T.C.
SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ
TANI TEST ÖLÇÜTLERĠNDE ROC EĞRĠSĠ VE SINIFLAMA ANALĠZLERĠNĠN KARġILAġTIRILMASINDA KULLANIMI
Mehmet Sinan ĠYĠSOY YÜKSEK LĠSANS TEZĠ
Ġstatistik Anabilim Dalı
Ocak-2014 KONYA Her Hakkı Saklıdır
TEZ BĠLDĠRĠMĠ
Bu tezdeki bütün bilgilerin etik davranıĢ ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalıĢmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.
DECLARATION PAGE
I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.
iv ÖZET
YÜKSEK LĠSANS TEZĠ
Tanı Test Ölçütlerinde ROC Eğrisi ve Sınıflama Analizlerinin KarĢılaĢtırılmasında Kullanımı
Mehmet Sinan ĠYĠSOY
Selçuk Üniversitesi Fen Bilimleri Enstitüsü Ġstatistik Anabilim Dalı
DanıĢman: Doç.Dr. Mustafa SEMĠZ
Yıl, 2014 43 Sayfa
Jüri
Doç.Dr.Mustafa SEMĠZ Yrd. Doç. Dr. Ġsmail KINACI Yrd. Doç. Dr. Murat ERĠġOĞLU
Tanı testleri sağlık alanında hastalıkların teĢhisinde kullanılır. Tanı testlerinin performansı ve daha kolay, daha uygun tanı testinin bulunması önemli bir sorundur. Tanı testlerinin performanslarının değerlendirilmesinde kullanılan duyarlılık ve seçicilik kavramları kullanılarak ROC eğrileri çizilir. Diskriminant (ayırma) analizi ve lojistik regresyon ikili sonuç değiĢkeni ile yapılacak olan sınıflamanın performanslarının değerlendirilmesi de yine ROC eğrileri ile yapılabilir. Bu çalıĢmada ayırma analizi ve lojistik regresyon analizinin performansları simülasyon çalıĢmasıyla karĢılaĢtırılmıĢtır.
Anahtar Kelimeler: tanı testi, duyarlılık, seçicilik, ayırma analizi, ROC eğrisi, lojistik regresyon
v ABSTRACT
MS THESIS
ROC Curves in Diagnostic Tests and a Comparison of Discriminant Analysis and Logistic Regression
Mehmet Sinan ĠYĠSOY
THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY
THE DEGREE OF MASTER OF SCIENCE IN STATISTICS
Advisor: Assoc. Prof. Dr. Mustafa SEMĠZ
Year, 2014 43 Pages
Jury
Assoc. Prof. Dr. Mustafa SEMĠZ Asst. Prof. Dr. Ġsmail KINACI Asst. Prof. Dr. Murat ERĠġOĞLU
Diagnostic tests are of special importance. It is an important issue to find the better, easy and performant diagnostic test. Sensitivity and specificity are two concepts which are used in ROC curves when interpreting the performances of diagnostic tests. Interpreting the performances of discriminant analysis and logistic regression when outcome variable is dichotomous is also possible with ROC curves. We will concentrate on interpreting performances of these analyses with simulations.
Keywords: diagnostic tests,sensitivity,specificity,ROC curves, discriminant analysis, logistic regression
vi ÖNSÖZ
Bu çalıĢma aileme ithaf edilmiĢtir. ÇalıĢmada yardımlarını esirgemeyen danıĢman hocam Doç.Dr. Mustafa Semiz‟e teĢekkürlerimi sunarım.
Mehmet Sinan ĠYĠSOY KONYA-2014
vii ĠÇĠNDEKĠLER ÖZET ... iv ABSTRACT ... v ÖNSÖZ ... vi ĠÇĠNDEKĠLER ... vii SĠMGELER VE KISALTMALAR ... ix 1. GĠRĠġ ... 1
2. TANISAL KESĠNLĠK ÖLÇÜTLERĠ VE ROC EĞRĠLERĠ ... 3
2.1. Duyarlılık ve Seçicilik ... 3
2.2. YanlıĢ Pozitif Oranı ve YanlıĢ Negatif Oranı ... 4
2.3. Kesinlik ... 5
2.4. Odds Oranı ... 7
2.5. Youden Ġndeksi ... 7
2.6. Pozitif Tahmini Değer ... 8
2.7. Negatif Tahmini Değer ... 8
2.8. Pozitif Olabilirlik Oranı ... 10
2.9. Negatif Olabilirlik Oranı ... 11
2.10. ROC Eğrileri ... 12
2.10.1. ROC eğrisinin çizilmesi ... 12
2.10.2. ROC eğrisi altında kalan alan ... 15
2.10.3. ROC eğrisinin değerlendirilmesi ... 16
2.10.4. Optimum kesim noktasını bulma ... 17
2.10.5. Belli bir seçicilik değerindeki duyarlılık ve ROC eğrisi altında kalan kısmi alan ... 17
2.10.6. ROC eğrisinin avantajları ... 18
3. SINIFLAMA ANALĠZLERĠ ... 19
3.1. Ayırma (Diskriminant) Analizi ... 19
3.1.1. Ayırma analizinin varsayımları ... 20
3.1.2. Ayırma analizindeki temel eĢitlikler ... 21
3.1.3. Örnek uygulama ... 23
3.2. Lojistik Regresyon ... 26
3.2.1. Lojistik regresyon modelini uydurma ... 27
3.2.2. Olabilirlik oranı testi ... 28
3.2.3. Wald testi ... 28
3.2.4. Çoklu lojistik regresyon modeli ... 29
3.2.5. Örnek uygulama ... 29
viii
5. ARAġTIRMA SONUÇLARI VE TARTIġMA ... 35
5.1. AraĢtırma Sonuçları ... 35
5.2. TartıĢma ... 40
6. SONUÇ VE ÖNERĠLER... 42
KAYNAKLAR ... 43
ix
SĠMGELER VE KISALTMALAR Simgeler
LR+ Positive Likelihood Ratio (Pozitif Olabilirlik Oranı) LR- Negative Likelihood Ratio (Negatif Olabilirlik Oranı) Se Sensitivity (Duyarlılık)
Sp Specifity (Seçicilik)
Kısaltmalar
AUC Area under the curve (Eğri Altında Kalan Alan) FPF False Positive Fraction (YanlıĢ Pozitif Oranı) FPR False Positive Rate (YanlıĢ Pozitif Oranı) OR Odds Ratio (Odds Oranı)
PPV Positive Predictive Value (Pozitif Tahmini Değer) NPV Negative Predictive Value (Negatif Tahmini Değer)
ROC Receiver Operating Characteristic (ĠĢlemci Uygulama Özelliği) TPF True Positive Fraction (Doğru Pozitif Oranı)
1. GĠRĠġ
Tanı testleri tıpta önemli bir rol oynar ve sağlık harcamalarında önemli bir paya sahiptirler. Tanı testleri bir hastalığa tanı koymada ya da koyulmuĢ olan bir tanıyı doğrulamada kullanılırlar. Tanı testi sonucunun yorumlanması hasta ile hasta olmayan kiĢiyi ayırmasına ve testin kullanıldığı duruma bağlıdır.
Bir tanı testi sonucuna göre sürekli, dikotom (ikili) veya ordinal (sıralı) olarak adlandırılır. Mesela kan basıncını veren bir test sürekli, hastanın HIV virüsü taĢıyıp taĢımadığını veren bir test dikotom ve hastanın bir hastalığa sahip olmasını kesinlikle, daha az kesin, muhtemelen değil, kesin değil Ģeklinde veren bir tanı testi ise ordinal olarak adlandırılır. En çok karĢılaĢılan tanı testleri sürekli olanlardır. Sürekli sonuç veren laboratuar çalıĢmaları oldukça çoktur ve bu yüzden sürekli tanı testleri ile ilgili yeni istatistiksel metodlar geliĢtirilmektedir. Dikotom sonuç veren laboratuar çalıĢmalarına da sıkça karĢılaĢılmakta ve bunların istatistiksel analizinde binomial oranlar ve 2x2 tabloları sıklıkla kullanılmaktadır. Sürekli tanı testleri için önerilmiĢ metodların çoğu özellikle radyolojik görüntüleme alanında sıklıkla kullanılan ordinal tanı testlerinden uyarlanmıĢtır (Shapiro,1999).
Tanı testlerinin iki amacı vardır:
a) Hastanın durumu hakkında doğru bilgi sağlamak b) Hastanın yönetimi için doktorun planına yön vermek.
Doktor tanı testinin nasıl yorumlanması gerektiğini biliyorsa bu amaçlar gerçekleĢebilir. Tanı testinin (ayırt edici) kesinliği (discriminatory accuracy) testin doğru sonuç verip vermemesi ile yani gerçek hasta ile hasta olmayanı ayırma gücündedir. Eğer test sonuçları hep aynıysa testin kesinliği önemsizdir ve eğer test sonuçları iki durum için kesiĢmiyorsa testin tanısal kesinliği mükemmeldir. Genelde bir testin kesinliği bu iki durumun arasındadır. Kaçınılması gereken en önemli hata, bir tanı testi sonucunun hastanın durumunu doğru olarak gösterdiğinin kabul edilmesidir. Çoğu tanı testi bilgisi mükemmel değildir, doktora bir fikir verir ama sonuçta bir belirsizlik olabileceği hiçbir zaman hatırdan çıkarılmamalıdır. Test sonucu negatifse hastanın hasta olmadığı anlamına mı gelmektedir? Doktor hastayı hasta olmadığından dolayı evine mi göndermelidir? Yoksa test sonucu pozitif olduğu için hemen tedaviye baĢlamalı ve hastaneye mi yatırmalıdır?
Bu sorulara cevap verebilmek için doktorun testin mutlak ve göreceli kapasitesi hakkında bilgi sahibi olması gerekir. Doktorun, bu testin gerçek hastaları nasıl tahmin ettiğini (duyarlılık) ve gerçek hasta olmayanı nasıl ayırt ettiğini (seçicilik)
değerlendirmesi gereklidir. Bu test daha önceki baĢka bir testin yerine mi konmuĢtur? Yoksa yanında baĢka testler de yapılmalı mıdır?
Eğer bir tanı testi tüm gerçek hastaları hasta olarak sınıflamıĢ, ve tüm hasta olmayanları hasta değil olarak belirlemiĢ ise o tanı testine “altın standart” denir. Altın standart tanı testleri kimi zaman diğerlerine göre pahalı, ya da zor ve daha çok kaynak, zaman gerektiren, ya da hastaya diğer testlere göre daha çok zarar veren testler veya yöntemler olabilir. Tanı testinin sonucunun doğruluğu altın standart sonucu ile belirlenir (Zhou ve ark.,2002).
Bu çalıĢmada tanı testlerinin kesinlik ölçütlerinden bahsedilecek ve tanı testlerinin karĢılaĢtırılmasında kullanımları anlatılacaktır.
ROC eğrileri ilk olarak 2. Dünya SavaĢında elektrik ve radar mühendisleri tarafından düĢman nesneleri ayırt etmede (cismin bir uçak mı? yoksa sadece bir kuĢ mu olduğunu bulmada) kullanılmıĢtır. Daha sonra psikoloji, tıp, biyometri ve sonraları ise makine öğrenmesi ve veri madenciliği alanlarında kullanılmaya baĢlamıĢtır.
ROC eğrileri tanı testlerinin performanslarını değerlendirmede ve uygun kesim noktasını bulmakta kullanılır. Bu çalıĢmada ROC eğrilerinin bu amaçla kullanımından bahsedilecektir.
ROC eğrilerinin baĢka bir uygulaması ise sınıflama analizlerine ait performansların karĢılaĢtırılmasında kullanımlarıdır. Dikotom bir sonuç değiĢkeni olduğunda sınıflama analizi bir tanı testi gibi düĢünülebilir. Çünkü sınıflama analizi sonucunda ikili bir sonuç çıkmaktadır (hasta ya da hasta değil, 1. gruba ait ya da 2. gruba ait gibi). ROC eğrileri aynı tanı testlerinde olduğu gibi, bu durumda da sınıflama analizinin performansını değerlendirmede kullanılacaktır. Ancak sadece ayırma analizi ve lojistik regresyon analizleri incelemeye alınmıĢtır. Diğer sınıflama analizleri çalıĢmanın kapsamı dıĢındadır.
ÇalıĢmanın ilk bölümünde tanı testlerini değerlendirmekte kullanılan kesinlik ölçütlerinden ve ROC eğrilerinden bahsedilmiĢtir. Ġkinci bölümde sınıflama analizlerinden ayırma analizi ve lojistik regresyondan bahsedilmiĢtir. Üçüncü bölümde ayırma analizi ve lojistik regresyonun performanslarını karĢılaĢtırmada kullanılacak yöntem anlatılmaktadır. Dördüncü bölümde uygulanan yöntem sonucunda çıkan sonuçlar tartıĢılmıĢtır.
2. TANISAL KESĠNLĠK ÖLÇÜTLERĠ VE ROC EĞRĠLERĠ
Bir testin tanı testi olarak kullanılabileceği anlaĢıldığında, o testin klinik durumlardaki rolü tanımlanmalı ve değerlendirilmelidir. Bu durumda sadece tanı testinin kendi iç kesinliğini değil aynı zamanda hastalığın prevalansı, hastanın durumu ve testin yanlıĢ tanılarının sonuçlarını değerlendirmek gerekir (Zhou ve ark.,2002).
2.1. Duyarlılık ve Seçicilik
Tanısal kesinliğin iki ölçütü duyarlılık (sensitivity) ve seçicilik (özgüllük, specificity) tir. Bunların tanımları en iyi 2x2 lik bir tablo (karar matrisi) yolu ile verilebilir. Bu tabloda sütunlar hastalığın, altın standart bir test sonucunda çıkan gerçekte varlığını ve yokluğunu, satırlar ise kullanılan tanı testi sonuçlarının pozitif ya da negatif olmasını gösterir.
Hastanın gerçekte hasta olmasını (D+) ve gerçekte hasta olmamasını (D-) , tanı testi sonucunun pozitif olmasını (T+) ve negatif olmasını (T-) ile gösterirsek, tüm test sonuçları Tablo 2.1 de olduğu gibi bir tablo (karar matrisi) ile özetlenir.
Tablo 2.1. Karar Matrisi
Hastalık Durumu
Var (D+) Yok (D-)
Test Sonucu
Pozitif (T+)
TP (Doğru pozitif) FP (YanlıĢ pozitif)
Negatif (T-)
FN (YanlıĢ negatif)
TN (Doğru negatif)
Tanısal kesinlik gerçek hastaları doğru bir Ģekilde sınıflayan Ģartlı olasılıklar ile ölçülür.
Bir testin duyarlılığı ) | (T D P
Se (2.1)
Ģeklinde tanımlanmıĢ bir Ģartlı olasılıktır. Daha açık bir ifadeyle, kiĢinin hasta olduğu bilindiğinde testin de hasta sonucu (pozitif) vermiĢ olması olasılığıdır. Dolayısıyla
FN TP
TP
Se (2.2)
vardır. Bu yüzden duyarlılık, doğru pozitif oranı (True Positive Rate, TPR,TPF) olarak da adlandırılır.
Bir testin seçiciliği
) |
(T D
P
Sp (2.3)
olarak tanımlanmıĢ bir Ģartlı olasılıktır. Diğer bir ifadeyle, kiĢinin hasta olmadığı bilindiğinde testin de hasta olmadığı sonucunu vermiĢ olması olasılığıdır. Dolayısıyla
FP TN
TN
Sp (2.4)
oranına eĢittir. TN + FP adet hasta olmayan kiĢi içerisinde test sonucu negatif olan TN adet hasta vardır. Bu yüzden seçicilik, doğru negatif oranı (True Negative Rate, TNR, TNF) olarak da adlandırılır.
Duyarlılık ve seçicilik tanı testlerinin değerlendirilmesinde kullanılan en önemli ölçütlerdendir (Shapiro,1999).
2.2. YanlıĢ Pozitif Oranı ve YanlıĢ Negatif Oranı
Yukarıda tanımlanan duyarlılık ve seçicilik değerlerinin tamamlayıcıları olarak yanlıĢ pozitif oranı ve yanlıĢ negatif oranı da tanımlanacaktır.
YanlıĢ negatif oranı (False Negative Rate, FNR, FNF) karar matrisindeki değerlere göre FN TP FN D T P FNR ( | ) (2.5)
Ģeklinde tanımlanır. Test sonucu negatif çıkan fakat hasta olduğu bilinen FN adet hastanın tüm hasta sayısına bölümüdür.
1 FNR
Se (2.6)
olduğu kolayca görülebilir.
YanlıĢ pozitif oranı (False Positive Rate, FPR, FPF) karar matrisindeki değerlere göre FP TN FP D T P FPR ( | ) (2.7)
Ģeklinde tanımlanır. Test sonucu pozitif çıkan fakat hasta olmadığı bilinen FP adet hastanın tüm hasta olmayan sayısına bölümüdür.
1
FPR
Sp (2.8)
2.3. Kesinlik
Kesinlik (accuracy) tanı testinin doğru sonuç verdiği popülasyon oranıdır.
Kesinlik=Doğru Karar Sayısı/ Tüm Durumlar
Ģeklinde tanımlanır.Tablo 2.1 kullanılarak ve toplam kiĢi sayısı N TP TF FP FN
olduğunda kesinlik N TN TP Kesinlik (2.9) Ģeklinde gösterilebilir.
Duyarlılık ve seçicilik kullanılarak, kesinlik aĢağıdaki gibi formüle edilebilir: Kesinlik=Duyarlılık* Hasta oranı + Seçicilik * Hasta olmayan oranı
Hasta popülasyon oranına hastalığın prevalansı denir ve P(D+) ile gösterilebilir. P(D-) ise hasta olmayan nüfus oranıdır.
Basit aritmetik iĢlemler kullanarak
N TN FP x TN FP TN N FN TP x FN TP TP N TN N TP Kesinlik ) ( . ) ( .P D S P D Se p (2.10)
Ģeklinde bulunur. Hastalığın prevalansı, tanı testinin duyarlılık ve seçiciliği bilindiğinde kesinlik yukarıdaki formüle göre hesaplanabilir.
Kesinlik bir tanısal kesinlik ölçütü olarak kullanılamaz, çünkü hastalığın prevalansından etkilenir. Bu durumu göstermek ve tanımlanan kavramları açıklamak için aĢağıda bir örnek verilecektir.
Varsayılsın ki 1200 kiĢiye bir A tanı testi uygulanmıĢ ve bu test sonucunda toplam 200 gerçek hasta içerisinde, A testi 140 hastaya pozitif sonuç vermiĢ ve kalan 60 hastaya negatif sonuç vermiĢ olsun. 1000 kiĢilik hasta olmayan grup içerisinde ise A testi 100 hastaya pozitif sonuç, 900 hastaya ise negatif sonuç vermiĢ olsun. A testine ait karar matrisi Tablo 2.2 de gösterilmiĢtir.
Tablo 2.2. A testi için karar matrisi
Hastalık Durumu
Var (D+) Yok (D-) Toplam
A Testi Sonucu Pozitif (T+) 140 100 240 Negatif (T-) 60 900 960 Toplam 200 1000 1200 Se= 140/200 = 0.7 , Sp= 900/1000=0.9 , P(D+)= 200/1200 = 0.17 ve Kesinlik1 = Se.P(D+) + Sp. P(D-) = 0.7*0.17 + 0.9*0.83 = 0.87 bulunur.
Bu hesaplamalardan, testin hasta olmayanları bulmakta daha baĢarılı (Sp= 0.9)
olduğunu, fakat hastaları bulmakta baĢarısının daha düĢük olduğu (Se= 0.7) anlaĢılır.
Eğer bu oranlar sabit tutulur ve hastalığın prevalansı 0.17 den 0.6 ya çıkartılırsa, yeni durumda testin kesinliği
Kesinlik2 = 0.7 * 0.6 + 0.9 * 0.4 = 0.78 olur. Görüldüğü gibi hastalığın
prevalansı değiĢtiğinde Kesinlik de değiĢmektedir.
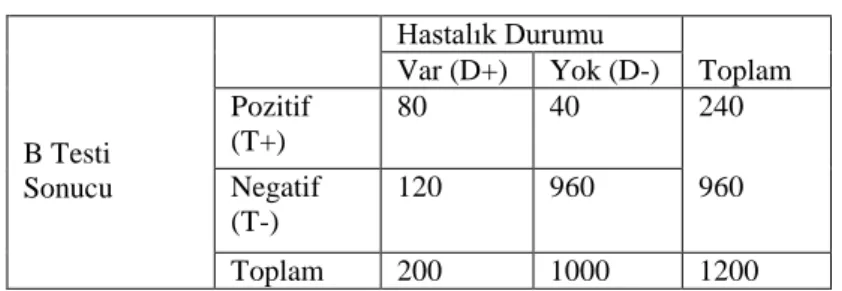
Genellikle iki tanı testi karĢılaĢtırılmak istenir. Mesela yukarıdaki örnekteki aynı popülasyona baĢka bir B testi ile de tanı konduğu varsayılsın. B testine ait sonuçlar Tablo 2.3‟te verilmiĢtir. Bu iki tablo karĢılaĢtırıldığında testlerin farklı sonuçlar vermesine rağmen kesinliklerinin aynı olduğu görülür. B testi gerçek hastaları bulmada A testinden kötü olmasına rağmen, hasta olmayanları bulmakta A testinden daha iyidir. Bu yüzden bu iki teste ait kesinlik değerleri eĢit çıkmaktadır. (Metz,1978)
Tablo 2.3. B testi için karar matrisi
Hastalık Durumu
Var (D+) Yok (D-) Toplam
B Testi Sonucu Pozitif (T+) 80 40 240 Negatif (T-) 120 960 960 Toplam 200 1000 1200 Se= 80/200 = 0.4 , Sp= 960/1000=0.96 , P(D+)= 200/1200 = 0.17 ve
Kesinlik = Se* P(D+) + Sp* P(D-) = 0.4*0.17 + 0.96*0.83 = 0.87.
2.4. Odds Oranı
Epidemiyolojide yaygın olarak kullanılan odds oranı (odds ratio) bir tanısal kesinlik ölçütü olarak da kullanılabilir. Tanısal kesinlik için odds oranı aĢağıdaki gibi tanımlanır. p p e e S S S S OR /(1 ) ) 1 ( (2.11)
Odds oranının 1 olması hasta olanlar ve olmayanlar için test sonucunun pozitif çıkma ihtimalinin eĢit olduğunu gösterir. Odds oranının 1‟den büyük olması, gerçek hastalarda test sonucu pozitif çıkmasının negatif çıkmasına göre daha yüksek ihtimalle olduğunu, 1‟den küçük olması ise hasta olmayanlar arasında test sonucu pozitif çıkmasının negatif çıkmasına göre daha yüksek olduğu anlamına gelir.
Odds oranı hastalığın prevalansından etkilenmez (Zhou ve ark.,2002).
2.5. Youden Ġndeksi
Bir tanı testi için Youden indeksi (Youden index)
Youden=Se + Sp - 1 (2.12)
Ģeklinde tanımlanır.
Bölüm 2.3.de tanımlanan kesinlikten farklı olarak, Odds oranı ve Youden indeksi hastalığın prevalansından etkilenmez. Dolayısıyla kesinlik ten daha iyi birer tanısal ölçüttürler. Fakat her ikisinin de doğru test sonucunu göstermede iki kısıtlılığı vardır. Ġlk olarak her ikisi de sadece bir karar kesim noktasına (decision threshold) dayanır ve ikinci olarak her ikisi de yanlıĢ pozitif ve yanlıĢ negatif sonuçları eĢit derecede istenilmez olarak değerlendirir. Mesela bir A testinin duyarlılığı 0.9 ve seçiciliği 0.4 ve bir baĢka B testinin duyarlılığı 0.4 ve seçiciliği 0.9 olsun.
Odds Oranı A = (0.9 / (1-0.9)) / ((1-0.4) / 0.4 ) = 6
Odds Oranı B = (0.4 / (1-0.4)) / ((1-0.9) / 0.9 ) = 6 ve
Youden A = 0.9 + 0.4 – 1 = 0.3
Youden B = 0.4 + 0.9 – 1 = 0.3 olur.
Odds oranı ve Youden indeksi her iki test için de aynı olmasına rağmen testler birbirlerinden farklı özelliklere sahiptir (Zhou ve ark. ,2002).
2.6. Pozitif Tahmini Değer
Doğru pozitif sonuçlarının tüm pozitif test sonuçlarına oranına Pozitif Tahmini Değer (Positive Predictive Value) denir. Karar matrisine göre
FP TP
TP
PPV (2.13)
Ģeklinde formüle edilir. Ya da koĢullu olasılık ile
) | (D T P PPV (2.14) Ģeklinde gösterilebilir.
Test sonucunun hangi oranda doğru olduğunu göstermesi açısından tanı testlerinin performansını değerlendirmede önemli bir ölçüttür. Hastalığın prevalansından etkilenir.
Bayes Teoremi kullanılarak
) | (D T P PPV ) ( ) ( ) | ( T P D P D T P = ) ( ) | ( ) ( ) | ( ) ( ) | ( D P D T P D P D T P D P D T P = )) ( 1 )( 1 ( ) ( ) ( D P S D P S D P S p e e (2.15) Ģeklinde bulunur. Eğer duyarlılık, seçicilik ve hastalığın prevalansı biliniyorsa pozitif tahmini değer yukarıdaki eĢitlik kullanılarak bulunabilir.
PPVnin düĢük olması pozitif test sonuçlarının çoğunun yanlıĢ pozitif olduğu anlamına gelir. Dolayısıyla böyle bir durumda baĢka bir test daha yaparak gerçekten hastalığın olup olmadığını anlamak gerekir.
2.7. Negatif Tahmini Değer
YanlıĢ negatif test sonuçlarının tüm negatif test sonuçlarına oranına Negatif Tahmini Değer (Negative Predictive Value) denir. Karar matrisine göre
FN TN
TN
NPV (2.16)
Ģeklinde formüle edilir. Ya da koĢullu olasılık ile
) | (D T P NPV (2.17) Ģeklinde gösterilebilir.
NPV nin yüksek olması test sonucu negatif çıkan bir kiĢinin gerçekte hasta olma olasılığının düĢük olduğunu gösterir. Hastalığın prevalansından etkilenir.
) | (D T P NPV = ) ( ) ( ) | ( T P D P D T P = ) ( ) | ( ) ( ) | ( ) ( ) | ( D P D T P D P D T P D P D T P = ) ( ) 1 ( ) ( ) ( D P S D P S D P S e p p (2.18)
Ģeklinde bulunur. Eğer duyarlılık, seçicilik ve hastalığın prevalansı biliniyorsa negatif tahmini değer yukarıdaki eĢitlik kullanarak bulunabilir.
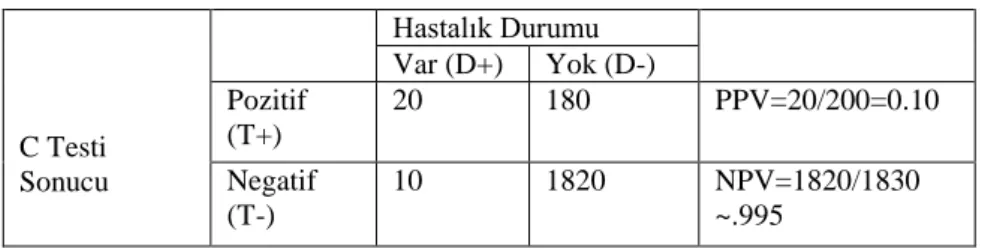
Örnek: Bir C tanı testi sonuçlarının aĢağıdaki gibi olduğu kabul edilsin.
Tablo 2.4. C testi için karar matrisi
Hastalık Durumu Var (D+) Yok (D-) C Testi Sonucu Pozitif (T+) 20 180 PPV=20/200=0.10 Negatif (T-) 10 1820 NPV=1820/1830 ~.995
PPV nin çok küçük %10 olması test sonucu pozitif çıkan bir kiĢinin büyük olasılıkla hasta olmadığı anlamına gelir. Bu durumda hasta teĢhisi konabilmesi için baĢka bir test kullanılmalıdır. Fakat, bu test yapılması çok kaynak gerektirmeyen ve kolay uygulanan bir test ise, yine de kullanılabilir. Çünkü NPV‟si çok yüksektir (%99.5). Dolayısıyla test sonucu negatif çıkan bir kiĢi çok yüksek olasılıkla hasta değildir.
PPV ve NPV nin hastalığın prevalansından etkilenmesi, testin kesinliğini ölçmek için bir problemdir. Ġncelenen popülasyonda hastalığın prevalansının, hastalığın gerçekteki prevalansından yüksek olması PPV değerini arttırır ve NPV değerini azaltır. Ġncelenen popülasyonda hastalığın prevalansının, hastalığın gerçekteki prevalansından az olması ise PPV değerini azaltır ve NPV değerini yükseltir. Bu durumdan kurtulmak için PPV ve NPV „yi, sadece test edilen gruptaki hasta ve sağlam oranının hastalığın gerçekteki prevalansına eĢit olduğu durumlarda kullanmak gerekmektedir.
Örnek: Duyarlılığı %80 ve seçiciliği %90 olan bir tanı testi ile prevalansı %60 olan bir hastalığın tanısını koymak istenildiği varsayılsın. Bu durumda
)) ( 1 )( 1 ( ) ( ) ( D P S D P S D P S PPV p e e formülü kullanılarak 92 . 0 ) 60 . 0 1 )( 90 . 0 1 ( 60 . 0 * 80 . 0 60 . 0 * 80 . 0 PPV
bulunur. Bu durumda eğer kiĢinin test sonucu pozitif ise %92 olasılıkla gerçekten hastadır.
Test sonucu negatif gelmiĢ ise, bu durumda NPV hesaplanarak
75 . 0 60 . 0 * ) 80 . 0 1 ( ) 60 . 0 1 ( * 90 . 0 ) 60 . 0 1 ( * 90 . 0 ) ( ) 1 ( ) ( ) ( D P S D P S D P S NPV e p p
olduğundan dolayı kiĢinin %75 ihtimalle gerçek hasta olmadığı hükmüne varılır.
Eğer bu testin duyarlılığı daha yüksek (%90), seçiciliği daha düĢük (%80) olsaydı, o zaman 87 . 0 ) 60 . 0 1 )( 80 . 0 1 ( 60 . 0 * 90 . 0 60 . 0 * 90 . 0 PPV ve 84 . 0 60 . 0 * ) 90 . 0 1 ( ) 60 . 0 1 ( * 80 . 0 ) 60 . 0 1 ( * 80 . 0 NPV
olacağından test sonucu pozitif çıkan bir kiĢinin %87 olasılıkla gerçek hasta, test sonucu negatif çıkan bir kiĢinin %84 olasılıkla sağlam olduğu anlaĢılacaktı.
2.8. Pozitif Olabilirlik Oranı
Pozitif Olabilirlik Oranı (Positive Likelihood Ratio) bir tanı testinin hasta kiĢide pozitif çıkma olasılığının, sağlam kiĢide pozitif çıkma olasılığına oranıdır. Duyarlılık ve seçicilik kullanılarak Pozitif LR = LR+ = p e S S 1 (2.19)
Ģeklinde ifade edilebilir. KoĢullu olasılıklar ile LR+ = ) | ( ) | ( ) | ( 1 ) | ( D T P D T P D T P D T P (2.20) Ģeklinde yazılabilir.
Sadece duyarlılık ve seçiciliğe bağlı olduğu için hastalığın prevalansından etkilenmeyen bir ölçüttür.
2.9. Negatif Olabilirlik Oranı
Negatif Olabilirlik Oranı (Negative Likelihood Ratio) bir tanı testinin hasta kiĢide negatif çıkma olasılığının, sağlam kiĢide negatif çıkma olasılığına oranıdır. Duyarlılık ve seçicilik kullanılarak
Negatif LR = LR- = p e S S 1 (2.21)
Ģeklinde ifade edilebilir. KoĢullu olasılıklar ile LR- = ) | ( ) | ( ) | ( ) | ( 1 D T P D T P D T P D T P (2.22) Ģeklinde yazılabilir.
Sadece duyarlılık ve seçiciliğe bağlı olduğu için hastalığın prevalansından etkilenmeyen bir ölçüttür.
Örnek: Duyarlılığı %80 ve seçiciliği %90 olan bir tanı testi için
LR + = 8 90 . 0 1 80 . 0
olduğu için bu tanı testi her 8 doğru pozitif sonuç için 1 yanlıĢ pozitif sonuç vermektedir. LR - = 0.22 9 2 90 . 0 80 . 0 1
olduğu için bu tanı testi her 2 yanlıĢ negatif sonuca karĢın 9 doğru negatif sonuç vermektedir.
LR + nın olabildiğince büyük olması ve LR – nin olabildiğince küçük olması istenen bir durumdur.
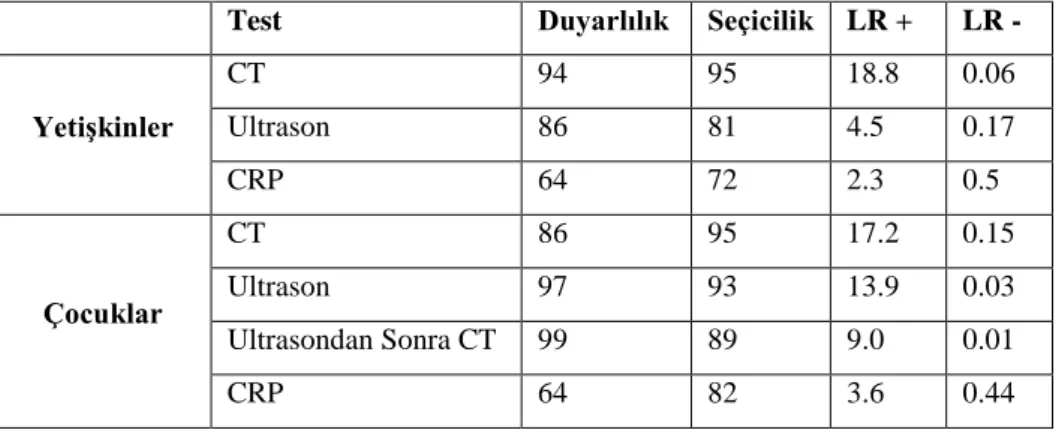
Örnek: www.essentialevidenceplus.com web sitesinden alınan bilgilere göre Apandisit teĢhisinde kullanılan 3 adet tanı testinin (CT, Ultrason, ve CRP değeri) duyarlılık, seçicilik, LR + ve LR – değerleri Tablo 2.5‟teki gibidir.
Tablo 2.5. Bazı tanı testleri için tanısal kesinlik ölçütleri
Test Duyarlılık Seçicilik LR + LR -
YetiĢkinler CT 94 95 18.8 0.06 Ultrason 86 81 4.5 0.17 CRP 64 72 2.3 0.5 Çocuklar CT 86 95 17.2 0.15 Ultrason 97 93 13.9 0.03 Ultrasondan Sonra CT 99 89 9.0 0.01 CRP 64 82 3.6 0.44 2.10. ROC Eğrileri
Bir tanı testinin duyarlılığı ile yanlıĢ pozitif oranlarının (1-seçicilik) oluĢturduğu grafiğe ROC eğrisi denir. Grafikteki her nokta farklı bir kesim noktası alınarak hesaplanan duyarlılık (TPR) ve 1-seçicilik (FPR) değerlerinden oluĢur. Daha sonra bu noktalar doğru parçaları ile birleĢtirilir ve uygun bir eğri kullanılarak kestirilir.
ROC eğrilerinin avantajı, sadece bir duyarlılık ve seçicilik değerine bağlı kalmadan, değiĢik duyarlılık ve seçicilik değerlerini bir arada değerlendirmeye imkan vermesindedir. Bu sayede maliyet, doğru ve yanlıĢ kararların getirileri her seviye için hesaplanabilir. Bu da doğru kesim noktasının bulunmasına yardım eder.
2.10.1. ROC eğrisinin çizilmesi
Bu bölümde gerçek hayattan bir örnek vererek ROC eğrisi çizilecektir.
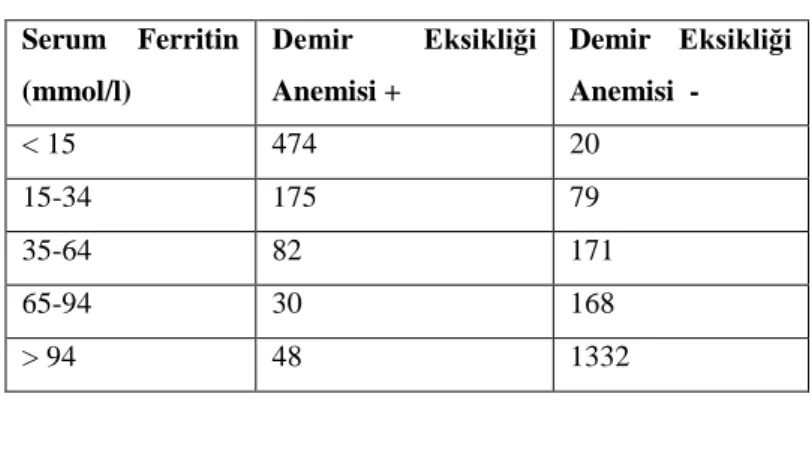
Demir eksikliği anemisi sık görülen bir kansızlık türüdür. Bu hastalığın teĢhisinde serum ferritin değerleri kullanılabilir. Belli bir grup kiĢide serum ferritin değerleri araĢtırılmıĢ, bu kiĢilerin demir eksikliği anemisine sahip olup olmadıkları belirlenmiĢ ve Tablo 2.6 oluĢturulmuĢtur1
.
1 Veriler
Tablo 2.6. Serum ferritin değerleri ve demir eksikliği anemisi olma durumu Serum Ferritin (mmol/l) Demir Eksikliği Anemisi + Demir Eksikliği Anemisi - < 15 474 20 15-34 175 79 35-64 82 171 65-94 30 168 > 94 48 1332
Bu tabloda ilk sütun serum ferritin miktarını, ikinci sütun demir eksikliği anemisi olan kiĢi sayısını, üçüncü sütun ise demir eksikliği anemisi olmayan kiĢi sayısını göstermektedir.
ROC eğrisini çizerken duyarlılık ve seçicilik değerlerine ihtiyaç olduğundan, yukarıdaki tabloyu iki farklı gruba bölmek gerekmektedir. Bir kesim noktası belirlenip, serum ferritin değeri o değerin altında olanları hasta, üstünde olanları sağlam kabul edilsin. Mesela 34 mmol/l değeri kesim noktası olarak alındığında aĢağıdaki gibi yeni bir tablo elde edilir.
Tablo 2.7. Bir kesim noktası (34) için değerler
Serum ferritin (mmol/l) Demir Eksikliği Anemisi + Demir Eksikliği Anemisi -
≤ 34 474+175=649 20+79=99
>34 82+30+48=160 171+168+1332=1671
Bu kesim noktası için
802 . 0 160 649 649 e S ve 944 . 0 99 1671 1671 p S olarak bulunur.
ROC eğrisini çizebilmek için baĢka duyarlılık ve seçicilik değerlerine de ihtiyaç vardır. Onlar da baĢka kesim noktaları seçilerek bulunur. Örnekte 15, 34, 64 ve 94
değerleri kesim noktaları olarak seçilerek, aĢağıdaki duyarlılık ve seçicilik tablosu elde edilir.
Tablo 2.8. Tüm kesim noktaları için duyarlılık ve seçicilik değerleri
Kesim Noktası Duyarlılık (Se) Seçicilik (Sp) 1-Seçicilik (1-Sp)
< 15 0.585 0.989 0.011
≤ 34 0.802 0.944 0.056
≤ 64 0.904 0.847 0.193
≤ 94 0.941 0.753 0.247
Tablodan görüleceği gibi Duyarlılık ve Seçicilik arasında bir yarıĢ vardır. Birisi arttıkça, diğeri azalır.
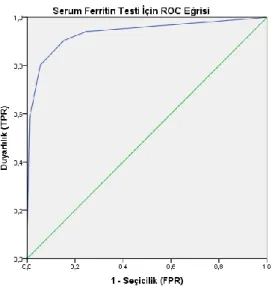
Bu tablodaki Duyarlılık ve 1-Seçicilik değerleri kullanılarak aĢağıdaki ROC eğrisi çizilir.
ġekil 2.1. deki eğri, ilgili tanı testine ait ROC eğrisini, köĢegenleri birleĢtiren doğru ise ayırt edici özelliği olmayan bir tanı testine ait ROC eğrisini göstermektedir.
ROC eğrisinin bu doğrudan yukarıya, eksenlere doğru uzaklaĢması tanı testinin ayırt edici özelliğinin artması anlamına gelmektedir. Eğer ROC eğrisinin tamamı bu doğrunun altında kalıyorsa bu durumda tanı testi değerlerini ters çevirerek eğriyi yukarı bölgeye çıkarmak gerekir.
Mükemmel bir tanı testi için ROC eğrisi, koordinat sisteminde (0,0) noktası ile sol üst köĢe noktasını birleĢtiren doğru ve sol üst köĢe noktası ile sağ üst köĢe noktasını birleĢtiren doğruların oluĢturduğu Ģekildir. Böyle bir eğriyi elde etmek gerçek hayatta oldukça zordur (Kumar ve Indrayan,2011).
2.10.2. ROC eğrisi altında kalan alan
Bir tanı testinin kesinliğini ölçmek için kullanılan ölçütlerden bir tanesi de teste ait ROC eğrisi altında kalan alandır. Bu alan 0 ile 1 arasında bir değer alır.
Yukarıda bahsedilen ve ayırt edici özelliği olmayan teste ait ROC eğrisini gösteren doğru altında kalan alan 0.5‟tir. Ve yine yukarıda bahsedilen mükemmel bir teste ait ROC eğrisi, tüm alanı içerdiğinden dolayı alanı 1.0‟dır. Dolayısıyla aslında herhangi bir tanı testine ait ROC eğrisinin altında kalan alanın 0.5-1.0 arasında olması beklenir.
ROC eğrisi altında kalan alan büyüdükçe tanı testinin kesinliği artar. ROC eğrisinin, sol üst köĢe noktasına ((1,0) noktası) yaklaĢması da testin tanısal kesinliğinin daha iyi olduğu anlamına gelir.
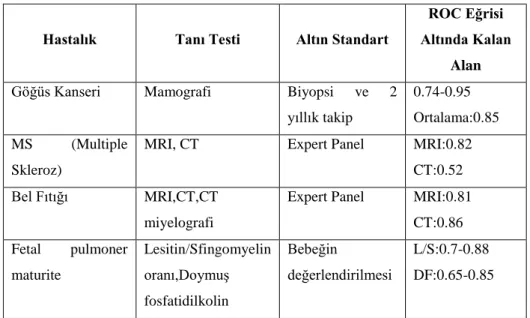
AĢağıdaki tabloda bazı hastalıklara ait tanı testleri ve bunların ROC eğrilerinin altında kalan alanlar verilmiĢtir (Zhou ve ark.,2002).
Tablo 2.9. Bazı tanı testlerine ait altın standart ve ROC eğrisi altında kalan alanlar
Hastalık Tanı Testi Altın Standart
ROC Eğrisi Altında Kalan
Alan
Göğüs Kanseri Mamografi Biyopsi ve 2 yıllık takip
0.74-0.95 Ortalama:0.85 MS (Multiple
Skleroz)
MRI, CT Expert Panel MRI:0.82
CT:0.52 Bel Fıtığı MRI,CT,CT
miyelografi
Expert Panel MRI:0.81 CT:0.86 Fetal pulmoner maturite Lesitin/Sfingomyelin oranı,DoymuĢ fosfatidilkolin Bebeğin değerlendirilmesi L/S:0.7-0.88 DF:0.65-0.85
2.10.3. ROC eğrisinin değerlendirilmesi
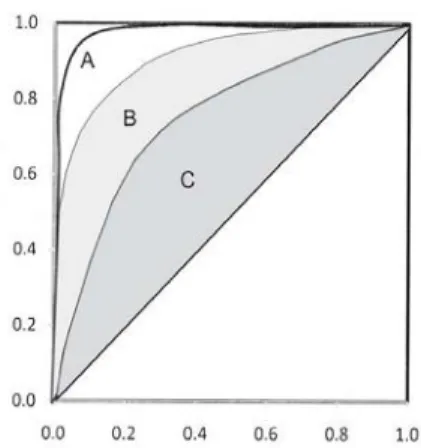
ROC eğrisi altında kalan alan tanı testinin performansını gösteren önemli bir ölçüttür. Alanın büyümesi tanı testinin hasta olanla olmayanı daha iyi ayırdığını gösterir. EĢit alana sahip iki eğri tanı testlerinin toplamda benzer performans gösterdiğini gösterir, ama bu durumda eğriler aynı olmak zorunda değildir. Eğriler birbirlerini kesebilir.
ġekil 2.2. de üç farklı ROC eğrisi gösterilmiĢtir. A eğrisi B ve C den üstündür ve mükemmele yakın bir performans göstermektedir. C ise en düĢük derecede performans gösteren tanı testine aittir (Kumar ve Indrayan,2011).
ġekil 2.3. de iki tanı testine ait kesiĢen ROC eğrileri görülmektedir. Alanlar birbirlerine yakın olmasına rağmen eğrilerin davranıĢları farklıdır. Yüksek duyarlılık isteniyorsa 1 numaralı ROC eğrisi, yüksek seçicilik isteniyorsa 2 numaralı ROC eğrisi tercih edilir.
ġekil 2.2. Üç tanı testi için ROC eğrileri
2.10.4. Optimum kesim noktasını bulma
ROC eğrisi üzerinde bulunacak optimum kesim noktası, tanı testinin en doğru sınıflamayı yapmasını sağlayan noktadır. Bu noktayı bulmak için 3 farklı kriter kullanılır. Bunlar eğri üzerindeki (0,1) noktasına en yakın nokta, Youden indeksi ve maliyeti minimize etme kriteridir.
Bu kriterlerden ilk ikisi duyarlılık ve seçiciliğe eĢit derecede önem verir ve etik, maliyet ve prevalans açısından her hangi bir sınırlamada bulunmayan kriterlerdir. Üçüncü kriter ise maliyetle ilgilenir. Maliyet sadece finansal maliyeti değil, aynı zamanda hastaya yapılacak müdahalenin getireceği zararları ve ileri tetkiklerin maliyetini de içeren bir kriterdir. Uygulaması zor olduğu için bu kriter sağlıkta pek kullanılmaz.
ROC eğrisi üzerinde olan her hangi bir nokta ile (0,1) noktası arasındaki uzaklık kolayca
d=(1-Se)2+(1-Sp)2 (2.23)
formülüyle bulunur. Optimum kesim noktasını bulmak için bu uzaklık eğri üzerindeki gözlenen tüm kesim noktaları için hesaplanır ve minimum olduğu nokta aranılan noktadır. Gözlenen duyarlılık ve seçicilik değerleri bilindiği için kolaylıkla hesaplanabilir.
Ġkinci kriter Youden indeksidir.Youden indeksi eğri üzerindeki bir noktanın (0,0) ve (1,1) doğrularını birleĢtiren ana köĢegene uzaklığı ile ilgilidir. Bu uzaklığın maksimum değeri Youden indeksini verir. Youden indeksinin amacı TPR ile FPR arasındaki farkı en büyük yapmaktır. DeğiĢik duyarlılık ve seçicilik değerleri denenerek Youden indeksi bulunabilir. Youden indeksi doğru sınıflandırma oranını maksimum olma eğilimini gösterdiği için tercih edilen bir kriterdir (Kumar ve Indrayan,2011).
2.10.5. Belli bir seçicilik değerindeki duyarlılık ve ROC eğrisi altında kalan kısmi alan
Belirli bir seçicilik değeri ya da aralığı, klinik ihtiyaçlara göre belirlenir. Mesela yüksek risk taĢıyan bir grupta kanser gibi ciddi bir hastalığı teĢhis etmek için, yanlıĢ pozitif oranı yüksek bile olsa, yüksek duyarlılığa sahip bir test tercih edilir. Çünkü yüksek yanlıĢ negatif sonuçlar veren bir test daha tehlikelidir.
Öte yandan düĢük risk taĢıyan bir grup incelendiğinde, yüksek seçicilik tercih edilir, çünkü sonraki doğrulayıcı test daha pahalı ve hastaya zarar veren bir test olabilir.
Dolayısıyla yanlıĢ pozitif oranı düĢük olmalıdır ve hasta gereksizce zarara uğratılmamalıdır.
Belirli bir seçicilik değerindeki duyarlılık değeri ve eğri altındaki kısmi alan bu Ģekildeki bir klinik durum için önemlidir.
Eğri altında kalan kısmi alan bir FPR aralığı ile eğri arasında kalan alan olarak tanımlanır. FPR aralığı alınabileceği gibi iki tane duyarlılık değeri ile bir TPR aralığı alınarak da kısmi alan bulunabilir.
Kısmi alanın mümkün en büyük alana bölünmesi ile standartlaĢtırılması tavsiye edilmiĢtir. Bu durumda standartlaĢtırılmıĢ eğri altında kalan alan belirli bir FPR (ya da TPR) aralığındaki ortalama duyarlılık olarak yorumlanabilir. StandartlaĢtırılmıĢ eğri altında kalan alanı yorumlamak daha kolaydır (Kumar ve Indrayan,2011).
2.10.6. ROC eğrisinin avantajları
Farklı kesim noktalarına göre ROC eğrisi oluĢturmanın avantajları aĢağıda listelenmiĢtir.
1. ROC eğrisi tüm muhtemel kesim noktalarını gösterdiği için optimum kesim noktası eğriye bakarak anlaĢılabilir.
2. ROC eğrisi hastalığın prevalansından etkilenmez.
3. Ġki veya daha fazla tanı testi ROC eğrilerine göre tek bir grafik üzerinde kıyaslanabilir.
4. Bazen duyarlılık seçiciliğe, bazen de seçicilik duyarlılığa tercih edilir. Her iki durumda da ROC eğrisi uygun kesim noktasının bulunmasına yardımcıdır. 5. Eğri altında kalan emprik alan doğrusal, log ya da karekök transformasyonu ile
3. SINIFLAMA ANALĠZLERĠ
Bu bölümde sınıflama analizlerinden ayırma analizi ve lojistik regresyon analizlerinden bahsedilecektir.
3.1. Ayırma (Diskriminant) Analizi
Ayırma analizinin amacı tahmin edici değiĢkenlere bakarak grup üyeliğini bulmaktır. Mesela kanser tanısı koymak için en kesin yöntem biyopsidir. Fakat biyopsi yapmak hem diğer yöntemlere göre pahalı hem de hastaya daha çok zarar veren bir yöntem olduğu için, biyopsi yapmaya gerek kalmadan hastaların bazı değerlerine bakarak kanser olup olmadıklarını tahmin etmek, kanser tanısı koymaya yardımcı olabilir. ĠĢte böyle bir durumda hastaya ait diğer verilere ayırma analizi uygulanarak hastanın kanser olup olmadığı tahmin edilebilir.
Ayırma analizi MANOVA‟nın tersi olarak düĢünülebilir. MANOVA‟da grup üyeliğinin bağımsız değiĢkenlerin ortalama farklılıklarıyla istatistiksel anlamlı bir iliĢkisi olup olmadığı araĢtırılır. Eğer anlamlı bir iliĢki varsa, ayırma analizi kullanarak ve tersten düĢünerek, bağımsız değiĢkenleri kullanarak grup üyeliği tahmin edilir.
MANOVA‟da bağımsız değiĢkenler gruplar ve bağımlı değiĢkenler tahmin edici değiĢkenler iken, ayırma analizinde ters olarak bağımlı değiĢken grupları gösteren değiĢken ve bağımsız değiĢkenler tahmin edici değiĢkenlerdir.
Ayırma analizi ile lojistik regresyon arasında da bazı farklılıklar vardır. Lojistik regresyonda bağımsız değiĢkenler için veri tipi, varyans-kovaryans matrislerinin homojenliği ve çok değiĢkenli normallik varsayımları yok iken ayırma analizinde bu varsayımlar vardır. Ayırma analizinde bağımsız değiĢkenler sürekli (ya da kesikli), varyans-kovaryans matrisleri homojen ve çok değiĢkenli normallik olmalıdır. Bazı yazarlar ayırma analizinde dikotom değiĢkenlerin de kullanılabileceğini söylemektedir.
Ayırma analizinde grup değiĢkeni bir dikotom ise bu ayırma analizine “iki gruplu ayırma analizi” denirken, grup değiĢkenindeki grup sayısı 2‟den fazla olduğu durumlarda “çoklu ayırma analizi” denir.
Ayırma analizi matematiksel olarak MANOVA ile aynıdır. Ayırma analizi yapılırken ilk aĢamada, tüm değiĢkenler dikkate alınarak gruplar arasında önemli farklılık olmadığı ya da bağımsız değiĢkenlerin doğrusal kombinasyonu ile grupların ayırt edilip edilmeyeceği belirlenir. Toplam varyans-kovaryans matrisi ve grup içi varyans-kovaryans matrisleri yardımıyla yapılacak çok değiĢkenli F testlerinden yararlanılır.
Çok değiĢkenli test sonucunda anlamlı fark bulunduğunda, hangi bağımsız değiĢkenlerin modele katkısının daha önemli olduğu belirlenebilir. Ayırma analizinde elde edilecek fonksiyonlar yardımıyla sınıflama iĢlemi, yani grup üyeliklerinin belirlenmesi yapılır.
3.1.1. Ayırma analizinin varsayımları
Ayırma analizinin iki temel varsayımı çok değiĢkenli normallik ve varyans-kovaryans matrislerinin homojenliğidir. Bazı kısıtlayıcıları da vardır ve bunlara da dikkat edilmesi gerekir.
3.1.1.1. Çok değiĢkenli normallik
Ayırma analizindeki çok değiĢkenli normallik varsayımı, bağımsız değiĢkenlerin çok değiĢkenli normal dağılıma sahip bir kitleden çekildiğini ve bağımsız değiĢkenlerin herhangi bir doğrusal kombinasyonunun örneklem dağılımının da normal olmasıdır.
Ayırma analizi bir dereceye kadar çok değiĢkenli normallik varsayımını tolere edebilir. Özellikle dağılımda biraz çarpıklığın olması durumunda ayırma analizi doğru sonuçlar verebilir. Fakat dağılımda aĢırı değerlerin olması durumunda ayırma analizi sonuçları daha yanıltıcı olabilir.
Özellikle örneklem büyüklüğünün küçük olduğu ve gruplardaki veri sayılarının aynı olmadığı durumda çok değiĢkenli normalliğin sağlanması için bazı dönüĢümler yapmak gerekebilir.
3.1.1.2. Varyans-kovaryans matrislerinin homojenliği
Özellikle grupların örneklem büyüklüğünün yetersiz ve dengesiz olduğu durumlarda sınıflama iĢlemi yanlıĢ sonuçlar verir.
Varyans-kovaryans matrislerinin homojenliğini test etmek için Box‟s M testinden faydalanılır. Fakat bu testin de çok duyarlı bir test olduğu unutulmamalıdır. Box‟s M testinin anlamlı çıktığı durumlarda yeterli örneklem büyüklüğü varsa, varyans-kovaryans matrislerinin log determinantları incelenebilir. Eğer log determinantlar benzer ise Box‟s M testi göz ardı edilerek iĢlemlere devam edilebilir.
Varyans-kovaryans matrislerinin homojenliğini sağlamak için dönüĢümlerden yararlanılabilir. Böyle bir durumda karesel ayırma fonksiyonundan ya da nonparametrik sınıflama yönteminden de faydalanılabilir.
Dolayısıyla istatistiksel çıkarımın temel amaç olduğu bir durumda, varyans-kovaryans matrisleri homojen değilse ve örneklem büyüklükleri eĢit ve yeterli değilse, değiĢken dönüĢümlerinden faydalanmak gereklidir. Eğer temel amaç sınıflama ve yaygınlıklar farklı ise ya farklı varyans-kovaryans matrislerini kullanmak veya
örneklem büyüklüğü yeterli ve normal dağılım olduğunda karesel ayırma fonksiyonunu kullanmak ya da örneklem büyüklüğü yetersiz ve normal dağılım olmadığında nonparametrik sınıflama yönteminden faydalanmak gereklidir.
3.1.1.3. Çoklu bağlantı sorununun olmaması
Bağımsız değiĢkenlerden biri diğerleri ile yüksek derecede iliĢkili ya da diğerlerinin bir fonksiyonu ise çoklu bağlantı sorunu ortaya çıkar. Bu durumda ayırma fonksiyonu katsayıları bağımsız değiĢkenin göreli önemini güvenilir bir Ģekilde belirleyemez. Çoklu bağlantı giderme yöntemleri kullanılarak bu sorunlar giderilmelidir.
3.1.1.4. Bağımsız değiĢkenler arası iliĢkilerin doğrusal olması
Ayırma analizi her grup içinde bütün bağımsız değiĢken çiftleri arasında doğrusal iliĢki olmasını varsayar. Bu varsayımın bozulması analizin gücünü azaltır. Bu sorun bazı değiĢkenlere dönüĢüm uygulayarak giderilebileceği gibi bu değiĢkenleri analizden çıkartmak bazen daha iyi bir yaklaĢım olarak kabul edilmektedir.
3.1.1.5. Aykırı değerler
Ayırma analizi aykırı değerlere çok duyarlıdır. Aykırı değerler olması durumunda sınıflama çok etkilenir. O yüzden ayırma analizi öncesinde tek değiĢkenli ve çok değiĢkenli aykırı değerler bulunmalı bunlar ya dönüĢüm yoluyla yok edilmeli ya da analizden çıkarılmalıdır.
3.1.2. Ayırma analizindeki temel eĢitlikler
Ayırma fonksiyonları elde edilmeden önce, bağımsız değiĢkenlerin oluĢturacağı kombinasyonların grupları belirlemede ne kadar baĢarılı olduğu araĢtırılmalıdır. Bu amaçla MANOVA‟daki gibi çeĢitli kareler toplamlarından yararlanılarak Wilk‟s Lambda istatistiğine ulaĢılır. Test iĢlemi ya Wilk‟s Lambda istatistiğini F dağılımına dönüĢtürerek ya da Ki kare dağılımı yaklaĢımı ile yapılır. Eğer değiĢkenlerin grupları belirlemede kullanılamayacağı anlaĢılırsa çalıĢma sonlandırılır.
Bağımsız değiĢkenlerdeki varyans, gruplar arası farklılığa iliĢkin varyans ve grup içi farklılığa iliĢkin varyans olacak Ģekilde ikiye bölünür
W B
T (3.1)
Burada
T: genel kareler toplamı matrisi
B: gruplar arası kareler toplamı matrisi W: grup içi kareler toplamı matrisidir. B ve W matrisleri
) )( ( 1 x x x x n B i k i i i (3.2) ve i k i i S n W ( 1) 1 (3.3)
Ģeklindedir.Bu bilgiler yardımıyla Wilk‟s Lambda λ istatistiği
B W
W
(3.4) bulunur.
Wilk‟s Lambda‟nın sıfıra yaklaĢması gruplar arasında bir fark olduğunun göstergesidir. Anlamlılığı F ya da ki kare dağılımı ile test edilir ve sonuçta bağımsız değiĢkenlerin grupları belirleyip belirleyemeyeceği bulunur.
Ayırma analizi tüm değiĢkenlerin hepsini birden analize katarak yapılabileceği gibi, değiĢken sayısını her adımda farklı alarak da yapılabilir. Bu Ģekilde hangi değiĢkenin modele anlamlı katkıda bulunduğu anlaĢılmıĢ olur. Ġstatistiksel yazılımlarda Wilk‟s lambda istatistikleri yer almaktadır.
Hangi değiĢkenin modele dahil edileceğini bulmak için farklı yaklaĢımlar da vardır. Bunlar açıklanmamıĢ varyans, Mahalanobis uzaklığı, en küçük F değeri ve Rho‟nun V değeri yaklaĢımıdır. Adımsal yöntemler kullanıldığında Mahalanobis uzaklığı ve Rho‟nun V değeri yaklaĢımının en iyi yaklaĢım olduğu bazı yazarlar tarafından belirtilmektedir (Alpar,2011).
Ayırma analizi kanonik korelasyon analizinin özel bir durumu gibi düĢünülebilir. Ayırma analizinde kanonik korelasyon, ayırma skorları yardımıyla gruplar arasındaki iliĢkinin büyüklüğünü ölçer. Bu nedenle her bir ayırma fonksiyonu için bir kanonik korelasyon hesaplanır.
Bağımsız değiĢkenlerin sınıflandırmadaki göreli önemini veren standartlaĢtırılmıĢ kanonik ayırma fonksiyon katsayıları, standartlaĢtırılmamıĢ kanonik ayırma fonksiyon katsayıları ile elde edilir. Bu katsayılar doğrusal regresyondaki beta katsayıları gibi yorumlanır.
StandartlaĢtırılmamıĢ kanonik ayırma fonsiyonları p ip i i i i c u x u x u x D 0 1 1 2 2 .... (3.5) Ģeklindedir.
Kanonik ayırma fonksiyon sayısı eğer bağımsız değiĢken sayısı bağımlı değiĢkendeki grup sayısından fazla ise değiĢken sayısı kadar, eğer fazla değilse bağımlı değiĢkendeki grup sayısından bir eksiktir. Kanonik fonksiyonlardan birincisi uygun değiĢkenler seçilerek, gruplar arasında en iyi ayrımı yapacak Ģekilde oluĢturulur. Daha sonraki kanonik fonksiyon ise ilk kanonik fonksiyona göre daha düĢük seviyede ayırım yapacak Ģekilde oluĢturulur. Ve diğer fonksiyonlar bu Ģekilde gider.
Ayırma fonksiyonları birbirinden bağımsız ya da birbirine diktir. Böylece fonksiyonların ayırma katkıları çakıĢmaz. Ġlk fonksiyon değiĢkenliğin en büyük miktarını açıklarken, diğer fonksiyonlar sırasıyla bir önceki fonksiyon tarafından açıklanmayan değiĢimin en büyük miktarını açıklar.
StandartlaĢtırılmamıĢ ayırma fonksiyonu sınıflandırma yapmak amacı ile kullanılır. Fisher ayırma fonksiyonu olarak da adlandırılan fonksiyon
p jp j j j c c x c x C 0 1 1 ... (3.6) Ģeklindedir.
Fisher ayırma fonksiyonları grup ortalamaları arasındaki farkın en büyüklenmesi temeline dayanır. Bağımlı değiĢkendeki grup sayısı kadar ayırma fonksiyonu üretilir.
Ayırma analizinde en küçük kareler yöntemi kullanılarak grup içi kareler toplamını en küçük yapan katsayıların kestiricileri elde edilir. Elde edilen parametre kestirimleri yardımıyla hesaplanan ayırma fonksiyonu skorları bağımlı, ayırma değiĢkenleri de bağımsız değiĢken olarak alınıp doğrusal regresyon analizi uygulandığında elde edilen regresyon katsayıları, standartlaĢtırılmamıĢ ayırma fonksiyonu katsayılarına eĢit çıkar (Alpar,2011).
3.1.3. Örnek uygulama
Ayırma analizi uygulaması için R versiyon 2.15.3 programı ile gelen Hindistanlı Pima Kadınlarında yapılmıĢ bir araĢtırmaya ait veriler kullanılmıĢtır. Pima.te adlı veri seti MASS kütüphanesi içindedir. Bu veri setinde 8 adet değiĢken vardır. Bağımlı değiĢken hastanın WHO kriterine göre Ģeker hastası olup olmadığını gösteren type adlı değiĢkendir.
Tablo 3.1. Ayırma analizinde kullanılacak
değiĢkenler ve açıklamaları
DeğiĢken Ġsmi Açıklaması
npreg Doğum sayısı
glu Glukoz konsantrasyonu
bp Diyastolik kan basıncı skin Trisep kalınlığı bmi Beden kitle endeksi
ped Diyabet pedigree fonksiyonu
age YaĢ
type Diyabet olup olmaması
type değiĢkeni hariç tüm değiĢkenler süreklidir. type değiĢkeni kategoriktir. Veri setinde 332 kadına ait veriler vardır ve eksik veri bulunmamaktadır. type değiĢkeni veri setinde “Yes”,”No” olarak kodlandığı için yeni bir dikotom diyabet değiĢkeni 0, 1 olarak üretilmiĢ ve bağımlı değiĢken olarak bu yeni değiĢken kullanılmıĢtır. Diğer tüm değiĢkenler bağımsız değiĢkenler olarak modele alınmıĢtır.
SPSS programının 21. versiyonunda ayırma analizi Analyze menüsü altındaki Classify->Discriminant seçeneğindedir. Grouping variable kısmına dikotom diyabet değiĢkeni atılmıĢ, Define Range kısmında Minimum:0 ve Maximum:1 olarak girilmiĢtir. Independents kısmına diğer tüm bağımlı değiĢkenler atanmıĢtır. Statistics kısmında Fisher‟s ve Unstandardized iĢaretlenmiĢ, Classify kısmında Summary Table seçilmiĢtir.
Ayırma analizi varsayımlarından çok değiĢkenli normallik varsayımı, R programı ile test edilmiĢtir. R programında mvnormtest paketindeki mshapiro.test komutu ile tüm değiĢkenlerin çok değiĢkenli normalliği test edilmiĢ ve çok değiĢkenli normal olmadığı bulunmuĢtur (p<0.001). Aynı değiĢkenler energy paketi içerisindeki etest fonksiyonu ile de test edilmiĢ ve yine çok değiĢkenli normallik Ģartının sağlanmadığı görülmüĢtür. Çok değiĢkenli normallik Ģartı sağlanmamasına rağmen analize devam edilmiĢtir.
Varyans-kovaryans matrislerinin homojenliği Box‟s M testi ile SPSS programında test edilmiĢ ve çok anlamlı bir p<0.001 bulunduğu için homojenliğin sağlanmadığı görülmüĢtür. Classify kısmında Use Covariance Matrix seçeneğinde Separate-groups iĢaretlenerek yeniden analiz yapılmıĢtır. SPSS programında karesel diskriminant analizi yapılamamaktadır. Fakat SPSS programına ait teknik destek
sayfalarında2
varyansların homojen olmadığı durumlarda Seperate-groups seçeneğinin iĢaretlenerek analize devam edilmesi tavsiye edilmektedir.
Bağımsız değiĢkenler arasındaki çoklu bağlantı sorunu incelendiğinde bmi ve skin değiĢkenleri arasında anlamlı ve yüksek seviyeli r=0.659 Pearson korelasyonu ve yine age ve npreg değiĢkenleri arasında anlamlı ve yüksek seviyeli r=0.676 Pearson korelasyonu bulunduğu için skin ve npreg değiĢkenleri analizden çıkarılarak analize devam edilmiĢtir.
Bağımlı değiĢken iki seviyeli olduğu için bir adet ayırma fonksiyonu elde edilmiĢtir. Çıkan sonuçlara göre grup kovaryans matrislerinin log determinantları sırasıyla, diyabet olmayan grup için 17.054 ve diyabet grup için 18.733 bulunmuĢtur. Wilk‟s lambda istatistiği λ=0.657 bulunmuĢ ve p<0.001 olduğu için değiĢkenlerin grupları istatistiksel anlamlı olarak ayırabileceği anlaĢılmıĢtır. λ1=0.521 olarak bir adet
özdeğer bulunmuĢ ve varyansın tamamını açıklamaktadır. Kanonik korelasyon katsayısı 0.585 olarak bulunmuĢtur.
StandartlaĢtırılmamıĢ kanonik ayırma fonksiyonu aĢağıdaki gibidir: age ped bmi bp glu D 6.206 0.028* 0.006* 0.056* 0.613* 0.034*
StandartlaĢtırılmıĢ kanonik ayırma fonksiyonu ise:
age ped bmi bp glu s D 0.735* 0.070* 0.385* 0.216* 0.349*
Ģeklindedir. Bu fonksiyondan anlaĢılacağı gibi ayırma skoruna en büyük katkıyı glu değiĢkeni yapmaktadır.
Bağımlı değiĢken iki seviyeli olduğu için iki adet Fisher ayırma fonksiyonu elde edilmiĢtir. Bu fonksiyonlar sırasıyla
age ped bmi bp glu C 27.057 0.115* 0.303* 0.438* 1.983* 0.147* 1 age ped bmi bp glu C 36.974 0.158* 0.294* 0.523* 2.923* 0.199* 2 Ģeklindedir.
Yapılan ayırma analizi ile 223 tane diyabeti olmayan kadından 184 tanesinin diyabeti yok, 39 tanesi ise diyabeti var olarak model tarafından tahmin edilmiĢtir.109 tane diyabetli hastanın ise 26 tanesi diyabeti yok ve 83 tanesi diyabeti var Ģeklinde tahmin edilmiĢtir. Bu durumda ayırma analizi ile %80.4 oranında doğru sınıflandırma yapılmıĢtır.
2
3.2. Lojistik Regresyon
Lojistik regresyonun amacı bağımlı değiĢken ve bağımsız değiĢkenler arasında en az değiĢken kullanan, en çok uyan ve teoriyle uyumlu modeli bulmaktır.
Bağımlı değiĢkenin ikili (dikotom) veya daha fazla kategorili kategorik bir değiĢken olduğu durumda, bu değiĢkeni baĢka değiĢkenleri kullanarak tahmin etmeye çalıĢtığımızda lojistik regresyon kullanabiliriz. Lineer regresyondan farkı, bağımlı değiĢkenin lineer regresyonda sürekli, lojistik regresyonda ise kategorik olmasıdır.
Sonuç değiĢkeni istenmeyen bir durumun (hastalık,ölüm gibi) ortaya çıkıp çıkmayacağını belirleyen bir değiĢken ise, lojistik regresyon kullanarak bağımsız değiĢkenlerin risk faktörü olup olmadığı anlaĢılır. Lojistik regresyon sonuçlarında her bir faktörün (bağımsız değiĢkenin) risk faktörü olarak istatistiksel anlamlılığı yanında, odds oranını da hesaplamayı sağlar.
Her hangi bir regresyon probleminde en önemli büyüklük, bağımsız değiĢkenin değeri verildiğinde bağımlı değiĢkenin aldığı ortalama değerdir. Bu büyüklüğe Ģartlı ortalama denir ve E(Y|x) olarak gösterilir. Burada Y bağımlı değiĢkeni, x ise bağımsız değiĢkeni gösterir. Doğrusal regresyonda bu değerin x‟in bir doğrusal ifadesi olduğu
x x Y E x) ( | ) 0 1 ( (3.7)
kabul edilir . Buradan x‟in ve arasında değerleri için E(Y|x) değerinin her hangi bir değeri alabileceği anlaĢılır.
Dikotom bir sonuç değiĢkeninin analizi için değiĢik dağılım fonksiyonları tavsiye edilmiĢtir. Lojistik regresyonun seçilmesinde iki temel sebep vardır
1- Matematiksel bir bakıĢ açısından oldukça kullanıĢlı ve kolay kullanılabilir olması
2- Biyolojik olarak anlamlı yorumlanabilmesi.
Lojistik regresyon modeli
) exp( 1 1 ) exp( 1 ) exp( ) ( 1 0 1 0 1 0 x x x x (3.8) Ģeklinde gösterilebilir. Lojit dönüĢümü ise x x x x g ) 0 1 ) ( 1 ) ( ln( ) ( (3.9) Ģeklindedir.
Bu dönüĢümün önemi ise g(x)‟in doğrusal regresyonda istenen bir çok özelliğe sahip olmasıdır. Lojit fonksiyonu g(x) doğrusaldır ve sürekli olabilir ve x‟in değerlerine bağlı olarak ve arasında değerler alabilir.
Lojistik regresyonun doğrusal regresyondan ikinci önemli farkı ise sonuç değiĢkeninin Ģartlı dağılımındadır. Doğrusal regresyon modelinde sonuç değiĢkeni
) |
(Y x
E
y Ģeklinde gösterilebilir. Buradaki ε gözlemin Ģartlı ortalamadan sapmasını gösteren hatadır. Doğrusal regresyondaki en yaygın varsayım ε‟nun ortalaması 0, varyansı bir sayı olan normal dağılıma sahip olduğudur. Buradan sonuç değiĢkeninin Ģartlı dağılımının ortalaması E(Y |x) ve varyansı sabit olan bir normal dağılım olduğu çıkar. Sonuç değiĢkeni dikotom olduğunda durum bu Ģekilde değildir. Lojistik regresyonda x değiĢkeni verildiğinde y değiĢkeni y (x) Ģeklinde belirtilir. Bu durumda ε iki farklı değer alabilir. y=1 olduğunda (x) olasılıkla
) (
1 x ve y=0 olduğunda 1 (x)olasılıkla (x) değerlerini alır. Böylece ε‟nun ortalaması 0 ve varyansı (x)1 (x) olan bir dağılımı olduğu anlaĢılır. Yani sonuç değiĢkeninin Ģartlı dağılımı bir (x) olasılıklı bir binomial dağılımdır.
3.2.1. Lojistik regresyon modelini uydurma
Uygun lojistik regresyon modelini bulmak için yukarıda bahsedilen β katsayılarını kestirmek gereklidir. Doğrusal regresyonda katsayıları kestirmek için kullanılan yöntem en küçük kareler yöntemidir. Bu metodda gözlenen ve tahmin edilen Y değerleri arasındaki karesel farkların toplamını minimize eden β katsayıları seçilir. Dikotom bir sonuç değiĢkeni olduğunda bu yöntemle yapılacak katsayı kestirimleri istatistiksel olarak uygun özelliklere sahip olmayan katsayıların üretilmesine yol açacaktır. O yüzden lojistik regresyonda farklı bir yöntem olan en çok olabilirlik yöntemi ile katsayılar kestirilir.
Genel bir ifadeyle, en çok olabilirlik yöntemi β katsayılarını gözlenen değerleri en büyük ihtimalle elde edecek Ģekilde hesaplar. Bu metodu uygulamak için önce olabilirlik fonksiyonu oluĢturulur. Bu fonksiyon gözlenen değerlerin olasılıklarını bilinmeyen katsayıların bir fonksiyonu olarak verir. En çok olabilirlik yöntemi ile kestirilen katsayı değerleri ise bu fonksiyonu maksimize eden değerlerdir.
Katsayıların kestirimi yapıldıktan sonra, değiĢkenlerin anlamlılıklarına bakmak gerekir. Bu da modeldeki bağımsız değiĢkenlerin bağımlı değiĢkenle anlamlı iliĢkileri olup olmadığına bakmak için kurulacak bir hipotez testi ile mümkündür. Buradaki hipotez testi yaklaĢımlarından bir tanesi Ģu Ģekildedir: “Bu değiĢkeni içeren model
içermeyen modele göre bize sonuç değiĢkeni hakkında daha çok bilgi verir mi? Yoksa vermez mi?”. Bu soruya sonuç değiĢkeni değerini her iki modelden çıkan değerlerle karĢılaĢtırılarak bir cevap verilebilir. Burada kullanılacak matematiksel fonksiyon gözlenen ve bilinen değerleri karĢılaĢtıran bir fonksiyondur. Eğer o değiĢken modele dahil edildiğinde modelin ürettiği değer daha iyi veya daha kesin ise o zaman değiĢkenin sonuç değiĢkeni ile anlamlı bir iliĢkisi olduğu düĢünülür.
3.2.2. Olabilirlik oranı testi
Bir bağımsız x değiĢkeninin anlamlılığını bulmak için aĢağıdaki istatistik kullanılır k olabilirli varken k olabilirli yokken ln 2 x x G (3.10).
β1 „in 0 olduğu kabul edilirse, G istatistiği 1 serbestlik dereceli bir ki kare
dağılımına sahip olacaktır. Lojistik regresyon yapabilen her hangi bir yazılımda G istatistiği hesaplanabilir. Bu sayede modele yeni değiĢkenler eklenerek, onların anlamlılıkları test edilebilir.
Tek değiĢkenin olduğu durumda, ilk önce sadece sabit terim kullanılarak model kurulur. Daha sonra o bağımsız değiĢkeni modele ekleyerek son modele ulaĢılır. Bu durumda olabilirlik oranı testini kullanarak eklenen değiĢkenin anlamlılığı test edilebilir.
3.2.3. Wald testi
Burada kullanılabilecek baĢka bir test ise Wald testidir. Wald test istatistiği
) ˆ ( ˆ 1 1 se W (3.11)
Ģeklindedir. Yine yazılımlar vasıtasıyla bu istatistik hesaplanabilir. Wald istatistiğinin bir dezavantajı ise β büyük değerler aldığında standart hatası ĢiĢer ve W olması gerekenden daha küçük değerler almaya baĢlar. Dolayısıyla aslında modele anlamlı katkı yapan bir değiĢkenin katkısının anlamlı olmadığı sonucunu doğurabilir. O yüzden Wald istatiğini kullanırken dikkatli olunmalı veya yerine olabilirlik oranı testi yapılmalıdır (Field, 2009).
Hem olabilirlik oranı testi hem de Wald testi β1‟in en çok olabilirlik yöntemi ile
kestirilmesini gerektirir. Tek bir değiĢken için bu çok zaman alıcı ve zor bir iĢlem değildir. Fakat değiĢken sayısı artınca döngüsel hesaplama zamanı ve güçlüğü de artacaktır.
3.2.4. Çoklu lojistik regresyon modeli
Birden çok bağımsız değiĢken olduğu durumlarda yine lojistik regresyon modeli kurulabilir. Bu durumda lojit
p px x x x g( ) 0 1 1 2 2 .... (3.12)
Ģeklindedir. Eğer bazı bağımsız değiĢkenler kategorik ise onları sürekli değiĢkenler gibi modele dahil etmek uygun değildir. Bu durumda tasarım değiĢkenleri (dummy variables) o kategorik değiĢkenler yerine modele dahil edilir. Eğer bir bağımsız değiĢkenin k tane seviyesi varsa, k-1 adet tasarım değiĢkeni modele dahil edilmelidir. Bir çok yazılım bu iĢi kolaylıkla yapmaktadır.
Diğer çok değiĢkenli modellerde olduğu gibi doğrudan lojistik regresyon yapma düĢüncesi ile analize giriĢmek genellikle yanlıĢtır. Tek değiĢkenli analizler ve lojistik regresyonda kullanılan tıbbi ve biyolojik modelin geçerliliği dikkate alınmalıdır (Armitage ve Colton,2005).
Modele dahil edecek değiĢkenlerin seçimi çok önemli bir konudur. Bu seçimi yaparken dikkat edilmesi gereken noktalar aĢağıdadır.
1-Örneklem büyüklüğü dikkate alınmalıdır. Modele dahil edilecek değiĢken sayısı, analize alınan denek sayısının en az 10 katı büyüklükte olmalıdır.
2-Tek değiĢkenli analizlerde anlamlı bulunan değiĢkenler modele dahil edilmelidir.
3-Tek değiĢkenli analizlerde istatistiksel anlamlı bulunmadığı halde p değeri 0.05‟e yakın olan değiĢkenler modele dahil edilmelidir. Genellikle p değeri 0.25 veya 0.10‟dan küçük olan değiĢkenler modele dahil edilir.
4-Aralarında yüksek korelasyon bulunan değiĢkenlerden biri modele dahil edilmelidir. Birden çok değiĢkenin yüksek derecede iliĢkili olması (multicollinearity) modelin geçerliliğini olumsuz yönde etkileyecektir.
5-Daha önce yapılmıĢ araĢtırma sonuçlarında sonucu etkilediği gösterilmiĢ değiĢkenler modele dahil edilmelidir.
6-Eksik veri bulunma oranı düĢük olmalıdır (Hayran ve Hayran, 2011).
3.2.5. Örnek uygulama
Bölüm 3.1.3‟teki veri setini kullanarak lojistik regresyon yapılacaktır. Dikotom diyabet değiĢkeni bağımlı değiĢken olarak diğer tüm değiĢkenler bağımsız değiĢkenler olarak modele alınmıĢtır.
SPSS versiyon 21 programında Analyze menüsü altında Regression->Binary Logistic seçilir. Dependent kısmına diyabet değiĢkeni, diğer tüm değiĢkenler Covariates kısmına atılır. Options kısmında Hosmer-Lemeshow goodness of fit ve CI for exp(B) seçilir.
SPSS çıktısında birinci adım olarak sadece sabitin olduğu lojistik regresyon denklemine ait sonuçlar verilir. Bu sonuçlarda tüm kiĢiler hasta olarak tahmin edilmiĢ ve doğru tahmin yüzdesi bu adımda %67.2 bulunmuĢtur. Bu adımda denkleme katılmayan diğer tüm değiĢkenler istatistiksel olarak anlamlı bulunmuĢ ve ikinci adımda hepsi modele dahil edilmiĢtir.
Ġkinci adımda model ve adım için hesaplanan Ki kare değerleri anlamlı bulunmuĢtur. Modele ait -2Log Olabilirlik değeri 285.791, Nagelkerke R kare değeri 0.464 bulunmuĢtur. Hosmer-Lemeshow uyum iyiliği testi sonucu 0.233 bulunmuĢtur bu değer modelin değiĢkenlere uyumu hakkında bir bilgi vermektedir.
Lojistik regresyon denklemi
) * 018 . 0 * 110 . 1 * 79 . 0 * 013 . 0 * 009 . 0 * 037 . 0 * 141 . 0 514 . 9 exp( 1 1 ) ( age ped bmi skin bp glu npreg x
olarak bulunur. Modeldeki değiĢkenlerin anlamlılık değerleri aĢağıdaki tabloda verilmiĢtir.
Tablo 3.2. DeğiĢkenlerin anlamlılık
değerleri
DeğiĢken Anlamlılık Değeri (p)
Sabit <0.001 npreg 0.018 glu <0.001 bp 0.491 skin 0.511 bmi 0.005 ped 0.013 age 0.325
Lojistik regresyon analizi 223 diyabeti olmayan kiĢiden 201 tanesi diyabeti yok Ģeklinde doğru tahmin etmiĢ, 22 tanesini diyabeti var olarak yanlıĢ tahmin etmiĢtir.
Diyabeti olan 109 kiĢiden 46 tanesini yanlıĢ olarak diyabeti yok, 63 tanesini de doğru olarak diyabeti var Ģeklinde sınıflamıĢtır. Doğru sınıflama oranı %79.5 olmuĢtur.
Bölüm 3.1.3‟teki analizde çoklu bağlantı sorunu nedeniyle skin ve npreg değiĢkenleri analiz dıĢına çıkartılmıĢtı. Bu değiĢkenler çıkartılarak yapılan lojistik regresyon analizinde modele ait -2Log Olabilirlik değeri 292.350 ve Nagelkerke R kare değeri 0.445 bulunmuĢtur. Modeldeki değiĢkenlerin anlamlılık değerleri aĢağıdaki tabloda verilmiĢtir.
Tablo 3.3.DeğiĢkenlerin anlamlılık değerleri
DeğiĢken Anlamlılık Değeri (p)
Sabit <0.001 glu <0.001 bp 0.419 bmi <0.001 ped 0.014 age 0.001
Yeni model 223 diyabetsiz kiĢiden 200‟ünü diyabetsiz 23‟ünü diyabetli ve 109 diyabetli kiĢiden 44‟ünü diyabetsiz ve 65‟ini diyabetli olarak sınıflamıĢtır. Yeni modelin doğru sınıflama oranı %79.8 olmuĢtur.