Bazı ısı problemlerinin dönüşüm yöntemi ile çözümü

(1)

1. GİRİŞ

1.1. Amaç ve Kapsam

Diferansiyel Dönüşüm Yöntemi yardımıyla karşılaşılan karmaşık ve yüksek mertebeden kısmi türevli diferansiyel denklemler (ısı iletim denklemi, dalga denklemi, poisson denklemi gibi) ve diğer mühendislik problemlerinin çözümünü elde etmek mümkündür. Kullanılan yöntem, kullanım açısından elverişli ve çabuk sonuca götüren bir yöntemdir. Laplace ve Fourier dönüşümleri gibi yöntemlerle karşılaştırıldığında, dönüşüm yöntemi daha pratik ve daha zaman kazandırıcı ve bilgisayar programlamasına uygundur.

Bu yöntem kullanılarak kısmi türevli diferansiyel denklemler(KTDD) cebirsel denklemlere dönüştürülebilir ve elde edilen cebirsel denklemler de bazı basit işlemlerle kolaylıkla sistematik bir şekilde çözülebilir. Ayrıca diferansiyel dönüşüm metodu diğer integral dönüşüm yöntemleriyle (Laplace ve Fourier dönüşümleri gibi) karşılaştırıldığında daha kolay çözüme ulaştırır. Çünkü integral yöntemleri kullanıldığında karmaşık ifadelerin integrallerinin alınması zor olabilir ve ters dönüşümlerinin alınmasında problemler ortaya çıkabilir.Diferansiyel dönüşüm metodunun ise lineer ve lineer olmayan problemlerin çözümünün yanı sıra, sürekli olmayan sınır şartlarına sahip problemlerin çözümünde de çalıştığını görebiliriz.

1.2. Literatür Özeti

Oturanç G. ve ark ;(2005).Bu çalışmada yatay düzlem üzerinde oluşan taşınım denklemlerinin diferansiyel dönüşüm metoduyla çözümü verilmiştir.Bu yöntemin özelliği lineer olmayan diferansiyel denklemlerin çözümünde daha etkin bir yöntem olduğu gösterilmiştir

(2)

Kurnaz A.ve ark ; (2005). Bu çalışmada KTDD in çözümleri için n boyutlu diferansiyel metodun genelleştirilmesi verilmiştir. Bu metodun diğerlerinden ayrı olarak özelliği özellikle lineer olmayan diferansiyel denklemleri çözmekte etkili olmasıdır. Sunulan metodu örneklerle açıklamak için bulunan sonuçlar birkaç başlangıç ve sınır değer problemlerine uygulanmıştır

Kurnaz A. ve ark; (2005). Bu çalışmada adi türevli diferansiyel denklem sistemlerinin çözümleri için diferansiyel dönüşüm metodunun bir genellemesi verilmiştir.

Ayaz F., Oturanç G.; (2004). Bu çalışmada diferansiyel dönüşüm metodu ile özel bir denklem olan Burgers denklemi çözümü araştırıldı. Başlangıç şartında verilerin değişmesiyle diferansiyel dönüşüm ile bulunan çözümler karşılaştırıldı.

Chen C. K. ve ark; (1999). Bu Çalışmada KTDD Çözümleri için iki boyutlu diferansiyel dönüşüm kullanıldı. Öncelikle iki boyutlu diferansiyel dönüşüm teorisine giriş yapıldı. İkinci olarak, bir KTDD probleminin iki boyutlu diferansiyel dönüşümü alınarak, fark denklemlerinin bir kümesi elde edildi. Bu denklemler üzerinde bazı basit matematiksel işlemler yapılarak, çözüm serisinin kapalı formu veya bir yaklaşık çözüm elde edilebilir. Son olarak değişken katsayılı ve sabit katsayılı PDE problemleri sunulan metot ile çözüldü. Hesaplanan bu sonuçlar diğer analitik veya yaklaşık metotlar ile karşılaştırıldı.

Ayaz F.; (2003) Bu çalışmada kismi türevli diferansiyel denklemlerin başlangıç değer problemlerini iki boyutlu diferansiyel dönüşüm metodu çözümü araştırıldı. Yeni teoremler eklendi ve bazı lineer ve lineer olmayan KTDD bu metot kullanılarak çözüldü. Bu metot lineer ve lineer olmayan problemler için kolayca uygulanabilir. Bu çalışmada, ek olarak iki difüzyon probleminin analitik çözümleri elde edildi ve bu çözümlerin ayrıştırma metodu ile elde edilen çözümleri karşılaştırıldı.

(3)

Ayaz F.; (2004). Bu çalışmada lineer diferansiyel-cebirsel denklemlerin nümerik çözümü, diferansiyel dönüşüm metodu ile ele alındı. İki farklı problem bu teknik kullanılarak çözüldü ve çözümler kesin çözümlerle karşılaştırıldı. Diferansiyel dönüşüm metodu DCD’ler için kolayca uygulanabilir ve çözüm serileri elde edilir. Bu dönüşümlerden sonra burada ele alınan problemler için basitçe katsayı serileri formülüze edildi.

Ayaz, F.; (2004). Bu çalışmada Üç boyutlu diferansiyel dönüşüm metoduna giriş yapılmış ve birinci adım için temel teoremler tanımlanmıştır. Ayrıca iki ve üç boyutlu diferansiyel dönüşümlerin bir uygulaması olarak lineer ve lineer olmayan KTDD sistemlerinin kesin çözümleri incelenmiştir. Sunulan metodun sonuçları ayrıştırma metodu ile karşılaştırılmıştır. Diferansiyel dönüşüm metodu lineer ve lineer olmayan problemlere kolayca uygulanabilir. Bu metot nümerik ve analitik çözümler için kullanışlı bir araç olduğu anlatılmış.

Abdel-Halim Hassan I. H.; (2004). Bu çalışmada Yüksek mertebeden başlangıç değer problemlerinin diferansiyel dönüşüm metodu ile çözümü ile uygulamaya yer verilmiş. Bulunan çözümler analitik çözümler ile karşılaştırılmıştır.

Chen C. K.ve ark.; (1996). Bu çalışmada diferansiyel dönüşümün tanımı verilmiş ve bu yöntem Strum-Lioville probleme uygulandı.Bu yöntem sayesinde bazı basit matematiksel işlemlerle i inci özdeğer ve öz vektör kolayca hesaplandı.

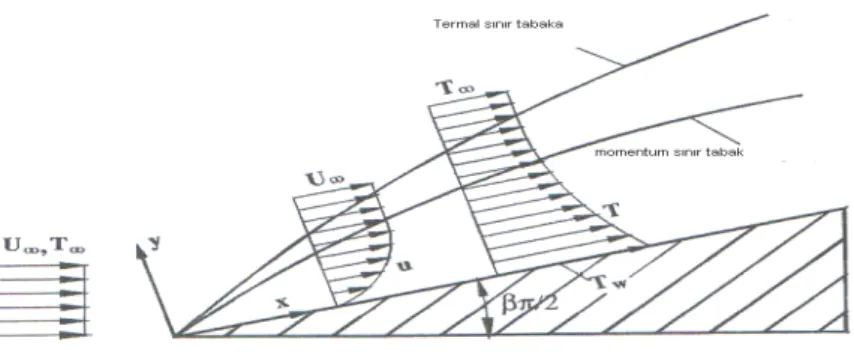
Bor–Lih K.; (2005).Bu çalışmada eğik düzlem üzerinde taşınım denklemlerinin diferansiyel dönüşüm metodu kullanılarak çözümü yapılmıştır.ve diğer nümerik metodlarla karşılaştırılması verildi.

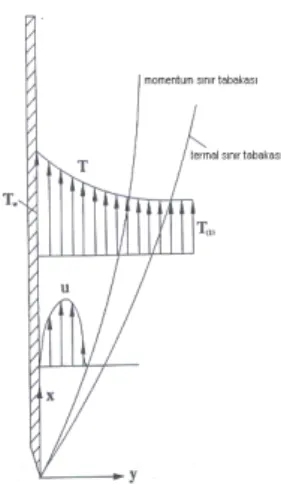
Bor –Lih K.; (2004).Bu çalışmada düşey düzlem üzerinde taşınım denklemlerinin diferansiyel dönüşüm metoduyla çözümü yapılmıştır.serbest ısı iletim sınır tabaka akışıyla,hız ve ısı dağılımı arası ilişkiyi araştırmak için diferansiyel dönüşüm metodu kullanılmıştır

(4)

2.TAŞINIM DENKLEMLERİ

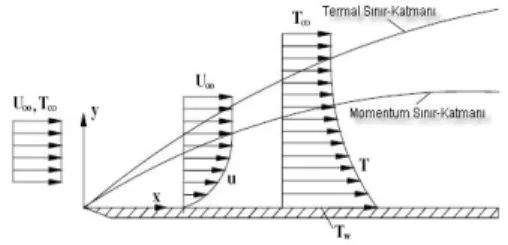
Literatürde, ısı transferi alanında, taşınım denklemleri oldukça önemlidir. Bu bölümde süreklilik, enerji ve momentum denklemleri kısaca tanımlanmışlardır. Bu konuda daha geniş bilgi,[Özışık M.N, 1980] ve [Altınışık K,2004] da mevcuttur.

2.1 Süreklilik Denklemi

Düz bir levha üzerinde tek fazlı değişmeyen özellikli akışkanın aktığını düşünelim.Akışkan hızı Vr ve hız bileşenleri u, ve v w olsun.Akış içinde

kenarlarıdx,dy vedz olan hacim kontrol elemanı göz önüne alınsın.Kontrol hacim

elemanına birim zamanda giren ve çıkan kütle akış miktarları kütlenin korunumu kanununa göre aşağıdaki gibi yazılabilir

t m m m m m m m ∂ ∂ = − + − + − ₂ ₃ ₄ ₅ ₆ 1 (2.1.1) burada 1

m :sol yüzden giren kütle m₁= udydzdtρ (2.1.2)

2

m : sağ yüzden çıkan kütle m₂=[ udx] x u ρ ρ ∂ ∂ + dydzdt (2.1.3) 3

m .alt yüzden giren kütle m = udxdzdt₃ ρ (2.1.4)

4

m üst yüzden çıkan kütle m₄=[ vdy] y v ρ ρ ∂ ∂ + dxdzdt (2.1.5) 5

m :ön yüzden giren kütle m = udydxdt₅ ρ (2.1.6)

6

m : arka yüzden çıkan kütle m =₆ [ wdz] z w ρ ρ ∂ ∂ + dxdydt (2.1.7)

(5)

Şekil 2.1 Hacim elemanına etki eden kuvvetler t

m

∂ ∂

: birim zamandaki hacim elemanındaki kütle artışı

t m ∂ ∂ = dxdydzdt t ∂ ∂ρ (2.1.8)

bu ifadeler (2.1.1) de yerine konursa ve gerekli düzenlemelerle aşağıdaki eşitlik elde edilir.

udydzdt

ρ + udxdzdtρ + udydxdtρ -[ udy]

y u ρ ρ ∂ ∂ + dydzdt -] [ vdy y v ρ ρ ∂ ∂ + dxdzdt- [ wdy] y w ρ ρ ∂ ∂ + dxdydt = dxdydzdt t ∂ ∂ρ ifadesi düzenlenerek ) ( u x ρ ∂ ∂ ) ( v y ρ ∂ ∂ + ( w) z ρ ∂ ∂ + + t ∂ ∂ρ =0 (2.1.9) bağıntısı elde edilir.Bu ifade genel anlamda süreksiz rejimde sıkıştırılabilir bir akışkanın kütle süreklilik denklemi adını alır. Vr nin hız bileşenleri vektörel formda

Vv=uiˆ+vˆj+wkˆ yazılabilir. ) ( u x ρ ∂ ∂ ) ( v y ρ ∂ ∂ + ( w) y ρ ∂ ∂ + =∇v( Vρv) olup (2.1.9) ifadesi + ∂ ∂ t ρ ) ( Vv v _ρ ∇ =0 (2.1.10)

(6)

şeklinde elde edilir.

DtD diferansiyel operatör olmak üzere

+ Dt Dρ ) ( Vv v _ρ ∇ =0 (2.1.11) yazılabilir.

DtD diferansiyel operatörü,akışkan hareketini izleyen gerçek türev olup,

= Dt D t ∂ ∂ + x u ∂ ∂ y v ∂ ∂ + z w ∂ ∂ + (2.1.12)

şeklinde verilebilir.Sürekli rejimde =0 ∂ ∂

t

ρ

ve sıkıştırılamayan akışkanlar için

x u ∂ ∂ y v ∂ ∂ = z w ∂ ∂ = =0 olacağından (2.1.11) bağıntısı ) ( Vv v _ρ ∇ =0 (2.1.13)

olacaktır.Eğer akışkan sıkıştırılamazsa (2.1.13) ifadesinde ρsabit olduğundan 0

)

( =

∇ Vv v (2.1.14)

şeklinde ifade edilebilir.Bu durumda sürekli rejim ve sıkıştırılamaz akış için (2.1.9) denklemi x u ∂ ∂ y v ∂ ∂ + z w ∂ ∂ + =0 (2.1.15)

olarak yazılır. Bu ifadeye kütle süreklilik denklemi denir.Burada (2.1.9) ifadesi yazılırken akışkan sıkıştırılabilir,süreksiz rejim ve sürtünme sıcaklık değişimi ihmal edilmiştir. Ayrıca sabit vizkozite ve iç ısı kaynağının olmadığı kabul edilmiştir. Verilen bağıntıyı iki boyutlu,sürekli rejim,sıkıştırılamaz ve levhaya dik yönde gelen basınç kuvvetlerinin olmadığı varsayılarak

x u ∂ ∂ y v ∂ ∂ + =0 (2.1.16)

yazmak mümkündür,[Özışık M.N, 1980] ,[Altınışık K, 2004].Bu ifade iki boyutlu akış için süreklilik denklemi adını alır.

(7)

2.2.Momentum denklemleri

Viskoz bir akışkan için kenarları dx,dy,dzolan hacim elemanı göz önüne

alınsın.Akışın hızı x ekseni boyunca değiştiği kabul edilsin.Hacim elemanı üzerine atalet kuvveti dinamik kuvvetler,sürtünme kuvvetleri etki eder.Bunlar daha genel olarak sürtünme kuvvetleri yer çekimi kuvvetleri basınç yoğunluk gibi kuvvetlerdir.Sürtünme kuvveti akışkan hızı x ekseni boyunca değiştiğinden sadece kenar yüzeyde görülür.Yer çekimi hacim elemanının merkezine uygulanır.Burada y ekseni üzerindeki izdüşümü,

1

F

dv =gyρudxdydz=gyρudv (2.2.1)

Şekil.2.2Hacim elemanı üzerine x yönünde etki eden kuvvetler

şeklinde verilebilir.Hacim elemanının sol yüzüne uygulanan basınç kuvveti pdydz bu basınç hacim elemanın sağ tarafında

- [ dx] x p ∂ ∂ + ρ dydz

şeklindedir.Hacim elemanı üzerine etki eden net basınç kuvveti dFv₂ olsun.

2 F dv = pdydz - [ dx] x p ∂ ∂ + ρ dydz= dxdydz x p ∂ ∂ − = dv x p ∂ ∂ − (2.2.2)

olacaktır ve y kesitinde sürtünme kuvveti akışa ters istikamette olup, dxdz alanına

dxdz

yx

τ

kadar bir kuvvetle etki edecektir y+ dy kesitinde ise,sürtünme kuvveti akış istikametindedir ve dxdzalanına,

(8)

[τyx + dy

yτyx

∂ ∂

] dxdz

büyüklüğünde bir kuvvetle etki eder. Net sürtünme kuvetidFv₃,

3 F dv =[τ_yx + dy yτyx ∂ ∂ ] dxdz- τ_yxdxdz= dv yτyx ∂ ∂ (2.2.3) olarak elde edilir. τyx sürtünme kuvveti,aşağıdaki gibi verilebilir.

yx τ = y V ∂ ∂r μ (2.2.4) F dv=dFv₁+ dFv₂+ dFv₃ yazılırsa F dv=[( ₂ ) 2 y V x p g_y ∂ ∂ + ∂ ∂ − μ v ρ dv (2.2.5)

olur.Newton’un 2.yasası gereği aşağıdaki eşitlik verilebilir.

F dv= ma dt V m d r _v = ) ( ( av akışkanın ivmesi) (2.2.6) av = dt V dr (2.2.7) olur ki av değeri yerine yazılırsa

F dv=m dt V dr = Dt V D dv r ρ (2.2.8)

bulunur. Bu ifade (2.2.5) de yerine yazılırsa

Dt V D r ρ =( 2₂) y V x p g_y ∂ ∂ + ∂ ∂ − μ v ρ

bulunur.V hızının bileşenleri u,v,w olsun ohalde akış denklemleri aşağıdaki gibi verilebilir. Dt Du ρ = ( 2₂ 2₂ 2₂) z u y u x u x p g_x ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − μ ρ (2.2.9) Dt Dv ρ = ( ₂) 2 2 2 2 2 z v y v x v y p gy ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − μ ρ (2.2.10) Dt Dw ρ = ( ₂ ) 2 2 2 2 2 z w y w x w z p gz ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − μ ρ (2.2.11)

(9)

t anında x,y,z noktasında bulunan kütlesi pdxdydz olan akışkan için toplam türev

fikrinden x,y,z ekseni için aşağıdaki ifadeler verilebilir.

= Dt Du t u ∂ ∂ + x u u ∂ ∂ y u v ∂ ∂ + z u w ∂ ∂ + (2.2.12) = Dt Dv t v ∂ ∂ + x v u ∂ ∂ y v v ∂ ∂ + z v w ∂ ∂ + (2.2.13) = Dt Dw t w ∂ ∂ + x w u ∂ ∂ y w v ∂ ∂ + z w w ∂ ∂ + (2.2.13) burada t u ∂ ∂ , t v ∂ ∂ , t w ∂ ∂

ifadeleri t zamanında hızın değişimini gösterir. (2.2.9), (2.2.10) (2.2.11) denklemleri taraf tarafa toplanırsa

Dt Dv ( ρ + Dt Dw + Dt Du )= ) ( ) ( ) ( 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 z w y w x w z v y v x v z u y u x u z p y p x p g g g_x _y _z ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ + ∂ ∂ − + + μ ρ (2.2.14) bulunur. Veya ) ( Dt V D v ρ = ( 2. ) V p gv−∇ +μ ∇ v ρ (2.2.15)

veya her yanı ρile bölersek

Dt V Dv = 1 ( 2. ) V p gv− ∇ + ∇ v ρ μ ρ (2.2.16)

elde edilir ve y yönünde viskoz gerilmeleri ihmal edildiğinde x- momentum için

Dt Du ρ = ₂ 2 y u x p g_x ∂ ∂ + ∂ ∂ − μ ρ (2.2.17) ifadesinde

(10)

= Dt Du t u ∂ ∂ + x u u ∂ ∂ y u v ∂ ∂ + z u w ∂ ∂ +

bağıntısı yerine konursa ve gerekli ihmaller yapılırsa ρ( x u u ∂ ∂ y u v ∂ ∂ + )= x p y u ∂ ∂ − ∂ ∂ 2 2 μ (2.2.18)

elde. edilir bu denkleme basitleştirilmiş momentum denklemi denir ve sıkıştırılamaz sürekli rejimde laminer akışlarda p sabit alınırsa

x u u ∂ ∂ y u v ∂ ∂ + = 2₂ y u ∂ ∂ ν (2.2.19)

elde edilir. [Özışık M.N, 1980] ,[Altınışık K, 2004]

2.3 Enerji Denklemi

Akışkan özelliklerinin sıcaklıkla değişmediğini ve sürtünme nedeni ile oluşan kayma gerilimleri üzerinde yapılan işin ihmal edilebilir olduğunu varsayarsak ,sınır tabaka içerisinde alınan kontrol hacme akışkanın taşıdığı enerji ρuhΔy+ρvhΔx

olacaktır.Burada h birim kütle başına entalpidir.Benzer şekilde akışkanın kontrol

hacimden taşıdığı enerji ise

ρ( x x uh uh Δ ∂ ∂ + ) yΔ + ρ( y x vh vh Δ ∂ ∂ + )Δx olarak yazılabilir.

(11)

Kontrol hacme iletimle transfer edilen ısı q&''xΔy+ q&''yΔx ve kontrol hacimden

iletimle transfer edilen ısı ise + Δ Δ ∂ ∂ + x y x q q x x ) ( '' &'' & y x y q q y y Δ Δ ∂ ∂ + ) ( '' &'' &

yazılabilir.Burada q& ,''x q& , x ve y yönünde ısı akılarıdır.sürekli rejimde kontrol ''y

hacme giren ve çıkan enerjiler eşit olacağından (termodinamiğin birinci yasası gereği ) + ∂ ∂ + ∂ ∂ ) ( y vh x uh ρ x q x ∂ ∂ '' & y q y ∂ ∂ + &'' =0 (2.3.1)

elde edilir.Süreklilik denklemi göz önüne alınarak (2.3.1) denkleminin sol tarafındaki ilk parantezin içerisindeki terimler,

) ( y vh x uh ∂ ∂ + ∂ ∂ ρ = ( ) y h v x h u ∂ ∂ + ∂ ∂ ρ (2.3.2)

yazılabilir.Sıkıştırılamaz akışkanlarda özgül entalpi değişimi dh=CdT,ideal

gazların özgül entalpi değişimide dh=CPdT olacağından

x T C x h ∂ ∂ = ∂ ∂ (2.3.3.a) y T C y h p ∂ ∂ = ∂ ∂ (2.3.3.b) yazılabilir.Sıkıştırılamaz akışkanlar için (2.3.3) deki C ile C değiştirilmelidir. _p

Fourier ısı iletim kanunundanda

x q x ∂ ∂ '' & = ₂ ) 2 x T ∂ ∂ −λ (2.3.4.a) y q y ∂ ∂ '' & ₌ 2 2 y T ∂ ∂ −λ (2.3.4.b)

yazılabilir. (2.3.4.) (2.3.3.) (2.3.2) eşitlikleri (2.3.1) de yerine yazılırsa

) ( ₂ 2 2 2 y T x T y T v x T u ∂ ∂ + ∂ ∂ = ∂ ∂ + ∂ ∂ _α (2.3.5)

(12)

elde edilir.Genellikle sınır tabakası içerisinde x yönünde iletimle ısı transferi,y yönündekinden küçük olacağından (2.3.5) in sağ tarafındaki birinci terim ihmal edilebilir.Bu durumda enerji denklemi

2 2 y T y T v x T u ∂ ∂ = ∂ ∂ + ∂ ∂ _α P C ρ λ

α = akışkan ısıl yayılım katsayısıdır. (2.3.6) indirgenir. [Özışık M.N, 1980] ,[Altınışık K, 2004]

(13)

3. DİFERANSİYEL DÖNÜŞÜM YÖNTEMİ

Lineer veya lineer olmayan, adi türevli ve kısmi türevli diferansiyel denklemlerin çözümü için kullanılan bu yöntem ilk olarak [ Zhou, 1986] da tanıttı. Zhou, bu çalışmasında elektirik ve elektirik devre analizinde karşılaşılan lineer ve lineer olmayan başlangıç değer problemlerini çözdü. [ Chen, 1999 ], lineer ve lineer olmayan başlangıç değer problemleri için kapalı seri çözüm formları elde ederek bu metodu geliştirdi. Dönüşüm metodu, Taylor serisi çözümünden farklıdır. Bu çözüm, diferansiyel denklem ve başlangıç bilgisi kullanarak Taylor serisinin çözümünün katsayılarını hesaplamayı kapsar. Bu yöntemi Taylor serisi metodu ile karşılaştıracak olursak taylor serisi büyük mertebeler için, daha çok hesaplama çalışması gerektirir. [Jang, 2001] de diferansiyel dönüşümü, diferansiyel denklemlerin Taylor serisi çözümünü elde etmek için bir iteratif prosedür olarak ele aldı..

Bu metod ile diferansiyel denklemler cebirsel denklemlere dönüştürülebilir ve elde edilen cebirsel denklemler de bazı basit işlemlerle kolaylıkla sistematik bir şekilde çözülebilir. Ayrıca diferansiyel dönüşüm metodu diğer integral dönüşüm yöntemleriyle (Laplace ve Fourier dönüşümleri gibi) karşılaştırıldığında daha kolay çözüme ulaştırır çünkü integral yöntemleri kullanıldığında karmaşık ifadelerin integrallerinin alınması zor olabilir ve ters dönüşümlerinin alınmasında problemler ortaya çıkabilir. Sonuçta bu yöntem ile lineer ve lineer olmayan problemlerin çözümünün yanı sıra, sürekli olmayan sınır şartlarına sahip problemlerin çözümünde de kullanılacağı görülebilir.

Diferansiyel dönüşüm yöntemi tek boyutlu, iki boyutlu, üç boyutlu ve n boyutlu diferansiyel dönüşüm yöntemi olmak üzere 4 ayrı durumda incelenebilir. Bir boyutlu diferansiyel dönüşüm yöntemi adi türevli diferansiyel denklemlerin ve denklem sistemlerinin çözümü için, iki ve üç boyutlu diferansiyel dönüşüm yöntemi kısmi türevli diferansiyel denklemlerin ve denklem sistemlerinin çözümü için ve n boyutlu diferansiyel dönüşüm yöntemi ise denklem sistemlerini ve bazı kısmi türevli diferansiyel denklemleri çözmekte kullanılır.

(14)

3.1. Tek Boyutlu Diferansiyel Dönüşüm Yöntemi

Bu yöntem tek değişken içerdiğinden adi türevli diferansiyel denklemlerin çözümleri için kullanılır bu yönteme geçmeden önce diferansiyel operatörünün özelliklerin inceleyelim. 1.

(

( ) ( )

)

( ) v(x) dx d x u dx d x v x u dx d _α _α ± = ± (α keyfi sabit) 2. ( ) ₂ ( ) 2 x u dx d x u dx d dx d = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ 3.

(

)

( ) ( ) ... 1 ) ( ) ( ) ( ) ( _⎟⎟ 1₁ + ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = −₋ u x dx d x v dx d n x u dx d x v x v x u dx d n n n n n n ( ) ( ) ( ) ( ) 1 1 1 x u dx d x u x u dx d x v dx d n n n n n n + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + −₋ Tanım 3.1.1.[Chen, 1996]

Tek bileşenli w(x) fonksiyonunun diferansiyel dönüşüm fonksiyonu W(k) olmak üzere, w(x)’ nin tek boyutlu diferansiyel dönüşümü

0 ) ( ! 1 ) ( = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = x k k x w dx d k k W (3.1.1) olarak tanımlanır. Tanım 3.1.2. [Chen, 1996]

W(k) dönüşüm fonksiyonunun tersi; diferansiyel ters dönüşüm fonksiyonu,

∑

∞ = = 0 ) ( ) ( k k x k W x w (3.1.2)

biçimde tanımlanır. (3.1.1) ve (3.1.2) eşitlikleri dikkate alınarak aşağıdaki (3.1.3) eşitliği elde edilir.

∑

∞ = ⎥⎦ ₌ ⎤ ⎢ ⎣ ⎡ = 0 ₀ ) ( ! 1 ) ( k k x k k x x w dx d k x w (3.1.3)

(3.1.1) ve (3.1.2) denklemleri kullanılarak temel matematiksel işlemle yardımıyla tek boyutlu diferansiyel dönüşümü için aşağıdaki teoremleri verebiliriz.

(15)

Teorem 3.1.1. [Chen, 1996]

Tek bileşenli w(x), u(x) ve v(x) fonksiyonlarını alalım. Eğer

w(x)=u(x) ± v(x)

ise sırasıyla W(k), U(k) ve V(k) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k)=U(k) ± V(k) eşitliği sağlanır. İspat u(x)→U(k)= 0 ) ( ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x k k x u dx d k ve v(x)→V(k)= ! ( ) ₀ 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x k k x v dx d k olmak üzere w(x)=u(x) ± v(x) ise W(k)=

(

)

0 ) ( ) ( ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ± x k k x v x u dx d k diferansiyel operatörünün 1. özelliğinden W(k)= 0 ) ( ) ( ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ± x k k k k x v dx d x u dx d k = 4 4 3 4 4 2 1 ) ( 0 ) ( ! 1 k U x k k x u dx d k ⎥_⎦ ₌ ⎤ ⎢ ⎣ ⎡ ± 4 4 3 4 4 2 1 ) ( 0 ) ( ! 1 k V x k k x v dx d k ⎥_⎦ ₌ ⎤ ⎢ ⎣ ⎡ W(k)=U(k) ± V(k) Teorem 3.1.2. [Chen, 1996]

Tek bileşenli w(x) ve u(x) fonksiyonlarını alalım. c ∈R olmak üzere eğer w(x)= c u(x)

ise sırasıyla W(k) ve U(k) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k)=c U(k)

(16)

İspat u(x)→U(k)= 0 ) ( ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x k k x u dx d

k olduğundan w(x)=cu(x) ise

W(k)= 0 ) ( ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x k k x u c dx d

k olur. Diferansiyel operatörünün 1. özelliğinden

W(k)= 0 ) ( ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x k k x u dx d k c = cU(k) olarak bulunur. Teorem 3.1.3. [Chen, 1996]

Tek bileşenli w(x) ve u(x) fonksiyonlarını alalım. Eğer

w(x)= dx

d u(x)

ise sırasıyla W(k) ve U(k) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere W(k)=(k+1)U(k+1) eşitliği sağlanır. İspat u(x)→U(k)= 0 ) ( ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x k k x u dx d k olduğunu biliyoruz. w(x)= dx x du( ) ise W(k)= 0 ) ( ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ x k k x u dx d dx d

k diferansiyel operatörünün 2. özelliğinden

W(k)= 0 1 1 ) ( ! 1 = + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x k k x u dx d k = 4 4 4 4 3 4 4 4 4 2 1 ) 1 ( 0 1 1 ) ( )! 1 ( 1 ) 1 ( + = + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + k U x k k x u dx d k k =(k+1)U(k+1)

Teorem 3.1.4.[Keskin Y,2005]

(17)

w(x)= _r r dx x u d ( )

ise sırasıyla W(k) ve U(k) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere W(k)=(k+1)(k+2)...(k+r) U(k+r)= ! )! ( k r k+ U(k+r) eşitliği sağlanır. Teorem 3.1.5. [Chen, 1996]

Tek bileşenli w(x), u(x) ve v(x) fonksiyonlarını alalım. r∈N olmak üzere eğer w(x)=u(x)v(x)

ise sırasıyla W(k),U(k) ve V(k) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k)=

∑

= − k r r k V r U 0 ) ( ) ( eşitliği sağlanır. İspat u(x)→U(k)= 0 ) ( ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x k k x u dx d k ve v(x)→V(k)= ! ( ) ₀ 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x k k x v dx d k olmak üzere w(x)=u(x) v(x) ise W(k)=

(

)

0 ) ( ) ( ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x k k x v x u dx d

k olur. Diferansiyel operatörünün 3.

özelliğinden

(

)

0 ) ( ) ( ! 1 ) ( = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = x k k x v x u dx d k k W + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = = − − 0 1 1 ) ( ) ( 1 ) ( ) ( ! 1 x k k k k x u dx d x v dx d k x u dx d x v k 0 1 1 2 2 2 2 ) ( ) ( ) ( ) ( 1 ... ) ( ) ( 2 − ₌ − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ x k k k k k k x u dx d x u x u dx d x v dx d k k x u dx d x v dx d k

(18)

W(k) _⎥ + ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = = − − = 0 1 1 0 ) ( ) ( 1 ! 1 ) ( ) ( ! 1 x k k x k k x u dx d x v dx d k k x u dx d x v k 0 0 1 1 0 2 2 2 2 ) ( ) ( ! 1 ) ( ) ( )! 1 ( ! ! 1 ... ) ( ) ( 2 ! 1 = = − − = − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ x k k x k k x k k x u dx d x u k x u dx d x v dx d k k k x u dx d x v dx d k k W(k) ( ) ( ) ... )! 1 ( ! ! 1 ) ( ) ( ! 1 0 1 1 0 + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = − − = x k k x k k x u dx d x v dx d k k k x v x u dx d k 0 0 1 1 ) ( ) ( ! 1 ) ( ) ( )! 1 ( ! ! 1 = = − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + x k k x k k x u dx d x u k x u dx d x v dx d k k k W(k)=U(k)V(0)+U(k-1)V(1)+...+U(1)V(k-1)+U(0)V(k) W(k)= W(k)=

∑

= − k r r k V r U 0 ) ( ) ( Teorem 3.1.6. [Chen, 1996]

Tek bileşenli w(x) fonksiyonunu alalım. m∈ N olmak üzere eğer w(x)=xm

ise sırasıyla W(k) verilen fonksiyonun diferansiyel dönüşüm fonksiyonu olmak üzere

W(k)= ⎩ ⎨ ⎧ = = − halde aksi m k m k , 0 , 1 ) ( δ eşitliği sağlanır. İspat İspata önce 0 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x m k k x dx d

ifadesinin eşitini araştıralım. Burada karşımıza 3 durum çıkmaktadır. 1. Durum: k<m durumu

[

( 1)...( 1)

]

₀ 0 0 = + − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − = x k m x m k k x k m m m x dx d 0 ! 0 ! 1 ) ( 0 = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = = k x dx d k k W x m k k 2. Durum: k=m durumu

[

( 1)...( 1)

]

₀ ! 0 m x m m m m x dx d x m m x m m m = + − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − =

(19)

1 ! ! 1 ! 1 ) ( 0 = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = = m m x dx d m m W x m m m 3. Durum: k>m durumu

[

( 1)...( 1)0

]

₀ 0 0 = + − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = = x x m k k m m m m x dx d olur. 0 ! 0 ! 1 ) ( 0 = = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = = k x dx d k k W x m k k

Bu 3 durum göz önüne alınarak w(x)=xm

olmak üzere W(k)= ⎩ ⎨ ⎧ = = − halde aksi m k m k , 0 , 1 ) ( δ olur.

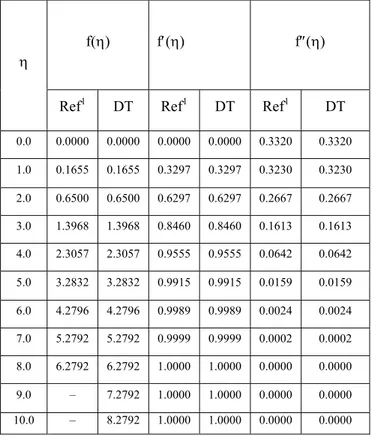
w(x) in bazı değerleri için elde edilen W(k) değerleri çalışmanın sonundaki

Tablo ’da verilmiştir. Bunlardan bazılarını

w(x) W(k) w(x)=16 W(k)=16δ(k) w(x)=8x W(k)=8δ(k-1) w(x)=5x2 W(k)=5δ(k-2) w(x)=7x5 W(k)=7δ(k-5) w(x)=3x8+4x3-9 W(k)=3δ(k-8)+ 4δ(k-3)- 9δ(k)

Teorem 3.1.7[Keskin Y,2005]

w(x)= u(x) ₂

2

dx d

v(x)

W(k)=

∑

= + − + − k r r k r k 0 ) 1 )( 2 ( U(r)V(k-r+2) eşitliği sağlanır.

(20)

İspat

Önce f(x)= ₂ 2

dx d

v(x)’ e karşılık gelen diferansiyel dönüşümü bulalım. Teorem

3.1.4 den r=2 için F(k)=(k+1)(k+2)V(k+2) olur Teorem 3.1.5 den iki fonksiyonun çarpımının diferansiyel dönüşüm fonksiyonundan

W(k)=

∑

= − k r r k F r U 0 ) ( ) ( şeklinde olur. Burada

F(k-r)=(k-r+1)(k-r+2)V(k-r+2)

olur. Bu iki ifadeden

W(k)=

∑

= + − + − k r r k r k 0 ) 1 )( 2 ( U(r)V(k-r+2) bulunur.

Teorem 3.1.8. [Keskin Y,2005]

w(x)= ( ) v(x) x d x u x d ∂ ∂

W(k)=

∑

= + − + + − + k r r k V r U r k r 0 ) 1 ( ) 1 ( ) 1 )( 1 ( eşitliği sağlanır. İspat f(x)= u(x) x d ∂ ve g(x)= xv(x) d

∂ olsun. Buradan F(k)=(k+1)U(k+1) ve

G(k)=(k+1)V(k+1) olur. Teorem 3.1.5 iki fonksiyonun çarpımının diferansiyel

dönüşüm fonksiyonundan W(k)=

∑

= − k r r k G r F 0 ) ( ) (

(21)

şeklindedir. Burada

F(r)=(r+1)U(r+1) ve G(k-r)=( k-r +1)V(k-r +1)

olur. Sonuç olarak

W(k)=

∑

= + − + + − + k r r k V r U r k r 0 ) 1 ( ) 1 ( ) 1 )( 1 ( Bulunur.

Teorem 3.1.9. [Keskin Y,2005]

Tek bileşenli w(x), u(x), v(x) ve s(x) fonksiyonlarını alalım. Eğer

w(x)=u(x)v(x)s(x)

ise sırasıyla W(k), U(k), V(k) ve S(k) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k)=U(k)⊗ V(k)⊗ S(k)=

∑∑

= − = − − k r r k t t r k S t V r U 0 0 ) ( ) ( ) ( eşitliği sağlanır. İspat

f(x)=v(x)s(x) olsun. Teorem 3.1.5 iki fonksiyonun çarpımının diferansiyel

dönüşüm fonksiyonundan F(k)=

∑

∞ = − 0 ) ( ) ( r r k S r

V olur. Burada w(x)=u(x)f(x)

olacaktır. Teorem 3.1.5 den

W(k)=

∑

= − k r r k F r U 0 ) ( ) ( olur. F(k−r)=

∑

− = − − r K t t r k S t V 0 ) ( ) ( denklemde yerine yazılırsa

W(k)=

∑∑

= − = − − k r r k t t r k S t V r U 0 0 ) ( ) ( ) ( olup ispat tamamlanmış olur.

(22)

Teorem 3.1.10. [Keskin Y,2005]

Tek bileşenli w(x), u(x), v(x) ve s(x) fonksiyonlarını alalım. Eğer

w(x)= u(x)v(x) ₂

2

dx d

s(x)

ise sırasıyla W(k), U(k), V(k) ve S(k) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k,h)=

∑∑

= − = + − − + − − k r r k t t r k t r k 0 0 ) 2 )( 2 ( U(r)V(t)S(k-r-t+2) eşitliği sağlanır. İspat g(x)= ₂ ( ) 2 x s dx d

olsun. Buna karşılık gelen diferansiyel dönüşüm fonksiyonu

G(k)=(k+1)(k+2)S(k+2) buradan f(x)=v(x)g(x) olur. Teorem 3.1.5 iki fonksiyonun

çarpımının diferansiyel dönüşüm fonksiyonundan

F(k)=

∑

∞ = − 0 ) ( ) ( r r k G r V Burada G(k-r)=(k-r+1)(k-r+2)S(k-r+2)

olur. Sonuç olarak w(x)=u(x)f(x) olacaktır. Teorem 3.1.5 den

W(k)=

∑

= − k r r k F r U 0 ) ( ) ( olur. F(k−r)=

∑

− = − − r k t t r k G t V 0 ) ( ) ( denklemde yerine yazılırsa

W(k) =

∑∑

= − = + − − + − − k r r k t t r k t r k 0 0 ) 2 )( 2 ( U(r)V(t)S(k-r-t+2)

(23)

Teorem 3.1.11. [Keskin Y,2005]

Tek bileşenli w(x) fonksiyonunu alalım. λ∈R olmak üzere eğer

w(x)=aλx

ise W(k) verilen fonksiyonun diferansiyel dönüşüm fonksiyonu olmak üzere

W(k)= ! ) (ln k a k k λ eşitliği sağlanır. İspat (3.1.1) den 0 ) ( ! 1 ) ( = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = x k k x w dx d k k W = 0 ! 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x x k k a dx d k

λ _{olur. Şimdi k nın aldığı}

değerlere göre W(k) değerlerini hesaplarsak

k=0 için W(0)=

[ ]

₀ ! 0 1 = x x aλ = ! 0 1 =1 k=1 için W(1)= 0 ! 1 1 = ⎥⎦ ⎤ ⎢⎣ ⎡ x x a dx d _λ =

[

ln

]

₀ ! 1 1 = x x aaλ λ = ! 1 1_λ lna k=2 için W(2)= 0 2 2 ! 2 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x x a dx d λ ₌

[

]

0 2 2_(ln ₎ ! 2 1 = x x a a λ λ = ! 2 1 _λ2 (lna)2 k=3 için W(3)= 0 2 2 ! 3 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ x x a dx d λ ₌

[

]

0 3 3_(ln ₎ ! 3 1 = x x a a λ λ = ! 3 1 _λ3 (lna)3

bu değerlerden anlaşılacağı gibi

W(k)= ! ) (ln k a k k λ eşitliği sağladığı görülür. Teorem 3.1.12. [Abdel-Halim, 2004]

w(x)=eλx

(24)

W(k)= ! k k λ eşitliği sağlanır. İspat

Teorem 3.1.11. den a=e alınırsa W(k)= ! ) (ln k e k k λ = ! k k λ

Teorem 3.1.13. [Keskin Y,2005]

w(x)=eλx+b

W(k)= ! k k λ eb eşitliği sağlanır. İspat

w(x)= eλx+b= eλxeb Teorem 3.1.2 diferansiyel dönüşümün lineerlik

özelliğinden u(x)= eλx

ve eb’ yi sabit olarak alırsak. W(k)=U(k)ebolur. Teorem 3.1.12. den U(k)=

!

k

λ

olduğu biliniyor. Sonuç

olarak W(k)= ! k k λ eb bulunur.

Teorem 3.1.14. [Keskin Y,2005]

Tek bileşenli w(x) fonksiyonunu alalım. Eğer

w(x)=sh(λx)

(25)

W(k)= ⎪⎩ ⎪ ⎨ ⎧ ise çift k ise tek k k k 0! λ eşitliği sağlanır. İspat w(x)= sh(λx )= 2 x x e eλ − −λ = 2 2 x x e eλ ₋ −λ

olur. Teorem 3.1.1 ve Teorem 3.1.2 den W(k)= 2 1 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − ! ) ( ! k k k k λ λ olur. k tek ise

W(k)= 2 1 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₋ − ! ) ( ! k k k k λ λ = ! k k λ k çift ise W(k)= 2 1 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₋ − ! ) ( ! k k k k λ λ = 0

Teorem 3.1.15. [Keskin Y,2005]

Tek bileşenli w(x) fonksiyonunu alalım. Eğer

w(x)=ch(λx)

W(k)= ⎪⎩ ⎪ ⎨ ⎧ ise çift k k ise tek k k ! 0 λ eşitliği sağlanır. Teorem 3.1.16. [Abdel-Halim, 2004]

Tek bileşenli w(x) fonksiyonunu alalım. a,b∈R olmak üzere eğer w(x)=sin(ax+b)

(26)

W(k)= ! k ak sin ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ b} k 2 π eşitliği sağlanır. İspat

w(x)=sin(ax+b) ise (3.1.1) den bu fonksiyonun diferansiyel dönüşüm

fonksiyonu 0 ) sin( ! 1 ) ( = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + = x k k b ax dx d k k W

Şimdi k nın aldığı değerlere göre W(k) değerlerini hesaplarsak

k=0 için W(0) =

[

sin( )

]

₀ ! 0 1 = +b _x ax = ! 0 1 sin(b) = ! 1 1 a0 sin ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ b} 2 0π k=1 için W(1) = 0 ) sin( ! 1 1 = ⎥⎦ ⎤ ⎢⎣ ⎡ ₊ x b ax dx d =

[

cos( )

]

₀ ! 1 1 = +b _x ax a = ! 1 1 a cos(b)= ! 1 1 a sin ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + b 2 π k=2 için W(2) = 0 2 2 ) sin( ! 2 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + x b ax dx d =

[

2_sin( ₎

]

₀ ! 2 1 = + −a ax b _x =-! 2 1 a2 sin(b) = ! 2 1 a2 sin ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ b} 2 2π k=3 için W(3) = 0 3 3 ) sin( ! 3 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + x b ax dx d =

[

3_cos( ₎

]

₀ ! 3 1 = + −a ax b _x = =-! 3 1 a3_cos(b)= ! 3 1 a3_sin _⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ b} 2 3π bu değerlerden anlaşılacağı gibi

W(k)= ! k ak sin ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ b} k 2 π dır.

(27)

Teorem 3.1.17. [Abdel-Halim, 2004]

Tek bileşenli w(x) fonksiyonunu alalım. a,b∈R olmak üzere eğer w(x)=cos(ax+b)

W(k)= ! k ak cos ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ b} k 2 π eşitliği sağlanır., Teorem 3.1.18. [Arikoglu, 2004]

Tek bileşenli w(x) ve u(x) fonksiyonlarını alalım. k∈N olmak üzere eğer w(x)=

∫

x x dt t u 0 ) (

ise W(k) ve U(k) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere W(k)= k k U( −1) eşitliği sağlanır. İspat

İspata geçmeden önce analizden iyi bilinen bir yardımcı teorem verelim. Yardımcı Teorem 3.1.

f: [a,b]→R fonksiyonu integrallenebilir olsun. [a,b] üzerinde F(x)=

∫

x a dt t f( )

Eşitliği ile tanımlanan F fonksiyonu f nin sürekli olduğu her noktada türevlidir ve

F′(x)=f(x)

dir.

(28)

(k+1)W(k+1)=U(k) W(k+1)= ) 1 ( ) ( + k k U W(k)= k k U( −1) Teorem 3.1.19. [Arikoglu, 2004]

Tek bileşenli w(x), u(x) ve v(x) fonksiyonlarını alalım.Eğer

w(x)= v(x)

∫

x x dt t u 0 ) (

ise W(k), U(k) ve V(k) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere W(k)= V(k)⊗ k k U( −1) eşitliği sağlanır. Teorem 3.1.20. [Arikoglu, 2004]

w(x)=

∫

x x dt t v t u 0 ) ( ) (

ise W(k), U(k) ve V(k) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere W(k)= k k V k U( −1)⊗ ( −1) eşitliği sağlanır.

(29)

3.2. İki Boyutlu Diferansiyel Dönüşüm Yöntemi

Tanım 3.2.1. [Zhou, 1986]

İki bileşenli w(x,y) fonksiyonunun diferansiyel dönüşüm fonksiyonu W(k,h) olmak üzere, w(x,y)’ nin iki boyutlu diferansiyel dönüşümü

0 0 ) , ( ! ! 1 ) , ( = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ = y x h k h k y x w y x h k h k W (3.2.1) olarak tanımlanır. Tanım 3.2.2. [Zhou, 1986]

W(k,h) dönüşüm fonksiyonunun tersi; diferansiyel ters dönüşüm fonksiyonu,

∑∑

∞ = ∞ = = 0 0 ) , ( ) , ( k h h k y x h k W y x w (3.2.2)

biçimde tanımlanır. (3.2.1) ve (3.2.2) eşitlikleri dikkate alınarak aşağıdaki (3.2.3) eşitliği elde edebiliriz.

∑∑

∞ = ∞ = ₌= + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ = 0 0 0 0 ) , ( ! ! 1 ) , ( k h h k y x h k h k y x y x w y x h k y x w (3.2.3)

(3.2.1) ve (3.2.2) denklemleri kullanılarak temel matematiksel operasyonlar yardımıyla iki boyutlu diferansiyel dönüşümü için aşağıdaki teoremler ispat edilebilir.

Teorem 3.2.1. [Zhou, 1986]

İki bileşenli w(x,y), u(x,y) ve v(x,y) fonksiyonlarını alalım. Eğer

w(x,y)=u(x,y) ± v(x,y)

ise sırasıyla W(k,h), U(k,h) ve V(k,h) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k,h)=U(k,h) ± V(k,h)

(30)

İspat u(x,y)→U(k,h)= 0 0 ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x u y x h k ve v(x,y)→V(k,h)= 0 0 ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x v y x h k

olmak üzere w(x,y)=u(x,y) ± v(x,y) ise

W(k,h)=

(

)

0 0 ) , ( ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ± ∂ ∂ ∂ y x h k h k y x v y x u y x h k

diferansiyel fonksiyonun 1. özelliğinden

W(k,h)= 0 0 ) , ( ) , ( ! ! 1 = = + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ ± ∂ ∂ ∂ y x h k h k h k h k y x v y x y x u y x h k = 4 4 4 4 3 4 4 4 4 2 1 ) , ( 0 0 ) , ( ! ! 1 h k U y x h k h k y x u dy dx d h k = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ± 4 4 4 4 3 4 4 4 4 2 1 ) , ( 0 0 ) , ( ! ! 1 h k V y x h k h k y x v dy dx d h k = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ W(k,h)=U(k,h) ± V(k,h) Teorem 3.2.2. [Zhou, 1986]

İki bileşenli w(x,y) ve u(x,y) fonksiyonlarını alalım. c∈R olmak üzere eğer w(x,y)=c u(x,y)

ise sırasıyla W(k,h) ve V(k,h) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k,h)=cU(k,h) eşitliği sağlanır. İspat u(x,y)→U(k,h)= 0 0 ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x u y x h

(31)

W(k,h)= 0 0 ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x u c y x h k

olur. Diferansiyel fonksiyonun 1. özelliğinden

W(k,h)= 0 0 ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x u y x h k c = cU(k,h) olarak bulunur. Teorem 3.2.3. [Zhou, 1986]

İki bileşenli w(x,y) ve u(x,y) fonksiyonlarını alalım. Eğer

w(x,y)= x y x u ∂ ∂ ( , )

ise sırasıyla W(k,h) ve U(k,h) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k,h)=(k+1)U(k+1,h) eşitliği sağlanır. İspat u(x,y)→U(k,h)= 0 0 ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x u y x h k olduğunu biliyoruz. w(x)= dx x du( ) ise W(k,h)= 0 0 ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ ∂ y x h k h k y x u x y x h

k diferansiyel fonksiyonunun 2. özelliğinden

W(k,h)= 0 0 1 1 ) , ( ! ! 1 = = + + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x u y x h k = 4 4 4 4 3 4 4 4 4 2 1 ) 1 ( 0 1 1 ) ( )! 1 ( 1 ) 1 ( + = + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + k U x k k x u dx d k k =(k+1)U(k+1,h) Teorem 3.2.4. [Ayaz, 2003]

(32)

w(x,y)= y y x u ∂ ∂ ( , )

W(k,h)=(h+1)U(k,h+1)

eşitliği sağlanır.

Teorem 3.2.5. [Ayaz, 2003]

İki bileşenli w(x,y) ve u(x,y) fonksiyonlarını alalım. r,s∈N olmak üzere eğer

w(x,y)= _r _s s r y x y x u ∂ ∂ ∂ + ₍ _, ₎

W(k,h)=(k+1)(k+2)...(k+r)(h+1)(h+2)...(h+s) U(k+r,h+s)

Teorem 3.2.5. [Ayaz, 2003]

w(x,y)=u(x,y)v(x,y)

W(k,h)=

∑∑

= = − − k r h s s r k U s h r V 0 0 ) , ( ) , ( eşitliği sağlanır. İspat u(x,y)→U(k,h)= 0 0 ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x u y x h k ve

(33)

v(x,y)→V(k,h)= 0 0 ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x v y x h k

olmak üzere w(x,y)=u(x,y)v(x,y) ise

W(k,h)=

(

)

0 0 ) , ( ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x v y x u y x h k

olur. Diferansiyel fonksiyonun 3. özelliğinden

W(k,h) =

(

)

0 0 ) , ( ) , ( ! ! 1 = = + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ y x h k h k y x v y x u y x h k = ( , ) ( , ) ... 1 ) , ( ) , ( 0 ! ! 1 1 1 + ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎜⎜ ⎝ ⎛ ∂ ∂ − − y x u x y x v x k y x u x y x v k y h k k k k k h h 0 0 1 1 ) , ( ) , ( ) , ( ) , ( 1 = = − − ⎟⎟ ⎠ ⎞ ∂ ∂ + ∂ ∂ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + y x k k k k y x u x y x u y x u x y x v x k k = ( , ) ( , ) ... 1 0 ) , ( ) , ( 0 0 ! ! 1 1 1 1 + ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ∂ ∂ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − − y x u y x y x v y h k y x u x y x v y h k h k k k h h k k h h ... ) , ( ) , ( 1 1 ) , ( ) , ( 1 0 1 1 1 1 1 + ∂ ∂ ∂ ∂ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ∂ ∂ ∂ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − − + y x u y x y x v x y h k y x u x y x v x y h k k k h h k k h h 0 0 ) , ( ) , ( ... ) , ( ) , ( = = − + − − + − ⎟⎟ ⎠ ⎞ ∂ ∂ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + ∂ ∂ ∂ ∂ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ y x h h k k s r k s r k r s h r s h y x u y y x v x h h k k y x u y x y x v x y s h r k = 0 0 0 0 ) , ( ) , ( ! ! 1 = = = = − + − − + − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ ∂ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

∑∑

y x k r h s s h r r s h s r k s r k y x v y x y x u y x s h r k h k = 0 0 0 0 ) , ( ) , ( ! )! ( 1 ! )! ( 1 = = − + − − + − = = ⎥⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ ∂ ∂ ∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − −

∑∑

y x s h r r s h s r k s r k k r h s y x v y x y x u y x s h r k r s h s r k W(k,h)=

∑∑

= = − − k r h s s r k U s h r V 0 0 ) , ( ) , ( Teorem 3.1.6. [Ayaz, 2003]

İki bileşenli w(x) fonksiyonunu alalım. m∈Z olmak üzere eğer w(x,y)=xmyn

(34)

ise sırasıyla W(k) verilen fonksiyonun diferansiyel dönüşüm fonksiyonu olmak üzere W(k,h)= ⎩ ⎨ ⎧ = = = − − halde aksi n h ve m k n h m k , 0 , 1 ) , ( δ eşitliği sağlanır. Teorem 3.2.7. [Ayaz, 2003]

w(x,y)= u(x,y) ₂ 2 ₍ _, ₎ x y x v ∂ ∂

W(k,h)=

∑∑

= = + − + − k r h s r k r k 0 0 ) 1 )( 2 ( U(r,h-s)V(k-r+2,s) eşitliği sağlanır. Teorem 3.2.8. [Ayaz, 2003]

w(x,y)= x y x v x y x u ∂ ∂ ∂ ∂ ( , ) ( , )

W(k,h)=

∑∑

= = + − − + + − + k r h s s r k V s h r U r k r 0 0 ) , 1 ( ) , 1 ( ) 1 )( 1 ( eşitliği sağlanır. Teorem 3.2.9. [Ayaz, 2003]

w(x,y)= y y x v y y x u ∂ ∂ ∂ ∂ ( , ) ( , )

(35)

W(k,h)=

∑∑

= = + − + − + − + k r h s s r k V s h r U s h s 0 0 ) 1 , ( ) 1 , ( ) 1 )( 1 ( eşitliği sağlanır. Teorem 3.2.10. [Ayaz, 2003]

w(x,y)= y y x v x y x u ∂ ∂ ∂ ∂ ( , ) ( , )

W(k,h)=

∑∑

= = + − + − + − + − k r h s s h r V s r k U s h r k 0 0 ) 1 , ( ) , 1 ( ) 1 )( 1 ( eşitliği sağlanır. Teorem 3.2.11. [Ayaz, 2003]

İki bileşenli w(x,y), u(x,y), v(x,y) ve s(x,y) fonksiyonlarını alalım. Eğer

w(x,y)=u(x,y)v(x,y)s(x,y)

ise sırasıyla W(k,h), U(k,h), V(k,h) ve S(k,h) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k,h)=

∑∑∑∑

= − = = − = − − − − k r r k t h s s h p p t r k S s t V p s h r U 0 0 0 0 ) , ( ) , ( ) , ( eşitliği sağlanır. Teorem 3.2.12. [Ayaz, 2003]

İki bileşenli w(x,y), u(x,y), v(x,y) ve s(x,y) fonksiyonlarını alalım. Eğer

w(x,y)= u(x,y)v(x,y) ₂ 2 ₍ _, ₎ x y x s ∂ ∂

ise sırasıyla W(k,h), U(k,h), V(k,h) ve S(k,h) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k,h)=

∑∑∑∑

= − = = − = + − − + − − k r r k t h s s h p t r k t r k 0 0 0 0 ) 2 )( 2 ( U(r,h-s-p)V(t,s)S(k-r-t+2,p) eşitliği sağlanır.

(36)

3.3. Üç Boyutlu Diferansiyel Dönüşüm Yöntemi

Tanım 3.3.1. [Ayaz, 2004]

Üç bileşenli fonksiyon w(x,y,t) olmak üzere, w(x,y,t)’nin üç boyutlu diferansiyel dönüşümü W(k,h,m)= ) 0 , 0 , 0 ( ) , , ( ! ! ! 1 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ ∂ + + t y x w t y x m h k k h m m h k (3.3.1)

olarak tanımlanır. Burada daha öncede olduğu gibi, dikkat edilecek olursa dönüşüm fonksiyonunu temsil etmek için büyük harfler, orijinal fonksiyonu ifade etmek için de küçük harfler kullanılmıştır.

Tanım 3.3.2. [Ayaz, 2004]

W(k,h,m) dönüşüm fonksiyonunun tersi; diferansiyel ters dönüşüm

fonksiyonu, w(x,y,t)=

∑∑∑

∞ = ∞ = ∞ = 0 0 0 ) , , ( k h p m h k t y x m h k W (3.3.2) olarak tanımlanır.

İki boyutlu diferansiyel dönüşüm yönteminde olduğu gibi (3.2.3) eşitliğine benzer şekilde (3.3.1), (3.3.2) denklemleri dikkate alınırsa,

w(x,y,t)=

∑∑∑

∞ = ∞ = ∞ = + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ ∂ 0 0 0 ₍₀_,₀_,₀₎ ) , , ( ! ! ! 1 k h p m h k m h k m h k t y x t y x w t y x m h k (3.3.3) yazabiliriz.

Üç boyutlu diferansiyel dönüşüm fonksiyonu için aşağıdaki teoremler ispat edilebilir.

Teorem 3.3.1. [Ayaz, 2004]

Üç bileşenli w(x,y,t), u(x,y,t) ve v(x,y,t) fonksiyonlarını alalım. Eğer

(37)

ise sırasıyla W(k,h,m), U(k,h,m) ve V(k,h,m) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k,h,m)=U(k,h,m) ± V(k,h,m)

Teorem 3.3.2. [Ayaz, 2004]

Üç bileşenli w(x,y,t) ve u(x,y,t) fonksiyonlarını alalım. c∈R olmak üzere

eğer

w(x,y,t)=c u(x,y,t)

ise sırasıyla W(k,h,m) ve U(k,h,m) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k,h,m)=c U(k,h,m)

Teorem 3.3.3. [Ayaz, 2004]

Üç bileşenli w(x,y,t) ve u(x,y,t) fonksiyonlarını alalım. Eğer

w(x,y,t)= x t y x u ∂ ∂ ( , , )

W(k,h,m)=(k+1)U(k+1,h,m)

Teorem 3.3.4. [Ayaz, 2004]

w(x,y,t)= y t y x u ∂ ∂ ( , , )

W(k,h,m)=(h+1)U(k,h+1,m)

(38)

Teorem 3.3.5. [Ayaz, 2004]

w(x,y,t)= _r _s _p p s r t y x t y x u ∂ ∂ ∂ ∂ + + ₍ _, _, ₎

W(k,h,m)= ! )! ( k r k+ ! )! ( h s h+ ! )! ( m p m+ U(k+r,h+s,m+p) eşitliği sağlanır. Teorem 3.3.6. [Ayaz, 2004]

w(x,y)=u(x,y,t)v(x,y,t)

W(k,h,m)=

∑∑∑

= = = − − − k r h s m p p s r k V p m s h r U 0 0 0 ) , , ( ) , , ( eşitliği sağlanır.

Teorem 3.3.7. [Keskin Y,2005]

w(x,y,t)= x ∂ ∂ u(x,y,t) y ∂ ∂ v(x,y,t)

W(k,h,m)=

∑∑∑

= = = − + − + − + − + − k r h s m p p m s h r V p s r k U s h r k 0 0 0 ) , 1 , ( ) , , 1 ( ) 1 )( 1 ( eşitliği sağlanır.

(39)

3.4. n Boyutlu Diferansiyel Dönüşüm Yöntemi

Tanım 3.4.1.

n bileşenli fonksiyon w(x1,x2,...,xn) olmak üzere, w(x1,x2,...,xn)’nin n boyutlu diferansiyel dönüşümü W(k1,k2,...,kn)= ! !... ! 1 2 1 k kn k 0 0 0 2 1 2 1 ... 2 1 2 1 2 1 ... ) ,..., , ( = = = + + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ ∂ n n n x x x k n k k n k k k x x x x x x w (3.3.1)

olarak tanımlanır. Burada daha öncede olduğu gibi, dikkat edilecek olursa dönüşüm fonksiyonunu temsil etmek için büyük harfler, orijinal fonksiyonu ifade etmek için de küçük harfler kullanılmıştır.

Tanım 3.4.2.

W(k1,k2,...,kn) dönüşüm fonksiyonunun tersi; diferansiyel ters dönüşüm fonksiyonu, w(x1,x2,...,xn) =

∑ ∑ ∑

∞ = ∞ = ∞ = 0 0 0 2 1 2 1 1 2 2 1 ... ... k k k k n k k n n n x x ) x ,...,k ,k W(k (3.3.2) olarak tanımlanır.

Üç boyutlu diferansiyel dönüşüm yönteminde olduğu gibi (3.2.3) eşitliğine benzer şekilde (3.3.1), (3.3.2) denklemleri dikkate alınırsa,

w(x1,x2,...,xn) =

∑ ∑ ∑

∞ = ∞ = ∞ = = = = + + + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ ∂ ∂ 0 0 0 2 1 0 0 0 2 1 2 1 ... 2 1 1 2 2 1 2 1 2 1 2 1 ... ... ) ,..., , ( ! !... ! 1 ... k k k k n k k x x x k n k k n k k k n n n n n n x x x x x x x x x w k k k (3.3.3) yazabiliriz.

n boyutlu diferansiyel dönüşüm fonksiyonu için aşağıdaki teoremler ispat

edilebilir.

Teorem 3.4.1. [Kurnaz, 2005]

(40)

w(x1,x2,...,xn)= u(x1,x2,...,xn)± v(x1,x2,...,xn)

ise sırasıyla W(k1,k2,...,kn), U(k1,k2,...,kn) ve V(k1,k2,...,kn) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k1,k2,...,kn)= U(k1,k2,...,kn)± V(k1,k2,...,kn) eşitliği sağlanır.

Teorem 3.4.2. [Kurnaz, 2005]

n bileşenli w(x1,x2,...,xn) ve u(x1,x2,...,xn) fonksiyonlarını alalım. c∈R olmak üzere eğer

w(x1,x2,...,xn)= c u(x1,x2,...,xn)

ise sırasıyla W(k1,k2,...,kn) ve U(k1,k2,...,kn) verilen fonksiyonların diferansiyel dönüşüm fonksiyonları olmak üzere

W(k1,k2,...,kn)= c U(k1,k2,...,kn) eşitliği sağlanır.

Teorem 3.4.3. [Kurnaz, 2005]

n bileşenli w(x1,x2,...,xn) ve u(x1,x2,...,xn) fonksiyonlarını alalım. Eğer

w(x1,x2,...,xn)= 1 x ∂ ∂ u(x1,x2,...,xn)

W(k1,k2,...,kn)= (k+1) U(k1+1,k2,...,kn) eşitliği sağlanır.

Teorem 3.4.4. [Kurnaz, 2005]

n bileşenli w(x1,x2,...,xn) ve u(x1,x2,...,xn) fonksiyonlarını alalım. Eğer

w(x1,x2,...,xn)= n n r n r r r r r x x x ∂ ∂ ∂ ∂ + + + ... 2 1 2 1 2 1 ... u(x1,x2,...,xn)

(41)

W(k1,k2,...,kn)= ! )! ( 1 1 1 k r k + ! )! ( 2 2 2 k r k + ... ! )! ( n n n k r k + U( k1+r1, k2+r2, ..., kn+rn ) eşitliği sağlanır.