Kalın cidarlı borularda dış yüzeyde periyodik değişen dış ortam sıcaklığı etkisinde taşınım sınır şartı ile geçici rejim birleşik ısı transferi

T.C.

SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ

KALIN CĠDARLI BORULARDA DIġ YÜZEYDE PERĠYODĠK DEĞĠġEN DIġ ORTAM SICAKLIĞI ETKĠSĠNDE TAġINIM SINIR ġARTI ĠLE GEÇĠCĠ REJĠM BĠRLEġĠK

ISI TRANSFERĠ

HAVVA DEMĠRPOLAT

DOKTORA TEZĠ

Makine Mühendisliği Anabilim Dalı

NĠSAN,2015 KONYA Her Hakkı Saklıdır

ÖZET

DOKTORA TEZĠ

KALIN CĠDARLI BORULARDA DIġ YÜZEYDE PERĠYODĠK DEĞĠġEN DIġ ORTAM SICAKLIĞI ETKĠSĠNDE TAġINIM SINIR ġARTI ĠLE GEÇĠCĠ

REJĠM BĠRLEġĠK ISI TRANSFERĠ

HAVVA DEMĠRPOLAT

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Makine Mühendisliği Anabilim Dalı

DanıĢman: Prof.Dr. Saim KOÇAK

2015, 115 Sayfa

Jüri

Prof. Dr. Saim KOÇAK Prof.Dr. ġefik BĠLĠR Doç. Dr. Yüksel KAPLAN Doç. Dr. Ali KAHRAMAN Yrd. Doç. Dr. ġ.UlaĢ ATMACA

Özet

Kalın cidarlı borularda, laminer akış ısıl gelişme bölgesi geçici rejim birleşik ısı transferi, iki boyutlu cidar ve eksenel akışkan iletimi dikkate alınarak incelenmiştir. Problem iki bölgeli ve başlangıçta eşit sıcaklıkta olan bir boruda, hidrodinamik olarak gelişmiş akış için, alt akış bölgesinde zamanla periyodik olarak değişen dış ortam sıcaklığı sınır şartı ile ele alınmıştır. Problem bir sonlu farklar yöntemi ile sayısal olarak çözülmüş ve problemi tanımlayan beş boyutsuz parametrenin, cidar kalınlık oranı, cidar-akışkan ısı iletkenlik katsayısı oranı, cidar-akışkan ısıl yayılım katsayısı oranı, Biot sayısı ve Peclet sayısı ile açısal frekansın ısı transferi karakteristikleri üzerindeki etkilerini belirleyebilmek için parametrik bir çalışma yapılmıştır.

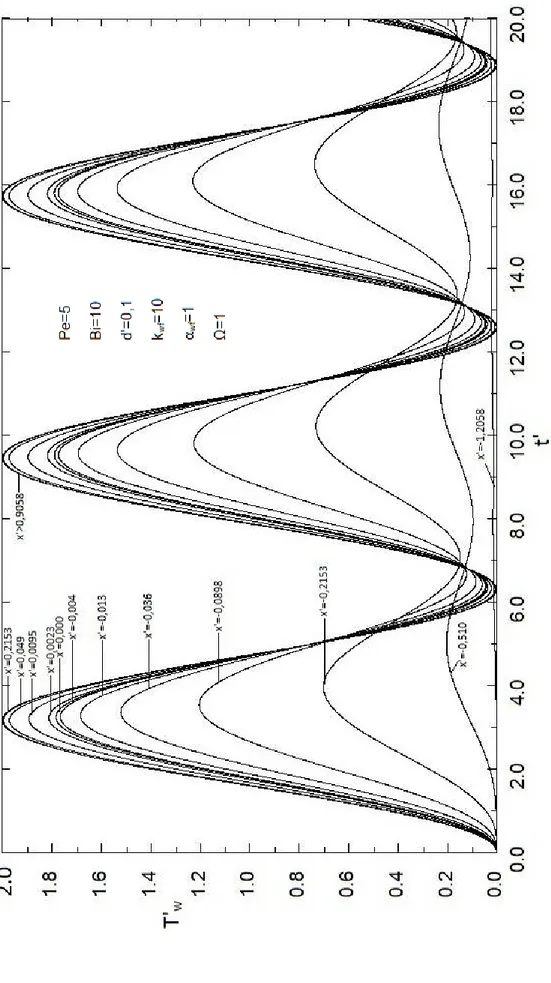
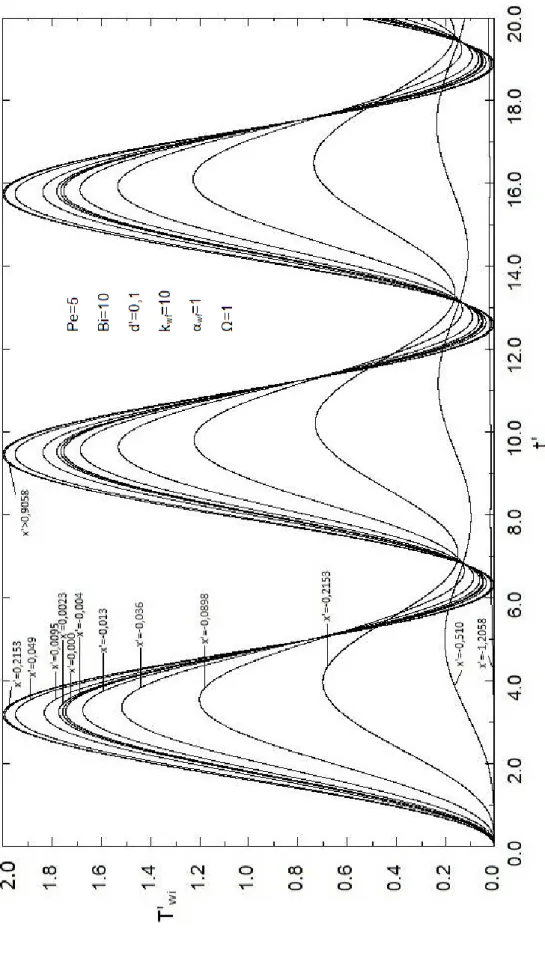
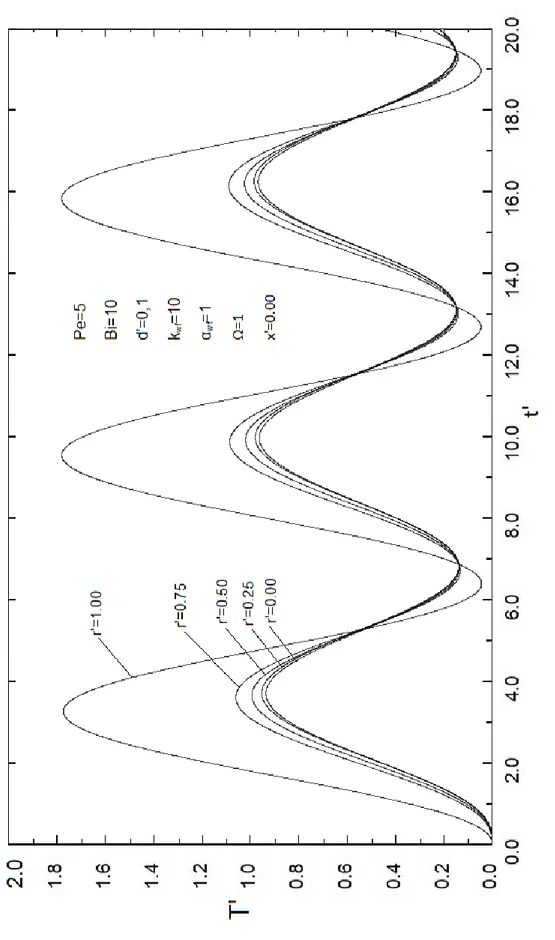
Gerek cidar ve gerekse akışkan eksenel iletimi nedeniyle üst akış bölgesine doğru önemli miktarda ısı transfer edilmektedir. Isı transferi karakteristiklerinin cidar dış yüzeyindeki periyodik sıcaklık değişimine benzer şekilde zamanla periyodik olarak değiştiği görülmüştür. Sonuçlar parametre değerlerinden ve açısal frekanstan büyük ölçüde etkilenmektedir.

Anahtar Kelimeler: Borularda birleşik ısı transferi, Laminer akış ısı transferi, Zamanla periyodik değişen sınır şartı, Akışkan eksenel iletimi.

ABSTRACT

Ph.D THESIS

TRANSIENT CONJUGATED FORCED CONVECTION HEAT TRANSFER IN THICK WALLED PIPES WITH PERIODIC CONVECTIVE BOUNDARY

CONDITIONS

Havva DEMĠRPOLAT

The GraduateSchool of Natural and Applied Science of SelcukUniversity The Degree of Doctor of Philosophy in Mechanical Engineering

Advisor: Prof.Dr. Saim KOÇAK

2015, 115 Page

Jüri

Prof. Dr. Saim KOÇAK Prof.Dr. ġefik BĠLĠR Assoc.Prof. Yüksel KAPLAN Assoc.Prof. Dr. Ali KAHRAMAN

Assis.Prof.Dr.ġ.UlaĢ ATMACA Abstract:

Transient conjugated heat transfer for thermally developing laminar flow in thick walled pipes is analysed involving two-dimensional wall and fluid axial conduction. A two-regional pipe is considered which is initially isothermal and the problem is handled for hydrodynamically developed flow with periodically time-varying external fluid temperature in the downstream region. The problem is solved numerically by a finite-difference method and a parametric study is done to analyse the effects of five defining parameters namely; wall thickness ratio, wall-to-fluid conductivity ratio, wall-to-fluid thermal diffusivity ratio, Biot number and the Peclet number and also the effect of angular frequency.

Considerable amount of heat is transferred through the upstream side due to both wall and fluid axial conduction. It is seen that the heat transfer chracteristics are changhing periodically in time in the similar manner to the periodic change in outside fluid temperatue. The results are found to be sensitive to the parameter values and angular frequency.

Key Words: Conjugate heat transfer in pipes, Laminar flow heat transfer, Time periodic boundary condition, Fluid axial conduction.

TEġEKKÜR

Bu çalışmada yardımlarından dolayı danışmanım Prof.Dr. Saim KOÇAK’a, vermiş olduğu tüm destek ve yardımlarından dolayı saygıdeğer hocam Prof.Dr. Şefik BİLİR’e, ve her türlü konuda yardımlarını esirgemeyen Yrd.Doç.Dr. Ali ATEŞ'e, Doç.Dr Ali KAHRAMAN’a, Yrd.Doç.Dr Aziz Hakan ALTUN’a,teşekkür ederim. Ayrıca tez çalışmam boyunca beni anlayışla karşılayan ve sabır gösteren eşime ve kızıma sonsuz teşekkür ederim.

Havva DEMİRPOLAT KONYA–2015

SĠMGELER VE KISALTMALAR

Simge Açıklama

a ayrıklaştırılmış denklem katsayısı

A alan

b kaynak (source) terim (denklem 3.32.f)

Bi Biot sayısı

cp özgül ısı

d cidar kalınlığı

D1, D2 integral sabitleri (denklem 3.12, 3.14)

f kütlesel kuvvet, ağırlık faktörü (denklem 2.1)

Fs güvenlik faktörü (denklem 4.5)

Fo Fourier sayısı

h ısı taşınım katsayısı, düğüm noktaları arası mesafe (denklem 4.1) J ısı akısı (denklem 3.6) k ısı iletkenlik katsayısı K Pe2 (1-r’2) (denklem 3.11) L uzunluk Nu Nusselt sayısı

p basınç, analiz seviyesi (denklem 4.3)

Pe Peclet sayısı

Pr Prandtl sayısı

q ısı akısı

r radyal koordinat, yarı çap, düğüm noktaları arasındaki mesafelerin oranı (denklem 4.1)

Re Reynolds sayısı

t zaman

T sıcaklık

T1 alt akış bölgesi dış ortam sıcaklığı

To sistemin başlangıç sıcaklığı

v radyal hız

w açısal hız

x eksenel koordinat

α ısıl yayılım katsayısı

δr radyal konum farkı

δx eksenel konum farkı

r radyal basamak uzunluğu

t zaman aralığı

T periyodik sıcaklık değişim genliği

x eksenel basamak uzunluğu

ε değer farkı (denklem 4.2)

 değer oranı (denklem 4.6)

θ açısal koordinat  dinamik viskozite  kinematik viskozite  yoğunluk  viskoz sönüm faktörü ω açısal frekans

Ω Boyutsuz açısal frekans

Alt Ġndisler

b yığık

c kesit

e, w, n, s e, w, n, s kontrol hacim yüzeylerinde

E, W, N, S,P E, W, N, S, P düğüm noktalarında

f akışkan

i ara yüzey (iç yüzey)

L uzunluk

m ortalama

o dış yüzey

r radyal

w cidar

wi cidar akışkan ara yüzeyi

wo cidar dış yüzeyi

x eksenel

Üst Ġndisler

' boyutsuz

0 önceki zaman adımında

11 ĠÇĠNDEKĠLER TEZ BĠLDĠRĠMĠ ... ĠĠĠ ÖZET. ... ĠV ABSTRACT ... VĠ TEġEKKÜR ... ĠĠX SĠMGELER VE KISALTMALAR ... ĠX 1. GĠRĠġ ... 13

1.1 Geçici Rejim, BirleĢik Isı Transferi ve Eksenel Ġletim ... 13

1.2. Kaynak AraĢtırması ... 14 1.3. Problemin Tanımı ... 17 2. TEORĠK ESASLAR ... 18 2.1 Temel Denklemler ... 18 2.2. BaĢlangıç ve Sınır ġartları ... 20 2.3 BoyutsuzlaĢtırma ... 22 2.3.1 Boyutsuz Parametreler ... 22

2.3.2 Enerji Denklemlerinin Boyutsuzlaştırılması ... 24

2.3.3 Başlangıç ve Sınır Şartlarının Boyutsuzlaştırılması ... 26

3. SAYISAL ÇÖZÜMLEME ... 32

3.1 Ağ Sistemi ve Düğüm Noktası Sayısı ... 32

3.2. Diferansiyel Denklemlerin AyrıklaĢtırılması ... 33

12

3.2.2 Akışkan Tarafı Diferansiyel Denklemlerin Ayrıklaştırılması ... 35

3.2.3 Başlangıç ve Sınır Şartlarının Ayrıklaştırılması ... 41

3.3 Çözüm ... 51

3.4 Program AkıĢ ġeması ... 53

4. AĞDAN BAĞIMSIZLIK (GCI) ANALĠZĠ ... 54

5. SONUÇLAR VE TARTIġMA ... 58

6. SONUÇ ... 110

7. KAYNAKLAR ... 112

EKLER ... 114

Ek 1. Sayısal Türev ve Sayısal Ġntegral ... 114

13 1. GĠRĠġ

1.1. Geçici Rejim, BirleĢik Isı Transferi ve Eksenel Ġletim

Bir ısı transferi probleminin incelenebilmesi için ortamın sıcaklık dağılımı bilinmelidir. Süreksiz ya da geçici (Transient veya Unsteady) sıcaklık alanı, bir ortamda sıcaklığın sadece bir noktadan diğerine değil aynı zamanda zamana bağlı olarak değiştiği durumdur. Geçici rejimde ısı geçişine; yeryüzü sıcaklık değişimi, gün boyunca ve mevsimsel periyotlarda binalarda meydana gelen sıcaklık değişimi, nükleer yakıt elemanlarında meydana gelen sıcaklık değişimi örnek gösterilebilir. Geçici rejim ısı transferi periyodik problemler ve periyodik olmayan problemler olarak iki grupta ele alınabilirler. Periyodik problemlerde herhangi bir mesafede ya da zamanda birbirini takip eden döngüler benzerdir.

Birleşik ısı transferi, genellikle cidar ile akışkan arasında ısı değişiminin olduğu yerlerde ortaya çıkan bir problemdir. Bu konu ile ilgili yapılmış çalışmaların çoğunda, boru cidarının dış yüzeyinde sınır şartı olarak, sabit yüzey ısı akısı veya sabit yüzey sıcaklığı sınır şartları kullanılmıştır. Ancak uygulamada bu iki sınır şartından başka üçüncü bir sınır şartı ile de karşılaşılır. Boru içinden akan akışkan genellikle boru dış yüzeyinden doğal veya zorlanmış taşınım ile ısı kaybına veya kazancına maruz kalır. Bu konu boru akışında zorlanmış taşınım ile ısı transferi olarak ele alındığı takdirde ısı transferinde cidarın kalınlığı ve ısı iletkenliğine ek olarak akışkanın fiziksel özelliklerinin ve akış karakterinin de etki olduğu görülür. Böylece problem tipik bir birleşik ısı transferi problemi olarak değerlendirilir.

Isı transferi analizlerinde genel olarak, akışkan-cidar ara yüzeyinde sıcaklık veya ısı akısı hesaplanır. Bunun için enerji denkleminin akış bölgesinde çözülmesi gerekir. Akışkan-cidar ara yüzeyinde önceden bilinmeyen koşullar, katı cidarın boyutlarına ve fiziksel özelliklerine bağlı olduğu gibi, akışkanın da akış şartlarına ve fiziksel özelliklerine bağlıdır. Cidardaki ısı iletimini ve akışkan içindeki taşınım ile ısı transferini birleştiren bu tip problemler literatürde “birleşik ısı transferi (conjugate heat transfer)”adı altında incelenir. Cidar kalın ve cidar malzemesinin ısı iletkenlik katsayısı

14

küçük ise ısı transferi büyük ölçüde etkilenir. Bu nedenle conjugation (iletim ve taşınımın aynı anda olması) bu tür problemlerde dikkate alınmalıdır.

Boru veya kanallarda laminer akış geçici rejim ısı transferi birçok araştırmacı tarafından sınır ya da giriş şartlarında ani veya periyodik değişme halinde incelenmiştir. Çoğu araştırmacı cidar iletiminin göz önünde bulundurulmadığı ince cidarlı borular için problemi ele almışlardır. Bu sayede dış yüzeydeki koşul iç yüzeyde de aynen geçerli olarak kabul edilebilir. Kalın cidarlı borular ise iki bölgeli olarak ele alınmalıdır ve ısı transferi karakteristikleri üst ve alt akış bölgeleri için ayrıca belirlenmelidir. Öte yandan akışkan eksenel iletiminin etkisi sadece ısıl gelişme bölgesinde görülür ve ısıl olarak gelişmiş bölgede yerel ısı transferi karakteristiklerini etkilemez.

Bu çalışmada, kalın cidarlı borularda, laminer akış ısıl gelişme bölgesi geçici rejim birleşik ısı transferi, zamanla periyodik olarak değişen dış ortam sıcaklığı sınır şartı altında, iki boyutlu cidar ve eksenel akışkan iletimi dikkate alınarak incelenmiştir.

1.2. Kaynak AraĢtırması

Boru ve kanallarda laminer akış geçici rejim ısı transferi pek çok araştırmacı tarafından sınır ya da giriş şartlarında ani değişim veya periyodik değişme halinde ele alınmıştır. İnce cidarlı borular için ele alınan problemlerde genellikle cidar iletimi her iki yön için de ihmal edilmiştir. Böylece dış yüzeydeki koşul iç yüzeyde de geçerli olarak kabul edilmiştir. Birleşik olarak adlandırılan problemlerde ise cidar-akışkan ara yüzeyindeki koşul önceden bilinemediği için enerji denklemleri hem cidar hem de akışkan bölgesi için ara yüzeyde sıcaklıkların ve ısı akılarının sürekliliği şartı ile birlikte çözülmelidir.

Periyodik olarak değişen çevre sıcaklığı sınır şartı ile boru ve kanallarda birleşik ısı transferi problemleri ile ilgili geniş bir kaynak araştırması Barletta ve Zanchini (1995) tarafından yapılmıştır. Periyodik rejim problemlerine ait ilk çalışmalar Patankar ve Sparrow (1978) tarafından yapılmıştır. Çalışmalarında kanal içinde zorlanmış taşınımda periyodik olarak değişen dış yüzey sıcaklığı sınır şartı ile bir ısı transferi problemi çözmüşlerdir. Eksenel iletim ve viskoz sönümün etkilerini ihmal ederek değişmeyen akışkan ve cidar özellikleri ile, hidrodinamik olarak gelişmiş akış için enerji denklemini analitik olarak çözmüşlerdir.

15

Faghri ve Welty (1978) Dış ortamda sinüzoidal değişen akışkan sıcaklığı etkisindeki dairesel kesitli bir kanalda, eksenel iletimi dikkate alarak bir ısı transferi problemini çözmüşlerdir. Sınır şartlarına bağlı olarak yerel ve ortalama Nusselt sayılarını belirlemişlerdir. Faghri ve Sparrow (1980) ince cidarlı bir kanalda ısı transferi problemini yüzeyde sinüzoidal değişen ısı akısı sınır şartı ile analitik olarak çözmüşlerdir. Çalışmalarında Foruier transform yöntemi ile düşük Peclet sayılı akışlar için yerel ısı transferi karakteristiklerini ve Peclet sayısındaki değişimin eksenel iletime etkisini belirlemişlerdir. Pearlstein ve Dempsey (1988), çalışmalarında düşük Peclet sayılı, hidrodinamik olarak gelişmiş laminer akış için bir problem çözmüşlerdir. Ebadian ve Zhang (1990) laminer gelişmiş akış bölgesinde eksenel iletimi dikkate alarak yüzeyde periyodik olarak değişen sıcaklığın etkisinde boru içi akış için ısı transferi problemini analitik olarak çözmüşlerdir. Peclet sayısının etkisini sıfır ve sonsuz aralığında incelemişlerdir.

Barletta ve Zanchini (1995) ince cidarlı, laminer ve gelişmiş akış için yüzeyde sinüzoidal değişen ısı akısının etkisindeki bir boru için enerji denklemini çözmüşlerdir. Eksenel iletim ve viskoz sönüm etkilerini ihmal etmişlerdir. Barletta ve Schio (1999), problemi ince cidarlı laminer ve gelişmiş akış için yüzeyde sinüzoidal değişen ısı akısı etkisindeki bir boru için viskoz sönüm etkisini dikkate alarak çözmüşlerdir. Barletta ve Schio (2000) benzer bir problemi sinüzoidal olarak değişen yüzey sıcaklığı ve ısı akısı sınır şartlarında eksenel iletimin etkilerini dikkate alarak analitik olarak çözmüşlerdir. Elde ettikleri yerel ve ortalama Nusselt sayılarını bir önceki çalışmalarıyla kıyaslamışlardır. Barletta ve Zanchini (2003) eğimli bir paralel plakalı kanalda, plakalardan birinde periyodik olarak değişen, diğerinde ise sabit yüzey sıcaklığı sınır şartı ile bir ısı transferi problemini analitik olarak çözmüşlerdir. Barletta ve Schio (2004) periyodik yüzey sıcaklığı sınır şartı ile ince cidarlı bir boru için eksenel iletim ve viskoz sönüm etkisini ihmal ederek bir problem çözmüşlerdir. Barletta ve Schio (2008) kalın cidarlı bir kanalda yüzeyde sinüzoidal olarak değişen sıcaklığın etkisinde, eksenel iletim ve viskoz sönüm etkisini ihmal ederek bir ısı transferi problemi çözmüşlerdir. Genellikle birleşik problemler, yüzeyde tanımlanan ısı akısı veya yüzey sıcaklığı sınır şartına bağlı olarak yerel ve ortalama Nusselt sayılarının belirlenmesi şeklinde yapılmıştır. Ancak gerçek uygulamalarda, yüzeyde sabit ısı akısı veya sıcaklık yerine sinüzoidal ve üssel bir fonksiyona bağlı olarak değişen sınır şartları da tanımlanabilir. Bu durumda problemin sınır şartı bir fonksiyona bağlı olarak değerlendirilmelidir.Bu

16

çalışmalarında Barletta ve Schio hidrodinamik ve ısıl olarak gelişmiş akış kabulü yaparak enerji denklemini analitik ve sayısal olarak çözmüşler ve her iki yöntemin sonuçlarını karşılaştırmışlardır. Her iki yöntemle yapılan çalışmalarda uyumlu sonuçlar elde etmişlerdir. Yüzeyden eksene doğru uzaklaştıkça benzer periyotta ancak gittikçe azalan bir genlik gözlemişlerdir. Simetri ekseni yakınlarında ise düzgün dağılımlı bir sıcaklık eğrisi elde etmişlerdir. Nusselt sayısının ise boyutsuz açısal frekansın değişimine bağlı olarak değiştiğini tespit etmişlerdir.

Literatürde cidar ve akışkan eksenel iletimlerini göz önüne alan, sayısal çözümler de bulunmaktadır. Bilir (1995, 2002)'de borularda sürekli ve geçici rejim için birleşik ısı transferi ile ilgili geniş kaynak araştırmaları vermiştir. Bilir ve Ateş (2003)’ de yaptıkları çalışmada, üst akış bölgesi cidarı sabit bir sıcaklıkta tutulurken alt akış bölgesinde cidar dış yüzeyinde taşınım sınır şartı ile problemi çözmüşlerdir. Benzer olarak Ateş ve ark. (2010) üst akış bölgesinde cidar dış yüzeyi yalıtılmış, alt akış bölgesinde ise sabit ısı akısı uygulanması durumunda problemi ele almışlardır. Bu çalışmalarda ısı transferi karakteristikleri sayısal olarak belirlenmiştir.

Kalın cidarlı borularda, zamanla periyodik olarak değişen dış ortam sıcaklığı etkisinde, cidar ve eksenel akışkan iletiminin dikkate alındığı, laminer akış ısıl gelişme bölgesi geçici rejim birleşik ısı transferi problemi ile ilgili çalışmaya literatürde rastlanılmamıştır.

17

1.3. PROBLEMĠN TANIMI

ġekil 1.1 Problemin şematik gösterimi

Bu çalışmada kalın cidarlı bir boruda, laminer akış ısıl gelişme bölgesi, geçici rejim birleşik ısı transferi problemi incelenmiştir. Cidarda iki boyutlu iletim ile düşük Peclet sayılı akışlar için akışkan eksenel iletiminin ısı transferine etkileri üçüncü tür sınır şartı ile ele alınmıştır. Problemin şematik görünümü ve koordinat sistemi Şekil 1.1’de görülmektedir.

Görüldüğü gibi akış iki bölgeli olarak ele alınmıştır. Dairesel kesitli boru her iki yönde sonsuz uzunluktadır, (-∞<x<+∞). Üst akış bölgesinin uzağında (x=-∞) akışkan uniform bir To sıcaklığı ile boruya girmektedir ve bu tüm sistemin başlangıç sıcaklığıdır. Üst akış bölgesi yalıtılmıştır ve akış hidrodinamik olarak gelişmiştir. Alt akış bölgesinde tüm dış yüzey boyunca sıcaklığı sinüzoidal olarak değişen akışkan ortam tanımlanmıştır ve çevre akışkanından sabit bir taşınım katsayısı h ile boruya ısı 0 transfer edilmektedir. Tüm akışkan ve cidar fiziksel özellikleri sabit kabul edilmiş, viskoz sönüm ihmal edilmiştir.

18 2. TEORĠK ESASLAR

2.1. Temel Denklemler

Boru içi akışta, silindirik koordinat sisteminde r,  ve x yönlerindeki hız bileşenleri sıra ile v, w, ve u olarak tanımlanırsa; sıkıştırılamaz ve özellikleri sabit bir akışkan için enerji denklemleri aşağıdaki gibi ifade edilebilir.(Kakaç ve Yener,1973)

r- yönünde

 

                                          2 2 2 2 2 2 f r 2 x v w r 2 v r 1 r rv r 1 r r P 1 f x v u r w v r w r v v t v      (2.1)  - yönünde

 

                                          2 2 2 2 2 2 f x w v r 2 w r 1 r rw r 1 r P 1 f x w u r vw w r w r w v t w        (2.2) x - yönünde                                       2 2 2 2 2 f x x u u r 1 r u r r r 1 x P 1 f x u u u r w r u v t u     (2.3)

Sürekli, hidrodinamik olarak gelişmiş, laminer, eksenel simetrik ve kütlesel kuvvetlerin olmadığı bir akışta eksenel yöndeki hız profili için;

                2 1 2 wi m r r u u (2.4)

19

elde edilir. Bu ifade borularda Hagen-Poiuselle hız profili olarak adlandırılır.

Silindirik koordinat sisteminde sıkıştırılamayan ve özellikleri değişmeyen bir akışkan için enerji denklemi,

    _                                        2 2 2 2 2 x T T r 1 r T r r r 1 k x T u T r w r T v t T c (2.5)

şeklinde yazılabilir (Kakaç ve Yener, 1993). Bu denklemdeki

2 2 x T   _{terimi, giriş} bölümünde bahsedilen eksenel iletim terimi, Φ ise viskoz sönüm terimidir. Silindirik koordinat sisteminde Φ aşağıdaki gibi ifade edilir.

                                                                                 _             2 2 2 2 2 2 r w r r v r 1 x w r u u r 1 x w x u v w r 1 r v 2       (2.6)

Laminer, hidrodinamik olarak gelişmiş, eksenel simetrik akış şartlarında ve viskoz sönümün ihmal edildiği bir problem için enerji denklemi şu şekilde sadeleşir.

                               2 2 x T r T r r r 1 k x T u t T c  (2.7)

Cidar tarafında enerji denklemi aşağıdaki şekilde ifade edilebilir.

                      2 w 2 w w w pw w x T r T r r r 1 k t T c  (2.8)

Hagen-Poiuselle hız profili (denklem 2.4), enerji denklemi (2.7)’ ye taşınarak akışkan tarafı enerji denklemi aşağıdaki gibi elde edilir.

20                                                   2 2 2 1 1 2 x T r T r r r k x T r r u t T c f f f f wi m f f f  (2.9) 2.2. BaĢlangıç ve Sınır ġartları

Problemin formülasyonunun tamamlanabilmesi için, başlangıç ve sınır şartlarının belirlenmesi gerekir.

Cidar tarafı enerji denklemi (2.8) için başlangıç ve sınır şartları;

Zamanın başlangıcında

o

w T

T

t0 da  (2.10.a)

Üst akış bölgesinin uzağında

o

w T

T

x da  (2.10.b)

Alt akış bölgesinin uzağında

0 da      x T x w (2.10.c) Dış Yüzeyde

Üst akış bölgesinde , rr_wi d de x0 için 0  

r Tw

(2.10.d) Alt akış bölgesinde, rr_wi d de x0 için w



_w



w h T T r T k     1 0 (2.10.e) Ara yüzeyde r T k r T k T T r r w _f f w f w wi _       de ve (2.10.f)

21

Akışkan tarafı enerji denklemi (2.9) için başlangıç ve sınır şartları;

Zamanın başlangıcında

o

f T

T

t0 da  (2.11.a)

Üst akış bölgesinin uzağında

o

f T

T

x da  (2.11.b)

Alt akış bölgesinin uzağında 0 da      x T x f (2.11.c) Ara yüzeyde r T k r T k T T r r _{wi f w f} f _w w        de ve (2.11.d) Boru ekseninde 0 da 0     r T r f (2.11.e)

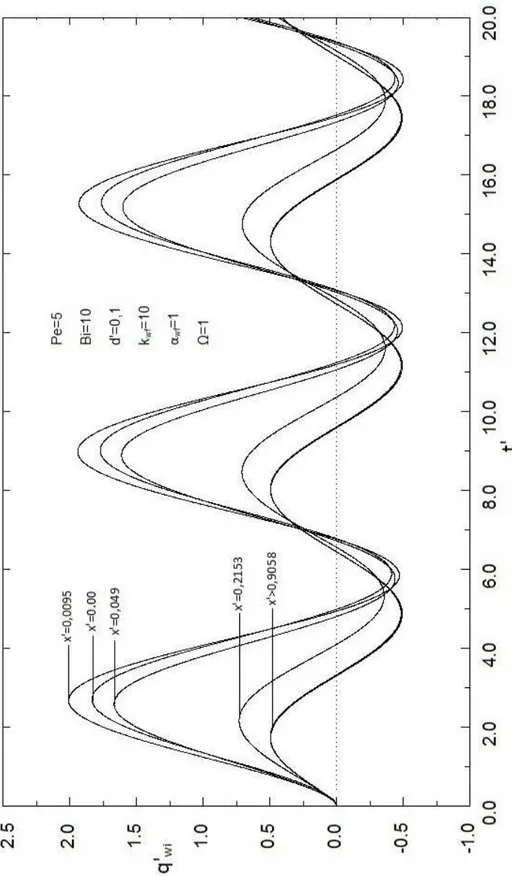
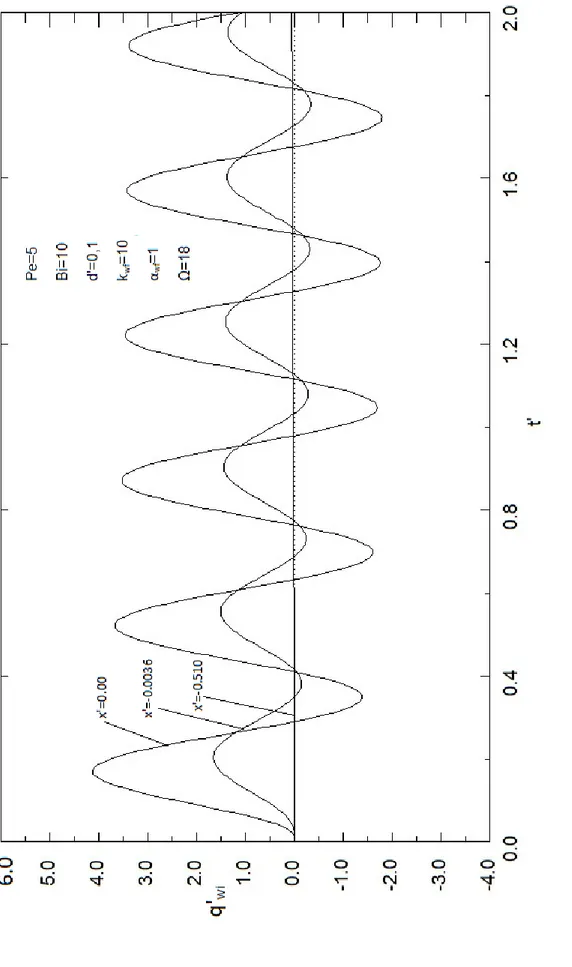
Enerji denklemlerinin başlangıç ve sınır şartları ile çözülmesi ile hem cidar hem de akışkan bölgesi için sıcaklık dağılımı belirlenir. Bunun yanı sıra akışkan yığık sıcaklığı, Tb, ara yüzey ısı akısı, qwi, ve ara yüzeydeki Nusselt sayısı, Nui sırası ile aşağıdaki ifadelerden hesaplanır.

c f A m c b uT dA u A T c



 1 (2.12)



_                 wi r f wi m m wi b c wi c rdr T r r u u r T rdr dA r A 0 2 2 2 2 1 2 1 ile (2.4) denklem ve 2 ,    

22



_               wi r 0 f 2 wi 2 wi b T dr r r 1 r r 4 T (2.13) w i r r f f wi r T k q            (2.14) ) ( _{wi b} i wi h T T q   ve f i wi i k h r Nu  2 ile ) ( 2 b wi r r f wi i T T r T r Nu wi             (2.15) 2.3 BoyutsuzlaĢtırma

Çözümlerden elde edilecek sonuçların genelleştirilebilmesi için, denklemlerin boyutsuz hale getirilerek çözüm yapılması daha uygundur. Bu nedenle denklemler ile başlangıç ve sınır şartları boyutsuz hale getirilmiştir. Boyutsuz parametrelerin tanımlanabilmesi için her bir değişken uygun bir referans değerine bölünmüştür.

2.3.1 Boyutsuz Parametreler Boyutsuz sıcaklık T T T T o     (2.16)

Boyutsuz eksenel koordinat

Gz Pe r x x wi 2    (2.17)

23

wi

r r

r (2.18)

Boyutsuz cidar kalınlığı (cidar kalınlık oranı)

wi

r d

d (2.19)

Cidar-akışkan ısı iletkenlik katsayısı oranı

f w wf k k k  (2.20)

Cidar-akışkan ısıl yayılım katsayısı oranı

f w wf _    (2.21) Boyutsuz zaman Fo r t t ₂ wi f _    (2.22) Peclet sayısı f pf f m wi k c u r PeRePr 2  (2.23)

Dış yüzeyin alt akış bölgesinde Biot sayısı

w wi k r h Bi₀  0 (2.24)

Boyutsuz açısal frekans

f 2 wi r     (2.25)

24 2.3.2 Enerji Denklemlerinin BoyutsuzlaĢtırılması

Yukarıda tanımlanan boyutsuz parametreler ile diferansiyel denklemler şu şekilde boyutsuz hale getirilebilir.

t T T r t r T T r t T T T t T f wi wi f wi f o                                 2 2 2 1 t T r T t T wi f           ₂ (2.26) r r T T r r T T T r T wi wi o                          1 1 r T r T r T wi          (2.27) r r r r r wi wi                r r r _wi        1 (2.28) x T T Pe r x Pe r T T Pe r x T T T x T _wi wi wi o                              1 1 x T Pe r T x T wi          (2.29)

25 2 2 2 2 2 2 2 2 1 x T T Pe r x T Pe r T Pe r x T T Pe r Pe r x x T x x T wi wi wi wi wi                                           2 2 2 2 2 2 x T Pe r T x T wi          (2.30)

(2.26-2.30) no’lu ifadeler denklem (2.8)’e uygulanırsa;

                                  2 2 2 2 2 1 1 x T Pe r T r T r T r r r r r r k t T r T c w wi w wi wi wi wi w w wi f pw w                                     w₂ 2 2 2 wi w 2 wi w w 2 wi f x T Pe 1 r T r T r r r 1 r T t T r T _    

ve cidar tarafı için boyutsuz diferansiyel denklem;

2 2 2 1 1 1 x T Pe r T r r r t T_{w w w} wf                           (2.31)

şeklinde elde edilir.

Yine (2.26-2.30) no’lu ifadeler denklem (2.9)’a uygulanırsa;

                                                                  2 2 2 2 2 2 1 1 1 2 x T Pe r T r T r T r r r r r r k x T Pe r T r r r u t T r T c f wi f wi wi wi wi f f wi wi wi m f wi f f f  

26





2 2 2 2 2 2 2 2 1 1 2 1 1 2 1 x T Pe r T r T r r r r T x T c k u r T r u t T r T f wi f wi f pf f f m wi m f wi f f                                                

ve akışkan tarafı için boyutsuz diferansiyel denklem





2 f 2 2 f f 2 f x T Pe 1 r T r r r 1 x T r 1 t T                                 (2.32)

şeklinde elde edilir.

Boyutsuz eksenel uzunluğun, x', tanımı için

wi r x yerine Gz 2 Pe r x wi  kullanılmıştır. Bu, denklemler (2.30) ve (2.31) de görüldüğü gibi Pe parametresinin sadece eksenel iletim terimi içerisinde yer almasını sağlar. Peclet sayısı büyüdükçe eksenel iletimin etkisi küçülür ve bu terim ihmal edilebilir.

2.3.3 BaĢlangıç ve Sınır ġartlarının BoyutsuzlaĢtırılması

Başlangıç ve sınır şartları, daha önce tanımlanan boyutsuz değişkenler ile aşağıdaki gibi boyutsuz hale getirebilir.

Cidar tarafı Zamanın başlangıcında (t=0) 0 T için ve 0 için 0   w   t T T t w o olur. Böylece 0 T da 0 _w    t (2.33.a) olur.

Üst akış bölgesinin girişinde (x)

0 için ve için x T T T x  _w  _{o w}  olur. Böylece

27 0 da T x _w  (2.33.b) olur.

Alt akış bölgesinin uzağında (x)      x x için ve 0 0               x T x T Pe r T x T w w wi w olur. Böylece,    x da 0     x T_w (2.33.c) Dış Yüzeyde (rrwi d) d r d r r _wi  için 1 olur.

Üst akış bölgesinde, x0 için x0 _ve 0     r T_w için T_w 0,

Alt akış bölgesinde, d r1  _{de ve} x0 için T_w 0 ve (2.33.d) d r1  _{de ve} x0 için Denklem (2.10.e)’den

 







w



W w h T T Cos t T r T k       _ 1 0 0 T T r t r Cos T r T h r T k w f wi wi f W wi w                              2 2 0 1







1

 

 





0      t Cos T Bi r T w w (2.33.e) olur. Ara yüzeyde (rr_wi ) wi r r için r1 ve Tf Tw için    w f T T       r T k r T k f f w w r T r T k r T r T k f wi f w wi w _{ }                     ve f w wf k k k  ile

28 1   r deT_f T_w ve r T k r T f wf w          1 (2.33.f,g) olur. AkıĢkan Tarafı Zamanın başlangıcında (t 0) 0 T T T 0 t 0

t  için  ve _f  _o için _f  olur. Böylece 0 T da 0 _f    t (2.34.a) olur.

Üst akış bölgesi uzağında (x)

0 için ve için x T T T x  f  o f  olur. Böylece 0 da T x _f  (2.34.b) olur.

Alt akış bölgesi uzağında (x)      x x için _ve 0   x T_f için 0 0               x T x T Pe r T x T _{f f} wi f olur. Böylece    x _da 0     x Tf (2.34.c) Boru ekseninde



r0



0  r _için r0 _ve 0   r T_f için 0     r T_f olur. Böylece 0   r _da 0     r T_f (2.34.d) olur. Ara yüzeyde (rr_wi ) wi r r için r1 ve T_f T_w için T_f T_w

29       r T k r T k w _f f w r T r T k r T r T k f wi f w wi w _{ }                     ve f w wf k k k  ile 1   r deT_f T_w ve r T k r T _w wf f          (2.34.e,f) elde edilir.

Problem boyutsuz formda yeniden şu şekilde ifade edilebilir.

Cidar tarafı için diferansiyel denklem;

2 2 2 1 1 1 x T Pe r T r r r t T_{w w w} wf                           (2.35) Başlangıç ve sınır şartları; 0 T da 0 _w    t (2.36.a) 0 da T x _w  (2.36.b)    x da 0     x Tw (2.36.c) d r1  _{de ve} x0 için 0    r T_w (2.36.d) d r1  _{de ve} x0 için 







1

 

 





0     t Cos T Bi r T_w (2.36.e) 1   r de T_f T_w ve r T k r T f wf w          1 (2.36.f,g)

30 Akışkan tarafı için diferansiyel denklem;





2 f 2 2 f f 2 f x T Pe 1 r T r r r 1 x T r 1 t T                                 (2.37) Başlangıç ve sınır şartları; 0 T da 0 _f   t (2.38.a) 0 da T x _f  (2.38.b)    x _da 0     x T_f (2.38.c) 0   r _da 0     r T_f (2.38.d) 1   r de Tf Tw ve r T k r T _w wf f          (2.38.e,f)

Yığık sıcaklık, ara yüzey ısı akısı ve Nusselt sayısı ise boyutsuz formda aşağıdaki gibi ifade edilebilir.

Boyutsuz yığık sıcaklık,

T T T Tb b

_

o    (2.39)

şeklinde tanımlanırsa, denklem (2.13), (2.16) ve (2.18) ile









T T r r d T T T r 1 r r r 4 T 0 wi 1 0 0 f 2 wi 2 wi b          _     



31









T r d T r r T r d T r r T _{f f}                     





1 1 4 1 4 1 0 2 0 1 0 2 ve 4



1



1 1 0 2    



r r dr olduğu için



r



T dr r T_b



   _f  1 0 2 1 4 (2.40)

Boyutsuz ara yüzey ısı akısı,

wi f wi wi r T k q q    (2.41)

şeklinde tanımlanırsa, denklem (2.14) ve (2.26) ile

1 r f wi f 1 r f wi f wi r T r T k r T r T k q                                  (2.42)

olur ve denklemler (2.15), (2.27) ve (2.39) ile

                     o b o wi r f wi wi i T T T T T T r T r T r Nu 1 2 b wi r f i T T r T Nu                1 2 (2.43)

32 3. SAYISAL ÇÖZÜMLEME

Problemi tanımlayan denklemler birbirine bağlı doğrusal olmayan kısmi diferansiyel denklemlerdir. Sistem kontrol hacimlere bölünmüş ve diferansiyel denklemler ayrıklaştırılmıştır.

3.1 Ağ Sistemi ve Düğüm Noktaları

Problemin sonlu farklar yöntemiyle çözülebilmesi için hem diferansiyel denklemlerin hem de başlangıç ve sınır şartlarının ayrıklaştırılması (diskritize edilmesi) gerekir. Denklem (2.35) ile denklem (2.37)’deki iletim terimleri merkezi fark formülleri ile, taşınım terimleri daha sonra açıklanacak bir kesin çözüm profili ile zamana bağlı terimler ise tam implicit yöntem ile ayrıklaştırılmıştır. Ayrıklaştırma Patankar’ın kontrol hacim yaklaşımı (Patankar 1980) ile Şekil 3.1’de verilen iki boyutlu bir ağ sistemindeki P noktası çevresinde gerçekleştirilmiştir. Şekil 3.1’de kontrol hacmi merkezi P noktası, komşu kontrol hacimlerinin merkezleri N, W, S ve E noktalarıdır. Komşu kontrol hacimlerinin yüzeyleri ise n, w, s ve e yüzeyleri olarak tanımlanmıştır. Şekildeki gösterim belirtilen kaynaktaki orijinal haline uygun olarak verilmiştir.

33

Çözüm bölgesinin gerek cidar ve gerekse akışkan tarafı, ara yüzeyde sıcaklıkların ve ısı akılarının sürekliliği şartları ile bir bütün olarak ele alındığı ve konum koordinatları ile her iki taraf belirgin bir şekilde tanımlanabildiği için, gösterimde sadelik sağlamak amacı ile bundan sonraki bölümlerde sıcaklıklar için w ve f indisleri kullanılmayacaktır.

3.2. Diferansiyel Denklemlerin AyrıklaĢtırılması

3.2.1 Cidar Tarafı için Diferansiyel Denklemin AyrıklaĢtırılması

Denklem (2.34), her iki tarafı r ile çarpılarak ve T_w yerine T yazarak

2 2 2 x T Pe r r T r r t T r wf                            (3.1)

şeklinde ifade edilebilir. Bu denklem P noktası çevresindeki kontrol hacminde ve tile t

t zaman aralığında integre edilirse; düğüm noktası sıcaklığının tüm kontrol hacim için geçerli olduğu varsayımı ile soldaki terim için





   

P P 0 P 1 P wf P n s e w t t t wf r x T T r r d x d t d t T r _{  }  _{    }     

 

       

elde edilir. Burada t anı 0 üst indisi ile ttanı ise 1 üst indisi ile gösterilmiştir. Denklem (3.1)’in sağ tarafındaki ilk terim

34

 

   

 

 





 

 

r

 

x t T T r r T T r f r T T r r T T r f t d x r T T r r T T r t d x d r T r r T r t d x d r d r T r r P s S P s n P N n s S P s n P N n P t t t s S P s n P N n t t t e w n s t t t e w n s                                                                                                                       



 

 

                     0 0 0 0 1 1 1 1 1

şeklinde gösterilebilir. Burada f bir ağırlık faktörüdür ve tam implict yöntemde f=1 alınır. Bu terim,

 

   

x t r T T r r T T r t d x d r d r T r r _s P 1 S 1 P s n 1 P 1 N n t t t e w n s                                     

 

         haline gelir.

Benzer şekilde sağdaki ikinci terim

 

 

   

r t x T T x T T Pe r t d r d x d x T Pe r P w 1 W 1 P e 1 P 1 E 2 P t t t n s e w 2 2 2                             

 

         şekline dönüşür.

Ayrıklaştırılmış terimler birleştirilerek ve sadeleştirmek için 1 üst indisi kaldırılarak cidar bölgesi için ayrıklaştırılmış denklem

   

_{ }

_{     }

 

     

r t x T T x T T Pe r t x r T T r r T T r r x T T r P w W P e P E 2 P P s S P s n P N n P P 0 P P wf P                                                _{  }             (3.2)

elde edilir. Bu denklem Δt’ye bölünerek ve yeniden düzenlenerek şöyle de ifade edilebilir.

35 0 0 P P S S N N W W E E P PT a T a T a T a T a T a          (3.3)

elde edilir. Buradaki katsayılar,

 

 

e P p E x r Pe r a       2 (3.4.a)

 

 

_wP p W x r Pe r a       2 (3.4.b)

 

 

 

 

P n p n P n N x r r r x r a _                 0.5  (3.4.c)

   

 

 

P s p P s s S x r r x r r a _                  0.5  (3.4.d)

   

 

t r x r a P P wf p P _         0 (3.4.e) 0 P S N W E P a a a a a a      (3.4.f)

3.2.2 AkıĢkan Tarafı için Diferansiyel Denklemin AyrıklaĢtırılması

Denklem (2.36)’da Tf yerine T yazılır, denklemin her iki tarafı r ile çarpılır ve

yeniden düzenlenirse,





                                      r T r r x T Pe r T r r x t T r 3 ₂ (3.5)

36 r J x J t T r x r                (3.6)

şeklinde de yazılabilir. Burada;





x T Pe r T r r Jx _            3 ₂ (3.7) x-yönündeki ıs akısı ve r T r J_r        (3.8)

r-yönündeki ısı akısı olarak tanımlanır.

Denklem (3.6)’nın sol tarafındaki birinci terim tam implict yöntem ile ayrıklaştırabilir. Sağ taraftaki terim ise sadece iletim terimleri içerdiği için cidar tarafında olduğu gibi merkezi fark formülleri ile ayrıklaştırılabilir.

Denklem (3.6)’nın sol tarafındaki ikinci terim ise hem iletim hem de taşınım terimleri içermektedir.

Taşınım problemlerin sonlu farklar ile çözümünde yakınsama için merkezi fark formülleri çok düşük Peclet sayılı (Pe<2) akışlar için güvenle kullanılabilir. Bu tarz problemlerde bir alternatif olan “üst akış” (upwind) formülü ise iletim etkisini tümüyle yok saydığı için ancak Pe>50 olan akışlar için uygundur (Patankar 1980 ). Bu çalışmada da etkisi göz önüne alınan akışkan eksenel iletimi genelde Pe<50 olan akışlar için söz konusudur. Bu nedenle burada bu akış şartları için geliştirilen bir ayrıklaştırma formülü kullanılacaktır. Problemin sürekli rejimde tek boyutlu halinin kesin çözümüne dayalı olarak geliştirilen formül, Patankar’ın kesin çözüm (exact profil ) olarak adlandırdığı genel profilin (Patankar, 1980) iki boyutlu (r, x)silindirik koordinat sitemleri için bir versiyonu olarak nitelendirilebilir. Daha önce bazı çalışmalarda (Bilir 1992, 1995) kullanılan profil ile ilgili bilgi (Bilir, 1992)’de ayrıntılı olarak verilmiştir ve aşağıda özetlenmiştir.

Denklem (3.6) ile karakterize edilen problemin x-yönünde bir boyutlu, sürekli hali için diferansiyel denklem

37 0  dx dJx (3.9) veya



3



_{2 }0              x T Pe r T r r dx d (3.10)

halini alır. Herhangi bir radyal konum için rsb ve K Pe2(1r2) alınarak bu denklem 0 2 2       x d T d K x d T d (3.11)

şeklinde yazılabilir. Bu ikinci dereceden tek bilinmeyenli, sabit katsayılı doğrusal ve homojen diferansiyel denklemin genel çözümü;

' 2 1 ) (x D DeKx T   (3.12)

ve0x'L' gibi bir çözüm aralığında aşağıdaki sınır şartları ile

0 ' x da T T₀ (3.13.a) ' ' L x de TT_L' (3.13.b) denklemin kökleri ' ' 0 0 1 1 KL L e T T T D        (3.14.a) ' ' 0 2 1 KL L e T T D      (3.14.b)

38

elde edilir. Bunlar genel çözümde yerlerine konularak ve K Pe2(1r2)yazılarak







1



1 exp 1 1 exp 2 2 2 2 0 ' 0               L ) r ( Pe x ) r ( Pe T T T T L (3.15)

elde edilir. Şekil 3.1’deki ağ sisteminde e noktasına bu profil şu şekilde uygulanabilir.

e T T , T₀T_P, T_L_' T_E, L'

 

x_e alınarak;

 

x 1 ) r 1 ( Pe exp 1 x ) r 1 ( Pe exp T T T T e 2 e 2 e 2 e 2 P E P e      _{  }      _{  }        (3.16) veya





 

               _{  }      _{  }       1 x ) r 1 ( Pe exp 1 x ) r 1 ( Pe exp T T T T e 2 e 2 e 2 e 2 P E P e  (3.17) yazılabilir. Buradan,





 

               _{  }     _{  }     _{ }         1 x ) r 1 ( Pe exp x ) r 1 ( Pe exp ) r 1 ( Pe T T x d T d e 2 e 2 e 2 e 2 2 e 2 P E e  (3.18)

yazılabilir. Denklem (3.18) e noktası için ifade edildiğinde;





e 2 e e 3 e e e x T Pe r T r r J                  (3.19)

39









 





 

               _{  }     _{  }     _{ }                              _{  }      _{  }         1 x ) r 1 ( Pe exp x ) r 1 ( Pe exp ) r 1 ( Pe T T Pe r 1 x ) r 1 ( Pe exp 1 x ) r 1 ( Pe exp T T T r r J e 2 e 2 e 2 e 2 2 e 2 P E 2 e e 2 e 2 e 2 e 2 P E P 3 e e e   (3.20) ve sadeleştirilerek;









 

               _{  }          1 x ) r 1 ( Pe exp T T T r r J e 2 e 2 E P P 3 e e e  (3.21)

elde edilir. Benzer şekilde Şekil 3.1’deki w noktası için





_



_{ }



_

                   1 ) 1 ( exp 2 2 3 w w P W W w w w x r Pe T T T r r J  (3.22)

yazılabilir. J_eJ_w yazılarak da denklem (3.5)’in sol tarafındaki ikinci terim ayrıklaştırılmış olur. re rw rp olduğu için ve ısı akısının tüm r ara yüzeyi

boyunca ve t zaman süresince geçerli olduğu varsayılarak









 









 





 

r t x r Pe T T T x r Pe T T T r r J J _p w p P w w e p E P P P P w e                                                            1 ) 1 ( exp 1 ) 1 ( exp 2 2 2 2 3   (3.23)

40

elde edilir. Denklem (3.5)’in sol tarafındaki birinci terim tam implict yöntem ile sağ taraftaki terim ise merkezi fark formülü ile ayrıklaştırılarak denklem (3.23) ile birleştirilirse akışkan tarafı için ayrıklaştırılmış denklem şu şekilde elde edilir.





   









 









 





 

 

   

r x t T T r r T T r t r x r Pe T T T x r Pe T T T r r r x T T r P s S P s n P N n P w p P W W e p E P P P P P P P P P                                                                                      1 ) 1 ( exp 1 ) 1 ( exp 2 2 2 2 3 0 (3.24)

Bu denklem tile bölünerek ve yeniden düzenlenerek şöyle de ifade edilebilir.

0 0 P P S S N N W W E E P PT a T a T a T a T a T a           (3.25)

 

 

x 1 ) r 1 ( Pe exp r r r a e 2 p 2 P 3 P P E      _{  }        _{  }    (3.26.a)

   

 

x 1 ) r 1 ( Pe exp r x ) r 1 ( Pe exp r r a w 2 p 2 P w 2 p 2 3 P P w      _{  }      _{  }       _{  }     (3.26.b)

 

 

n P n N r x r a       =

 

 

P n p x 5 . 0 r r             (3.26.c)

 

 

s P s S r x r a       =

 

 

P s p x 5 . 0 r r             (3.26.d)

   

t r x r a P P P 0 P     







(3.26.e)