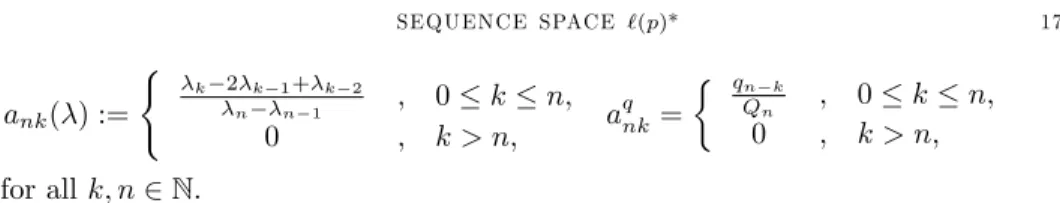IS S N 1 3 0 3 –5 9 9 1
SOME GEOMETRIC PROPERTIES OF THE DOMAIN OF THE
TRIANGLE eA IN THE SEQUENCE SPACE `(p)*
ESRA SÜMEYRA YILMAZ AND FEYZI BA¸SAR
Abstract. The sequence space `( eA; p)of non-absolute type is the domain of the triangle matrix eAde…ned by the strictly increasing sequence = ( n)of
positive real numbers tending to in…nity in the sequence space `(p), where `(p) denotes the space of all sequences x = (xk) such thatPkjxkjpk < 1 and
were de…ned by Maddox in [Spaces of strongly summable sequences, Quart. J. Math. Oxford (2) 18 (1967), 345–355]. The main purpose of this paper is to investigate the geometric properties of the space ` eA; p, like rotundity, Kadec-Klee property.
1. Introduction
By !, we denote the space of all sequences with complex elements which contains , the set of all …nitely non-zero sequences, that is,
! := fx = (xk) : xk 2 C for all k 2 Ng ;
where C denotes the complex …eld and N = f0; 1; 2; : : :g. By a sequence space, we understand a linear subspace of the space !. We write `1, c, c0and `p for the
clas-sical sequence spaces of all bounded, convergent, null and absolutely p-summable sequences which are the Banach spaces with the norms kxk1 = supk2Njxkj and
kxkp = (
P
kjxkjp)1=p; respectively, where 1 p < 1. For simplicity in notation,
here and in what follows, the summation without limits runs from 0 to 1. Also by bs and cs, we denote the spaces of all bounded and convergent series, respectively. bv is the space consisting of all sequences (xk) such that (xk xk+1) in `1 and bv0
is the intersection of the spaces bv and c0.
Received by the editors : 01.11.2013, accepted: 07.09.2014.
2010 Mathematics Subject Classi…cation. 47A10, 47B37.
Key words and phrases. Paranormed sequence spaces, triangle matrix, alpha-, beta- and gamma-duals, matrix transformations and rotundity of a sequence space.
*The main results of this paper were presented in part at the conference Algerian-Turkish International Days on Mathematics 2013 (ATIM’ 2013) to be held September 12–14, 2013 in ·
Istanbul at the Fatih University.
c 2 0 1 4 A n ka ra U n ive rsity
A linear topological space X over the real …eld R is said to be a paranormed space if there is a subadditive function g : X ! R satisfying the following conditions for all x; y 2 X:
(i) g( ) = 0. (ii) g(x) = g( x).
(iii) Scalar multiplication is continuous, i.e., j n j ! 0 and g(xn x) ! 0
imply g( nxn x) ! 0 for all ’s in R and all x’s in X, where is the
zero vector in the linear space X.
Assume here and after that (pk) be a bounded sequence of strictly positive real
numbers with sup pk = H and M = maxf1; Hg. Then, the linear space `(p) was
de…ned by Maddox [2] (see also Simons [3] and Nakano [4]) as follows: `(p) := ( x = (xk) 2 ! : X k jxkjpk< 1 ) ; (0 < pk H < 1)
which is complete paranormed space paranormed by
g(x) = X
k
jxkjpk
!1=M
:
We assume throughout that pk1+ (p0k) 1= 1 provided inf pk H < 1 and
de-note the collection of all …nite subsets of N by F. The beta-dual of a sequence space is de…ned by
= fx = (xk) 2 ! : xy = (xkyk) 2 cs for all y = (yk) 2 g:
Let , be any two sequence spaces and A = (ank) be an in…nite matrix of
complex numbers ank, where k; n 2 N. Then, we say that A de…nes a matrix
transformation from into and we denote it by writing A : ! ; if for every sequence x = (xk) 2 the sequence Ax = f(Ax)ng, the A-transform of x, is in ;
where
(Ax)n =
X
k
ankxk (1.1)
provided the series on the right side of (1.1) converges for each n 2 N. By ( : ), we denote the class of all matrices A such that A : ! . Thus, A 2 ( : ) if and only if Ax exists, i.e. An 2 for all n 2 N and is in for all x 2 , where An
denotes the sequence in the n-th row of A.
A matrix A = (ank) is called a triangle if ank= 0 for k > n and ann6= 0 for all
n 2 N. It is trivial that A(Bx) = (AB)x holds for triangles A; B and any sequence x. Further, a triangle matrix U uniquely has an inverse U 1= V which is also a triangle matrix. Then, x = U (V x) = V (U x) holds for all x 2 !.
The matrix domain A of an in…nite matrix A in a sequence space is de…ned
by
If A is triangle, then one can easily observe that the sequence spaces A and are
linearly isomorphic, i.e. A= .
We consider the strictly increasing sequence = ( k)1k=0of positive reals tending
to 1, that is
0 < 0< 1< 2< < k < k+1< and lim
k!1 k= 1:
Via the sequence = ( k)k2N, we de…ne the triangle matrix eA = (eank) by
eank( ) =
(
k 2 k 1+ k 2
n n 1 ; 0 k n;
0 ; k > n
for all k; n 2 N. It is easy to show that eA is a regular matrix and a straightforward calculation yields that the inverse eA 1= fb
nk( )g of the matrix eA is given by the
following double band matrix as bnk( ) =
(
( 1)n k k k 1
n 2 n 1+ n 2 ; n 1 k n;
0 ; 0 k < n 1 or k > n
for all k; n 2 N. We study some geometric properties of the sequence space `( eA; p) of non-absolute type which is the domain of the triangle matrix eA in the sequence space `(p), that is `( eA; p) := 8 < :(xk) 2 ! : X k k X j=0 j 2 j 1+ j 2 k k 1 xj pk < 1 9 = ; which is a complete linear metric space paranormed by the paranorm
g1(x) = 0 @X k k X j=0 j 2 j 1+ j 2 k k 1 xj pk1 A 1=M
and has the AK property. In the special case pk = p for all k 2 N, the space `( eA; p)
is reduced to the space `p( eA), i.e.,
`p( eA) := 8 < :(xk) 2 ! : X k k X j=0 j 2 j 1+ j 2 k k 1 xj p < 1 9 = ;; (0 < p < 1) which is a BK-space with the norm
kxk = 0 @X k k X j=0 j 2 j 1+ j 2 k k 1 xj p1 A 1=p ; where 1 p < 1
and is a complete p-normed space with the p-norm kxk =X k k X j=0 j 2 j 1+ j 2 k k 1 xj p ; where 0 < p < 1:
One can see from Theorem 2.3 of Jarrah and Malkowsky [5] that the domain T of
an in…nite matrix T = (tnk) in a sequence space has a basis if and only if has
a basis, if T is a triangle. As an immediate consequence of this fact, we derive the following result:
Corollary 1. Let 0 < pk H < 1 and k = ( eAx)k for all k 2 N. De…ne the
sequence b(k)= b(k)
n n2Nof the elements of the space `( eA; p) by
b(k)n := (
( 1)n k k k 1
n 2 n 1+ n 2 ; n 1 k n;
0 ; otherwise (1.2)
for every …xed k 2 N. Then, the sequence fb(k)gk2N given by (1.2) is a basis
for the space `( eA; p) and any x 2 `( eA; p) has a unique representation of the form x :=Pk kb(k).
Since the algebraic and topological properties of the space rq(p) were studied
by Altay and Ba¸sar in [6], we essentially emphasize the geometric properties of the space `( eA; p).
2. The rotundity of the space `( eA; p)
In this section, we focus on the rotundity and some geometric properties of the space `( eA; p). For details, the reader may refer to [7], [8] and [9]. The main purpose of this study is to characterize the rotundity and some other geometric properties of the space `( eA; p), the domain of the triangle matrix eA in the sequence space `(p). De…nition 2.1. Let S(X) be the unit sphere of a Banach space X. Then a point x 2 S(X) is called an extreme point if 2x = y + z implies y = z for every y; z 2 S(X). A Banach space X is said to be rotund (stricly convex) if every point of S(X) is an extreme point.
De…nition 2.2. A Banach space X is said to have the Kadec-Klee property (or property(H)) if every weakly convergent sequence on the unit sphere is convergent in norm.
De…nition 2.3. Let X be real vector space. A functional : X ! [0; 1) is called a modular if
(i) (x) = 0 if and only if x = ;
(ii) ( x) = (x) for all scalars with j j = 1;
(iv) The modular is called convex if ( x + y) (x) + (y) for all x; y 2 X and ; > 0 with + = 1.
A modular on X is called
(a) right continuous if ( x) ! (x), as ! 1+ for all x 2 X .
(b) left continuous if ( x) ! (x), as ! 1 for all x 2 X . (c) continuous if it is both right and left continuous, where
X := x 2 X : lim
!0+ ( x) = 0 :
We de…ne p on the real sequence space `( eA; p) by
p(x) = X k 1 k k 1 k X j=0 ( j 2 j 1+ j 2)xj pk :
If pk 1 for all k 2 N, by the convexity of the function t 7! jtkjpk for each k 2 N, p is a convex modular on `( eA; p).
Proposition 1. The modular p on `( eA; p) satis…es the following properties with
pk 1 for all k, we have M = H :
(i) If 0 < 1, then M
p(x= ) p(x) and p( x) p(x).
(ii) If 1, then p(x) M p(x= ).
(iii) If 1, then p(x) p(x= ).
(iv) The modular p is continuous on the space `( eA; p).
(i) Let 0 < 1, then M= pk 1. So, we have M p x = MX k 1 Xk j=0 j 2 j 1+ j 2 k k 1 xj pk = MX k 1 pk 1 k k 1 k X j=0 ( j 2 j 1+ j 2)xj pk = X k M pk 1 k k 1 k X j=0 ( j 2 j 1+ j 2)xj pk X k 1 k k 1 k X j=0 ( j 2 j 1+ j 2)xj pk = p(x); p( x) = X k k k 1 k X j=0 ( j 2 j 1+ j 2)xj pk = X k pk 1 k k 1 k X j=0 ( j 2 j 1+ j 2)xj pk X k 1 k k 1 k X j=0 ( j 2 j 1+ j 2)xj pk = p(x):
(ii) Let 1. Then, M= pk 1 for all p
k 1. So, we have p(x) M pk p(x) = M p x : (iii) Let 1. Then, = pk 1 for all p
k 1. So, we have p(x) pk p(x) = p
x : (iv) One can immediately see by Part (ii) for > 1 that
p(x) p(x) p( x) M p(x): (2.1)
By passing to limit as ! 1+ in (2.1), we have p( x) ! p(x). Hence, p is
right continuous. If 0 < < 1, we have by Part (i) that
M
p(x) p( x) p(x): (2.2)
By letting ! 1 in (2.2), we observe that p( x) ! p(x). Hence, p is left
Now, we consider the space `( eA; p) equipped with the Luxemburg norm given by kxk = infn > 0 : p
x
1o:
Proposition 2. For any x 2 `( eA; p), the following statements hold: (i) If kxk < 1, then p(x) kxk.
(ii) If kxk > 1, then p(x) kxk.
(iii) kxk = 1 if and only if p(x) = 1.
(iv) kxk < 1 if and only if p(x) < 1.
(v) kxk > 1 if and only if p(x) > 1.
Proof. Let x 2 `( eA; p).
(i) Let " > 0 be such that 0 < " < 1 kxk. By the de…nition of k k, there exists an > 0 such that kxk + " > and p(x) 1. From Parts (i) and
(ii) of Proposition 1, we obtain
p(x) p
h
(kxk + ")x i (kxk + ") p
x
kxk + ": Since " is arbitrary, we have (i).
(ii) If we choose " > 0 such that 0 < " < 1 (1=kxk), then 1 < (1 ")kxk < kxk. By the de…nition of k k and Part (i) of Proposition 1, we have
1 < p
x (1 ")kxk
1
(1 ")kxk p(x):
So (1 ")kxk < p(x) for all " 2 (0; 1 (1=kxk)): This implies that kxk < p(x):
(iii) Since p is continuous, we directly have (iii).
(iv) This follows from Parts (i) and (iii). (v) This follows from Parts (ii) and (iii).
Theorem 2.4. `( eA; p) is a Banach space with the Luxemburg norm.
Proof. Let Sx= f > 0 : p(x= ) 1g and kxk = inf Sxfor all x 2 `( eA; p). Then,
Sx (0; 1). Therefore, kxk 0 for all x 2 `( eA; p).
For x = , p( ) = 0 for all > 0. Hence, S0 = (0; 1) and k k = inf S0 =
inf(0; 1) = 0.
Let x 6= and Y = fkx : k 2 C and x 2 `( eA; p)g be a non-empty subset of `( eA; p). Since Y S[`( eA; p)], there exists k1 2 C such that k1x =2 S[`( eA; p)]. Obviously
k16= 0. We assume that 0 < < 1=k1 and 2 Sx: Then, (x= ) 2 S[`( eA; p)]. Since
jk1 j < 1, we get
k1x = k1
x
which contradicts the assumption. Hence, we obtain that if 2 Sx, then > 1=jk1j.
This means that kxk 1=jk1j > 0. Thus, we conclude that kxk = 0 if and only if
x = .
Now, let k 6= 0 and 2 Skx. Then, we have p kx 1 and kx 2 S[`( eA; p)]: Therefore, we obtain jkjx = jkj k kx 2 S[`( eA; p)] and jkj 2 Sx:
That is, kxk =jkj and jkjkxk for all 2 Skx. So, jkjkxk kkxk. If we take
1=k and kx instead of k and x, respectively, then we obtain that 1
k kkxk 1
kkx = kxk and kkxk jkjkxk: Hence, we see kkxk = jkjkxk which also holds when k = 0.
To prove the triangle inequality, let x, y 2 S[`( eA; p)] and " > 0 be given. Then, there exist 2 Sx and 2 Sy such that < kxk + " and < kyk + ". Since
S[`( eA; p)] is convex, x 2 S[`( eA; p)]; y 2 S[`( eA; p)]; x + y + = + x + + y 2 S[`( eA; p)]: Therefore, + 2 Sx+y. Then, we have kx + yk + < kxk + kyk + 2". Since
" > 0 was arbitrary, we obtain kx + yk kxk + kyk. Hence, kxk = inff > 0 :
p(x= ) 1g is a norm on `( eA; p).
Now, we show that every Cauchy sequence in `( eA; p) is convergent with respect to the Luxemburg norm. Letnx(n)k obe a Cauchy sequence in `( eA; p) and " 2 (0; 1). Thus, there exists n0such that kx(n) x(m)k < " for all n; m n0. By Part (i) of
Proposition 2, we have
p x(n) x(m) x(n) x(m) < " (2.3)
for all n; m n0. This implies that
X k h e A x(n) x(m) i k pk < ": (2.4)
Then, for each …xed k and for all n; m n0,
h e A x(n) x(m) i k pk = Axe (n) k e Ax(m) k < ":
Hence, the sequence f( eAx(n))
kg is a Cauchy sequence in R. Since R is complete,
there is ( eAx)k2 R such that eAx(m)
by (2.4) we have X k h e A x(n) x i k pk < " for all n n0.
Now, we have to show that (xk) is an element of `( eA; p). Since Axe (m) k ! ( eAx)k, as m ! 1, we have lim m!1 p x (n) x(m) = p x(n) x : (2.5)
Then, we see by (2.3) that p x(n) x kx(n) xk < " for all n n0. This
implies that x(n) ! x, as n ! 1. So, we have x = x(n) x(n) x 2 `( eA; p). Therefore, the sequence space `( eA; p) is complete with respect to Luxemburg norm. This completes the proof.
Theorem 2.5. The space `( eA; p) is rotund if and only if pk> 1 for all k 2 N.
Proof. Let `( eA; p) be rotund and choose k 2 N such that pk = 1. Consider the
following sequences given by
x = 1; 0 1 2 0 ; 0; 0; : : : and y = 0; 1 0 1 2 0 ; 1 0 2 2 1+ 0 ; 0; 0; : : : : Then, obviously x 6= y and p(x) = p(y) = p x+y2 = 1: By Part (iii) of
Proposition 2, x, y, (x + y)=2 2 S[`( eA; p)] which leads us to the contradiction that the sequence space `( eA; p) is not rotund. Hence, pk> 1 for all k 2 N. Conversely,
let x 2 S[`( eA; p)] and v; z 2 S[`( eA; p)] with x = (v + z)=2. By convexity of p and
Part (iii) of Proposition 2, we have
1 = p(x) p (v) + p(z) 2 1 2+ 1 2 = 1 which gives that p(v) = p(z) = 1 and
p(x) = p((v + z)=2) = p
(v) + p(z)
2 : (2.6)
Also, we obtain from (2.6) that 1 k k 1 k X j=0 i (vj+ zj) 2 2 j 1 (vj+ zj) 2 + j 2 (vj+ zj) 2 pk (2.7) =1 2 k X j=0 j 2 j 1+ j 2 k k 1 vj pk +1 2 k X j=0 j 2 j 1+ j 2 k k 1 zj pk
for all k 2 N. Since the function t 7! jtjpk is strictly convex for all k 2 N, it follows
by (2.7) that vk = zk for all k 2 N. Hence, v = z. That is, the sequence space
`( eA; p) is rotund.
Theorem 2.6. Let x 2 `( eA; p). Then, the following statements hold: (i) 0 < < 1 and kxk > imply p(x) > M.
(ii) 1 and kxk < imply p(x) < M.
Proof. Let x 2 `( eA; p).
(i) Suppose that kxk > with 0 < < 1. Then, kx= k > 1. By Part (ii) of Proposition 2, kx= k > 1 implies p(x= ) kx= k > 1. That
is, p(x= ) > 1. Since 0 < < 1, by Part (i) of Proposition 1, we get M
p(x= ) p(x). Thus, we have M < p(x).
(ii) Let kxk < with 1. Then kx= k < 1. By Part (i) of Proposition 2, kx= k < 1 implies p(x= ) kx= k < 1. That is, p(x= ) < 1. If = 1,
then p(x= ) = p(x) < 1 = M. If > 1, then by Part (ii) of Proposition
1, we have p(x) M p(x= ). This means that p(x) < M.
Theorem 2.7. Let (xn) be a sequence in `( eA; p). Then, the following statements
hold:
(i) kxnk ! 1, as n ! 1 implies p(xn) ! 1, as n ! 1.
(ii) p(xn) ! 0, as n ! 1 implies kxnk ! 0, as n ! 1.
Proof. Let (xn) be a sequence in `( eA; p).
(i) kxnk ! 1, as n ! 1 and " 2 (0; 1). Then, there exists n02 N such that
1 " < kxnk < " + 1 for all n n0. By Parts (i) and (ii) of Theorem
2.6, 1 " < kxnk implies p(xn) > (1 ")M and kxnk < " + 1 implies p(xn) < (1 + ")M for all n n0. This means " 2 (0; 1) and for all n n0
there exists n02 N such that (1 ")M < p(xn) < (1 + ")M for all n n0.
That is, p(xn) ! 1, as n ! 1.
(ii) We assume that kxnk 9 0, as n ! 1 and " 2 (0; 1). Then, there exists
a subsequence (xnk) of (xn) such that kxnkk > " for all k 2 N. By Part
(i) of Theorem 2.6, 0 < " < 1 and kxnkk > " imply p(xnk) > "
M. Thus, p(xn) 9 0, as n ! 1. Hence, we obtain that p(xn) ! 0, as n ! 1
implies kxnk ! 0, as n ! 1.
Theorem 2.8. Let x 2 `( eA; p) and x(n) `( eA; p). If
p x(n) ! p(x), as
Proof. Let " > 0 be given. Since p(x) =
P
k ( eAx)k pk
< 1, x 2 `( eA; p) there exists k02 N such that
1 X k=k0+1 ( eAx)k pk < " 3(2M +1): (2.8)
It follows from the equality lim n!1 " p(x(n)) k0 X k=0 e Ax(n) k pk # = p(x) k0 X k=0 e Ax k pk
that there exists n02 N and for all k 2 N
p(x(n)) k0 X k=0 e Ax(n) k pk < p(x) k0 X k=0 e Ax k pk + " 3(2M) (2.9)
and for all k 2 N
k0 X k=0 e A(x(n) x) k pk < " 3: (2.10)
Therefore, we obtain from (2.8), (2.9) and (2.10) that
p(xn x) = 1 X k=0 f eA(x(n) x)gk pk < k0 X k=0 f eA(x(n) x)gk pk + 1 X k=k0+1 f eA(x(n) x)gk pk < " 3+ 2 M " 1 X k=k0+1 ( eAx(n))k pk + 1 X k=k0+1 ( eAx)k pk # < " 3+ 2 M " p(x(n)) k0 X k=0 ( eAx(n))k pk + 1 X k=k0+1 ( eAx)k pk # < " 3+ 2 M " p(x) k0 X k=0 ( eAx)k pk + " 3(2M)+ 1 X k=k0+1 ( eAx)k pk # < " 3+ " 3 + 2 M " 2 1 X k=k0+1 ( eAx)k pk # < 2" 3 + 2M +1 3(2M +1) = ":
This means that p x(n) x ! 0, as n ! 1. By Part (i) of Theorem 2.7, p x(n) x ! 0, as n ! 1 implies kxn xk ! 0, as n ! 1. Hence, xn! x, as
n ! 1.
Theorem 2.9. The sequence space `( eA; p) has the Kadec-Klee property. Proof. Let x 2 S
h `( eA; p)
i
and x(n) `( eA; p) such that kx(n)k ! 1 and x(n) w! x be given. By Part (ii) of Theorem 2.7, we have p x(n) ! 1 as n ! 1. Also
x 2 S h
`( eA; p) i
implies kxk = 1. By Part (iii) of Proposition 2, we obtain p(x) = 1.
Therefore, we have p(x(n)) ! p(x), as n ! 1:
Since x(n) ! x, as n ! 1 and qw
k : `( eA; p) ! R de…ned by qk(x) = xk is
continuous, x(n)k ! xk, as n ! 1 for all k 2 N. Therefore, x(n)! x, as n ! 1.
Because of any weakly convergent sequence in `( eA; p) is convergent, the sequence space `( eA; p) has the Kadec-Klee property.
Conclusion
Let 0 < r < 1, q = (qk) be a sequence of non-negative reals with q0 > 0 and
Qn =
Pn
k=0qk for all n 2 N, er = (rk) andes = (sk) be the convergent sequences.
Suppose that the sequences u = (uk) and v = (vk) consist of non-zero entries;
u; s 2 R, and = ( n) be the strictly increasing sequence of positive real numbers
tending to in…nity with n+1 2 n.
Let us de…ne the Riesz matrix Rq= (rq
nk) with respect to the sequence q = (qk),
the double band matrix F = (fnk) de…ned by the sequence (fn) of Fibonacci
num-bers, the matrix Ar= (ar
nk), the generalized di¤erence matrix B(u; s) = fbnk(u; s)g,
the matrix Au= (au
nk), the double sequential band matrix B(er; es) = fbnk(rk; sk)g,
the matrix eA = fank( )g and the Nörlund matrix Nq = (aqnk) with respect to the
sequence q = (qk) by rqnk:= qk Qn ; 0 k n; 0 ; k > n; fnk:= 8 > < > : fn+1 fn ; k = n 1; fn fn+1 ; k = n; 0 ; 0 k < n 1 or k > n; arnk:= ( 1+rk n+1uk ; 0 k n; 0 ; k > n; bnk(u; s) := 8 < : u ; k = n; s ; k = n 1; 0 ; 0 k < n 1 or k > n; aunk:= ( 1) n ku k ; n 1 k n; 0 ; 0 k < n 1 or k > n; bnk(rk; sk) = 8 < : rk ; k = n; sk ; k = n 1; 0 ; 0 k < n 1 or k > n;
ank( ) := ( k 2 k 1+ k 2 n n 1 ; 0 k n; 0 ; k > n; a q nk= qn k Qn ; 0 k n; 0 ; k > n; for all k; n 2 N.
For concerning literature about the geometric properties of the domain of the in…nite matrix A in the sequence space `(p), the following table may be useful:
A the space geometric properties of A refer to:
Ar `(p) ar(u; p) [10] B(u; s) `(p) `(p)b [11] Au `(p) bv(u; p) [12] B(er; es) `(p) `( eB; p) [13, 14] F `(p) `(F; p) [15] Nq `(p) Nq(p) [16]
Table 1: The domains of some triangle matrices in the spaces `(p). In the special case qk = k 2 k 1+ k 2 and Qn= n n 1, Rq is reduced
to eA. So, the space `( eA; p) can be seen as a special case of the space rq(p), the
domain of the Riesz mean Rq in the Maddox’space `(p) introduced by Altay and
Ba¸sar [6]. Since the geometric properties of the space rq(p) was not investigated the main results of the present paper are not contained in Altay and Ba¸sar [6]. So, the main results of the present study can be seen as the complementary results for Altay and Ba¸sar [6].
Acknowledgements
The authors would like to thank Mustafa Ayd¬n for his kindly giving the results concerning the topological properties of the space `( eA; p), in Section 1. The authors also record their gratitude to Esmehan Uçar for her careful reading and valuable suggestions on the earlier version of this paper which improved the presentation and readability.
References [1]
[2] I.J. Maddox, Spaces of strongly summable sequences, Quart. J. Math. Oxford (2) 18 (1967), 345–355.
[3] S. Simons, The sequence spaces `(pv) and m(pv), Proc. London Math. Soc. (3), 15 (1965),
422–436.
[4] H. Nakano, Modulared sequence spaces, Proc. Japan Acad. 27 (2) (1951), 508–512.
[5] A.M. Jarrah, E. Malkowsky, BK spaces, bases and linear operators, Rendiconti Circ. Mat. Palermo II 52 (1990), 177–191.
[6] B. Altay, F. Ba¸sar, On the paranormed Riesz sequence spaces of non-absolute type, Southeast Asian Bull. Math. 26 (5) (2002), 701–715.
[7] S. Chen, Geometry of Orlicz Spaces, Dissertationes Math. 356 (1996), 1–224. [8] J. Diestel, Geometry of Banach Spaces - Selected Topics, Springer - Verlag, 1984.
[9] L. Maligranda, Orlicz Spaces and Interpolation, Inst. Math. Polish Academy of Sciences, Poznan, 1985.
[10] C. Ayd¬n, F. Ba¸sar, Some generalizations of the sequence space arp, Iran. J. Sci. Technol.
Trans. A, Sci. 30 (2006), No. A2, 175–190.
[11] C. Ayd¬n, F. Ba¸sar, Some topological and geometric properties of the domain of the gen-eralized di¤ erence matrix B(r; s) in the sequence space `(p), Thai J. Math. 12 (1) (2014), 113–132.
[12] F. Ba¸sar, B. Altay, M. Mursaleen, Some generalizations of the space bvpof p-bounded
vari-ation sequences, Nonlinear Anal. 68 (2) (2008), 273–287.
[13] H. Nergiz, F. Ba¸sar, Some topological and geometric properties of the domain of the double sequential band matrix B(r;ees) in the sequence space `(p), AIP Conference Proceedings 1470 (2012), 163–168, doi: 10.1063/1.4747665.
[14] H. Nergiz, F. Ba¸sar, Some geometric properties of the domain of the double sequential band matrix B(er;es) in the sequence space `(p), Abstr. Appl. Anal. 2013, Article ID 421031, 7 pages, 2013. doi: 10.1155/2013/421031.
[15] E. Uçar, F. Ba¸sar, Some geometric properties of the domain of the double band matrix de…ned by Fibonacci numbers in the sequence space `(p), AIP Conference Proceedings 1611 (2014), 316–324, doi: 10.1063/1.4893854.
[16] M. Ye¸silkayagil, F. Ba¸sar, On the paranormed Nörlund sequence space of non-absolute type, Abstr. Appl. Anal. 2014, Article ID 858704, 9 pages, 2014. doi:10.1155/2014/858704. [17] E.E. Kara, Some topological and geometrical properties of new Banach sequence spaces, J.
Inequal. Appl. 2013, 15 pages, 2013. doi:10.1186/1029-242X-2013-38.
[18] M. Ba¸sar¬r, F. Ba¸sar, E.E. Kara, On the spaces of Fibonacci di¤ erence null and convergent sequences, arXiv:1309.0150v1 [math.FA], (2013).
Current address : Esra Sümeyra YILMAZ; The Graduate School of Sciences and English, Department of Mathematics, Fatih University, The Had¬mköy Campus, Büyükçekmece, 34500– ·
Istanbul, TURKEY, Feyzi Ba¸sar;Faculty of Arts and Sciences , Department of Mathematics, Fatih University, The Had¬mköy Campus, Büyükçekmece, 34500–·Istanbul, TURKEY.
Current address : ß
E-mail address : esrasumeyraylmz@gmail.com,, fbasar@fatih.edu.tr, feyzibasar@gmail.com URL: http://math.science.ankara.edu.tr/