SOME SPECIAL INTEGER SEQUENCES RELATED TO BIPARTITE GRAPHS

(1)

T.R.

SİİRT UNIVERSİTY

GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE

SOME SPECIAL INTEGER SEQUENCES RELATED TO

BIPARTITE GRAPHS

M.Sc. THESIS

DIYAR OMAR MUSTAFA ZANGANA

(153114021)

Department of Mathematics

Supervisor: Asst. Prof. Dr. Abdulkadir KARAKAŞ

Co-Supervisor: Res. Asst. Dr. Ahmet ÖTELEŞ

August-2017

SİİRT

(2)

ACCEPTANCE AND APPROVAL OF THESIS

The thesis entitled “SOME SPECIAL INTEGER SEQUENCES RELATED TO

BIPARTITE GRAPHS” submitted by Diyar Omar Mustafa Zangana has been approved

as Master Thesis at Department of Mathematics, Graduate School of Natural and Applied

Sciences, Siirt University with unanimity/majority of votes by the committee listed below

on …/…/…….

Committee Members

Signature

Head

………..

Supervisor

………..

Member

………..

I approve the above results.

Assoc. Prof. Dr. Koray ÖZRENK

Director of the Graduate School of Natural and Applied Sciences

(3)

ACKNOWLEDGMENTS

Firstly the name of Allah we started and starting.

Before of all things, I want to thank God for helping me to finish my thesis, this

is a great opportunity to acknowledge and to thanks all persons without their support, and

help this thesis would have been impossible.

I would like to add a few heartfelt words for the people who were part of this thesis in

numerous ways.

I wish to thanks my supervisors Arş.Gör.Dr.Ahmet Öteleş and

Asst.Prof.Dr.Abdulkadir Karakaş for our indefatigable guidance, valuable suggestion,

moral support, constant encouragement and contribution of time for the successful

completion of thesis work. I am very grateful to there, for providing all the facilities

needed during the thesis development.

My special thanks to my family for indispensable support and encouragement

thing my study. Finally, I would like to thank all those who helped me directly or

indirectly.

Diyar Omar Mustafa ZANGANA

SİİRT-2017

(4)

Page

ACKNOWLEDGMENTS ... iii

TABLE OF CONTENTS ... iv

LIST OF TABLES ... vi

LIST OF FIGURES ... vii

LIST OF SYMBOLS ... viii

ÖZET ... ix

ABSTRACT ... x

1. INTRODUCTION ... 1

1.1. Structure of the Thesis ... 2

2. LITERATURE RESEARCH ... 3

3. PRELIMINARIES ... 14

3.1. Special Types of Matrices ... 14

3.1.1. Diagonal matrices ... 14

3.1.2. Triangular matrices ... 14

3.1.3. Permutation matrices ... 14

3.1.4. Circulant matrices ... 15

3.1.5. Toeplitz matrices ... 15

3.1.6. Hankel matrices ... 16

3.1.7. Hessenberg matrices ... 16

3.1.8. Tridiagonal matrices ... 17

3.2. Graph Theory ... 17

3.3. Graphs and Matrices ... 22

3.3.1. Incidence Matrix ... 22

3.3.2. Adjacency Matrix ... 23

3.3.3. Laplacian Matrix ... 24

3.4. Bipartite Graph and Perfect Matching ... 25

3.5. Permanents ... 27

3.6. Number Sequences ... 29

4. SOME SPECIAL INTEGER SEQUENCES RELATED TO BIPARTITE

GRAPHS ... 36

4.1. Jacobsthal Numbers and Associated Bipartite Graphs ... 36

4.1.1. Maple procedure ... 40

4.2. Bipartite Graphs Associated with Circulant Matrices ... 41

(5)

5. CONCLUSION ... 50

6. REFERENCES ... 51

(6)

LIST OF TABLES

Page

(7)

LIST OF FIGURES

Page

Figure 3.1. A graph with 6-vertices and 5-edges ... 18

Figure 3.2. A graph with 5-vertices and 7-edges ... 18

Figure 3.3. A graph with 5-vertices and 8-edges is called a (5; 8) graph ... 19

Figure 3.4. Directed graph ... 19

Figure 3.5. Undirected graph ... 20

Figure 3.6. Directed multiple graph ... 20

Figure 3.7. Un-directed multiple graph ... 20

Figure 3.8. Un-directed Pseudo graph ... 21

Figure 3.9. Directed Pseudo graph ... 21

Figure 3.10. A graph with 6-vertices and 5-edges ... 21

Figure 3.11. A graph with 5-vertices and 8-edges ... 22

(8)

LIST OF SYMBOLS

Symbol

Explanation

𝑮

: Graph

𝑨

_𝒏

= (𝒂

_𝒊𝒋

)

: Matrix

𝐴

_𝑛

of order 𝑛 with entries 𝑎

_𝑖𝑗

𝑨

_(𝒏,𝒌)

= (𝒂

_𝒊𝒋

)

: Matrix

𝐴

_(𝑛,𝑘)

of order 𝑛 with entries 𝑎

_𝑖𝑗

𝑎

𝑖𝑗

= {

1, if − 1 ≤ |𝑗 − 𝑖| ≤ 𝑘 − 1

_{0, otherwise}

𝑮(𝑨

_𝒏

)

: Graph with adjacency matrix

𝐴

_𝑛

𝑱(𝒏)

:

𝑛th Jacobsthal number

𝑭(𝒏)

:

𝑛th Fibonacci number

𝑳(𝒏)

:

𝑛th Lucas number

𝑨

_𝒏𝒌

_:

_{𝑘th contraction of the matrix 𝐴}

𝑛

𝐩𝐞𝐫𝑨

_𝒏

: Permanent of the matrix

𝐴

_𝑛

(9)

ÖZET

YÜKSEK LİSANS

İKİ PARÇALI GRAFLARLA İLİŞKİLİ BAZI ÖZEL TAMSAYI DİZİLERİ

Diyar Omar Mustafa ZANGANA

Siirt Üniversitesi Fen Bilimleri Enstitüsü

Matematik Anabilim Dalı

Danışman

: Yrd. Doç. Dr. Abdulkadir KARAKAŞ

II. Danışman : Arş. Gör. Dr. Ahmet ÖTELEŞ

2017, 53 Sayfa

Bu tezde, iki parçalı komşuluk matrisleri 𝑛 × 𝑛 (0,1) − matrisler olan bazı belli tip iki parçalı grafları ele aldık. Sonra bu iki parçalı grafların mükemmel eşlemeleri sayılarının çok iyi bilinen sayı dizilerine (örneğin; Fibonacci Lucas Jacobsthal) eşit olduğunu gösterdik. Daha sonra, ele aldığımız bu graflar ve onların mükemmel eşlemeleriyle ilgili bazı örnekler verdik. Son olarak, bu iki parçalı grafların mükemmel eşlemeleri sayılarını hesaplamak için Maple 2016 prosedürleri sunduk.

Anahtar Kelimeler: Fibonacci dizisi, İki parçalı graf, Jacobsthal dizisi, Lucas dizisi, Mükemmel eşleme, Permanent.

(10)

x

ABSTRACT

M.Sc. THESIS

SOME SPECIAL INTEGER SEQUENCES RELATED TO

BIPARTITE GRAPHS

Diyar Omar Mustafa ZANGANA

The Graduate School of Natural and Applied Science of Siirt University

The Degree of Master of Science

In Mathematics

Supervisior

: Asst. Prof. Dr. Abdulkadir KARAKAŞ

Co-Supervisior : Res. Asst. Dr. Ahmet ÖTELEŞ

2017, 53 Pages

In this thesis, we consider some certain types of bipartite graphs whose bipartite adjacency matrices are the 𝑛 × 𝑛 (0,1) − matrices. Then we show that the numbers of perfect matchings (1 − factosrs) of these bipartite graphs are equal to the famous integer sequences (e.g. Fibonacci, Lucas, Jacobsthal). After that, we give some examples concerned with these graphs and their perfect matchings. Finally, we present Maple procedures in order to calculate the numbers of perfect matchings of the bipartite graphs.

Keywords: Bipartite graph, Fibonacci sequence, Jacobsthal sequence, Lucas sequence, Perfect matching, Permanent.

(11)

1. INTRODUCTION

Bipartite graph is a graph in which the vertices can be divided into two parts

such that no two vertices in the same part are joined by an edge. The investigation of

the properties of bipartite graphs was begun by König. His work was motivated by

an attempt to give a new approach to the investigation of matrices on determinants

of matrices. As a practical matter, bipartite graphs form a model of the interaction

between two di¤erent types of objects. For example; social network analysis, railway

optimization problem, marriage problem etc (Asratian et al., 1998).

A perfect matching (1-factors) of a graph is a matching (i.e., an independent

edge set) in which every vertex of the graph is incident to exactly one edge of

the matching. "The enumeration or actual construction of perfect matching of a

bipartite graph has many applications, for example, in maximal ‡ow problems and

in assignment and scheduling problems arising in operational research" (Minc, 1978).

The number of perfect matchings of bipartite graphs also plays a signi…cant role in

organic chemistry (Wheland, 1953).

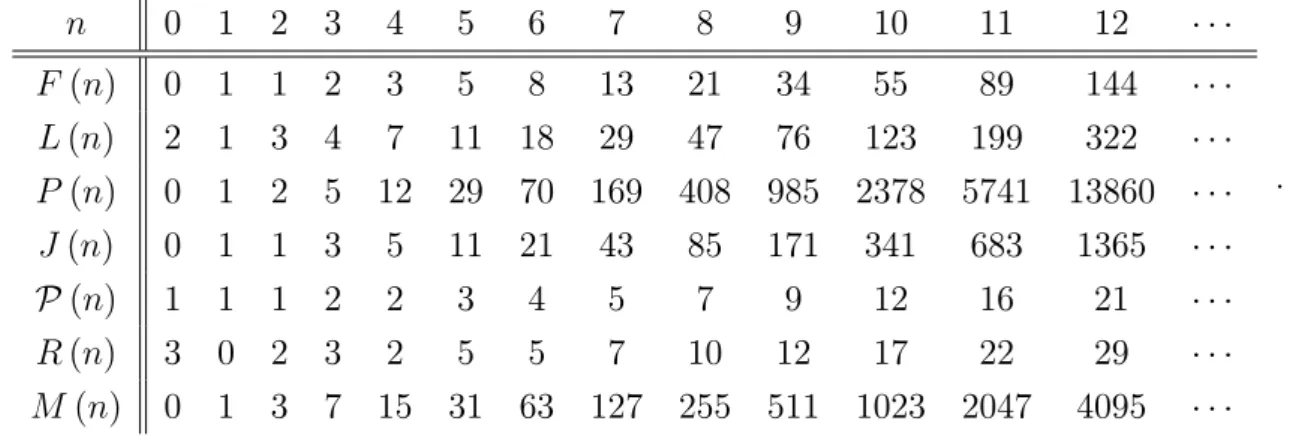
Fibonacci, Lucas and Jacobsthal numbers which are respectively de…ned by

the recurrence relation

F (n) = F (n

1) + F (n

2) ;

F (0) = 0

and F (1) = 1

L (n) = L (n

1) + L (n

2) ;

L (0) = 2

and L (1) = 1

J (n) = J (n

1) + 2J (n

2) ;

J (0) = 0

and J (1) = 1,

for n

2, belong to a large family of positive integers. They have many interesting

properties and applications to almost every …eld of science and art. They continue

to contribute signi…cant innovations for investigations, and reveal the niceness of

mathematics in many …elds, particularly number theory (Koshy, 2001; Koshy, 2011;

Horadam, 1988).

"The permanent of an n

n

matrix A = (a

ij

)

is de…ned by

per (A) =

X

Sn n

Y

i=1

a

i (i)

where the summation extends over all permutations

of the symmetric group S

n

.

The permanent of a matrix is analogous to the determinant, where all of the signs

used in the Laplace expansion of minors are positive" (Minc, 1978). Permanents have

many applications in physics, chemistry, electrical engineering, graph theory etc.

Some of the most important applications of permanents are via graph theory. A more

di¢ cult problem with many applications is the enumeration of perfect matchings of

(12)

has been very popular problem.

1.1. Structure of the Thesis

The rest of the thesis is structured as follows.

In Chapter 2, we present a discussion of previously published work that I

did in this area in conjunction with other authors.

In Chapter 3, we give the fundamental de…nitions, structures and theorems

which are necessary to better understand the topics contained within this text.

In Chapter 4, we consider a bipartite graph. Then we show that the

num-bers of perfect matchings of this graph generate the Jacobsthal numnum-bers by the

contraction method. Finally, a Maple procedure is presented in order to compute

the numbers of perfect matchings of the graph.

In Chapter 5, we …rstly introduce two lemmas ralated to bipartite graphs

as-sociated with Fibonacci numbers. After that, we de…ne a bipartite graph asas-sociated

with n

n (0; 1)-circulant matrix whose the numbers of perfect matchings generate

the Lucas numbers. Finally, two Maple procedures are presented to compute the

numbers of perfect matchings in these graphs.

(13)

2. LITERATURE RESEARCH

The purpose of this chapter is to further motivate the rest of the thesis

by presenting a discussion of previously published work that I did in this area in

conjunction with other authors.

Lee et al. (1997) consider "a bipartite graph G F

(n;2)

= (f

i;j

)

with bipartite

adjacency matrix is the n

n

tridiagonal matrix of the form

F

(n;2)

=

0 B

B

@

1

0

1

1 . ..

..

.

0

1 . .. ... ... ...

..

.

. .. ... ... 1 0

..

.

. .. 1

1

0

1

1 C

C

A

;

(1)

with the entries are

f

ij

=

(

1;

_{if jj}

i

_j

1;

0;

otherwise

". Then they obtain "the number of perfect matchings of G F

(n;2)

is the (n + 1)st

Fibonacci number F (n + 1)". In other words,

per

_F

(n;2)

= F (n + 1) :

(2)

They also consider "a bipartite graph G F

(n;k)

= (f

i;j

)

with bipartite adjacency

matrix is the n

n (0; 1)-matrix of the form

F

(n;k)

=

0 B

B

@

1

0

1

0

1

0

0 . .. ... ... ...

. .. ... ...

..

.

. ..

. .. 0

..

.

. ..

1 . .. ... ... ...

0

1

1 C

C

A

(3)

with the entries are

f

ij

=

(

1;

if

1 _jj

i

_j

k

1;

(14)

". Then they obtain "the number of perfect matchings of G F

(n;k)

is g

k

(n + k

1) ;

where

g

k

_(n)

_{is the nth k-Fibonacci number" (Lee et al., 1997). This time, they consider}

"an another bipartite graph G (U

n

= (u

i;j

))

with bipartite adjacency matrix is the

n

n (0; 1)-matrix of the form

U

n

=

0 B

B

@

1

0

1

0

1

0

1

1 ..

.

. .. ... ... ... ...

..

.

. .. 1

0

1

0

1

1 C

C

A

with the entries are

u

ij

=

8 >

<

>

:

1;

if i = j = 1 or i = j = n;

1;

if i < j or j

i =

1 0;

otherwise

". Then they obtain "the number of perfect matchings of G (U

n

)

is the (n + 1)st

Fibonacci number F (n + 1)" (Lee et al., 1997).

Lee (2000) considers "a bipartite graph G L

(n;2)

= (l

i;j

)

with bipartite

adjacency matrix is the n

n

matrix of the form

L

(n;2)

=

0 B

B

@

1

0

1

0

1

0 ..

.

0

1 . .. ... ... 0

..

.

. .. ... ... ... 0

..

.

. .. ... ... 1

0

1

1 C

C

A

;

with the entries are

l

i;j

=

8 >

>

<

>

:

1;

if i = j = 1 or i = 1 and j = 3;

1;

_{if i > 2 and jj}

i

_j

1;

0;

otherwise

". Then he shows that "the number of perfect matchings of G L

(n;2)

is (n

1)st

Lucas number L (n

1)

for n

3 _{". He also considers "a bipartite graph G L}

(n;k)

with bipartite adjacency matrixL

(n;k)

=

F

(n;k)

+ E

1;k+1

P

k_j=2

E

1;j

for n

3, where

(15)

j)-entry and zeros elsewhere". Namely,

L

(n;k)

=

0 B

B

@

1

0

1

0

1

0

1

0

0 . .. ... ... ...

. .. ... ...

..

.

. ..

. .. 0

..

.

. ..

1 . .. ... ... ...

0

1

1 C

C

A

Then he shows that "the number of perfect matchings of G L

(n;k)

is l

k

(n

1) ;

where

l

k

_(n)

_{is the nth k-Lucas number" (Lee, 2000). This time, he de…nes "the matrix}

B

n

as

B

n

=

F

(n;2)

+ E

13

E

23

+ E

24

E

34

where F

(n;2)

is the matrix in (1) and E

i;j

denotes the n

n

matrix with 1 at the

(i; j)-entry and zeros elsewhere". Let G (B

n

)

be the bipartite graph with bipartite

adjacency matrix B

n

:

Then he shows that "the number of perfect matchings of

G (B

n

)

is (n

1)st Lucas number L (n

1)" (Lee, 2000).

Shiu et al. (2003) …rstly de…ne the (k; )-sequences s

k

_{(n) :}

_{Then they give}

the following result:

"For a …xed m

1, suppose n; k

2 and n

m:

_{Let G B}

(n;k)

a bipartite

graph with bipartite adjacency matrix has the form

B

(n;k)

=

0 B

B

@

a

1

a

2

: : :

a

m

0 : : : 0

1

0 _F

(n 1;2)

..

.

0

1 C

C

A

;

for some elements a

1

; a

2

; : : : ; a

m

in a ring R:Then the number of perfect matching

of G B

(n;k)

is nth (k; )-number s

k

(n)

with

= (a

1

; a

2

; : : : ; a

m

)".

(16)

bi-partite adjacency matrix has the form

V

n

=

0 B

B

@

1

0

1

0

0 ..

.

. .. ... ... ... ... ...

..

.

. .. ... ... ... 0

..

.

. .. ... ... 1

0

1

1 C

C

A

with the entries are

v

ij

=

(

1;

if

1 j

i

1 or i = 1;

0;

otherwise

". Then they obtain that "the number of perfect matchings of G (V

n

)

is

P

n

i=0

F (i) =

F (n + 2)

1;

where F (n) is the nth Fibonacci number". They also consider "a

bipartite graph G (W

n

)

with bipartite adjacency matrix W

n

= V

n

+ Y

n

;

where Y

n

de-notes the n

n

matrix with

1 at the (1; 2)-entry, 1 at the (2; 4)-entry and zeros

elsewhere". Clearly,

W

n

=

0 B

B

@

1

0

1

0

1

0

0 ..

.

. .. ... ... ... ... ...

..

.

. .. ... ... ... 0

..

.

. .. ... ... 1

0

1

1 C

C

A

Then for n

4;

they obtain that "the number of perfect matchings of G (W

n

)

is

P

n 2

i=0

L (i) = L (n)

1;

where L (n) is the nth Lucas number" (K¬l¬ç and Ta¸

sc¬,

2008a).

K¬l¬ç and Ta¸

sc¬(2008b) consider "a bipartite graph G M

(n;k)

with bipartite

adjacency matrix M

(n;k)

=

F

(n;k)

+U

(n;k)

;

where F

(n;k)

is the matrix given by (3) and

(17)

0": Clearly,

M

(n;k)

=

0 B

B

@

1

0

1

0

1

0

0 ..

.

. .. ... ... ... ... ... ... ... ...

..

.

0

1

0

0 ..

.

0

1

0

0 ..

.

0

1

0

1

0

1

0

1

1 C

C

A

:

(4)

Then for n

3;

they obtain that "the number of perfect matchings of G M

(n;k)

is

the nth k-Lucas number, l

k

(n)". They also consider "a bipartite graph G T

(n;k)

with bipartite adjacency matrix T

(n;k)

=

F

(n;k)

+ V

(n;k)

for 2

k < n;

where F

(n;k)

is the matrix given by (3) and V

(n;k)

= (v

ij

)

is the n

n (0; 1)-matrix with v

1j

= 1

if k + 1

j

n

and otherwise 0": Clearly,

T

(n;k)

=

0 B

B

@

1

0

1

0

0 ..

.

. .. ... ... ... ... ... ... ...

..

.

..

.

0

1

1 . .. ...

..

.

0

1

0 ..

.

0

1

0

1

0

1

0

1

1 C

C

A

:

Then they obtain that "the number of perfect matchings of G T

(n;k)

is the sums

of k-Fibonacci numbers,

P

n_j=1

g

k

(j)

for n

3" (K¬l¬ç and Ta¸

sc¬, 2008b). This

time, they consider "a bipartite graph G E

(n;k)

with bipartite adjacency matrix

E

(n;k)

= M

(n;k)

+ D

(n;k)

for 2

k < n;

where M

(n;k)

is the matrix given by (4) and

(18)

0": Clearly,

E

(n;k)

=

0 B

B

@

1

0

1

0

0 ..

.

. .. ... ... ... ... ... ... ... ... ...

..

.

0

1

0

0 ..

.

0

1

0

0 ..

.

0

1

0

1

0

1

0

1

1 C

C

A

:

Then they obtain that "the number of perfect matchings of G E

(n;k)

is the sums

of k-Lucas numbers,

P

n 1_j=1

l

k

(j)

for n

3" (K¬l¬ç and Ta¸

sc¬, 2008b).

K¬l¬ç and Stakhov (2009) consider "a bipartite graph G M

(n;p)

with

bipar-tite adjacency matrix M

(n;p)

= (m

ij

)

with m

i+1;i

= m

i;i

= m

i;i+p

= 1

for a …xed

integer p and otherwise 0": Clearly,

M

(n;p)

=

0 B

B

@

1

0

1

0

1

0

1 . .. ...

0

1

0

1

0

1

0

1 ..

.

. .. ... ... ... ...

0 ..

.

. .. ... ... ... ... ...

..

.

. .. ... ... ... 0

0

1

1 C

C

A

:

(5)

Then they obtain that "the number of perfect matchings of G M

(n;p)

is the (n + 1)st

generalized Fibonacci p-number F

p

(n + 1)

for n

3". They also consider a bipartite

graph G T

(n;p)

with bipartite adjacency matrix has the form

T

(n;p)

=

0 B

B

@

1 1 1

1 1

1

0 M

(n 1;p)

..

.

0

1 C

C

A

;

(19)

where M

(n 1;p)

is the matrix of order (n

1)

given by (5)". Then they obtain

that "the number of perfect matchings of G T

(n;p)

is the sums of the consecutive

generalized Fibonacci p-numbers,

P

n_i=1

F

p

(i)

for n

3" (K¬l¬ç and Stakhov, 2009).

Akbulak and Ötele¸

s (2013) give the following results for the number of

per-fect matchings in bipartite graphs with upper Hessenberg adjacency matrix related

to Fibonacci, Lucas and Padovan numbers.

"Let G(U

n

= (u

ij

))

be a bipartite graph with bipartite adjacency matrix is

the n

n (0; 1)-upper Hessenberg matrix de…ned by

U

n

=

0 B

B

@

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

1 C

C

A

(6)

where

u

ij

=

8 >

<

>

:

1;

if j

i =

1;

if i

j

and j

i

0 (mod 2) ;

0;

otherwise.

Then the number of perfect matchings of G(U

n

)

is the nth Fibonacci number F (n)

for n

3" (Akbulak and Ötele¸

s, 2013).

"Let G(V

n

= (v

ij

))

be a bipartite graph with bipartite adjacency matrix is

the n

n (0; 1)-upper Hessenberg matrix de…ned by

V

n

=

0 B

B

@

1 1 1

1 1 0 1

0

1 0 1

0 0

U

n 2

..

.

..

.

0 0

1 C

C

A

;

where U

n 2

is the matrix of order (n

2)

in 6. Then the number of perfect matchings

of G(V

n

)

is the (n

1)st Lucas number L (n

1)

for n

3" (Akbulak and Ötele¸

s,

2013).

(20)

the n

n (0; 1)-upper Hessenberg matrix de…ned by

W

n

=

0 B

B

@

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1 C

C

A

;

where

w

ij

=

8 >

<

>

:

1;

if i = 1 or j

i =

1;

if i

j

and j

i

1 (mod 3) ;

0;

otherwise.

Then the number of perfect matchings of G(W

n

)

is the nth Padovan number P (n)

for n

3" (Akbulak and Ötele¸

s, 2013).

Ötele¸

s (2017) gives the following results for the number of perfect matchings

in bipartite graphs related to the well-known integer sequences (Fibonacci, Lucas

i.e.).

"Let G (H

n

= (h

i;j

)) (n = 2t; t

2 N) be a bipartite graph with bipartite

adjacency matrix is the n

n (0; 1)-tridiagonal matrix has the form

H

n

=

0 B

B

@

1

0

1

0

1 . ..

..

.

0

1

1 . ..

..

.

..

.

. .. 1

0

1 . .. ...

..

.

. .. 1 ... 1 0

..

.

. .. ...

1

0

1

1 C

C

A

;

(7)

where

h

i;j

=

8 >

>

<

>

:

1;

_{if jj}

i

_{j = 1;}

1;

if i = j = 2m

1 (m

_{2 N) ;}

0;

otherwise.

Then the number of perfect matchings of G (H

n

)

is 1" (Ötele¸

s, 2017).

"Let G (H

n

) (n = 2t + 1; t

2 N) be a bipartite graph with bipartite

adja-cency matrix H

n

given by (7). Then the number of perfect matchings of G (H

n

)

is

n+1

2

" (Ötele¸

s, 2017).

(21)

the n

n (0; 1)-tridiagonal matrix has the form

K

n

=

0 B

B

@

1

0

1

0

1 . ..

..

.

0

1

1 . ..

..

.

..

.

. .. 1

0

1 . .. ...

..

.

. .. 1

1

0 ..

.

. .. ... ... 1

0

1

1 C

C

A

;

where k

2;2

= k

4;4

= 0;

all other terms on the main diagonal are 1; all terms on the

sub-diagonal and superdiagonal are 1 and otherwise k

i;j

= 0. Then for n

3, the

number of perfect matchings of G (K

n

)

is the (n

3)rd Lucas number L (n

3)"

(Ötele¸

s, 2017).

"Let G (B

n

= (b

i;j

))

be a bipartite graph with bipartite adjacency matrix is

the n

n (0; 1)-anti-tridiagonal matrix has the form

B

n

=

0 B

B

@

0

1

1 ..

.

. .

.

1

1 ..

.

. .

.

. .

.

. .

.

1

0

0 . .

.

. .

.

. .

.

. .

.

..

.

1

1 . .

.

. .

.

..

.

1

0

1 C

C

A

;

where

b

i;j

=

(

1;

_{if ji + j mod (n + 1)j}

1;

0;

otherwise.

Then for n

2, the number of perfect matchings of G (B

n

)

is the (n + 1)st Fibonacci

number F (n + 1)" (Ötele¸

s, 2017).

"Let G (D

n

= (d

i;j

))

be a bipartite graph with bipartite adjacency matrix

has the form

D

n

=

0 B

B

@

0

1

0

1 ..

.

0

1

1 ..

.

. .

.

. .

.

. .

.

1

0

0 . .

.

. .

.

. .

.

. .

.

..

.

1

1 . .

.

..

.

1

0

1 C

C

A

(22)

where

d

i;j

=

8 >

>

<

>

:

1;

if i = 1 and j = n

2; j = n;

1;

_{if ji + j mod (n + 1)j}

_{2 i n}

1;

0;

otherwise.

Then for n

3, the number of perfect matchings of G (D

n

)

is the (n

1)st Lucas

number L (n

1)" (Ötele¸

s, 2017).

"Let G (U

n

= (u

i;j

))

be a bipartite graph with bipartite adjacency matrix

has the form

U

n

=

0 B

B

@

1

0

1

1 ..

.

. .

.

1

0 ..

.

. .

.

. .

.

. .

.

1 . .

.

0

1 . .

.

. .

.

. .

.

..

.

1

1 . .

.

0

1

0

1 C

C

A

where

u

i;j

=

8 >

>

<

>

:

1;

if i = 1 and 1

j

n;

1;

_{if ji + j mod (n + 1)j}

_{2 i n}

1;

0;

otherwise.

Then for n

2, the number of perfect matchings of G (U

n

)

is F (n + 2)

1, where

F (n)

is the nth Fibonacci number" (Ötele¸

s, 2017).

"Let G (V

n

= (v

i;j

))

be a bipartite graph with bipartite adjacency matrix

has the form

V

n

=

0 B

B

@

1

0

1

0

1

1 ..

.

. .

.

0

1

0 ..

.

. .

.

. .

.

. .

.

1

0

0 . .

.

. .

.

. .

.

1 . .

.

. .

.

..

.

0

1

1 . .

.

. .

.

. .

.

..

.

1

0

1

0

1 C

C

A

where

v

i;j

=

8 >

>

<

>

:

1;

if i = 1 and 1

j

n

2; j = n;

1;

if i = 2 and j = n

3;

1;

_{if ji + j mod (n + 1)j}

_{2 i n}

1;

0;

otherwise.

(23)

is the nth Lucas number" (Ötele¸

s, 2017).

"Let G (P

n

= (p

ij

))

be a bipartite graph with bipartite adjacency matrix is

the n

n (0; 1)-pentadiagonal matrix has the form

P

n

=

0 B

B

@

1

0

1

0

1

0

1 . ..

..

.

1

0

1 . .. ... ... ...

0

1 . .. ... ... 1 0

..

.

. .. ... ... ... 0 1

..

.

. .. 1

0

1

0

1

0

1

1 C

C

A

:

Then the number of perfect matchings of G (P

n

)

is obtained as

per (P

n

) =

8 <

:

F

n+1₂

F

n+3₂

;

if n is odd,

F

n₂

+ 1

2

;

if n is even,

(24)

3. PRELIMINARIES

In this chapter, we give the fundamental de…nitions, structures and theorems

which are necessary to better understand the topics contained within this text.

3.1. Special Types of Matrices

3.1.1. Diagonal matrices

"A matrix D = [d

ij

]

2 M

n;m

(F )

is diagonal if d

ij

= 0

whenever j 6= i" (Horn

and Johnson, 1990).

3.1.2. Triangular matrices

"A matrix T = [t

ij

]

2 M

n;m

(F )

is upper triangular if t

ij

= 0

whenever

i > j. If t

ij

= 0

whenever i

j

, then T is said to be strictly upper triangular.

Analogously, T is lower triangular (or strictly lower triangular) if its transpose is

upper triangular (or strictly upper triangular). A triangular matrix is either lower

or upper triangular; a strictly triangular matrix is either strictly upper triangular

or strictly lower triangular" (Horn and Johnson, 1990).

3.1.3. Permutation matrices

"A square matrix P is a permutation matrix if exactly one entry in each

row and column is equal to 1 and all other entries are 0. Multiplication by such

matrices e¤ects a permutation of the rows or columns of the matrix multiplied. For

example,

₀

B

@

0 1 0

1 0 0

0 0 1

1 C

A

0 B

@

1

2

3

1 C

A =

0 B

@

2

1

3

1 C

A

illustrates how a permutation matrix produces a permutation of the rows (entries)

of a vector: it sends the …rst entry to the second position, sends the second entry

to the …rst position, and leaves the third entry in the third position" (Horn and

Johnson, 1990).

(25)

3.1.4. Circulant matrices

"A matrix A 2 M

n

(F )

of the form

A =

0 B

B

@

a

1

a

2

a

n

a

n

a

1

a

2

a

n 1

a

n 1

a

n

a

1

a

n 2

..

.

..

.

. .. ...

..

.

a

2

a

3

a

n

a

1

1 C

C

A

is a circulant matrix. Each row is the previous row cycled forward one step; the

en-tries in each row are a cyclic permutation of those in the …rst. The n n permutation

matrix

C =

0 B

B

@

0 1

0

0 ..

.

0

1 ..

.

. .. ... 0

0

1 1 0

0

1 C

C

A

=

0 I

n 1

1 0

1;n 1

!

is the basic circulant permutation matrix. A matrix A 2 M

n

(F )

can be written in

the form

A =

n 1

X

k=0

a

k+1

C

nk

(a polynomial in the matrix C

n

) if and only if it is a circulant. We have C

n0

= I =

C

n

;

and the coe¢ cients a

1

; : : : ; a

n

are the entries of the …rst row of A" (Horn and

Johnson, 1990).

3.1.5. Toeplitz matrices

"A matrix A = a

ij

2 M

n+1

(F )

of the form

A =

0 B

B

@

a

0

a

1

a

2

a

n

a

1

a

0

a

1

a

2

a

n 1

a

2

a

1

a

0

a

1

a

n 2

..

.

..

.

. .. ... ...

..

.

..

.

..

.

. .. ...

a

1

a

n

a

n+1

a

1

a

0

1 C

C

A

is a Toeplitz matrix.

The entry a

ij

is equal to a

j i

for some given sequence

(26)

the diagonals parallel to the main diagonal. The Toeplitz matrices

B =

0 B

B

@

0 1

0

0 . ..

. .. 1

0

1 C

C

A

and

F =

0 B

B

@

0

1

0 . .. ...

0

1

0

1 C

C

A

are called the backward shift and forward shift because of their e¤ect on the elements

of the standard basis fe

1

; : : : ; e

n+1

g. Moreover, F = B

T

and B = F

T

. A matrix

A

_{2 M}

n+1

can be written in the form

A =

n

X

k=1

a

k

F

k

+

n

X

k=0

a

k

B

k

if and only if it is a Toeplitz matrix. Toeplitz matrices arise naturally in problems

involving trigonometric moments" (Horn and Johnson, 1990).

3.1.6. Hankel matrices

"A matrix A 2 M

n+1

(F )

of the form

A =

0 B

B

@

a

0

a

1

a

2

a

n

a

1

a

2

. .

.

a

n+1

a

2

. .

.

..

.

..

.

a

n

a

2n 1

a

n

a

n+1

a

2n 1

a

2n

1 C

C

A

is a Hankel matrix . Each entry a

ij

is equal to a

i+j 2

for some given sequence

a

0

; a

1

; a

2

; : : : ; a

2n 1

; a

2n

:

The entries of A are constant along the diagonals

perpen-dicular to the main diagonal. Hankel matrices arise naturally in problems involving

power moments" (Horn and Johnson, 1990).

3.1.7. Hessenberg matrices

(27)

be an upper Hessenberg matrix if a

ij

= 0

for all i > j + 1 :

A =

0 B

B

@

a

11

F

a

21

a

22

a

32

. ..

0 a

n;n 1

a

nn

1 C

C

A

An upper Hessenberg matrix A is said to be unreduced if all its sub-diagonal entries

are nonzero, that is, if a

i+1

; i = 0

for all i = 1; : : : ; n

1;

the rank of such a matrix

is at least n

1 since its …rst n

1 columns are independent" (Horn and Johnson,

1990).

3.1.8. Tridiagonal matrices

"A matrix A = [a

ij

]

2 M

n

(F )

that is both upper and lower Hessenberg is

called tridiagonal, that is, A is tridiagonal if a

ij

= 0

whenever ji

j

j > 1:

A =

0 B

B

@

a

1

b

1

0 c

1

a

2

. ..

. .. ... b

n 1

0 c

n 1

a

n

1 C

C

A

" (Horn and Johnson, 1990).

3.2. Graph Theory

De…nition 1

_{"A graph G consists of a set of objects V = fv}

1

; v

2

; v

3

; : : :

g called

ver-tices (also called points or nodes) and other set E = fe

1

; e

2

; e

3

; : : :

g whose elements

are called edges (also called lines or arcs)" (Vasudev, 2006).

De…nition 2

"The set V (G) is called the vertex set of G and E(G) is the edge set.

Usually the graph is denoted as G = (V; E)" (Vasudev, 2006).

Let G be a graph and fu; vg an edge of G. Since fu; vg is 2-element set, we may

write fv; ug instead of fu; vg. It is often more convenient to represent this edge by

uv

or vu: If e = uv is an edge of a graph G, then we say that u and v are adjacent in

G

and that e joins u and v. (We may also say that each that of u and v is adjacent

to or with the other).

(28)

and

E(G) =

_{fuv; uw; wx; xy; xzg:}

Now we have the graph in the Figure 3.1 by considering these sets.

Figure 3.1. A graph with

6

-vertices and

5

-edges

Every graph has a diagram associated with it. The vertex u and an edge e

are incident with each other as are v and e. If two distinct edges say e and f are

incident with a common vertex, then they are adjacent edges.

Example 4

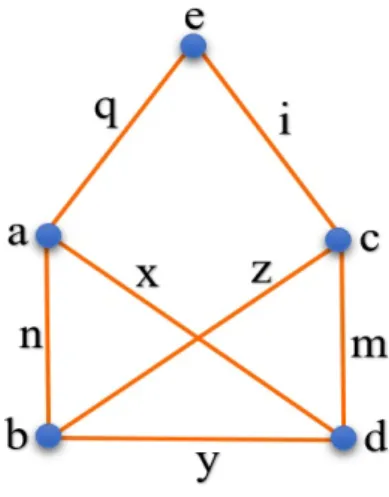
In Figure 3.2 the vertices a and b are adjacent but a and c are not.

The edges x and y are adjacent but x and z are not. Although the edges x and z

intersect in the diagram, their intersection is not a vertex of the graph.

5

-vertices and

7

-edges

De…nition 5

"A graph with p-vertices and q-edges is called a (p; q) graph. The

(1; 0) graph is called trivial graph" (Vasudev, 2006).

Example 6

_{Let V = f1; 2; 3; 4g and E = ff1; 2g; f1; 3g; f3; 2g; f4; 4gg:Then G(V; E)}

is a graph.

Example 7

_{Let V = f1; 2; 3; 4g and E = ff1; 5g; f2; 3gg:Then G(V; E) is not a}

(29)

5

-vertices and

8

-edges is called a

(5; 8)

graph

De…nition 8

"A directed graph or digraph G consists of a set V of vertices and a

set E of edges such that e 2 E is associated with an ordered pair of vertices. In other

words, if each edge of the graph G has a direction then the graph is called directed

graph" (Vasudev, 2006).

In the diagram of directed graph, each edge e = (u; v) is represented by an

arrow or directed curve from initial point u of e to the terminal point v. Figure 3.4

is an example of a directed graph.

Figure 3.4. Directed graph

Suppose e = (u; v) is a directed edge in a digraph, then

(i) u is called the initial vertex of e and v is the terminal vertex of e

(ii) e is said to be incident from u and to be incident to v.

(iii) u is adjacent to v, and v is adjacent from u.

De…nition 9

"An un-directed graph G consists of set V of vertices and a set E of

edges such that each edge e 2 E is associated with an unordered pair of vertices. In

other words, if each edge of the graph G has no direction then the graph is called

(30)

We

can refer to an edge joining the vertex pair i and j as either (i; j) or

(j;

i): Figure 3.5 is an example of an undirected graph.

Figure 3.5. Undirected graph

De…nition 10

"An edge of a graph that joins a node to itself is called loop or self

loop" (Vasudev, 2006).

For example, a loop is an edge (v

i

; v

j

)

where v

i

= v

j

.

De…nition 11

"A multi-graph is a graph which is permitted to have multiple edges

(also called parallel edges) that is, edges that have the same end nodes" (Vasudev,

2006).

Two edges (v

i

; v

j

)

and (v

f

; v

r

)

are parallel edges if v

i

= v

f

and v

j

= v

r

.

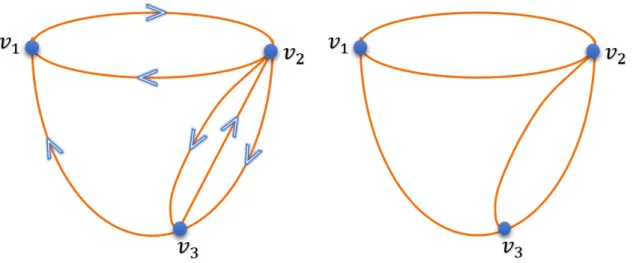
Figure 3.6. Directed multiple graph Figure 3.7. Un-directed multiple graph

In Figure 3.6, there are two parallel edges associated with v

2

and v

3

. In Figure 3.7,

there are two parallel edges joining nodes v

1

and v

2

and v

2

and v

3

(Vasudev, 2006).

De…nition 12

"A graph in which loops and multiple edges are allowed, is called a

pseudo graph.

(31)

Figure 3.8. Un-directed Pseudo graph Figure 3.9. Directed Pseudo graph

". (Vasudev, 2006).

De…nition 13

"A graph which has neither loops nor multiple edges. i.e., where

each edge connects two distinct vertices and no two edges connect the same pair of

vertices is called a simple graph" (Vasudev, 2006).

Figure 3.4 and 3.5 represents simple un-directed and directed graph because

the graphs do not contain loops and the edges are all distinct.

De…nition 14

"A graph with …nite number of vertices as well as a …nite number of

edges is called a …nite graph. Otherwise, it is an in…nite graph" (Vasudev, 2006).

De…nition 15

"The number of edges incident on a vertex v

i

with self-loops counted

twice (is called the degree of a vertex v

i

and is denoted by deg

G

(v

i

) or degv

i

or d(v

i

)"

(Vasudev, 2006).

The degrees of vertices in the graph G and H are shown in Figure 3.10 and

3.11.

(32)

and

5

-vertices and

8

-edges

In G as shown in Figure 3.10, deg

G

(v

2

) = 2 = deg

G

(v

4

) = deg

G

(v

1

), deg

G

(v

3

) = 3

and

deg

_G

(v

5

) = 1

In H as shown in Figure 3.11 deg

H

(v

2

) = 5; deg

H

(v

4

) = 3; deg

H

(v

3

) =

5; deg

_H

(v

1

) = 4

and deg

H

(v

5

) = 1

(Vasudev, 2006).

"The degree of a vertex is some times also referred to as its valency"

(Va-sudev, 2006).

3.3. Graphs and Matrices

3.3.1. Incidence Matrix

"Let G be a graph with V (G) = f1; : : : ; ng and E(G) = fe

1

; : : : ; e

m

g .

Suppose each edge of G is assigned an orientation, which is arbitrary but …xed. The

(vertex-edge) incidence matrix of G, denoted by Q(G), is the n

m

matrix de…ned

as follows. The rows and the columns of Q(G) are indexed by V (G) and E(G),

respectively. The (i; j)-entry of Q(G) is 0 if vertex i and edge e

j

are not incident,

and otherwise it is 1 or

1 according as e

j

originates or terminates at i, respectively.

We often denote Q(G) simply by Q. Whenever we mention Q(G) it is assumed that

the edges of G are oriented" (Bapat, 2010).

(33)

:

Then Its incidence matrix is given by Q as

Q =

0 B

B

@

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

1 C

C

A

:

3.3.2. Adjacency Matrix

"Let G be a graph with V (G) = f1; : : : ; ng and E(G) = fe

1

; : : : ; e

m

g . The

adjacency matrix of G, denoted by A(G); is the n

n

matrix de…ned as follows. The

rows and the columns of A(G) are indexed by V (G). If i 6= j then the (i; j)-entry

of A(G) is 0 for vertices i and j non-adjacent, and the (i; j)-entry is 1 for i and

j

adjacent. The (i; i)-entry of A(G) is 0 for i = 1; : : : ; n. We often denote A(G)

simply by A" (Bapat, 2010).

(34)

:

Then its adjacency matrix is given A (G) as

A (G) =

0 B

B

@

0 1 1 1 0

1 0 1 0 0

1 1 0 1 1

1 0 1 0 1

0 0 1 1 0

1 C

C

A

:

Clearly A is a symmetric matrix with zeros on the diagonal. For i 6= j; the principal

sub-matrix of A formed by the rows and the columns i; j is the the zero matrix if

i

j

and otherwise it equals

0 1

1 0

!

.

3.3.3. Laplacian Matrix

"Let G be a graph with V (G) = f1; : : : ; ng and E(G) = fe

1

; : : : ; e

m

g . The

Laplacian matrix of G, denoted by L(G), is the n

n

matrix de…ned as follows. The

rows and columns of L(G) are indexed by V (G). If i 6= j then the (i; j)-entry of

L(G)

is 0 if vertex i and j are not adjacent, and it is

1 if i and j are adjacent. The

(i; i)-entry of L(G) is d

i

, the degree of the vertex i; i = 1; 2; : : : ; n" (Bapat, 2010).

"Let D(G) be the diagonal matrix of vertex degrees. If A(G) is the adjacency

matrix of G, then note that L(G) = D(G)

A(G)" (Bapat, 2010).

"Suppose each edge of G is assigned an orientation, which is arbitrary

but …xed. Let Q(G) be the incidence matrix of G. Then observe that L(G) =

Q(G)Q(G)

0

:

This can be seen as follows. The rows of Q(G) are indexed by V (G).

The (i; j)-entry of Q(G)Q(G)

0

is the inner product of the rows i and j of Q(G): If

i = j

then the inner product is clearly d

i

, the degree of the vertex i. If i 6= j; then

the inner product is

1 if the vertices i and j are adjacent, and zero otherwise"

(Bapat, 2010).

(35)

:

Then its Laplacian matrix is given by L(G) as

L(G) =

0 B

B

@

3

1

0

1

0

1

3

1

0

1

0

1

2

0

1

0

1

0

2

1

0

1

5

1

0

1

1 C

C

A

:

3.4. Bipartite Graph and Perfect Matching

De…nition 19

"A bipartite graph G is a graph whose vertex set V can be partitioned

into two subsets V

1

and V

2

such that every edge of G joins a vertex in V

1

and a

vertex in V

2

:

In other words, there are no edges which connect two vertices in V

1

or

in V

2

" (Diestel, 2005).

(36)

Bipartite graphs have a huge of applications in modern science. For example;

When modeling relations between two di¤erent classes of objects, bipartite

graphs very often arise naturally. For instance, "a graph of football players

and clubs, with an edge between a player and a club if the player has played

for that club, is a natural example of an a¢ liation network, a type of bipartite

graph used in social network analysis" (Wasserman and Faust, 1994).

Another example where bipartite graphs appear naturally is in the railway

optimization problem, in which "the input is a schedule of trains and their

stops, and the goal is to …nd a set of train stations as small as possible such

that every train visits at least one of the chosen stations. This problem can be