IS S N 1 3 0 3 –5 9 9 1
SOME BASIC RESULTS ON THE SETS OF SEQUENCES WITH GEOMETRIC CALCULUS
CENG·IZ TÜRKMEN AND FEYZ·I BA¸SAR
Abstract. As an alternative to the classical calculus, Grossman and Katz [Non-Newtonian Calculus, Lee Press, Pigeon Cove, Massachusetts, 1972] in-troduced the non-Newtonian calculus consisting of the branches of geometric, anageometric and bigeometric calculus. Following Grossman and Katz, we construct the …eld C(G) of geometric complex numbers and the concept of geometric metric. Also we give the triangle and Minkowski’s inequalities in the sense of geometric calculus. Later we respectively de…ne the sets !(G), `1(G),
c(G), c0(G)and `p(G)of all, bounded, convergent, null and p-absolutely
sum-mable sequences, in the sense of geometric calculus and show that each of the set forms a vector space on the …eld C(G) and a complete metric space.
1. Preliminaries, Background and Notation
During the renaissance many scholars, including Galileo, discussed the follow-ing problem: Two estimates, 10 and 1000, are proposed as the value of a horse, which estimates, if any, deviates more from the true value of 100? The scholars who maintained that deviations should be measured by di¤erences concluded that the estimate of 10 was closer to the true value. However, Galileo eventually main-tained that the deviations should be measured by ratios, and he concluded that two estimates deviated equally from the true value.
From the story, the question comes out this way what if we measure by ratios? The answer is the main idea of non-Newtonian calculus which is consist of many calculuses such as; the classical, geometric, ana-geometric, bi-geometric calculus. Even you can create your own calculus by choosing generator di¤erent function. Although all arithmetics are structurally equivalent, only by distinguishing among
Received by the editors June 26, 2012, Accepted: Nov. 27, 2012. 2010 Mathematics Subject Classi…cation. 26A06, 11U10, 08A05.
Key words and phrases. Geometric calculus, algebraic structures with respect to geometric calculus, geometric sequence spaces.
The main results of this paper were presented in part at the International Conference On Applied Analysis and Algebra to be held on 29-30 June and 1-2 July 2011 in ·Istanbul, Turkey at the Y¬ld¬z Technical University.
c 2 0 1 2 A n ka ra U n ive rsity
them do we obtain suitable tools for constructing all the non-Newtonian calculus. But the usefulness of arithmetics is not limited to the construction of calculus; we believe there is a more fundamental reason for considering alternative arith-metics: They may also be helpful in developing and understanding new systems of measurement that could yield simpler physical laws.
Bashirov et al. [1] have recently emphasized on the non-Newtonian calculus and gave the results with applications corresponding to the well-known properties of de-rivative and integral in the classical calculus. Quite recently, Uzer [7] has extended the multiplicative calculus to the complex valued functions and interested in the statements of some fundamental theorems and concepts of multiplicative complex calculus, and demonstrated some analogies between the multiplicative complex cal-culus and classical calcal-culus by theoretical and numerical examples. Bashirov and R¬za [2] have studied on the multiplicative di¤erentiation for complex-valued func-tions and established the multiplicative Cauchy-Riemann condifunc-tions. Bashirov et al. [3] have investigated various problems from di¤erent …elds can be modeled more e¢ ciently using multiplicative calculus, in place of Newtonian calculus. Quite re-cently, Çakmak and Ba¸sar [4] have emphasized that each of the set !(N), `1(N), c(N), c0(N) and `p(N) of all, bounded, convergent, null and p-absolutely summable
sequences forms a vector space on the …eld R(N) of non-Newtonian real numbers and a complete metric space.
Geometric calculus is an alternative to the usual calculus of Newton and Leibniz. It provides di¤erentiation and integration tools based on multiplication instead of addition. Every property in Newtonian calculus has an analog in multiplicative calculus. Generally speaking, multiplicative calculus is a methodology that allows one to have a di¤erent look at problems which can be investigated via calculus. In some cases, for example for growth related problems, the use of multiplicative calculus is advocated instead of a traditional Newtonian one.
The set R(G) of positive real numbers are de…ned by R(G) := fex: x 2 Rg := R+n f0g. Throughout this document, geometric calculus is denoted by (GC) and classical calculus is denoted by (CC). A generator is one-to-one function whose domain is C and whose range is a subset of C, the set of complex numbers. As a generator, we choose the function exp from Cstr to the set C(G) := C n f0g,(see
: Cstr ! C(G) z 7 ! (z) = ez= w and 1: C(G) ! Cstr w 7 ! 1(w) = ln w = z; where Cstr:= fz = x + iy : x 2 R; < y g:
In this situation, geometric zero is e0= 1 and geometric one is e1= e. Similarly,
the set Z(G) of geometric integers is given by Z(G) =: fem: m 2 Zg, where Z
denotes the set of integers.
Remark 1.1. Since it is known that the base e of natural logarithm is transcendental, one can easily see that e 2 Z(G) but e =2 Z n f0g. This reveals that Z(G) 6= Z n f0g.
We de…ne the set C(G) of geometric complex numbers, as follows: C(G) := n w = u ig v : u; v 2 R(G) and ig = p 1 eG o = n ez= ex (ey)ln ei : ex; ey 2 R(G) and ei= ep 1 o = ex+iy: x 2 R; < y and i =p 1 = fez: z 2 Cstrg :
It is easy to see that C(G) = C n f0g. It is clear by the de…nition of complex exp function that (z) = ez 6= 0 for all z 2 C
str. Since -generator is a bijective
function, it maps all complex numbers without zero to the range set. Each generator generates exactly one arithmetic, and conversely each arithmetic is generated by exactly one generator.
A complete …eld is a system consisting of a set A and four binary operations , , , . We call A the realm of complete …eld. By an arithmetic, we mean complete …eld whose realm is a subset of C.
Consider any generator with range A C. By -arithmetic we mean the arithmetic whose realm is A and whose operations are de…ned as follows: For z; w 2 C and any generator ,
addition : z w = f 1(z) + 1(w) g subtraction : z w = f 1(z) 1(w) g multiplication : z w = f 1(z) 1(w) g division : z w = f 1(z) 1(w) g
Particularly if we choose the -generator as the identity function then (z) = z for all z 2 C which implies that 1(z) = z, that is to say that -arithmetic is reduced
to the classical arithmetic.
addition : z w = f 1(z) + 1(w)g = fz + wg = z + w : classical addition subtraction : z w = f 1(z) 1(w)g = fz wg = z w : classical subtraction multiplication : z w = f 1(z) 1(w)g = fz wg = z w : classic multiplication
division : z w = f 1(z) 1(w)g = fz wg = z w : classical division
If we choose the -generator as exp, then (z) = ez for all z 2 C which gives
that 1(z) = ln z, that is to say that -arithmetic is reduced to the Geometric
arithmetic.
addition : z w = f 1(z) + 1(w)g = efln z+ln wg= z w : geometric addition subtraction : z w = f 1(z) 1(w)g = efln z ln wg= z w : geometric subtraction multiplication : z w = f 1(z) 1(w)g = efln z ln wg= zln w : geometric multiplication
division : z w = f 1(z) 1(w)g = efln z ln wg= zln w1 : geometric division
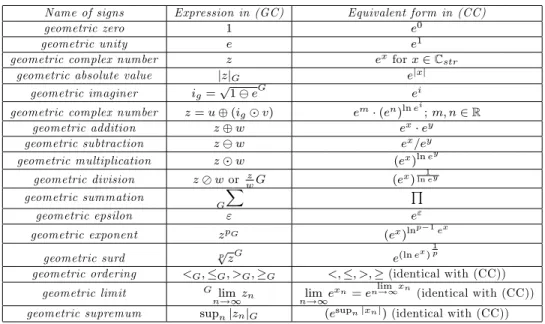
Now we express signs and their equivalent forms in classical calculus by the fol-lowing table:
Following Bashirov et al. [1] and Uzer [7], the main purpose of this paper is to construct the classical sequence spaces with respect to geometric calculus over com-plex numbers. To do this, we need some preparatory knowledge about geometric calculus.
The rest of the paper is organized, as follows:
In Section 2, it is showed that the set C(G) of geometric complex numbers forms a …eld with the binary operations addition and multiplication . Further, the geometric exponent, surd and absolute value are de…ned and their some properties are given. Section 3 is devoted to the vector spaces over the …eld C(G) of geo-metric complex numbers. Additionally, some required inequalities are presented in the sense of geometric calculus and the concepts of geometric metric and geo-metric norm are introduced. In Section 4, subsequent to giving the corresponding results for the sequences of geometric complex numbers concerning the convergent sequences of real or complex numbers, it is stated and proved that the n-dimensional geometric complex space Cn(G) is a complete metric space. In Section 5, prior to
showing the sets !(G), `1(G), c(G), c0(G) and `p(G) of all, bounded, convergent,
null and absolutely p summable sequences are the complete metric spaces it is proved that each of those sets forms a vector space over the …eld C(G) with respect
Name of signs Expression in (GC) Equivalent form in (CC)
geometric zero 1 e0
geometric unity e e1
geometric complex number z exfor x 2 C
str
geometric absolute value jzjG ejxj
geometric imaginer ig=p1 eG ei
geometric complex number z = u (ig v) em (en)ln e
i ; m; n 2 R geometric addition z w ex ey geometric subtraction z w ex=ey geometric multiplication z w (ex)ln ey geometric division z wor z wG (e x)ln ey1 geometric summation G X Q geometric epsilon " e" geometric exponent zpG (ex)lnp 1ex geometric surd ppzG e(ln ex) 1 p
geometric ordering <G; G; >G; G <; ; >; (identical with (CC))
geometric limit G lim
n!1zn nlim!1e
xn= en!1lim xn(identical with (CC)) geometric supremum supnjznjG (esupnjxnj)(identical with (CC))
Table 1. Notation in (GC) and equivalent form in (CC)
to the algebraic operations addition and scalar multiplication . In the …nal section of the paper, we note the sicni…cance of the geometric calculus and record some further suggestions.
In the foundations of science (formerly titled, Physics: The Elements), Norman Robert Campbell, a pioneer in the theory of measurement, clearly recognized that alternative arithmetics might be useful in science, for he wrote, we must recognize the possibility that a system of measurement may be arbitrary otherwise than in the choice of unit; there may be arbitrariness in the choice of process of addition, [5].
We should know that all concept in classical arithmetic have natural counterparts in arithmetic. For instance; zero and one turn out to be (0) and
(1). Similarly the integers turn out to be the following: : : : ; ( 3); ( 2); ( 1); (0); (1); (2); (3); : : : :
Particularly by choosing generator (x) = ex then the set Z(G) of geometric integers and the set R(G) of geometric real numbers are given by
Z(G) =: fex: x 2 Zg = Z n f0g; R(G) =: fex: x 2 Rg = R+
2. Geometric Complex Field and Related Properties
In the present section, we construct the geometric complex …eld C(G) and give its some properties.
De…ne the binary operations addition and multiplication on the set C(G) of geometric complex numbers by
: C(G) C(G) ! C(G)
(z; w) 7 ! z w = z w;
: C(G) C(G) ! C(G)
(z; w) 7 ! z w = zln w= wln z for all z; w 2 C(G). Then we have:
Theorem 2.1. (C(G); ; ) is a …eld.
Proof. Since one can easily observe by routine veri…cation that (i) (C(G); ) is an Abelian group,
(ii) (C(G) n f1g; ) is an Abelian group,
(iii) The operation is distributive over the operation , we conclude that (C(G); ; ) is a …eld.
Now, we emphasize on the concepts of geometric exponent, surd and absolute value.
Let x 2 C(G). Then, x-square, x-cube and pth power of x are de…ned in the sense of (GC) as follows: x2G = x x = xln x x3G = x x x = xln x ln x= xln2x .. . xpG = x x x : : : x | {z } p times = xln x ln x ln x ln x = xlnp 1x As a consequence of the concept geometric square x2G of x 2 C(G), we de…ne the
geometric square rootpG by
x =pyG= e(ln y)1=2 if y = x2G = xln x:
Since x 2 C(G) with x = ey for y 2 Cstr, we have
p
x2GG= e(ln x2G) 1=2
= e[ln (xln x)]1=2
= e[(ln ey)2]1=2= epy2 = ejyj= jeyjG= jxjG
which gives the following property about geometric surd: p
x2GG= jxj G
Similarly, we de…ne pth root of geometric surd, as follows: Let x 2 C(G) with x = ey and y 2 C str. Then, pth root p p xpGG is de…ned by p p xpGG = e(ln xpG) 1 p = e[ln (xln(p 1) x)] 1 p = e[(y)p] 1 p = eppyp= ejyj= jxjG ; if p even; ey = x ; if p odd:
-absolute value jxj of x 2 A R is de…ned by jxj = 8 < : x ; x > (0); (0) ; x = (0); (0) x ; x < (0);
and -distance is given by jx1 x2j for all x1; x2 2 A. Particularly choose I as
-generator, we obtain classical absolute value jxj of x 2 R is de…ned, as usual, by jxj = 8 < : x ; x > 0; 0 ; x = 0; x ; x < 0;
and classical distance is given by jx1 x2j for all x1; x22 R.
Similarly, if we choose exp as -generator, then we derive the geometric absolute value jxjG of x 2 R(G) with x = ey is de…ned by
jxjG= 8 < : x ; x > 1; 1 ; x = 1; x 1 ; x < 1; = jeyjG= 8 < : ey ; ey> 1; 1 ; ey= 1; e y ; ey< 1;
and geometric-distance is given by jx1 x2jG = jx1=x2jG for all x1; x2 2 R(G)
or ejy1 y2j = jey1=ey2j
G for all y1; y2 2 R. Now, we can list some properties of
geometric absolute value:
1) u 2 R(G) with u > 1 is called as geometric positive number. Also, u 2 R(G) with u < 1 is called as geometric negative number. u 2 R(G) with u = 1 is called as geometric unsigned number.
2) For x1; x22 R(G) with x1= ey1; x2= ey2 it is immediate that
jx1 x2jG = jx1=x2jG = jey1=ey2jG = jey1 y2jG = ejy1 y2j
= ejy2 y1j
= jey2=ey1
jG= jx2=x1jG= jx2 x1jG:
That is to say that j jG is also symmetric with respect to subtraction.
3) In (CC), it is known that jx yj = jxj jyj for all x; y 2 C. Now, we are going to give the corresponding equality in (GC). For u; v 2 C(G) with et= u; ez= v, since ju vjG = juln vjG = j(et)ln (e z ) jG = ejtj ln (e jzj) = ejtj ejzj= jujG jvjG
we derive that the equality
ju vjG= jujG jvjG
holds, as desired.
In (CC), the usual distance is given by jz1 z2j =
p
(x1 x2)2+ (y1 y2)2,
where z1; z22 C with z1= x1+ iy1; z2= x2+ iy2. In (GC), the geometric distance
is de…ned by ju1 u2jG = p (u1 u2)2G (v1 v2)2G G = e ln j u1 u2jGlnj u1 u2jG jv1 v2jG lnjv1v2jG 1=2 ; where u1; u22 C(G) with u1= ez1; u2= ez2 such that
z1= x1+ iy1; z2= x2+ iy22 Cstr:
So ez1 = u
1; ez2 = u2 2 C(G) and u1 = u1 v1ln i ; u2 = u2 v2ln i it is clear that
u1= ex1; u2= ex2; v1= ey1; v2= ey2
We can de…ne another way, replacing each exp function by its corresponding statement. ju1 u2jG = p (u1 u2)2G (v1 v2)2G G = e ln j u1 u2jG lnju1u2jG jv1v2jG lnjv1v2jG 1=2 = e ln j ex1 ex2jG lnjex1ex2jG jey1 ey2jG lnjey1ey2jG 1=2 = e ln je x1 x2jGlnjex1 x2 jG jey1 y2jGlnjey1 y2 jG 1=2 = e ln e
jx1 x2jln ejx1 x2jejy1 y2jln ejy1 y2j 1=2
= e h ln ejx1 x2j2ejy1 y2j2 i1=2 = e h ln ejx1 x2j2 +jy1 y2j2 i1=2 = epjx1 x2j2+jy1 y2j2 = epj ln u1 ln u2j2+j ln v1 ln v2j2
3. Geometric Metric Spaces
In this section, we deal with the vector spaces over the …eld C(G) of geometric complex numbers. Prior to giving the theorems on the geometric vector spaces, we prove the required inequalities in the sense of (GC).
Lemma 3.1. [Triangle inequality] Let x; y 2 C(G). Then,
Proof. Let x; y 2 C(G) with x = eu, y = ev. Then, by bearing in mind the triangle
inequality in (CC) one can easily see that
jx yjG = jeu+vjG = eju+vj
ejuj+jvj= jeujG jevjG
= jxjG jyjG;
i.e., the geometric triangle inequality in (3.1) holds.
Lemma 3.2. Let u; v 2 C(G). Then, ju vjG 1 ju vjG G jujG 1 jujG G jvjG 1 jvjG G: (3.2)
Proof. For this purpose we use the auxiliary function f de…ned on C(G) by f (t) = t=G(1 t). Geometric derivative f0G
of f is f0G(t) = e1+t21 which is positive
in the sense of (GC). Hence f is monotone increasing. Consequently, the triangle inequality in (3.1) implies that f (ju vjG) f (jujG jvjG). Therefore, we have
ju vjG 1 ju vjG G jujG jvjG 1 jujG jvjG G = jujG 1 jujG jvjG G jvjG 1 jujG jvjG G jujG 1 jujG G jvjG 1 jvjG G; as desired.
Now, we state and prove the Minkowski’s inequality in the sense of (GC). Lemma 3.3. [Minkowski’s inequality] Let p 1 and ak; bk 2 C(G) with ak = eck,
bk = edk for k 2 f1; 2; 3; : : : ; ng. Then, p v u u t n G X k=1 jak bkjpGG G p v u u t n G X k=1 jakjpGG G p v u u t n G X k=1 jbkjpGG G : (3.3)
Proof. Suppose that p 1 and ak; bk 2 C(G) with ak= eck, bk = edk for
sense of (CC) a direct calculation leads us to p v u u t n G X k=1 jak bkjpGG G = e(lnQnk=1jakbkjlnp 1 jak bkj) 1 p = e ln Qn k=1(ejck+dkj) lnp 1(ejck +dk j) 1 p = e ln Qn k=1(ejck+dkj)jck+dkj p 1 1p = e h ln ePnk=1 jck+dkjp i1 p e(Pnk=1jckjp) 1 p+(Pn k=1jdkjp) 1 p = n Y k=1 jakjln p 1 jakj ! n Y k=1 jbkjln p 1 jbkj ! = p v u u t n G X k=1 jakjpGG G p v u u t n G X k=1 jbkjpGG G ; as asserted.
Now, we can give the de…nition of the concepts metric and norm, in the sense of geometric calculus.
De…nition 3.4. Let X be any non-empty set. Then, a geometric metric space is a pair (X; dG), where dG is a geometric metric function dG: X X ! R+(G) such
that the following geometric metric axioms hold: GM1 dG(x; y) = 1 if and only if x = y,
GM2 dG(x; y) = dG(y; x), (symmetry)
GM3 dG(x; y) dG(x; z) dG(z; y), (triangle inequality)
for all x; y; z 2 X.
De…nition 3.5. Let X be a vector space over the …eld C(G) and k kGbe a function
from X to R+(G) satisfying the following properties: For x; y 2 X and 2 C(G), GN1 kxkG = 1 if and only if x = G,
GN2 k xkG= j jGkxkG,
GN3 kx ykG kxkG kykG, (triangle inequality).
Then, (X; k kG) is said a geometric normed space.
It is trivial that a geometric norm k kG on X de…nes a geometric metric dG on
X which is given by
dG(x; y) = kx ykG; (x; y 2 X)
It is not hard to show that (R(G); dG) is a metric space with the usual metric
dG de…ned by
dG: R(G) R(G) ! R+(G)
(x; y) 7 ! dG(x; y) = jx yjG:
Geometric complex metric: Assuming z1 = x1+ iy1; z2 = x2+ iy2 2 Cstr so
ez1 = w
1; ez2 = w2 2 C(G) and w1= u1 i v1, w2 = u2 i v2 it’s clear that
u1= ex1; u2= ex2; v1= ey1; v2= ey2 so we de…ne the metric as follows
dG(w1; w2) = jw1 w2jG=
p
(u1 u2)2G (v1 v2)2G G
= epj ln u1 ln u2j2+j ln v1 ln v2j2
Theorem 3.6. n-dimensional geometric complex Euclidian space Cn(G) consists
of all ordered n-tuples of geometric complex numbers is a metric space with the metric dG de…ned by dG: Cn(G) Cn(G) ! R+(G) (x; y) 7 ! dG(x; y) = r G Xn k=1(xk yk) 2G G = eln Qn k=1j xk ykjG lnjxkykjG 1=2 ; (3.4) where x = (x1; x2; : : : ; xn); y = (y1; y2; : : : ; yn) 2 Cn(G).
Proof. One can easily see that the relation dG given by (3:4) satis…es the axioms
(GM1) and (GM2). (GM3) also follows from (3:3) with p = 2, the Cauchy-Schwarz inequality. So, we omit the detail.
4. Convergence and Completeness in (GC)
De…nition 4.1 (Geometric convergent sequence). A sequence (xn) in a metric
space (X; dG) is said to be convergent if there is an x 2 X such that
limn!1dG(xn; x) = 1 then x is called the geometric limit of (xn) and we write G
lim
n!1xn= x or xn G
! x; as n ! 1:
De…nition 4.2. [Geometric Cauchy sequence] A sequence (xn) in a geometric
metric space X = (X; dG) is said to be geometric Cauchy if for every " > 1 in
R+(G), there is an N = N (") such that jxm xnj < " for all m; n > N. The space
X is said to be geometric complete if every geometric Cauchy sequence converges in X.
Theorem 4.3. Every geometric convergent sequence is a geometric Cauchy se-quence.
Proof. Suppose that (xn) be a geometric convergent sequence with the limit x in a
geometric metric space X = (X; dG). Then, for every " > 1 there is an N = N (")
such that dG(xn; x) <2"G for all n > N . Hence by the geometric triangle inequality,
we obtain for m; n > N that
dG(xm; xn) dG(xm; x) dG(x; xn) <
" 2G
" 2G = "; which shows that (xn) is geometric Cauchy, as asserted.
Theorem 4.4. Let X = (X; dG) be a geometric metric space. Then, a convergent
sequence in X is bounded and its geometric limit is unique.
Proof. Suppose that (xn) be a convergent sequence in a geometric metric space X
with xn G
! x. Then, taking " = e, we can …nd an N such that dG(xn; x) < e for
all n > N . Hence by the geometric triangle inequality (GM3), for all n we have dG(xn; x) < e a, where a = maxfdG(x1; x); : : : ; dG(XN; x)g. This shows that (xn)
is bounded. Assuming that xn G ! x and xn G ! z, we obtain from (GM3) 1 dG(x; z) dG(x; xn) dG(xn; z) G ! 1 1 = 1 and the uniqueness x = z of the geometric limit follows from (GM1).
Now, we can give the theorem on the completeness of the metric space (Cn(G); d G).
Theorem 4.5. (Cn(G); d
G) is complete.
Proof. It is known by Theorem 3.6 that dG de…ned by (3.4) is a metric on Cn(G).
Suppose that (xm) =
n x(m)k
o
is a Cauchy sequence in Cn(G), where
xm= x(m)1 ; x (m) 2 ; x
(m)
3 ; : : : ; x(m)n
for each …xed m 2 N. Since (xm) is a geometric Cauchy, for every " > 1 there is an
N 2 N such that dG(xm; xr) = v u u t n G X k=1 x(m)k x(r)k 2G G < " for all m; r > N: (4.1) Geometric squaring, we have for all m; r > N and all k 2 f1; 2; 3; : : : ; ng that
x(m)k x(r)k 2G < "2G
which is equivalent to
x(m)k x(r)k
G < ":
This shows that for each …xed k 2 f1; 2; : : : ; ng, x(1)k ; x(2)k ; x(3)k ; : : : is a con-vergent sequence with x(m)k ! xG k, as m ! 1. Using these n limits, we de…ne
dG(xm; x) " for all m > N which shows that (xm) converges in Cn(G).
Conse-quently, (Cn(G); d
G) is a complete metric space.
Since it is known that Cn(G) is a complete metric space with the metric d G
de…ned by (3:4) induced by the norm k kG, as a direct consequence of Theorem
4.5, we have:
Corollary 1. Cn(G) is a Banach space with the norm k k
G de…ned by kxkG= v u u t n X k=1 jxkj2GG G ; x = (x1; x2; : : : ; xn) 2 Cn(G):
5. Sequence Spaces in the Field C(G)
In this section, we de…ne the sets !(G), `1(G), c(G), c0(G) and `p(G) of all,
bounded, convergent, null and absolutely p summable sequences over the geometric complex …eld C(G) which correspond to the sets !, `1, c, c0and `pover the complex
…eld C, respectively. That is to say that
!(G) = fx = (xk) : xk2 C(G) for all k 2 Ng ; `1(G) = x = (xk) 2 !(G) : sup k2NjxkjG< 1 ; c(G) = x = (xk) 2 !(G) : Glim k!1jxk `jG= 1 ; c0(G) = x = (xk) 2 !(G) : Glim k!1xk = 1 ; `p(G) = ( x = (xk) 2 !(G) : 1 G X k=0 jxkjpGG < 1 ) :
One can easily see that the set !(G) forms a vector space over C(G) with respect to the algebraic operations addition and scalar multiplication de…ned on !(G), as follows:
: !(G) !(G) ! !(G)
(x; y) 7 ! x y = (xk) (yk) = (xkyk);
: C(G) !(G) ! !(G)
( ; y) 7 ! y = (yk) = ( ln yk);
where x = (xk); y = (yk) 2 !(G) and 2 C(G). It is not hard to show that the sets
`1(G), c(G), c0(G) and `p(G) are the subspaces of the space !(G). This means
that `1(G), c(G), c0(G) and `p(G) are the classical sequence spaces over the …eld
Theorem 5.1. De…ne dG on the space !(G) by dG(x; y) = 1 G X k=1 jxk ykjG 2kG (1 jx k ykjG) G;
where x = (xk); y = (yk) 2 !(G). Then, (!(G); dG) is a metric space.
Proof. Since the axioms (GM1) and (GM2) are easily satis…ed, we omit the detail. Since the inequality
jxk ykjG 1 jxk ykjG G jxk zkjG 1 jxk zkjG G jzk ykjG 1 jzk ykjG G (5.1)
holds by(3:2) for all xk; yk; zk 2 C(G), multiplying the inequality (5.1) by 2kG1 G
and nextly summing over 1 k n one can derive that
n G X k=1 jxk ykjG 2kG (1 jx k ykjG) G (5.2) n G X k=1 jxk zkjG 2kG (1 jx k zkjG) G n G X k=1 jzk ykjG 2kG (1 jz k ykjG) G:
Additionally, since the inequalities jxk ykjG 2kG (1 jx k ykjG) G 1 2kGG; jxk zkjG 2kG (1 jx k zkjG) G 1 2kGG; jzk ykjG 2kG (1 jz k ykjG) G 1 2kGG
hold for all k 2 N, the comparison test yields that the series
1 G X k=1 jxk ykjG 2kG (1 jx k ykjG) G; 1 G X k=1 jxk zkjG 2kG (1 jx k zkjG) G; 1 G X k=1 jzk ykjG 2kG (1 jz k ykjG) G:
are geometric convergent. Therefore, by letting n ! 1 in (5:2) that dG(x; y) = 1 G X k=1 jxk ykjG 2kG (1 jx k ykjG) G 1 G X k=1 jxk zkjG 2kG (1 jx k zkjG) G 1 G X k=1 jzk ykjG 2kG (1 jz k ykjG) G = dG(x; z) dG(z; y);
i.e., (GM3) holds. This step completes the proof. Theorem 5.2. The inclusion !(G) ! strictly holds.
Proof. Let x = (xk) 2 !(G) with xk = eyk for all k 2 N. Then, x 2 ! which
shows that !(G) !. Although y = (yk) = (0; 0; 0; : : :) = 2 !, 62 !(G) since
xk= eyk6= 0 for all k 2 N. Hence, the inclusion !(G) ! is strict.
Theorem 5.3. De…ne dG1 on the geometric space (G) by
dG1(x; y) = sup k2Njxk
ykjG;
where denotes any of the spaces `1, c and c0, and x = (xk); y = (yk) 2 (G).
Then, ( (G); dG1) is a complete metric space.
Proof. Since the proof is similar for the spaces c(G) and c0(G), we prove the theorem
only for the space `1(G). Let x = (xk); y = (yk); z = (zk) 2 `1(G). Then,
(i) Suppose that dG1(x; y) = 1. This implies for all k 2 N that
xk yk = xk=yk = 1, i.e., x = y.
Conversely, let x = y. Then, we have xk=yk = xk yk = 1 which yields that
dG1(x; y) = 1.
That is to say that (GM1) holds.
(ii) It is immediate that dG1(x; y) = dG1(y; x), i.e., (GM2) holds.
(iii) By taking into account the triangle inequality in (3:1) we see that dG1(x; y) = sup k2Njx k ykjG = sup k2Njxk yk zk zkjG sup k2Njxk zkjG sup k2Njyk zkjG = dG1(x; z) + dG1(z; y): Hence, (GM3) is satis…ed.
Since the axioms (GM1)–(GM3) are satis…ed, (`1(G); dG1) is a metric space.
It remains to prove the completeness of the space `1(G). Let (xm) be any Cauchy sequence in the space `1(G), where xm=nx(m)
1 ; x (m) 2 ; : : :
o
" > 1 there is an N such that for all m; n > N , dG1(x m; xn) = sup k2N x(m)k x(n)k G < ":
A fortiori, for every …xed k 2 N and for m; n > N x(m)k x(n)k
G< ": (5.3)
Hence for every …xed k 2 N, the sequence xm =
n
x(1)k ; x(2)k ; : : :o is a Cauchy sequence of geometric complex numbers. Since C(G) is a complete metric space by Theorem 4.5 with n = 1, it converges, say x(m)k ! xk as m ! 1. Using
these in…nitely many limits x1; x2; : : :, we de…ne x = (x1; x2; : : :) and show that
x 2 `1(G). From (5:3) letting n ! 1 and m > N we have
x(m)k xk
G ": (5.4)
Since (xm) = x(m)k 2 `1(G), there is a geometric real number km such that
x(m)k
G kmfor all k 2 N. Thus, (5:4) gives together with the triangle inequality
in (3:1) for m > N that jxkjG xk x(m)k G+ x (m) k G " + km: (5.5)
It is clear that (5:5) holds for every k 2 N whose right-hand side does not involve k. Hence (xk) is a bounded sequence of geometric complex numbers, i.e.,
x = (xk) 2 `1(G). Also from (5:4) we obtain for m > N that
dG1(x
m; x) = sup k2Njx
(m)
k xkjG ":
This shows that xm G! x, as m ! 1. Since (xm) is an arbitrary geometric Cauchy
sequence, `1(G) is complete.
Since it is known by Theorem 5.3 that the spaces `1(G), c(G) and c0(G) are
the complete metric spaces with the metric dG1 induced by the norm k kG1, we
have:
Corollary 2. `1(G), c(G) and c0(G) are the Banach spaces with the norm k kG1
de…ned by
kxkG1 = sup k2NjxkjG
; x = (x1; x2; : : : ; xn) 2 (G); 2 f`1; c; c0g:
To avoid undue repetition in the statements, we give the …nal theorem is on the complete metric space `p(G) without proof.
Theorem 5.4. Let dGp be de…ned on the space `p(G) by dGp(x; y) = 1 G X k=0 jxk ykjpGG !(1 p)G ; where x = (xk); y = (yk) 2 `p(G):
Then, (`p(G); dGp) is a complete metric space.
Theorem 5.5. `p(G) is a Banach space with the norm k kGp de…ned by
kxkGp = 1 G X k=0 jxkjpGG !(1 p)G ; x = (x1; x2; : : : ; xn) 2 `p(G): 6. Conclusion
Some of the analogies between (CC) and the (GC) are demonstrated by the-oretical examples. Some important inequalities such as triangle, Minkowski and some other inequalities in the sense of (GC) which are frequently used, are proved. We derive classical sequence spaces in the sense of geometric calculus and try to understand their structure of being geometric vector space. Generally we work on vector spaces which concern physics and computing. There are lots of techniques that have been developed in the sense of the (CC). If the (GC) is employed together with the (CC) in the formulations, then many of the complicated phenomena in physics or engineering may be analyzed more easily.
Quite recently, Talo and Ba¸sar have studied the certain sets of sequences of fuzzy numbers and introduced the classical sets `1(F ), c(F ), c0(F ) and `p(F ) consisting
of the bounded, convergent, null and absolutely p-summable sequences of fuzzy numbers in [6]. Nextly, they have de…ned the -, - and -duals of a set of sequences of fuzzy numbers, and gave the duals of the classical sets of sequences of fuzzy numbers together with the characterization of the classes of in…nite matrices of fuzzy numbers transforming one of the classical set into another one. Following Bashirov et al. [1] and Uzer [7], we have given the corresponding results for geometric calculus to the results derived for fuzzy valued sequences in Talo and Ba¸sar [6], as a beginning. As a natural continuation of this paper, we should record from now on that it is meaningful to de…ne the -, - and -duals of a set of sequences of geometric complex numbers, and to determine the duals of classical spaces `1(G), c(G), c0(G) and `p(G). Further, one can obtain the similar results by using another
type of calculus instead of geometric calculus. Acknowledgements
The authors wish to express their pleasure to Professor Agamirza E. Bashirov, Department of Mathematics, Eastern Mediterranean University, Gazimagusa - North Cyprus, via Mersin 10 - Turkey, for his careful reading of an earlier version of this paper and constructive suggestions which led to some improvements of the paper.
The authors also would like to thank Professor Ali Uzer, Department of Electri-cal and Electronics Engineering, Fatih University, 34500 Büyükçekmece ·Istanbul, TURKEY, for his making some useful comments which improved the presentation of the paper.
Özet: Klâsik hesap tarz¬na bir alternatif olarak Grossman ve Katz, [Non-Newtonian Calculus, Lee Press, Pigeon Cove, Massa-chusetts, 1972] künyeli eserlerinde geometrik, anageometrik ve bi-geometrik adl¬çe¸sitleriyle Newtonyen olmayan hesap tarz¬n¬liter-atüre sunmu¸slard¬. Bu çal¬¸smada; Grossman ve Katz takip edil-erek geometrik kompleks say¬lar¬n C(G) cismi ve geometrik metrik kavram¬in¸sa edilmi¸stir. Daha sonra geometrik hesap tarz¬na göre üçgen ve Minkowski e¸sitsizlikleri ispat edilerek geometrik kom-pleks de¼gerli bütün dizilerin !(G), s¬n¬rl¬dizilerin `1(G), yak¬nsak dizilerin c(G), s¬f¬ra yak¬nsayan dizilerin c0(G) ve p-mutlak
toplan-abilen dizilerin `p(G) cümlelerinin C(G) cismi üzerinde birer
vek-tör uzay¬te¸skil ettikleri ve üzerlerinde tan¬mlanan metriklere göre birer tam metrik uzay olduklar¬gösterilmi¸stir.
References
[1] A.E. Bashirov, E.M. Kurp¬nar, A. Özyap¬c¬, Multiplicative calculus and its applications, J. Math. Anal. Appl. 337(2008), 36–48.
[2] A. Bashirov, M. R iza, On complex multiplicative di¤ erentiation, TWMS J. App. Eng. Math. 1(1)(2011), 75–85.
[3] A.E. Bashirov, E. M¬s¬rl¬, Y. Tando¼gdu, A. Özyap¬c¬, On modeling with multiplicative di¤ er-ential equations, Appl. Math. J. Chinese Univ. 26(4)(2011), 425–438.
[4] A.F. Çakmak, F. Ba¸sar, On the classical sequence spaces and non-Newtonian calculus, J. Inequal. Appl. 2012, Art. ID 932734, 13 pp.
[5] M. Grossman, R. Katz, Non-Newtonian Calculus, Lowell Technological Institute, 1972. [6] Ö. Talo, F. Ba¸sar, Determination of the duals of classical sets of sequences of fuzzy numbers
and related matrix transformations, Comput. Math. Appl. 58(2009), 717–733.
[7] A. Uzer, Multiplicative type complex calculus as an alternative to the classical calculus, Com-put. Math. Appl. 60(2010), 2725–2737.
Current address : Cengiz Türkmen: The Graduate School of Sciences and Engineering, Fatih University, The Had¬mköy Campus, Büyükçekmece, 34500–·Istanbul, TURKEY
Feyzi Ba¸sar: Fatih University, Faculty of Art and Sciences, Department of Mathematics, The Had¬mköy Campus, Büyükçekmece, 34500–·Istanbul, TURKEY
E-mail address : cturkmen10@gmail.com, fbasar@fatih.edu.tr, feyzibasar@gmail.com URL: http://communications.science.ankara.edu.tr/index.php?series=A1