Bour 's Theorem on Timelike Helicoidal Surfaces with (L,L)-Type in Minkowski 3- Space

©BEYKENT UNIVERSITY

BOUR S THEOREM ON TIMELIKE

HELICOIDAL SURFACES WITH (L,L)-TYPE IN

MINKOWSKI 3-SPACE

Erhan GÜLER

Etimesgut Anatolian Commercial Vocational High School 06930, Ankara, TURKEY

ergler@gmail.com

Received: 6 February 2007, Revised: 4 December 2007, Accepted: 27 December 2007

ABSTRACT

In this work, it is given that a timelike generalized helicoid of (null axis, null

profile curve)-type is isometric to a timelike rotation surface of same type by

Bour's theorem in Minkowski 3-space. In addition, it is obtained that these surfaces are not minimal and have not got the same Gauss map. Moreover, some relations between the mean, Gauss, the second Gaussian and the second mean curvature of the helicoidal surfaces of (L,L)-type are investigated in Minkowski 3-space.

Key words: Timelike helicoidal surfaces, Gauss map, second mean curvature,

second Gaussian curvature.

MİNKOWSKİ 3-UZAYINDA (L,L) -TÜRÜNDEKİ

TİMELİKE HELİSOİDAL YÜZEYLER

ÜZERİNDE BOUR TEOREMİ

ÖZET

Bu çalışmada, 3-boyutlu Minkowski uzayında, (null eksen, null üreteç

eğrisi)-türünde verilen bir timelike genelleştirilmiş helisoidin, aynı tipteki bir timelike

dönel yüzeye izometrik olduğu Bour teoremi ile verildi. İlaveten, bu yüzeylerin minimal olmadıkları ve aynı Gauss dönüşümüne sahip olmadıkları belirlendi. Ayrıca, Minkowski 3-uzayında (L,L)-türünde helisoidal yüzeylerin ortalama, Gauss, ikinci Gauss ve ikinci ortalama eğrilikleri arasındaki bazı bağıntılar araştırıldı.

Anahtar kelimeler: Timelike helisoidal yüzeyler, Gauss dönüşümü, ikinci

ortalama eğriliği, ikinci Gauss eğriliği.

2000 Mathematics Subject Classification: Primary; 53A35; Secondary;

53C45.

1. INTRODUCTON

The right helicoid (resp. catenoid) is the only ruled (resp. rotation) surface which is minimal in Euclidean space. Moreover, these surfaces have interesting properties. That is, they are both members of a one-parameter family of isometric minimal surfaces. The pair of the right helicoid and the catenoid has following generalization.

Bour's Theorem. A generalized helicoid is isometric to a rotation surface so

that helices on the helicoid correspond to parallel circles on the rotation surface [3].

In this generalization, original properties that they are minimal and preserve the Gauss map are not generally kept. In [7], T. Ikawa showed that a generalized helicoid and a rotation surface have isometric relation by Bour's theorem in Euclidean 3-space by using a result of E. Bour [3]. He determined pairs of surfaces with an additional condition that they have the same Gauss map on Bour's theorem. Ikawa classified the spacelike and timelike surfaces as

(axis, profile curve) -type in [8]. He proved an isometric relation between a

spacelike (timelike) generalized helicoid and a spacelike (timelike) rotation surface of spacelike (timelike) axis (S,S), (S,T), (T,S) and (T,T)-type by Bour's theorem. Since Brioschi's formulas in Euclidean ([6, p.504]) and Minkowski 3-spaces are the same, we are able to compute K n of a surface M by replacing the components of the first fundamental form E, F, G by the components of the second fundamental form L, M, N respectively in Brioschi's formula. Consequently, the second Gaussian curvature Kn of M is

given by

K n (1)

' 1 1 1 1 ^ - 2 LUU + Mu v - - Nv v 2 Lu MU - 2 L Q = det Mv - 2 Nu L M - N M N 2 v ¥ = det 0 2 L 1 L Nu 0 2 L L M N„ u M N

and A = |det / / | . It is well known that a minimal surface has vanishing second Gaussian curvature but that a surface with vanishing second Gaussian curvature need not be minimal [9]. Koutroufiotis [11] has shown that a closed

ovaloid is a sphere if Kn = cK for some constant c or in

1974. Koufogiorgos and Hasanis [10] proved that the sphere is the only closed ovaloid satisfying Kn = H in 1977. Baikoussis and Koufogiorgos [1] proved

that the helicoidal surfaces satisfying Ku = H are locally characterized by

the constancy of the ratio of the principal curvatures. Blair and Koufogiorgos [2] investigated a non-developable ruled surface in E3 such that a Ku + bH ,

2a + b ^ 0 , is a constant along each ruling in 1992. Also, they proved that a ruled surface with vanishing second Gaussian curvature is a helicoid.

On the other hand, in 2005, Dillen and Sodsiri [4] studied ruled linear Weingarten surfaces in Minkowski 3-space such that the linear combination a Kn + bH + cHn + dK is constant along each ruling for some constants

a , b , c , d with a2 +b2 + c2 ^ 0 . They used the second mean curvature formula as follow

H,, = H

11 H

2VÂ f r du'

' duJ J

(2) where A =

|det //|, j

G

{1,2}, h

are the coefficients of the second fundamental form II, u1 and u2 stand for u , v and H, K are the mean and Gauss curvatures respectively.

In 2006, Güler and Vanli [5] showed that a generalized helicoid and a rotation surface with lightlike axis have isometric relation by Bour's theorem in Minkowski 3-space. They classified the spacelike (timelike) helicoidal (rotation) surfaces with lightlike axis of (L,S)-type and (L,T)-type in Minkowski 3-space.

W e say that a surface in R3 is timelike if the discriminant Q = EG — F is negative, where E , F, G are coefficients of its first fundamental form.

Now, let's give some basic notions of the Lorentzian geometry. The 3 3 Minkowski 3-space R j is the Euclidean space \ provided with the inner product

< u, v >

L

= u

l

v

l

+ u

2

v

2

- u

3

v

3

where

u

=

(u

x

,u

2

,u

3

), v

=

(vj,v

2

,v

3

)G

E3. We say that a Lorentzian vector u in R13 is spacelike (lightlike and timelike) if u = 0 or

< u, u >L > 0 (u ^ 0; < u, u > L = 0 and < u, u > L < 0) respectively. The

norm of the vector u G R3 is defined by ||w || = u, u >L \ . Lorentzian

vector product u X v of u and v is defined as follows:

u X v =

ei e2 e3

Uj U2 U3

Now we define a non degenerate rotation surface and generalized helicoid in R3. For an open interval I C R, let Y: I > n be a curve in a plane in R3, and let I be a straight line in n which does not intersect the curve J . A

3

rotation surface in R j is defined as a non-degenerate surface rotating a curve

J around a line £ (these are called the profile curve and the axis, respectively). Suppose that when a profile curve J rotates around the axis £ , it simultaneously displaces parallel to £ so that the speed of displacement is proportional to the speed of rotation. Then the resulting surface is called the

generalized helicoid with axis £ and pitch a .

W e classified a surface by types of axis and profile curve, and write as (axis's

type, profile curve's type)-type; for example, (L,L)-type mean that the surface

has a lightlike axis and a lightlike(line) profile curve. In section 3, we study an isometric relation between a timelike generalized helicoid and a timelike rotation surface of lightlike axis by Bour's theorem. Then, we give these

surfaces have not got zero mean curvature (CMC), have not got the same Gauss map. W e show some results of curvatures for the helicoidal surfaces with lightlike axis of (L,L)-type in Minkowski 3-space in section 4. In addition, we study helicoidal surfaces of (L,L)-type such that the linear combination pH + qK + rHu + sKn is constant along each ruling for

some non-zero constants p , q , r, s.

2. PRELIMINARIES

In this section, we will obtain some rotation and helicoidal surfaces with lightlike axis in Minkowski 3-space. In the rest of this paper we shall identify a vector (a, b , c) with its transpose (a, b, c)t.

If the axis I is lightlike in Minkowski 3-space R 3, then we may suppose that I is the line spanned by the vector (0,1,1). The semi-orthogonal matrix given as follow is the subgroup of the Lorentzian group that fixes the above vector as invariant

A(v)

- v

1 —

2

2

;

2

v

v2

1+v_

v e

R.

2 ;

Suppose that the axis of rotating is lightlike line, or equvalently the line of the plane

x

2

x

3 spanned by the vector (0,1,1). Since the surface is n o n -degenerate, we may assume that the profile curve Y1 lies in the x2 x3- p l a n e without loss of generality and its parametrization is given by

Y

1

(u) = (0,p(u) + u,p(u) - u)

where <p(u) + u and <p(u) — u are functions on I such that

<p(u)

+

u

±

p(u) — u

for all

u e

R

— {0}.

Hence the matrix A can be found by solving the following equations simultaneously;

1

2

v

2

v

1.

Al = i

,

2.

AeA

= £ where £ =

diag(l,1,-l),

3.

det A = 1.

A helicoidal surface in Minkowski 3-space with the lightlike axis which is spanned by (0,1,1), and which has pitch ae R — {0} is as follows

f

H(u,v) =

\ — i

v

v

2 2

V V

v 1 —

2 2

2 2

v

v

v 1 + —

V 2 2 ;

(

0

^

(o

^

(p+

u + a V

. (3)

VP

-u

V

v

When a = 0 , H(u, v) reduces to a rotation surface. Hence, we have < Y1, Y > = 4 ^ ' . For a moment, we assume that (p = 0. If, (p = c G R ^ Y profile curve is lightlike line, then rotation (helicoidal) surfaces are timelike with lightlike axis and they are (L,L)-type. Then timelike rotation (helicoidal) surfaces reduces to as follows respectively

R(u, v) = (-2uv,c

+

u

-

uv

2

,c

-

u

-

uv

2

),

H (u, v) = (-2uv, c

+

u

-

uv

2

+ av, c

-

u

-

uv

2

+ av)

where

cG

R,

u,v,aG R-{0}.

3. BOUR'S THEOREM ON TIMELIKE SURFACES WITH

LIGHTLIKE AXIS

Case. (L,L)-type.

First of all, we consider the (L,L)-type surfaces, namely, the axis is lightlike and the profile curve is lightlike line.

Theorem 3.1. A timelike generalized helicoid

is isometric to a timelike rotation surface

a2 a2

R(u, v) = (-4uv + 2a, c 2uv

2

+ 2av + 2u, c 2uv

2

+ 2av - 2u )

u u

so that helices on the generalized helicoid correspond to parallel circles on the rotation surface.

Proof. W e assume that the profile curve is on the x2 x3 -plane. Since a

generalized helicoid is given by rotating the profile curve around the axis and simultaneously displacing parallel to the axis, so that the speed of displacement is proportional to the speed of rotation, from (3), we have the following representation of a generalized helicoid

H(u

H

,v

H

) = (-2u

H

v

H

,c + u

H

- u

H

v

2H

+ av

H

,c - u

H

- u

H

v

2H

+ av

H

) (4)

where a ^ 0 is a constant.

The coefficients of the first fundamental form and the line element of the generalized helicoid (4) are given by

EH =

0,

FH =

2a,

GH =

4uH,

ds

2H

= 4adu

H

dv

H

+ 4v

2H

dv

2H

.

Because of

Q

H

= E

H

G

H

— F H = -4a

2

< 0

then

H (u

H

, v

H

)

is timelike. Helices in

H(u

H

, v

H

)

are curves defined by

u

H

= const.,

so curves in

H (uH, vH ) that are orthogonal to helices satisfy the following orthogonality

condition

2adu

H

+ 4u

2

'

7

"

2 Thus we obtain

2adu

H

+ 4u

H

dv

H

= 0.

i—:rdu„ + c

J 2

u 2 H lH

where c is constant. Hence if we put

_ a

2u

H

then curves that are orthogonal to helices are given by

v

H

= const..

Substituting the equation

dv

H

= dv

H

——-- du

H

2U

H

into the line element, we have

a2 dsH

=——

duH

+

4U

2H dvHH. (S) UH By putting (S) reduces to a2 Y D U H , F H ( U H ) = 2UH

ds

2H

= duH + fH (u

H

)dvH. (6)

On the other hand, an (L,L)-type rotation surface

R(u

R

,v

R

) = (-2u

R

v

R

,c

+

u

R

-u

R

v

2R

,c

-u

2 -u2vR) (7)

has the line element

dsR = 4uR dvR. (8) Hence, if we put U r =

0,

fR ( U R

) =

2 U R

,

V R = V R , then (8) reduces to dsR = duR + f R

(u

R

)dvR.

(9) Comparing (6) with (9), if UH = UR , vH = vR , f H (uH

) =

fR (UR

)

,

then we have an isometry between H(uH, vH) and R(UR , vR). Therefore it

follows that a2

—du

H

= Odu

R UH and we have 2 cR cH

a

uH

Theorem 3.2. The non-zero mean curvatures and Gauss maps of the

helicoidal (rotation) surfaces in Theorem 3.1. are different definitely .

Proof. First we consider a helicoid (4). Differentiating Hu and Hv, we

obtain

Huu = (0,0,0), Hu

V

=-2(1, v, v), H

vv

= (0,-2u,-2u).

The Gauss map eH of the generalized helicoid is

- 2uv + a

u - uv

2

+ av

2

^ - u - uv + av j

Hence, the mean curvature HH is given by

H,

1

(10)

by virtue of the first and second fundamental forms

Eh

= 0,

Fh =

2a,

G h =

4u

2

,

2a 4u

2

LH =

0,

MH

= ^ t

T

,

NH

= -

T 7

a a

Next we calculate the Gauss map eR and the mean curvature HR of the

rotation surface. Since

2 2

R

u

=

( - 4 v ,

_{u2 u2} T

-

-

2v

2

+ 2 ,

T

r

-

2v

2

- 2),

R

v

=

(-4u,-4uv + 2a,-4uv + 2a)

the Gauss map eR of the rotation surface is given by

ef i

=

V2

lal

2uv + a

2

a

2

+ u - uv + av

8u

2 (11)

a

2

u - uv + av

V 8u j

By the straight calculation, we have the coefficients of the second fundamental form as follows Lr =

-42a

2

, , 442a

-,

M r =

-au

N =

R -

-842u

2

e

_H 2

a

a

a

Hence the mean curvature H R is

V2

H r = - — (12)

2a

where a ^ 0 is a constant. This means that the generalized helicoid and the rotation surface have (non-zero) constant mean curvature (CMC).

•

Corollary 3.1. The relation between two surfaces Gauss map in Theorem 2.1.

is as follow

4le

H

-

e

R

= V 2 $ ( u ) (13)

a 2 a 2

where $ ( u ) = (0, , ).

8u 8u

Corollary 3.2. The relation between two surfaces that have non-zero constant

mean curvature in Theorem 3.1. is as follow

H h + 2HR =

0.

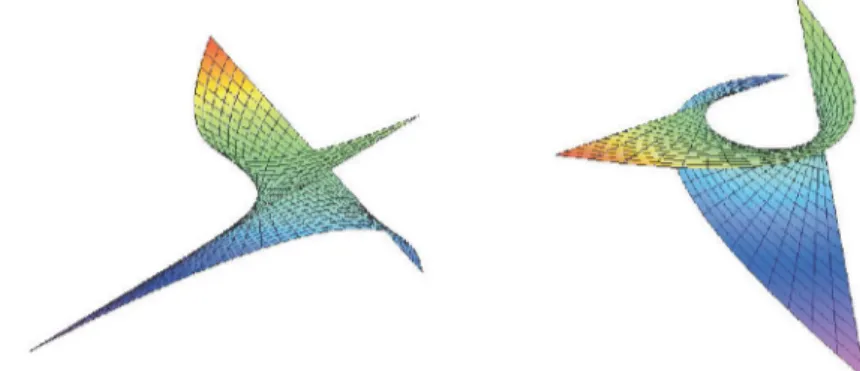
(14)

Example 3.1. A timelike helicoidal surface with lightlike axis (Figure 1) is isometric to a timelike rotation surface with lightlike axis (Figure 2) where

(

=

c

=

1.

Figure 2. a-b Timelike rotation surface with lightlike axis ( ( = 1).

4. RELATIONS BETWEEN H, K, H „ AND K „ FOR

(L,L)-TYPE

W e obtain some results of curvatures for the helicoidal surfaces with lightlike axis of (L,L)-type in Minkowski 3-space.

Theorem 4.1. The mean and the second mean curvatures of the helicoidal

surfaces of (L,L)-type are related as follow equation

H

=

H

n (15)

in Minkowski 3-space, where p(u) = c, c G R, a G R — {0}.

Proof. If p(u) = c, c G R then the mean and the second mean curvature of the helicoidal surfaces (L,L)-type are equal as follow

H

=

H

n = — 1

a

where a G R —{0}.

•

Theorem 4.2. The second mean and Gauss curvatures of the helicoidal

surfaces of (L,L)-type are related as follow equation

Hi

=

K

(16)

Proof. If p ( u ) = c, c e R then the second mean and Gauss curvature of the helicoidal surfaces of (L,L)-type are

H

n

= —

- ,

K =

a a

where

a

e

R-{0}.

Theorem 4.3. The second Gaussian curvature of the helicoidal surfaces of

(L,L)-type is

K„

=

0

(17)

in Minkowski 3-space, where p(u) = c, c e R, a e R — {0}.

Proof. Firstly we compute the Eq. (1) for helicoidal surfaces of (L,L)-type. We obtain the following equation

K . = 1 _{- LuuLN + LuuM2 + - L}2 1 1 2 _{uNuN - NuMMu + - LN¡ (18)} 2(| LN\ — M2)2

If <p(u) = c, c e R then the second Gaussian curvature of the helicoidal surfaces of (L,L)-type is Kn = 0 where a e R — {0}.

Corollary 4.1. Let H (u, v) be the helicoidal surfaces of (L,L)-type, and let p , q, r, s be real constants. Then

pH + qK + rH

n +

sK

n =

0

(19) where a( p + r) = q.

REFERENCES

[1] Baikoussis, C. and Koufogiorgos, Th.; On the inner curvature of the second fundamental form of helicoidal surfaces, Arch. Math. J. 68 (1997), 169-176. [2] Blair, D.E. and Koufogiorgos, Th.; Ruled surfaces with vanishing second Gaussian

curvature, Monatsh. Math. 113 (1992), 177-181.

[3] Bour, E.; Memoire sur le deformation de surfaces, Journal de l'Ecole Polytechnique, XXXIX Cahier (1862), 1-148.

[4] Dillen, F. and Sodsiri, W.; Ruled surfaces of Weingarten type in Minkowski 3-space, J. Geom. 83 (2005), 10-21.

[5] Güler, E. and Turgut Vanli, A.; Bour's theorem in Minkowski 3-space, J. Math. Kyoto, 46-1 (2006), 47-63.

[6] Gray, A.; Modern differential geometry of curves and surfaces with Mathematica, CRC Press, Florida, 1998.

[7] Ikawa, T.; Bour's theorem and Gauss map, Yokohama Math. J. 48 (2000), 173-180. [8] Ikawa, T.; Bour's theorem in Minkowski geometry, Tokyo J. Math. 24 (2001), 377-394.

[9] Kim, Y.H. and Yoon, D.W.; Classification of ruled surfaces in Minkowski 3-spaces, J.Math. Geom. Phys. 49 (2004), 89-100.

[10] Koufogiorgos Th.; and Hasanis, T.; A characteristic property of the sphere, Proc. Am. Math. Soc. 67 (1977), 303-305.

[11] Koutroufiotis, D.; Two characteristic properties of the sphere, Proc. Am. Math. Soc. 44 (1974), 176-178.