Selçuk J. Appl. Math. Selçuk Journal of Vol. 7. No.2. pp. 69-79, 2006 Applied Mathematics
Training Based Method For Heat Flux Function Estimation Using Sensed Temperatures
Morteza Mohmmadzaheri , Orang Asef-Afshar, Ali Mirsepahi, Mansur Bornak, Islamic Azad University, Semnan Branch, Iran-Tehran-P.O.Box: 16535-335 e-mail: m m zahery@ gm ail.com
Summary.Suggested Running Head: Neural Solution of Heat Flux Estimation Category of IHCP Problems. Heat flux function estimation problems are in-verse heat conduction problems which heat flux functions (boundary or initial conditions) are the unknowns and temperature distribution (at present and ear-lier times) is available. There are several algorithms for solving this type of IHC problems. In all of these methods the computational cost is very heavy and all of common IHCP algorithm requires finding the solution of the direct heat conduction problem numerous times. In this paper the neural networks is utilized to estimate the "filter coefficients" needed to estimate heat flux in a particular system. In developing the training phase of the network inspiration is drawn from the Burgraff’s exact solution of the IHCP as well as the filter method. Thus, the estimation phase neither requires any temperature field nor the sensitivity coefficients calculations which are common in classical methods. The neural network used in this work is a 2-layer perceptron. It is shown via classical triangular heat flux test cases that the method can yield very accurate, very efficient as well as stable estimations.
Key words: inverse heat conduction, artificial neural networks, inverse mod-eling
1. Introduction
Heat conduction problems may be put into two distinct categories: direct and inverse problems. In direct problems thermophysical properties, boundary, and initial conditions are all known, and the problem is to obtain a temperature distribution for a geometrically well-defined domain. Mathematically, direct heat conduction problems are considered to be “well-posed”. That is, error in the either of the input data to the heat conduction model will induce an error in the same order of magnitude in the calculated temperatures. Inverse heat
conduction problems (IHCP’s), on the other hand, are considered to be mathe-matically “ill-posed”. In these types of problems, there is lack of knowledge in either the boundary or initial conditions, or the thermophysical properties. In fact these unknowns are to be estimated using measured temperature data at one or several locations within the body of the domain. Being mathematically ill-posed means that unavoidable random errors (noise) in the measured data may induce errors amplified by several orders of magnitudes in the estimated unknowns. It is mainly for this reason that the IHCP’s are considered to be considerably more “difficult” than direct heat conduction problems [1].
The inverse heat conduction problems IHCP’s are in general solved by minimiz-ing a sum of squares of errors function; (i.e., the objective function) which is defined based on the difference between the calculated and the measured tem-peratures. The parameters, (i.e., thermophysical properties) boundary or initial conditions that minimize the aforementioned error function are the solution of the IHCP problem. If thermophysical properties are the unknowns, the IHCP is classified as the parameter estimation problem. On the other hand, the func-tion estimafunc-tion IHCP is the type in which boundary or initial condifunc-tions (i.e., functions) are the unknowns. An IHCP may be simultaneously of parameter and function estimation type.
From one view point the solutions of IHCP may be classified into two sequential and whole domain groups. Most noted of the former group is the sequential function specification method [1](chapter 4), while examples for the latter are the Tikhonov regularization [2], the conjugate gradient [3] and the variable metric [4] methods. The whole domain methods require temperature data for the entire time domain in order to estimate the heat flux history; therefore, technically they cannot be used for real time estimation of the heat flux function. As the traces of a heat flux component occurring at a given time exist only in the future temperatures, an efficient solution would be the one which uses temperatures subsequent to that heat flux component. This is the incentive behind the sequential methods, which makes them to be more efficient than their whole domain counterparts. Nonetheless, even these methods do not render readily to real time heat flux estimation as they require a direct (or forward) temperature solver, which makes the computational cost to become very heavy. This is particularly true when the problem in hand is multidimensional. In Filter forms of IHCP ([1], Chapter 5) or the transformation matrices method (Behbahaninia and Kowsary [5]) heat flux components are estimated sequen-tially by performing simple algebraic (the former) or matrix operations (the latter) on measured data. As the filter coefficients or the transformation ma-trices are determined prior to temperature measurements, these methods are considerably more efficient and can be used for real time heat flux estimations. Determination of the filter coefficients or the transformation matrices is, how-ever, a formidable analytical task. In this paper via a classical test case, it
is shown that the artificial neural networks (ANN) is quite useful in acquiring these filter coefficients.
The use of the artificial neural networks on the subject of the inverse heat transfer is nothing new. The earliest works sited by the present authors are those by Dumek et al. [6] and Raudensky et. Al [7]. Other works worthy of mentioning are those by Jambunathan et al [8], Sablani [9], Sreekanth et al [10], and Sablani et al [11], and Hao, et al [12]. The common approach in all the sited works is that the ANN is trained by several "experiments" using the temperature data for the entire time domain all at once. That is, the network learns to estimate the unknown parameter or function once the temperature data for the entire time domain is made available. This makes the network unnecessarily complex and precludes the online heat flux estimation. In the work by Hao et al. [12] the IHCP solution by the conjugate gradient method is taught to the network once again using the data for the entire time domain; therefore: (1-) the advantage of the ANN method is not utilized fully in the solution, and (2-) the network resulting for this type of analysis was again multilayered and complex. In this work it is shown that the heat flux at any given time can be represented as a linear function of the temperatures around that time and the linear coefficients are estimated by the use of the artificial neural networks (ANN) method. It is shown via a classical IHCP test case that this approach leads to a very efficient as well as accurate IHCP solution technique suitable for real time heat flux estimation.
2. Theory
The Burgraff exact solution of the linear one dimensional IHCP (Fig. 1), as de-tailed in the classic IHCP text by Beck et al [1] (chapter 2), ends up representing the heat flux applied to one of the surfaces of a one dimensional slab at a given time by an infinite series of the time derivative of the measured temperature data at that time. That is:
(1) = 0 + 1 + 2 2 2 + +
In the above equation is represents the term beyond which the infinite series is truncated.
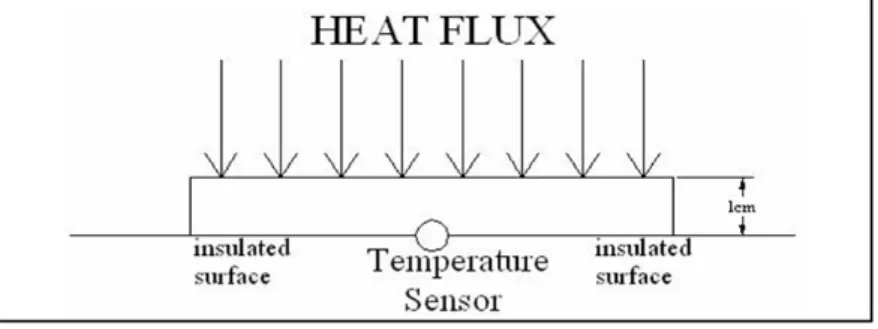
Fig. 1 A schematic of the test case
In real applications, only the discrete values of temperatures are available rather than continuous functions. Therefore, derivatives are expressed as numerical central derivatives. Consequently, Eq.(1) is transformed to
(2)
= −−+ +−2−2+−1−1+−1+0+1+1+2+2+ ++
In other words, although it may come as a surprise to some, the heat flux at a given time can be expressed as a linear combination of some measured temper-atures around that time and can be estimated by a "moving average filter" in time. In linear IHCP problems the coefficients are functions of the thermophys-ical properties, geometry, sensor location, and of course the data acquisition sampling rate. If the coefficients of Eq.(2) are obtained somehow, heat flux may become readily available using some temperature data prior to and after the time of the occurrence of the desired heat flux component. Techniques such as the filter method (discussed previously) are devised to obtain these coefficients using a particular type of regularization. In this paper these coefficients are obtained using training-based artificial neural networks method.
As discussed by Dumek et al [6] the neural network is a structure for parallel information processing, which may be considered as a "black box" or a transfer function. Consider, for example, a one dimensional slab which is being heated from one side, and for which the temperature history at its inactive surface is available. If a controlled heat flux is applied on the active surface and the tem-perature is recorded, a data set of “heat flux versus temtem-perature” is obtained. Such a data set can be obtained as accurately as one would wish by performing experiments or direct heat conduction calculations. In this paper training data set is obtained by direct solution of the heat conduction equation. If we train these data to a proper model inversely, that model can predict heat flux using temperatures. Achieving a good and effective inverse model depends on devising a proper:
1) Structure selection, 2) Data preparation, and
3) The training algorithm.
3. Model And Training Characteristics
A functional solution as depicted by Eq. (2) provides a useful structure for linear inverse model, and provides a basis for the data preparation procedure. Accordingly, +, = − are proper inputs of the inverse model whose
output is to be .
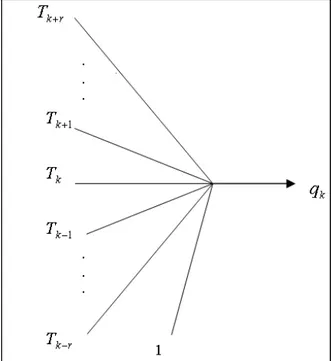
This inverse model can be a simple neural network as depicted in Fig.2. All activation functions of ANN are linear with slope of 1 and the weights of this ANN are the coefficients of Eq.(2). In this paper two methods are applied for obtaining the coefficients (weights). The first one is the least square of errors method (LSE). It is mathematically proven that LSE is an ideal method for linear systems’ modeling [13]. The only problem is its sensitivity against noise or sensor error. The second method is the error back propagation using the Levenberg-Marquardt algorithm. Application of both these methods will be discussed later for a test case.
Fig. 2 The neural network for the inverse model as presented by Eq. (2) 4. Case Study
The following test case is used as an example to elaborate on the general scenario described above. As shown in Fig. 1, the test case involves a one dimensional slab, 1cm thick, made of a steel alloy having thermophysical properties: k=63.9
W/m/K, C=434 J/kg/K, and =7832 kg/ 3 The slab is exposed to an
un-known heat flux from one side (i.e., the active surface), while the other side of the plate (i.e., the inactive side) is insulated. Thus, the governing differential equation (i.e., the heat equation) for the direct heat conduction, and boundary and initial conditions are given as:
(3) 2 2 = 1 (4) |=0 = () (5) |= = 0 (6) ( 0) = 0
As mentioned previously, in the inverse problems the time history of the heat flux is unknown and is to be estimated. Instead, a set of temperature data for every 0.1sec (i.e., sampling rate of 10 Hz ) at the inactive (insulated) side is available.
5. Implementation Of The Method
For test case introduced above, the first order time derivative representation of the temperature data was found to be sufficient for heat flux estimation according to the model given by Eq. (2). In other words, heat flux at any time is estimated by only using the temperature of the same time and the temperature at one instant (0.1 sec) after and before current time. Therefore, Eq.2 is simplified as
(7) = −1−1+ −1+ 0+ 1+1
Fig.3 The heat flux history used in training phase.
As the coefficients in Eq. (7) are independent of the heat flux or temperature, one set of heat flux vs. temperature data obtained by this "experiment" (or di-rect solution) is ample enough for their accurate determination. In the training phase the data were made noisy with random errors having Gaussian distribu-tion with standard deviadistribu-tions of 1◦ as well as 3◦. Recorded
“temperature-heat flux” data are arranged as was previously explained. Two models are trained by the prepared data. The first model is without −1 and is trained using the least squares of errors LSE; therefore, this model is defined with only three parameters. A similar procedure is used for obtaining the transfer func-tions in automatic control [14]. The second model is exactly as given by Eq.4 (i.e., with four parameters) and trained using Levenberg-Marquardt back prop-agation algorithm (with only 7 iterations).This algorithm is commonly used in training ANNs. The neural network used in this work is a 2-layer perceptron (like ANN shown in Fig.2). Estimated coefficients, achieved by training ANNs by heat-flux-temperature data, are shown in Table1.
6. Results And Discussion
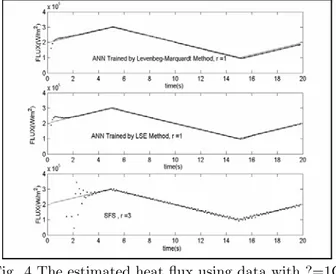
After completing the inverse model, a heat flux function (see Fig. 3), different from that used in the training phase (Fig. 2), is used to assess the performance of the proposed models in heat flux estimation. Relevant sensed temperatures (manipulated by errors having a Gaussian distribution) are used as inputs of the model. Estimated heat fluxes are compared with exact values and the estimation of the classical sequential function specification (SFS) method.
Fig. 4 The estimated heat flux using data with ?=1C
Fig. 5 The estimated heat flux using data with ?=3C
The error norm in estimation of the heat flux by the ANN method was 2.2kW/m2. (Heat flux ranges between 0 to 200kW/m2.), whereas that for the SFS is higher
by a factor of 30. ANN (using either LSE or Levenberg-Marquardt method) can resolve the heat flux function, at much earlier times than the SFS method as indicated in Fig.s 4 and 5.
By recalling the fact that temperature sensors were located on the inactive surface; i.e, furthest location from the exposed surface, one can possibly conclude that the ANN estimator is not affected much by the well-known damping and lagging effects which hamper use of classical IHCP algorithms. It should also be mentioned that we were able to estimate heat flux using only one future data as well. This is particularly difficult using the classical IHCP solutions. The main advantage of the suggested approach is once again its efficiency, as presented in Table 2, which makes it particularly useful for real time (or online) heat flux estimation.
Table..2, Comparison of the estimation time of heat flux shown in Fig. 4 for the SFS and ANN methods both for ANN trained by LSE (with 3 parameters) or Levenberg Marquardt(LM) method(with 4 parameters)
7. Conclusion
In this paper training-based method for heat flux estimation problem, one of inverse heat conduction problems, is presented. This method is divided to two completely separate stages, the first, inverse modeling or training which is done by a set of “temperature-heat flux” data namely training data and the second, the estimation phase. By using a classical test case the suggested method was shown to be very promising both from the view point of accuracy and the efficiency. The method is shown to be particularly useful for real time heat flux estimation. Nonetheless, admittedly, further studies are needed to investigate the applicability of the method to multidimensional IHCP problems in which more than one spatial heat flux component may exist. It should further be noted that the proposed method is suitable only for linear IHCP’s.
8. Nomenclature
Constant pressure specific heat ,J/kg/)
Total error of training
Thermal conductivity , Number of ANN inputs
Number of future temperature used in estimation Temperature, centigrade degree
Distance from active surface , Greek Letters
Density (kg/m3)
Modification factor used in training Subscripts
Indicator of layer number of ANN
Indicator of connection number of each layer
References
1. J. V. Beck, B. Blackwell, and C. R. St. Clair, "Inverse Heat Conduction: Ill-posed problems", Wiley Intersciences, NY, 1985
2. A. N. Tikhonov and V. Y. Arsenin, "Solution of Ill-posed Problems", V. H. Winston & Sons, Washington D.C., 1977.
3. M. N. Özicik and R. B. Orlande, "Inverse Heat Transfer’s Fundamentals and Ap-plications", Taylor and Francis, London, 2000.
4. F. Kowsary, A. Behbahaninia, A. Pourshaghaghy"Transient Heat Flux Function Estimation Utilizing the Variable Metric Method", Accepted and soon to be published in International Communications in Heat and Mass Transfer (Elsevier).
5. Behbahaninia, A. and F. Kowsary, "A Direct transformation Matrices Method For Solving Inverse Heat Conduction Problems", Journal of Numerical Heat Transfer Part B, 46 (2004) 16-22.
6. Dumek, M. Druckmüller, K. Raudensky, K. Woodbury, "Novel Approaches to IHCP: Neural Networks and Expert Systems", Proceedings of the First International Conference on Inverse Problems in Engineering: Theory and Practice, June 13-18, Palm Coast, Florida, ASME. Book No. I00357, 1993, pp. 275-282.
7. M. Raudensky, J. Horsky, and J. Krejsa, "Usage of Neural Network for Coupled Pa-rameter and Function Specification Inverse Heat Conduction Problem", International Communications in Heat and Mass Transfer, Vol. 22 (5) (1995) 661-670.
8. K. Jambunathan, S. Hartle, S. Ashforth-frost, V. N. Fontama, "Evaluating Con-vective Heat Transfer Coefficients Using Neural Networks", International Journal of Heat and Mass Transfer, 39 (1996) 2329-2332.
9. S. S. Sablani, "A Neural Network Approach for Non-Iterative Calculation of Heat Transfer Coefficient in Fluid-Particle Systems", Chemical Engineering and Processing, 40 (2001) 363-369.
10. S. Sreekanth, H. S. Ramaswamy, S. S. Sablani, S. O. Prasher, "A Neural Network Approach for Inverse Heat Conduction Problem", Proceedings of the ASME National Heat Transfer Conference, Baltimore, MD, August 10-12 1997, pp. 37-34
11. S. S. Sablani, A. Kacimov, J. Perret, A. S. Mujumdar, A. Kampo, "Non-Iterative Estimation of Heat Transfer Coefficient Using an Artificial Neural Network Model", International Journal of Heat and Mass Transfer, 48 (2005) 665-679.
12. D. Hao, G. Sofiane, G. Montayon, H. Liao, C. Coddet, D. Benkrid, S. Abouddi, "Combination of Inverse and Neural Network Methods to Estimate Heat Flux", Nu-merical Heat Transfer Part A, 47 (2005) 593-607.
13. S. Haykin, "Neural Networks a Comprehensive Foundation", 2edition, Prentice-Hall Inc. London, 1999.
14. A. Ghafari, M. Nikkhah Bahrami and M. Mohammad-Zaheri, "Linear Modeling of Nonlinear Systems Using Artificial Neural Networks Based on I/O Data and Its Application in Power Plant Boiler Modeling (in Farsi)", Journal of Engineering Faculty of University of Tehran/ Mechanics and Metallurgy, 39 (1) (2005) 53-60.