Sirkülant matrislerin sayısal işaret işlemede kullanımı

T.C.

SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ

SĠRKÜLANT MATRĠSLERĠN SAYISAL ĠġARET ĠġLEMEDE KULLANIMI

Ahmet ÖTELEġ YÜKSEK LĠSANS TEZĠ Matematik Anabilim Dalını

Ağustos-2011 KONYA Her Hakkı Saklıdır

IV

ÖZET

YÜKSEK LĠSANS TEZĠ

SĠRKÜLANT MATRĠSLERĠN SAYISAL ĠġARET ĠġLEMEDE KULLANIMI Ahmet ÖTELEġ

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı

DanıĢman: Prof. Dr. DurmuĢ BOZKURT 2011, 50 Sayfa

Jüri

Prof. Dr. AĢır GENÇ Prof. Dr. DurmuĢ BOZKURT Yrd. Doç. Dr. Yıldıray KESKĠN

Sirkülant matrisler son yıllarda nümerik hesaplamalarda, işaret işlemede, kodlama teorisinde ve petrol araştırmalarında sıklıkla kullanılmaktadır. Bu çalışmada, sayısal işaret işlemenin önemli alanlarından olan ayrık Fourier dönüşümünün (AFD) ve dairesel konvolüsyonun sirkülant matrislerle ilişkisi ele alındı. Öncelikle; ayrık Fourier dönüşümü (AFD), onun özellikleri ve AFD tabanlı elde edilen hızlı Fourier dönüşümü (HFD) verildi. Daha sonra sirkülant matrislerin AFD matrisiyle köşegenleştirilmesi, sirkülant matrislerin öz değerlerinin HFD yardımıyla hesaplanması, yine bu matrisin öz vektörlerinin AFD matrisinin satır veya sütun vektörleri olduğu ve sirkülant matris katsayılı lineer denklem sistemlerinin HFD ile hızlı bir şekilde çözüldüğü gösterildi. Son olarak; dairesel konvolüsyon ve onun sirkülant matrislerle ilişkisi verildikten sonra bu defa sirkülantlı matris katsayılı lineer denklem sistemlerinin dairesel konvolüsyon metoduyla çözüm yöntemi verildi. Bütün bu yapılanları somutlaştırmak için çalışmamız örneklerle zenginleştirildi.

Anahtar Kelimeler: Ayrık Fourier Dönüşümü (AFD), Dairesel Konvolüsyon, Hızlı Fourier

V

ABSTRACT MS THESIS

ON USING OF CIRCULANT MATRICES IN DIGITAL SIGNAL PROCESSING

Ahmet ÖTELEġ

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE IN MATHEMATICS

Advisor: Prof. Dr. DurmuĢ Bozkurt 2011, 50 Pages

Jury

Prof. Dr. AĢır GENÇ Prof. Dr. DurmuĢ BOZKURT Asst. Prof. Dr. Yıldıray KESKĠN

The circulant matrices have applied in numerical computation, signal processing, coding theory and oil investigation in recent years, and so on. In this study; we have discussed relationship with the circulant matrices of Discrete Fourier Transform (DFT) and the circular convolution. Firstly, we have presented DFT, its properties and Fast Fourier Transform (FFT) obtained from DFT-based. Then, we have showed the diagonalization of the circulant matrices with DFT matrix, the calculation of the eigenvalues of the circulant matrices with FFT. We have also showed that the eigenvectors of these matrices correspond to the row or the column vectors of DFT matrix and the linear equations system having the circulant matrices could easily be solved with FFT. Finally, after the discussing the circular convolution and its relationship with the circulant matrices, we have given the solution method the linear equations system having the cirrculant matrices with the circular convolution method. To embody all the work that we have done, we have tried to enrich them with the examples.

Keywords: Circulant matrices, Digital Signal Processing, Discrete Fourier Transform (DFT),

VI

ÖNSÖZ

Bu tez çalışması Selçuk Üniversitesi Fen Fakültesi Matematik Bölümü öğretim üyesi, Prof. Dr. Durmuş BOZKURT danışmanlığında yapılarak, Selçuk Üniversitesi Fen Bilimleri Enstitüsü’ne yüksek lisans tezi olarak sunulmuştur.

Bu tez; 1. Bölüm Giriş bölümü, 2. Bölüm Kaynak Araştırması, 3. Bölüm Temel Kavramlar, 4. Bölüm Sayısal İşaret İşlemede Sirkülant Matrislerin Kullanımı, 5. Bölüm Sonuç ve Öneriler, 6. Bölüm Kaynaklar olmak üzere toplam altı bölümden oluşmaktadır.

Çalışmalarım boyunca beni yönlendiren ve yardımlarını esirgemeyen danışmanım Prof. Dr. Durmuş Bozkurt’a teşekkürü bir borç bilirim.

VII ĠÇĠNDEKĠLER ÖZET ... IV ABSTRACT ... V ÖNSÖZ ... VI ĠÇĠNDEKĠLER ... VII 1. GĠRĠġ ... 1 1.1. Tezin Yapısı ... 2 2. KAYNAK ARAġTIRMASI ... 4 3. TEMEL KAVRAMLAR ... 5

3.1. Bazı Özel Matrisler ... 5

3.2. Öz değerler ve Öz vektörler ... 6

3.3. Bir Matrisin Köşegenleştirilmesi ... 7

3.4. Lineer Denklem Sistemleri ve Çözümleri ... 9

3.5. Sirkülant Matrisler ve Özellikleri ... 11

4. SAYISAL ĠġARET ĠġLEMEDE SĠRKÜLANT MATRĠSLER ... 17

4.1. Sayısal İşaret İşleme ... 17

4.2. Sirkülant Matrislerin Ayrık Fourier Dönüşüm (AFD) ile İlişkisi ... 19

4.2.1. Ayrık Fourier dönüşüm (AFD) matrisi ... 19

4.2.2. Ayrık Fourier dönüşümü (AFD) ... 22

4.2.3. Matris formunda AFD ve ters AFD gösterilimi ... 22

4.2.4. Hızlı Fourier dönüşümü ... 23

4.2.5. Matris gösterimi yardımıyla HFD ... 24

4.2.6. AFD ile HFD’nin karşılaştırılması ... 25

4.2.7. AFD matrisi ile sirkülant matrislerin köşegenleştirilmesi ... 26

4.2.8. Sirkülant matrisin öz değerlerinin HFD yardımıyla hesaplanması ... 28

4.2.9. Sirkülant matrisin öz vektörlerinin AFD matrisiyle ilişkisi ... 31

4.2.10. Sirkülant matris katsayılı lineer denklem sistemlerinin HFD yardımıyla çözümü ... 32

4.3. Lineer ve Dairesel Konvolüsyonda Sirkülant Matrisler ... 35

4.3.1. Lineer konvolüsyon ... 35

4.3.2. Dairesel konvolüsyon ... 37

4.3.3. Dairesel konvolüsyonun matris gösterimi ... 37

4.3.4. Dairesel konvolüsyonun hesaplanmasında AFD ve ters AFD metodu ... 42

4.3.5. Sirkülant matris katsayılı lineer denklem sistemlerinin çözümü için dairesel konvülasyon metodu ... 43

5. SONUÇLAR VE ÖNERĠLER ... 47

VIII

5.2. Öneriler ... 47

6. KAYNAKLAR ... 48 ÖZGEÇMĠġ ... 50

1. GĠRĠġ

Sayısal İşaret İşleme (Digital Signal Processing) DSP, sayısal işaretler ve bu işaretlerin işleme yöntemlerini inceler. Amacı genellikle analog sinyalleri ölçmek ya da filtrelemek olan DSP bu işlemi yapabilmek için öncelikle bir analog-sayısal dönüştürücü (A/D) kullanır ve sinyalleri işleyebileceği bir hale getirir. Yapılmak istenen işlemler yapıldıktan sonra da sayısal-analog dönüştürücü (D/A) kullanarak tekrar analog sinyal elde edilir (Karaboğa, 1995).

Bir Sayısal işaret İşlemenin Blok Diyagramı

İşaretlerin işlenmesi, elektrik mühendisliğinin en önemli konularından biridir. Çeşitli nedenlerden dolayı işaretler işlenmektedir. Haberleşmede işareti gürültüden ayırmak, radar ve sonar sistemlerinde hedefi belirlemek için işaretler işlenir. Ayrıca işaretler çeşitli uygulamalarda kullanılmak amacıyla da işlenebilir. Televizyonda görüntüleme, haberleşmede transmisyon ve sayısal sistemlerin kontrolünde kullanmak için işaretler işlenir.

Ayrık Fourier Dönüşümü (AFD), ayrık zamanlı işaret işleme algoritma ve sistemlerin analizi, tasarımı, gerçekleştirilmesi ile doğrusal filtreleme, korelasyon analizi ve spektrum analizi gibi işaret işleme uygulamalarında önemli bir rol oynar. AFD’nin bu öneme sahip olmasının ardındaki temel neden AFD’yi hesaplamakta kullanılan verimli algoritmaların varlığıdır.

ij

C   c nkare _{bir matris olmak üzere elemanları} ; (mod ) ( , 1, 2, , ) ij j i

c c _ j i k n i j n

0 1 2 1 1 0 1 2 0 1 1 2 1 0 3 1 2 3 0 ( , , , ) n n n n n n n c c c c c c c c C circ c c c c c c c c c c c                          biçimindedir. ,

C bir sirkülant matris ve  da köşegen elemanları C sirkülant matrisinin özdeğerleri olan köşegen bir matris olmak üzere

* CF F

şeklinde AFD matrisi ile köşegenleştirilebilir. Bir sirkülant matrisin öz değerleri, bu sirkülant matrisin ilk satırının veya sütununun AFD’sinden oluşur. Bu da hızlı Fourier dönüşümü (HFD) ile hızlı bir şekilde hesaplanabilir. Ayrıca sirkülant matrislerin öz vektörleri AFD matrisinin sütun vektörleridir. Yine sirkülant matris katsayılı lineer denklem sistemlerinin çözümleri de HFD yardımıyla hızlı bir şekilde yapılabilir.

Lineer ve dairesel konvolüsyon, sayısal işaret işlemede çok sık uygulanılan hesaplama metotlarından birisidir.

a ve ,b n bileşenli iki vektör ve C a da a vektöründen üretilmiş bir sirkülant ( ) matris olmak üzere bu iki vektörün dairesel konvolüsyonu

( )

a b C a b

biçimindedir. Yine, sirkülant matris katsayılı lineer denklem sistemleri dairesel konvolüsyon yardımıyla çözülebilirler.

Sonuç olarak bütün bunlar bize sirkülant matrislerin sayısal işaret işlemede önemli bir yerinin olduğunu gösterir. Bu tez çalışmasında sirkülant matrisler bu yönden ele alındı ve yukarıda anlatılanlara tezin esas kısmında ayrıntılı olarak değinildi.

1.1. Tezin Yapısı

Bu tez altı bölümden oluşmaktadır.

1. Bölüm: Giriş bölümü olup bu bölümde tez konusu hakkında önceden yapılan çalışmalar ve tez konusu kısaca tanıtılmıştır.

2. Bölüm: Tez konusu ile ilgili literatürde yer alan kaynaklar araştırılıp; kaynak araştırması başlığı altında bu kaynaklar hakkında bilgi verilmiştir.

3. Bölüm: Tez boyunca faydalanılacak bazı kavramlar hakkında ön bilgiler verilmiştir.

4. Bölüm: Tezin esas kısmını oluşturmaktadır. Bu bölümde sayısal işaret işlemede çok önemli olan ayrık fourier dönüşümü, hızlı fourier dönüşümü ve dairesel konvolüsyonun sirkülant matrislerle olan ilişkisi detaylı bir şekilde ele alınmıştır.

5. Bölüm: Tezin sonuç ve öneriler bölümü olup bu bölümde, bu konuda ileride ne tür çalışmalar yapılabileceği ifade edilmiştir.

2. KAYNAK ARAġTIRMASI

X. Liu ve P. Wei (2009), sirkülant matrislerin bir çeşidi olan permütasyon sirkülant

matrisler, sayısal işaret işlemede uygulama alanı olan matrislerdir. Bu çalışmada hızlı Fourier dönüşümü yardımıyla ninci mertebeden permütasyon çarpan sirkülant matrislerin çarpımı ve kıncı kuvveti için hızlı bir algoritma verilmiştir.

G. Zhao (2009), sirkülant matrislerin bir çeşidi olan rsirkülant matrisler sayısal işaret işlemede kullanılmaktadır. Bu çalışmada, tekil olmayan rsirkülant matrislerin sadece ilk satır elemanları kullanılarak sirkülant matrislerin ters problemi incelenmiştir.

M. Teixeira ve D. Rodriguez (1994) çalışmalarında, dairesel konvolüsyon yardımıyla,

biçimsel olarak AFD matrisinin bazı çarpanlarının sirkülant matrisin çarpanlarıyla ilişkili olduğunu göstermiştir.

H. Li, X. Liu ve P. Wang (2009), hızlı Fourier dönüşümü yardımıyla ninci mertebeden permütasyon faktör sirkülant matrislerin kıncı kökü için hızlı bir algoritma verilmiştir.

W. Zhao (2009), sayısal işaret işlemede, ters sirkülant matrislerin ters problemini ele

almıştır.

N. L. Tsitsas, E. G. Alivizatos ve G.H. Kalogeropoulos (2007), sirkülant bloklu

matrislerin sayısal işaret işlemede birçok uygulama alanı vardır. Bu tip matrislerin tersi ayrık Fourier dönüşümü yardımıyla her bir sirkülant bloğun köşegenleştirilmesine dayanmaktadır. Bu çalışmada sirkülant bloklu matrislerin tersi için rekürsif (yinelemeli) bir agoritma ele alınmıştır.

H. Karner, J. Schneid ve C. W. Ueberhuber (2003) çalışmalarında, sirkülant

matrisleri sağ ve sol sirkülant matris olarak sınıflandırmışlardır. Ayrıca ters sağ sirkülant ve ters sol sirkülant matrisler tanımlanarak, bu matrislerin öz değer ve singüler değer ayrışımları Fourier matrisi kullanılarak elde edilmiştir.

D. S. G. Pollock (2002), sirkülant matrislerin spektral ayrışımını Fourier matrisi

yardımıyla elde etmiştir. Buna ek olarak simetrik sirkülant matrisleri tanımlamış ve bu matrisin Fourier dönüşümlerini incelemiştir.

H. Li ve X. Liu (2009), sayısal işaret işlemde önemli bir yeri olan rsirkülant matrislerin sadece ilk satır elemanları kullanılarak bazı özellikler verilmiştir.

C. Dong (2009), sayısal işaret işlemde önemli bir yeri olan simetrik rsirkülant matrislerin sadece ilk satır elemanları kullanılarak bazı özellikler verilmiştir.

3. TEMEL KAVRAMLAR

3.1. Bazı Özel Matrisler

Tanım 3.1. _ij

n n

A a



 

   bir kare matris olmak üzere eğer i j için her zaman 0

ij

a  oluyorsa, o takdirde A matrisine köşegen matris denir ve diag A( ) şeklinde gösterilir.

Üçüncü mertebeden bir köşegen matrise, örnek olarak

11 22 33 0 0 ( ) 0 0 0 0 a diag A a a           

matrisini verebiliriz (Taşcı, 2005).

Tanım 3.2. Eğer verilen bir kare matrisin transpozesini alarak elde edilen matris,

verilen matrisin kendisine eşit oluyorsa bu matrise simetriktir denir. Başka bir ifade ile A kare matrisi için

T

A  A

ise bu matrise simetrik matris denir.

Üçüncü mertebeden bir simetrik matrise, örnek olarak

11 22 33 a b c A b a d c d a           

matrisini verebiliriz (Taşcı, 2005).

Tanım 3.3. 



1, 2, , n



kümesinin bir,

1 2 (1) (2) ( ) n n           

permütasyonu olsun. E , ._j j bileşeni 1 diğer bileşenleri 0 olan



0, , 0,1, 0, , 0



j

E 

şeklinde gösterilen n bileşenli birim satır vektör olmak üzere n. mertebeden permütasyon matris

(1) (2) ( )n E E P P E            _{ }      

biçimindedir. Yani, i1, 2,...,n olmak üzere P' nin i. satırının ( ).i sütunundaki elemanı 1, diğer elemanları 0 olan matrise permütasyon matris denir.

En genel anlamda bir permütasyon matris, birim matrisin satırlarını ya da sütunlarını değiştirmekle elde edilen bir matristir.

Üçüncü mertebeden permütasyon matrisine, örnek olarak

0 1 0 0 0 1 1 0 0 P           

matrisini verebiliriz (Davis, 1979).

Tanım 3.4. U kompleks bir kare matris olmak üzere

* *

U UUU I ise bu matrise üniter matris denir. Burada *

,

U U' nuneşlenik transpozesi ve I birim matristir (Taşcı, 2005).

3.2. Öz değerler ve Öz vektörler

Tanım 3.5. A_, nkare bir matris olmak üzere

A( ) det(I A)

  

polinomuna A matrisinin karakteristik polinomu denir. Tanım 3.5 ile verilen polinomu

1 2 A( ) 1 2 1 n n n n n a a a a               

şeklinde açık bir şekilde de yazabiliriz (Bozkurt ve ark., 2005).

Tanım 3.6. A( ) 0 denklemine A matrisinin karakteristik denklemi denir

(Bozkurt ve ark., 2005).

Tanım 3.7. _A( ) 0 denkleminin köklerine A matrisinin öz değerleri veya karakteristik değerleri veya aygen değerleri denir (Bozkurt ve ark., 2005).

Tanım 3.8. (1_i  i n) için

(IA x) 0

denkleminin x çözüm vektörüne _i A matrisinin öz vektörü veya karakteristik vektörü veya aygen vektörü denir (Bozkurt ve ark., 2005).

Teorem 3.1. n mertebeden bir kare matrisin karakteristik polinomu . n . dereceden bir polinomdur ve en yüksek dereceli terimin katsayısı 1, polinomdaki sabit terim a_n  ( 1)n A ve 1

'in n  

katsayısı - (A)'dır.iz Eğer A matrisinin öz değerleri

1, 2, , n

   ise

n

i=1

(a)= _i

iz



 ve det( )A  _{1 2} _n şeklindedir (Bozkurt ve ark., 2005).

Teorem 3.2. A n, . mertebeden herhangi bir kare matris ise, A matrisinin her öz değerine en az bir öz vektör karşılık gelir (Bozkurt ve ark., 2005).

3.3. Bir Matrisin KöĢegenleĢtirilmesi

Tanım 3.9. A ve B herhangi iki kare matris olsun.

1 BP AP

olacak şekilde P düzgün (tersi olan) matris varsa A ve B matrislerine benzer matrisler, P' ye dönüşüm matrisi ve dönüşüme de benzerlik dönüşümü denir (Bozkurt ve ark., 2005).

Teorem 3.3. Benzer matrislerin karakteristik polinomları ve dolayısıyla öz

değerleri aynıdır (Bozkurt ve ark. 2005).

Ġspat: A ve B benzer matrisler olsun. Bu durumda

1 BP AP dir. 1 1 1 det( ) det( ) det( ( ) ) det det( ) det det( ) B I P AP I P A I P P A I P A I                 

Teorem 3.4. A herhangi bir kare matris olsun. A matrisi, _i(1 i n) öz değerlerine karşılık

(AiI x) i 0, xi 0

denklemini sağlayan x x₁, ₂, ,x şeklinde _n n tane lineer bağımsız öz vektöre sahip

olsun. Bu durumda;



1 2 n



ve ( ,1 2, , n) P x x x  diag    olmak üzere 1 1 P AP   veya A P P

dir (Bozkurt ve ark. 2005).

Ġspat: 1 i n  için

i i i

Ax x

olduğundan A matrisi ile P matrisini çarparsak;













1 2 1 2 1 1 2 2 n n n n AP A x x x A x Ax Ax x x x P        

elde edilir. P matrisinin sütun vektörleri lineer bağımsız olduğundan detP0

olup P1 vardır. Bu durumda elde edilen AP P eşitliği soldan 1 P ile çarpılırsa; 1 P AP   sağdan 1 P ile çarpılırsa da 1 A P P elde edilir.

Teorem 3.5. A köşegenleştirilebilen bir kare matris ise herhangi bir pozitif k

tamsayısı için

1

k k

A  P P

dir (Bozkurt ve ark. 2005).

Ġspat: A köşegenleştirilebilir olduğundan

1 A P P

olacak şekilde P düzgün matrisi vardır. k tane 1

P P  matrisini çarpım şeklinde yazarsak; 1 1 1 tane ( )( ) ( ) k k A  P P  P P  P P 

olur. Matrislerde çarpma işlemi, birleşme özelliğine sahip olduğundan;

1 1 1 ( ) ( ) k A  P P P  P P P şeklinde yazılabilir. 1 P P I

olduğundan, sonuç olarak

1

k k

A  P P

dir.

Sonuç 3.1. Herhangi bir nkare matrisin benzerlik dönüşümü ile köşegenleştirilmesi için gerek ve yeter şart matrisin n tane lineer bağımsız öz vektöre sahip olmasıdır ( Bozkurt ve ark. 2005).

3.4. Lineer Denklem Sistemleri ve Çözümleri

Tanım 3.10. K bir cisim olsun. b b₁, ₂, b ve _m a_ij(1 i m,1 j n), K cisminin verilen elemanları; x x1, 2, x de bilinmeyenler olmak üzere n

11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b           _        _ (3.1)

sistemine n bilinmeyenli m denklemden oluşan bir lineer denklem sistemi denir

(Bozkurt ve ark., 2005). (3.1) ile verilen sistem

11 12 1 1 1 21 22 2 2 2 1 2 n n m m mn n n a a a x b a a a x b a a a x b                  _                  

şeklinde matris notasyonu ile gösterilebilir. Bunu da; A, m n matris; x, n1 ve b de 1

Axb

olarak gösterebiliriz (Bozkurt ve ark., 2005).

Tanım 3.11. (3.1) ile verilen sistemi sağlayan ( ,x x_{1 2}, x (_n) x_i'ler K' nın elemanları) nlisine sistemin çözüm takımı denir.

Tanım 3.12. Herhangi iki lineer denklem sisteminin çözüm takımı aynı ise bu

sistemlere denk sistemler denir.

Teorem 3.6. Bir lineer denklem sistemindeki herhangi bir denkleme diğer

denklemlerin lineer kombinasyonlarını eklemekle veya denklemlerden birisini sıfırdan farklı bir skalerle çarpmakla elde edilen yeni lineer denklem orijinal sisteme denktir (Bozkurt ve ark., 2005).

(3.1) sistemi verilsin ve sistemin çözümü var olsun. Eğer A katsayılar matrisinde a₁₁0 ise (eğer a₁₁0 ise uygun bir satır değişikliğiyle a pozisyonuna ₁₁

sıfırdan farklı bir eleman getirilir.) sistemin ilk satırı 21 11

a a

 ile çarpılıp ikinci satıra,

31 11

a a

 ile çarpılıp üçüncü satıra ve bu işleme bu şekilde devam ederek 1 11

m

a a

 ile çarpılıp son satıra eklenirse

11 1 12 2 1 1 (1) (1) (1) 22 2 2 2 (1) (1) (1) 2 2 n n n n m mn n m a x a x a x b a x a x b a x a x b          _       _ (3.2)

elde ederiz. a₂₂(1) 0 ise ( eğer a₂₂(1)0 ise uygun bir satır değişikliğiyle a(1)₂₂ pozisyonuna sıfırdan farklı bir eleman getirilir.) sistemin ikinci satırı

(1) 32 (1) 22 a a

 ile çarpılıp üçüncü satıra,

(1) 42 (1) 22 a a

 ile çarpılıp dördüncü satıra ve bu işleme bu şekilde devam ederek

(1) 2 (1) 22 m a a  ile çarpılıp son satıra eklenirse

11 1 12 2 1 1 (1) (1) (1) 22 2 2 2 (2) (2) (2) 33 3 3 3 (2) (2) (2) 3 3 n n n n n n m mn n m a x a x a x b a x a x b a x a x b a x a x b             

elde edilir. k eleminasyon sayısını göstermek üzere ( 1) ( ) ( 1) ( 1) (0) ( 1) ; 1, 2, , 1; 1, , ; , , ; k k k ik k ij ij k kj ij ij kk a a a a k m i k m j k m a a a            

seçmek suretiyle işleme A katsayılar matrisini satır indirgenmiş forma getirene kadar devam edilir. Elde edilen sistem, verilen sisteme denk bir sistem olup buradan çözüme gidilir (Bozkurt ve ark., 2005).

3.5. Sirkülant Matrisler ve Özellikleri

Tanım 3.13. _ij

n n

C c



 

   nkare _{bir matris olmak üzere elemanları}

0, ; (mod )

ij j i j i

c c _ c _ j i k n şartını sağlayan n n mertebeliC matrisine sirkülant matris denir ve

0 1 2 1

( , , , , _n )

Ccirc c c c c _

şeklinde gösterilir. Ayrıca açık olarak

0 1 2 1 1 0 1 2 2 1 0 3 1 2 3 0 n n n n n n c c c c c c c c C c c c c c c c c                        biçimindedir.

n n _{mertebeli sirkülant bir matris n elemanlı bir vektör ile temsil edilir ve bu}

vektör, matrisin ilk satırını oluşturur. Böylece takip eden satırlar önceki satırın son elemanını başa alarak devam eder. Bir sirkülant matrisin esas köşegeni üzerindeki elemanları ile esas köşegene paralel olan doğrultu üzerindeki elemanları aynıdır.

0 1 2 1

( , , , , _n ) _ij

Ccirc c c c c _    a olsun ve bunu açık şekilde yazalım.

0 1 2 1 11 12 13 1 1 0 1 2 21 22 23 2 2 1 0 3 31 32 33 3 1 2 3 0 1 2 3 n n n n n n n n n n n n nn c c c c a a a a c c c c a a a a C c c c c a a a a c c c c a a a a                                         Yukarıdaki eşitlikten, 1, 1 1,1 1, 1 11 ; 1 , 1 ; 1 ; 1 ij i j in i nj j nn a a i n j n a a i n a a j n a a                

dir. Bunu da aşağıdaki gibi genelleştirebiliriz.



1, 2, , n



  , n uzunluğunda bir devir olmak üzere

( ), ( ); 1 , 1

ij i j

a a   i n  j n (3.3)

olur (Davis, 1979; Gray, 2001).

Sonuç 3.2. A’nın sirkülant olması için gerek ve yeter şart (3.3)’ün sağlanmasıdır (Davis, 1979).

Sirkülant matrislere örnek verecek olursak

; ; a b c d a b c a b d a b c c a b b a c d a b b c a b c d a    _{  }  _{    }  _{    }  _{   }     

sırasıyla 2 2, 3 3 ve 4 4 mertebeli sirkülant matrislerdir.

Teorem 3.7. A   a_ij nkare _{bir matris olsun. O zaman} A' nın sirkülant olması için gerek ve yeter şart

A  A

olmasıdır (Davis, 1979).

Ġspat:

) A   a_ij nkare bir matris ve A  A olsun. Eşitliğin her iki yanını sağdan * ile çarparsak * * * * * ( ) ( ) ( ) A A A A I             

olup, bu son eşitlikten

*

A A (3.4)

elde ederiz. P, permütasyon matris olmak üzere PAP_* a_{( ), ( )i  j} _ olup ayrıca,  de bir permütasyon matris olduğundan P_  dir. O halde

* ( ), ( )i j A a_{ }   _{ } _ (3.5) dir. (3.4) ve (3.5) eşitliklerinden ( ), ( ) ij i j a a_{ } olur ki, Sonuç 3.2’ye göreA sirkülanttır.

) A n - kare matrisi sirkülant olsun.  



1, 2,..., n



n uzunluğunda bir devir

olmak üzere ( ), ( ) ij i j a a_{ } (3.6) dir. (3.5) ifadesinden * ( ), ( )i j A a_{ }   _{ } _ (3.7)

olduğunu biliyoruz. (3.6) ve (3.7)’den

*

A A (3.8)

elde ederiz. (3.8) eşitliğini sağdan  ile çarparsak

* * * ( ) ( ) ( ) A A A I A              

elde ederiz ki, bu da ispatı tamamlar.

Sonuç 3.3. A’nın sirkülant olması için gerek ve yeter şart A ’ın sirkülant *

olmasıdır (Davis, 1979).

Ġspat: (3.4)’ den

*

A A olup, her iki tarafın eşlenik transpozesini aldığımızda

* * * * * * * * * * * * * * * ( ) ( ) ( ) ( ) A A A A A A A A I A A                      

olur bu da Teorem 3.7 gereği *

A sirkülanttır.

A ve B, n n iki sirkülant matris olsun. Yani;

0 0 ; (mod ) ij k ij k A a ve B b j i k n olsun. 1 0 0 1 0 0 ( ) ( ) n ij r rk r n r k r r k AB a b a b AB        





veya ve

A B 'yi Acirc a a( , ,_{0 1} a_n1) ve Bcirc b b( , ,_{0 1} b_n1) biçiminde gösterip

0 1 1 0 1 1 0 0 1 0 1 0 1 1 0 1 2 1 1 1 2 1 0 1 , , , , , , , , , , , n n n n n n n n a a a b b b a b a b a b a b a b a b a b a b a b        

şeklinde düzenlersek, her sütunun toplamı bize AB’nin ilk satır elamanlarını verir. Yani;

0 0 1 1 1 0 2 1 1 0 0 1

( _n , _n , , _{n n} )

ABcirc a b  a b_ a b  a b_ a b_  a b_

dir (Davis, 1979).

Teorem 3.8.A ve B nkare sirkülant matrisler  da bir skaler olmak üzere aşağıdaki özellikler mevcuttur:

i) A B , A ve AB de sirkülant matrislerdir.

ii) Aynı mertebeli iki sirkülant matrisin çarpımının değişme özelliği vardır.

Yani; ABBA'dır.

iii) Eğer bir sirkülant matris tekil değilse, tersi de sirkülant matristir. Yani;

detA0 _ise 1

A mevcut ve sirkülant matristir.

iv)A sirkülant matristir. T

v) Sirkülant matrisler normal matrislerdir (Davis, 1979). Ġspat:

i) Ave B sirkülant ise A  A ve B  Bdir. Bu iki eşitliği taraf tarafa toplarsak ( ) ( ) A B A B A B A B



 



 

     

olur ki, A B _{toplam matrisi sirkülanttır.}

A sirkülant ise A  A _dır.  da bir skaler olmak üzere, eşitliğin her iki tarafını ile çarparsak,

(

)

(

)

(

)

(

)

A

A

A

A

 

 

   





elde edilir. Bu da, A _{matrisinin sirkülant olmasıdır.}

Şimdi de AB’nin sirkülant olduğunu gösterelim. O halde (AB)  (AB) olduğunu göstermek yeterlidir.

A _ve B sirkülant olsun. O halde A  A’dir. Eşitliğin her iki tarafını sağdan

Bile çarparsak

( ) ( )

( ) ( ) matris çarpımının birleşme özelliği ( ) ( ) sirkülant olduğundan ( ) ( ) A B A B A B AB A B AB B AB AB            

olur ki, istenendir.

ii) Sirkülant matris çarpımından açıktır. iii-iv) İspat, Sonuç 3.3’ den açıktır.

v) Sirkülant matrislerde çarpmanın değişme özelliği olduğundan, açıktır.

Bir n n sirkülant matrisi oluşturabilmek için öncelikle n n temel sirkülant matrisi tanımlamak gerekir.

Tanım 3.14.



permütasyon matrisi ilk satırı (0,1, 0, , 0) olan n n sirkülant matris ise



’e temel sirkülant matris denir.

3 3 temel sirkülant matrisi

0 1 0 0 0 1 1 0 0             dir (Davis, 1979).

İlk satırı  



c c c₀, ,_{1 2}, ,c_n1



olan n n sirkülant matrisi oluşturmak için katsayıları C ’nin ilk satır elemanları olan

2 1 0 1 2 ... 1 ( ) n n c c c p z c  z z   z  polinomu tanımlansın. Bu durumda C p_( ) şeklindedir.

Örneğin 3 3 sirkülant matris oluşturmak için p z_( ) c₀ c z c z₁  ₂ 2

polinomunu ele alalım. O halde

2 0 1 2 0 1 2 0 1 2 1 2 2 0 1 1 2 1 2 0 2 2 0 1 2 2 0 1 1 2 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 1 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 ( ) p c I c c c c c c c c c c c c c c c c c c c c c c c c c c c c c C _                    _{ } _{ } _{ }                         _{  } _{ } _                        

elde edilir (Davis, 1979).

Sonuç 3.4. İlk sütunu 



c c c₀, ,_{1 2}, ,c_n1



T olan n n sirkülant matrisi oluşturmak için katsayıları CT ' nin _{ilk sütun elemanları olan}

2 1 0 1 2 ... 1 ( ) n n c c c p z_ c  z z   _z 

4. SAYISAL ĠġARET ĠġLEMEDE SĠRKÜLANT MATRĠSLER

Bu bölüm tezin esas kısmını oluşturmakta olup üç başlık altında toplanmıştır.

4.1. Sayısal ĠĢaret ĠĢleme

İşaret; zamanla, uzayla veya diğer bağımsız değişken veya değişkenlere bağlı olarak değişen herhangi bir fiziksel büyüklük olarak tarif edilir. Konuşma, radyo dalgaları işarete örnek olarak verilebilir. Bir işaret üzerine, herhangi bir işlemi uygulayan fiziksel cihaz da sistem olarak tanımlanır ve işaret bir sistemden geçirildiği zaman bu işlem işaret işleme olarak adlandırılır.

İşaretlerin işlenmesi, elektrik mühendisliğinin en önemli konularından biridir. Çeşitli nedenlerden dolayı işaretler işlenmektedir. Haberleşmede işareti gürültüden ayırmak, radar ve sonar sistemlerinde hedefi belirlemek için işaretler işlenir. Ayrıca işaretler çeşitli uygulamalarda kullanılmak amacıyla da işlenebilir. Televizyonda görüntüleme, haberleşmede transmisyon ve sayısal sistemlerin kontrolünde kullanmak için işaretler işlenir.

Bilim ve mühendislikte karşılaşılan işaretler tabii olarak analog formda olan işaretlerdir. Yani, işaretler zaman ve uzay gibi sürekli bir değişkenin fonksiyonlarıdır. Bunlar sürekli olan bir sahada (domain) değer alırlar. Böyle işaretler, direkt olarak karakteristiklerini değiştirmek veya bazı arzu edilen özelliklerini çıkarıp değerlendirmek gayesiyle filtreler, frekans analiz cihazları, frekans çarpanları gibi uygun analog sistemlerde işleme tabii tutulmaktadırlar. Bu durumda işaretin direkt analog formda işlendiği söylenebilir. Şekil 4.1’de böyle bir sistem görülmektedir.

ġekil 4.1. Analog işaret işleme

Sayısal işaret işleme ise analog işaretlerin işlenmesi için alternatif bir yoldur. Böyle bir sistem Şekil 4.2’de gösterilmektedir. İşlemeyi sayısal olarak gerçekleştirmek için analog işaret ile sayısal işaret işleyici arasında analog-sayısal (A/D) kullanılır ve

işaretleri işleyebileceği bir hale getirir. Yapılmak istenen işlemler yapıldıktan sonra da sayısal-analog dönüştürücü (D/A) kullanarak tekrar analog işaret elde edilir.

ġekil 4.2 Bir sayısal işaret işlemenin blok diyagramı

İşaretleri, zamana göre değişimleri dikkate alınarak sürekli-zamanlı ve ayrık-zamanlı işaretler olarak iki gruba ayırmak mümkündür. Biz bu tezde ayrık ayrık-zamanlı işaretleri ele alacağız.

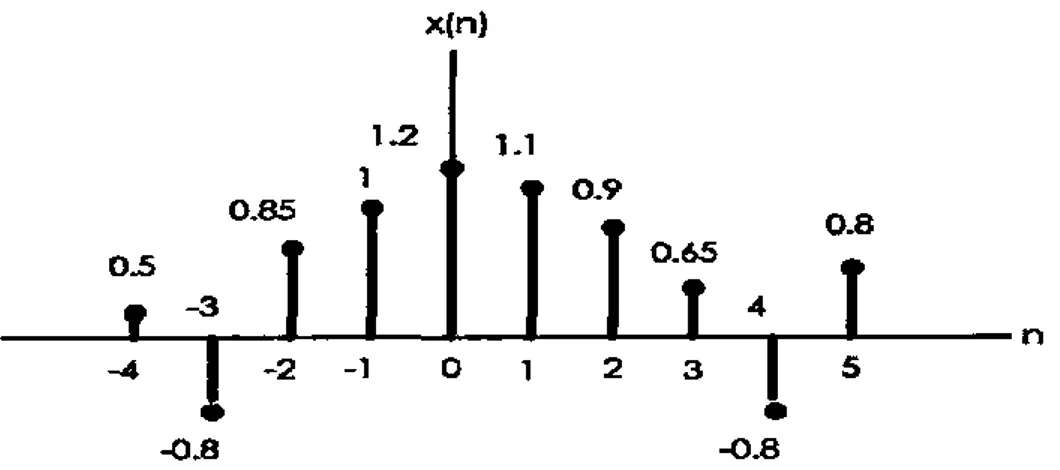
Ayrık zamanlı işaret, bir dizi sayıdan oluşur ve genellikle dizi, fonksiyon vektör, grafik veya tablo şeklinde gösterilir. Bir ayrık zamanlı işaretin grafik gösterimi Şekil 4.3’de gösterilmiştir.

ġekil 4.3. Bir ayrık zamanlı işaretin grafik gösterimi

Bir ayrık zamanlı işaret, dizi olarak





( ) 0, 0,1, 2 1,3, 4, 0

x n  

şeklinde gösterildiği gibi bu işareti vektörel olarak da



0, 0,1, 2 1,3, 4, 0



x 

şeklinde gösterebiliriz (Tolimieri ve ark., 1997; Kayran ve Ekşioğlu, 2010; Karaboğa, 1995).

4.2. Sirkülant Matrislerin Ayrık Fourier DönüĢüm (AFD) ile ĠliĢkisi

Ayrık Fourier Dönüşümü (AFD), ayrık zamanlı işaret işleme algoritma ve sistemlerin analizi, tasarımı, gerçekleştirilmesi ile doğrusal filtreleme, korelasyon analizi ve spektrum analizi gibi işaret işleme uygulamalarında önemli bir rol oynar. AFD’nin bu öneme sahip olmasının ardındaki temel neden AFD’yi hesaplamakta kullanılan verimli algoritmaların varlığıdır (Oppenheim, 1999; Proakis ve Manolakis, 2007).

Ayrık Fourier dönüşümü (AFD), bir sayısal işaretin zaman bölgesindeki karşılığını eş değer frekans bölgesindeki karşılığına dönüştürür. Ters AFD ise geri işlemi gerçekleştirerek işaretin frekans bölgesindeki karşılığını zaman bölgesindeki karşılığına dönüştürür (Oppenheim, 1999).

Ayrık Fourier dönüşüm matrisi, AFD’yi anlamamızda kolaylık sağlayacağından, bu matrisi ve onun özelliklerinin bilinmesi yararlı olacağı düşüncesiyle AFD’den önce verilmiştir.

4.2.1. Ayrık Fourier dönüĢüm (AFD) matrisi

1 n bir tamsayı ve 2 2 2 cos sin , 1 i n w e i i n n  _{     }   _{ } _{ }       olmak üzere; a) wn 1 b) ww1 c) 1 ww d) wk wk wn k e) 2 1 1 n 0 w w w     

eşitlikleri vardır. Gerçekten

a) 2 2 ( ) 1 i n i n w e e   

b) (c)’yi gösterirsek eşitlik kolayca görülür. c)

2 2 1 1 2 2 ( ) ( ) cos( ) sin( ) 2 2 cos( ) sin( ) i i n n w e e i n n i w n n   _  _{    }      _{ }   d) 2 2 (2 ) 2 2 ( ) 2 2 ( ) cos( 2 ) sin( 2 ) 2 2 cos( ) sin( ) ( ) i k i n k n n k n k i i k k n n k k w e e i n n k k i e e w n n     _{ }                 _     _  _   e) 2 1 1 1 1 1 0 1 1 n n w w w w w w            

elde edilir (Davis, 1979).

Tanım 4.1. ninci mertebeden ayrık Fourier dönüşüm matrisi

2 1 * ( 1)( 1) _{2 4 2( 1)} ( 1) 2( 1) ( 1)( 1) 1 1 1 1 1 1 1 n j k _n n n n n w w w W w w w w w w w                           olmak üzere * * ( 1)( 1) 1 1 ( j k ) F W n w n    

olan Fmatrisine ayrık Fourier dönüşüm matrisi denir (Davis, 1979).

*

ve

F F matrislerinin tanımdan simetrik oldukları açık olup

* * *

, ( ) ,

T T

FF F  F F FF

dir.

Ayrık Fourier dönüşüm matrisinin en temel özelliği üniter olmasıdır. Şimdi Davis’in aşağıdaki teoremini verelim.

Teorem 4.1. F matrisi üniterdir. Yani,

* * -1 *

veya F n

F F FF I F (4.1)

Ġspat: * * 1 ( 1)( 1) ( 1)( 1) 1 ( 1)( 1) ( 1)( 1) 1 ( 1)( 1 1) 1 1 ( ) 0 ( ) ( ) ( ) 1 1 ( ) ( ) 1 ( )( ) 1 ( ) 1 n jk jr rk r n j r r k r n j r r k r n r j k r n r j k r F F F F w w n n w w n w n w n                         











elde ederiz. Buradan jk için

1 1 1 ( ) 0 0 0 0 1 1 1 1 1 1 n n n r j k r r r w w n n n n n            







jk için 1 1 1 ( ) 1 1 1 0 1 1 ( ) 1 1 ( ) 1 1 1 1 ( ) ( ) ( ) 0 1 1 1 j k n n j k n r j k j k j k j k r w w w n n w n w n w                       



olur. O halde * 1, ise ( ) 0, ise jk j k F F j k     _ 

olur ki, bu da F F* 'ınbirim matris olmasından başka bir şey değildir. Benzer şekilde;

* n FF I olduğunu da gösterilebiliriz. Teorem 4.2. * * n WW W W nI dır (Davis, 1979; Kayran ve Ekşioğlu, 2010).

Ġspat: (4.1)’den * n FF I olduğundan * * 1 n n WW I n WW nI  

olur. Benzer şekilde

*

n

W W nI olduğu da kolayca görülebilir.

4.2.2. Ayrık Fourier dönüĢümü (AFD)

Tanım 4.2. x, n bileşenli bir vektör olmak üzere x'inayrık Fourier dönüşümü (AFD) ve ters AFD eşitlikleri şu şekilde yazılır.

2 1 0 , 0,1, , 1 ijk n n k j j X x e k n    



  (4.2) ve 2 1 0 1 , 0,1, , 1 ijk n n j k k x X e j n n     



  (4.3) şeklinde yazılır. 2 i n w e 

 olduğu dikkate alınırsa (4.2) ve (4.3) dönüşüm ikilisi,

1 0 , 0,1, , 1 n jk k j j X x w k n   



  (4.4) ve 1 0 1 , 0,1, , 1 n jk j k k x X w j n n    



  (4.5)

olarak da yazılabilir. Burada hesaplanan n tane X değeri, _k x_j vektörünün nnoktalı AFD’si olarak adlandırılır. x_j ise X_k vektörünün nnoktalı _{ters AFD’si olarak} adlandırılır.

AFD yardımıyla sınırlı ve ayrık işaret için sınırlı ve ayrık bir frekans gösterimi elde edilmektedir (Kayran ve Ekşioğlu, 2010).

Not 4.1. Literatürde bazen X_k' nın negatif üstel fonksiyon ve buna karşılık gelen xj' nin de pozitif üstel fonksiyon yardımıyla tanımlandığı görülmektedir.

1

n

terimi yine denklemlerden herhangi biriyle kullanılabilir (Kayran ve Ekşioğlu, 2010).

4.2.3. Matris formunda AFD ve ters AFD gösterilimi bileşenli

n _{x vektörünün AFD’sinin (4.4)’den}

1 0 , 0,1, , 1 n jk k j j X x w k n   



 

2 0 0 2 ( 1) 1 1 2 4 2( 1) 2 2 ( 1) 2( 1) _{( 1)} 1 1 1 1 1 1 1 1 1 n n n n _n n n X x w X w w x X w w w x X w w _w x                                                       (4.6)

biçimindedir. (4.6) ifadesi, AFD’nin matris gösterimi olup Tanım 4.1’den

*

n

X W x (4.7)

şeklinde sembolize edebiliriz. (4.7) ve Teorem 4.2’den ters AFD’nin matris gösterimi 1 n x W X n  biçimindedir. *

W ve W matrisinin elemanları, w' nin özelliklerinden faydalanarak n farklı

sayıdan oluşan



2 1



1, ,w w , ,wn

kümesi yardımıyla basitleştirilebilir. Burada k, ( 0,1, , 1)

w k n dizisinin elemanları, 1 0

n

z   denkleminin kökleridir.

Örneğin, n4 için W matrisinin elemanları * z4 1 0 denkleminin kökleri olan



1, 1, , i i



kümesinin elemanlarından oluşur. Gerçekten

2 3 2 3 * 4 2 4 6 2 0 2 3 6 9 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 w w w w w w W w w w w w w w w w w w w i i i i                              _{ }          _{ }   

olup bu kolayca görülebilir (Kayran ve Ekşioğlu, 2010).

4.2.4. Hızlı Fourier dönüĢümü

Ayrık Fourier dönüşümünün (AFD) doğrudan hesaplanmasında her bir X _k

nedenle n adet AFD değeri bulunurken, n çarpma ve 2 n n( 1) toplama işlemi gereklidir. Ayrıca, her karmaşık çarpma işlemi dört gerçel çarpma ve iki gerçel toplama işlemi ve her bir karmaşık toplama, iki gerçel toplama işlemi ile gerçekleşmektedir. Sonuç olarak, işaretin boyutu olan n' nin büyük olması durumunda AFD nin doğrudan hesaplanması çok fazla miktarda işlem gerektirmektedir. Yani, n sayısı artarken gereken işlem sayısı yüksek hızla artmaktadır. AFD hesaplanmasında etkin ve bugün kullanılan yaklaşım, hızlı Fourier dönüşümü (HFD) algoritmalarıdır. HFD terimi bazen karışıklıklara neden olmaktadır. Her ne kadar dönüşüm olarak adlandırılsa da, hızlı Fourier dönüşümü (HFD) ayrık Fourier dönüşümü (AFD)’den farklı değildir. HFD, AFD hesaplanması için etkili, ekonomik bir algoritmadır (Kayran ve Ekşioğlu, 2010; Cooley ve Tukey, 1965; Kunt, 1987).

AFD’nin sayısal işaret işleme alanında spektrum analizi, konvolüsyon ve korelasyon gibi işlemlerin gerçekleşmesinde önemli rol oynamasının önemli bir sebebi HFD algoritmalarıdır. Genel olarak HFD ile ilgili birçok algoritma olmasına karşın konumuzun bütünlüğü açısından biz burada HFD’yi matris formunda inceleyeceğiz.

4.2.5. Matris gösterimi yardımıyla HFD

AFD için matris gösterimi, (4.6) ve (4.7) ifadeleriyle verilmişti. Hızlı Fourier dönüşümü ile sağlanmak istenen, bu matris çarpımını daha az sayıda işlem uygulayarak gerçekleştirebilmektir. Bunu yapmanın yolu ise, (4.7)’deki *

n

W matrisinin, bol sıfırlar içeren matrislerin çarpımı şeklinde ayrıştırılması olacaktır. *

'ı n

W oluşturan w jk

terimlerinin özelliği sayesinde bu mümkün olmaktadır. ' nin

n 2 ' nin bir kuvveti olduğu (n2 )m varsayımı altında, 2 tabanlı bir HFD algoritması geliştirilecektir. HFD’yi gerçekleyecek matris ayrıştırması için izlenecek yol, W_n* matrisinin W_n*_{/ 2} matrisiyle ilişkilendirilmesi olacaktır.

Örnek olarak n4 durumunu ele alalım. n4 için

2 3 * * 2 4 2 4 6 * 2 3 6 9 1 1 1 1 1 1 0 0 1 0 1 0 0 1 0 0 0 1 1 1 0 0 1 w w w W w W ve w w w W w w w w       _{ }        _{ }   _{ }           olmaktadır. * 4 W matrisini

* 4 1 0 1 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 0 1 0 0 0 1 1 0 1 0 0 0 1 0 0 0 1 0 0 0 1 w w W w w                            _           

şeklinde ayrıştırmak mümkündür. En sağdaki matris bir permütasyon matrisidir. Çift ve tek indisli vektör elemanlarını birbirinden ayırmaktadır. Ortadaki matris iki tane 2noktalı AFD işlemi gerçekleştirmektedir. W₄* için sağlanan bu ayrıştırma, çarpımda yer alan matrislerin bol sıfırlı olmasından dolayı matris çarpımında işlem sayısında bir azalma getirmektedir. n4 için geliştirilen bu ayrıştırma genel bir n için

* / 2 / 2 * / 2 * / 2 / 2 / 2 çift-tek indis 0 ayrıştırması 0 n n n n n n n I W W I W        _{   }  _{ }    

şeklinde yapılabilir. Burada ( 0,1, 2, , 1) 2

n

k  olmak üzere I birim matrisi, _k _k ise

köşegen elemanları 2 1

(1, ,w w , ,wk ) olan köşegen matrisi göstermektedir (Kayran ve Ekşioğlu, 2010; Strang, 1998).

Tablo 4.1. AFD için Doğrudan Hesaplama ve HFD Algoritmasının Gerektirdiği Çarpma İşlemleri

Adım Sayısı Nokta Sayısı HFD Çarpma Sayısı AFD’nin Doğrudan Hesaplanmasındaki Çarpma Sayısı Oran l n nlnlog2n n 2 2 n nl 1 4 8 10 2 16 256 1024 2 64 2048 10240 4 256 65536 1048576 2 4 32 102,4

4.2.6. AFD ile HFD’nin karĢılaĢtırılması

(4.4) bağıntısı ile verilen AFD’nin hesaplanmasında n karmaşık çarpım ve 2

( 1)

n n karmaşık toplama gereklidir. Oysa HFD yardımıyla n2l noktadan oluşan bir dizinin ayrık Fourier dönüşümünün hesabında nl/ 2 karmaşık çarpma ve nl karmaşık toplama işlemi yeterlidir. Adım sayısı llog₂n yazılırsa, işlem yoğunluğu açısından

AFD ile HFD’nin karşılaştırılması Tablo 4.1’de gösterildiği gibidir. Tablo incelendiğinde 10

2 1024

n  noktalı AFD için yüz katın üzerinde bir kazanç sağlanmaktadır. Başka bir deyişle, n1024 için HFD dönüşüm algoritmasının gerektirdiği çarpım sayısı doğrudan yöntemin yüzde birinden daha azdır (Kayran ve Ekşioğlu, 2010).

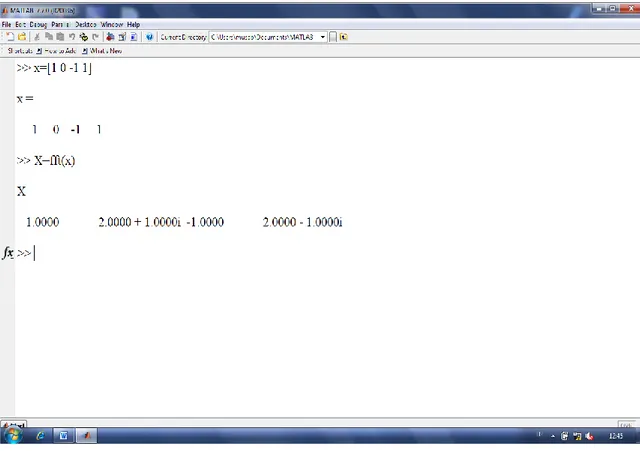
Bir vektörün AFD’si HFD yardımıyla MATLAB’da fft komutuyla hesaplanır. Örneğin x(1, 0, 1,1) vektörünün AFD’si X olmak üzere MATLAB’da Şekil 4.4’deki gibi hesaplanır.

ġekil 4.4. Bir vektörün AFD’sinin MATLAB’da hesaplanması

4.2.7. AFD matrisi ile sirkülant matrislerin köĢegenleĢtirilmesi

Sirkülant matrisleri AFD matrisi ile köşegenleştirmede,  temel sirkülant matrisin köşegenleştirmesinden yararlanacağız.

Tanım 4.3. n1 bir tamsayı,

2 /

cos(2 / ) sin(2 / ), i n

ve 2 1 (1, , , , n ) n diag w w w      olsun. Bu durumda 2 ( 1) (1, , , , ) k k k n k diag w w w    dır (Davis, 1979). Teorem 4.3. * F F    dir (Davis, 1979). Teorem 4.3’den * * * 1 ( ) ( ) ( ) ( (1), ( ), , ( n )) C circ p p F F F p F F diag p p w p w F                

olup, biz sirkülant matrisler için aşağıdaki temel teoreme ulaşmış oluruz.

Teorem 4.4. C bir sirkülant matris ise, bu matris bir AFD matrisi ile köşegenleştirilebilir.

Daha açık olarak, 1

( (1), ( ), , ( n )) C diag p p w p w      olmak üzere * CF F (4.8) dir (Davis, 1979). Sonuç 4.1. * T F F    _(4.9) dir (Davis, 1979).

Ġspat: Teorem 4.3’den açıktır.

Sonuç 4.2. C bir sirkülant matris olmak üzere

1 * ( (1), ( ), , ( )) T n C Fdiag p_ p w_ p w_  F (4.10) dir (Davis 1979). Ġspat: (4.9)’dan

* * 1 * ( ) ( ) ( ) ( (1), ( ), , ( )) T T n C circ p p F F Fp F Fdiag p p w p w F                 olur ki, istenendir.

4.2.8. Sirkülant matrisin öz değerlerinin HFD yardımıyla hesaplanması

Bu kısımda, C sirkülant matrisinin öz değerlerinin, bu sirkülant matrisin sadece ilk satır elemanlarını kullanarak, HFD yardımıyla bulunabileceği gösterilecektir. (4.8)’den * * * * * * * = = ( ) C I F F I F F F F F I F F I F I F F I F F I I I                                

elde ederiz ki, C ve  aynı karakteristik polinoma sahiptir. O halde bu iki matrisin öz değerleri de aynıdır.

, esas köşegen üzerindeki elemanları 2 1

(1), ( ), ( ), , ( n )

p_ p w p w_{ } p w_  olan köşegen bir matris olduğundan bu değerler aynı zamanda ' nın öz değerleridir. O halde 2 1 1 (1) , 2 ( ) , 3 ( ), , ( ) n n p_ p w_ p w_ p w_  _  _  _  _ 

dir. Bunu da genelleştirecek olursak C sirkülant matrisinin öz değerleri j1, 2, ,n olmak üzere 1 ( j ) j p w  _  (4.11) dir. 1 2 ( , , , _n) diag      olmak üzere

1 0 2 1 1 ; T n n c c L c     _                           olsun. (4.11)’den 1 0 1 1 1 2 0 1 1 1 1 ( 1)( 1) 0 1 1 (1) ( ) ( ) n n n n n n n n n p c c c p w c c w c w p w c c w c w                             

yazabiliriz. Bu denklem sisteminin matris formu

1 0 1 2 1 1 ( 1)( 1) 1 1 1 1 1 1 n n n n n n c c w w c w w                    _                   şeklindedir. Buradan * T L nF  elde ederiz. Ayrıca yukarıdaki eşitlikten

1 T

FL n

 

dir. AFD matrisinin tanımından * 1 *

F W

n

 eşitliğini kullanarak yukarıdaki eşitliklerden * T LW  (4.12) ve 1 T WL n  

elde edilir. Sirkülant matrisin ilk sütunu için de benzer şeyler yapılabilir (Davis, 1979). Böylece bir sirkülant matrisin öz değerleri, bu sirkülant matrisin ilk satırının veya sütununun AFD’sinden oluşur. Sonuç olarak bir sirkülant matrisin ilk satırı veya sütunu da bu sirkülant matrisin öz değerlerinin ters AFD’sinden oluşur. Bu da HFD ile hızlı bir şekilde hesaplanır.

1 2 1 3 3 1 2 1 1 3 1 2 2 1 3 1 C     _        _   

4 4 sirkülant matrisinin öz değerlerini AFD yardımıyla MATLAB’da hesaplayalım.

Çözüm: c vektörü, C matrisinin ilk satırı ve L vektörü de, bu matrisin öz değerleri olsun. (4.12) eşitliğinden faydalanarak işlem MATLAB’da Şekil 4.5’deki gibi yapılır.

ġekil 4.5. Örnek 4.1’in MATLAB’da çözümü

Teorem 4.5. ,A n n bir sirkülant matris olsun. Eğer

* 1 2 , ( , , , n) AF F  diag    ise A' nıntersi 1 1 1 1 1 2 ( , , , _n ) diag          olmak üzere 1 * 1 A F  F (4.13) dir (Davis, 1979).

4.2.9. Sirkülant matrisin öz vektörlerinin AFD matrisiyle iliĢkisi

,

C n n bir sirkülant matris olsun. Bu matrisin öz vektörleri F veya F*'ın sütun vektörleridir. Yani X_j, C sirkülant matrisinin öz vektörleri olmak üzere

1 2( 1) ( 1)( 1) 1 (1, j , j , n j )T j X w w w n      dir. Örneğin ,_C 0 1 2 2 0 1 1 2 0 C= c c c c c c c c c          

şeklinde bir sirkülant matris olsun ve 3 3 tipinde bir F matrisinin sütun vektörler *

kümesi 2 1 2 3 2 1 1 1 1 1 1 1 , , 3 3 3 1 X X w X w w w         _   _   _    _{     }  _{     }         olup 0 1 2 0 1 2 1 2 0 1 0 1 2 1 2 0 0 1 2 0 1 2 1 1 1 c c c 1 c c c 1 1 c c c 1 c c c 3 3 c c c 1 c c c 1 1 (c c c ) 1 (1) 3 1 CX p_ X X               _{   } _   _                      _{ }      olur ki X ₁, C' ninöz bir vektörüdür.

2 0 1 2 0 1 2 2 2 2 0 1 2 0 1 2 2 1 2 0 1 2 0 2 0 1 2 2 2 2 2 c c c 1 c c c 1 1 c c c c c c 3 3 c c c c c c 1 1 (c c c ) ( ) 3 w w CX w w w w w w w w w p w X X w                 _{   } _   _                      _{ }     

2 0 1 2 0 1 2 2 2 3 2 0 1 2 0 1 2 1 2 0 1 2 0 2 2 2 0 1 2 3 3 3 c c c 1 c c c 1 1 c c c c c c 3 3 c c c c c c 1 1 (c c c ) ( ) 3 w w CX w w w w w w w w w p w X X w                 _{   } _   _                      _{ }     

olup, bu da X₃' ün de C' ninöz vektörü olduğu görülmüş olur (Easton, 2010).

Sonuç 4.3. Aynı mertebeli bütün sirkülant matrislerin öz vektörleri

aynıdır.(Easton, 2010).

4.2.10. Sirkülant matris katsayılı lineer denklem sistemlerinin HFD yardımıyla çözümü

,

C n n bir sirkülant matris olmak üzere

Cxb

lineer denklem sistemi verilmiş olsun. Teorem 4.4’den C bir sirkülant matris ise

*

1 2

( , , , _n)

CF diag    F dir. C aynı zamanda tekil de değilse Teorem 4.5’den

1 * 1 1 1

1 2

( , , , n )

C F diag      F dir. O halde Cxb lineer denklem sisteminin çözümü

1 xC b

ifadesinde C1'ineşitini yazarsak

* 1 1 1 1 2 ( , , , n ) xF diag     Fb (4.14) olur (Chen, 1985). Bir vektörü *

F veya F matrisi ile çarpmak, o vektörün AFD’si ile ilişkili olduğundan bu da HFD yardımıyla hızlı bir şekilde hesaplanabilir. C' ninöz değerleri

' nin

C ilk satırının veya sütununun AFD’si olduğundan HFD yardımıyla hesaplarız. Bu algoritmayı aşağıdaki gibi verebiliriz:

Algoritma 4.1. CIRS(CIRculant Solver)

1985 yılında Chen tarafından önerilen bu algoritma sirkülant matris katsayılı lineer denklem sistemlerini çözer.

1. Adım bFb, HFD ile hesaplanır.

2. Adım C' nin öz değerleri HFD ile hesaplanır.

3. Adım 1 1 1 1 2 ( , , , _n ) b diag      b hesaplanır. 4. Adım * xF b HFD yardımıyla bulunur. Örnek 4.2. 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 2 3 5 3 2 0 3 2 0 2 3 5 x x x x x x x x x x x x x x x x                 

sirkülant matris katsayılı lineer denklem sistemini yukarıdaki algoritmayı kullanarak çözünüz.

Çözüm: Bu lineer denklem sisteminin matris formu

1 2 3 4 1 2 1 3 5 3 1 2 1 0 1 3 1 2 0 2 1 3 1 5 x x x x                   _           _        

şeklinde olup c, C' ninbirinci satırının transpozesi olmak üzere

1 5 2 0 ve 1 0 3 5 c b                          

dir. (4.14)’den lineer denklem sisteminin çözümü

* 1 1 1

1 2

( , , , n )

xF diag      Fb olup, şimdi algoritmayı uygulayalım.

1. Adım 1 1 ( ) b Fb Wb n Wb n n   

eşitliğindeki son ifade b vektörünün ters AFD’sinin n ile çarpımı olduğundan HFD