Kısa Cevaplı Matematik Yazılı Sınavının Genellenebilirlik Kuramı ve Test Tekrar Test Yöntemiyle Güvenirliğinin Kıyaslanması

KISA CEVAPLI MATEMATİK YAZILI SINAVININ

GENELLENEBİLİRLİK KURAMI VE TEST TEKRAR TEST

YÖNTEMİYLE GÜVENİRLİĞİNİN KIYASLANMASI

AYŞEDUDU ŞALGAM

YÜKSEK LİSANS TEZİ

EĞİTİM BİLİMLERİ ANA BİLİM DALI

GAZİ ÜNİVERSİTESİ

EĞİTİM BİLİMLERİ ENSTİTÜSÜ

i

TELİF HAKKI ve TEZ FOTOKOPİ İZİN FORMU

Bu tezin tüm hakları saklıdır. Kaynak göstermek koşuluyla tezin teslim tarihinden itibaren 6 (altı) ay sonra tezden fotokopi çekilebilir.

YAZARIN

Adı : Ayşedudu Soyadı : ŞALGAM

Bölümü : Eğitimde Ölçme ve Değerlendirme İmza :

Teslim tarihi : 03/11/2016

TEZİN

Türkçe Adı: Kısa Cevaplı Matematik Yazılı Sınavının Genellenebilirlik Kuramı ve Test Tekrar Test Yöntemiyle Güvenirliğinin Kıyaslanması

İngilizce Adı: The Comparison Of Reliability Of The Generalizability Theory And The Test-Retest Technique For The Short Answered Maths Exam

ii

ETİK İLKELERE UYGUNLUK BEYANI

Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu, yararlandığım tüm kaynakları kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dışındaki tüm ifadelerin şahsıma ait olduğunu beyan ederim.

Yazar Adı Soyadı: Ayşedudu ŞALGAM

iii

JÜRİ ONAY SAYFASI

Ayşedudu ŞALGAM tarafından hazırlanan “Kısa Cevaplı Matematik Yazılı Sınavının Genellenebilirlik Kuramı ve Test Tekrar Test Yöntemiyle Güvenirliğinin Kıyaslanması’’adlı tez çalışması aşağıdaki jüri tarafından oy birliği / oy çokluğu ile Gazi Üniversitesi Eğitimde Ölçme ve Değerlendirme Anabilim Dalı’nda Yüksek Lisans tezi olarak kabul edilmiştir.

Danışman: Doç. Dr. Şeref TAN

Eğitimde Ölçme ve Değerlendirme Ana Bilim Dalı, Gazi Üniversitesi

Başkan: Prof. Dr. Mehtap ÇAKAN

Eğitimde Ölçme ve Değerlendirme Ana Bilim Dalı, Gazi Üniversitesi

Üye: Prof. Dr. Selahattin GELBAL

Eğitimde Ölçme ve Değerlendirme Ana Bilim Dalı, Hacettepe Üniversitesi

Tez Savunma Tarihi: 03/11/2016

Bu tezin Eğitimde Ölçme ve Değerlendirme Anabilim Dalı’nda Yüksek Lisans tezi olması için şartları yerine getirdiğini onaylıyorum.

Prof. Dr. Ülkü Eser ÜNALDI Eğitim Bilimleri Enstitüsü Müdürü

iv

v

TEŞEKKÜR

Öncelikle çalışmamda bana yol gösterici olan, yapıcı önerileri ve yorumları ile tezimin tamamlanmasında hiçbir desteğini benden esirgemeyen, benimle birlikte emek sarf eden değerli hocam ve tez danışmanım Doç. Dr. Şeref Tan’a ; süreç boyunca benden desteğini hiç esirgemeyen Esra Sözer ve Sinem Şenferah’a; uygulamalarım sırasında bana çok yardımcı olan dostların en güzelleri Öznur Calp, Esra Küçüksoku, ve Halime Alibekiroğlu’na; Ankara’da bana evini açan yuva özlemini aratmayan ders dönemini sayesinde tamamlayabildiğim kuzenlerin bitanesi, ablaların en güzeli Gülistan Durmaz’a; tez dönemimde hayatıma giren ve tezimin uzamasına sebep olan ama hayatıma iyi ki de girmiş dediğim eşim Abdüssamed Şalgam’a; her an yanımda olan, bana her zaman destek veren bu hayatta gördüğüm en güçlü kadın olan biricik annem Gülşen Çınar’a ; her zaman arkamda olduğunu bildiğim babama ve kardeşlerime çok teşekkür ederim.

vi

KISA CEVAPLI MATEMATİK YAZILI SINAVININ

GENELLENEBİLİRLİK KURAMI VE TEST TEKRAR TEST

YÖNTEMİYLE GÜVENİRLİĞİNİN KIYASLANMASI

(YÜKSEK LİSANS TEZİ)

AYŞEDUDU ŞALGAM

GAZİ ÜNİVERSİTESİ

EĞİTİM BİLİMLERİ ENSTİTÜSÜ

KASIM, 2016

ÖZ

Bu çalışmada ilköğretim 7.sınıf öğrencilerine yönelik olarak hazırlanmış ‘Kısa Cevaplı Matematik Yazılı Sınavından’ elde edilen ölçümlerin güvenirliğinin incelenmesi amaçlanmıştır. Bu amaçla yazılı sınavın üç bağımsız puanlayıcı tarafından puanlanmasıyla elde edilen ölçümler Klasik Test Kuramının Test Tekrar Test Yöntemi ve Genellenebilirlik (G) Kuramının çaprazlanmış deseniyle kıyaslanmıştır. Her iki kuramda yapılan güvenirlik analizleri sonucu elde edilen güvenirlik katsayıları karşılaştırılarak aralarında manidar bir farklılık olup olmadığı test edilmiştir. Araştırmanın çalışma grubunu, Çorum ilinde 2014-2015 eğitim öğretim yılında yedinci sınıfta eğitim görmekte olan 99 öğrenci oluşturmuştur. Öğrencilere ‘Kısa Cevaplı Matematik Yazılı Sınavı’ uygulanmış ve öğrenci cevapları 3 bağımsız puanlayıcı tarafından cevap anahtarı ile puanlanmıştır. Genellenebilirlik Kuramında birey (b), madde (m) ve puanlayıcı (p) değişkenleri olmak üzere her bireyin her maddeye ulaştığı ve puanlayıcıların her biri tarafından puanlandığı b x m x p çaprazlanmış desen kullanılmıştır. Klasik Test Kuramında ise Test Tekrar Test yöntemi kullanılmıştır. Kısa Cevaplı Matematik Yazılı Sınavı iki hafta arayla aynı öğrencilere uygulanmış ve aynı puanlayıcı tarafından puanlanmıştır. Araştırma sonucunda her iki kuramdan elde edilen güvenirlik katsayıları kıyaslandığında aralarında manidar bir farklılık olmadığı gözlenmiştir. Dolayısıyla her iki kuramda benzer sonuçlar vermiştir.

Anahtar Kelimeler: Klasik test kuramı, genellenebilirlik kuramı, test tekrar test, güvenirlik, G çalışması, K çalışması.

vii Sayfa Adedi:51

viii

THE COMPARISON OF RELIABILITY OF THE GENERALIZABILITY

THEORY AND THE TEST-RETEST TECHNIQUE FOR THE SHORT

ANSWERED MATHS EXAM

(M.S THESIS)

AYŞEDUDU ŞALGAM

GAZI UNIVERSITY

GRADUATE SCHOOL OF EDUCATIONAL SCIENCES

NOVEMBER, 2016

ABSTRACT

In this study, it was aimed to evaluate the reliability of testing obtained from the Short Answer Maths Examination prepared for elementary school grade 7 students. For his purpose, the measurements obtained by the written exam scored by three in dependent raters were compared with the Test-Retest method of Classical Test Theory and crossed pattern of Generalizability (G) Theory. It was tested whether there is meaningful difference between both theories by comparing the reliability coefficients obtained as a result of reliability analysis. 99 students of 7th grade who studies in school in Çorum during 2014-2015 education year, consist the study group of this research. Students were applied Short Answer Mathematics Examination and students responses were scored by 3 independent scores with an answer key. In Generalizability Theory p x i x r crossed pattern in which each person could reach each item including person (p), item (i) and raters (r) and scored by each raters. In the Classical Test Theory Test-Retest method was used. Short Answer Mathematics Examination was applied to the same group of student in two week time interval and obtained measurement results were scored by the same raters. When compared to the results of two theories, it is observed that there is no differences between the reliability coefficient.

KeyWords: Classical test theory, generalizability theory, test-retest, reliability, G study, D study.

Page Number: 51

ix

İÇİNDEKİLER

TELİF HAKKI VE TEZ FOTOKOPİ İZİN FORMU

………....i

ETİK İLKELERE UYGUNLUK BEYANI

………....ii

JURİ ONAY SAYFASI

……….………...iii

TEŞEKKÜR

………...…………v

ÖZET..

………vi

ABSTRACT

…..………..viii

İÇİNDEKİLER

…...……….ix

TABLOLAR LİSTESİ

……..………...xii

ŞEKİLLER LİSTESİ

………..xiii

SİMGELER VE KISALTMALAR

………....xiv

BÖLÜM I

………...1

GİRİŞ

………..………….……1

Problem Durumu……….1

Eğitimde Kullanılan Ölçme Araçları……….2

Kısa Cevaplı Yazılı Sınav……….3

Kısa Cevaplı Yazılı Sınavların Özellikleri………..3

Araştırmada Kullanılan Kuramlar.………...5

Klasik Test Kuramı……….5

x

Genellenebilirlik Kuramı……….10

Genellenebilirlik Çalışması………..11

Çalışmada Genellenebilirlik Kuramı’nda Uygulanan Desen…………...12

Karar Çalışmaları……….15 Araştırmanın Amacı ………..17 Araştırmanın Önemi ………...………...17 Problem Cümlesi….………18 Alt Problemler….………18 Sayıltılar……….………..18 Sınırlılıklar..………..…...………...19 İlgili Araştırmalar……….…….……….……..………19

Yurt İçinde Yapılan Araştırmalar……….19

Yurt Dışında Yapılan Araştırmalar………..26

BÖLÜM II

………31

YÖNTEM

……….31

Araştırmanın Modeli………….……….31

Evren ve Örneklem………31

Veri Toplama Yöntemi………..31

Verilerin Analiz Edilmesi..………33

BÖLÜM III

………..34

BULGULAR VE YORUMLAR

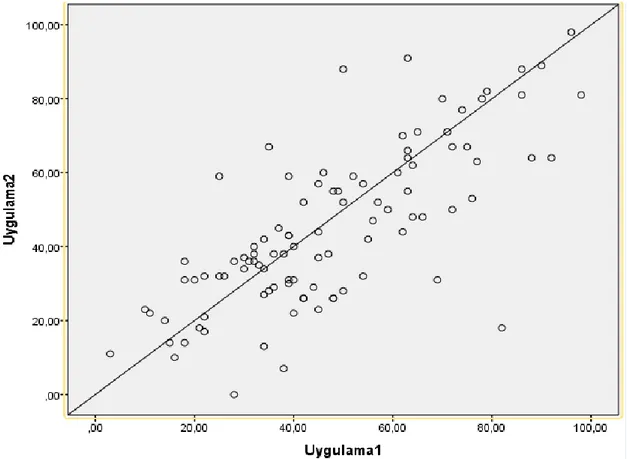
………...34

Birinci Alt Probleme İlişkin Bulgu ve Yorumlar………...34

İkinci Alt Probleme İlişkin Bulgu ve Yorumlar…………...……….37

Üçüncü Alt Probleme İlişkin Bulgu ve Yorumlar ……...……….39

Dördüncü Alt Probleme İlişkin Bulgu ve Yorumlar…...………..41

BÖLÜM IV

………...43

SONUÇ, TARTIŞMA VE ÖNERİLER

……….43

Birinci Alt Probleme İlişkin Sonuçlar ve Tartışma………...43

İkinci Alt Probleme İlişkin Sonuçlar ve Tartışma……….44

Üçüncü Alt Probleme İlişkin Sonuçlar ve Tartışma………..45

xi

Öneriler………..46

xii

TABLOLAR LİSTESİ

Tablo 1. Klasik Test Kuramı (KTK) Ve Genellenebilirlik Kuramı (G Kuramı) Karşılaştırması……….11 Tablo 2. G Kuramında b x m x p Deseninden Elde Edilen Puanlara Ait Eşitlikler…………..13 Tablo 3. İki Değişken Kaynaklı (Facet) Tesadüfî Desen İçin Varyans Bileşenlerinin Kestirilmesine Ait Eşitlikler………..14 Tablo 4. İki Yüzeyli Çaprazlanmış bxmxp Deseni İçin Kestirilen Kareler Ortalaması Formülleri……….15 Tablo 5. Öğrencilere Uygulanan Kısa Cevaplı Matematik Yazılı Sınavının Kazanımları…...32 Tablo 6. Birinci Sınav ile İkinci Sınav Puanları Arasındaki Pearson Momentler Çarpım Katsayısı...35 Tablo 7. Kısa Cevaplı Matematik Yazılı Sınavı İle Elde Edilen Puanların bxmxp Desenine Ait G Çalışması Sonucunda Kestirilen Varyans Bileşenleri Ve Toplam Varyansı Açıklama Yüzdeleri………...36 Tablo 8. Kısa Cevaplı Matematik Yazılı Sınavı Değerlendirmesinin Madde Sayısı Sabitken K Çalışması İle G Ve Phi Katsayıları……….38 Tablo 9. Kısa Cevaplı Matematik Yazılı Sınavı Değerlendirmesinin Puanlayıcı Sayısı Sabitken K Çalışması İle G Ve Phi Katsayıları……….40 Tablo 10. Kısa Cevaplı Matematik Yazılı Sınav Sonucu Elde Edilen Puanların Klasik Test Kuramı Ve Genellenebilirlik Kuramı’na Göre Güvenirlikleri...40 Tablo 11. Kısa Cevaplı Matematik Yazılı Sınav Sonucu Elde Edilen Puanların Klasik Test Kuramı Ve Genellenebilirlik Kuramı’na Göre Güvenirlikleri………...41

xiii

ŞEKİLLER LİSTESİ

Şekil 1.İki yüzeyli desende ortak etkileşim alanı………..13

Şekil 2. Varyans bileşenleri………...………15

Şekil 3. Bağıl hata kaynakları……….………...16

Şekil 4. Mutlak hata kaynakları……….………17

xiv

SİMGELER VE KISALTMALAR LİSTESİ

G Kuramı Genellenebilirlik Kuramı

KTK Klasik Test Kuramı

G Çalışması Genellenebilirlik Çalışması

K Çalışması Karar Çalışması

1

BÖLÜM I

GİRİŞ

Bu bölümde araştırmanın problem durumuna, amacı ve önemine, problem cümlesine, alt problemlerine, sayıltılarına ve sınırlılıklarına yer verilmiştir.

Problem Durumu

Eğitim bireyde bazı davranışlarını değiştirmek ve bireyde var olmayan bazı davranışları kazandırmak amacıyla yapılır. Verilen eğitimin sonunda bireyin davranışlarında istenen yönde değişiklikler olması beklenir. Uygulanan bir eğitim programının başarılı olup olmadığı öğrencilerde meydana gelen davranış değişikliklerinin ölçülüp değerlendirilmesiyle mümkündür (Baykul ve Turgut, 2012, s.1).

Ölçme sonuçları uygulanan tekniklere göre farklılıklar göstermektedir. Bireyler hakkında doğru kararlar verebilmek için ölçümlerimizdeki hata miktarını azaltma amacıyla ölçümleri elde etmede uygulanan teknikler büyük öneme sahiptir. Bireylere uygulanan sınavların sonuçlarına birden çok hata karışabilmektedir. Bu hata kaynakları ölçülenden, ölçmeciden, zamandan, ortamdan vb. birçok değişkenden kaynaklanmaktadır. Hata kaynakları kullanılan tekniklere göre farklılıklar göstermektedir ve bu farklılıklar güvenirlik sonuçlarını da etkilemektedir (Büyüköztürk, Kılıç Çakmak, Akgün, Karadeniz ve Demirel, 2012, s.104). Öğrenciler hakkında bilgi toplayabilmek, öğrenciye davranışını nasıl değiştireceği, nasıl geliştireceği hakkında bilgi vermek ve çeşitli kararlar alabilmek için farklı ölçme ve değerlendirme araç ve yöntemlerinden yararlanılır. Bu araç ve yöntemler yazılı yoklamalar, kısa cevaplı, doğru yanlış ve çoktan seçmeli testler, performans görevleri, projeler, gelişim dosyaları gibi etkinlikler ve kontrol listeleri, dereceleme ölçekleri, dereceli puanlama anahtarları şeklinde sıralanabilir.

2

Her ölçme aracının kullanım yeri farklıdır. Ölçme araçlarını kullanırken kazanıma, sınıf mevcuduna, sınıf seviyesine, öğretim yöntemine vb. uygun olan ölçme araçlarını seçmeliyiz. Öğrenci başarısını değerlendirirken ölçme sonucunu bir ölçütle karşılaştırırız. Ölçme sonucunun tesadüfi hatalardan arınık olması ise yani güvenirliğin yüksek olması öğrenci başarısı hakkında doğru karar vermemizi sağlar. Güvenirlik ne kadar yüksek ise öğrenci başarısı hakkında verilen karar da o kadar doğrudur.

Bu çalışmada öğrencilerin matematiksel zihinsel becerilerini ölçmek amacıyla kısa cevaplı matematik yazılı sınavı uygulanmıştır. Sınav aynı cevap anahtarıyla, aynı puanlayıcının aynı bireylere iki hafta arayla uygulanan kısa cevaplı matematik yazılı sınavının puanlamasından elde edilen puanlar arasındaki uyum klasik test kuramının test tekrar test yöntemiyle elde edilen Pearson momentler çarpımı güvenirlik katsayısı ile belirlenmiştir. Aynı zamanda aynı bireylere uygulanan aynı kısa cevaplı matematik sınavı üç puanlayıcının puanlamasından elde edilen puanlar arasındaki uyum ise Genellenebilirlik kuramından elde edilen güvenirlik katsayısı ile belirlenmiştir. Daha sonra her iki kuramla elde edilen güvenirlik katsayıları arasında anlamlı bir farklılık olup olmadığı incelenmiştir.

Eğitimde Kullanılan Ölçme Araçları

Bir derse ilişkin öğrenmelerin ölçülmesinde çeşitli ölçme araçlarından yararlanılır. Hangi ölçme aracının kullanılacağı, yapılacak ölçmenin amacına, konu kapsamına, hangi davranış düzeylerinde sorular sorulacağına, birey sayısına, ölçme aracını hazırlayacak kişinin bu konudaki deneyimlerine vb. etkenlere bağlıdır.

Derse ilişkin öğrenmelerde bilişsel, duyuşsal ve devimsel davranışlar ölçülebilmektedir. Ancak eğitim çalışmalarında daha çok, bilişsel davranışları ölçen araçlar kullanılmaktadır. Bu araçların kullanıldığı sınav türlerinin başlıcaları şunlardır: Yazılı yoklamalar, sözlü sınavlar, kısa cevaplı sınavlar, çoktan seçmeli sınavlar, doğru-yanlış (sınıflama gerektiren) sınavları, eşleştirmeli sınavlar, ödevler, performans görevleri ve projelerdir.

Geleneksel yöntemlerde öğrenci başarısının değerlendirilmesi, genellikle öğretim sürecinden ayrı ve daha çok ürüne ağırlık verecek bir şekilde ele alınmakta; bu amaçla daha çok seçmeli ve kısa cevaplı testlerle, yazılı ve sözlü yoklamalara önem verilmektedir (Gelbal ve Kelecioğlu, 2007,s.136). Geleneksel öğretim programlarında yer alan ve sadece ürünü ölçen değerlendirmenin dışında süreci ölçen yeni yaklaşımlar da geliştirilmiştir. Ancak öğretmenlerin alışık olması sebebiyle daha çok geleneksel ölçme araçları tercih edilmektedir.

3

Geleneksel olarak kullanılan kağıt-kalem testleri ile birlikte, öğrencinin sınıf içi ve sınıf dışındaki davranışlarını izleyerek, süreç içindeki performansını gözleyerek, ilgisini ve tutumunu ölçerek ve öğrenciyi de değerlendirme sürecine katarak öğrenci performansını her yönüyle değerlendirebilmek mümkün olabilmektedir (Gelbal ve Kelecioğlu, 2007,s.136). Araştırmada kullanılan ölçme aracı geleneksel ölçme araçlarından biri olan kısa cevaplı yazılı sınav olduğu için burada yalnızca kısa cevaplı yazılı sınavların özelliklerine değinilmiştir.

Kısa Cevaplı Yazılı Sınav

‘Cevaplayıcının, bir kelime, bir rakam, bir ibare veya en çok bir cümle ile cevaplayabileceği sorulardan oluşturulmuş ölçme aracına denir.’ (Baykul ve Turgut, 2012, s.165). Kısa cevaplı yazılı sınavlar yazılı yoklamalara alternatif olan sınav türlerinden biridir. Cevabı yazılı yoklamalarda olduğu gibi uzun değildir. Kısa cevaplı yazılı sınavlarda ki maddeler ;

Eksik cümle olarak sorulabileceği gibi direkt soru cümlesi olarak da sorulabilir.

Üç köşesi, üç kenarı ve üç açısı olan kapalı şekillere……….denir. Sorusu eksik cümle tipinde maddeye örnektir.

Üç köşesi, üç kenarı ve üç açısı olan kapalı şekillere ne ad verilir? Sorusu ise direkt soru cümlesi tipindeki maddeye örnek verilebilir.

Kısa cevaplı yazılı sınavlar eğitimin her basamağında kullanılabilir. Genellikle bilgi ve kavrama basamağında kullanılmasının yanında çok yaygın olmasa da uygulama basamağında da kullanılmaktadır.

Kısa Cevaplı Yazılı Sınavların Özellikleri

Tekin (1984,s.126)’e göre ‘bir testin özelliklerini, o testin kapsadığı maddelerin sayısı ve yapısı belirler. Kısa cevaplı testler, kısa cevaplı maddelerden oluştuğuna göre, söz konusu testlerin özellikleri kısa cevaplı maddelerin özelliklerine bağlı kalarak belirlenebilir.’ Kısa cevaplı yazılı sınavların özellikleri aşağıda kısaca açıklanmıştır.

1.Hazırlama Kolaylığı: Kısa cevaplı testlerin hazırlanması yazılı yoklamalara göre daha zor

ama diğer objektif testlere göre daha kolaydır.

2.Sorulabilecek Soru Sayısı: Kısa cevaplı test maddelerinin cevaplanması yazılı yoklamalara

göre daha az zaman alır. Cevap kısa olduğu için kısa cevaplı test maddelerinin cevaplandırılası kompozisyon yeteneği gerektirmez. Cevaplandırılması daha az zaman aldığı

4

için daha fazla soru sorma olanağı verir. Daha çok soru sorulması da genellikle testin kapsam geçerliğini arttırır. Cevapların kısa ve sınırlandırılmış olması puanlama hatalarının da az olmasını sağlar. Kısa cevaplı yazılı sınavlarda genellikle yazılı yoklama sınavlarından daha çok soru sorulabilmekteyken çoktan seçmeli testlerden daha az soru sorulmaktadır. Genellikle de kapsam geçerliliği yazılı yoklamalara göre yüksek olurken çoktan seçmeli testlere göre daha düşük çıkmaktadır (Tan, 2013, s.329).

3.Cevaplayıcı Bağımsızlığı: Kısa cevaplı yazılı sınavlarda cevaplayıcının cevaplama

bağımsızlığı vardır. Çoktan seçmeli testlerde olduğu gibi olası cevapların verilmemiş olması ve yanıtlayıcının cevabı düşünüp yazmasını gerektirmektedir. Bu yüzden bu testlerde şans başarısı hemen hemen yoktur.

4.Cevaplama İşlemi: Kısa cevaplı yazılı sınavlar, cevabı öğrenci tarafından hatırlanıp yazılan

sınavlardır. Bu tür sınavlarda sorulan soruların cevaplarını da öğrenci, uzun cevaplı yazılı sınavlarda olduğu gibi düşünerek bulup yazmak zorundadır. Ancak, cevap kısadır.

5.Uygulama Alanları: Kısa cevap gerektiren sorular çok çeşitli bilgi ve yetenek alanlarını

uygulanabilir. .Kısa cevaplı sorular oldukça geniş bir alanda ve her eğitim düzeyinde kullanılabilir. Çünkü cevaplayıcıdan kısa bir cevaplama ve kolay bir cevap kaydı istendiğinden eğitimin her basamağında kolaylıkla uygulanabilir (Tekin,1984,s.127).

6. Soruların Hazırlanması: Sorular açık ifade edilmeli ve yanlış anlaşılmalara yol açmamalı,

her soru bir davranışı yoklamalıdır. İfadeler, cevaplayıcının tanıdığı kaynaklardan birebir alınmamalı ve bir soru başka bir sorunun cevabını içermemelidir.

7.Puanlama: Puanlama işlemi nispeten kolaydır, fakat tamamen objektif değildir.

Puanlamaya; yazı güzelliği, kağıt düzeni vb. gibi değişkenler karışmadığı için ve cevapların sınırlı, kısa ve kesin oluşundan kolaydır. Fakat bu sorulara cevaplayıcıların istedikleri cevabı verme bağımsızlığı vardır. Cevapların kısmen doğru olması, doğruluk derecesinin kestirilememesi de mümkündür. Puanlayıcının kısa da olsa, soruları cevap anahtarına göre okuyup doğru olup olmadığına karar vermesi gerekir.

Puanlama işlemine başlamadan önce bir cevap anahtarı hazırlanmalıdır. Anahtar her soruya verilmesi beklenen doğru cevapları ayrıntılı olarak listelemelidir.

5

Araştırmada Kullanılan Kuramlar

Bu kısımda Klasik test kuramı ile Genellenebilirlik kuramına değinilmiştir.

Klasik Test Kuramı

Ölçmede gözlenen bir özelliğin gerçek değeri bulunmak istenir fakat ölçmeye karışan çeşitli hatalar sebebiyle bu gerçek değer, ölçme yoluyla doğrudan elde edilemez ve gözlenen puanlarla kestirilmeye çalışılır. Kestirmeyi yapabilmek için bazı teoriler geliştirilmiştir. Bunlardan biri klasik test kuramı adıyla bilinen ve üzerinde çok çalışılan bir kuramdır ve Klasik gerçek puan modeli olarak da adlandırılmaktadır (Baykul, 2010, s. 107).

Klasik gerçek puan modeli İngiliz psikolog Charles Spearman’ın ilgilendiği konulardan birisidir. Hatalı ölçümler ile gerçek nesnel değerleri açıklamak için tekrarlanan girişimlerle Spearman (1907-1913) klasik gerçek puanın temelini attı ve yıllar içerisinde kuram birçok yazar tarafından geliştirildi.

Spearman gözlenen test puanın iki varsayımsal bileşenden (gerçek puan ve rastgele hata bileşeni) oluştuğunu öngördü. Sistematik hata yapılmadığı gibi bazı sayıltılar sağlandığında… X=T+E…….(1)

X gözlenen puan , T bireylerin gerçek puanı , E rastgele hata bileşenini temsil ediyor (Crocker ve Algina, 1986, s. 106 -107).

Klasik test kuramının varsayımları (Baykul, 2010, s. 113 - 114);

i. Hata puanlarının beklenen değeri sıfıra eşittir.

ii. Gerçek puanlarla hata puanları arasındaki korelasyon sıfıra eşittir.

iii. İki farklı ölçmeye ait hata puanları ile gerçek puanlar arasındaki korelasyon sıfıra eşittir.

iv. İki farklı ölçmeye ait hata puanları arasındaki korelasyon sıfıra eşittir.

Ölçme hatası, ölçülen nesnenin gerçek değeri ile ölçme sonucundan elde edilen değeri arasındaki farka denir. Ölçmede hata sabit hata, sistematik hata ve tesadüfî hata olmak üzere üç gruba ayrılır (Turgut, 1977, s.28). Sabit hata ölçümden ölçüme aynı miktarda ve yönde yansıyan ölçümden ölçüme değişmeyen hatadır. Sistematik hata ölçümden ölçüme belli bir oranda artar ya da azalır hatta bazı ölçme işlemlerine karışmayan hatadır. Tesadüfî hata ölçme sonuçlarına karışan miktarı ve kaynağı kesin olarak belli olmayan hatalardır.

6

Sabit, sistematik ve tesadüfî hatalar ölçme işlemine karışarak ölçme sonuçlarının gerçek değerinin bulunmasına engel olur. Bu hatalar ölçme sonuçlarına farklı kaynaklar aracılığıyla etki ederler. Bu hata kaynakları:

 Ölçmeyi yapan kişiden kaynaklanan hatalar

 Ölçme aracından kaynaklanan hatalar

 Ölçme işleminin yapıldığı ortamdan kaynaklanan hatalar

 Ölçme işleminin yapıldığı kişiden kaynaklanan hatalardır (Atılgan, 2009, s. 91-96). Klasik test kuramında güvenirlik sabit ve sistematik hatadan etkilenmez çünkü ölçme sonuçlarına karışan hatanın miktarı, yönü ve kaynağı bellidir. Tesadüfi hatanın miktarı, yönü ve kaynağı belli olmadığı için güvenirlik etkilenir. Güvenirlik, ölçülmek istenen belli bir niteliğin, sürekli olarak aynı sembolleri alması ve ölçmenin tesadüfî hatalardan arınık olmasıdır.

Klasik test kuramında güvenirlik katsayısı, gerçek puan varyansının gözlenen puan varyansına oranı olarak tanımlanır. Gözlenen puan varyansı gerçek puan varyansı ve hata puan varyansının toplamından oluşmaktadır (Güler, 2008, s.16).

𝜎

_{𝑔ö𝑧𝑙𝑒𝑛𝑒𝑛} 2



𝜎

_{𝑔𝑒𝑟ç𝑒𝑘}2



𝜎

_{ℎ𝑎𝑡𝑎}2





𝜎 𝑔𝑒𝑟ç𝑒𝑘2

𝜎 _{𝑔ö𝑧𝑙𝑒𝑛𝑒𝑛}2



Klasik test kuramında güvenirlik katsayısı 0 ile 1 arasında değer alır. Güvenirliği kestirmede kullanılan klasik test kuramının en yaygın yöntemleri test tekrar test ve iç tutarlılık yöntemleridir. Aşağıda güvenirlik katsayısı hesaplanmasında kullanılan test tekrar test yöntemi ile iç tutarlılık yöntemi açıklanmıştır.

 Test tekrar test  İç tutarlılık

Test Tekrar Test Yöntemi:

Test tekrar test yöntemi ile elde edilen güvenirlik katsayısı kararlılık katsayısı olarak adlandırılır. Kararlılık, bir testin birden çok uygulanması sonucu benzer sonuçlar elde edilmesidir. Kararlılık katsayısı ne kadar yüksekse güvenirlik de o derece yüksek olacaktır. Bu yöntemle aynı değişkenin birden fazla ölçülmesi sonucu elde elden ölçümler arasındaki

7

benzerliği veya ilişkiyi belirleyerek ölçümlerin güvenirliği kestirilir. Bu yöntemle test tekrar tekrar uygulandığında elde edilen ölçümler arasındaki uyum korelasyon tekniği ile hesaplanabilir. Korelasyon katsayısı –1.00 ile + 1.00 arasında değişmekle birlikte, güvenirlik katsayıları hemen hemen her zaman 0.00 ile +1.00 arasında değişmektedir. Korelasyon günümüzde çok geniş bir kullanım alanına sahiptir. İki değişken arasındaki doğrusal ilişkinin bir ölçüsü olarak en çok kullanılan korelasyon katsayısı Pearson Momentler Çarpımı Korelasyon Katsayısı’dır. Elde edilen korelasyon bize güvenirlik hakkında bilgi verir. Test tekrar test yöntemi; tek form ve alternatif form yöntemi olarak iki şekilde uygulanmaktadır.

Tek Form Yöntemi: Bu yöntemle test güvenirliğini kestirmek için, bir test aynı gruba belli

bir zaman aralığıyla genelde iki kez uygulanır. Daha sonra bireylerin birinci uygulamada aldıkları puanlarla ikinci uygulamada aldıkları puanlar arasındaki korelasyon bulunur. Elde edilen korelasyon katsayısı testin güvenirlik katsayısıdır. Bu korelasyon katsayısı iki uygulamadan elde edilen puanların ne derece kararlı olduğunu gösterir. Korelasyon katsayısı 1’e yaklaştıkça iki uygulamadaki puanların birbirine yaklaştığını, 0’a yaklaştıkça iki uygulamadaki puanların birbirinden uzaklaştığını gösterir. Bu yöntemle kestirilen güvenirlik katsayısına ‘kararlılık katsayısı’ denir.

Test tekrar test yöntemlerinden tek form yöntemiyle güvenirlik katsayısı kestirilirken aynı ölçme aracının iki kez uygulanmasından elde edilen ölçümler arasındaki korelasyonun güvenirlik katsayısı olarak yorumlanması için sağlanması gereken iki temel koşul vardır. Bunlar;

1. İki uygulama arasında geçen süre içinde, öğrencilerin ölçülen değişkene ait gerçek puanlarında bir değişikliğin olmaması ve

2. Birinci uygulamanın ikinci uygulamadan elde edilecek puanı etkilememesidir (Tan, 2013, s.138).

Alternatif (Eşdeğer) Form Yöntemi: Birbirine paralel yani aynı davranışları ölçen, fakat

farklı sorulardan oluşan iki paralel testin, aynı gruba uygulanmasına dayanan yöntemdir. Paralel iki testin eşdeğer olabilmesi için her iki test içindeki maddelerin sayısı, niteliği ve ölçtükleri davranışlar bakımından birbirlerine benzer olmaları gerekmektedir.

Bu yöntemde önemli olan kullanılacak olan eşdeğer testin aşağıdaki özellikleri taşımasıdır. 1. Aynı değişkeni ölçmeli

2. Aritmetik ortalaması birinci testin aritmetik ortalamasına eşit olmalı 3. Standart sapması birinci testin standart sapmasına eşit olmalı

8

Bu testlerin uygulanmasından elde edilen puanlar arasında hesaplanan Pearson momentler çarpım korelasyon katsayısı ‘kararlılık ve eşdeğerlik’ anlamında güvenirliği verir. Elde edilen korelasyon yüksekse ölçümlerin kararlı olduğu aynı zamanda testlerin de eşdeğer olduğu anlamına gelir.

İç Tutarlılık Yöntemi

Testin bir kez uygulanması ile güvenirliğin kestirilmesi yöntemlerini içerir. Bu yöntemlerden bazıları, testi yarılama, Cronbach alfa ve Cronbach alfanın 0-1 puanlama yöntemi için özel bir eş değeri olan Kuder-Richardson güvenirlik katsayılarıdır.

Testi Yarılama Yöntemi: testi yarılama yönteminde belirli yöntemlerle iki paralel alt test

oluşturulur. Oluşturulan bu iki paralel test tek bir form halinde düzenlenerek uygulanır. Bir gruba uygulanan test uygulamadan sonra testin iki yarısından aldığı puanlar ayrı ayrı hesaplanır. Grubun ilk yarıdan elde ettiği puanlar ile ikinci yarıdan elde ettiği puanlar arasındaki korelasyon katsayısı hesaplanır. İki yarıdan elde edilen puanlar arasındaki korelasyonla bulunan güvenirlik katsayısı iç-tutarlılık katsayısı olarak adlandırılır. Testin bütününün güvenirliği Spearman-Brown formülü ile hesaplanır. İki yarıya bölme yöntemiyle bulunan güvenirlik katsayısı, testin iki yarısı arasındaki iç-tutarlılık anlamına gelir. Bu katsayı, test gelişigüzel cevaplanmışsa ya da testin iki yarısı arasında paralellik yeterince sağlanamamışsa düşük çıkar. İki yarı arasındaki tutarsızlığın tesadüfî hatalardan çok iki yarının yeterince paralel olmamasından ileri geldiği sonucuna ulaşılır. Bu katsayı yüksek bulunmuşsa test puanlarının tesadüfî hatalardan arınık olduğu ve iki yarının eşdeğer olduğu söylenebilir.

Kuder-Richardson Yöntemi: Bu yöntemle maddeler doğruysa 1 yanlışsa 0 olacak şekilde

ikili puanlanan testlere uygulanır. Yani iki kategorili seçeneklerin kullanıldığı testlerde kullanılır. Test maddelerinin birbiriyle ne derece tutarlı olduğunu (yani iç-tutarlılığı) gösteren yöntemdir. Kuder-Richardson formülleri, testteki her maddenin aynı değişkeni ölçtüğü, yani testin ölçtüğü şeyin homojen olduğu sayıltısına dayanır. Testin iki yarısı yerine testteki tüm maddeler arasındaki tutarlılığın ölçümünü verir ve iç-tutarlılık katsayısı olarak adlandırılır. KR-21 madde analizi yapılmamış testlerin güvenirliğin alt sınırını kestirmede uygulanır; ve testteki maddelerin madde güçlükleri eşit farz edilir. KR-21 her zaman için KR-20’den küçüktür.(KR-20> KR-21)(Tan, 2013, s.143-144). Yüksek bir KR-20 güvenirlik katsayısının testin tek boyutlu olduğunu belirtmenin yanlış olacağı belirtilmektedir:

…ölçülen değişkenin faktör analizi sonucu çok boyutlu olmasına rağmen KR-20 güvenirlik katsayısının yine de çok yüksek çıkabileceğini belirtmiştir. Testi oluşturan maddelerin homojen

9

olduğunun bir göstergesi olarak KR-20’nin kullanılması yanıltıcı olabilir. Bu nedenle tek boyutlu bir değişkenin ölçüldüğü sayıltısına dayalı olan KR-20’yi uygulamadan önce faktör analizi uygulanarak testin tek boyutluluğu kontrol edilmelidir (Tan, 2013, s.143-144).

Cronbach Alfa (𝜶) Yöntemi: KR 20 güvenirlik kestirme formülünün çok kategorili veya dereceleme yöntemiyle puanlamaya da uygulanabilen genel halidir. Anlaşılacağı üzere, tek bir uygulamaya dayalı olan güvenirlik kestirme yöntemlerinden biridir. Özellikle cevapların dereceleme ölçeğinde elde edildiği durumlarda sıklıkla kullanılır. Alfa katsayısı KR 20 güvenirlik katsayısının genelleştirilmiş bir şeklidir. Alfa güvenirlik katsayısı da bir tutarlılık katsayısıdır ve 0 ile 1.00 arasında değer almaktadır. Alfa güvenirlik katsayısı bir iç-tutarlılık katsayısı olduğundan dolayı; ölçülen değişken tek boyutlu olmalıdır. Araştırmada uygulanan Kısa cevaplı matematik yazılı sınavının iki kez uygulanması ve bir puanlayıcı tarafından puanlanması sonucu elde edilen veriler ile güvenlik kestirimi yapılacaktır. Dolayısıyla Test tekrar test yönteminde Pearson momentler çarpımı korelasyon katsayısı incelenecektir.

Test Tekrar Test Yöntemi

Bu çalışmada Klasik test kuramında test tekrar test yöntemi uygulanmıştır. 7.sınıfa devam eden 99 öğrenciye uygulanmış olan kısa cevaplı matematik yazılı sınavı iki hafta arayla tekrar aynı öğrencilere uygulanmıştır. İki uygulama sonunda elde edilen veriler ile Pearson momentler çarpımı ile güvenirlik katsayısı bulunmuştur.

Pearson momentler çarpımı ile güvenirlik katsayısı formülü aşağıda verilmiştir. Formülde; n testi cevaplayan kişi sayısı,

𝑋_𝑖; i. kişinin ilk uygulama da aldığı puan, 𝑌_𝑖, i.kişinin ikinci uygulama da aldığı puan,

∑𝑛_𝑖=1𝑋_𝑖𝑌_{𝑖 ;} X ve Y puanlarının çarpımlarının toplamını, ∑𝑛_𝑖=1𝑋_𝑖; X puanlarının toplamını,

∑𝑛_𝑖=1𝑌_𝑖; Y puanlarının toplamını göstermektedir.

𝑟_𝑥𝑦= ∑ 𝑋𝑖 𝑛 𝑖=1 𝑌𝑖 − [∑𝑛_𝑖=1𝑋_𝑖][∑𝑛_𝑖=1𝑌_𝑖] 𝑛 √[∑𝑛_𝑖=1𝑋_𝑖2−[∑ 𝑋𝑖 𝑛 𝑖=1 ]2 𝑛 ] [∑ 𝑌𝑖2 𝑛 𝑖=1 − [∑𝑛𝑖=1𝑌𝑖]2 𝑛 ]

10

Genellenebilirlik Kuramı

Genellenebilirlik (G) kuramı hatanın birden fazla kaynaktan geldiği ölçme durumlarında tek bir analizle farklı hata kaynaklarını kestirebilen bir kuramdır. İstatistiksel olarak varyans analizini(ANOVA) esas alan G kuramı hem klasik test kuramının hem de varyans analizinin bir uzantısıdır.

G kuramının kavramlarını ve yöntemlerini derinlemesine açıklayan Cronbach, Gleser, Nanda, ve Rajaratnam (1972) ve Brennan olmuştur. G kuramının temel özelliklerine genel bir bakış Feldt ve Brennan (1989) Shavelson ve Webb (1991) tarafından sağlanmıştır.

Klasik Test Kuramı bir seferde bir hata kaynağını tahmin edebilirken G kuramı birden fazla kaynaktan gelen hatayı tek bir analizle tahmin edebilmektedir (Shavelson ve Webb, 1991, s.1-2). Klasik test kuramı her bir hata kaynağı için farklı güvenirlik kestirimi yapmaktayken G kuramı Klasik test kuramının bu sınırlılığını ortadan kaldırmak için geliştirilmiş olup daha esnek bir yapıya sahiptir. G kuramı potansiyel değişkenlik kaynaklarından gelebilecek hataları birlikte ve eş zamanlı olarak değerlendirerek kapsamlı tek bir güvenirlik katsayısı hesaplanmasına imkân vermektedir (Güler, 2008, s.23).

G kuramının amacı ölçme sonuçlarını farklı varyans kaynaklarına ayırıp yorumlamak ve tanımlayarak ölçme konusu olan bireyler ya da nesnelerin gözlenen puanlarının KTK’daki gerçek puan kavramının karşılığı olan evren puanlarına genellenmesini sağlamaktır (Atılgan, 2004, s.16).

G Kuramı dört farklı açıdan klasik test kuramının genişletilmiş halidir (Shavelson ve Webb,1991, s.127-128):

1. Bir analizle hata kaynağının her birinin büyüklüğünü tahmin eder ve ölçme güvenirliğini iyileştirmek için bir düzenek sağlar

2. Ölçmeyi etkileyen hata kaynaklarının her birinin varyans büyüklüğünün belirlenmesini sağlar.

3. Bağıl kararlar ve mutlak kararlar alınmasını sağlayan güvenirlik katsayılarının hesaplanmasına olanak verir.

4. Belirli bir amaca bağlı olarak, ölçme hatasının en aza indirgenebileceği ölçmelerin düzenlenmesine (K- çalışmaları) imkân tanır.

KTK ‘na göre bireylerin birbirlerine göre durumları kıyaslanırken G Kuramında ise hem bireylerin birbirlerine göre durumu hem de bireyin bağımsız olarak düzeyinin belirlenmesine

11

olanak sağlar. KTK bağıl karar vermeyi sağlarken G Kuramı hem bağıl karar vermeyi hem de mutlak karar vermeyi sağlar.

G kuramı ölçme sorunlarına geniş bir kavramsal çerçeve ve güçlü bir istatistiksel işlem sunuyor. Bir ölçüde G kuramı KTK’nın ve ANOVA’nın bir uzantısı olarak görülebilir (Brennan,2001,s.2). Fakat G Kuramının KTK’dan farklı olduğu birçok nokta bulunmaktadır. Brenanan bu farklılıkları aşağıdaki tablo ile göstermektedir.

Tablo 1

Klasik Test Kuramı (KTK) Ve Genellenebilirlik Kuramı (G ) Karşılaştırması

Konu KTK G Kuramı Formlar ve paralellik Gerçek puan Varsayımlar Öncelikli artıları Öncelikli eksileri Kullanım ve anlaşırlık

Klasik paralel, eşdeğerli vb. Formlar üzerinden

kestirim Oldukça zayıf Basitlik, yaygın olarak

kullanım

Hataların ayrılamaması Kolay

Paralel

Paralel formlar üzerinden kestirim Oldukça zayıf

Kavramsal genişlik, farklı hata kaynaklarına ayrıştırabilme, sabit

ve rastgele yüzeylerin arasındaki farkı ayırt etme

Kavramsal karmaşıklık Bazı koşullarda zorlayıcı

Brennan,R. L.(2011).Generalizability Theory and Classical Theory. Applied Measurement in Education, 24,1-21

G Kuramında G çalışmasının amacı olası gözlemler evreni ile ilgili varyans bileşenlerini kestirebilmektir. K çalışması ise ölçme süreciyle ilgili karar verebilmek amacıyla G çalışmasından elde edilen varyans bileşenlerinin kestirimi, kullanımı ve yorumlanması süreçlerini gerçekleştirir.

Genellenebilirlik Çalışması

G çalışmasının ya da Genellenebilirlik çalışmasının temel amacı belirli bir ölçme işleminin özelliklerini ve ölçme hassasiyetini(kesinliğini) değerlendirmektir. Bu amaca yönelik olarak, öncelikle çalışmadaki ölçme hatasının farklı kaynakları tespit edilmelidir, böylece hata katkısı olarak bu kaynakların göreceli önemi nicel olarak gösterilebilir. Göreceli önem, genellikle klasik ANOVA kullanılarak tahmin edilen tahmini varyans bileşenlerinin göreceli boyutları ile gösterilir. Bu tahmini bileşenler; G katsayısını ve ölçme hatasını hesaplamak için kullanılır. G teorisindeki bir yüzey ANOVA'daki bir faktör ile eş anlamlıdır. Bu yeni terim

12

faktör analizinin faktörleri ile ilgili psikometrik çevrelerdeki karışıklığı önlemek için Guttman tarafından tanıtıldı (Cardinet, Johnson ve Pini, 2010, s.11-12).

Genellenebilirlik kuramına göre değişkenlik kaynakları çapraz (crossed) ya da yuvalanmış (nested) şekilde olabilir. Veri setinde yüzeylerden birinin her seviyesi ile diğerinin her seviyesi birleştirildiğinde iki yüzey "çapraz" olur ve yüzeyler arasına ‘x’ işareti konulur. Bir yüzeyin her seviyesi ile diğer yüzeyin yalnızca bir seviyesi ilişkili ise iki yüzeyi ‘yuvalanmış’ olur ve iki yüzey arasına ‘:’ işareti konulur (Cardinet vd., 2010, s.13).

Genellenebilirlik kuramında görev, zaman, puanlayıcı gibi ölçmenin benzer durumlarının setine, değişkenlik kaynağı ya da yüzey (facet) denir. Bir değişkenlik kaynağının düzeyleri ise koşullar olarak adlandırılır.

Örneklemin ötesinde genelleme evrenine genelleme yapılıyorsa değişkenlik kaynağı tesadüfî değişkenlik kaynağıdır. Eğer örneklemin ötesinde genelleme yapılmıyorsa değişkenlik kaynağı sabit değişkenlik kaynağıdır (Alharby’den aktaran Güler, 2008).

Çalışmada Genellenebilirlik Kuramı’nda Uygulanan Desen

Çalışma da kısa cevaplı matematik yazılı sınavı yedinci sınıfa devam etmekte olan 99 öğrenciye uygulanmıştır. 9 maddeden oluşan kısa cevaplı matematik yazılı sınavı 3 puanlayıcı tarafından puanlanmıştır. Puanlayıcıların her biri tüm soruları puanlamış ve her öğrenci tüm sorulara ulaştığı için desen b x m x p (b: birey, m:madde, p: puanlayıcı) şeklinde çaprazlanmış desendir.

Bu çalışmada ölçmenin hedefi bireyler olacağı için bireyler değişkenlik kaynağı yani facet olarak adlandırılmaz. Bireyler çalışmada ölçmenin objesi olarak adlandırılır. Değişkenlik kaynakları madde ve puanlayıcıdır. Madde ve puanlayıcının seviyeleri de koşullar olarak adlandırılmaktadır. Bu desen için iki-yüzeyli deseni kullanılmıştır. Değişkenlik kaynağı, ölçme yapılan durumla sınırlı kalmadığı için tesadüfî değişkenlik kaynağıdır.

İki yüzeyli desende puanlayıcıların her biri tüm bireylerin tüm maddelerini puanlamıştır. Bu desende tüm değişkenlik kaynakları birbiriyle çaprazlanmıştır. Şekil 1’de iki yüzeyli desende ortak etkileşim alanı gösterilmektedir.

13

Şekil 1.İki yüzeyli desende ortak etkileşim alan

Bireylerin her bir puanlayıcı tarafından puanlandığı çaprazlanmış bxmxp deseninde gözlenen puan şu şekilde gösterilebilir.

Tablo 2

G Kuramında b x m x p Deseninden Elde Edilen Puanlara Ait Eşitlikler

Xbmp= μ + μb – μ + μm – μ + μp – μ +μbm - μb – μm + μ +μbp - μb – μp + μ +μmp - μm – μp + μ + Xbmp -μb - μm – μp + μbm + μbp + μmp + μ Genel ortalama Birey Etkisi Madde Etkisi Puanlayıcı Etkisi Birey x Madde Etkisi Birey x Puanlayıcı Etkisi Madde x Puanlayıcı Etkisi Ortak (artık) Etki

Genel ortalama dışındaki her bir bileşenin birer dağılımı vardır. Örneğin verilen cevaplar bir bireyden diğerine değişebilir. Her bir dağılımın ortalaması sıfırdır ve her birinin kendine özgü varyansı vardır.

İki değişkenlik kaynaklı tamamıyla çaprazlanmış rastgele desende gözlenen varyans;

𝜎

2

𝑋

_{(𝑏𝑚𝑝)} = 𝜎2_𝑏+𝜎2_𝑚+𝜎2_𝑝+𝜎2_𝑏𝑚+𝜎2_𝑏𝑝+𝜎2_𝑚𝑝+𝜎2_{𝑏𝑚𝑝,𝑒}…

14 Tablo 3

İki Değişken Kaynaklı (Facet) Tesadüfî Desen İçin Varyans Bileşenlerinin Kestirilmesine Ait Eşitlikler

Varyans Kareler Serbestlik Kareler Kestirilen Kaynağı Toplamı Derecesi Ortalaması Varyansın Bileşenleri Birey (b) SSb 𝑛𝑏-1 𝑀𝑆𝑏 = SSb/𝑛𝑏-1 𝜎2(𝑏) Madde (m) SSm 𝑛_𝑚-1 𝑀𝑆_𝑚 = SSm/𝑛_𝑚-1 𝜎2_(𝑚) Puanlayıcı (p) SSp 𝑛𝑝-1 𝑀𝑆𝑝 = SSp/𝑛𝑝-1 𝜎2(𝑝) b x m SSbm (𝑛_𝑏-1).(𝑛_𝑚-1) 𝑀𝑆_𝑏𝑚= SSbm/𝑛_𝑏𝑚-1 𝜎2 (𝑏𝑚) b x p SSbp (𝑛_𝑏-1).(𝑛_𝑝-1) 𝑀𝑆_𝑏𝑝= SSbp/𝑛_𝑏𝑝-1 𝜎2 (𝑏𝑝) m x p SSmp (𝑛_𝑚-1).(𝑛_𝑝-1) 𝑀𝑆_𝑚𝑝 = SSmp/𝑛_𝑚𝑝-1 𝜎2_(𝑚𝑝) b x m x p, e SSbmp,e(𝑛𝑏-1).(𝑛𝑚-1).(𝑛𝑝-1) 𝑀𝑆𝑏𝑚𝑝 = SSbmp/𝑛𝑏𝑚𝑝-1 𝜎2(𝑏𝑚𝑝)

ANOVA’daki her bir kareler ortalaması, varyans bileşenlerinin kestirimini çözmek için ona karşılık gelen beklenen kareler ortalamasının temsilidir. Ayrıca G Kuramında F testi ve F istatistiği yer almaz (Brennan,2011,s.9).

Tablo 2 deki değişkenlik kaynakları şunlardır:

1. Birey (b)

𝜎

2_𝑏

:

Sınavı cevaplayanlardan kaynaklanan değişkenlik kaynağı. Evren puan varyansıdır.

2. Madde (m)

𝜎

2_𝑚

:

Bir maddeden diğerine cevaplamadaki farklılıklardır. Sınavdaki maddelerin güçlüğünden kaynaklanan değişkenlik kaynağı

3. Puanlayıcı (p)

𝜎

2_𝑝: Puanlayıcıların cevapları puanlamadaki farklılıklarıdır. Puanlayıcının (cömertlik-katılık) kaynaklanan değişkenlik kaynağıdır.

4. Birey madde etkileşimi (bm)

𝜎

2_𝑏𝑚: Bireylerin bir maddeden diğerine cevaplardaki değişikliği gösterir.

5. Birey puanlayıcı etkileşimi(bp)

𝜎

2_𝑏𝑝

:

Bireylerin puanının puanlayıcıdan puanlayıcıya farklılık gösterip göstermediğini gösterir.

6. Madde puanlayıcı etkileşimi (mp)

𝜎

2_𝑚𝑝

:

Puanlayıcılarını bir maddeden diğerine olan puanlamadaki farklılığını gösterir.

7. Birey madde puanlayıcı (bmp)

𝜎

2_{𝑏𝑚𝑝,𝑒}: Ölçme hatasından kaynaklı değişkenlik kaynağıdır.

15

b bireyi, m maddeyi, p puanlayıcıyı göstermek üzere bxmxp desenine ait varyans bileşenleri şekildeki gibidir.

Şekil 2. Varyans bileşenleri

bxmxp iki yüzeyli çaprazlanmış desen için kestirilen kareler ortalaması formülleri Tablo 4’de verilmiştir.

Tablo 4

İki Yüzeyli Çaprazlanmış bxmxp Deseni İçin Kestirilen Kareler Ortalaması Formülleri

Varyans Varyans Kestirilen Kareler Ortalaması Kaynağı Bileşeni Birey (b) 𝜎2_𝑏 𝜎2_{𝑏𝑚𝑝,𝑒}+ 𝑛_𝑝 𝜎2_𝑏𝑚+𝑛_𝑚 𝜎2_𝑏𝑝 +𝑛_𝑚 𝑛_𝑝 𝜎2_𝑏 Madde (m) 𝜎2 𝑚 𝜎2𝑏𝑚𝑝,𝑒 + 𝑛𝑏 𝜎2𝑚𝑝+𝑛𝑝 𝜎2𝑏𝑚 +𝑛𝑏 𝑛𝑝 𝜎2𝑚 Puanlayıcı (p) 𝜎2 𝑝 𝜎2𝑏𝑚𝑝,𝑒 + 𝑛𝑏 𝜎2𝑚𝑝+𝑛𝑚 𝜎2𝑏𝑝 +𝑛𝑏 𝑛𝑚 𝜎2𝑝 b x m 𝜎2 𝑏𝑚 𝜎2𝑏𝑚𝑝,𝑒 + 𝑛𝑝 𝜎2𝑏𝑚 b x p 𝜎2 𝑏𝑝 𝜎2𝑏𝑚𝑝,𝑒+ 𝑛𝑚 𝜎2𝑏𝑝 m x p 𝜎2𝑚𝑝 𝜎2𝑏𝑚𝑝,𝑒+ 𝑛𝑏 𝜎2𝑚𝑝 b x m x p, e(artık) 𝜎2 𝑏𝑚𝑝,𝑒 𝜎2𝑏𝑚𝑝,𝑒 Karar Çalışmaları

G çalışması belirli koşullar altında elde edilen ölçümlere dayanır. Bu ölçümlerle elde edilen varyans değerleri K çalışmasında alınacak kararlar için kullanılır. K çalışmalarında G çalışmalarında elde edilen sonuçlar kullanılarak hataları azaltacak ölçmeler tasarlanmaktadır.

16

Karar çalışmasında hem genellenebilirlik katsayısı (G) ve hem de Phi ( Φ ) katsayısı katsayısı hesaplanabilir. Hesaplanan bu güvenirlik katsayıları hata varyansına göre değişiklik göstermektedir. Bu hata varyansları mutlak hata ve bağıl hata varyansı olarak adlandırılmaktadır. Mutlak hata; bir kişinin gözlenen puanı ve onun evren puanı arasındaki fark olarak tanımlanır. Bağıl hata ise gözlenen sapma puanı ve evren sapma puanı arasındaki farklılıktır. Bağıl hata varyansı

𝜎

_𝛿2 sembolü ile gösterilir ve klasik test kuramındaki hata varyansına karşılık gelir (Brennan, 2001,s.31-34).

Genellenebilirlik Katsayısı

G kuramı güvenilir puanlar elde etmek için gerekli ortamlar, test formları ve uygulayıcıların belirlenmesi için karar vermeye olanak sağlar ve kuramın güvenirlik düzeyini klasik test kuramının güvenirlik katsayısına benzer bir genellenebilirlik katsayısı verir (Shavelson ve Webb,1991, s.1-2).

Genellenebilirlik Katsayısı

G katsayısı, evren puan varyansının gözlenen puan varyansına oranı olarak ifade edilir.

G= 𝜎 2

𝑏 𝜎2_𝑏+𝜎_𝛿2

Genellenebilirlik katsayısı bağıl hata varyansı (

𝜎

_𝛿2 ) kullanılarak hesaplanır. Bağıl hata varyansı;

𝜎

_𝛿2 = 𝜎 2 𝑏𝑚 𝑛_𝑚 + 𝜎2_𝑏𝑝 𝑛_𝑝 + 𝜎2_𝑏𝑚𝑝 𝑛_{𝑚 .}𝑛_𝑝 (Brennan,2011, s. 10 -11)

İki yüzeyli çaprazlanmış bxmxp deseni için bağıl hata kaynakları şekildeki gibidir.

17 Phi (Ф) Katsayısı Ф= 𝜎 2 𝑏 𝜎2_𝑏+𝜎2_𝛥ile hesaplanır.(Brennan,2011,s. 11)

Phi katsayısı mutlak hata varyansı (

𝜎

2_𝛥) kullanılarak hesaplanır.

Mutlak hata varyansı;

𝜎

2_𝛥

=

𝜎 2 𝑚 𝑛_𝑚

+

𝜎2_𝑝 𝑛_𝑝

+

𝜎2_𝑏𝑚 𝑛_𝑚

+

𝜎2_𝑏𝑝 𝑛_𝑝

+

𝜎2_𝑚𝑝 𝑛_{𝑚.𝑛𝑝}

+

𝜎2_𝑏𝑚𝑝 𝑛_{𝑚 .}𝑛_𝑝

Şekil 4’te iki yüzeyli çaprazlanmış bxmxp deseni için mutlak hata kaynakları gösterilmektedir.

Şekil 4. Mutlak hata kaynakları

Araştırmanın Amacı

Bu araştırmanın amacı, aynı cevaplayıcıların kısa cevaplı matematik yazılı sınavına verdikleri cevapların güvenirlik katsayılarının Klasik test kuramındaki test tekrar test yöntemi ve Genellenebilirlik kuramına göre incelenmesidir.

Araştırmanın Önemi

Bu araştırma; öğrencilere uygulanan kısa cevaplı matematik yazılı sınavının, iki hafta arayla aynı öğrencilere uygulanması sonucunda puanlanması ile aynı öğrencilere uygulanan aynı kısa cevaplı matematik yazılı sınavının üç puanlayıcı tarafından puanlanmasıyla elde edilen

18

ölçümlerin güvenirliklerini karşılaştırmayı amaçlamaktadır. Bu amaçla sınav sonucunda elde edilen puanların güvenirlikleri hem Klasik test kuramı ile hem de Genellenebilirlik kuramı ile incelenmiştir. Bu araştırma seçilen yöntemlerin hatalardan ne derece arınık olduğunu göstermiştir. Ayrıca KTK ve G kuramına dayalı yapılan çalışmalar incelendiğinde test tekrar test yönteminden elde edilen güvenirlikle G kuramından elde edilen güvenirlik kıyaslanmıştır. K çalışması sonucu ölçümlerin güvenirliğinin iyileştirilmesine yönelik öneriler de fayda sağlayacaktır. Bu araştırmadan elde edilen bilgilerin hem kuramlardan elde edilen bilgilerin karşılaştırılmasına, hem gelecek araştırmalara, hem de öğretmenlerin ölçme ve değerlendirme sürecine yönelik bir katkı sağlayabileceği düşünülmektedir.

Problem Cümlesi

7. sınıfa devam etmekte olan 99 öğrenciye uygulanan kısa cevaplı matematik yazılı sınavının aynı puanlayıcılar tarafından puanlanması sonucu elde edilen puanlarının güvenirliğini kestirmede klasik test kuramı ve genellenebilirlik kuramına göre güvenirlik kıyaslaması nedir?

Alt Problemler

1.Klasik test kuramına göre test tekrar test yöntemiyle elde edilen güvenirlik katsayısı nedir? 2.Genellenebilirlik kuramına göre;

a. Kısa cevaplı matematik yazılı sınavından elde edilen puanların değerlendirilmesinde kestirilen genellenebilirlik kuramı parametreleri nasıldır?

b. Genellenebilirlik çalışması sonucunda kısa cevaplı matematik yazılı sınavından elde edilen puanların değerlendirilmesinde kestirilen varyansları ve toplam varyansları açıklama yüzdeleri nasıldır?

3. Madde sayılarının ve puanlayıcı sayılarının artırılıp azaltılmasıyla yapılan karar (K) çalışması sonucunda elde edilen G ve Phi katsayıları nasıl değişmektedir?

4. Yedinci sınıflara uygulanan kısa cevaplı matematik yazılı sınavının Klasik test kuramındaki test tekrar test yöntemi ile elde edilen güvenirlik katsayısı ile Genellenebilirlik kuramıyla elde edilen güvenirlik katsayıları arasında manidar farklılıklar var mıdır?

19

Sayıltılar

1.Puanlayıcılar puanlamayı benzer şartlarda yapmıştır. 2.Öğrencilere uygulama benzer ortamlarda yapılmıştır.

3. Puanlayıcılar her öğrencinin sınav kağıdını aynı titizlikle ve dikkatle puanlamışlardır.

Sınırlılıklar

1.Araştırma 7. Sınıf kazanımlarına yönelik kısa cevaplı matematik yazılı sınavının içeriği ile sınırlıdır.

2.Araştırma Çorum ilinde yedinci sınıfta öğrenim gören 99 öğrenci ile sınırlıdır.

3.Ölçme aracı geliştirme süreci için pilot uygulama yapılmadığından araçtan kaynaklanan hatalar ile sınırlıdır

İlgili Araştırmalar

Yurt İçinde Yapılan Araştırmalar

Bu bölümde Klasik test kuramı ile Genellenebilirlik kuramına yönelik yurt içinde yapılan araştırmalara yer verilmiştir.

Atılgan (2004), “Genellenebilirlik Kuramı ve Çok Değişken Kaynaklı Rasch Modelinin Karşılaştırılması” adlı çalışmasında 2002 ve 2003 yıllarında yapılan müzik öğretmenliği özel yetenek seçme sınavı verileri ile birden çok görev için bireylerin gözlenmesi ve puanlanması durumunda Genellenebilirlik kuramı ve çok değişkenlik kaynaklı Rasch modeli ile kestirilen istatistikleri karşılaştırmıştır. 2002 yılında 499 öğrenci, 3 puanlayıcı ve 19 madde; 2003 yılında ise 689 öğrenci, 4 puanlayıcı ve 28 madde ile çalışma yürütülmüştür. Araştırma sonuçlarına göre, G kuramı ve çok değişkenlik kaynaklı Rasch yaklaşımlarıyla elde edilen sonuçların kısmen tutarlı sonuçlar verdiği görülmüştür.

Atılgan (2005)’ın çalışmasında G kuramına bir giriş yapılarak temelleri vurgulanmış ve kuramın Klasik test kuramına göre avantajları açıklanmıştır. Ayrıca farklı ve çok hata kaynaklı bir ölçe durumu olarak, puanlayıcıların ölçme sürecine katıldığı bir örnekle; ölçüt dayanaklı ölçmeler için Phi ve norm dayanıklı ölçmeler için G katsayılarının elde edilerek kullanılması gösterilmiştir. Çalışmada örnek olarak 10 adaya uygulanmış dört görevden oluşan testin, dört bağımsız puanlayıcı tarafından puanlamasına ilişkin hipotetik bir veri çizelge ile verilmiştir. Her bireye aynı dört madde yöneltildiğinden ve dört puanlayıcının

20

bütün bireyleri aynı dört madde üzerinden puanladığı için çaprazlanmış desen kullanılmıştır. Yapılan ANAVO çalışması sonrasında ise KTK’nın potansiyel hata kaynaklarının birden fazla olması durumunda güvenirliğin hesaplanmasının tek bir analizle yapılmasına olanak sağlamazken G Kuramı olası hata kaynaklarının tamamını bir analizle kapsamlı tek bir güvenirlik katsayısını bağıl ve mutlak değerlendirme için ayrı ayrı kestirebilen bir kuramdır. Yelboğa (2007)’ın araştırmasında, ortak performans ölçüt ve standartlarına dayalı yöntem yaklaşımı ile geliştirilmiş İş Performansı Ölçeği’nin güvenirliği, Klasik test kuramı ve Genellenebilirlik kuramı yardımıyla incelenmiştir. Aynı zamanda Kendall’ın uyum katsayısı yardımıyla değerlendiriciler arası tutarlılığa bakılmıştır. Genellenebilirlik kuramında çok değişkenli modelle G ve Phi katsayıları; Klasik test kuramında ise test tekrar test ve Cronbach alfa güvenirlik katsayıları hesaplanmıştır. Araştırma sonucunda, İş Performansı Ölçeği’nde aynı ölçme durumu için Klasik test kuramında ve Genellenebilirlik kuramının çok değişkenli modelle elde edilen güvenirlik katsayılarının birbirleriyle uyumlu sonuçlar ürettiği belirlenmiştir.

Güler (2008) tarafından 2007 yılında yapılan bu araştırma TİMMS-1999’da yer alan açık uçlu matematik sorularının 24’ü 2007 yılı bahar döneminde 203 öğrenciye uygulanmış; öğrencilerin verdikleri cevaplar dört puanlayıcı tarafından bütüncül rubrikle puanlanmıştır. Puanlayıcıların yaptıkları puanlamalara ilişkin güvenirlik Klasik test kuramı, Genellenebilirlik kuramı ve çok değişkenlik kaynaklı Rasch ölçme modeli yardımıyla incelenmiştir. Klasik Test Kuramı’nda Cronbach alfa katsayısı 0,92 ve Kendall’ın uyum katsayısı 0,52 ve puanlayıcılar arası korelasyon katsayısı 0,90 ile 0,97 arasında değişen bir değer almaktadır.; Genellenebilirlik Kuramı’nda b x g x p (b: birey; p: puanlayıcı; g: görev) tümüyle çaprazlanmış desen kullanılarak genellenebilirlik katsayısı 0,92 ve güvenirlik katsayısı 0,90 ; Rasch ölçme modelinde ise öğrenci boyutunun güvenirliği 0,95 ve puanlayıcılar arası güvenirlik ise 0,99 bulunmuştur. Araştırma sonucunda, puanlayıcıların puan ortalamaları arasında fark olmakla birlikte, birbirleriyle uyumlu puanlamalar yaptıkları belirlenmiştir. Yelboğa (2008), tarafından yapılan çalışmada 2007 yılında 18 aday mühendisi; her biri Otomotiv Firmasında farklı birimlerden sorumlu yedi kişilik bir komisyon tarafından altı görev üzerinden birbirinden bağımsız olarak 1 –10 puanları arasında yapılandırılmış mülakat formuyla puanlandırılmıştır. G kuramı tamamıyla çaprazlanmış desenin kullanıldığı bu çalışmada, görevlerin güçlük bakımından birbirine yakın olduğu, puanlayıcıların birbirlerinden oldukça farklı değerlendirme yaptıkları, puanlayıcıların adayları bir görevden diğerine kararlı puanlamış oldukları sonucuna varmıştır. Yelboğa çalışmasında G katsayısının

21

0,80’den büyük ve yeterli olduğunu; ancak Phi katsayının 0,80’den küçük olduğunu bulmuştur. Yapılan karar çalışmasında G ve Phi katsayılarını artırmak için puanlayıcı sayısının artırılmasından ziyade madde sayısının artırılması gerektiği belirtilmiştir.

Alkan (2009) bu araştırmada, PISA 2009 Okuma Becerileri performansını değerlendirmede kullanılan açık uçlu soruların, birden fazla puanlayıcı tarafından birlikte ve dönüşümlü olarak puanlanmasıyla elde edilen farklı desenler Genellenebilirlik Kuramına göre karşılaştırılmıştır. Bu çalışmanın örneklemini, PISA 2009 uygulamasına katılan 4996 öğrenciden, okuma becerileri alanında yer alan soruları yanıtlayan ve yanıtladıkları kitapçıklar birden fazla puanlayıcı tarafından puanlanan 886 öğrenci oluşturmaktadır. Araştırmada, iki farklı senaryo üzerinden Genellenebilirlik kuramında kullanılmak üzere iki desen tasarlanmıştır. Bu desenlerden ilki, öğrenci (ö), soru (s) ve puanlayıcı (p) değişkenleri olmak üzere, öğrencilerin aynı beceriler konusunda puanlayıcıların her biri tarafından puanlandığı ö x s x p çapraz desendir. İkinci desen ise, her bir puanlayıcının öğrencilerden sadece bir kısmını puanlamasıyla oluşan, öğrenci ve puanlayıcı değişkenlerinin yuvalanmış olduğu, soruların ise bu değişkenlerle çaprazlanmış olduğu (ö:p) x s desenidir. Ö x S x P ve (Ö:P) x S desenleri karşılaştırıldığında, (Ö:P) x S deseni ile kestirilen bağıl ve mutlak hata varyanslarının ÖxSxP desenine göre daha küçük olduğu, dolayısıyla G ve Phi katsayılarının daha büyük değerler aldığı görülmektedir. Bu iki desende yapılan Karar çalışmaları incelendiğinde, her iki desende de puanlayıcı sayısını artırmanın G ve Phi katsayılarında artış sağladığı görülmüştür. 2, 4, 5, 6 ve 7 nolu Kitapçıklarda, puanlayıcı sayısını yarıya indirerek ya da madde sayısını yarıya indirerek, çoğu zaman her ikisinin sayısını da yarıya indirerek kabul edilebilir düzeylerde G katsayısına ulaşmanın mümkün olduğu görülmektedir. 2, 4, 5, 6, 7 nolu Kitapçıklarda madde ve puanlayıcı sayısının indirilip, 8 ve 12 nolu Kitapçıklarda madde sayısı sabit tutularak, puanlayıcı sayısının artırılmasının zaman, işgücü ve ekonomi açısından uygun olacağı sonucuna ulaşılmıştır.

Deliceoğlu (2009) futbolcuların teknik yeterliliklerini tespit etmek için uyguladığı ölçeğin KTK ve G Kuramına ait güvenirlikleri hesaplanmış ve birbiri ile kıyaslanmıştır Çalışma grubu 2007 – 2008 yılları arasında Ankara ilindeki profesyonel spor kulüplerin futbol takımlarının alt yapılarındaki toplam 72 futbolcu oluşturmuştur. Futbolcuların teknik yetilerinin (pas, şut çekme, top sürme ve top kontrolü) ölçülmesi amacıyla 56 maddeden oluşan “Futbol Yetilerine İlişkin Dereceleme Ölçeği” (Luxbacher, 1991) kullanılmıştır. KTK ile ilk puanlama ve ikinci puanlama arasındaki tutarlılık için “Pearson momentler çarpımı” korelasyon katsayısı, maddelerin iç tutarlılık güvenirliği için Cronbach α (alfa) katsayısı,

22

puanlayıcılar arasındaki tutarlılık için Kendall uyuşum katsayıları hesaplanmıştır. G kuramında ana ve ortak etkilerin varyans bileşenlerin kestirilmesi için MGENOVA paket programında G ve Phi katsayıları bulunmuştur. Araştırmadaki potansiyel hata kaynaklarının fazla olduğu durumlara benzer çalışmalarda G Kuramı, KTK’ na alternatif oluşturmaktadır. Bununla birlikte, Futbol Yetilerine İlişkin Dereceleme Ölçeği’nin ve ölçeğe ait alt boyutların güvenirliğinin yüksek olması, ölçeğin güvenilir bir ölçek olarak değerlendirebileceğini göstermektedir.

Güler (2009) Genellenebilirlik kuramında, birden fazla kaynaktan meydana gelen hataların her birinin ve etkileşimlerinin büyüklüklerini aynı anda tek bir analizle kestirmek mümkündür. Genellenebilirlik kuramı Klasik test kuramını da kapsayan, onun uzantısı olan bir kuram niteliği taşımaktadır. Genellenebilirlik kuramına ilişkin analizler genellikle GENOVA paket programıyla yapılmıştır. Ancak bu programın kullanımının zor ve karmaşık olması, genellenebilirlik çalışmalarının yapılmasındaki en büyük sınırlılık olarak araştırmacıların karşısına çıkmaktadır. Musquash ve O’Connor (2006), Genellenebilirlik kuramına ilişkin tüm analizlerin yapılabileceği bir SPSS programı geliştirmişlerdir. Bu çalışmada, Genellenebilirlik kuramına ve terminolojisine ilişkin genel bir bakış açısı oluşturulmaya çalışılmıştır. Ayrıca, genellenebilirlik kuramına bağlı Genellenebilirlik (G) ve Karar (K) çalışmalarında elde edilen genellenebilirlik ve güvenirlik katsayılarının yukarıda ifade edilen iki farklı paket programıyla elde edilen değerleri bir arada sunulmuştur.

Nalbantoğlu (2009)’nun araştırmasının temel amacı genellenebilirlik kuramına göre performans puanlamada öğrencilerin birden fazla puanlayıcı tarafından birlikte ve dönüşümlü olarak puanlanmasıyla oluşturulan desenlerden elde edilen G ve K çalışmaları sonuçlarını karşılaştırmaktır. Araştırmanın çalışma grubunu, 2007- 2008 öğretim yılı Hacettepe Üniversitesi Tıp Fakültesi üçüncü sınıf öğrencilerinden tesadüfî olarak seçilen 48 öğrenci oluşturmaktadır. Ayrıca araştırmada öğrencilerin iletişim becerileri istasyonundaki hasta görüşmelerinin puanlanmasında üç puanlayıcı görev almıştır. Araştırmada puanlayıcıların öğrencileri aynı iletişim becerileri değerlendirme formuyla 15 görev doğrultusunda birlikte ve dönüşümlü olarak puanlamasıyla oluşturulan ö x g x p ve (ö: p) x g desenleri (ö: öğrenci, g: görev, p: puanlayıcı) için ayrı ayrı G ve K çalışması yapılmıştır. Araştırmanın son kısmında ise iki desen için yapılan G ve K çalışmaları karşılaştırılmıştır. Sınavda puanlayıcıların öğrencileri puanlamada aralarında farklılıklar olmadığı bulunmuştur.

Taşdelen (2009), çalışmasında Nedelsky ve Angoff standart belirleme yöntemleri ile elde edilen kesme puanları Genellenebilirlik Kuramı kullanılarak karşılaştırılmıştır. Araştırmada

23

kullanılan veriler 2008 yılı ilköğretim 6.sınıf SBS (Seviye Belirleme Sınavı)’de yer alan ve 16 maddeden oluşan fen ve teknoloji sorularının Ankara ilinde görev yapan 40 fen ve teknoloji uzmanı tarafından adı geçen standart belirleme yöntemlerine uygun Şekilde puanlanması sonucu elde edilmiştir. Araştırmanın birinci aşamasında her bir yöntem için farklı hesaplanan ve farklı uzman görüşlerine dayanan kesme puanları kullanılarak yöntemler karşılaştırılmıştır. Araştırmanın ikinci aşamasında ise aynı veriler ile genellenebilirlik çalışması yürütülmüş ve genellenebilirlik katsayıları ve varyans bileşenleri elde edilmiştir. Ayrıca bu yöntemlerin uygulanması için gereken en uygun puanlayıcı sayısı da belirlenmeye çalışılmıştır. Çalışmadan elde edilen G ve Φ katsayılarına bakıldığında ise Angoff ve Nedelsky yöntemleri ile standart belirleme çalışılırken 10 puanlayıcının yeterli olacağı sonucuna varılmıştır.

Güler (2011) Klasik test kuramı ve Genellenebilirlik kuramına göre güvenirlik değerlerini rastgele veriler üzerinde karşılaştırdığı çalışmada daha önce yapılan çalışmalardan farklı olarak burada yer alan örnek, 125 öğrencinin 18 maddeye verdiği cevapları 4 farklı puanlayıcı puanlamış düşüncesiyle tamamen rastgele oluşturulmuş verilere dayanmaktadır. Oluşturulan bu rastgele verinin GK ve KTK’ya dayalı güvenirlik sonuçları hesaplanarak tartışılmıştır. Değişkenlik kaynağının maddeler olduğu tek değişken kaynaklı çapraz desen ( b x m) için hesaplanan G katsayısı ile Cronbach α değerleri her bir puanlayıcı için ayrı ayrı hesaplanmış ve çok düşük değerler elde edilmiştir. Değişkenlik kaynağının maddeler ve puanlayıcılar olduğu tümüyle çapraz desen ( b x m x p) için GK’ya dayalı G katsayısı ve Ф katsayısı sırasıyla .457 ve .456 olarak hesaplanmıştır.

Öztürk (2011), “Voleybol Becerileri Gözlem Formu İle Elde Edilen Puanların Genellenebilirlik ve Klasik Test Kuramı’na Göre Karşılaştırılması” adlı çalışma 2009-2010 yılları arasında Türkiye Voleybol Federasyonun belirlemiş olduğu 10 bölgede görevlendirilen antrenörlerin seçmiş olduğu 102 erkek voleybolcu oluşturmuştur. Voleybolcuların teknik becerilerinin (pas, manşet, smaç, blok ve voleybol zekası) ölçülmesi amacıyla 5 görevden oluşan “Voleybol Becerilerine İlişkin Gözlem Formu” kullanılmıştır. Gözlem Formuna ait maddeler, beş dereceli ölçekte puanlayıcılardan (4 puanlayıcı),“Görülmedi”, “Yetersiz”, “Yeterli”, “Oldukça Yeterli” ve “Mükemmel” seçeneklerinden birini işaretlemeleri istenmiştir. Voleybolcuların teknik becerilerinin tespit edilmesi için kullanılan voleybol becerilerine ilişkin dereceleme ölçeğinden elde edilen ölçmelerin; Klasik test kuramı ve Genellenebilirlik kuramına dayalı olarak belirlenen güvenirlik katsayılarının düzeyleri saptanmış ve birbirleriyle karşılaştırılmıştır. Voleybol becerilerine ilişkin dereceleme ölçeğinin puanlamasından elde edilen güvenirlik katsayıları iç ölçütlere göre incelendiğinde G