Robust exponential stabilization of networked switched control systems

Abstract—The use of networks in control systems to connect

controllers and sensors/actuators has become a common practice. A networked switched control system, a special case of such systems, is studied in this paper by making use of linear descriptor system theory. Such a control system is modeled as switched delay systems involving network-induced delay and packet dropout. Sufficient conditions for robust exponential stability are given for a class of switching signals with average dwell time. A design method to stabilize a continuous-time, linear switched plant under a given communication network via a hybrid state feedback controller is proposed. The design solution for hybrid controllers is network-dependent and given in terms of linear matrix inequalities.

I. INTRODUCTION

ETWORKED Control Systems (NCS) are feedback control systems whose feedback paths are implemented by a real-time operating network. This type of system allows for reduced wiring, as well as a lower installation cost. It also permits greater agility in diagnosis and maintenance. Examples of such systems can be found in automobile industry, tele-robotics, aircraft, and automated manufacturing systems [1-2, 4-5, 8]. However, this new technology has also posed a novel theoretical control problem of how to design the controller subjected to the network.

The limitation of network bandwidth and the differences of various transmission protocols have affected transmission timing and accuracy, so network-induced delays [1] and packet dropout [1, 7] often occur. Generally speaking, packet dropout results from transmission errors in physical network links (which is far more common in wireless than in wired networks) or from buffer overflow due to congestion and node failure occasionally occur, depending on the network protocol employed. Packets can be lost and are

Manuscript received 2008. This research was supported in part by the NSF of P.R. of China (grant 60574013), the Ministry of Education & Science of Republic of Macedonia (grant 14-3154/1/17.12.2007).

Dan Ma (madan@ ise.neu.edu.cn) and Jun Zhao are with Key Laboratory for Integrated Automation of Process Industry, Ministry of Education and College of Information Science and Engineering, Northeastern University, Shenyang, 110004, P.R. China. Also, Jun Zhao is also with Australian National University, Research School of Information Science and Engineering, Canberra ACT 0200, Australia (jun.zhao@ anu.edu.au).

Georgi M. Dimirovski, the corresponding author, is with FEIT College of Electrical Engineering & Information Technologies, SS Cyril & MethodiusUniversity, Karpos II b.b., P.O. Box 574 1000 Skopje, R. Macedonia, and also with Computer Engineering Department, Dogus University, 34722 Istanbul, Acibadem, Zeamet Sk 21, R. Turkey (phone: +90-216-5445555; fax: +90-216-5445535; e-mail: author@ dogus.edu.tr).

often not recoverable. In real time systems, in control systems in particular, network-induced delays and packet dropout will degrade the performance of control systems and even make systems unstable.

The study of NCS with network-induced delays or/and packet dropout have drawn considerable attention in the recently past years. The research focus has been put mainly on stability analysis and design for networked linear/nonlinear (with uncertainty/disturbance) plant [1-8]. Networked switched control systems (NSCS) are those all sensors/actuators of switched subsystems and hybrid controllers are connected by communication channel hence a special class of NCS. When the maximal delay is less than one sample period and the switching signal is synchronous with the sampling instant, stabilization of arbitrary switched systems with a computer is studied [9]. The method for uncertain systems with polytopic uncertainties has been used. However, it is more useful and challenging to this type of systems when the delay is larger than one period or packet dropout happens. As known, one of the basic problems of switched systems is the design of (a class of) switching rules to stabilize the systems. We can deal with the above problems via designing the switching signal, nonetheless, insertion of the communication channel into the switched control system architecture makes the analysis and design much more complex. Thus, the design of switching rule under the network-induced delay and packet dropout must be investigated in its own turn.

The stability and stabilization of switched systems have attracted much attention in the last decade [10-21]. A common Lyapunov function under arbitrary switching and multiple Lyapunov functions [12] for each of the individual subsystems being switched are given to analyze this type of systems. The stability analysis under slow switching, i.e., average dwell time technique has been used as an effective tool [16, 19-20]. However, these important methods for switched systems must be reevaluated before they become applicable to the networked switched control systems. In this paper, we study the exponential stabilization for networked switched control systems with network-induced delay and packet dropout. Firstly, we present a new concept of networked switched control systems. We also model this type of systems as switched delay systems, which describe NSCS with network-induced delay and packet dropout. Under this framework all components, including sensors, actuators, and controllers, are assumed to be connected

Robust Exponential Stabilization of Networked Switched Control

Systems

Dan Ma, Georgi M. Dimirovski, Senior Member, IEEE., and Jun Zhao

N

18th IEEE International Conference on Control Applications Part of 2009 IEEE Multi-conference on Systems and Control Saint Petersburg, Russia, July 8-10, 2009

through a network transmission channel. Secondly, a descriptor representation and the Lyapunov-Krasovskii technique are used to analyze the switched control systems with time-varying delay. Then the result is extended to the case of networked switched systems with uncertainty. For the networked switched control systems, we develop the Lyapunov-Krasovskii functional to present network-dependent criteria, which guarantee the exponential stability of NSCS. The switching rule and hybrid controller design are network-dependent and given in the form of linear matrix inequalities (LMI).

II. PROBLEM FORMULATION

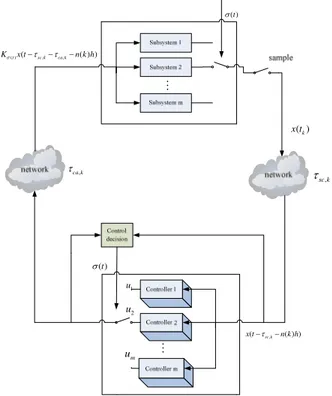
The NSCS to be studied in this paper is shown in Fig 1. The plant interacts with the controller through a network transmission channel and can be modeled as a continuous-time linear switched system described by

( ) ( ) ( )

( )

_t

( )

_{t t}

( )

x t

&

=

A

_σ

x t

+

B

_σ

u

_σ

t

₍₁₎

and a hybrid state feedback controller

( )t

( )

( )t

ˆ

( ),

k

[ ,

k k 1

)

u

_σ

t

+

=

K

_σ

x t

t

∈

t t

₊ (2) where:

_{x t}

( )

_∈

_R

n

denotes the state;

u t

( )

∈

R

mis the control input;

σ

( ) :[0, )

t

∞ → ϒ =

{

1, 2,...

m

}

is the switching signal depending on

t

directly or via the state

( )

x t

;

A

iand

B

i

(

∀ ∈ ϒ

i

)

are constant system matrices; k

t

denotes the sampling instant;

h

is the sampling period, which is bounded; and K_i(∀ ∈ ϒi )is the controller gain. Note that

u t

_i

( )

+

(

∀ ∈ ϒ

i

)

is piecewise continuous and only changes value at

t

_k, and that

ˆx

denotes the received state signal via network transmission.

The output of the plant is transmitted to a controller via the network transmission channel (Fig. 1). If network congestion or node failure occurs, depending on the network protocol employed, network-induced delay and packet dropout happen inevitably. For analysis purpose, the whole delay in each sampling period is considered as

k ca k sc k

τ

,

τ

,

τ

=

+

,

where:

τ

_{sc k,} is the sensor-to-controller delay and

τ

_ca,k is the controller-to-actuator delay [1]. Packets are often lost and not recoverable owing to link failure or they are dropped purposefully to avoid network congestion. The received signals by the controller, whether packet dropout happens or not, can be described as follows:

ˆ( ) ( )_k

x t =x t denotes no packet dropout at time

t

_k; ˆ( ) (_k )

x t =x t −h denotes one packet dropout at time

t

_k;

ˆ( )

(

k

( ) )

x t

=

x t

−

n k h

denotes

n k

( )

packets dropout at

t

_k. Therefore, the network-induced delay and packet dropout

can be lumped into a general description

x t

ˆ( )

=

x t

(

_k

−

n k h

( )

−

τ

_k

)

(3) By replacing

t

−

(

t

_k

−

n k h

( )

−

τ

_k

)

by a new variable

( )

t

τ

[3], we have the following expression

ˆ( )

(

( ))

x t

=

x t

−

τ

t

(4) where

τ

( )

t

is time-varying delay satisfying

≤

+

+

−

=

≤

τ

(

t

)

t

t

_k

n

(

t

)

h

τ

_k

0

,

t

∈

[

t

_k

,

t

_k+1

)

(5)

( )

t

d

τ

&

≤

₍₆₎ where

τ

>

0

and

0

< <

d

1

are known constants. The condition (6) means network-induced delay and packet dropout are time varying, and yet the variation rate is not too fast, which is the case in many communication networks.

The closed-loop NSCS can be described by means of

( ) ( ) ( ) 1

( )

( )

(

( )),

[ ,

)

( )

( ),

[

, 0)

t t t k k

x t

A

x t

B

K

x t

t

t

t t

x

σ σ σ

τ

θ

φ θ

θ

τ

+

=

+

−

∈

=

∈ −

&

(7) where the switching signal

σ

( )

t

and hybrid controller gain

, (

)

i

K

∀ ∈ ϒ

i

are to be designed,

φ θ

( )

∈

C

_nis a differentiable vector-valued initial function on

[

−

τ

, 0]

.

From the above analysis, a switched delay system model has been given to describe the NSCS with network-induced delay and packet dropout. In the following section, we will discuss the exponential stabilization of the NSCS (7). Firstly, we study its exponential stability.

1 u 2 u m u M M ( )t σ ( )t σ ( )k x t , ( sc k ( ) ) x t−τ −n k h , sc k τ , ca k τ ( )t ( sc k, ca k, ( ) ) Kσ x t−τ −τ −n k h

Fig. 1. NSCS architecture with network-induced delay and packet dropout.

III. EXPONENTIAL STABILITY AND ROBUST EXPONENTIAL

STABILITY OF NSCS

For the switching signal

σ

( )

t

, we give the switching sequences as follows

{

x

t0

;( , ), ( , ),

i t

0 0

i t

1 1

,( , ),

i t

k k

,|

i

k

,

k

{0,1 } ,

}

Σ =

L

L

∈ ϒ ∈

L

which means the

i th

_k subsystem is activated when

t

∈

[ ,

t t

_{k k+1}Å. We assume that the state of system (7) is continuous at the switching time.

Definition 1. The equilibrium

x

*

=

0

of system (7) is said

to be exponential stable under switching signal

σ

( )

t

, if the solution of system (7) satisfies

0 0 ( ) 0

( , )( )

t t t

,

r

x t

φ

t

≤ Γ

x

e

−γ −

∀ ≥

t

t

0 (8)

for constants

Γ ≥

1

and

γ

>

0

, where

•

denotes the Euclidean norm, and

x

_{t r}

=

sup

_{− ≤ ≤τ θ 0}

{ (

x t

+

θ

), (

x t

&

+

θ

)}

.

We denote the number of discontinuities of a switching signal

σ

on an interval

[ , ]

t T

by N_σ( , )T t . We say [16] that

σ

has average dwell time, if there exist two numbers

0

0

N

≥

and

τ

_a

>

0

such that

0

( , )

a

T

t

N T t

_σ

N

τ

−

≤

+

,

∀ ≥ ≥

T

t

0

(9)

As commonly done in the literature, we choose

N

₀

=

0

.

Theorem 1. For given constants

α

>

0

,

τ

>

0

,

0

< <

d

1

and controller gain matrices

K

_i, suppose (5)-(6) holds and there exist matrices

P

i1

>

0

,

P P

i2

,

i3,

Q

i

>

0

,

Z

i

,

R

i

>

0

such that 0 0 0 0 0 (1 ) i T T i i i i i i i i Q P A A P Z EP R d e ατQ

τ

α

τ

−     + + + +    _<      _{− −}    (10)

(

0

)

0

T T i i i i i

R

K B

P

Z





≥







_∗







(11) hold for any

i

∈ ϒ

. Then the NSCS (7) is exponential stable for any switching signal with average dwell time satisfying *

ln

a a

µ

τ

τ

α

>

=

(12) Moreover, an estimate of state decay is given by

0 0 0 ( )

|| ( ) ||

x t

b

e

t t

||

x

_t

||

_r

a

λ − −

≤

(13) where

µ

≥

1

satisfies 1 1

,

,

,

,

i j i j i j

P

≤

µ

P Q

≤

µ

Q R

≤

µ

R

∀

i j

∈ ϒ

0

1

ln

(

)

2

_a

µ

λ

α

τ

=

−

, _i

0

i i i

I

A

A

B K

I





= 

₊

₋







, 1 2 3

0

i i i i

P

P

P

P





= 







, 1 2 3 i i i i

Z

Z

Z

Z





= 

_∗







min 1

min

(

_i

),

i

a

λ

P

∀ ∈ϒ

=

2

max 1 max max

max

(

)

max

(

)

max

(

).

2

i i i i i i

b

λ

P

τ

λ

Q

τ

λ

R

∀ ∈ϒ ∀ ∈ϒ ∀ ∈ϒ

=

+

+

Proof: We first change the system (7) into an equivalent

descriptor form similar to the one in references [21, 23]:

( ) ( ) ( )

( )

( )

0

( )

_t

( )

_{t t}

(

( ))

x t

y t

y t

A

_σ

x t

B

_σ

K

_σ

x t

τ

t

=

= −

+

+

−

&

(14) or ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) _{( )}

( )

( )

( )

( )

( ), if

[0, )

0

_{( ) (}

_{) ( )}

( )d , if

t t t t t t t t t _{t t}

x t

y t

y t

A

x t

B

u

t

t

y t

A

B

K

x t

B

K

y s s

t

σ σ σ σ σ σ σ σ _τ

τ

τ

−

=

−

+





₊

_∈



= −

+

+





₋

_≥



∫

&

(15)

( )

( ),

[

, 0]

x

θ

=

φ θ

θ

∈ −

τ

is the initial condition in (7). Choose the piecewise Lyapunov-Krasovskii functional candidate as 1 2 3 ( ) ( ) ( ) ( )

( )

_{t t}

( )

_{t t}

( )

_t

( )

_t

( )

V x

=

V

_σ

x

=

V

_σ

t

+

V

_σ

t

+

V

_σ

t

(16) where 1 ( )

( )

( )

( )

( )

T t t

V

σ

t

=

s t EP

σ

s t

( )

( )

0 2 ( ) ( )

( )

( )

d d

t T s t t _t t

V

_σ

t

y

s e

α

R

_σ

y s

s

τ θ

θ

− − +

=

_{∫ ∫}

( )

( )

3 ( ) ( ) ( ) ( )

( )

t T s t

d

t t t t

V

_σ

t

x

s e

α

Q

_σ

x s s

τ − −

=

_∫

,

( )

( )

( )

x t

s t

y t





= 







,

0

0

0

n

I

E

= 





_





, 1 2 3

0

i i i i

P

P

P

P





= 







,

and where

P

_{σ( )t} ,

Q

_{σ( )t} ,

R

_{σ( )t} are positive matrices for every switching signal

σ

( )

t

. Along the trajectory of system (7) it follows 1 1

( )

( )

2

( )

( )

2

( )

0

T T T i t i i

x t

V x

=

x t P x t

=

s t P



_



_





&

&

_&

. (17) Substituting (15) into (17) gives

1

( )

T

( )(

T T

) ( )

i t i i i i i

( )

0

2

T

( )

_iT t

( )d

t t i i

s t P

y s s

B K

τ

η

−





= −

_

_





∫

,

0

i i i i

I

A

A

B K

I





= 

₊

₋







.

From the reference [22], we know that the inequality 2 T _T T T a R Y N a b Na b Y N Z b  −      − ≤_{    } −     

holds for any

a

∈

R ,

n

b

∈

R ,

2n

N

∈

R

2n n×

,

R

∈

R

2n n×

,

2 2 2

R

n n

,

R

n n

Y

∈

×

Z

∈

× , where

R

Y

0

Z





≥



_∗







. Therefore, taking i iT

0

,

( ),

( )

i i

N

P

b

s t a

y s

B K





=

_

_

=

=





, we have ( ) ( ) 0 2 ( ) ( )d ( ) ( ) d ( ) ( ) t T T i i t t i i T _T t i i i t t i s t P y s s B K y s R Y N y s s s t Z s t τ τ

η

− −   = − _{ }    −      ≤   _∗       

∫

∫

(19)

where

R Y Z

_i

, ,

_{i i}are constant matrices with appropriate dimensions such that i i

0

i

R

Y

Z





≥



_∗







hold. Choosing

Y

_i

=

[0

K B P

_{i i}

]

_i, we have ( )

( )

( )d

( )

( )

t _{T T} i _{tτ t}

y

s R y s

i

s

s t Z s t

i

η

τ

−

≤

_∫

+

(20)

Since

α

>

0

and

τ τ

≥

( )

t

>

0

, we know

( ) ( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

t _{T T} i _{t t} i i t _{T s T} i i t t t _{T s T} i i t

y

s R y s ds

s t Z s t

y

s e R y s ds

s t Z s t

y

s e R y s ds

s t Z s t

τ α τ α τ

η

τ

τ

τ

− − −

≤

+

≤

+

≤

+

∫

∫

∫

(21)

( )

( )

0 2 ( ) ( ) 2 ( )

( )

d d

( )

( )

( )

( )

( )

( )

( )

( )

( )

t T s t i t _t i t T T s t i _t i T i i t T s t i t

V

x

x

s e

R x s

s

y t R y t

y s e

R y s ds

V t

y t R y t

y s e

R y s ds

α τ θ α τ α τ

α

θ

τ

α

τ

− − + − − − −

= −

+

−

= −

+

−

∫ ∫

∫

∫

&

_&

_&

(22)

( )

( )

3 ( ) ( ) ( ) 3 ( ) ( ) ( ) (1 ( )) ( ( )) ( ( )) ( ) ( ) ( ) (1 ) ( ( )) ( ( )) t _{T s t T} i t i i t t T t i T i i T i V x x s e Q x s ds x t Q x t t x t t e Q x t t V t x t Q x t d x t t e Q x t t α τ ατ ατ

α

τ

τ

τ

α

τ

τ

− − − − = − + − − − − ≤ − + − − − −

∫

& & (23) Applying (18), (21)-(23) leads to 1 2 3

( )

( )

( )

( )

( )

( )

( )(

) ( )

( )

( )

( )

( )

( )

( )

( )

( )

(1

)

(

( ))

(

( ))

t t i t i t i t t T T T i i i i T T i i T T i i T i

V x

V x

V x

V x

V x

V x

s t P A

A P s t

s t Z s t

y t R y t

x t Q x t

s t

EPs t

d x t

t e

ατ

Q x t

t

α

α

τ

τ

α

τ

−

τ

+

=

+

+

+

≤

+

+

+

+

+

− −

−

−

&

&

&

&

(24) That is

( )

( )

T

( )

( )

t t i

V x

&

+

α

V x

≤

ξ

t

Ψ

ξ

t

(25) where

(

)

( )

_t

_{x t}

T

( )

_{y t}

T

( )

_{x t}

T

(

( ))

_t

T

ξ

=

−

τ

0

0

0

0

(1

)

i T T i i i i i i i i i

Q

P A

A P

Z

EP

R

d e

ατ

Q

τ

α

τ

−









+

+

+

+









Ψ =

_

_

_

_



_{− −}







(26) Thus, given (10)-(11), the system (7) is exponentially stable for any

i

∈ ϒ

. For

t

∈

[

t t

k

,

k+1

)

, we have ( ) ( ) ( )

( )

( )

k

(

)

k k t t t t t t t

V x

=

V

_σ

x

<

e

−α −

V

_σ

x

(27) From (10)-(11), at the switching instant

t

_i, we obtain

( )t_k

(

t_k

)

V

_σ

x

(tk)

(

tk

)

V

_σ

x

µ

− −

≤

(28) Therefore, from (27)-(28) and the switching number

0 a

t

t

N

_σ

τ

−

≤

it follows: 1 1 1 1 1 2 2 2 0 0 0 0 ( ) ( ) ( ) ( ) ( 1) 1 ( ) ( 1) 1 ( ) 2 ( ) ( ) 2 ( ) ( ) ( ) ln ( )( )

( )

(

)

(

)

(

)

(

)

(

)

(

)

k k k k k k k k k k k k k k k k k a t t t _t t t t t t t t t t t t t t t t t t t t t t N t t t t

V x

e

V

x

e

e

V

x

e

V

x

e

V

x

e

V

x

e

V

x

e

V

σ α σ α α σ α σ α σ α σ α σ µ α τ

µ

µ

µ

µ

µ

µ

− − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −

≤

≤

=

≤

≤

≤

≤

≤

L

0 ( )t

( ( ))

x t

0 σ (29) Since

a x t

|| ( ) ||

2

≤

V x

( )

t and _{0 0} 2

(

_t

)

||

_t

||

_r

V x

≤

b x

, we get 0 0 ln ( )( ) 2

1

2

|| ( ) ||

( )

a

||

||

t t t t r

b

x t

V x

e

x

a

a

µ α τ − − −

≤

≤

(30)

And this completes the proof. ø

Theorem 1 can be used to solve robust exponential stabilization problem for system (7). The NSCS (7) with

uncertainty is described by ( ) ( ) ( ) ( ) 1

( ) (

) ( )

(

( )),

[ ,

)

( )

( ),

[ ,0)

t t t t k k

x t

A

A

x t

B K

x t

t

t

t t

x

σ σ σ σ

τ

θ φ θ θ

τ

+

=

+∆

+

−

∈

=

∈ −

&

(31) where

∆

A

_i(

∀ ∈ ϒ =

i

{

1, 2,...

m

}

) denote the uncertainty of the controlled plant and satisfies

( )

i i i i

A

D F t H

∆ =

(32) with

D

iand

H

iconstant matrices,

F t

i

( )

an unknown,

real-valued and possibly time-varying matrix. Furthermore,

( )

i

F t

has Lebesgue-measurable elements and satisfies

( ) ( )

,

T

i i

F

t F t

≤ ∀

I

t

(33)

Theorem 2. For given constants

α

>

0

,

τ

>

0

,

0

< <

d

1

, and controller gain matrices

K

_i, if there exist matrices

P

i1

>

0,

P P Q

i2

,

i3

,

i

>

0,

Z R

i

,

i

>

0

such that

2 3 0 0 0 (1 ) 0 0 T T T T i i i i i i i i i i i T i i i i Q H H P D P A A P Z EP R P D d e Q I ατ τ α τ −   +    + + + +            _{∗ − −} _<   ∗ ∗ −         (34) and (11) hold for any

i

∈ ϒ

, then the NSCS (7) is robust exponentially stable for a switching signal with average dwell time satisfying (12), where

A P Z

_i

, ,

_{i i}are the same as in Theorem 1. Moreover, an estimate of the state decay is the same as in Theorem 1.

Proof. Let

A

i

=

A

i

+ ∆

A

i, if the inequalities

0 0 0 0 0 (1 ) i T T i i i i i i i i Q P A A P Z EP R d e ατQ τ α τ −     + + + +    _<      _{− −}    (35) and (11) hold, the result follows from Theorem 1. Apparently, inequalities (35) can be rewritten as

(

)

(

)

2 2 3 3 0 0 0 ( ) 0 ( ) 0 0 T T i i i i i T T T T i i i T i i i i i i P A A P P D H F t H F t D P D P P D  ∆ + ∆  Ψ +         = Ψ +_{ } +_{ }     < (36) where

Ψ

_i is defined as in (26). By virtue of Lemma 2.4 in Xie [25], a sufficient condition for the above is

(

)

(

)

2 2 2 3 3 0 0 0 T T T T i i i T i i i i P D H D P D P H P D λΨ +λ _ _ +_ _ <     (37) for some

λ

>

0

. (!?? Replacing

λ λ

P

_i

,

Q

_i

,

λ

R

_i

,

λ

Z

_iwith

,

,

,

i i i i

P Q R Z

, respectively, and using Schur complement formula [23] yields the inequality (34)). ø

IV. DESIGN OF HYBRID STATE FEEDBACK CONTROLLERS

In this section, we will design hybrid state feedback controller gains under switching rule (12) such that the NSCS (7) with the effects of network-induced delay and packet dropout is exponential stabilization.

Theorem 3. For given scalars

α

>

0

τ

>

0

,

0

< <

d

1

,

suppose that there exist matrices

M

_i1

>

0,

M

_i2

,

M

_i3

,

Z

_i1,

2

,

3

,

0,

0,

i i i i i

Z

Z

R

>

Q

>

X

, such that the following linear matrices inequalities 1 2 2 1 3 3 0 0 0 0 (1 ) 0 0 0 T T i i T i T i i i M M M d e Q R Q ατ

ψ ψ

τ

ψ

τ

τ

−     ∗   _{∗ ∗ −  <}   ∗ ∗ ∗ −   _{∗ ∗ ∗ ∗ −}    (38) 1 1 1 2 3

0

0

T T T i i i i i i i i

M

M

R

X B

Z

Z

Z



+

−







∗

≥







_∗

_∗







(39)

hold for any

i

∈ ϒ

. Then the hybrid state feedback control laws of (2) for any switching signal with average dwell time satisfying (12) exponentially stabilize the NSCS (7). Furthermore, the hybrid state feedback controller gain is

K

_i

=

X M

_{i i1}−1,

i

∈ ϒ

. Moreover, an estimate of state decay is given by (13), where

µ

is a constant satisfying

1 1 1 1 1 1 1 1

,

,

,

,

i j i j i j

M

−

≤

µ

M

−

Q

−

≤

µ

Q

−

R

−

≤

µ

R

−

∀

i j

∈ ϒ

1 2 2 1 1 T T i i i i

M

M

Z

M

ψ

=

+

+

τ

+

α

ø 2 3 2 1 2 T T T T i i i i i i i

M

M

M A

X B

Z

ψ

=

−

+

+

+

τ

ø 3 3 3 3 T i i i

M

M

Z

ψ

= −

−

+

τ

ø 0

1

ln

(

)

2

_a

µ

λ

α

τ

=

−

,

min

_min

(

_i1 1

),

i

a

λ

M

− ∀ ∈ϒ

=

2 1 1

max 1 max max

max

(

)

max

(

)

max

(

).

2

i i i i i i

b

λ

M

−

τ

λ

Q

τ

λ

R

− ∀ ∈ϒ ∀ ∈ϒ ∀ ∈ϒ

=

+

+

Proof. Let it be defined:

1 1 2 3

0

i i i i i

M

M

P

M

M

−





=

_{= }

_





, 1 2 3

,

T i i i i i i i

Z

Z

Z

M Z M

Z





=

_{= }

_

∗





1

,

i i

R

=

R

−

Q

i

Q

i 1

,

−

=

X

i

=

K M

i i1.

1

diag{ , (

I Q

_i−

) }

T and

diag{ ,

I Q

_i−1

}

on the left and right sides of (10), and then multiplying

diag{

M

_iT

, }

I

and its transpose on the left and right sides of the above result, respectively, and applying Schur complement formula at the last step.

Multiplying

diag{

1

,

}

T

i i

M

M

and its transpose on the left and right sides of (11), we obtain

1 1 1 1 2 2

0

0

T T T i i i i i i i i

M R M

Y B

Z

Z

Z

−







_∗



_≥







_∗

_∗







(40)

Since we known,

R

_i

=

R

_i−1

>

0

and

(

) (

1

)

1 1

0

T i i i i i

M

−

R R

−

M

−

R

>

, the inequalities 1 1 1 1 1 T i i i i i i

M R M

−

≥

M

+

M

−

R

(41) apparently hold. Therefore inequality (39) is guaranteed by the inequalities (41). The proof is thus completed.ø

Remark 1. The inequalities (10)-(11) in Theorem 1 give

network-dependent conditions for exponential stability for NSCS (7). Notice that the NSCS preserves its exponential stability under switching rule (12) in the presence of largest

τ

(corresponding to the upper bound of network-induced delay and packet dropout).

Remark 2: Notice that Theorem 2 gives a sufficient

condition of exponential stability for NSCS (7) in terms of LMI, which may be conveniently solved using Matlab LMI toolbox.

V. CONCLUSIONS

The robust exponential stabilization for a class of networked switched delay systems with uncertainty is studied. Linear switched subsystems with uncertainty and the hybrid state feedback controller are connected via network transmission channel, which is subjected to network-induced delay and packet dropout. Using the descriptor systems representation, we developed network-dependent conditions on exponential stabilization for NSCS. The hybrid controllers stabilize the switched systems in the sense that the overall control system is maximally tolerant to the network-induced delay and packet dropout. The design of hybrid network-dependent controllers is given in terms of linear matrix inequalities, thus fairly easy solvable by Matlab LMI toolbox.

REFERENCES

[1] W. Zhang, M. S. Branicky, S. M. Phillips. Stability of networked control systems. IEEE Control Systems Magazine, vol. 21(1), pp. 84–99, 2001.

[2] J. Nilsson. Real-time control systems with delays. Dept. of Automatic Control, Lund Institute of Technology, Lund, Sweden, Jan. 1998.

[3] M. Yu, L. Wang, T. Chu, and F. Gao. An LMI approach to networked control systems with data packet dropout and transmission delays. International Journal of Hybrid Systems, vol. 3(11), pp. 291-303, 2003.

[4] W. S. Wong, R. W. Brocket. System with finite communication bandwidth constraints-II: stabilization with limited information feedback. IEEE Trans. on Automatic Control, 44(5), pp. 1049-1053, 1999.

[5] P. Seiler and R. Sengupta. An H_∞approach to networked control.

IEEE Trans. on Automatic Control, 50(3), pp. 356-364, Mar.2005. [6] P. Naghshtabrizi and J. P. Hespanha. Designing an observer-based

controller for a network control system. Proceedings of the 44th

IEEE Conference on Decision and Control, Seville, Spain, pp.848-853, Dec.12-15, 2005.

[7] Q. Ling and M. D. Lemmon, Optimal dropout compensation in networked control systems, IEEE Conference on Decision and

Control, Maui, Hawaii USA, pp.670-675, Dec. 2003.

[8] Y. Tipsuwan and M. Y. Chow, Control methodologies in networked control systems, Control Engineering Practice, 11(10), pp. 1099-1111, 2003.

[9] L. Hetel, J. Daafouz, and C. Iung, Stabilization of arbitrary switched linear systems with unknown time-varying delays. IEEE

Transactions on Automatic Control, vol. 51 (10), pp1668-1674, 2006.

[10] D. Liberzon. Switching in Systems and Control, Birkhauser, Boston, 2003.

[11] Z. D. Sun, S. S. GE. Switched Linear Systems-Control and Design, New York: Springer –Verlag, 2004.

[12] M. S. Branicky. Multiple Lyapunov functions and other analysis tools for switched and hybrid systems. IEEE Transaction on

Automatic Control, vol. 43(4), pp. 475-482, 1998.

[13] J. Zhao and G. M. Dimirovski, Quadratic stability of a class of switched nonlinear systems, IEEE Transactions on Automatic

Control, vol. 49 (4), pp574-578, 2004.

[14] J. Zhao and D. J. Hill. On stability and

L

₂-gain for switched system,

Proceedings of the 44th IEEE Conference on Decision and Control,

Seville, Spain, pp. 3279-3284, Dec. 2005.

[15] A. S. Morse. Supervisory control of families of linear set-point controllers-Part II: exact matching, IEEE Transactions on Automatic

Control, 41(10), pp. 1413–1431, 1996.

[16] J. P. Hespanha, A. S. Morse. Stability of switched systems with average dwell-time. Proceedings of the 38th IEEE Conference on

Decision and Control, Phoenix, Arizona, pp2655–2660, 1999. [17] Y. J. Wang, G. M. Xie, L. Wang. Controllability of switched

time-delay systems under constrained switching. J. Maths. Anal. Appls., vol. 286, pp 397- 421, 2003.

[18] X. R. Mao. Exponential stability of stochastic delay interval systems with Markovian switching. IEEE Transactions on Automatic

Control, 47(10), pp. 1604-1612, 2002.

[19] G. S. Zhai, B. Hu, K.Yasuda and A. Michel. Disturbance attenuation properties of time-controlled switched systems. Journal of the

Franklin Institute, vol. 338, pp. 765-779, 2001.

[20] X. M. Sun, J. Zhao, D. J. Hill. Stability and -gain analysis for switched delay systems: a delay-dependent method, Automatica, 42, pp. 1769-1774, 2006.

[21] E. Fridman, A. Seuret, and J. P. Richard. Robust sampled-data stabilization of linear systems: an input delay approach, Automatica, vol. 40, pp. 1441-1446, 2004.

[22] Y. S. Moon, P. Park, W. H. Kwon, and Y. S. Lee. Delay-dependent robust stabilization of uncertain state-delay systems. Intl. J. Control, vol.74, pp. 1447-1455, 2001.

[23] E. Fridman, U. Shaked. An improved stabilization method for linear time-delay systems. IEEE Transactions on Automatic Control, 47 (11), pp. 1931-1937, 2002.

[24] S. Boyd, L. El Ghaoui, E. Feron et al. Linear Matrix Inequalities in

System and Control Theory. SIAM, Philadelphia, PA, 1994. [25] L. Xie. Output feedback

H

_∞ control of systems with parameter