Un Approximation To Neutron Transport Equation In Slab Geometry; Computation Of General Eigenvalue Spectrum

©BEYKENT UNIVERSITY

U

TRANSPORT EQUATION IN SLAB GEOMETRY;

COMPUTATION OF GENERAL EIGENVALUE

SPECTRUM

Ahmet BÜLBÜL Fikret ANLI*

ahmetbulbul@gmail.com fikretanli@gmail.com

Kahramanmaraş Sutcu Imam University, Faculty of Sciences and Letters, Department of Physics, 46100 Kahramanmaraş, Turkey

ABSTACT

General theoretical scheme for the UN method and evolution of general

eigenvalue spectrum are described. Firstly, applicability of UN method to one

dimensional slab geometry neutron transport problem is discussed and then eigenvalue spectrum is calculated for isotropic scattering with different values of parameter c (where c is the mean number of secondary neutrons per collision and known as the fundamental eigenvalue). Results of the UN method

showed that both discrete and continuum eigenvalues are present as in the case of PN method. All the results computed by both methods i.e. UN and PN

methods are presented side by side in the Tables for the comparisons.

Keywords : Chebyshev Polynomials, neutron transport in slab geometry, eigenvalue spectrum.

1. INTRODUCTION

In applied science, some special classical orthogonal polynomials such as Legendre, Chebyshev [1, 2], Hermite etc. have a great importance. Especially, Legendre polynomials have an extensive usage area in the solution of physics and engineering problems. In neutron transport theory, Legendre polynomials have an extraordinary importance. Angle and position dependent angular flux of neutrons are expanded [3, 4] in terms of Legendre polynomials and then the method is called PN approximation. As well known, the variables or the roots

of both polynomials Legendre and Chebysev are in the interval of [-1, 1]. If the PN method gives the appropriate solutions, then the Chebyshev polynomials

should also give the appropriate solutions for the neutron transport equation in plane geometry.

The Chebyshev polynomial method was first proposed by Aspelund [5] and Conkie [6]. By TN method (first kind Chebyshev polynomial approximation),

the necessary condition for reactor criticality and the values of extrapolated end point were discussed by Yabushita [7]. In his work, it was shown that TN

method gave the results closer to exact value than PN method for the strong absorber but for weak absorber PN method gave the results closer to exact value than TN method. In recent published papers, Anli et al. showed that the eigenvalue spectrum and critical half thickness of neutron transport equation in slab geometry can be calculated by modified TN method [8, 10].

One of the important problem in the solution of neutron transport equation is the calculation of eigenvalues. As well known, these eigenvalues depend on the c values. In nuclear reactor physics, the important coefficients such as diffusion length, diffusion coefficient and buckling also depend on the parameter c which is known as the fundamental eigenvalue in the neutron transport theory.

The spherical harmonics approximation, PN method, [3, 4, 11] has been

explored in the early years of the nuclear age for the solution of neutron transport equation. In the present work, we describe a new theoretical scheme for the solution of neutron transport equation in plane geometry. We expanded the neutron angular flux in terms of Chebyshev polynomials of the second kind instead of Legendre polynomials and then we called this application as UN

method.

2. THEORY

2.1. PN APPROXIMATION

We consider the one-dimensional Boltzman integro-differential equation. This equation, for isotropic scattering and with no sources present, is

dw( x,u) Js 1 , ,

¡ 1 ^ ^ — + Jt^(X,/U) = / ) d/u , - a < x < a, - 1 < / < 1. ( 1 )

dx 2 -1

where y/(x, ¡¡¡) is the angular flux or flux density of neutrons at position x traveling in direction p, aT and aS are total and scattering differential cross section, respectively.

In order to solve Eq.(1), it is well known that in the PN approximation the

M) = £ (x)Pn

The orthogonality and recurrence relations of Legendre polynomials are given by, respectively

1 |2/(2n +1) , n = m

J

M)

' (3)

- [0 , n ^ m

( 2 n + 1 ) MPn ( M ) = ( n + 1 ) Pn+i ( M ) + ( M ) (4)

and then, inserting Eq.(2) into Eq.(1) and using the recurrence and orthogonality relations of the Legendre polynomials defined in Eq.(4) and Eq.(3) respectively, we obtain the PN moments of the angular flux as

d<( x) . . . . . .

< <

< <

dx

dx dx

(x)

<

dx dx

(n +1) d< + '( x ) + nd<n -'( x ) + a T (2n + 1)<(x) = <s<a(x)8na , (5d)

dx dx

For the solution of Eqs.(5) we assume [11,12]

<n ( x ) = Gn ( V ) e xp(& T x / V ) (6)

and putting this in Eqs(5) we obtain analytical expressions for all Gn(V) as,

G0V) =

1,

c)

and in generally,

(n + 1)Gn+1(v) + nGn-1(v) + (2n + 1 ) G ( V ) - v c G 0 { v ) 8n0 = 0, n = 1,2,...N ( 7 b ) where c = aS / <JT, and Sn0 is the kronecker delta and V is a constant

appearing as an eigenvalue associated with the eigenfunction GN (V) . The

eigenvalues

Vk

,

k = 1,2,.. N +1 can be calculated by setting G

0.

2.2. CHEBYSHEV POLYNOMIAL APPROXIMATION (UN APPROXIMATION)

We expand the neutron angular flux in terms of Chebyshev polynomial as,

2 / N

W ( x , n ) = - V l - V_- n 2 n ( x ) U n (M), _ a < x < a, _1 <M< 1 (8)

n n=0

The orthogonality and recurrence relations of Chebyshev polynomials of the second kind are given by, respectively

in/2, n = m

f

I

/ 2,

n = m

f Un MU m ( ^ ) V1 - V dV = \ ' (9)

- [0,

n

m

2 v Un (M) = Un+i (M) + Un-1 (V), - 1 < V < 1 (10)

Inserting Eq.(8) into Eq.(1) and using the recurrence and orthogonality relations of the Chebyshev polynomials of the second kind defined in Eq.(10) and Eq.(9) respectively, we obtain the UN moments of the angular flux as,

^

2aT

(x)

2aS

(x)

dx

dO 2

x) d O

x) „

^

+ —

2 o

0

dx dx

and in general, assuming O _ ( x ) = 0

+ + ( x ) = n t f ^ « , ( . 1 0

dx dx n

Here we clarify an important point; As well known, in the diffusion approximation it is assumed that all the flux moments O N + 1 ( x ) equal to zero

for all N > 1. Applying this rule to Eq.(11b) for n = 1, which is the

U1 approximation, we obtain

. 1 d O

(x)

O 1

(x)

2a

dx

where O0( x ) is the scalar flux and O j ( x ) i s the neutron current at the

position x . The general relation between the scalar flux and current is given by the Fick's law [3, 4, 11] which is defined for a general geometry as

J ( r )

= -D

Eq.(12) for one dimension. If Eq.(12) is used in Eq.(11a) it is obtained that

d

°

-4a

(1 - c ) O

( x ) = 0, c = ct

/ G

(14)

dx

which is the neutron diffusion equation with no source. As a result, in the U1 approximation diffusion coefficient and diffusion length are found to be

D = 1 /(2o> ) and L = 1 /(2oy VT - c ) respectively, but in the P approximation (Legendre polynomial approximation) these are given by

D = 1/(3<r

) and L = 1/(ct

/3(1 - c)) .

For the solutions of Eqs.(11), again we assume [11,12]

o n (x) = An (v)exp(^Tx/v) (15)

and putting this in Eqs.(11) we obtain analytical expressions for all An (v) as

Ac(v)

1

A

c)A

(v), c = a

/ a

1

(

1)

An+1 (v) + 2vAn (v) + An-! (v) = (v), n > 1 (1 6c)

n +1

As An (v) depends on v, we obtain the permissible values of V from

Eq.(16c), that is since ON + 1 (x) is neglected in the UN approximation, we

should thus have AN+1 (v) = 0 . Hence the permissible values of V will be

obtained from the solution of

AN+1(v) = 0 (17) The other way to compute V eigenvalues is to use the determinant of the

coefficients matrix of An (v) , that is

[M(v)]A(v) = 0, (18)

where A ( v ) is the column vector given by

[A

(v), Aj(v),...., A

(V)]

and M(v) is a (N +1) x (N +1) square

2v(1 - c) 1 0 0 0 0

1 2v 1 0 0 0

2

1 2v 1 0 0

—vc

3

M (v) = 0

0 1 2v 1 0

2

0 0 1 2v 1

—vc

5

1 + (-1)

1 2v

2n +1

If one solves the equation det M ( v ) = 0 for any order N+l, it is clear that same results are obtained with the results of Eq.(17). The discrete

[vk < 0, vk > 0] and continuum [_ 1 <vk < 1] eigenvalues for different

values of c are given in the Tables for any given value of the approximation order N.

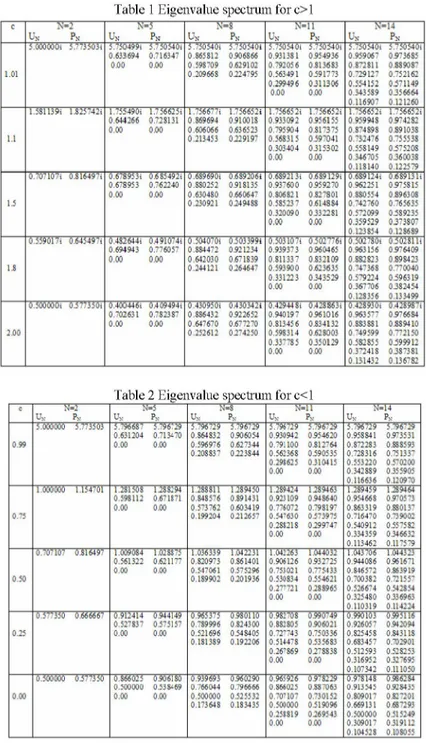
In this work, we investigated the applicability of second kind of Chebyshev polynomial approximation method for the solution of neutron transport equation in slab geometry and then we attempted to compute the general eigenvalue spectrum of neutron transport equation. In all Tables, generated numerical results were calculated by using Maple Software. The numerical results for c>1 are presented in Table 1 and c<1 are presented in Table 2. Results obtained by both methods are given side by side for the comparison. It is seen that the results obtained by UN method are in good agreement with the results obtained by PN method.

As seen Eqs.(16) the analytical expressions for all An (v) are present and by

using these analytical expressions the discrete and continuum v eigenvalues can be calculated by setting AN+1 (v) = 0 for various c values. This comes

from essential idea of the UN method for which O N+1 (x) = 0 as in the case of PN method. As seen in Table 1, when c>1 then one pair of the roots is

purely imaginary and the others are the pairs in the interval [-1,1]. These are

the expected results, because it is possible to see in literature [4,11] that, when c>1 asymptotic roots or discrete eigenvalues are purely imaginary. When c=1 then one pair of the roots is + ro i and the remaining roots are the pairs in the interval [-1,1]. As seen in the Table 2, all the roots are real and absolute value of only one pair of them is greater than 1 and these are known as the discrete eigenvalue of transport equation. Some values of V lie on the real line between - 1 and +1 and these are called continuum eigenvalues. Thus, for c<1 it is clear that the discrete eigenvalues may change between V=1 and V = ro. When c = 0 , then all the roots of AN+1 (V) = 0 are identical to the roots of

UN+I (V) = 0 , i.e. to the roots of second kind Chebyshev polynomials. For N

even, AN (V) = 0 gives symmetric eigenvalues as ±Vk, therefore the system

has N eigenvalues. For odd N, AN (V) = 0 gives the eigenvalues such that one

of them is zero and remaining N -1 pairs are symmetric according to V = 0 . Only positive values of Vk are presented in the Tables. As seen in the

Tables, UN approximation also gave the eigenvalues; two of them discrete

and the others are the continuum as in the case of PN approximation. It should

be noted that when - 1 < V < 1, the continuous solutions of the neutron scalar flux change very faster with x than the asymptotic solutions.

As a result, neutron transport equation can also be solved by the Chebyshev polynomials (with both kinds TN and UN) not only by Legendre polynomials. For the solution of neutron transport equation, we suggested the appropriate expansion as seen in Eq.(8) but we could have suggested the expansion as

complications to compute the eigenvalues. If the above expansion was used, we could not obtained the exact analytical expressions of An (V) in terms of

the variable V.

2

Table 1 Eigenvalue spectrum for c>l c N = 2 U „ PK N = 5 U „ PK N = S U „ PK N = l l U „ PK N = 1 4 U „ PK 1.01 5.0000001 5.7735031 5.7504991 5.7505401 0.633694 0.716347 0.00 0.00 5.7505401 5.750 5401 0.865812 0.906866 0.598709 0.629102 0.209668 0 2 2 4 7 9 : 5.750 5401 5.750 5401 0.931581 0.954936 0.792056 0.813683 0.56349 1 0 . 5 9 1 " " : 0.255496 0.311306 0.00 O.OO 5 7 5 0 5 4 0 1 5.7505401 0.959067 0.973685 0.872811 O.E89087 0.721127 0.752162 0 . 5 : 4 1 : 1 0.571145 0.343589 0 356664 0.116907 0.121260 1.1 1.5811391 1.8257421 I.7554901 1.7566251 0.614266 0.728131 0.00 0.00 1.7566771 1.7566521 0.B65654 0.910018 0.606066 0.636523 0.213453 0 2 2 3 1 5 " 1 7 5 6 6 5 2 1 1.7566521 0.93305 2 0 956155 0.795904 0.817375 0.568315 0.597041 0.303404 0 3 1 : : Ol O.OO O.OO I.7566521 1.7566 521 0 . 5 3 9 4 8 0.9742 E2 0.874 858 0.B51038 0.732476 0.755538 0.558149 0 5 7 5 2 0 8 0.346705 0 3 6 0 0 3 8 0.118140 0.122579 1.5 0.7071071 0.8164971 0.6789531 0 6 854921 0.678953 0.76224« 0.00 0.00 0.6856501 0 6 892061 0.880252 0.91 El 35 0.630480 0.660647 0.230921 0 2 4 9 4 8 8 0.6852131 0 6 8 9 I 2 9 i 0.937600 0.959270 0.80682 1 0.827801 0.585237 0 614884 0.320050 0 332281 0.30 O.OO 0 . 6 0 1 2 4 1 0.6851311 0.962251 0 . 9 7 : 8 1 : 0.880554 0.856308 0.742760 0.765635 0.572099 0 5 8 5 1 : : 0 . 5 :5 : : 5 0 3 7 3 8 0 7 0.123854 0.128685 1 3 0.5590171 0.6454971 0.4826441 0.4910741 0.694943 0.77605" 0.30 0.00 0.5010701 0.5033951 0.884472 0.921234 0.642030 0.671839 0.244121 0 2 6 4 6 4 7 0.5031071 0.5027761 0.939373 0.960465 0.81133 7 0.832105 0.593900 0.623635 0.331223 0 343529 O.OO O.OO 0.5027801 0.50281 H 0.5631:6 0.976405 0.8K2S23 0.B5842: 0.747368 0.770040 0.579224 0.596315 0.367706 0 382454 0.128356 0.133495 2.00 0.5000001 0 5773501 0.4004461 0.4094941 0.702631 0 7 8 2 3 8 7 0.00 0.00 0.4309501 0.4303421 0.886432 0.922652 0.647670 0.677270 0.252612 0 274250 0.4154481 0.428B631 0.94015" 0.961016 0.813456 0.834132 0.598314 0.628003 0.337785 0 350129 O.OO O.OO 0.4289301 0.4289871 0 . 5 6 3 ; " " 0.976684 0.883881 0.E89410 0.749599 0.772150 0.5K2855 0.599912 0.372418 0 3 8 7 3 8 1 0.131432 0.1367B2

Table 2 Eigenvalue spectrum for c<l N=2 PK N=5 UH PK N=8 UH PH N=11 UH PK N=14 Pk 0-99 5.000000 :.773503 5.796687 5.796725 0.631204 0.713470 O.OO 0.00 5.796729 5.796729 0.864832 0.906054 0.596976 0.627344 0.208837 0 223844 5.796729 5.796729 0.530942 0.954620 0.791100 0.812764 0.562368 0 5 9 0 : : : 0.29S62 5 0 310415 0.00 0.00 5.796729 5.796729 0.95884 1 0 9 7 5 5: 1 0.872283 0.888593 0.728316 0.751337 0.553220 0.570200 0.342889 0 355905 0.116636 0.120970 0.75 1.000000 1.154701 1.281508 1 2 8 8294 0.55811: 0.671S71 O.OO 0.00 1.288811 1289450 0.848576 0.8914:1 0.573762 0.603419 0.199204 0 2 1 2 5 : " 1.289424 1 289463 0.923109 0.948640 0.776072 0.798197 0.547630 0.573975 0.288218 0 299747 0.00 0.00 1.289459 1 289464 0.954668 0 970573 0.863:19 0.880137 0.716470 0.739002 0.540912 0 . ; ; 7 5 8 2 0.3345:9 0 346632 0.113462 0.117579 0.50 0.707107 0.816497 1-009084 1.028875 0.561322 0.621177 O.OO 0.00 1.036339 1.042231 0.820973 0.861401 0.54706 1 0 575296 0.185902 0 201936 1.042263 1.044032 0.906126 0 . 9 3 : " : ; 0.7530:1 0.775433 0.530834 0.554621 0.27-721 0 2 8 8 9 6 5 0.00 0.00 1.043706 1.044323 0.944086 0.9616"! 0-846572 0.863919 0.700382 0.721557 0.526674 0.542854 0.325480 0 336963 0.110319 0.114224 o . : : 0.577350 0.666667 0.912414 0.944149 0.527837 0.575157 O.OO 0.00 0.965375 0.980110 0.785956 0.824300 0 521696 0.548405 0.181389 0.192206 0.982708 0.990749 0.88280 5 0.906021 0.727743 0.750336 0.51447 8 0 535683 0.267869 0 278838 0.00 0.00 0.990103 0.99:116 0.926057 0.942094 0.825458 0.845118 0.683457 0.702901 0.512593 0 528253 0 . 5 1 6 9 : : 0327695 0.107342 0.111050 0.00 0.500000 0 577350 0.86602 5 0.906180 0.500000 0.538469 O.OO 0.00 0.539653 0.960290 0.766044 0.796666 0.500000 0.525532 0.173648 0.183435 0.965926 0.978229 0.86602 5 0.887063 0.707107 0 . 7 3 0 1 ; : 0.500000 0.519096 0.25! 819 0 2 6 9 5 4 3 0.00 0.00 0.978148 0.986284 5 . 9 0 545 0.92843: 0.809017 0.827201 0.6691:1 0 687293 0.500000 0 515249 0.309017 0.51911: 0.10452 8 0.10805:

REFERENCES

[1] Bell, W.W.; Special Functions for Scientists and Engineer, D. Van Nostrand Company Ltd., London, (1967).

[2] Arfken, G.; Mathematical Methods for Physics, 2ed., Academic Press Inc., New York, (1970).

[3] Davison, B.; Neutron Transport Theory, Oxford University Press, London, (1957).

[4] Bell, G. I., Glastone, S.; Nuclear Reactor Theory, Van Nostrand Reinhold Company, New York, (1970).

[5] Aspelund, O.; PICG, 16 (1958), 530.

[6] Conkie, W. R. ; Polynomial approximations in neutron transport theory, Nucl. Sci. and Eng. 6 (1959), 260-266.

[7] Yabushita, S.; Tschebyscheff polynomials approximation method of the neutron transport equation, Journal of Mathematical Physics. 2 (1961), 543-549.

[8] Yaşa, F., Anli, F., and Güngör, S.; Eigenvalue spectrum with chebyshev polynomial approximation of the transport equation in slab geometry, JQSRT. 97 (2006), 51-57.

[9] Anli, F., Yaşa, F., Güngör, S., and Öztürk, H.; TN approximation to neutron transport equation and application to critical slab problem, JQSRT. 101 (2006), 129-134.

[10] Anli, F., Yaşa, F., Güngör S., and Öztürk, H.; TN approximation to reflected slab and computation of the critical half thicknesses, JQSRT. 101 (2006), 135-140.

[11] Case, K. M., Zweifel, P.F.; Linear Transport Theory, Reading MA, Addison Wesley, (1967).