DERS 3 : Üyelik fonksiyonları formülasyonları ve parametreleri, T-norm ve S-norm
Aşağıda, ÜF’leri tanımlamak için kullanılan bir takım parametreli fonksiyon grupları sunulmuştur..
Bu şekildeki parametreli ÜF fonksiyonları, adaptif bulanık sonuçlu sitemler için çok önemli bir rol üstlenmektedir.
Üçgen ÜF fonksiyonları
Üçgen ÜF, üç köşenin X koordinatlarını belirleyen üç parametre {a,b,c} tarafından belirlenir.
x c c x b b x a a x , 0 , b c x c , ≤ ≤ ≤ ≤ ≤ ≤ ⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎨ ⎧ − − = b-a a -x0, ) c , b , a , x ( üçgen
veya üçgen(x ;a,b,c)=max ⎟⎟
⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − − 0 , , min b c x c a b a x
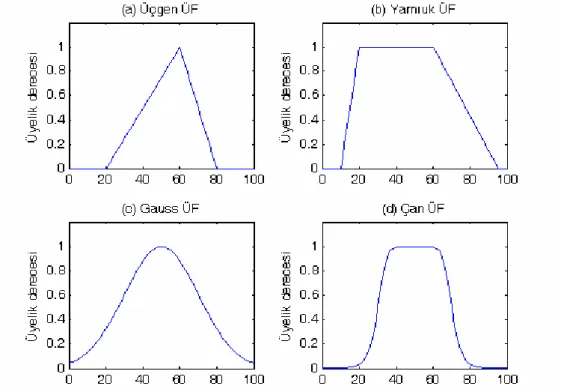
Şekil 3.1 (a) , üçgen ( x ; 20 , 60 , 80 ) olarak tanımlanan bir üçgensel ÜF fonksiyonuna ait bir örneği göstermektedir.
Yamuk ÜF fonksiyonu
Yamuk bir ÜF aşağıdaki gibi belirtilen dört parametre {a ,b, c, d} tarafından belirlenir.
⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ≤ ≤ ≤ − − ≤ ≤ ≤ ≤ ≤ = x d , 0 d x c , c d x d c x b , 1 b x a , a x a -b a -x 0, ) d c, , b , a , x ( yamuk veyayamuk(x;a,b,c,d)=max ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − − 0 , , 1 , min c d x d a b a x
Şekil 3.1 (b) , yamuk ( x ; 10 , 20 , 60 , 95 ) olarak tanımlanan bir yamuk ÜF fonksiyonuna ait örneği açıklamaktadır. Açıktır ki, üçgen ÜF, yamuk ÜF’nin özel bir durumudur.
Basit formülleri ve hesaplanmasındaki verimliliği dolayısıyla hem üçgen ÜF, hem de yamuk ÜF’ler özellikle de gerçek -zaman uygulamalarında yaygın olarak kullanılmaktadır. Bununla birlikte ÜF fonksiyonları, doğru parçalarının birleşiminden oluştuğu için, bu fonksiyonların parametrelerce belirlenmiş dönüm noktalarındaki geçişi düzgün değildir. Aşağıda, düzgün ve lineer olmayan fonksiyonlar tarafından tanımlanan diğer ÜFler sunulmaktadır.
Gauss ÜF fonksiyonları
Gauss ÜF fonksiyonu iki parametre { σ , c } ile tanımlanır. gauss (x; σ, c) = 2 c x 2 1 e ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ σ − −
Βurada c, ÜF’nin merkezini ve σ, genişliğini belirtir. Şekil 3.1 (c) , gauss (x ;20,50 ) olarak tanımlanan bir Gauss ÜF fonksiyonunun grafiğini göstermektedir.
Genelleştirilmiş çan ÜF fonksiyonları
Genelleştirilmiş çan ÜF ( veya çan ÜF ) üç parametre {a, b, c} tarafından belirlenir. çan (x ; a , b , c ) = b a c x 2 1 1 − +
Burada b parametresi genelde pozitiftir. Eğer b negatif olursa çan eğrisi baş aşağı olur.Bu ÜFnin, olasılık teorisinde kullanılan Cauchy dağılımının doğrudan genelleştirilmiş şekli olduğuna dikkat edilmelidir. Bu sebeple bu ÜFye Cauchy ÜF de denilir. Şekil 3.1 (d) çan( x ; 20 , 4 , 50 ) olarak tanımlanmış bir genelleştirilmiş çan ÜF fonksiyonunu göstermektedir.
Şekil 3.1 Çeşitli ÜF fonksiyonları örnekleri, (a); Üçgen (x; 20,60,80), (b); Yamuk (x; 10,20,60,95), (c); Gauss (x;20,50), (d); Çan (x; 20,4,50)
Akıcılığı ve kısa notasyonları ile Gauss ÜF fonksiyonları ve çan ÜF fonksiyonları bulanık kümelerin belirlenmesinde gitgide artan bir şekilde popüler ÜFler haline gelmektedir.
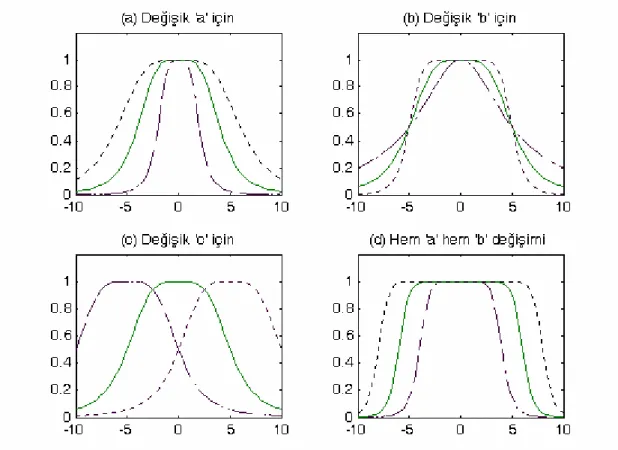
Şekil 3.2 Genelleştirilmiş bir çan fonksiyonunda parametrelerin değişim etkileri (d) için a/b oranı sabit olmak kaydıyla hem a hem de b eşzamanlı değişiyor.
Sigmoidal ÜF fonksiyonları , sigma ( x ; a , c ) = )] ( exp[ 1 1 c x a − − +
c parametresi yine ÜFnin merkezini, a parametresi ise x = c geçiş noktalarındaki eğimi belirleyen parametredir. 'a' parametresinin işaretine bağlı olarak bir sigma ÜF sağa açık veya sola açıktır. Böylece "çok büyük" veya ''çok eksi" gibi dilsel olarak tanımlanan kavramları karakterize etmek bu ÜF2ler ile mümkün olabilmektedir. Bu tür sigma fonksiyonları , yapay sinir ağlarının geçiş fonksiyonları olarak da yaygın bir biçimde kullanılmaktadır. Bu yüzden bir sinir ağını, bulanık girişimli sistem davranışına benzetmekte karşılaşılan ilk problem , kapalı bir ÜF fonksiyonunu sigma fonksiyonu boyunca nasıl sentezleyebileceğimizdir. Bu sorunu gidermenin basit iki yolu vardır: Birincisi, iki sigma ÜF fonksiyonunun bileşkesini almaktır. Diğeri de iki sigma fonksiyonunun mutlak farkını almaktır. Şekil 3.4’de bu yaklaşım resmedilmiştir.
S biçimli ÜF : ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ < ≤ < + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − − + ≤ < ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ≤ = x , 1 r x , l r x r 2 1 x l r l x 2 , 0 ) r ,l ; x ( S 2 2 r 2 r l 2 r l l , l x ; (l<r) Z biçimli ÜF : Z(x;l,r)=1- S(x;l,r) ;(l<r) π biçimli ÜF: π(x;a,c)=⎧⎩⎨SZ((xx;;cc,−ca+,ca),), x x≤>cc
iki taraflı π biçimli ÜF:
⎪ ⎪ ⎪ ⎩ ⎪⎪ ⎪ ⎨ ⎧ ≤ < < ≤ ≤ < < ≤ = π x d d x c c x b 1, b x a a x , 0 ), d , c ; x ( Z ), b , a ; x ( S , 0 ) d , c , b , a ; x ( _ İT
iki taraflı Gauss ÜF:
⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ≤ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ σ − − < < ≤ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ σ − − = σ σ x c , c x 2 1 exp c x c , 1 c , c x 2 1 exp ) , c , , c ; x ( Gauss _ İT 2 2 2 2 2 1 1 2 1 1 2 2 1 1 x
Bu bölümde sunulan ÜF fonksiyonları kullanıla gelen en popüler ÜF’lerdir. Diğer özel ÜF fonksiyonları gerekli olması halinde özel uygulamalar için oluşturulabilir .
İKİ BOYUTLU ÜYELİK FONKSİYONLARI
Bazen iki girişli üf kullanmak avantajlı olabilir. İki boyutlu bir ÜF elde etmenin en kolay ve doğal yolu, tek boyutlu bir ÜF’den silindirik genişletme ile iki boyutlu ÜF elde etmektir.
Tanım: Tek boyutlu bit bulanık kümenin silindirik genişletimi
A bulanık kümesi X nesnel uzayında tanımlı olsun. Bu kümenin XxY uzayında silindirik genişletimi c(A)bulanık kümesidir. ∫ μ = XxY A(x)/(x,y) ) A ( c
Şekil 3.5 Silindirik genişletme
İki boyutlu Üfler iki kategoride ele alınabilir: karma (composite) ve karma olmayan (noncomposite). Eğer iki boyutlu bir ÜF, analitik olarak tek boyutlu iki ÜF ile ifade edilebiliyorsa bu ÜF karmadır. Aksi halde karma değildir.
Örnek: Karma ve karma olmayan iki boyutlu ÜF
Bir A bulanık kümesi A=”(x,y) (3,4)’ün civarındadır” dilsel olarak ifade edilsin. Buna ilişkin ÜF de şöyle tanımlansın: ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − = μ 2 2 A (y 4) 2 3 x exp ) y , x (
bu ÜF karma bir ÜF’dir. Çünkü iki tek boyutlu gauss tipi ÜF’nin çarpımı biçiminde ifade edilebilir.
1) gauss(y;4, 2). gauss(x;3, = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − = μ 2 2 A 1 4 y exp 2 3 x exp ) y , x (
Eğer a bulanık kümesi aşağıda verilen ÜF ile karakterize edilmiş olsa idi, A kümesi karma olmaya bir küme olurdu. 5 , 2 A 4 y 3 x 1 1 ) y , x ( − − + = μ
Şekil 3.6’da iki farklı kartezyen çarpım sonucunda iki tek boyutlu yamuk ve çan ÜF’den elde edilmiş 4 adet iki boyutlu ÜF resmedilmiştir.
Şekil 3.6 İki tek boyutlu yamuk ve çan eğrisi ÜF’den min ve max işlemleri ile elde edilmiş iki boyutlu ÜFler
BULANIK BİRLEŞİM, KESİŞİM VE EVİRME üzerine detaylar
Geçen derste tanımlamış olduğumuz bulanık birleşim, kesişim ve evirme tanımları bu işlemlerin yapılabilmesi için tek yol değildir. Bu işlemler için literatürde tanımlanmış bir çok yol vardır. Bu kısımda bu yollar üzerinde tartışacağız.
Bulanık evirme operatörü: Bulanık evirme operatörü N: [0,1]→[0,1] eşlemesini yapan aşağıda belirtilen şartları sağlayan sürekli bir fonksiyondur.
N(0)=1 ve N(1)=0 (sınır koşulu)
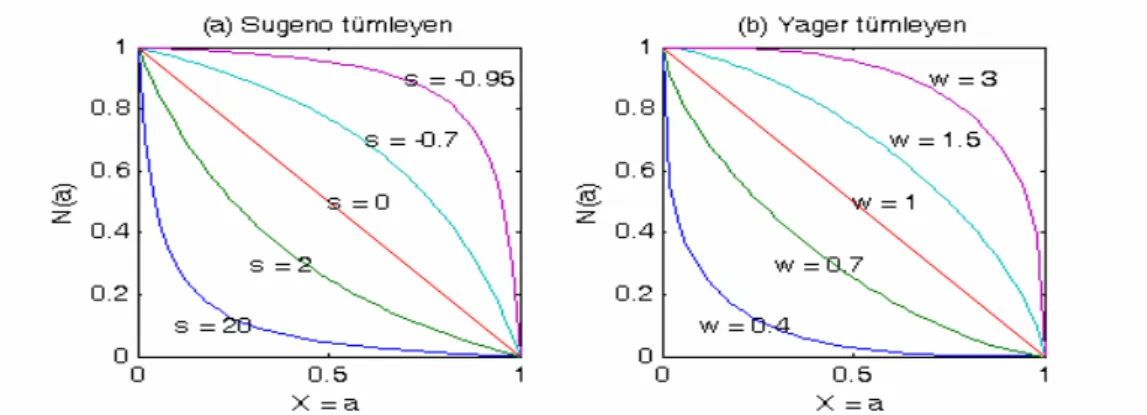
N(a) ≥ N(b) (a≤b için) (azalan eğilimlilik koşulu) N(N(a))=a (involution) (iki defa evrimle şartı) Sugeno opreratörü: s≥-1 + − = , sa 1 a 1 ) a ( N Yager opreratörü: N (a) (1 aw)1/w, 0 w = − w>
Bulanık Kesişim operatörleri: A ve B iki bulanık küme olmak üzere, bunların kesişimi
T: [0,1]x[0,1]→[0,1] fonksiyonu ile belirtilir. Sonuç ÜF iki ÜF’nin derecesi ile şöyle ifade edilir.
) x ( * ~ ) x ( )) x ( ), x ( ( T ) x ( A B A B B A = μ μ =μ μ μ ∩
Eşitliğin en sağındaki ifadenin ortasındaki simge T fonksiyonunun ikili operatörüdür. Bu tipten bulanık küme kesişimi T-norm olarak adlandırılır.
Bir T-norm operatörü aşağıdaki koşulları sağlamalıdır:
T(0,0)=0, T(a,1)= T(1,a)=a (sınır koşulu)
T(a,b) ≤ T(c,d) (a≤c ve b≤d için) (azalan eğilim koşulu) T(a,b)=T(b,a) (değişme koşulu) T(a,T(b,c)= T(T(a,b),c) (birleşme koşulu) En sık kullanılan T-norm operatörleri:
Minimum : Tmin(a,b)=min (a,b)=a∧b
Cebirsel çarpım : Tcç(a,b)=ab
Sınırlı çarpım : Tsç(a,b)=0∨(a+b-1)
Sert (Drastic) çarpım :
⎪⎩ ⎪ ⎨ ⎧ < = = = 1 b a, a , 0 1 , b 1 b , a Tdç
Şekil 3.8 Dört popüler T-norm operatör yüzeyi (üst satır) ve bu operatörlerle a=yamuk (x,3,8,12,17) ve b=yamuk(x,3,8,12,17) bulanık kümelerinin T-norm yüzeyleri (alt satır)
Bulanık Birleşim operatörleri: A ve B iki bulanık küme olmak üzere, bunların kesişimi
S: [0,1]x[0,1]→[0,1] fonksiyonu ile belirtilir. Sonuç ÜF iki ÜF’nin derecesi ile şöyle ifade edilir.
) x ( ~ ) x ( )) x ( ), x ( ( S ) x ( A B A B B A = μ μ =μ +μ μ ∪
Eşitliğin en sağındaki ifadenin ortasındaki simge S fonksiyonunun ikili operatörüdür. Bu tipten bulanık küme birleşimi T-conorm (S-norm) olarak adlandırılır.
Bir S-norm operatörü aşağıdaki koşulları sağlamalıdır:
S(1,1)=1, S(a,0)= S(0,a)=a (sınır koşulu)
S(a,b) ≤ S(c,d) (a≤c ve b≤d için) (azalan eğilim koşulu) S(a,b)=S(b,a) (değişme koşulu) S(a,S(b,c)= S(S(a,b),c) (birleşme koşulu) En sık kullanılan S-norm operatörleri:
Maximum : Smax(a,b)=max (a,b)=a∨b
Cebirsel toplam : Sct(a,b)=a+b-ab
Sınırlı toplam : Sst(a,b)=1∧(a+b) Sert (Drastic)toplam : ⎪⎩ ⎪ ⎨ ⎧ > = = = 0 , 1 0 , b 0 b , a Sdt b a, a
Şekil 3.8 Dört popüler S-norm operatör yüzeyi (üst satır) ve bu opretörlerle a=yamuk (x,3,8,12,17) ve b=yamuk(x,3,8,12,17) bulanık kümelerinin S-norm yüzeyleri (alt satır)