Kompleks mertebeli Salagean tipli harmonik yalınkat fonksiyonlar üzerine

KOMPLEKS MERTEBELİ SALAGEAN TİPLİ

HARMONİK YALINKAT FONKSİYONLAR

ÜZERİNE

GÜLBAHAR BAYKARA

YÜKSEK LİSANS TEZİ

(MATEMATİK ANABİLİM DALI)

DİYARBAKIR

HAZİRAN-2008

TEŞEKKÜR

Öğrencisi olduğum için kendimi ayrıcalıklı bulduğum, her konuda desteğini hep yanımda hisettiğim değerli danışman hocam,

Doç.Dr. H.Özlem GÜNEY’e

Yüksek Lisans Öğrenimim boyunca araştırmalarımda bana yardımcı olan sayın

Prof. Dr. Om P. AHUJA’ya

Tezin yazımı aşamasında hep yanımda olan, benden hiçbir yardımı esirgemeyen sevgili eşim Orhan BAYKARA’ya

Yaşamım boyunca benden esirgemedikleri sevgi, anlayış ve güvenle kendimi gerçekleştirmeme fırsat veren ve desteklerini her zaman hissettiğim sevgili anneme ve

babama

Son olarak bu çalışmayı 06-FF-80 nolu projeyle destekleyen Dicle

Üniversitesi Bilimsel Araştırma Projeleri Komisyonu - DÜBAP’ a katkılarından dolayı,

Sonsuz Teşekkürler…

AMAÇ

i

ÖZET

ii

ABSTRACT

iii

SEMBOLLER

iv

GİRİŞ

v

1. BÖLÜM : YALINKAT FONKSİYONLAR

1.1 Temel Tanım ve Teoremler 1

1.2 Yalınkat Fonksiyonların Bazı Alt Sınıfları 4

2. BÖLÜM : HARMONİK FONKSİYONLAR

2.1 Harmonik Fonksiyonlar 8

2.2 Bazı Temel Özellikler 9

2.3 Harmonik Yalınkat Fonksiyonlar 14

2.4 Harmonik Yıldızıl Fonksiyonlar 17

2.5 Harmonik Konveks Fonksiyonlar 19

2.6 Salagean Operatörü 21

3. BÖLÜM : SALAGEAN TİPLİ BAZI ÖZEL SINIFLAR

25

4. BÖLÜM: SALAGEAN TİPLİ HARMONİK YALINKAT

FONKSİYONLARIN

SINIFI

30 4.1UHmn

(

,k,t

)

, γ Sınıfının Katsayı Hesabı 31 4.2 U_Hm,n

(

γ,k,t

)

Sınıfının Extreme Noktaları 34 4.3 Umn

(

k t

)

H , , , γ Sınıfının Büyüme Teoremleri 35 4.4 U_Hm,n

(

γ,k,t

)

Sınıfının Kapalılık Özellikleri 37

KAYNAKLAR

ÖZGEÇMİŞ

AMAÇ

Bu çalışmanın amacı, günümüzde hâlâ açık bir problem olarak kalan harmonik yalınkat fonksiyonların SH sınıfının yeni bir alt sınıfını tanımlayarak bu alt sınıf için

gerekli olan bazı önemli özellikleri ispatlamaktır.

Diğer bir amacımız ise, özellikle analitik ve harmonik fonksiyonlar arasında bir karşılaştırma yapmaktır.

ÖZET

Bu çalışma dört bölümden oluşmaktadır.

Birinci bölümde; Çalışmamızın temel taşı olan yalınkat fonksiyonlarla

ilgili birtakım önemli tanımlar, teoremler ve bunların sonuçları verilmektedir.

İkinci bölümde; Harmonik fonksiyonların tanımı ve ilgili önemli

teoremler verilerek üçüncü bölüm için bir taban oluşturulmaktadır.

Üçüncü bölümde; Gereksiz tekrarlardan kaçınmak ve konunun

bütünlüğünü bozmamak amacıyla, ispatlar için doğrudan ulaşılabilecek kaynak gösterilmesi yoluyla konumuz ile ilgili daha önce yapılmış olan çalışmalara yer verilmektedir.

Çalışmamızın esas kısmını oluşturan dördüncü bölümde ise, Kompleks mertebeli Salagean tipli harmonik yalınkat fonksiyonların yeni bir sınıfı tanımlanmaktadır. Ayrıca bu sınıf ile ilgili Katsayı tahmini, ekstreme noktaları… verilmektedir.

ABSTRACT

This work consist of four chapters.

İn the first chapter, some important definitions, theorems, these associated with univalent functions which consist of main part of our study are given.

İn the second chapter, by giving the definition of harmonic functions and theorems connected them, a bas efor third chapter is formed.

İn the third chapter, by the aim to avoid unnecesarry repeats and not to damage the completeness of topics, to be straighford word obtained references are prefered.

İn the fourd chapter, which consistof the main part of our study, a new subclasses of salagean type harmonic univalent functions is defined. Furthermore, coefficient estimates, extreme points… are calculated.

SEMBOLLER

N : Doğal Sayılar Kümesi 0

N : N∪

{ }

0

R : Gerçel Sayılar Kümesi

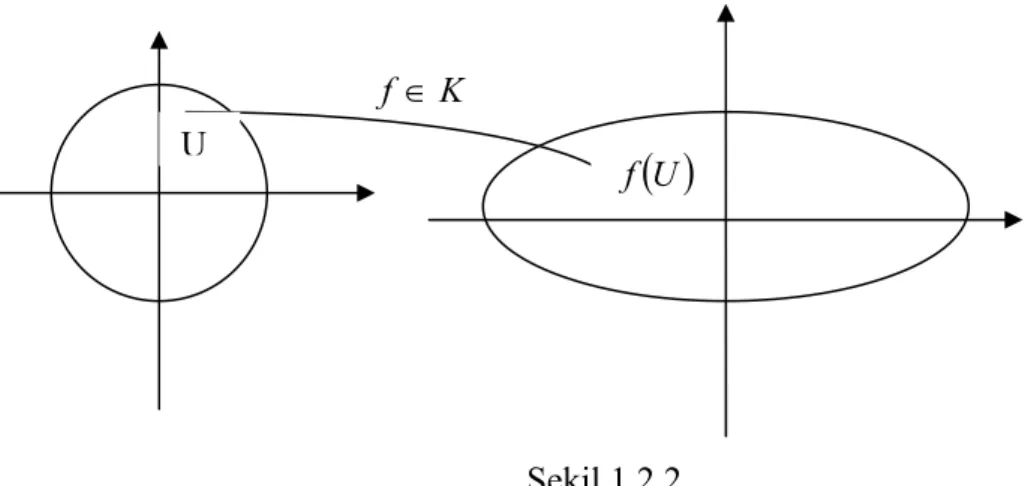
C : Karmaşık Sayılar Kümesi U : Birim disk

( )

U

f : U nun f altındaki görüntüsü

z

f : f nin z ye göre türevi g : g nin eşleniği f Im : f nin imajiner kısmı f Re : f nin reel kısmı U ∂ : U nun sınırı

S : Normalleştirilmiş Yalınkat Fonksiyonların Sınıfı ∗

S : Yıldızıl Fonksiyonlar Sınıfı H

K : Harmonik Konveks Fonksiyonlar ∗

H

S : Harmonik Yıldızıl Fonksiyonlar g

f ≺ : f fonksiyonu g Fonksiyonuna Subordine

k UCV− :k−düzgün konveks fonksiyonların sınıfı k−ST : k−yıldızıl fonksiyonların sınıfı

( )

k UCV− α : α mertebeli k−düzgün konveks fonksiyonların sınıfı

( )

GİRİŞ

Karmaşık Analizin, amaçlarından biri fonksiyonun analitik özellikleri ile analitik bir fonksiyonun görüntüsünün geometrik özellikleri arasındaki bağıntıyı anlatmak olan, Geometrik Fonksiyonlar Kuramıdır. Daha sonra ise diferansiyel geometriciler tarafından keşfedilen Harmonik Fonksiyonlar üzerine çalışmaktır. Harmonik fonksiyon demek, reel ve imajiner kısımlarının eşlenik olması gerekmeyen karmaşık değerli fonksiyonlardır. Harmonik fonksiyonlar konformal dönüşümlerin genelleştirilmişidir ve harmonik fonksiyonlar karmaşık analizde ilk olarak 1980 yılında dikkat çekmiştir.

Harmonik Dönüşümler teorisinin gelişimi iki aşamadan oluşmaktadır. İlk olarak 1920 yılında minimal yüzeylerin kutup noktaları için Diferansiyel Geometriciler tarafından çalışılmış ve Gauss eğrilik gibi minimal yüzeylerin özellikleri harmonik dönüşümler de etkili olmuştur. Tibor Rado, Lipmon Bers, Erhard Heinz, Johannes

Nitsche ve diğerleri harmonik dönüşümler ile minimal yüzeyler arasındaki bağlantıya

1960 yılndan önce katkıda bulunmuştur.

Son zamanlarda Kompleks Analizciler Konformal dönüşümlerin genelleştirilmişi olarak bilinen harmonik dönüşümlerle ilgilenmişlerdir. İlk olarak 1984 yılında James

Clunie ve Terry Sheil-Small ilgilenmişlerdir. Clunie ve Sheil-Small genişletilmiş

tahminlerin kesin sonuçlarını bulmamalarına rağmen klasik olan büyüme, bükülme, katsayı tahminleri geliştirmişlerdir. Ayrıca klasik Koebe fonksiyonunun extreme değerleriyle oynayarak Harmonik Koebe fonksiyonunu elde ettiler. Bu sonuçlar bazı özel geometrik özelliklerle harmonik dönüşümler için doğrulanmıştır. Böylece Clunie ve

Sheil-Small diğer Kompleks analizcilerin dikkatlerini çekmiştir ve harmonik dönüşüm

araştırmalarında etkili olmuştur.

Teorinin diğer bir yönü Riemann dönüşüm teoremi için uygun araştırmalar yapmaktır. Buradaki amaç kısmi türevli eşitlikler ve hemen hemen konformal dönüşümlerin gelişimine katkıda bulunmaktır. 1980 yılında Hengartner ve Glenn

Schober bunlarla ilgili makaleler yazmışlardır. Hemen hemen konformal dönüşümler

hakkındaki standart sonuçlar, özellikle Beltrami denkleminin bir çözümü olan hemen hemen konformal homeomorfizması için Riemann teoreminin genişletilmişini öne sürmüşlerdir.

1.BÖLÜM

YALINKAT FONKSİYONLAR

Bu bölümde yalınkat fonksiyonlar ile ilgili birtakım önemli tanımlar, teoremler ve bunların sonuçları verilmektedir.

1.1 Temel Tanım ve Teoremler

Karmaşık düzlemde bir bölge, açık bağlantılı bir kümedir. Herhangi bir D bölgesinde ve en fazla bir kutup noktası hariç tüm düzlemde analitik bir f fonksiyonu

için, z₁, z₂∈D olmak üzere,

( )

1

( )

2 2

1 z f z f z

z ≠ ⇒ ≠

önermesi doğru oluyorsa, f fonksiyonuna D bölgesinde yalınkattır denir.D

bölgesindeki yalınkatlık doğal olarak D bölgesinin her alt bölgesinde de sağlanır. Bir

D bölgesinde tanımlı herhangi bir f fonksiyonu , bir z₀∈D noktasının en az bir komşuluğunda yalınkat ise bu f fonksiyonuna z₀∈D noktasında yerel yalınkat

fonksiyon denir. Bir bölgede yerel yalınkat olan bir analitik fonksiyon yalınkat

olmayabilir.

Analitik yalınkat bir fonksiyon eğriler arasındaki açıyı koruduğundan dolayı

konformal dönüşüm olarak bilinmektedir.

Riemann dönüşüm teoremi her basit bağlantılı D⊂C, D≠C ve ζ ∈D keyfi noktası için f

( )

ζ =0 ve f′

( )

ζ >0 koşullarıyla D ’yi birim disk olan U ’ya dönüştüren bir tek konformal dönüşümün olduğunu ileri sürer. Riemann Dönüşüm teoremine göre, karmaşık düzlemde herhangi basit bağlantılı bir bölge yerine açık birim diski alabildiğimizden, bu çalışma boyunca bölge olarak U =

{

z: z <1

}

birim diskini gözönüne alacağız.

{

: <1

}

= z z

U birim diskinde analitik, yalınkat ve f

( )

0 = f′

( )

0 −1=0

normalize koşullarını sağlayan fonksiyonların sınıfı S ile gösterilir. Her f ∈ S

fonksiyonu,

( )

n n n z a z z a z z f

∑

∞ = + = + + = 2 2 2 ...

şeklinde bir Taylor serisi ile ifade edilebilir.

Bununla beraber, bir f ∈ fonksiyonu ile birlikte temel dönüşümler olarak S

bilinen eşlenik, dönme, genişleme, disk otomorfizmi, erim, atılmış değer ve karekök dönüşümleri S sınıfındadır.

S sınıfındaki fonksiyonların en öncelikli örneği olan, ... 3 2 2 3 1 + + + =

∑

∞ = z z z nz n n

şeklinde Taylor serisi açılımına sahip

( )

2

(

) (

₍

2

₎

₂

)

2

₍

₎

₂ 1 1 4 1 1 1 1 1 4 1 z z z z z z z z k − = − − − + = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + =

Koebe fonksiyonu, U =

{

z: z <1

}

birim diskini , − ∞ dan −1₄ e kadar kesik doğru hariç tüm karmaşık düzlemin içine konform olarak dönüştürür (Şekil 1.1.1) ♦ z w k Şekil 1.1.1

Rezidüsü 1 olan, sonsuz basit bir kutup hariç, U bölgesinin dışı olan

{

: >1

}

=

Δ z z bölgesinde analitik ve yalınkat olan

U 0 −14

( )

k U 1 0 1

( )

_∑

∞ = − − − _{+ + = + +} + + = 1 0 2 2 1 1 0 ... n n nz b b z z b z b b z z g

fonksiyonlarının sınıfı ∑ ile gösterilir. Ayrıca g

( )

z ≠0 fonksiyonlarının altsınıfları

0

∑ şeklinde gösterilir.

Teorem 1.1.1 ( Alan Teoremi ):

∑ sınıfından alınan her g fonksiyonu için ,

∑

∞ = ≤ 1 2 1 n n b n

eşitsizliği sağlanır. Eşitlik, g fonksiyonunun, b₀∈C ve α ∈ℜ olmak üzere,

( )

2 1 0+ − + = z b e z z g iα

şeklinde seçilmesi durumunda gerçekleşir [13]. ♦ “S sınıfındaki her f fonksiyonu n=2,3,4,... için a_n ≤n eşitsizliğini sağlar” ifadesi Bieberbach kestirimi olarak bilinmektedir. 1916 yılında Bieberbarch

tarafından ortaya atılan ve uzun yıllar kestirim olarak kalan ve kısmen ispatlanan bu kestirimin tam ispatı 1984 yılında Louis de Branges tarafından yapılmıştır.

Teorem 1.1.2 ( Bieberbach Teoremi ):

S sınıfından alınan her

( )

_∑

∞ = + = 2 n n nz a z z f fonksiyonu için 2 2 ≤ a

eşitsizliği sağlanır. Eşitliğin sağlanması için f fonksiyonunun

( )

( ) (

₎

₂ 1 e z z z e k e z f i i i α α α − + − − = =

şeklinde Koebe fonksiyonunun bir dönmesi olması gerekli ve yeterlidir [13]. ♦ Bieberbach’a ait a₂ ≤2 eşitsizliği, konform dönüşümlerin geometrik teorisinde daha ileri uygulamalara sahiptir. En önemli sonuç, f ∈ iken S f ′

( )

z için kesin üst ve alt sınırları veren Koebe Bükülme Teoremidir. Bükülme Terimi, geometrik olarak,

( )

z

f ′ nin f dönüşümü altında sonsuz küçük büyütme çarpanı ya da f ′

( )

z 2

Jacobien’inin, alanın sonsuz küçük büyütme çarpanı olması gerçeğinden çıkmıştır.

Teorem 1.1.3 ( Bükülme Teoremi ):

Her bir f ∈ ve S z = r <1 için,

(

)

3

( )

(

)

3 1 1 1 1 r r z f r r − + ≤ ′ ≤ + −

eşitsizliği sağlanır. Eşitlik durumu Koebe fonksiyonu için vardır [13]. ♦

Teorem 1.1.4 ( Büyüme Teoremi ):

Her bir f ∈ ve S z = r <1 için,

(

)

2

( )

(

)

2 1 1 r r z f r r − ≤ ≤ + eşitsizliği sağlanır [13]. ♦

Aşağıdaki teoremle, Bükülme ve Büyüme Teoremlerinin birleşmesiyle elde edilen eşitsizlik verilmektedir.

Teorem 1.1.5:

S sınıfındaki her bir f fonksiyonu için z = r <1 olmak üzere

( )

( )

r r z f z f z r r − + ≤ ′ ≤ + − 1 1 1 1

eşitsizliği doğrudur. Bu eşitsizlik kesindir. Eşitlik hali

( )

(

_{1 z}

)

2 z z f − = fonksiyonu için sağlanır [13]. ♦

1.2 Yalınkat Fonksiyonların Bazı Alt Sınıfları

Bu kesimde, yalınkat fonksiyonların bazı özel alt sınıfları tanıtılmakta ve bu alt sınıfların özelliklerinden söz edilmektedir.

Tanım 1.2.1 ( Yıldızıl Fonksiyon):

0

w , düzlemdeki bir D kümesinden alınan bir iç nokta olsun. w noktasını her _o D

w∈ noktasına birleştiren doğru parçası tamamen D içinde kalıyorsa , D kümesine

0

w ∈ noktasına göre yıldızıl küme denir. Başka bir deyişle; D kümesinin her D

noktası w noktasından görülebilir ise D kümesine yıldızıl küme olur. ₀

Bir f fonksiyonu U birim diskini w noktasına göre yıldızıl bir bölge üzerine ₀

dönüştürüyorsa f fonksiyonuna w noktasına göre yıldızıl fonksiyon denir. Özel ₀

olarak, 0w₀ = alınırsa f fonksiyonuna yıldızıl fonksiyon denir. Yıldızıl fonksiyonların sınıfı S ile gösterilir. ∗

Şekil 1.2.1

Tanım 1.2.2 (Konveks Fonksiyon):

Düzlemdeki bir D kümesinin içinden alınan w₁ ve w₂ noktalarını birleştiren doğru parçası tamamen D kümesinde kalıyorsa, D kümesine konveks’tir denir. Konveks bir kümeyi konveks bir kümeye dönüştüren fonksiyona da konveks

fonksiyon denir. Konveks fonksiyonlarının sınıfı

K

ile gösterilir.

∗ ∈ S f

( )

U f U

Şekil 1.2.2 Konveks ve Yıldızıl fonksiyon sınıfları için

S S K ⊂ ∗ ⊂ şeklinde kapsama bağıntısı yazılabilir.

Teorem 1.2.1:

f fonksiyonu UR :

{

z: z ≤R

}

kapalı diskinde analitik ve yalınkat olsun. Bu

durumda f fonksiyonu UR diskini konveks bir bölgeye dönüştürmesi için gerekli ve

yeterli koşul C_R :

{

z: z =R

}

üzerindeki her z için Re 1

_{( )}

( )

_⎥≥0 ⎦ ⎤ ⎢ ⎣ ⎡ ′ ′′ + z f z f z olmasıdır [1].

Bununla birlikte f

( )

0 =0 kabul edelim. Bu durumda f fonksiyonunun UR

bölgesini w=0 noktasına göre yıldızıl bir bölgeye dönüştürmesi için gerekli ve yeterli koşul C_R :

{

z: z =R

}

üzerindeki her z için Re

_{( )}

( )

_⎥≥0

⎦ ⎤ ⎢ ⎣ ⎡ ′ z f z f z olmasıdır [1]. Konveks ve yıldızıl fonksiyonlar arasında çok kullanışlı olan bir bağıntı ilk olarak J.W Alexander tarafından

∗ ∈ ′ ⇔ ∈K zf S f şeklinde verilmiştir [13]. ♦

Yukarıdaki tanımlara örnek olarak

( )

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + = z z z f 1 1

log fonksiyonu konvekstir, ancak

( )

(

_{1 z}

)

2 z z k − = fonksiyonu yıldızıl olup konveks değildir.

( )

U f

K f ∈ U

Tanım 1.2.3 (Pozitif Gerçel Kısımlı Fonksiyonlar) :

U bölgesindeki tüm z noktaları için

( )

(

)

0

Re f z >

koşulunu sağlayan ve analitik olan

( )

_∑

∞ = + = + + + + + = 1 2 2 1 ... ... 1 1 n n n n nz p z p z p z p z f

şeklindeki fonksiyonların oluşturduğu kümeye pozitif gerçel kısımlı fonksiyonlar sınıfı denir ve bu sınıf ℘ ile gösterilir. Örnek olarak

( )

_∑

∞ = + = + + + = − + = 1 2 0 1 2 2 ... 1 2 1 1 n n z z z z z z L

şeklindeki Mobius fonksiyonu verilebilir. Gerçekten L fonksiyonu ₀ U birim diskini sağ yarı düzlem içine dönüştürür.

Şekil 1.2.3

U bölgesinde analitik olan ve f

( )

0 = f′

( )

0 =1 normalize koşullarını sağlayan bir f fonksiyonu için,

( )

( )

z P f z f z S f ∈ ∗ ⇔ ′ ∈ ve

( )

( )

z P f z f z K f ∈ ′ ′′ + ⇔ ∈ 1 önermeleri doğrudur [13]. x

( )

z z z f w − + = = 1 1 y u v

k UCV− sınıfını, Kanas ve Wisniowska [15] geometrik tanımı ve konik bölge ile arasındaki ilişkiyi göz önünde bulundurarak çalışmışlardır. k ST− sınıfı da, [16] de araştırılmıştır. Gerçekten bu sınıf konveks ve yıldızıl fonksiyonların sınıfları arasında iyi bilinen Alexander Teoremi ile ilişkilidir. Özellikle k =1 alındığında, C ve S∗ _sırasıyla, U da konveks ve yıldızıl fonksiyonların sınıflarını göstermek üzere,

0−UCV ≡C ve 0₋ST _≡S∗

eşitlikleri yazılır.

Ayrıca, U birim diskinde 0≤ <α 1 için α mertebeli k−düzgün konveks ve α mertebeli k−yıldızıl fonksiyonlardan oluşan S’ nin iki alt sınıfı da sırasıyla

( )

k UCV− α ve k ST−

( )

α ile gösterilir. Bu sınıflar,

ve

şeklinde tanımlıdırlar. . Özel olarak α =0 alındığında,

k UC−

( )

0 = −k UC ve k ST−

( )

0 = −k ST

eşitlikleri yazılır.

Konumuzla çok yakından ilgili olan Subordinasyon ilkesi karmaşık analizde önemli rol oynamaktadır. Son yıllarda karmaşık analiz ile ilgilenen bir çok matematikçi, subordinasyon konusunda çalışmalar yapmıştır. Subordinasyon kavramı, ilk olarak E. Lindelöf [2] tarafından ortaya atılmış, ancak temel bağıntılar J.E. Littlewood [7] ve W.W. Rogosinski [20] tarafından bulunmuştur.

( )

: 1 "( ) "( )

(

: 0 ,0 1

)

'( ) '( ) zf z zf z k UCV f S k z U k f z f z α ⎧ ⎛ ⎞ α α ⎫ − =_⎨ ∈ ℜ +_{⎜ ⎟}> + ∈ ≤ < ∞ ≤ < _⎬ ⎝ ⎠ ⎩ ⎭

( )

: '( ) '( ) 1

(

: 0 ,0 1

)

( ) ( ) zf z zf z k ST f S k z U k f z f z α ⎧ ⎛ ⎞ α α ⎫ − =_⎨ ∈ ℜ_{⎜ ⎟}> − + ∈ ≤ < ∞ ≤ < _⎬ ⎝ ⎠ ⎩ ⎭

Tanım 1.2.4 ( Subordinasyon İlkesi ):

f ve g fonksiyonları f

( )

0 = g

( )

0 olacak şekilde U birim diskinde analitik olsunlar. U bölgesinde

( )

z g

(

w

( )

z

)

f = ve

w

( )

z < z

koşullarını sağlayan analitik w fonksiyonu varsa f fonksiyonu g fonksiyonuna subordinedir denir ve f ≺ şeklinde gösterilir. g

Örneğin, n bir tamsayı olmak üzere U birim diskinde zn _{≺ şeklindedir.} z

( )

w

g nin yalınkat olması gerekmez. U birim diskinde _z2n _{≺ z}2 _{şeklindedir fakat z}2n+1_, 2

2.BÖLÜM

HARMONİK FONKSİYONLAR

Bu bölümde, çalışmamızın esas konusu olan harmonik fonksiyonların tanımı ve ilgili önemli teoremler verilerek üçüncü bölüm için bir taban oluşturulacaktır.

2.1 Harmonik Fonksiyonlar

D karmaşık düzlemde bir bölge ve u:D→IR, ikinci dereceden sürekli kısmi türevlenebilir bir fonksiyon olsun. Eğer ∀z∈D için u fonksiyonu ,

0 2 2 2 2 = ∂ ∂ + ∂ ∂ = ∇ y u x u u

Laplace’s denklemini sağlarsa u fonksiyonuna D ’de harmoniktir denir.

xy - düzlemdeki bir D bölgesinden uv- düzlemindeki bir Ω bölgesine tanımlı

u ve v fonksiyonları harmonik iseler z = x+iy ve w=u+iv olmak üzere

( ) ( ) ( )

z u z iv z f

w= = + birebir dönüşümüne harmonik dönüşüm denir. Böylece karmaşık değerli harmonik bir fonksiyonun D⊂C bölgesinin harmonik dönüşümü olması için gerekli ve yeterli koşul fonksiyonun D de yalınkat olmasıdır. Bu çalışma boyunca harmonik dönüşüm denildiğinde yalınkat karmaşık değerli harmonik fonksiyon anlaşılacaktır.

D , C de bir bölge olsun ve f =u+iv kompleks değerli fonksiyonunu alalım. Her bir z∈ noktasında D f ′

( )

z türevi varsa f =u+iv fonksiyonuna D bölgesinde

analitik denildiğini biliyoruz. Bunun bir sonucu olarak

y v x u ∂ ∂ = ∂ ∂ , x v y u ∂ ∂ − = ∂ ∂

Cauchy-Riemann denklemlerini yazmak mümkündür. Aksine eğer f , birinci kısmi

türevlere sahip ve Cauchy-Riemann denklemlerini sağlarsa f , D de analitiktir [10].

Cauchy-Riemann denklemlerinden, her analitik fonksiyonun harmonik olduğu söylenebilir. Cauchy-Riemann denklemlerini sağlayan

( )

u,v fonksiyonlarının bir ikilisine bir eşlenik ikili denir ve v fonksiyonuna , u fonksiyonunun harmonik

Harmonik dönüşümler konformal dönüşümlerin genelleştirilmiş durumudur. Harmonik dönüşümlerin sınırdaki davranışı konformal dönüşümlerinkinden daha zordur. Bundan dolayı konformal dönüşümlerin klasik teoremi bizi harmonik dönüşümlere götürecektir. Örnek 2.1.1: β α β α + ≠ = z z,

w lineer dönüşümü, bir harmonik dönüşümdür, fakat konformal olmayabilir.

iv u

f = + fonksiyonunun Jacobian matrisi

( )

y x x y y y x x f _{u v} v u vu v u z J = = −

şeklinde tanımlanır. Eğer f fonksiyonu analitik ise f fonksiyonunun Jacobiani

( )

z

J_f =

( ) ( )

u_x 2 + v_x 2 = f′

( )

z 2

şeklinde olur. Analitik olan f fonksiyonları için J_f

( )

z ≠0 sonucunun doğru olması için gerekli ve yeterli koşul f fonksiyonunun , z noktasında yerel olarak yalınkat

olmasıdır. 1936 da, Hans Lewy bu ispatın harmonik fonksiyonlar içinde doğru olduğunu göstermiştir. Lewy teoremine göre, f fonksiyonunun analitik olduğu D

bölgesi boyunca harmonik fonksiyon ya J_f

( )

z >0 ile yön koruyan yada J_f

( )

z <0 ile

yön değiştiren olur. Eğer f fonksiyonu yön koruyan ise f fonksiyonu yön değiştiren olur. Özellikle, konformal dönüşümler yön koruyandırlar.

2.2 Bazı Temel Özellikler

Karmaşık analizde, z= x+iyolmak üzere,

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂ = ∂ ∂ y i x z 2 1 ve _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ = ∂ ∂ y i x z 2 1

diferansiyel operatörleri sıkça kullanılır.

z ∂ ∂ ve z ∂ ∂

operatörleri lineerdir ve bunlar diferansiyel operatörlerinin genel özelliklerine sahiptirler. Örneğin; çarpım ve bölüm kurallarını sağlarlar ve

( )

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ + ∂ ∂ = ∂ ∂ − z g f z f g g g f z z f g z g f fg z 2 , şeklindedir ve z ∂ ∂

içinde benzer eşitlikler yazılabilir. Karmaşık değerli f fonksiyonu için , =0

∂ ∂

z f

eşitliği, Cauchy-Riemann denklemlerini yazmanın başka bir yoludur. Diğer taraftan basit bir hesaplama ile f fonksiyonun Laplacian’ı

z z f f ∂ ∂ ∂ = Δ 4 2

şeklinde yazılabilir. Böylece ikinci basamaktan sürekli kısmi türevlenebilir

f fonksiyonları için, f harmoniktir ⇔ z f ∂ ∂ analitiktir

önermesinin doğru olduğu açıktır. Eğer f fonksiyonu analitik ise f

( )

z z f _{= ′} ∂ ∂ olur. Bununla birlikte = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ − z f z f ∂ ∂

eşitliği iki türevi birbirine bağlar. Yine

dy y f dx x f df ∂ ∂ + ∂ ∂ = diferansiyeli, z d z f dz z f df ∂ ∂ + ∂ ∂ =

olarak yazılabilir, bununla beraber

z f f_z ∂ ∂ = ve z f f_z ∂ ∂ =

gösterimini kullanmak daha uygun ve kullanışlı olur. Bileşke fonksiyonların türevleri için zincir kuralını da aşağıdaki gibi yazabiliriz. Eğer w= f

( )

z ve z= g

( )

ζ şeklinde ise, h= f g olmak üzere w=h

( )

ζ şeklinde olur.

ζ ζ ζ ζ d g d g dz ∂ ∂ + ∂ ∂ = ve ζ ζ ζ ζ ζ ζ ζ ζ d g d g d g d g z d ∂ ∂ + ∂ ∂ = ∂ ∂ + ∂ ∂ = yazılıp gerekli düzenlemeler yapılırsa,

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ∂ ∂ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∂ ∂ + ∂ ∂ ∂ ∂ = ζ ζ ζ ζ ζ ζ ζ ζ d g d g z f d g d g z f dh

elde edilir. Böylece

ζ ζ ζ ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ g z f g z f h ve ζ ζ ζ ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ = ∂ ∂ g z f g z f h bulunur. iv u f = + fonksiyonu için f_z =

(

f_x−if_y

)

2 1 ; f_z =

(

f_x+if_y

)

2 1 eşitlikleri göz önüne alındığında f ’in Jacobianı

2 2 z z f f f J = −

şeklinde de ifade edilebilir. Sonuç olarak , f fonksiyonu f_z > f_z iken f yerel yalınkat ile yön koruyan ve f_z < f_z iken yalınkat ve yön değiştirendir. J_f

( )

z >0 iken f_z

( )

z ≠0 olur. w= f

( )

z yön koruyan dönüşümleri için

(

fz − f_z

)

dz ≤ dw ≤

(

fz + f_z

)

dz

olduğu görülür. Bu kesin eşitsizlikler, büyük ve küçük eksenlerin oranı olan

z z z z f f f f f D − + =

ile f in sonsuz bir çemberi sonsuz bir elipse dönüştürdüğü geometrik yoruma sahiptirler. D_f =D_f

( )

z , z noktasındaki f ’ in genişletilmişi olarak adlandırılır.

( )

<∞ ≤D_f z

1 olduğu da açıktır. K , 1≤ K <∞ şeklinde bir sabit olmak üzere, verilen bölge boyuncaD_f

( )

z ≤ K ise yön koruyan f homeomorfizmasına

hemen-hemen konformal yada K-hemen-hemen konformal denir. Hemen hemen konformal fonksiyonlar basit konformal fonksiyonlardır.

z z

f _f

f

=

μ oranı f ’in karmaşık genişletilmişi olarak adlandırılmaktadır. Böylece, f yön koruyan ise 0≤ μ_f <1 olur. D_f

( )

z ≤ K koşulunun sağlanması için gerekli ve yeterli koşul μ_f ≤

(

K−1

)

₍

_K+1

₎

eşitsizliğin sağlanmasıdır. Bu da gösterir ki, yön koruyan bir homeomorfizmin hemen hemen konformal olması için gerekli ve yeterli koşul μ_f kompleks genişleme verilen bölgede 1 den küçük sayılar için sınırlandırılmalıdır yani ; μ_f ≤ k <1 şeklinde olmalıdır. f dönüşümünün konformal olması için gerekli ve yeterli koşul 0μ_f = olmasıdır.

Harmonik fonksiyonlar teorisinde, ikinci karmaşık genişleme olarak bilinen

z z

f _f

f

v = eşitliği, birinci kompleks genişleme olan μ_f den daha uygundur. v_f = μ_f olduğundan dolayı , f in hemen hemen konformal olması için gerekli ve yeterli koşulun v_f ≤ k <1 olduğu da açıktır.

Şimdi f , bir D⊂C bölgesinde sürekli ikinci kısmi türeve sahip karmaşık değerli bir fonksiyon olsun. f fonksiyonun J_f

( )

z >0 ile D bölgesinde yerel

yalınkat olduğunu kabul edelim.

z z

f _f

f v

w= = olsun. Bu durumda D bölgesinde

( )

z <1 w olur. z ye göre _z z wf f = eşitliğinin diferansiyeli z z z z z z f w f w f = + olarak bulunur.

Eğer f fonksiyonu D bölgesinde harmonik ise, f_zz = Δf

4 1

olur. Böylece w

analitik olmak üzere, D bölgesinde w_z =0 olduğu bulunur. Tersine, eğer w analitik ise, o zaman f_zz = f_zzw olur. Fakat w

( )

z <1 olduğundan, bu f_zz =0 ifadesini sağlar ve f harmonik olur. Böylece f fonksiyonun harmonik olması için gerekli ve yeterli koşul w nin analitik olmasıdır.

Aşağıdaki tabloda şu ana kadar yazdığımız analitik fonksiyonlar ile harmonik fonksiyonlar arasındaki kıyaslama verilmiştir.

ANALİTİK FONKSİYONLAR HARMONİK FONKSİYONLAR

Harmoniktir Analitik olmayabilir

Birleşimleri altında korunurlar Birleşimleri altında korunmazlar

( )

D

A cebirdir H

( )

D cebir değildir

f fonksiyonu analitik ise _{f yada} 2 1

−

f analitiktir

f fonksiyonu harmonik ise _f 2

yada _{f harmonik olması gerekmez} −1

Reel ve imajiner kısımları eşleniktir Reel ve imajiner kısımları eşlenik olması gerekmez

( )

z ≠0

J_f jacobian ile yön

koruyandır

( )

z > 0

Jf ise yön koruyan , Jf

( )

z < 0 ise yön

değiştirendir

2.3 Harmonik Yalınkat Fonksiyonlar

Bu kesimde, kısmen analitik yalınkat fonksiyonların genelleştirilmiş durumu olarak da düşünülebilen harmonik yalınkat fonksiyonlar verilmektedir.

Tanım 2.3.1: Harmonik Yalınkat Fonksiyon

Basit bağlantılı bir D⊂C bölgesinde, karmaşık değerli f harmonik

fonksiyonu, h ve g fonksiyonları D bölgesinde analitik olmak üzere f =h+g gösterimine sahiptir. Bu gösterim tektir. Gerçekten, f harmonik ise f_z nin analitik olduğunu biliyoruz. h, D bölgesinde analitik olmak üzere h′= f_z olsun. Yine

g f

g = − olsun ve h’ın tanımıyla D ’de g_z = f_z −h_z =0 olduğunu varsayalım. Böylece g , D ’de analitiktir. Gösterimin tekliği hem analitik hem de anti analitik olan fonksiyonun sabit olması gerçeğine bağlıdır ( Burada anti analitik, analitik bir fonksiyonun eşleniği anlamındadır ). Eğer f gerçel değerli ise 2h, f ’in analitik

tamamlayıcısı olmak üzere gösterim, imajiner bir ek sabite kadar,

{ }

h h

h

f = + =Re 2 ’a indirgenir.

U birim diskindeki f harmonik dönüşümü için g

( )

0 =0 olacak şekilde ek sabit seçmek uygundur. Bu durumda f =h+g gösterimi tektir ve f ’in kanonik

gösterimi olarak adlandırılır.

D bölgesinde h ve g analitik olmak üzere f fonksiyonunu

( ) ( ) ( )

z h z g z

f = +

şeklinde yazabiliriz. f

( ) ( ) ( )

z =h z +g z fonksiyonu D bölgesinde yalınkat ve yön koruyan olması için gerekli ve yeterli koşul h′

( )

z > g′

( )

z , z∈ koşulunun D

sağlanmasıdır. U’da analitik

( )

_∑

∞ = + = 2 n n nz a z z h ve

( )

∑

∞ = = 1 n n nz b z g (1)

fonksiyonları için U ’da yön koruyan harmonik yalınkat f

( ) ( ) ( )

z =h z +g z

fonksiyonları ile ilgili ilk çalışma Clunie ve Sheil-Small [6] tarafından yapılmıştır.

U’da analitik h ve g fonksiyonları (1) ifadesindeki gibi verilmek üzere, f =h+g şeklindeki yön koruyan harmonik yalınkat fonksiyonların sınıfı S_H ile gösterilir.

g′

( )

0 =0 şartını sağlayan f ∈S_H fonksiyonlarının sınıfı da 0 H S ile gösterilir ve H H S S0 ⊂ şeklinde yazılabilir.

S sınıfına ait fonksiyonların bir

{ }

f dizisi bir fonksiyona düzgün yakınsak _n

ise bu fonksiyon ya S sınıfına ait yada sabit olmalıdır. Fakat bu durum S sınıfı için _H

geçerli değildir. Örneğin; genel terimi

( )

z n n z z f_n 1 + + =

olan S sınıfına ait fonksiyonlardan oluşan _H

{ }

f dizisi için _n

( )

z z z

f_n

n→∞ = +

lim

limit fonksiyonu S sınıfına ait değildir. _H

F, D bölgesinde sürekli fonksiyonların bir ailesi olsun. F her bir dizisi, D ’nin kompakt alt kümelerinde düzgün yakınsak bir alt diziye sahipse F ailesine normaldir denir.

F , normal bir aile ve ϕ, U’dan U'ya analitik bir fonksiyon olsun. Eğer her

F

f ∈ için f F fonksiyonlarının oluşturduğu aile normal ise, f ’e normal fonksiyon

denir.

H

S sınıfı normaldir ancak kompakt değildir. 0

H

S sınıfı normal ve kompakttır.

Analitik yalınkat fonksiyonların S sınıfı üzerindeki bir çok problemde Koebe fonksiyonu extremal fonksiyon olarak önemli rol oynamaktadır. Analitik yalınkat fonksiyonlar için tanımlanan Koebe fonksiyonun bir benzeri, Clunie-Sheil Small [6] tarafından

S

H0 sınıfı için tanımlanmıştır. Clunie ve Sheil Small tarafından tanımlanan

Tanım 2.3.2 : Harmonik Koebe Fonksiyonu

( )

0 = g

( )

0 =0 h varsayımı ile

( )

₍

₎

₃ 3 2 1 6 1 2 1 z z z z z h − + − = ,

( )

(

)

3 3 2 1 6 1 2 1 z z z z g − + =

olmak üzere K =h+g fonksiyonuna Harmonik Koebe fonksiyonu denir.

Harmonik Koebe fonksiyonu birim diski harmonik olarak , −∞<t <−1₆ şeridi çıkarılmış tüm C düzlemi üzerine dönüştürür. Ayrıca z =1 hariç birim diskteki her z değeri için K

( )

z =−1₆ şeklindedir.

Teorem 2.3.1 : 0 H S f ∈ ise

( )

(

)

2 1 4 1 z z z f + ≥ şeklindedir. Özellikle her 0

H S

f ∈ için

{

w∈C w < 1₆

}

⊂ f

( )

U şeklinde olur [6]. Teorem 2.3.1 de verilen sonuç kesin olmamakla birlikte, Harmonik Koebe fonksiyonu

16

1 _{yarıçapının 61 olarak alınabileceğini söyler. Ancak bu hâlâ bir kestirimdir. ♦}

Kestirim 2.3.1: Her 0 H S f ∈ fonksiyonu için

{

w∈C w < 1₆

}

⊂ f

( )

U kapsaması doğrudur [6]. ♦

Bununla birlikte Clunie ve Sheil-Small [6] ,

S

_H0 ailesi için Bieberbach kestirimini aşağıdaki harmonik şeklini tahmin etmişlerdir.

Kestirim 2.3.2 : 0

H S g h

f = + ∈ fonksiyonu (1) ile verilsin. Bu durumda

n b a_n − _n ≤ n=2,3,...

(

2 1

)(

1

)

6 1 + + ≤ n n a_n

(

2 1

)(

1

)

6 1 − − ≤ n n b_n

şeklindedir. Eşitlik durumu K Harmonik Koebe fonksiyonu için sağlanır. ♦ Daha sonra Sheil-Small [18] Kestirim 2.3.2’yi geliştirmişler ve Bieberbach kestiriminin aşağıdaki genelleştirilmişini önermişlerdir.

Kestirim 2.3.3 :

( )

H n n n n n nz a z S a z z f = +

∑

∞ +

∑

∈ = ∞ = − 2 1

ise n = 2,3,.... olmak üzere a_n

3 1 2 2₊ < n şeklindedir. ♦ H S ve 0 H

S sınıfındaki fonksiyonlarla ilgili katsayı tahminleri hâlâ devam

etmekte olup b₂ için kesin bir üst sınır elde edilmesine rağmen a₂ katsayısı için henüz kesin bir üst sınır bulunamamıştır. Ancak [6] da, her f ∈S_H için a₂ <12,173 olduğu bulunmuştur. Bu sonuç her 0

H S f ∈ için ise 2 1 2 ≤

b kesin eşitsizliği doğrudur [18].

Yine, 0

H S

f ∈ sınıfındaki bütün fonksiyonlar için ,

2 1

2 ≤

b kesin eşitsizliği

doğrudur.

Tanım 2.3.3: Harmonik Fonksiyonların Hadamard Çarpımı (Konvolüsyon )

∑

∞

∑

= ∞ = + + = + = 2 1 n n n n n nz b z a z g h f ve

∑

∞

∑

= ∞ = + + = + = 2 1 n n n n n nz B z A z G H F

şeklindeki harmonik fonksiyonlar için,

(

f ∗F

) (

= h∗H

)

+

( )

g∗G ile gösterilen Hadamard çarpım ( konvolüsyon )

(

)( )

_∑

_∑

∞ = ∞ = + + = ∗ 1 2 n n n n n n n nAz b B z a z z F f

olarak tanımlanır.

2.4 Harmonik Yıldızıl Fonksiyonlar

Yön koruyan bir f ∈S_H harmonik dönüşümünün görüntü bölgesi orjine göre yıldızıl olan fonksiyona yıldızıldır denilir. Bu tüm değer bölgesinin orjinden görülebilmesi anlamına gelir. Başka bir deyişle w₀ = f

( )

z₀ noktası f ’in görüntü bölgesinde ise 0dan w noktasına birleştiren doğru parçası vardır. Eğer f , kapalı ₀

diskte düzgün bir genişlemeye sahip ise eşdeğer bir ifade,_arg

{

_f

( )

_eiθ

}

_{nın θ ’nın}

azalmayan fonksiyonu olması veya

( )

(

arg

)

≥0, ∈ .0≤ ≤2 , 0≤ ≤1 ∂ ∂ r ve re z re f i i _{θ π} θ θ θ olmasıdır. Şekil 2.4.1 Analitik f fonksiyonları için bu koşul

( )

( )

0 Re > ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ′ z f z f z ; z∈U

şeklindeki bilinen formda olur. Aşağıdaki teorem 0

H

S harmonik yıldızıl fonksiyonlar için kesin olan katsayı

sınırları verilecektir. Bu teorem Sheil-Small [18] tarafından ileri sürülmüştür.

H S f ∈ 0 w U

Teorem 2.4.1 : Her yıldızıl 0 H S f ∈ fonksiyonunun katsayıları

(

2 1

)(

1

)

6 1 _{+ +} ≤ n n a_n

(

2 1

)(

1

)

6 1 _{− −} ≤ n n b_n ve a_n − b_n ≤n n=2,3,...

kesin eşitsizliklerini sağlar. ♦

Sonuç 2.4.1 : H

S sınıfındaki yıldızıl fonksiyonların katsayıları

(

2 1

)

3 1 2₊ < n a_n

(

2 1

)

3 1 2₊ < n b_n n=2,3,... kesin eşitsizliklerini sağlar.

Teorem 2.4.1’in aşağıdaki diğer sonucu yıldızıl harmonik dönüşümlerin büyümesi üzerindeki kesin üst sınırını verir.

Sonuç 2.4.2: Her 0 H S f ∈ fonksiyonu için

( )

₍

₎

₃3 1 3 3 1 r r r z f − + ≤ ; z = r <1

kesin eşitsizliği her yıldızıl 0

H S

f ∈ fonksiyonu için sağlanır. Eşitlik durumu Harmonik Koebe fonksiyonu için sağlanır.

2.5 Harmonik Konveks Fonksiyonlar

f harmonik fonksiyonunun görüntü kümesinden alınan herhangi iki noktayı

birleştiren doğru parçası görüntü kümesinin içinde kalıyorsa f fonksiyonuna konveks

fonksiyon denir. Bir konveks fonksiyonu

( )

0, ,0 2 ,0 1 arg arg ≥ = ≤ ≤ ≤ ≤ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ r re z re f i i _{θ π} θ θ θ θ şeklinde nitelendirebiliriz.

Şekil 2.5.1

Klasik Koebe 1 teoremi, ₄ U birim diskinde yalınkat ve analitik olan her bir

( )

2 ... 2 + + =z a z z f fonksiyonunun f

( )

U daki 4 1 <

w diskin tamamını kapsadığını söyler.

( )

(

1

)

2 3 ... 3 2 2 = + + + − = z z z z z z k

Koebe fonksiyonunun, U =

{

z: z〈1

}

birim diskini konformal olarak ,

z z w − + = 1 1 dönüşümü altında −1₄ den ∞ ’a kadar kesik doğru hariç tüm karmaşık düzlemin içine dönüştürmesi ve ‘Her f fonksiyonunun katsayıları a_n ≤n, n=2,3,4,... şeklindeki eşitsizliği sağlar’ ifadesi ile bilinen Bieberbach tahmininden, f in değer kümesinin konveks olduğunu varsayılabilir. K , birim diski konformal olarak bir konveks bölgeye dönüştüren

( )

2 ...

2 +

+ =z a z z

f şeklindeki fonksiyonların

sınıfı olsun. f ∈K şeklindeki her fonksiyonun değer kümesi 2 1 < w diskini kapsar ve katsayıları a_n ≤1 sınırını sağlar.

( )

... 1 3 2 _{+ +} + = − = z z z z z z

fonksiyonu U birim diskini konformal olarak

{ }

2 1

Re w >− yarı düzlem üzerine dönüştürür [13]. Bu sonuçlardan konveks konformal dönüşüm konveks harmonik dönüşümlere genişletebilir. K_H sınıfı, h

( )

0 = g

( )

0 =0 ve h′

( )

0 =1 normalize koşulları ile , birim diski konveks bölgeye dönüştüren yön koruyan f =h+g

H

K f ∈

şeklindeki harmonik dönüşümlerden meydana gelir. g′

( )

0 < h′

( )

0 =1 olduğunu kabul edelim ( çünkü f yön koruyandır ve Jacobianı pozitiftir ). Konveksliği koruyan

( )

₂ 1 1 1 b w b w w − − = ϕ , b₁ =g′

( )

0

yön koruyan afin dönüşümü ile f =h+g∈K_H fonksiyonu birleştirilerek daha ileri

( )

0 =0 ′

g normalize koşulu elde edilebilir. Bu sonuçlardan 0

H

K sınıfı elde edilir. Böylece , yön koruyan f =h+g harmonik fonksiyonu 0

H

K sınıfına ait olması demek

f ’in birim diski yalınkat bir şekilde konveks bölge üzerine dönüştürmesi ve h ve g analitik fonksiyonlarının

( )

2 ... 2 + + =z a z z h ,

( )

3 ... 3 2 2 + + =b z b z z g

yapılarına sahip olmasıdır.

H

K

f ∈ dan f₀ =(ϕ ο ₎ 0

H K

f ∈ a olan dönüşüm f = f₀+b₁f₀ ile tersine çevirilebilir.

Aşağıdaki teoremler Clunie ve Sheil-Small [6]’a aittir.

Teorem 2.5.1 : Her bir 0

H K

f ∈ fonksiyonu f

( )

U değer bölgesindeki

2 1 <

w

diskinin tamamını kapsar. ♦

Teorem 2.5.2 : Her bir 0

H K f ∈ fonksiyonunun katsayıları , 2 1 + ≤ n a_n 2 1 − ≤ n b_n ve a_n − b_n ≤1 n=2,3,.... için

kesin eşitsizlikleri sağlar. Eşitlik durumu

( )

z

{ }

( )

z i

{ }

k

( )

z

[

( ) ( )

z k z

]

[

( ) ( )

z k z

]

L = + = + + − 2 1 2 1 Im Re

2.6 Salagean Operatörü

( )

_∑

∞ = + = 2 , k k kz a z z h

( )

∑

∞ = = 1 k k kz b z g , b₁ <1 olmak üzere g h

f = + fonksiyonu için Salagean [3] tarafından tanımlanan _Dm _diferansiyel

operatörü ile, Jahangiri ve arkadaşları [9] bu f =h+g fonksiyonu için Salagean operatörünü

( )

_∑

∞ = + = 2 k k k m m_{h z z k a z} D ,

( )

∑

∞ = = 1 k k k m m_{g z k b z} D olmak üzere

( )

z D h

( ) ( )

z D g

( )

z f Dm ₌ m _{+ −1}m m ₍₂₎ şeklinde tanımlamışlardır.

3.BÖLÜM

SALAGEAN TİPLİ BAZI ÖZEL SINIFLAR

Bu kesimde, daha önce çalışılmış, S_H sınıfının bazı altsınıflarınının katsayı problemleri ile ilgili teoremler yer almaktadır. Bu bölüm çalışmamızın esasını oluşturan 4. bölüm için taban oluşturmaktadır.

Yalçın [14] tarafından tanımlanan S_H

(

m,n;α

)

sınıfı ile ilgili katsayı tahminleri ile S_H

(

m,n;α

)

nin S_H

(

m,n,α

)

alt sınıfına ait bazı teoremler aşağıdaki gibidir.

1

0≤α < , m∈IN , n∈IN₀ , m >n ve z∈U için S_H

(

m,n;α

)

, (2) de tanımlanan Dmf _{türev operatörü}

( )

( )

_⎭⎬⎫>α ⎩ ⎨ ⎧ z f D z f D n m Re (3)

olacak şekilde harmonik fonksiyonlarının ailesini tanımlasın.

(

m,n,α

)

S_H alt sınıfı,

( )

∑

∞ = − = 2 k k kz a z z h ,

( )

∑

∞ = = 1 k k k m z b z g ; a_k,b_k ≥0 (4) şeklindeki f_m =h+g_m harmonik fonksiyonlarından oluşsun.

(

m,n,α

)

S_H sınıfı iyi bilinen S_H sınıfının alt sınıflarını kapsar. Örneğin,

(

α

)

F

( )

α

SH 1,0, ≡ , [8], U ’da α mertebeli yıldızıl, yön koruyan f harmonik yalınkat

fonksiyonların sınıfıdır, SH

(

2,1,α

)

U’da α mertebeli konveks, yön koruyan f harmonik yalınkat fonksiyonların sınıfıdır ve SH

(

n+1,n,α

)

≡ H

( )

n,α , [9], Salagean tipte harmonik fonksiyonların sınıfıdır.

0

1 =

b olmak üzere , (1) ifadesindeki f harmonik fonksiyonlar için Avcı ve Zlotkiewicz[19]

∑

∞

(

)

= ≤ + 2 2 ₁ k k k b a

k ise f ∈HK olduğunu göstermişler, Silverman [5] ise, negatif katsayıya sahip ise gerekli olan katsayı durumlarını ispatlamıştır. Daha sonra, Silverman ve Silvia [4] b₁’in sıfır olmadığı durumda [5] ve [19] sonuçlarını geliştirmişlerdir.

1 =

m olmak üzere , (4) ifadesindeki f harmonik fonksiyonlar için Jahangiri [8], f ∈F

( )

α olması için gerekli ve yeterli koşulun

(

−α

)

+

(

+α

)

≤ −α

∑

∞

∑

= ∞ = 2 1 1 k k k k k b a k ve f ∈SH

(

2,1,α

)

, ayrıca

∑

∞

(

−α

)

+

∑

(

+α

)

≤ −α = ∞ = 2 1 1 k k k k k kb a k k

olması gerektiğini göstermiştir.

Teorem 3.1.1 : h ve g , (1) de tanımlanan fonksiyonlar olmak üzere f =h+g

şeklinde olsun. Bu durumda , f ∈S_H

(

m,n;α

)

ve U bölgesinde harmonik yalınkat ve yön koruyan iken 0≤α <1

,

m∈IN

,

n∈IN₀

,

m>n

değerlerinde katsayı eşitsizliği

( )

2 1 1 1 1 ≤ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − + − −

∑

∞ = − k k n n m m k n m b k k a k k α α α α (5) şeklindedir [14] . ♦

Aşağıdaki teorem (5) şartının, f_m =h+g_m∈SH

(

m,n;α

)

için aynı zamanda

gerekli olduğunu da söyler.

Teorem 3.1.2 : (4) te verilen fonksiyonlarla f_m =h+g_m şeklinde olsun. Bu durumda f_m∈SH

(

m,n;α

)

⇔

∑

[

(

)

(

( )

)

]

(

)

∞ = − _{≤ −} − − + − 1 1 2 1 k k n n m m k n m _{k a k k b} k α α α (6) olmasıdır. ♦

Kapalı konveks kabuk, bir M kümesini kapsayan en küçük kapalı konveks kümedir. M ’nin kapalı konveks kabuğu H

( )

M ile gösterilir.

(

m,n;α

)

SH sınıfının clcoSH

(

m,n;α

)

ile tanımlanan kapalı konveks kabuğunun

Teorem 3.1.3 : f , _m (4) te verildiği gibi olsun. Bu durumda f ∈S_H

(

m,n,α

)

olması için gerekli ve yeterli koşul

( )

( )

k n m k z k k z z h z z h α α − − − = = , 1 1

(

k =2,....

)

ve

( )

( )

_{( )}

k n n m m m m z k k z z g _k α α − − − − − − + = 1 1 1 1

(

k =1,2,...

)

, 0 , 0 ≥ ≥ _j j y x

∑

∞

(

)

= ≥ + − = 2 1 1 0 k k k y x x

olmasıdır. SH

(

m,n;α

)

sınıfının extreme noktaları

{ }

h_k ve

{ }

k

m

g fonksiyonlarıdır. ♦ Görüntü kümesinin davranışı hakkında bilgi veren büyüme teoremi de aşağıdaki gibidir.

Teorem 3.1.4 : f_m∈SH

(

m,n,α

)

olduğunu kabul edelim. O halde z = r <1 için

( ) (

)

( )

, 2 1 1 2 1 2 1 1 2 1 r r b z f _{m n} n m n m n m ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − − − − + + ≤ ₋ − − _α α α α z = r <1, ve

( ) (

)

( )

, 2 1 1 2 1 2 1 1 2 1 r r b z f _{m n} n m n m n m ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − − − − − − ≥ ₋ − − _α α α α

, 1 < = r z şeklindedir. ♦ Aşağıda vereceğimiz örtü teoremi Teorem 3.1.4’ün direkt bir sonucudur.

Sonuç 3.1.5 : (4) ifadesi ile, f_m∈SH

(

m,n,α

)

olsun . Bu durumda

(

)

(

( )

)

_{( )}

U f b w w _{m n m} n m n m n m n m ⊂ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − − − − − − − − − < − 1 2 2 1 2 1 2 2 2 1 2 1 2 : α α α α olur. ♦

Yine , SH

(

m,n;α

)

sınıfının Hadamard çarpım altında kapalı olduğunu gösteren aşağıdaki teorem önemlidir.

Teorem 3.1.6 :

1

0≤β ≤α < için f_m∈SH

(

m,n;α

)

ve F_m∈S_H

(

m,n;β

)

olsun. Bu

Teorem 3.1.7 :

(

m,n;α

)

SH sınıfı konveks birleşimi altında kapalıdır. ♦

Son zamanlarda Rosy ve arkadaşları [17] Re

(

1 α

)

_{( )}

( )

α ≥γ, ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − ′ + i _ei z f z f z e 0≤γ <1, α∈ℜ (7) eşitsizliğini sağlayan f harmonik yalınkat fonksiyonların G_H

( )

γ ⊂ S_H alt sınıfını tanımlamışlardır. (1) ifadesinde verilen f =h+g fonksiyonu için

∑

∞ = ≤ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + + + − − − 1 , 2 1 1 2 1 1 2 n n n b n a n γ γ γ γ 0≤γ <1 (8) sağlanır. Bu durumda f , U sınıfında Goodman-Ronning tipte harmonik yalınkat fonksiyon olarak adlandırılır. Bu koşul eğer h ve g fonksiyonları

( )

_∑

∞ = − = 2 n n n z a z z h ,

( )

∑

∞ = = 1 n n n z b z g (9) şeklinde olursa sağlanmış olur.

( )

k,γ RS_H ,

(

α

)

_{( )}

( )

α _≥γ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − + + i k k i _e z f D z f D e 1 1 Re , 0≤γ <1, α ∈ℜ (10) olacak şekilde (1) ifadesinde tanımlanan f harmonik fonksiyonlarının ailesi olarak tanımlansın. Ayrıca , RSH

( )

k,γ sınıfı , h ve g_k

( )

_∑

∞ = − = 2 n n n z a z z h ,

( ) ( )

∑

∞ = − = 1 1 n n n k k z b z g (11) olacak şekilde RS_H

( )

k,γ sınıfındaki f_k =h+g_k harmonik fonksiyonlarını kapsayan bir altsınıfı olsun.

Aşağıdaki teoremlerle de G_H

( )

γ sınıfı için [17] de verilen katsayı eşitsizliğinin (10) ifadesindekiRS_H

( )

k,γ sınıfına genişletildiği verilir. Ayrıca RSH

( )

k,γ sınıfındaki fonksiyonlar için konveks birleşimleri , hadamard çarpımları, bükülme teoremini ve uç noktalarını vereceğiz.

Teorem 3.1.8: f =h+g fonksiyonu (1) ifadesindeki gibi olsun. Eğer a₁ =1 ve 1 0≤γ < şeklinde iken

(

)

(

)

[

− −γ + + +γ

]

≤

(

−γ

)

∑

∞ = 1 2 1 2 1 2 1 n n n k _{n a n b} n (12) eşitsizliği sağlanırsa f , U sınıfında harmonik yalınkat , yön koruyan ve

( )

k,γ

RS

f ∈ _H olduğu görülür. ♦

Aşağıdaki teoremle (11) ifadesinde tanımlanan h ve g_k fonksiyonları için

k k h g

f = + fonksiyonu için gerekli ve yeterli olan katsayı eşitsizliğini verelim.

Teorem 3.1.9: f_k =h+g_k fonksiyonu (11) ifadesindeki gibi olsun. O zaman

( )

⇔ ∈RS k,γ f_k H

∑

[

(

− −γ

)

+

(

+ +γ

)

]

≤

(

−γ

)

∞ = 1 2 1 2 1 2 1 n n k _{n a n} n (13) olur. ♦

Şimdiki teoremde de RSH

( )

k,γ sınıfındaki fonksiyonlar için bir teorem betimleyeceğiz.

Teorem 3.1.10: f _k , (11) ifadesinde verildiği gibi tanımlansın. O zaman

( )

( )

_∑

∞

(

( )

( )

)

= + = ⇔ ∈ 1 , n n n n k k H k RS k f z X h z Y g z f n γ (14)

( )

, 1 z z h =

( )

₍

_{) (}

, 2,3,..

)

1 2 1 ₌ − − − − = z n n n z z h n k n _γ γ

( )

_{( ) (}

₎

,

(

1,2,3,...

)

1 2 1 1 = + + − − + = _z− _n n n z z g n k k kn γ γ

(

)

∑

∞ = = + 1 1 n n n Y X , X_n ≥0,Y_n ≥0. Özellikle ,

{ }

h_n ve

{ }

n k g , RSH

( )

k,γ sınıfının extreme fonksiyonlarıdır. ♦

Aşağıdaki teoremde bu sınıf için katsayıyı sağlayan RSH

( )

k,γ sınıfındaki fonksiyonlar için büyüme sınırlarını verelim.

Teorem 3.1.11: f_k∈RSH

( )

k,γ olsun. O zaman z = r<1 için

( ) (

)

2 1 1 3 3 3 1 2 1 1 b r b r z f_{k k ⎟⎟} ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + − − − + + ≤ γ γ γ γ ve

( ) (

)

2 1 1 3 3 3 1 2 1 1 b r b r z f_{k k ⎟⎟} ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + − − − − − ≥ γ γ γ γ

eşitsizlikleri elde edilir. ♦

Teorem 3.1.12: 0≤β ≤γ <1 için f_k∈RSH

( )

k,γ ve F_k∈RSH

( )

k,β şeklinde

olsun. Bu durumda

(

f_k∗F_k

)

∈RSH

( )

k,γ ⊂ RSH

( )

k,β

olur. ♦

Teorem 3.1.13: RSH

( )

k,γ sınıfı konveks birleşimleri altında kapalıdır. ♦