EĞİTİM BİLİMLERİ ENSTİTÜSÜ İLKÖĞRETİM ANABİLİM DALI
İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ BİLİM DALI
İLKÖĞRETİM 8. SINIF MATEMATİK DERSİ ÜÇGENLER ALT ÖĞRENME ALANININ ÖĞRETİMİNDE AKTİF ÖĞRENME YAKLAŞIMININ ÖĞRENCİLERİN BAŞARISINA
VE KALICILIĞINA ETKİSİ
YÜKSEK LİSANS TEZİ
Hazırlayan Hilal BOZTAŞ
Ankara Haziran, 2012
EĞİTİM BİLİMLERİ ENSTİTÜSÜ İLKÖĞRETİM ANABİLİM DALI
İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ BİLİM DALI
İLKÖĞRETİM 8. SINIF MATEMATİK DERSİ ÜÇGENLER ALT ÖĞRENME ALANI KAZANIMLARININ AKTİF ÖĞRENME YAKLAŞIMINA UYGUN OLARAK
ÖĞRETİMİNİN ÖĞRENCİ BAŞARISINA VE KALICILIĞA ETKİSİ
YÜKSEK LİSANS TEZİ Hilal BOZTAŞ
Danışman: Yrd. Doç. Dr. Devrim ÇAKMAK
Ankara Haziran, 2012
başlıklı tezi 06.06.2012 tarihinde, jürimiz tarafından İlköğretim Matematik Öğretmenliği Anabilim Dalında Yüksek Lisans Tezi olarak kabul edilmiştir.
Adı Soyadı İmza
Başkan : Yrd.Doç.Dr. Dursun SOYLU ……… Üye ( Tez Danışmanı) : Yrd.Doç.Dr. Devrim ÇAKMAK ……… Üye : Doç.Dr. Melek ÇAKMAK ………
i
öğrenme yaklaşımının öğrenci başarısına ve kalıcılığına etkisini incelemek amacıyla yapılmıştır.
Araştırmayı gerçekleştirdiğim süre içerisinde bana yol gösteren ve yardımlarını esirgemeyen değerli danışman hocam Yrd. Doç. Dr. Devrim ÇAKMAK’ a ve Yrd. Doç. Dr. Nusret KAVAK’ a teşekkürü bir borç bilirim.
Araştırmanın uygulama aşamasında tüm imkanlarını sunarak rahat bir ortamda çalışmamı sağlayan okulların yönetici, öğretmen ve öğrencilerine teşekkürlerimi sunarım.
Son olarak; araştırma konusunda beni destekleyen, hep yanımda olan aileme ve araştırmanın başından sonuna kadar karşılaştığım tüm zorluklarda beni yalnız bırakmayan, desteğini hiç eksik etmeyen eşim Mustafa BOZTAŞ’ a sonsuz teşekkürlerimi sunarım.
Hilal BOZTAŞ Haziran-2012
ii
İLKÖĞRETİM 8. SINIF MATEMATİK DERSİ ÜÇGENLER ALT ÖĞRENME ALANININ ÖĞRETİMİNDE AKTİF ÖĞRENME YAKLAŞIMININ ÖĞRENCİ
BAŞARISINA VE KALICILIĞINA ETKİSİ
BOZTAŞ, Hilal
Yüksek Lisans, İlköğretim Matematik Öğretmenliği Bilim Dalı Tez Danışmanı: Yrd. Doç. Dr. Devrim ÇAKMAK
Haziran-2012, 123 Sayfa
Bu araştırmanın amacı, 8. sınıf matematik dersi üçgenler alt öğrenme alanının öğretiminde aktif öğrenme yaklaşımının öğrenci başarısına ve kalıcılığına etkisini incelemektir.
Araştırmada, öntest-sontest kontrol gruplu deneysel araştırma modeli kullanılmıştır. Araştırma, belirli amaçlar için daha önce şekillenmiş olan gruplar üzerinde yapılmıştır. Ön test-son test kontrol gruplu modelin kullanıldığı araştırmalarda iç-geçerliliği tehdit edebilecek tarih, olgunluk, test etme ve araç gibi kaynaklardan gelen hatalar ya da etkiler diğer modellere kıyasla daha çok kontrol altında tutulabilmektedir. Bu da öntest-sontest kontrol gruplu modeli diğer modellere oranla daha güvenilir ve kullanışlı kılmaktadır.
Araştırma 2011-2012 eğitim-öğretim yılında, Ankara İli Etimesgut İlçesi’ nde bulunan bir ilköğretim okulunda gerçekleştirilmiştir. Uygulamaya 8. sınıfların iki farklı şubesinde öğrenim gören toplam 68 öğrenci katılmıştır. Sınıflardan biri deney grubu diğeri ise kontrol grubu olarak rastgele belirlenmiştir. Deney grubunda 35, kontrol grubunda 33 öğrenci bulunmaktadır.
Deney grubunda dersler aktif öğrenme yaklaşımı ile kontrol grubunda ise geleneksel öğretim yöntemi ile yürütülmüştür. Araştırmada veri toplama aracı olarak Matematik Başarı
iii
Araştırma sonucunda aktif öğrenme yaklaşımına göre öğretimin öğrencilerin matematik başarısını artırmada geleneksel öğretim yöntemine göre daha etkili olduğu görülmüştür. Ayrıca aktif öğrenme yaklaşımı, öğrencilerinin konu ile ilgili kalıcılık düzeylerini de artırmıştır.
Anahtar Kelimeler: Matematik, Matematik Öğretimi, Aktif Öğrenme Yaklaşımı, Geleneksel Öğrenme Yaklaşımı, Başarı.
iv
GRADES’ MATHEMATICS LESSONS ACCORDING TO ACTIVE LEARNING APPROACH ONTO THE ACHIEVEMENT AND PERMANENCE OF THE
STUDENTS
BOZTAŞ, Hilal
Master Thesis, Primary Mathematics Teaching Department Thesis Advisor: Assist Prof. Devrim ÇAKMAK
June-2012, 123 page
The purpose of this study, to examine the effect of teaching triangle lower learning area gains 8th grades’ mathematics lessons according to active learning approach onto the achievement and permanence of the students.
In the study pretest – posttest control group experimental research model was used. Pretest – posttest control group experimental research model is more reliable and convenient than other models.
The study took place in 2011-2012 academic ( educational ) years on 68 students studying a primary school in Etimesgut, Ankara. One of the classes was determined as experimental group, the other one was decided as control group, randomly. There were 35 students in experimental group and 33 students in control group.
The lessons were carried out with active learning approach on control group and with traditional teaching method on experimental group. In the study, Mathematics Achievement Test was used as data collection device. Achievement test was the researcher. The data analyzed by the SPSS 15.00 statistic program.
v
permanence of the students.
Key Words: Mathematics, Mathematic Education, Active Learning Approach, Traditional Teaching Method, Achievement.
vi ÖN SÖZ………..i ÖZET……….ii ABSTRACT………..iv İÇİNDEKİLER………....vi
TABLOLAR LİSTESİ ………ix
BÖLÜM I 1.GİRİŞ……….………...1 1.1 Problem Durumu………..………...5 1.2 Araştırmanın Amacı……….………..7 1.3 Araştırmanın Önemi……….………..8 1.4 Araştırmanın Varsayımları……….………....9 1.5 Araştırmanın Sınırlılıkları……….10 1.6 Tanımlar / Terimler………...12 BÖLÜM II 2. KAVRAMSAL ÇERÇEVE………..13 2.1. Aktif Öğrenme………..14
2.2. Aktif Öğrenme Yaklaşımında Öğretmen ve Öğrencinin Rolü……….15
2.3. Aktif Öğrenme Yaklaşımında Sınıf Düzeni ………16
2.4. Aktif Öğrenme Yaklaşımının Temel Düşünceleri………...17
2.5. Aktif Öğrenme Yaklaşımının Uygulanmasında Karşılaşılan Zorluklar………..18
2.6. Aktif Öğrenme Yaklaşımında Kullanılabilecek Yöntem ve Teknikler ………..19
vii
YÖNTEM………..34
3.1 Araştırmanın Modeli ...………..………..34
3.2 Evren ve Örneklem ...………..…………35
3.3 Veri Toplama Yöntemi ve Araçları ...……….35
3.4 Verilerin Analizi ..………...39
BÖLÜM IV 3. BULGULAR VE YORUMLAR………..40
4.1 Birinci Alt Probleme İlişkin Bulgular ve Yorumlar………...40
4.2 İkinci Alt Probleme İlişkin Bulgular ve Yorumlar ..……….41
4.3 Üçüncü Alt Probleme İlişkin Bulgular ve Yorumlar……….42
4.4 Dördüncü Alt Probleme İlişkin Bulgular ve Yorumlar ..………..43
4.5 Beşinci Alt Probleme İlişkin Bulgular ve Yorumlar………..44
BÖLÜM V 4. SONUÇ VE ÖNERİLER………46
5.1 Sonuçlar……….46
5.2 Öneriler………..48
viii
Ek-2. Deney Grubu Ders Planları……….66 Ek-3. Öğrenci Çalışmalarından Örnekler………94 Ek-4. İzin Yazıları………...112
ix
Tablo.4.1. Deney ve Kontrol Grubu Öğrencilerinin Öntest Sonuçları………...41
Tablo.4.2. Deney Grubu Öğrencilerinin Öntest-Sontest Sonuçları………42
Tablo.4.3. Kontrol Grubu Öğrencilerinin Öntest-Sontest Sonuçları……….43
Tablo.4.4. Deney ve Kontrol Grubu Öğrencilerinin Sontest Sonuçları………...44
BÖLÜM I
1.GİRİŞ
‘Matematik nedir?’ sorusunun cevabı, insanların matematiğe başvurmadaki amaçlarına, belli bir amaç için kullandıkları matematik konularına, matematikteki tecrübelerine ve matematiğe olan ilgilerine göre değişmektedir (Baykul, 2009). İnsanlık tarihi kadar eski olan matematik için çok çeşitli tanımlar yapılmıştır.
Matematik Terimler Sözlüğü’nde (2000) matematik; “Biçim, sayı ve çoklukların yapılarını, özelliklerini ve aralarındaki ilişkileri inceleyen bilimdir.” şeklinde tanımlanmaktadır.
Matematik, düşüncenin tümden gelimli bir iletişim yolu ile sayılar, geometrik şekiller, fonksiyonlar, uzaylar gibi soyut varlıkların özelliklerini ve bunların arasında kurulan ilişkileri inceleyen bilimler grubuna verilen genel ad olarak tanımlanmıştır (MEB, 1976).
Matematik, insanlık tarihinin en eski bilimlerinden biridir. Çok eskiden matematik, sayıların ve şekillerin ilmi olarak tanımlanırdı. Ancak geçen zaman içinde büyük bir gelişme gösterdiği için artık birkaç cümleyle tanımlanamamaktadır. Matematik, bir yönüyle resim ve müzik gibi bir sanattır. Matematikçilerin büyük bir çoğunluğu onu sanat olarak icra eder. Bu açıdan bakınca yapılan bir işin, geliştirilen bir
teorinin işe yararlılığı değil estetiği, matematik için işe yaraması önemlidir. Matematik başka bir yönüyle dildir. Eğer bilimin gayesi evreni tanımak, evrende olan her şeyi anlamak, onlara hükmetmek ve yönlendirmekse bunları yapabilmek için matematik dilini bilmemiz gerekmektedir.
Matematik sözcüğü, ilk kez M.Ö. 550’lerde Pisagor okulu üyeleri tarafından kullanılmıştır. Yazılı literatüre girmesi Platon’la M.Ö. 380’lerde olmuştur. Bu tarihlerden önce matematik kelimesi yerine yer ölçümü manasına gelen geometri ya da eski dilde ona eş olan sözcükler kullanılıyordu. Matematiğin nerede ve nasıl başladığı hakkında kesin bir şey söylemek mümkün değildir. Ancak yorum gerektirmeyecek yazılı kaynaklara bakarsak M.Ö. 3000-2000 yılları arasında Mısır ve Mezopotamya’da başladığı söylenebilmektedir.
Geometri, uzayın ve uzayda tasarlanabilen biçimlerin kurallara uyularak incelenmesini konu alan matematik dalıdır. Yunanca da “geo” yer ve “metron” ölçü anlamına gelmektedir.
Geometrinin uğraş alanı, cisimleri ve şekilleri içermektedir. Günlük hayatta karşılaştığımız ve kullandığımız eşyalar içinde oldukça fazla geometrik şekil, desen ve biçimler yer almaktadır. Bunun nedeni eşyanın ergonomik olmasının ve görevini daha iyi yapmasının sağlanmasıdır. Ayrıca eşyaya estetik de kazandırmaktadır (Pesen, 2008). Bu durum çok eski tarihlerden günümüze kadar insanlar için bir uğraş alanı olmuş ve bunun sonucunda Matematik içinde yeni bir dal olan Geometri ortaya çıkmıştır.
Geometrinin Nil kıyılarında doğduğu düşünülmektedir. Bu ırmağın düzenli aralıklarla taşması tarlaların sınırlarını silerek Mısırlıları güç sorunlarla karşı karşıya bırakıyordu. Çünkü tarlaların sınırlarını yeniden çizmek, herkese kendi yerini vermek, bunun için de tarlaların yüzölçümünü hesaplamak, nirengiler dikmek, kısaca geometri yapmak gerekiyordu (MEB, 2008). Ancak Geometri ile ilgili ulaşılan tarihi gerçekler bunlarla sınırlı değildir. Örneğin M.Ö. 25.000’li yıllarda ilkel geometrik şekiller saptanmıştır. Gerçek gelişme M.Ö. 3000’lerde Mezopotamya’da yazı ve rakamların icadıyla başlamaktadır. Mezopotamya’da Sümerler, daha sonra Babil ve Akadlar, M.Ö. 3500-2000 yıllarında üçgen ve çokgenlerin alanlarının hesaplanması, ispat olmamakla birlikte Pisagor teoremiyle ilgili bilgileri, bazı basit cisimlerin hacim formüllerini, çapı gören çevre açının dik olduğunu bilmektedirler (Baykul, 2009).
Geometriyle çok sayıda bilim adamı uğraşmıştır. Bunlardan biri de Farabi’dir. Farabi, “Geometri konusuna bir sıra dahilinde inmek gerekir. Bu sıra iki türlü olur. Birincisi kavramsal alana en yakın olandan başlamalı, ikincisi ise duyusal alana en yakın olandan başlamalı. Duyusal alana en yakın olanı cisimdir. Sonra yüzey ve çizgi gelir. Duyusal alana en uzak olan da noktadır. Kavramsal alana en yakın olan ise noktadır. Noktadan sonra çizgi, yüzey ve cisim gelmektedir. Öğretim gerektiğinde duyusal alana daha yakın olduğumuzdan çözümleme yoluyla cisimden noktaya ulaşılmalıdır.” görüşünü ortaya koymuştur (Türker, 1992). Farabi’ nin görüşleri son yıllara kadar uygulanması devam eden bir modelin temelini oluşturmuştur.
Bu model eğitim sistemimizde bir dönem Geometri öğretimine temel oluşturan ilke olarak yer almıştır. 1990 yılında kabul edilen ilköğretim matematik programında kavramsal alana yönelik nokta, doğru, düzlem ve cisim sırası takip edilirken 1998 yılında hazırlanan programda duyusal alana yönelik, cisim, düzlem, doğru ve nokta sırası takip edilmeye başlanmıştır. 1998 yılında hazırlanan programda kabul edilen bu yapıya 2004 yılında hazırlanmaya başlanan programda da aynı şekilde devam edilmiştir (Pesen, 2008).
Geometri öğretimine yönelik son yıllarda oldukça üzerinde durulan bir diğer model ise Van Hiele geometrik düşünme modelidir. Bu model Hollandalı matematik öğretmenleri Dina Van Hiele Geldof ve eşi Pierre Marie Van Hiele’nin Utrecht Üniversitesi’nde 1957 yılında tamamladıkları doktora çalışmalarının bir ürünüdür. 1958 yılında Dina doktora tezini tamamladıktan hemen sonra öldüğü için eşi Pierre kuramı geliştirmiştir. Bu model ilk ortaya çıktığında çok fazla gündeme gelmemiş, yeterli ilgiyi görmemiştir. Sovyetlerin dışında Van Hiele modeli uzunca bir süre batının da dikkatini çekmemiştir. Sovyetler, Hiele’lerin çalışmasından etkilenerek 1960 yılında kendi geometri programlarında büyük bir reforma gitmişlerdir. Amerika ve diğer batı ülkeleri ise 1970’lerin ortalarında kuramdan haberdar olmuşlardır. Fakat asıl önemli çalışmaların İngilizceye çevirisi 1984 yılında yapılmıştır. Kuram bugün hala geçerliliğini korumaktadır (Olkun ve Toluk, 2007).
1.1.Problem Durumu
Matematiğin ne olduğu ve nasıl öğretilmesi gerektiği konularında son yıllarda önemli düşünce değişiklikleri olmuştur. Geleneksel matematik eğitimi anlayışında öğretmenler, matematiksel bilgileri küçük parçalar halinde öğrencilere sunar. Verilen alıştırmalarla öğrencilerin bu bilgileri tekrar etmeleri beklenir. Soruların tek bir yanıtı ve bu yanıtlara ulaşmak için öğretmen tarafından önceden belirlenmiş yöntem veya yöntemler vardır. En çok soruyu, belirlenmiş olan en kısa yoldan ve en hızlı yanıtlayan öğrenci en başarılı öğrenci olarak kabul edilir. Böyle bir eğitim ortamında öğrenciler pasiftirler. Öğrenciler, en iyi ve en doğruyu ancak öğretmenden öğrenmek durumundadırlar. Öğrencilere bir neden gösterilmeden veya ispat yapılmadan bir yığın bağıntı, kural ve simgeler verilir. Bu durum, öğrencileri ezbere dayalı öğrenmeye sevk eder ve öğrencilerin daha önce çözümünü görmedikleri herhangi bir problemi çözemez hale gelmesine neden olur (Olkun ve Toluk, 2007). Geleneksel eğitim programındaki bu olumsuzluklar yeni arayışlara neden olmuş ve yeni öğretim programları geliştirilmiştir.
Milli Eğitim Bakanlığı (MEB) tarafından 2008 yılında yenilenen eğitim programında kavram öğretimi ile öğrencilerin sezgilerini kullanarak ve somut deneyimlerinden matematiksel anlamları oluşturmaları ve buradan hareketle soyutlamalar yapabilmeleri amaçlanmıştır. Ayrıca öğrencilerin matematiğin eğlenceli ve zevkli yönünü keşfetmelerini sağlamak da yeni programın büyük önem taşıyan amaçlarındandır (MEB, 2008).
Yeni eğitim programında öğrencilerin matematiğin eğlenceli ve zevkli yönünü keşfetmelerini, onların derse aktif bir şekilde katılımlarını ve tartışma ortamları yaratarak onların daha anlamlı öğrenmelerini sağlayabilmek içi görsel araçların kullanımına da oldukça yer verilmiştir. Yeni eğitim programları ders içerikleri ve ders işleyişleri bakımından incelendiğinde aktif öğrenme yaklaşımının uygulanmaya çalışıldığı görülmektedir.
Aktif öğrenme, öğrenenin öğrenme sürecinin sorumluluğunu taşıdığı, öğrenene öğrenme sürecinin çeşitli yönleriyle ilgili kararlar ve öz düzenleme yapma olanaklarının verildiği ve karmaşık öğretimsel işlerle öğrenenin öğrenme sırasında zihinsel yeteneklerini kullanmaya zorlandığı bir öğrenme süreci olarak tanımlanmaktadır (Açıkgöz, 2002).
Aktif öğrenmenin öz düzenleme ve karmaşık öğretimsel işler olmak üzere aşağıda kısaca açıklanan iki koşulu vardır.
Öz düzenleme: Öğrenenin kendi öğrenmesinin sorumluluğunu taşıması ve kendi öğrenmesi ile ilgili kararları kendinin alması ve uygulamasıdır. Öğrenen birey neyi öğreneceği, zamanını nasıl kullanacağı, bu süreçte hangi stratejileri izleyeceği, nasıl yoğunlaşacağı gibi birçok konuda kararı kendisi verir. Aktif öğrenme teknikleri, öğrenenlere bu olanakları verecek şekilde tasarlanmıştır.
Karmaşık öğretimsel işler: Öğrenme sürecinde çocuğun zihninin aktifleşmesini, öğrenilenlerin derinlemesine işlenmesini, analiz, sentez, değerlendirme gibi üst düzey düşünme süreçlerinin harekete geçmesini sağlar. (Açıkgöz, 2002)
Eğitim literatüründe yıllarca öğretmen özellikleri, öğretmen davranışları ve eğitim programları gibi dışsal kontrol öğeleri üzerinde durulmuş öğrencinin ne yaptığı, ne düşündüğü ve ne algıladığı pek dikkate alınmamıştır. Ancak son yapılan çalışmalarda öğrencinin algıları, davranışları ve bilişsel süreçleri üzerinde durulmaya başlanmıştır.
Aktif öğrenme ile ilgili yapılan pek çok araştırmada elde edilen veriler aktif öğrenmenin etkililiğini ortaya koymaktadır. Bu araştırmada da geleneksel öğretime kıyasla aktif öğrenme kuramına uygun olarak yapılan öğretimin akademik başarıya ve kalıcılığa etkisi incelenecektir.
1.2. Araştırmanın Amacı
Bu araştırmanın amacı, geleneksel öğretime kıyasla aktif öğrenme kuramına uygun olarak yapılan öğretimin ilköğretim 8. sınıf öğrencilerinin matematik dersi geometri öğrenme alanı üçgenler alt öğrenme alanındaki başarılarına ve kalıcılığına etkisini araştırmaktır.
Bu amaç doğrultusunda aşağıdaki sorulara cevap aranmıştır:
1. Konunun aktif öğrenme kuramına göre anlatıldığı öğrenciler (deney grubu) ile geleneksel öğretimle öğrenim gören öğrencilerin (kontrol grubu) uygulamadan önceki başarı puanları arasında anlamlı bir fark var mıdır? 2. Deney grubu öğrencilerinin uygulamadan önce (öntest) ve sonraki (sontest)
başarı puanları arasında anlamlı bir fark var mıdır?
3. Kontrol grubu öğrencilerinin uygulamadan önce ve sonraki başarı puanları arasında anlamlı bir fark var mıdır?
4. Deney ve kontrol grubu öğrencilerinin uygulamadan sonraki başarı puanları arasında anlamlı bir fark var mıdır?
5. Deney ve kontrol grubu öğrencilerinin kalıcılık düzeyleri arasında anlamlı farklılıklar var mıdır?
1.3.Araştırmanın Önemi
Günümüzde eğitim, öğrencilere mevcut bilgileri aktarmak yerine bilgiye ulaşma yollarını öğretmeye yöneliktir. Bu tür öğrenme ezberden çok kavramayı ve karşılaşılan yeni durumlarla ilgili problem çözebilme sürecine yönelik becerileri gerektirir. Bu becerilerin kazandırılması sürecinde matematiğin önemi oldukça fazladır. Son yıllarda matematik eğitimine bakış açılarında önemli değişiklikler olmuştur. Artık matematik eğitimi, yalnız matematik bilen değil sahip olduğu bilgiyi uygulayan, matematik yapan, problem çözen insanlar yetiştirmeyi hedeflemektedir (Soylu ve Aydın, 2006).
Yeni ilköğretim programının içinde yer alan matematik öğretimi programı, matematiği anlayabilen, günlük hayatında kullanabilen bireyler yetiştirmeyi ve öğrencilerin bağımsız düşünebilme ve karar verebilme, öz düzenleme gibi bireysel yetenek ve becerilerini geliştirmeyi hedeflemektedir (MEB, 2005). Ancak yapılan araştırmalar ve çevreden elde edilen gözlemler sonucu yeni öğretim programlarının temelinde yer alan aktif öğrenme yöntem ve tekniklerinin okullarda öğretmenler tarafından pek uygulanmadığı, hala eski öğretim yöntemlerine devam edildiği görülmektedir. Bu amaçla aktif öğrenmenin etkililiği ve uygulanmasında yaşanabilecek olumlu ve olumsuz faktörlerin tespit edilmesi, öğretimde başarıya ve kalıcılığa etkisinin belirlenmesini sağlayacak çalışmaların yapılması gerekmektedir.
Bu araştırma, 8. sınıf matematik dersi üçgenler alt öğrenme alanının aktif öğrenme yaklaşımı ile öğretiminin öğrenci başarısına ve kalıcılığa etkisini incelemek amacıyla yapılmaktadır. Elde edilecek bulguların matematik dersindeki diğer konulara da yol göstereceği ve gelecekte yapılacak diğer çalışmalara da fikir vereceği düşünülmektedir.
1.4. Araştırmanın Varsayımları
1. Öğrencilerin araştırmada kullanılan başarı testini tüm ciddiyet ve içtenlikleriyle cevaplayacakları,
2. Deney ve kontrol grubu öğrencilerinin araştırmanın sonucunu etkileyecek derecede bir etkileşimde bulunmayacakları,
3. Başarı testi geliştirmek için görüşülen uzmanların alanlarında yeterli oldukları,
4. Araştırmaya etki edebilecek değişkenlerin her iki grubu da eşit derece etkilediği,
varsayılmıştır.
1.5. Araştırmanın Sınırlılıkları
Bu araştırma
1. Ankara ilindeki bir ilköğretim okulunun 8. sınıf öğrencileri ile,
2. 2011-2012 eğitim-öğretim yılının I. döneminde 3 hafta süren 12 ders saati ile,
3. İlköğretim 8. sınıf matematik dersi üçgenler alt öğrenme alanı 6 kazanımı ile,
sınırlandırılmıştır.
MEB Program Kitabı’ nda üçgenler alt öğrenme alanı ile ilgili 9 kazanım bulunmaktadır. Ancak, yeni eğitim sistemimizde kullanılan sarmal yapıdan dolayı bu kazanımlar yıl içerisine dağılmış durumdadır. Bu da bütün kazanımların birlikte
işlenmesine olanak sağlamamaktadır. 8. sınıf üçgenler alt öğrenme alanı kazanımları aşağıda verilmiştir.
1. Atatürk’ün matematik alanında yaptığı çalışmaların önemini açıklar.
2. Üçgenin iki kenar uzunluğunun toplamı veya farkı ile üçüncü kenarının uzunluğu arasındaki ilişkiyi belirler.
3. Üçgenin kenar uzunlukları ile bu kenarların karşısındaki açıların ölçüleri arasındaki ilişkiyi belirler.
4. Yeterli sayıda elemanının ölçüleri verilen bir üçgeni çizer.
5. Üçgende kenarortay, kenar orta dikme, açıortay ve yüksekliği inşa eder.
6. Üçgenlerde eşlik şartlarını açıklar. 7. Üçgenlerde benzerlik şartlarını açıklar. 8. Pythagoras (Pisagor) bağıntısını oluşturur.
9. Dik üçgendeki dar açıların trigonometrik oranlarını belirler.
Uygulamanın yapılacağı 6 kazanım; 1,2,3,4,5 ve 8. kazanımlardır. Bu kazanımlar Bloom Taksonomisine göre bilişsel alana uygundur. 1. ve 8. kazanım bilişsel alanın kavrama düzeyinde yer alırken, 2,3,4 ve 5. kazanımlar bilişsel alanın uygulama düzeyindedir.
1.6. Tanımlar
Bağımlı Değişken: Araştırmacı tarafından incelenerek ölçümü yapılan değişkendir (Arıkan. 2007).
Bağımsız Değişken: Araştırmacı tarafından gerektiğinde değiştirilen veya manipüle edilen değişkendir (Arıkan, 2007).
Matematik: Aritmetik, cebir, geometri gibi sayı ve ölçü temeline dayanarak niceliklerin özelliklerini inceleyen bilimlerin ortak adıdır (Ağakay, 1974).
Geleneksel Öğretim Yöntemi: Öğretim programına uygun olarak bütün öğretmenler tarafından kullanılan ve bütün faaliyetlerin öğretmende olup öğrencinin pasif kaldığı öğretim yöntemidir (Fidan, 1996).
Aktif Öğrenme: Öğretimin merkezinde öğrencinin bulunduğu ve her aşamaya öğrencinin katıldığı öğrenme sürecidir (Açıkgöz, 2009).
Başarı Testi: Belli bir programa dayalı bir öğretimin sonunda katılımcıların bilgi, kavram ve anlayış yönlerinden sağladıkları gelişmeyi tespit etmek amacı ile hazırlanan ve kullanılan testlerdir (Yıldırım, 1996).
Yapılandırmacı Yaklaşım: Öğrencilerin öğrenme sürecinin merkezinde yer aldığı ve öğrenme sürecinde kendi bilgilerini, zihinsel süreç içerisinde keşfedip algıladıkları biçimde zihinde algoritmik esaslara dayalı olarak yapılandırdıkları bir öğrenme anlayışıdır (Saban, 2004).
BÖLÜM II
KAVRAMSAL ÇERÇEVE
Eğitim, bireyin davranışlarında kendi yaşantısı yoluyla istendik değişme meydana getirme sürecidir (Ertürk, 1972). Bu tanım incelendiğinde eğitime katılan bireylerde bazı davranış değişiklikleri meydana geleceği, bu değişikliklerin amaçlanan doğrultuda ve bireylerin kendi yaşantıları sonucunda gelişen bir süreç olduğu görülmektedir. Buradaki süreç kavramını, istenmeyen davranışların değiştirilmesi veya istendik davranışların yenilerinin oluşturulması için yapılan etkinlikler olarak açıklayabiliriz. Sürecin işleyişinde kullandığımız yöntem ve teknikler benimsediğimiz öğretim yaklaşımına göre şekillenmektedir.
Eğitimde sürecin işleyişine dair kullanılan yöntem ve teknikler son yıllarda yapılandırmacı yaklaşım üzerinde yoğunlaşmaktadır. Yapılandırmacılık giderek popülerleşen bir bilme (knowing) kuramıdır. Bazı düşünceleri eskiden de dile getirilmiştir. Örneğin bilginin bilen tarafından yapılandırıldığı düşüncesi M.Ö. 5 ve 6. yüzyıllarda şüpheciler tarafından savunulmuştur. Locke’ ın, doğanın insanlara yansıttığı basit düşüncelerin zihin tarafından birleştirilip daha büyük düşünce donanımlarına dönüştüğü fikri de bu noktada iyi bir örnek oluşturmaktadır (Phillips, 1995). Kant, Jung ve Herbart gibi düşünürlerin de yapılandırmacı düşünceleri vardır. Örneğin Herbart, yaşantıların önceden bilinen kavramlarla ilişkilendirilmesi sürecinden bahsetmektedir (Duit, 1995). Ancak bunlar, çeşitli kuramlarda tek tek yer alan düşüncelerden öteye
gidememiştir. Bu nedenle böyle düşünceler içeren kuramlara da yapılandırmacı kuramlar denilememektedir (Açıkgöz, 2009).
Yapılandırmacılık 20. yüzyılın başlarından itibaren gelişmeye ve uygulamalara temel oluşturmaya başlamıştır. Yapılandırmacılık bir bilme kuramı olduğu için bilme, bilen, bilinen, bilgiyi yapılandırma süreci, bu süreci etkileyen etkenlerle ilgili birçok açıklama içermektedir. Yapılandırmacılığa göre bilgi, duyularımızla ya da çeşitli iletişim kanallarıyla edilgin olarak alınan ya da dış dünyada bulunan bir şey değildir. Tersine bilgi, bilen (öğrenen) tarafından yapılandırılır, üretilir. Bu nedenle yapılar kişiye özgüdür (Açıkgöz, 2009).
Aktif öğrenmenin kuramsal temelleri yapılandırmacılığa ve onun öğrenme alanındaki karşılığı olan bilişselciliğe dayanmaktadır. Gerek yapılandırmacılık gerekse bilişselcilik öğretim süreciyle değil öğrenme süreciyle ilgili çeşitli açıklamalar ve önermeler sunmaktadır (Açıkgöz, 2009).
2.1.Aktif Öğrenme
Aktif öğrenme, öğrenenin öğrenme sürecinin sorumluluğunu taşıdığı, öğrenene öğrenme sürecinin çeşitli yönleriyle ilgili kararlar ve öz düzenleme yapma olanaklarının verildiği ve karmaşık öğretimsel işlerle öğrenenin öğrenme sırasında zihinsel
yeteneklerini kullanmaya zorladığı bir öğrenme süreci olarak tanımlanmaktadır (Açıkgöz, 2002).
Aktif öğrenme, öğrencinin aktif olduğu öğrenme sürecinin merkezinde bulunduğu öğrenme yaklaşımıdır. Öğrenciyi pasif dinleyici durumundan alır öğrenme sürecinin içine çeker. Öğrencinin düşünmesine, yeteneklerini kullanmasına, öğrenilenler hakkında yorum yapmasına ve sürece katılmasına imkan sağlayan bir yöntemdir.
2.2.Aktif Öğrenme Yaklaşımında Öğretmen ve Öğrencinin Rolü
Aktif öğrenme yaklaşımında öğretmen ve öğrencinin rolü, bugüne kadar alışageldiğimiz öğretmen ve öğrenci rollerinden farklıdır. Aktif öğrenme yaklaşımının uygulandığı sınıflarda öğretmen rahat ve demokratik bir ortam oluşmasını sağlayacak rehber rolündedir.
Bugüne kadar bildiğimiz, uyguladığımız geleneksel öğrenme yönteminde öğretmen, sınıfta olayları kontrol eden, bilgiyi aktaran, konuşmaların çoğunu yapan, soru soran, cezalandıran, ödüllendiren yani en aktif, en baskın ve sürecin bütün sorumluluğunu taşıyan kişidir. Ancak aktif öğrenme yaklaşımında öğretmen, bunları yapmak yerine öğrencilere yön gösteren, önerilerde bulunan, fikir veren, rehber olan ve onların gelişimlerini gözlemleyen kişidir. Burada önemli olan, öğretmenin kendi
kararlarını öğrenciye dayatmaması ve onun yerine kararlar almaması, buna karşılık öğrencinin kendi öğrenmesinin sorumluluğunu üstlenmesidir.
Aktif öğrenme yaklaşımında öğrenci, araştırır, düşünür, soru sorar, keşfeder, tartışır, fikir üretir, karşılaştırma yapar, açıklar, örnek verir, anlam çıkarır. Önceki öğrenilenlerle bağ kurar, değerlendirme yapar, çıkarımlarda bulunur, tahmin eder. Neyi, nasıl öğreneceğine karar verir, eksikliklerinin farkına varır. Bilgiyi yeniden yapılandırır, sınıflar ve öğrenmek için uğraşır.
Aktif öğrenme yaklaşımı ile etkili iletişim becerilerine, yaratıcı düşünceye sahip, yaşam boyu öğrenen ve kendini geliştiren, yaşadığı toplumda etkili olan ve etkili insan ilişkileri kurabilen bireyler yetişir.
2.3.Aktif Öğrenme Yaklaşımında Sınıf Düzeni
Geleneksel öğrenme yaklaşımında öğrencilerin hareketsiz oturduğu, etkileşimin çok sınırlı olduğu bir sınıf düzeni vardır. Oysa aktif öğrenme yaklaşımında sınıf düzeni sabit değil hareketlidir. Öğrenciler, çeşitli biçimlerde (küme, köşelenme, U, O, V veya iç içe halkalar vb.) otururlar. Sınıfın önü, arkası belli değildir. Aynı anda her köşesinde etkinlik sürmekte ve öğrenciler birbirleriyle sürekli etkileşim içinde bulunmaktadırlar. Sınıf düzeninin sürekli değişiklik göstermesi öğrencinin güdülenme düzeyini
artırmaktadır. Öğrenme ortamında meydana gelen her bir yenilik öğrenci için ilgi uyandırıcı, dikkat çekici bir anlam taşımaktadır (Açıkgöz, 2009).
2.4.Aktif Öğrenme Yaklaşımının Temel Düşünceleri
Açıkgöz (2009), aktif öğrenme yaklaşımının temel düşüncelerini aşağıdaki şekilde sıralamıştır:
• Öğrenen, öğrenme sürecinin aktif bir öğesidir. • Öğrenme birikimli bir süreçtir.
• Öğrencilerin öğrenme kapasiteleri artırılabilir.
• Öğrenme malzemesi öğrenene bildiği bağlamda sunulmalıdır. • Kalıcılık için öğrenilenlerin kullanılması gerekir.
• Etkileşim, insanı ve beyni geliştirir.
• Öğrenme sürecinde etkili olmak öğreneni güdüler. • Öğrenmede ezber değil anlam önemlidir.
• Uğraştırıcılık, öğrenme sürecinin etkililiğini artırır. • Farklı kişiler, farklı biçemlerde öğrenir.
Tezin uygulama aşamasında kullanılan aktif öğrenme yaklaşımına göre hazırlanan ders planlarının içeriğinin oluşturulmasında ve sınıf ortamında gerçekleştirilmesinde bu temel düşünceler dikkate alınmaya çalışılmıştır.
2.5. Aktif Öğrenme Yaklaşımının Uygulanmasında Karşılaşılan Zorluklar
Literatürde aktif öğrenme yaklaşımının uygulanmasında karşılaşılan bazı zorluklar vardır. Bu zorluklar sınıf içinde öğrencilerden ve/veya öğretmenlerden kaynaklanacağı gibi sınıf dışı etkenlerden olan ailelerden ve/veya okullardan da kaynaklanabilir.
Öğrenciler aktif öğrenmeyi farklı algılayabilirler. Bu öğrenme şeklinin kitaptakileri veya öğretmenin söylediklerini ezberleme olarak gerçekleştiğini düşünebilirler. Oysa aktif öğrenmede ezber eğilimli çalışmak, uygulamada sorunlara neden olur. Çünkü aktif öğrenmede ezber değil bilgiyi öğrencinin kendisinin yapılandırması, anlamlandırması esastır.
Öğretmenler aktif öğrenmenin tam olarak ne anlama geldiğini ve/veya nasıl uygulanması gerektiğini benimseyemediklerinde aktif öğrenme gerçekleşemez. Bu sebeple aktif öğrenme yaklaşımının öncelikle öğretmenlere anlatılması ve uygulama noktasında aktif öğrenmeyi benimsemeleri sağlanmalıdır.
Aileler açısından bakıldığında ise yıllardır geleneksel öğrenme yaklaşımına alışıldığından aktif öğrenme uygulamalarından tatmin olmayabilir, oyun, eğlence olarak algılayabilirler. Çocukların önceden daha çok şey öğrendiğini şimdi ise derslerin içinin çok boşaltıldığını, müfredattaki bilgilerin de yetersiz olduğunu
düşünebilirler. Çünkü her ne kadar 2004 yılından bu yana eğitim sistemimiz yapılandırmacı yaklaşıma göre şekillenmiş ve öğrencilerin aktif olması benimsenmiş olsa da hala bazı öğretmenler geleneksel öğretimin etkilerinden kurtulamamakta ve aileler de yeni eğitim sisteminin ne olduğunu tam olarak anlayamamaktadır.
Son olarak okul açısından bakıldığında ise öğretmenler arasında iletişim, etkileşim olmadan yeterli materyal ve öğrenme ortamları hazırlanmadan aktif öğrenme yaklaşımının uygulanması neredeyse imkansızdır.
2.6. Aktif Öğrenme Yaklaşımında Kullanılabilecek Yöntem ve Teknikler
Aktif Öğrenme Yaklaşımının uygulandığı deney grubu ders planlarında (Ek-2) adı geçen ve ders işleyiş esnasında kullanılan bazı yöntem ve teknikler aşağıda kısaca açıklanmaya çalışılmıştır.
Kartopu
Verilen bir problem ya da konu ile ilgili olarak, öğrenciler önce tek başına düşünüp sonra iki, daha sonra dört ve sekiz kişilik gruplarla tartışırlar. Yönteme kartopu denmesinin nedeni grubun giderek büyümesidir. En son grupta ulaşılan sonuçlar, sınıfa sunulur Açıkgöz (2009).
Akvaryum
Sınıf içi tartışmaları canlandırmak, mümkün olduğu kadar çok sayıda öğrenciyi tartışmaya katmak için kullanılır. Uygulanması sırasında sıralar iç içe iki çember halinde oturulacak şekilde düzenlenir. Öğrencilere ne yapılacağı söylenir ve problem açıklanır. Tartışmaya katılacak olan öğrenciler iç çembere, dinleyiciler dış çembere oturur, tartışma başlatılır ve sonuca bağlanır Açıkgöz (2009).
Vızıltı
Küçük öğrenci grupları verilen bir problem, soru ya da konu üzerinde görüşme yaparlar. Öğrencilerden bir hipotez geliştirmeleri ya da konu ile ilgili bir örnek bulmaları gibi işler istenebilir. Daha sonra gruplar sözcüleri aracılığıyla sonucu sınıfa sunarlar. Sunum bazen sözcüler aracılığı ile sırasıyla bazen de büyük grup tartışması içinde yapılabilir. Vızıltı grupları geçicidir. Bazen, anlatım sırasında dinleyicilerin birbirine anlatılanlar hakkında aklına geleni söylemesiyle kendiliğinden oluşabilir. Böyle zamanlarda anlatıma biraz ara vererek bu fırsat değerlendirilebilir. Öğrenenlerin öğrendikleri hakkında konuşmaları daima yararlıdır Açıkgöz (2009).
Şiir yazma
Öğrenciler küçük gruplar halinde otururlar. Her birinde kağıt bulunur. Verilen konu ile ilgili bir dize yazmaları söylenir. Yanındakiyle kağıtlar değişilir. Yeni kağıda ikinci dize yazılır. Süre bitene kadar devam edilir. Grupların elinde üye sayısı kadar şiir bulunur. Daha sonra şiirler sınıfa okunur. Tezin uygulaması sırasında bu yöntemi
kullanarak öğrencilere yaptırılan çalışmaların bazıları ekler bölümünde verilmiştir (Ek-3).
Kavram Haritaları
Kavramlar eşyaları, olayları, insanları ve düşünceleri benzerliklerine göre gruplandırdığımızda bu gruplara verilen addır. Kavramlar bilgilerin yapı taşlarını, kavramlar arası ilişkiler de bilimsel ilkeleri oluştururlar. Günümüzde öğrenmenin işlemsel değil kavramsal olduğu kabul edilmekte ve bazı kavramların öğrencinin zihninde oluşmasını sağlamak olarak tanımlayabileceğimiz kavram öğretimine önem verilmektedir (Turgut ve arkadaşları, 1997).
Kavram öğrenmede en önemli nokta, öğrencilerin daha önce öğrendiği kavramların, yeni öğrendiği kavramlarla ilişkilendirilmesidir. Kavramlar arası ilişki kurmada en önemli araç kavram haritalarıdır. Kavram haritaları 1970’li yılların sonlarında Cornell Üniversitesi’nde Prof. J. D. Novak tarafından geliştirilmiştir (Çavaş ve Pekmez, 2001). Bilgilerin grafiksel olarak gösterimini içeren bir tekniktir. Kavram haritaları kavramlar arası bağlantıyı gösteren görsel bir şemadır.
Tereyağı-Ekmek
Verilen bir problem, bir soru ya da konu üzerinde öğrenciler önce tek başlarına düşünür, daha sonra arkadaşları ile bir araya gelerek düşüncelerini tartışırlar. Sonunda, ulaştıkları sonucu sınıfa sunarlar. Öğrenciler fikirlerini iki aşamada sunmaktadır ve
birinci aşamanın üzerine ikinci aşama konuşma yapılırken arkadaşları ile paylaştıklarını da düşünerek daha verimli bir sunuş gerçekleştirir. Teknik, birinci aşamanın üstüne bir daha konuşma fırsatı verdiği için bu adı almıştır (Açıkgöz, 2009).
Örnek Olay
Belirli bir öğretim konusu ile ilgili gerçek hayatta karşılaşılan problemlerin sınıf ortamında neden, nasıl ve sonuç ilişkisine göre incelenerek çözülmesi yöntemidir. Bu yöntemin amacı öğrencilerin konu ile ilgili bilgi, beceri ve tutum kazanmasını sağlamak ve benzer olaylar karşısında daha hızlı ve etkin çözüm yolları bulmalarına yardımcı olmaktır (Yılmaz ve Sünbül, 2000).
Kart Gösterme
Kart gösterme yöntemi öğrencilere öğrendiklerini gözden geçirme, değerlendirme yapma, karar verme vb. fırsatlar sunar. Önce öğrencilere çeşitli renklerde 3-5 adet küçük kart ya da kağıt parçalarından oluşmuş desteler dağıtılır. Her renge bir anlam verilir. Örneğin yeşil tümüyle katılıyorum, mavi katılıyorum, beyaz kararsızım gibi. Sonra öğretmen işlenen konu ile ilgili bazı cümleleri okur. Bu cümleleri dinleyen öğrenciler önce hangi kartı seçeceklerini düşünürler. Daha sonra seçtikleri kartı sıranın üzerine koyarlar. En sonunda her öğrenci neden o kartı seçtiğini yani neden öyle düşündüğünü açıklar (Açıkgöz, 2009).
Beyin Fırtınası
Beyin Fırtınası yöntemi, birden fazla kişinin bir araya gelerek bir konuyla ilgili fikirlerini tartışmaksızın açıklayarak birbirleriyle fikir alışverişinde bulundukları, bireyin yaratıcı düşünme gücünü geliştiren bir öğretim tekniğidir. Bu teknik bir problemi çözmek, bir konuyu netleştirmek gibi amaçlarla kullanılır. Sınıftaki öğrencilerin tümünün katılmasına elverişli olması, onların yaratıcılığını teşvik etmesi, dersi ilginç duruma getirmesi ve kullanışlı olması nedeniyle önerilmektedir.
Beyin fırtınası yaparken öğrenciler gruplara ayrılır. Öğretmen bir problem ortaya atar, bu bir olay veya deney olabilir. Bu problemin çözümünü bütün gruplar kendi aralarında tartışır ve çözüm üretmeye çalışırlar. Her grup bir sonuca varır. Grup sözcüleri çözümü sınıfa sunar. Öğretmen olumlu veya olumsuz bir cevap vermez. Çok ilgisiz cevaplar gelse de “evet” ya da “hayır” diye cevap vermez. Sadece dinler, başını sallayıp “hı hı” diye öğrencilerin konuşmasını teşvik eder. Grup sözcüleri sonuçların sunumunu bitirince zaman varsa gruplar arası tartışma açılabilir. Sonuçlar tahtaya yazılır. Saçma ve yanlış olanlar elenir. Doğruya ulaşılmaya çalışılır. En sonunda öğretmen problemin doğru çözümünü, olayın nedenini, deneyin neden öyle olduğunu açıklar. Tartışma, grup yerine bireysel olarak da yapılabilir (Gürdal, Şahin, Çağlar, 2001).
Günlük Tutma
Öğrencilerin belirli aralıklarla öğrendikleriyle ilgili düşüncelerini, olayları ve izlenimlerini kaydetmeleridir. Bu uygulama öğrencilerin öğrendiklerini gözden geçirmelerini, öğretim sonucunda kendilerinin nereden nereye geldiklerini ve ne kadar ilerlediklerini görmelerini sağlar. Tezin uygulaması sırasında bu yöntemi kullanarak öğrencilere yaptırılan çalışmaların bazıları ekler bölümünde verilmiştir (Ek-3).
Çalışma Yaprağı
Öğrenilenlerle ilgili tekrar ve uygulamayı sağlayan öğrenilenlerin kullanılmasına ve dönüştürülmesine imkan tanıyan bir tekniktir. Tezin uygulaması sırasında deney grubu öğrencilerine yaptırılan çalışma yaprağı örnekleri ekler bölümünde verilmiştir. (Ek-2). Uygulama sırasında çalışma yapraklarının öğrencilerin konuyu kavramalarında ve pratik düşünme becerisi kazanmalarında oldukça faydalı olduğu görülmüştür.
Hızlı Tur
Öğrencilere öncelikle konu ya da soru verilir. Bir müddet düşündükten sonra sırayla konuşmaları sağlanır. Konuşanlar daha önce söylenmiş bir şeyi tekrar edemezler. Söyleyecek bir şeyleri olmayanlar “geçiniz” diyerek bir sonraki öğrenciye sırasını verir.
Her öğrenciye konuşma fırsatı veren ve bütün sınıfı içine alan bir tekniktir. Çekingen öğrencilere konuşma fırsatı verirken onların konuşup konuşmama noktasında olsa bile ufak da olsa yaşamları ile ilgili karar vermelerini sağlar. Konunun gözden geçirilmesine yardımcı olur (Açıkgöz, 2007).
Drama
Drama, insanın kendini başkalarının yerine koyarak çok yönlü gelişmesi, bireyin eğitim ve öğretimde aktif rol alması, kendini doğru ifade edebilme, yaratıcı olma, yaşamı çok yönlü algılama istek ve duygusunun gelişmesi, eğitim ve öğretimin buyurgan, kısırlaştırıcı ve angarya haline dönüşmesine karşın bireyin eğitim ve öğrenme isteğini artırıcı eğitim yöntemi olarak tanımlanmıştır (Koç ve Dikici, 2002).
Problem Çözme
Problem, bireyin içinde bulunduğu durumla olmasını istediği durum arasında engelin olması ve bunun bireyde gerilim yaratması durumudur. Problem çözme ise bireyin amacına ulaşmasını engelleyen sorunlarla başa çıkabileceği bir çözüm bulmasıdır (Ülgen, 2001).
Problem çözme sürecinde yer alan başlıca işlemler sırasıyla aşağıdaki gibidir:
2. Problemi tanımlama,
3. Problemin çözümünü, olabilecek seçenekleri saptama,
4. Seçenekleri değerlendirmede kullanılabilecek verileri toplama, 5. Verileri değerlendirme,
6. Genellemelere ve sonuçlara ulaşma,
7. Çözümü uygulamaya koyma ve etkinliliğini değerlendirme.
Problemlerin ve problem çözmenin öğretim tekniği olarak kullanılması öğrencileri araştırma yapmaya, kaynakları tamamlamaya ve öğrendiklerini birbirleriyle paylaşmaya yönlendirir (Açıkgöz, 2009).
Aktif öğrenme yeni bir düşünce değildir. Yüzyılın başından beri çeşitli yazarlar tarafından zaman zaman dile getirilmiş olmasına rağmen psikoloji ve eğitim gibi bilim dallarında davranışçılık akımının egemen olması bu düşüncenin yayılmasını geciktirmiştir.
Aktif öğrenme anlayışına göre öğrenme yeteneği durağan değil değişkendir. Eğitim yoluyla öğrencilerin öğrenme kapasiteleri artırılabilir. Bu nedenle eskiden olduğu gibi öğrencilerin yeteneklerine göre sınıflanması ve yeteneğin değişmeyen bir özellik olduğu doğru değildir. Tersine bir yandan öğrencinin bir konu alanına özgü bilgi ve becerileri öğrenirken diğer yandan öğrenmeyi öğrenmesi sağlanabilir.
Yapılan araştırmalarda bu görüşleri destekleyen bulgular elde edilmiştir. Başarısız öğrencilerin başarılı öğrencilerden farkının ön öğrenmelerindeki ve bilişsel
strateji kullanımlarındaki farklılıklar olduğu saptanmıştır. Başarılı öğrenciler bilgiyi başarılı olmayanlardan daha hızlı işlemektedirler. Ancak daha önce de belirtildiği gibi bu farklılıklar durağan değildir. Çünkü bilişsel stratejiler öğrenilebilirdir. Yetişme ile daha iyi öğrenen olunabilir. Önemli olan öğrencilere bu fırsatların sağlanmasıdır.
2.7. İlgili Araştırmalar
Senk (1983) tarafından yapılan "İspat Yapabilme Başarısı ve Ortaokul Öğrencilerinin Van Hiele Düzeyleri" adlı araştırmada, öğrencilerin geometrik düşünce düzeyleri ile ispat yapabilme başarıları arasındaki ilişkiye bakılmıştır. 1520 ortaokul öğrencisine Van Hiele geometri testi ve geometri başarı testi uygulanmıştır. Analiz sonuçlarına göre ispat yapabilme becerilerinin düşük olduğu ve Van Hiele geometri testinin ispat yapabilme başarısını arttırmada kullanılabileceği saptanmıştır.
Rosenthal (1995), üst düzey matematik sınıflarında aktif öğrenme stratejileri uygulamak ve değerlendirmek amacıyla yaptığı çalışmada, küçük gruplarla işbirlikli öğrenme ve teknik konularda deneme yazma görevlerini içeren alternatif öğrenme yaklaşımlarını kullanmanın desteklenmesi gerektiğini belirtmiştir. Öğrencilerin katılımlarının ve etkileşimde bulunmalarının artırılması, bakış açılarının geliştirilmesi vurgulanmaktadır. Araştırma sonucunda elde edilen bulgular, çeşitli aktif öğrenme yöntemlerinin uygulanmasının öğrencilerin öğrenmesini olumlu etkilediğini ortaya koymuştur.
Uysal (1996), öğrenme sürecine etkin öğrenci katılımının öğrenme sonuçlarına etkisini incelemiştir. Bu araştırmasında etkin öğrenci katılımının sağlandığı öğretim ortamında yer alan deney grubu öğrencileri ile geleneksel öğretim ortamında yer alan kontrol grubu öğrencilerinin başarı puanları arasında anlamlı bir fark tespit edilmiştir. Araştırma sonucunda, öğrenme sürecine etkin öğrenci katılımının başarıyı artırdığı ve öğrencinin öğrenme sürecine etkin katılım düzeyi ile başarısı arasında olumlu bir ilişki gözlemlenmiştir.
Nakiboğlu ve Altıparmak (2002), “Aktif Öğrenmede Bir Grup Tartışması Yöntemi Olarak Beyin Fırtınası” isimli yaptıkları çalışma ile beyin fırtınasının öğrencilerin derse yönelik ilgilerini artırdığını, bilgileri hangi alanda nasıl kullanacaklarını, verilen bilgilerin gerekliliğini ve önemini kavrama bilincini, bilgi birikimlerini ve gözlemlerini analiz ederek sonuca ulaşmayı geliştirdiklerini ortaya koymuştur.
Altun ve Olkun (2003), “İlköğretim Öğrencilerinin Bilgisayar Deneyimleri ile Uzamsal Düşünme ve Geometri Başarıları Arasındaki İlişki” üzerine yaptıkları çalışmada farklı sosyo-ekonomik çevrelerden gelen öğrencilerin bilgisayarda edindikleri deneyimlerin geometri ve uzamsal düşünme becerileri üzerinde fark yaratıp yaratmadığını incelemişlerdir. Araştırma Bolu il sınırı içerisinde bulunan 4 okulun 4 ve 5. sınıflarında öğrenim gören toplam 297 öğrenci ile yürütülmüştür. Araştırmada elde edilen bulgular öğrencilerin bilgisayarlı ortamda daha çok geometri öğrenebildiğini ve farkın gittikçe arttığını destekler niteliktedir. Ancak bu iddianın daha kesin şekilde
desteklenebilmesi için deneysel araştırmalara gereksinim vardır. Cinsiyet değişkeninin bu çalışmada bir fark yaratmadığı görülmüştür.
Demirci (2003), ilköğretim 5. sınıf Fen Bilgisi dersinde aktif öğrenme yaklaşımının uygulandığı deney grubu ile geleneksel öğretimin uygulandığı kontrol grubunun erişileri üzerine etkisini incelemiştir. Çalışmasında öntest, sontest ve kontrol gruplu deneysel desen kullanmıştır. Sonuç olarak aktif öğrenme yaklaşımının uygulandığı deney grubu ile geleneksel öğretimin uygulandığı kontrol grubunun erişi puanları arasında deney grubunun lehine anlamlı bir fark bulunmuştur.
Fife (2003), Doğu Tennessee Üniversitesi’nde yaptığı araştırmada etkinliklerle yapılan öğretimle geleneksel öğretimin birinci sınıf öğrencilerinin Matematik bilgilerini hatırda tutmalarına etkisini sınamıştır. Öntest, sontest ve kontrol gruplu deneysel desen kullanılan araştırma 6 hafta sürmüştür. Kontrol grubunda geleneksel yöntem, deney grubunda ise etkinlikler kullanarak gerçekleştirilen aktif öğrenme yaklaşımı kullanılmıştır. p<.05 anlamlılık düzeyinde gerçekleştirilen araştırma sonucunda deney ve kontrol grubu arasında anlamlı fark gözlenmediğinden araştırmanın hipotezi geçersiz bulunmuştur. Araştırmacı bu durumu araştırma süresinin kısa olmasına bağlamıştır.
Memnun (2003), ilköğretim 8. sınıf matematik dersinde permütasyon ve olasılık konusunun aktif öğrenme yöntemi ile yapılan öğretimin, öğrenci başarısında yarattığı farklılıkları belirlemek amacıyla bir araştırma yapmıştır. Deney grubunda 90, kontrol grubunda 107 öğrenci bulunmaktadır. Deney grubunda aktif öğrenme, kontrol grubunda
geleneksel yöntemle ders işlenmiştir. Uygulama sonunda aktif öğrenme ile yapılan öğretimin öğrenci başarısını arttırdığı görülmüştür.
Seyhan (2003), 7. sınıf matematik dersinde aktif öğrenme ve geleneksel öğretim metotlarını karşılaştırdığı çalışmasında öntest, sontest ve kontrol gruplu deneysel desen kullanılmıştır. Deney grubunda ‘pi sayısı ve çemberin çevresi’ ve ‘dairenin alanı’ ile ilgili aktif öğrenme etkinliklerini, kontrol grubunda ise geleneksel ders anlatma yöntemi kullanılmıştır. Araştırma sonucunda, aktif öğrenme yönteminin öğrenci başarısı açısından geleneksel öğretim yönteminden daha etkili olduğu öğrencilerin olumlu tutum ve görüş sergilediği görülmüştür.
Duatepe ve Ubuz (2004), drama temelli geometri ders planının geliştirilmesi ve uygulanması üzerine yaptıkları çalışmada 7. sınıf geometri konularının öğretilmesi ve öğrenilmesinde dramanın kullanılmasını amaçlayan ders planlarının geliştirilmesi ve uygulanması örnekler verilerek sunulmaktadır. Ayrıca, bu çalışmada bazı deneysel sonuçlar da kısaca verilmektedir. Çalışma 2002-2003 eğitim-öğretim yılı ikinci döneminde bir devlet okulunda bulunan 3 yedinci sınıf üzerinde gerçekleştirilmiştir. Her sınıfta 34 öğrencinin yer aldığı örneklem 102 öğrenciden oluşmaktadır. Grupların ders saatleri dikkate alınarak ikisi deney biri kontrol grubu olarak atanmıştır. Deney grubunda dersler drama yöntemi kullanılarak geliştirilen ders planları ile birinci araştırmacı tarafından sürdürülmüştür. Kontrol grubunda ise matematik öğretmeni tarafından düz anlatım yöntemi kullanılarak gerçekleştirilmiştir. Bunun yanında öğrencilerin geometrik düşünme seviyelerini ölçmek için Van Hiele geometrik düşünme
testi (Usiskin, 1982) ve matematiğe karşı tutumlarını ölçmek için matematik tutum ölçeği ana çalışmadan önce öğrencilere uygulanmıştır. Uygulamada her iki ünite bittikten sonra üniteler ile ilgili erişi testleri uygulanmıştır. İki erişi testinin yanı sıra matematiğe ve geometriye karşı tutumu ve geometrik düşünme seviyesini gelişimin belirlenebilmesi için tutum ölçekleri ve geometrik düşünme testi uygulamanın bitiminde tekrar uygulanmıştır. Araştırma sonucunda drama ile geometri öğrenen grubun lehine olmak üzere açılar ve çokgenler; ve çember, daire ve silindir konularındaki erişi ve kalıcılık testlerinden, Van Hiele geometrik düşünme testinden, matematik ve geometri tutum ölçeklerinden aldıkları puanlar arasında istatistiksel olarak anlamlı bir fark görülmüştür. Bu sonuçlar dramanın değişik konu alanlarında erişiyi artırdığı ve hatırlamayı desteklediği yönündeki bulguları desteklemektedir. Bu bulguları, yapılan yüz yüze görüşmeler de desteklemektedir. Yapılan görüşmelerde deney grubundaki öğrenciler drama temelli geometri derslerinin eğlenceli, kalıcı, istek ve merak uyandırıcı olduğundan söz etmişlerdir.
Ünal (2004), ilköğretim 6. sınıf matematik dersinde “Nokta, doğru, düzlem, doğru parçası, uzay ve ışın” konusunun aktif öğrenme yöntemiyle öğretiminin öğrenci başarısı üzerine etkisini belirlemek amacıyla bir araştırma yapmıştır. Araştırmada deney grubu 36, kontrol grubu 29 öğrenciden oluşturulmuştur. Deney grubunda aktif öğrenme, kontrol grubunda geleneksel yöntemle ders işlenmiştir. Son test sonuçları dikkate alındığında deney grubunun kontrol grubuna göre daha başarılı olduğu görülmüştür.
Köseoğlu (2005), kesirler konusunun öğretiminde aktif öğrenme yönteminin öğrenci başarısına etkisini belirlemek amacıyla deneysel bir çalışma yapmıştır. 6. sınıf
kesirler ünitesi deney grubunda aktif öğrenme, kontrol grubunda geleneksel yöntemle anlatılmıştır. Çalışmalar sonucunda her iki grupta da başarı artışı görülmüştür fakat deney grubundaki başarı artışının kontrol grubundaki başarı artışından daha fazla olduğu belirlenmiştir.
Acar (2005), açı ve üçgen çeşitleri konusunun öğretiminde aktif öğrenme yönteminin matematik dersi başarısı üzerine etkisini belirlemek amacıyla deneysel bir çalışma yapmıştır. 48 öğrenciden oluşan deney ve kontrol gruplarından deney grubunda aktif öğrenme yöntemi ile kontrol grubunda ise geleneksel yöntemle ders anlatılmıştır. Elde edilen verilere göre aktif öğrenme ile işlenen dersin başarıyı arttıracağı kanısına varılmıştır.
Aksu (2005) tarafından yapılan araştırmada, ilköğretimde aktif öğrenme modeli ile geometri öğretiminin başarıya, kalıcılığa, tutuma ve geometrik düşünme düzeyine etkisi incelenmiştir. Araştırmada dersler deney grubunda aktif öğrenme yöntemi ile kontrol grubunda ise geleneksel yöntem kullanılarak işlenmiştir. Verileri toplamak için Matematik Başarı Testi, Matematik Tutum Ölçeği ve Van Hiele Geometri Testi kullanılmıştır. Sonuç olarak, aktif öğrenme yönteminin öğrenci başarısını artırmada, matematiğe karşı olumlu tutum geliştirmede ve kalıcılık düzeyinde geleneksel öğretim yöntemine göre daha etkili olduğu görülmüştür.
Ciritli (2006), ilköğretim 4 ve 5. sınıf öğretmenlerinin aktif öğrenme metodunu algılama ve sınıflarında uygulama durumlarını araştırmıştır. Araştırma sonucunda
öğretmenlerin aktif öğrenme metodu hakkında bilgi sahibi oldukları ancak sınıflarında aktif öğrenme metoduna yer vermedikleri, geleneksel öğretim yöntemiyle ders anlatmaya devam ettikleri görülmüştür.
Seyhan ve Gür (2006), ilköğretim 7. sınıf matematik öğretiminde aktif öğrenmenin öğrenci başarısı üzerine etkisini araştırmak amacıyla yaptıkları çalışmada, çember ve daire konusu deney grubuna aktif öğrenme yöntemi kullanılarak kontrol grubuna ise geleneksel yöntem kullanılarak anlatılmıştır. Araştırma sonucunda aktif öğrenme yönteminin kullanıldığı deney grubu öğrencilerinin geleneksel yöntemin kullanıldığı kontrol grubu öğrencilerine göre daha başarılı olduğu gözlenmiştir.
Şen (2008), ilköğretim 7. sınıflarda matematik dersi birinci dereceden bir bilinmeyenli denklemler konusunun aktif öğrenme yöntemiyle işlenmesinin öğrenci başarısına etkisini incelemiştir. Deney grubunda 29, kontrol grubunda 28 öğrencinin yer aldığı araştırmada, deney grubunda aktif öğrenme yöntemi, kontrol grubunda geleneksel yöntem kullanılmıştır. Aktif öğrenme yönteminin uygulandığı deney grubu öğrencilerinin kontrol grubu öğrencilerine göre daha başarılı olduğu saptanmıştır.
BÖLÜM III
YÖNTEM
Bu bölümde araştırmanın modeli, evreni ve örneklemi, araştırmada kullanılacak veri toplama araçları ve elde edilen verilerin analiz edilmesinde kullanılacak olan yöntemle ilgili gerekli bilgiler verilmiştir.
3.1.Araştırmanın Modeli
Bu araştırmada, 8. sınıf matematik dersi üçgenler alt öğrenme alanının öğretiminde aktif öğrenme yaklaşımının öğrenci başarısına ve kalıcılığına etkisi incelenmiştir.
Araştırmada, ön test-son test kontrol gruplu deneysel araştırma modeli kullanılmıştır. Araştırma, belirli amaçlar için daha önce şekillenmiş olan gruplar üzerinde yapılmıştır. Ön test-son test kontrol gruplu modelin kullanıldığı araştırmalarda iç-geçerliliği tehdit edebilecek tarih, olgunluk, test etme ve araç gibi kaynaklardan gelen hatalar ya da etkiler diğer modellere kıyasla daha çok kontrol altında tutulabilmektedir. Bu da ön test-son test kontrol gruplu modeli diğer modellere oranla daha güvenilir ve kullanışlı kılmaktadır (Kaptan, 1998).
Bu çalışmada, uygulamanın yapılacağı okulunun 8. sınıflarından rastgele iki şube seçilmiş ve yine rastgele bu iki şubeden biri kontrol diğeri deney grubu olarak atanmıştır. Ön test sonuçlarına göre seçilen grupların denk hale getirilmesi eğitim sistemimizin buna olanak sağlamaması nedeniyle yapılamamıştır. Deney grubunda dersler aktif öğrenme yöntemiyle kontrol grubunda ise geleneksel öğretim yöntemleriyle işlenmiştir. Her iki gruba da başarı testi deney öncesi ve sonrasında uygulanmıştır. Ayrıca öğretimden yaklaşık bir ay sonra tekrar aynı başarı testi uygulanarak öğretimin kalıcılığına bakılmıştır.
3.2. Evren ve Örneklem
Bu araştırmanın evrenini Ankara ilinde bulunan ilköğretim 8. sınıf öğrencileri, örneklemini ise 2011-2012 eğitim-öğretim yılında yine Ankara ilinde bulunan bir ilköğretim okulundaki iki şube oluşturmaktadır. A şubesi deney grubu, B şubesi kontrol grubu olarak rastgele seçilmiştir. Deney grubunda dersleri araştırmacı, kontrol grubunda ise sınıf öğretmeni anlatmıştır. Uygulama toplam 3 hafta ve 12 ders saati sürmüştür.
3.3.Veri Toplama Yöntemi ve Araçları
Bu araştırmada, araştırmacı tarafından geliştirilmiş olan başarı testi kullanılmıştır. Başarı testi araştırmacı tarafından uygulama yapılacak 6 kazanımı kapsayacak şekilde 29 sorudan oluşturulmuş, başarı testinin taslağı oluşturulduktan
sonra uzman görüşleri alınmış ve bu görüşler doğrultusunda gerekli düzenlemeler yapılarak testin geçerliği sağlanmıştır. Uzman görüşleri doğrultusunda düzenlenerek oluşturulan taslak form uygulama yapılacak olan grupla benzer özelliklere sahip daha önce bu konuları görmüş Ankara ilindeki bir Anadolu lisesinin 9. sınıf öğrencilerinden oluşan 164 öğrenci üzerinde uygulanmıştır. Testin uygulanması için enstitü aracılığıyla İl Milli Eğitim Müdürlüğü’nden yazılı izin alınmıştır (Ek-4). Uygulama okulundaki yöneticiler ve öğretmenler gerekli desteği sağlamıştır ve bu sayede hiçbir sorunla karşılaşılmadan kısa sürede verilere ulaşılmıştır. Elde edilen veriler MS Excel programı yardımıyla hesaplanarak başarı testinin güvenirliğine ilişkin elde edilen sonuçlar Tablo 3.1’ de verilmiştir.
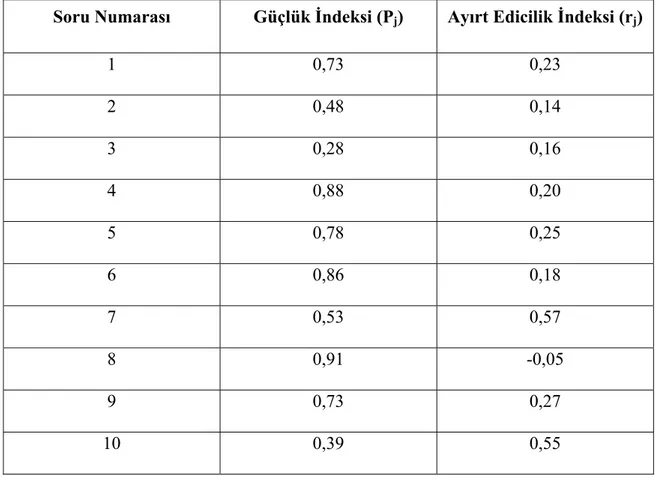
Tablo 3.1. Geliştirilen başarı testinin sorulara göre güçlük ve ayırt edicilik indeksleri
Soru Numarası Güçlük İndeksi (Pj) Ayırt Edicilik İndeksi (rj)
1 0,73 0,23 2 0,48 0,14 3 0,28 0,16 4 0,88 0,20 5 0,78 0,25 6 0,86 0,18 7 0,53 0,57 8 0,91 -0,05 9 0,73 0,27 10 0,39 0,55
11 0,67 0,39 12 0,67 0,25 13 0,75 0,14 14 0,17 0,20 15 0,17 -0,02 16 0,24 0,02 17 0,80 0,27 18 0,66 0,41 19 0,61 0,41 20 0,26 0,39 21 0,63 0,61 22 0,41 0,55 23 0,42 0,57 24 0,69 0,52 25 0,38 0,43 26 0,50 0,55 27 0,48 0,59 28 0,81 0,34 29 0,73 0,41
Tablo 3.1.’ deki sonuçlara göre başarı testinin güçlük indeksi 0,66 olarak hesaplanmıştır. Bu sonuçlar doğrultusunda testin güvenirliğini artırmak için ayırt edicilik düzeyi düşük olan 8 ve 15. sorular uzman görüşleri doğrultusunda başarı
testinden çıkarılmıştır. Son haliyle başarı testinin güçlük indeksi 0,69 olarak bulunmuştur.
Ders planları ve başarı testi hazırlandıktan sonra çalışmanın yapılacağı okul ile irtibata geçilerek üçgenler alt öğrenme alanının bulunduğu ünitenin başlayacağı tarih belirlenmiş ve uygulama için tekrar İl Milli Eğitim Müdürlüğü’ nden yazılı izin alınmıştır (Ek-4).
Dersler başlamadan birkaç gün önce deney grubundaki öğrencilere yapılacak çalışma ile ilgili bilgi verilmiş ve ilk ders için yapmaları gereken hazırlıklardan bahsedilmiştir. Uygulamadan bir gün önce ise başarı testi deney ve kontrol gruplarına ön test olarak uygulanmıştır.
Uygulama sürecinde deney grubunda aktif öğrenme yaklaşımına uygun olarak hazırlanan ders planları araştırmacı tarafından anlatılmıştır. Kontrol grubunda ise ders öğretmeni her zaman olduğu gibi geleneksel yaklaşımla dersleri anlatmaya devam etmiştir.
Uygulama süreci tamamlandıktan bir gün sonra başarı testi deney ve kontrol gruplarına son test olarak uygulanmıştır. Yaklaşık bir ay sonra başarı testi son bir kez daha uygulanarak uygulamanın kalıcılığına dair bulgular elde edilmiştir.
3.4.Verilerin Analizi
Deney öncesinde ve sonrasında uygulanan başarı testinden (öntest ve sontest) elde edilen veriler SPSS programı ile analiz edilip yorumlanmıştır. Elde edilen veriler parametrik test istatistiklerinin varsayımlarının karşılanması durumunda ilişkisiz ölçümler için varyans analizi, ilişkili ölçümler için varyans analizi ve tekrarlı ölçümler için varyans analizi kullanılarak test edilmiştir. Bulguların yorumlanmasında 0,05 hata düzeyi dikkate alınmıştır.
BÖLÜM IV
BULGULAR VE YORUM
İlköğretim 8. sınıf öğrencilerinin matematik dersi geometri öğrenme alanı üçgenler alt öğrenme alanındaki kazanımların aktif öğrenme yaklaşımına uygun öğretiminin akademik başarılarına ve kalıcılığına etkisini incelemek amacıyla yapılan araştırmanın bu bölümünde toplanan verilerden elde edilen bulgular tablolar halinde verilmiştir.
4.1.Birinci Alt Probleme İlişkin Bulgular ve Yorum
Birinci alt problemde “Konunun aktif öğrenme kuramına göre anlatıldığı öğrenciler (deney grubu) ile geleneksel öğretimle öğrenim gören öğrencilerin (kontrol grubu) uygulamadan önceki başarı puanları arasında anlamlı bir fark var mıdır?” sorusunun cevabı aranmıştır. Deney ve kontrol gruplarından elde edilen veriler SPSS programı kullanılarak hesaplanmıştır. Tablo 4.1’ de görüldüğü gibi deney grubu 35, kontrol grubu 33 öğrenciden oluşmuştur. Uygulama öncesi deney grubunun aritmetik ortalaması 9,60 bulunurken, kontrol grubunun aritmetik ortalaması 9,51 bulunmuştur. Grupların ön test puanlarına ait aritmetik ortalamaları arasındaki fark t-testi ile karşılaştırılmış ve p=0,05 düzeyinde anlamlı bir fark bulunamamıştır (0,924>0,05). Görüldüğü gibi uygulama öncesi grupların aritmetik ortalamaları birbirine çok yakın
değerler almıştır. Yani uygulama öncesi deney ve kontrol grupları birbirleriyle hemen hemen aynı seviyededir. Deney ve kontrol grubu öğrencilerinin matematik başarı puanlarının uygulama öncesinde aynı seviyede olması diğer alt problemlerin yorumlanmasında kolaylık sağlaması açısından önemlidir.
Tablo.4.1. Deney ve Kontrol Grubu Öğrencilerinin Ön test Sonuçları
Grup N ss t sd p
Deney 35 9.60 4.34
0.095 66 0.924
Kontrol 33 9.51 2.76
4.2. İkinci Alt Probleme İlişkin Bulgular ve Yorum
İkinci alt problemde “Deney grubu öğrencilerinin uygulamadan önce (ön test) ve sonraki (son test) başarı puanları arasında anlamlı bir farkı var mıdır?” sorusunun cevabı aranmıştır. Deney grubundan elde edilen veriler SPSS programı kullanılarak hesaplanmıştır. Tablo 4.2.’ de görüldüğü gibi deney grubu öğrencilerinin uygulamadan önceki ön test aritmetik ortalaması 9,60 iken uygulamadan sonraki aritmetik ortalaması 14,51’e kadar yükselmiştir. Yapılan t-testi sonucuna göre bu değer 0,05 düzeyinde anlamlıdır (p<0,05). Yani deney grubu öğrencilerinin uygulama sonrasındaki aritmetik
ortalamasında gözlenen artış aktif öğrenme yaklaşımının başarıyı artırmada etkisi olduğu sonucunu ortaya çıkarmaktadır.
Tablo.4.2.Deney Grubu Öğrencilerinin Ön test-Son test Sonuçları
Grup N ss t sd p
Deney 35 9.60 4.34
13.717 34 .000 Deney 35 14.51 4.38
4.3. Üçüncü Alt Probleme İlişkin Bulgular ve Yorum
Üçüncü alt problemde “Kontrol grubu öğrencilerinin uygulamadan önce ve sonraki başarı puanları arasında anlamlı bir fark var mıdır?” sorusunun cevabı aranmıştır. Kontrol grubundan elde edilen veriler SPSS programı kullanılarak hesaplandığında; Tablo 4.3.’ de görüldüğü gibi kontrol grubu öğrencilerinin uygulamadan önceki ön test aritmetik ortalaması 9,51 iken uygulamadan sonraki aritmetik ortalamasının 11,72’ye kadar yükseldiği görülmüştür. Yapılan t-testi sonucuna göre bu değer 0,05 düzeyinde anlamlıdır (p<0,05). Yani kontrol grubu öğrencilerinin uygulama sonrasındaki aritmetik ortalamasında anlamlı bir artış gözlenmiştir. Bu durum geleneksel öğretimin öğrenci başarısını artırmada olumlu bir etkisi olduğu sonucunu ortaya koymaktadır.
Tablo.4.3. Kontrol Grubu Öğrencilerinin Ön test-Son test Sonuçları
Grup N ss t sd p
Kontrol 33 9.51 2.76
6.317 32 .000 Kontrol 33 11.72 2.99
4.4. Dördüncü Alt Probleme İlişkin Bulgular ve Yorum
Dördüncü alt problemde “Deney ve kontrol grubu öğrencilerinin uygulamadan sonraki başarı puanları arasında anlamlı bir fark var mıdır?” sorusunun cevabı aranmıştır. Deney ve kontrol gruplarından elde edilen veriler SPSS programı kullanılarak hesaplandığında Tablo 4.4’ de görülen sonuçlar ortaya çıkmıştır. Deney grubunun son test aritmetik ortalaması 14,51 iken kontrol grubu öğrencilerinin uygulamadan sonraki aritmetik ortalaması 11,72’dir. Bu değerler arasında t-testi puanına göre anlamlı bir fark vardır ve bu fark deney grubu lehinedir (p<0,05). Yani aktif öğrenme yaklaşımına göre ders işlenen grup geleneksel yönteme göre ders işlenen gruba göre daha başarılı olmuştur. Uygulama öncesi hemen hemen aynı seviyede olan gruplar uygulama sonrasında başarılarını artırmıştır ancak aktif öğrenme yaklaşımının uygulandığı deney grubunda başarı geleneksel yöntemle uygulamanın yapıldığı kontrol grubuna göre daha fazla artmış, öğretim yöntemleri daha etkili olmuştur.
Tablo.4.4. Deney ve Kontrol Grubu Öğrencilerinin Son test Sonuçları
Grup N ss t sd p
Deney 35 14.51 4.38
3.04 66 .003 Kontrol 33 11.72 2.99
4.5. Beşinci Alt Probleme İlişkin Bulgular ve Yorum
Beşinci alt problemde “Deney ve kontrol grubu öğrencilerinin kalıcılık düzeyleri arasında anlamlı farklılıklar var mıdır?” sorusunun cevabı aranmıştır. Deney ve kontrol gruplarından elde edilen veriler SPSS programı kullanılarak hesaplanmıştır. Tablo 4.5.’ de görüldüğü gibi deney grubunun kalıcılık testi aritmetik ortalaması 13,82 iken kontrol grubu öğrencilerinin kalıcılık testi aritmetik ortalaması 10,12’dir. Bu değerler arasında t-testi puanına göre anlamlı bir fark vardır ve bu fark deney grubu lehinedir (p<0,05). Yani aktif öğrenme yaklaşımına göre ders gören deney grubu öğrencilerinin geleneksel yaklaşıma göre ders gören kontrol grubu öğrencilerine göre kalıcılık düzeyleri daha fazla olmuştur. Aktif öğrenme yöntemi ile anlatılan konular geleneksel yönteme göre daha uzun süreli ve daha etkili olarak öğrenci zihninde yer edinmiştir.
Tablo.4.5. Deney ve Kontrol Grubu Öğrencilerinin Kalıcılık Testi Sonuçları
Grup N ss t sd p
Deney 35 13.82 4.28
4.207 66 .000 Kontrol 33 10.12 2.76
BÖLÜM V
SONUÇ VE ÖNERİLER
Geleneksel öğretime kıyasla aktif öğrenme kuramına uygun olarak yapılan öğretimin ilköğretim 8. sınıf öğrencilerinin matematik dersi geometri öğrenme alanı üçgenler alt öğrenme alanındaki başarılarına ve kalıcılığına etkisinin araştırıldığı araştırmanın bu bölümünde araştırmanın bulguları ve yorumlarına dayalı olarak elde edilen sonuçlara ve bu sonuçlar kapsamında geliştirilen önerilere yer verilmiştir.
5.1. Sonuçlar
Araştırmada toplanan verilerden elde edilen sonuçlar araştırmanın her bir alt problemi için ayrı ayrı maddelenmiştir.
i. Birinci alt problemle ilgili elde edilen veriler, deney ve kontrol grubu öğrencilerinin uygulama öncesindeki matematik başarı testi aritmetik ortalamaları arasında anlamlı bir fark olmadığını ortaya koymuştur. Buna göre aktif öğrenme yaklaşımının uygulandığı deney grubu öğrencileri ile geleneksel öğretim yönteminin uygulandığı kontrol grubu öğrencilerinin uygulama öncesi matematik başarılarının birbirine neredeyse eşit seviyede olduğu sonucuna varılmıştır.