Cooper instability in the occupation dependent hopping Hamiltonians

H. Boyaci, and I. O. Kulik

Citation: Low Temperature Physics 25, 625 (1999); View online: https://doi.org/10.1063/1.593807

View Table of Contents: http://aip.scitation.org/toc/ltp/25/8

Cooper instability in the occupation dependent hopping Hamiltonians

H. Boyaci

Department of Physics, Bilkent Universilty, Ankara 06533, Turkey

I. O. Kulik

Department of Physics, Bilkent University, Ankara 06533, Turkey;

B. Verkin Institute for Low Temperature Physics and Engineering, National Academy of Sciences of Ukraine, Lenin Ave. 47, 310164 Kharkov, Ukraine*

共Submitted April 13, 1999兲

Fiz. Nizk. Temp. 25, 838–849共August–September 1999兲

A generic Hamiltonian, which incorporates the effect of the orbital contraction on the hopping amplitude between nearest sites, is studied both analytically at the weak coupling limit

and numerically at the intermediate and strong coupling regimes for a finite atomic cluster. The effect of the orbital contraction due to hole localization at atomic sites is specified with

two coupling parameters V and W共multiplicative and additive contraction terms兲. The singularity of the vertex part of the two-particle Green’s function determines the critical temperature Tc and the relaxation rate ⌫(T) of the order parameter at temperature above Tc. Unlike the case in conventional BCS superconductors, ⌫ has a non-zero imaginary part which may influence the fluctuation conductivity of the superconductor above Tc. We compute the ground state energy as a function of the particle number and magnetic flux through the cluster, and show the

existence of the parity gap⌬ appearing at the range of system parameters consistent with the appearance of the Cooper instability. Numeric calculation of the Hubbard model共with U⬎0兲 at arbitrary occupation does not show any sign of superconductivity in a small cluster. © 1999 American Institute of Physics.关S1063-777X共99兲00708-2兴

1. FORMULATION OF THE MODEL

High temperature superconductivity in lanthanum,1 yttrium2 and related copper-oxide compounds remains the subject of intensive investigation and controversy. It was suggested that the electron-phonon interaction mechanism, which is very successful in understanding conventional 共‘‘low temperature’’兲 superconductors within the Bardeen– Cooper–Schrieffer scheme,3 may not be adequate for high-Tc cuprates, and even the conventional Fermi liquid model of the metallic state may require reconsideration. This opens an area for investigation of mechanisms of electron-electron interaction which can be relevant in understanding the pecu-liarities of superconducting, as well as normal state, proper-ties of cuprates. Specific to all of them is the existence of oxide orbitals. Band calculations4,5suggest that hopping be-tween the oxygen px, py orbitals and between the copper dx2_⫺y2 orbitals may be of comparable magnitude. On the

experimental side, spectroscopic studies6,7clearly show that the oxygen band appears in the same region of oxygen con-centration in which superconductivity in cuprates is the strongest. Therefore there exists the possibility that specific features of oxide compounds may be related to oxygen-oxygen hopping, or to the interaction between the copper and the rotational p_x⫺p_y collective modes. If the oxygen hop-ping is significant, then it immediately follows that the in-trinsic oxygen carriers 共px, py oxygen holes兲 should be dif-ferent from the more familiar generic s-orbital derived itinerant carriers. The difference is related to low atomic number of oxygen such that removing or adding of one

electron to the atom induces a substantial change in the Cou-lomb field near the remaining ion and therefore results in a change of the effective radius of atomic orbitals near the ion. This will strongly influence the hopping amplitude between this atom and the atoms in its neighborhood. Such an ‘‘or-bital contraction’’ effect represents a source of strong inter-action which does not simply reduce to the Coulomb 共or phonon兲 repulsion 共or attraction兲 between the charge carriers. It was suggested by Hirsch and coauthors,8–10 and by the present authors11–14that the occupation dependent hopping can have relevance to the appearance of superconductivity in high-temperature oxide compounds. In the present paper, we investigate the generic occupation-dependent hopping Hamiltonians with respect to peculiarities of the normal state, and to the range of existence of the superconducting state. Theoretical investigation of the Cooper instability is supplemented by numeric study of pairing and diamagnetic currents in finite atomic clusters. We study the effect of Coo-per pairing between the carriers and show that at certain values and magnitudes of the appropriate coupling param-eters, the system is actually superconducting. The properties of such superconducting state are in fact only slightly differ-ent from the properties of convdiffer-entional 共low-T_c兲 supercon-ductors. Among those we so far can only mention the change in the fluctuation conductivity above or near the critical tem-perature Tc. Relaxation of the pairing parameter to equilib-rium acquires a small real part due to the asymmetry of contraction-derived interaction between the quasi-particles above and below the Fermi energy.

LOW TEMPERATURE PHYSICS VOLUME 25, NUMBER 8–9 AUGUST–SEPTEMBER 1999

625

Oxygen atoms in the copper-oxygen layers of the cuprates共Fig. 1兲 have a simple quadratic lattice. We assume that pz orbitals of oxygen共z is the direction perpendicular to the cuprate plane兲 are bound to the near cuprate layers whereas carriers at the px, pyorbitals may hop between the oxygen ions in the plane.

Let t1 be the hopping amplitude of px( py) and t2 the

hopping amplitude of py( px) oxygen orbitals between the nearest lattice sites in the x(y ) direction in a square lattice with a lattice parameter a. Then the non-interacting Hamil-tonian is H0⫽⫺t1

兺

具i j典_x ai⫹aj⫺t2

兺

具i j典_y ai⫹aj ⫺t1

兺

具i j典_y b_i⫹bj⫺t2

兺

具i j典_x b_i⫹bj 共1兲

where ai⫹(ai) is the creation 共annihilation兲 operator for px and correspondingly b_i⫹(bi) for py orbitals. The interaction Hamiltonian includes the terms

H1⫽

兺

具i j典 a_i⫹aj关Vmimj⫹W共mi⫹mj兲兴 ⫹

兺

具i j典 b_i⫹bj关Vninj⫹W共ni⫹nj兲兴 共2兲

where ni⫽ai⫹ai; mi⫽bi⫹bi. This corresponds to the depen-dence of the hopping amplitude on the occupation numbers ni, miof the form

共tˆi j兲a_i→a_j⫽␶0共1⫺mi兲共1⫺mj兲⫹␶1关共1⫺mi兲mj

⫹mi共1⫺mj兲兴⫹␶2mimj 共3兲 and correspondingly ( tˆ_{i j})_b

i→bj of the same form with mi

replaced with ni. The amplitudes ␶0,␶1,␶2 correspond to

the transitions between the ionic configurations of oxygen: ␶0:Oi⫺⫹Oj 2⫺_→O i 2⫺_⫹O j ⫺_, ␶1:Oi⫹Oj 2⫺_→O i 2⫺_⫹O j, 共4兲

␶2;Oi⫹Oj⫺→Oi⫺⫹Oj.

O corresponds to the neutral oxygen ion whereas O⫺to the single charged and O2⫺to the double charged negative ions. Since oxygen atom has 1s22 p42s2 configuration in its ground state, filling of the p shell to the full occupied con-figuration 2 p6 is the most favorable. Amplitudes V and W relate to the parameter␶0,␶1,␶2 according to

V⫽␶₀⫺2␶₁⫹␶₂, W⫽␶₁⫺␶₂. 共5兲

Assuming t1⫽t2⫽t and replacing ai,bi with ai with the pseudo-spin indices ␴⫽↓,↑ we write the Hamiltonian Eq. 共1兲 in the form H⫽⫺t

兺

具i j典␴ a_i⫹_␴aj␴⫹HU⫹HV⫹HW 共6兲 where HU⫽U

兺

i ni↑ni↓; 共7兲 HV⫽V

兺

具i j典␴ a_i⫹_␴aj␴ni␴¯nj,␴¯; 共8兲 HW⫽W

兺

具i j典␴ a_i⫹_␴aj␴共ni,␴¯⫹nj,␴¯兲 共9兲

where we also included the in-site Coulomb interaction 共U兲 between the dissimilar orbitals at the same site.␴can also be considered as a real spin projection of electrons at the site. In that case, the pairing will originate between the spin-up and spin-down orbitals, rather than between px and py orbitals. More complex mixed spin- and orbital-pairing configurations can also be possible within the same idea of orbital contrac-tion共or expansion兲 at hole localization but are not considered in this paper. The following discussion does not distinguish between the real spin and the pseudo-spin pairing. The Hamiltonian, Eq. 共6兲, is a model one which cannot refer to the reliable values of the parameters appropriate to the oxide materials. The purpose of our study is rather to investigate the properties of superconducting transition specific to the model chosen and to find the range of the U, V, W values which may correspond to superconductivity. This will be done along the lines of the standard BCS model15 in the weak coupling limit, U, V, W→0, and by an exact diagonal-ization of the Hamiltonian for a finite atomic cluster at large and intermediate coupling.

In the momentum representation, the Hamiltonian be-comes H⫽H₀⫹H₁⫹H₂ with H0⫽

兺

p␴ ␰p a_p⫹_␴ap␴, 共10兲 H₁⫽1 4 p₁p₂p

兺

₃p₄,␣␤␥␦ a_p 1␣ ⫹ _a p₂␤ ⫻⌫_␣␤␥␦0 _共p 1, p2, p3, p4兲ap₄␦ap₃␥ 共11兲 where ␰p⫽⫺t␴p⫺␮, ␴p⫽2共cos pxa⫹cos pya兲, 共12兲 and␮is the chemical potential.⌫_␣␤␥␦0 is the zero order ver-tex part, defined as

FIG. 1. Site configuration in the CuO2plane of cuprates. Dotted line

repre-sents the effect of orbital contraction/expansion due to the localization/ delocalization of an extra hole at a specific site. The enlarged orbital attains the larger value of the hopping amplitude to the nearest sites.

⌫_␣␤␥␦0 _共p 1, p2, p3, p4兲⫽

冋

U⫹

冉

W⫹ 1 2vV

冊

共␴p1⫹␴p2 ⫹␴p₃⫹␴p₄兲

册

␶␣␤ x _␶ ␥␦ x _共␦ ␣␥␦␤␦ ⫺␦␣␦␦␤␥兲␦p₁⫹p₂•p₃⫹p₄ 共13兲 where␶_␣␤x is the Pauli matrix

冉

0 1

1 0

冊

.

For reasons which will be clear later, we separated HV and put some part of it into the H1term, while the remaining part

is included in the H2 term, thus giving

H2⫽V

兺

具i j典␴

a_i⫹_␴aj␴共ai⫹␴¯ai␴¯⫺v/2兲共a⫹j␴¯aj␴¯⫺v/2兲 共14兲 withv⫽

具

ni

典

being the average occupation of the site. 2. THE COOPER INSTABILITY IN THE

OCCUPATION-DEPENDENT HOPPING HAMILTONIANS The Cooper instability is realized at certain temperature T⫽Tcas a singularity in a two-particle scattering amplitude at zero total momentum. We introduce a function

⌫共p1, p2,␶⫺␶

⬘

兲⫽

具

T␶ap₁↑共␶兲a⫺p₁↓共␶兲a¯⫺p₂↓共␶

⬘

兲a¯p₂↑共␶

⬘

兲

典

共15兲 where ¯ap␣(␶)⫽exp(H␶)a⫹p␣exp(⫺H␶), ap␣⫽exp(H␶)ap␣ ⫻exp(⫺H␶) are the imaginary time共␶兲 creation and annihi-lation operators. At p1⫽⫺p2, p3⫽⫺p4, the kernel of

⌫_␣␤␥␦ is proportional to G_␣␤x G_␥␦x 共G is the one-electron Green’s function兲. We keep the notation ⌫(p,p

⬘

) for such a reduced Green’s function specifying only momenta p⫽p1

⫽⫺p2 and p

⬘

⫽p3⫽⫺p4. By assuming temporarily V⫽0,

this Hamiltonian results in an equation for the Fourier trans-form⌫(p,p

⬘

,⍀) ⌫共p,p

⬘

,⍀兲⫽⌫0共p,p

⬘

兲⫺T ⫻

兺

␻

兺

k ⌫ 0_共p,k兲G ␻共k兲G⫺␻⫹⍀共⫺k兲 ⫻⌫共k,p

⬘

,⍀兲 共16兲

corresponding to summation of the Feynmann graphs shown in Fig. 2. In the above formulas, ␻⫽(2n⫹1)␲T and ⍀ ⫽2␲mT 共n, m integers兲 are the discrete odd and even fre-quencies of the thermodynamic perturbation theory15. G(k,␻) is a one-particle Green’s function in the Fourier rep-resentation

G共k,␻兲⫽ 1

␰k⫺i␻. 共17兲

Diagrams of Fig. 2 are singular since equal momenta of two parallel running lines bring together singularities of both Green’s functions G(k,␻) and G(⫺k,␻).

The 6-vertex interaction, Eq.共8兲, is not generally consid-ered in the theories of strongly-correlated fermionic systems. Such interaction also results in singular diagrams for p→ ⫺p scattering shown in Fig. 3. Since a closed loop in this figure does not carry any momentum to the vertex, it reduces to the average value of G¯ which in turn is the average of the number operator,

具

a⫹a

典

. Taking such diagrams into consid-eration is equivalent to replacing one of the ni’s in Eq.共8兲 to its thermodynamical average v⫽

具

a_i⫹_␴ai␴

典

. Then the V term can be added to the renormalized value of W,

W→W⫹1

2vV.

We shall check to what extent such an approximation may be justified by numeric analysis in Sec. 3.

Solution of Eq.共16兲 can be obtained by putting ⌫共p,p

⬘

,⍀兲⫽A共⍀兲⫹B1共⍀兲␴p⫹B2共⍀兲␴p⬘

⫹C共⍀兲␴p␴p⬘. 共18兲

Substituting this expression into Eq.共16兲 and introducing the quantities

Sn共⍀兲⫽T

兺

␻

兺

k ␴k

n_G

␻共k兲G⫺␻⫹⍀共⫺k兲 共19兲

we obtain a system of coupled equations for A, B1, B2, C

冉

1⫹US0⫹W˜ S1 US1⫹W˜ S2 0 0 W˜ S0 1⫹W˜1 0 0 0 0 1⫹US₀⫹W˜ S₁ US₁⫹W˜ S₂ 0 0 W˜ S0 1⫹W˜ S1

冊

冉

A B₁ B2 C

冊

⫽

冉

U W˜ W˜ 0

冊

共20兲

where W˜⫽W⫹(1/2)vV, which are solved to give

A⫽U⫺W ˜2_S 2 D , B₁⫽B₂⫽W ˜_{共1⫹W˜ S1兲} D , C⫽⫺ W˜2S0 D 共21兲 where D is a determinant

FIG. 2. Feynmann diagrams for 4-vertex interactions, U and W.

627

D⫽

冏

1⫹US0⫹W˜ S1 US1⫹W˜ S2

WS0 1⫹WS1

冏

. 共22兲

The determinant becomes zero at some temperature which means an instability in the two-particle scattering am-plitude (⌫→⬁). This temperature is the superconducting transition temperature Tc. At Tc, Eq.共16兲 is singular, which means that two-particle scattering amplitude becomes infi-nite. Below Tc, the finite value of⌫ is established by includ-ing the non-zero thermal averages 共the order parameters兲,

具

a_p⫹a_⫺p⫹

典

,

具

apa_⫺p

典

. We first analyze the case of non-retarded, non-contraction interaction U, and after that will consider the effect of the occupation-dependent hopping terms, V and W.

2.1. Direct non-retarded interaction

Neglecting contraction parameters V, W, the solution of Eq. 共16兲 reduces to ⫺1 U⫽T

兺

_␻

兺

k 1 ␰k 2_⫹␻2 共23兲

which, after the summation over the discrete frequencies, reduces to the conventional BCS equation共at negative U兲

1 兩U兩 ⫽

兺

k

1⫺2nk

2␰_k , 共24兲

with nk⫽关exp(␤␰k)⫹1兴⫺1. At finite frequency ⍀, Eq. 共23兲 reduces to lnT Tc⫽T

兺

␻

冕

⫺E1 E₂ d␰ ⫺i⍀ 共␰2_⫹␻2_{兲共␰⫹i␻⫹i⍀兲} 共25兲

where, for simplicity, we replaced an integration over the Brillouin zone 兰d3_{k by the integration over the energy}

as-suming that the density of states near the Fermi energy ␮is flat.⫺E₁ and E₂ are the lower and upper limits of integra-tion equal to⫺4t⫺␮ and 4t⫺␮, respectively. Such an ap-proximation is not very bad since most singular contributions to integral comes from the point␰p⫽0 where the integrand is the largest.

Above Tc, Eq.共25兲 determines the frequency of the or-der parameter relaxation.16–18There is a small change in this frequency compared to the BCS model in which limits of the integration (⫺E1,E2) are symmetric with respect to the

Fermi energy, and small in comparison to␧F; therefore we shall briefly discuss it now.

To receive a real-time relaxation frequency, Eq. 共25兲 needs to be analytically continued to a real frequency domain

from the discrete imaginary frequencies

i␻n⫽(2n⫹1)␲iT.15Using the identity

T

兺

␻

1

共␻⫹i␰1兲共␻⫹i␰2兲...共␻⫹i␰n兲

⫽共⫺i兲n

兺

i⫽1 n

兿

i⫽ j n共␰i兲 ␰i⫺␰j 共26兲

where n(␰) is a Fermi function n(␰)⫽关exp(␤␰)⫹1兴⫺1gives lnT Tc ⫽i⍀ 2

冕

_⫺E1 E_{2 tanh}共␰_/2T兲 ␰共2␰⫹i⍀兲d␰ 共27兲 where Tc⫽ 2␥ ␲

冑

E1E2exp

冉

⫺ 1 N共␧F兲兩U兩

冊

, ln␥⫽C⫽0.577, 共28兲 C is the Euler constant. Analytic continuation is now simple: we change ⍀, to i(␻⫺i␦), ␦⫽⫹0, to receive a function which will be analytic in the upper half plane of complex␻, Im␻⬎0. The order parameter relaxation equation becomes

冉

lnT Tc⫺ ␻ 4

冕

_⫺E 1 E_{2 tanh}共␰_/2T兲 ␰共␰⫺␻/2⫹i␦兲d␰

冊

⌬⫽0. 共29兲 At ␻ⰆTc and T⫺TcⰆTc, the real and imaginary parts of Eq. 共29兲 are easily evaluated to give

冉

T⫺Tc⫺ ␲i␻ 8Tc ⫹␻E1⫺E2 4E1E2

冊

⌬⫽0. 共30兲

Thus, the order parameter relaxation equation at T⬎Tc be-comes 共1⫹i␭兲⳵_⳵⌬_t ⫹⌫⌬⫽0 共31兲 where ⌫⫽_␲8 共T⫺Tc兲, ␭⫽ 2共E1⫺E2兲 ␲E1E2 Tc. 共32兲

In comparison to the BCS theory in which E1⫽E2⫽␻D共␻D is the Debye frequency兲 and therefore ␭⫽0, we obtain a relaxation which has a non-zero ‘‘inductive’’ component, ⫺i␭⌫. Typically, E1⬃E2⬃␧F and therefore 兩␭兩 is a small quantity. It increases however near the low (vⰆ1) or near

the maximal (v⯝2) occupation where E1 or E2 become

small. Such mode of relaxation is specific to a non-retarded 共non-phonon兲 interaction which is not symmetric near ␧F and spans over the large volume of the k-space rather than is restricted to a narrow energy␻DⰆ␧F near the Fermi energy.

2.2. Occupation-dependent hopping instability and relaxation

Neglecting direct interaction, we put U⫽0 in Eq. 共22兲 and obtain

⫺ 1 W˜

⫽S1共␻兲⫾

冑

S0共␻兲S2共␻兲 共33兲

where at finite frequency␻ Sn共␻兲⫽N共␧F兲T

兺

␻

冕

⫺E1 E₂

冉

␰⫹␮ ⫺t

冊

n_{tanh共␰/2T兲} 2␰⫺␻⫹i␦d␰. 共34兲 Putting␻⫽0 we obtain a transition temperature Tcfrom Eq. 共33兲. The equation has a solution at W˜_{⬍0, ␮⬍0, or at W}˜ ⬎0,␮⬎0 共we assume that t⬎0兲. The plus or minus sign is chosen to obtain the maximal value of T_c共the second solu-tion corresponding to smaller T, then, has to be disregarded since the order parameter will be finite at T⬍Tc and there-fore Eqs.共20兲–共22兲 do not apply兲. This gives us an expres-sion for Tc Tc⫽ 2␥ ␲

冑

E1E2exp

冋

E1⫺E2 2兩␮兩t 共t⫺兩␮兩兲⫹ E2 2_⫺E 1 2 8␮2

册

⫻exp

冉

⫺ t 2兩W˜兩N共␧F兲

冊

共35兲 where␮⬍0, W˜⬍0 共second exponent is dominating the first one in the weak coupling limit W˜→0兲. Real and imaginary parts of S_n(␻) are calculated at␻ⰆT_c

Im Sn共␻兲⯝⫺ ␲␻ 8Tc

冉

⫺ ␮ t

冊

n N共␧F兲. 共36兲 Re Sn共␻兲⫽ ␻ 4 N共␧F兲

冉

⫺ ␮ t

冊

n ⫻

冦

E2⫺E1 E1E2 , n⫽0, E2⫺E1 E₁E₂ ⫹ 2 ␮ln ␥

冑

E1E2 T_c , n⫽1, E2⫺E1 E1E2 ⫹E1⫺E2 ␮2 ⫹ 2 ␮ln ␥

冑

E1E2 Tc , n⫽2. 共37兲

Equation for ␭ is received with a value larger than the pre-vious one关Eq. 共32兲兴

␭⯝T_␮c

冉

3 ln2␥

冑

E1E2 ␲Tc ⫹ 2␮共E2⫺E1兲 E1E2 ⫹ E1⫺E2 2␮

冊

. 共38兲 The eigenvalue equation gives the p-dependence of the two particle correlator⌫(p,p

⬘

)⫽

具

a_p⫹_↑a⫹_⫺p↓a_⫺p⬘↓a_p⬘↑

典

near T_c

⌫共p,p

⬘

兲⫽C关S2⫺S1共␴p⫹␴p⬘兲⫹S0␴p␴p⬘兴. 共39兲 Since C diverges at T_c, this determines that the order param-eter becomes macroscopic at T⬍Tc. Then, the pair creation operator, a_p⫹a_⫺p⫹ , will almost be a number, i.e., we may decompose Eq.共39兲 into a product

⌬p*⌬p⫽

具

ap⫹↑a⫺p↓⫹

典具

a⫺p⬘↓ap⬘↑

典

共40兲 and, to be consistent with the p, p

⬘

dependences, by putting ␰p⫽␰p⬘ we obtain

⌬p⫽C1关exp共i␪/2兲

冑

S2共0兲

⫹exp共⫺i␪/2兲

冑

S0共0兲兴exp共i␸兲 共41兲

where

cos␪⫽⫺S1共0兲/

冑

S0共0兲S2共0兲 共42兲

and ␸ is an overall phase which is irrelevant for a single superconductor but is important for calculating currents in multiple or weakly coupled superconductors. Therefore, the system undergoes a pairing transition at a temperature found from Eq.共35兲. Since the pairs are charged, the state below T_c cannot be non-superconducting.

We have not calculated the Meissner response but in the following section we present a numerical calculation of flux quantization which supports the above statement.

3. EXACT DIAGONALIZATION OF THE OCCUPATION-DEPENDENT HOPPING HAMILTONIANS IN A FINITE CLUSTER

We calculate the ground state energy of a cubic system as shown in Fig. 4. A magnetic flux ⌽ is produced by a solenoid passing through the cube. The corners of the cube are the lattice sites that can be occupied by electrons. With the inclusion of the magnetic flux, model Hamiltonian, Eq. 6, becomes

H⫽⫺t

兺

具i j典␴

ai⫹_␴aj␴exp共i␣i j兲⫹h.c.⫹U

兺

i ni↑ni↓ ⫹

兺

具i j典␴ a_i⫹_␴aj␴关Vni␴¯nj␴¯⫹W共ni␴¯⫹nj␴¯兲兴 ⫻exp共i␣i j兲⫹h.c. 共43兲 where ␣i j⫽共2␲/⌽0兲

冕

r_i r_j A•dl 共44兲

and⌽0⫽hc/e is the magnetic flux quantum. Throughout the

calculations we take t⫽1.

We start with constructing the model Hamiltonian. In the Hilbert space of one electron

a⫽

冉

0 1

0 0

冊

, a

⫹_⫽

冉

0 0

1 0

冊

, 共45兲

FIG. 4. Sample configuration. The flux⌽ through the cube is produced by a solenoid.

629

with a basis specified as ␺₀⫽(0,1) for the ground state (n ⫽0) and␺1⫽(1,0) for the excited state (n⫽1). In case of N

states, the operator of annihilation an takes the form

a_n⫽vn⫺1_丢a丢uN⫺n _共46兲

where u is the unit matrix and v is unitary matrix

u⫽

冉

1 0

0 1

冊

, v⫽

冉

1 0

0 ⫺1

冊

共47兲

and 丢 stands for the Kronecker matrix multiplication. Ex-plicitly, we have

a1⫽a丢u丢u丢u...丢u

a2⫽v丢a丢u丢u...丢u

... aN⫽v丢v丢v...丢v丢a Thus, for example, for two states

a1⫽

冉

0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0

冊

, a2⫽

冉

0 0 1 0 0 0 0 ⫺1 0 0 0 0 0 0 0 0

冊

. 共48兲

These matrices, which are annihilation operators, and the corresponding Hermitian conjugate matrices, which are the creation operators, satisfy the Fermi anti-commutation rela-tion. These operators are sparse matrices with only N/2 non-zero elements, which are equal to ⫾1. Next we solve the Schro¨dinger equation H_␺⫽E_␺. We implemented a novel al-gorithm for solving such sparse systems, which will be de-scribed elsewhere.

The cubic cluster within the Hubbard Hamiltonian and no external flux applied to the system was studied previously by Callaway et al.19 Quantum Monte Carlo methods appli-cable to large systems within the Hubbard model 共both at-tractive and repulsive兲, but not the occupation-dependent hopping Hamiltonians, are reviewed in a paper of Dagotto.20

3.1. The number parity effect

Superconductivity reveals itself in the lowering of the ground state energy as electrons get paired. Therefore the energy needs to be minimal for an even number of electrons n and will attain a larger value when n is odd. We consider a ‘‘gap’’ parameter21

⌬l⫽E2l⫹1⫺

1

2共E2l⫹E2l⫹2兲 共49兲

as a possible ‘‘signature’’ of superconductivity 共where Em corresponds to the ground state energy for m fermions兲. For all interaction parameters set to zero (U⫽V⫽W⫽0), no sign of pairing is observed. To check our analytic results of Sec. 2.2 and the argument following Eq.共34兲, we calculated ⌬ above and below the half-filling 共n⫽8 in the case of cubic cluster兲. Below the half-filling chemical potential is negative (␮⬍0) and above the half-filling it is positive (␮⬎0). We first checked that the W→0⫹, W→0⫺ and V→0⫹, V

→0⫺ _{calculation is consistent with an exact solution} avail-able for a non-interacting system of n electrons.

We then test our program for the case of negative-U Hubbard Hamiltonian 共U⬍0, V⫽0, W⫽0兲 which is known to be superconducting 共e.g., Refs. 22 and 23兲. Positive-U Hubbard model does not show any sign of superconductivity, in disagreement with some statements in the literature.24Our calculations cannot disprove the 共possible兲 non-pairing mechanisms of superconductivity but these seem to be un-likely models for the problem of superconductivity in oxides which clearly shows pairing of electrons 共holes兲 in the Josephson effect and in the Abrikosov vortices. The relation 2eV⫽ប␻ is justified in the first case25and flux quantum of a vortex is hc/2e in the second,26both with the value of the charge equal to twice the electronic charge, e.

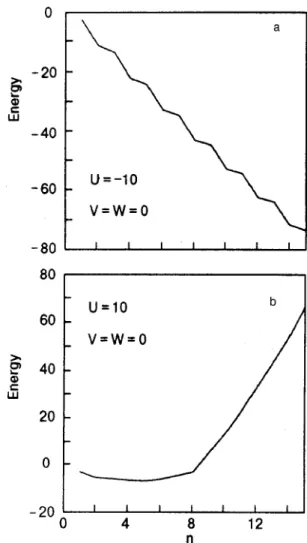
Figure 5 shows the dependence of the ground state en-ergy upon the number of particles in case of negative-U and positive-U Hubbard models assuming V⫽0 and W⫽0. Such dependences are typical for any value of兩U兩. There clearly is the pairing effect when U⬍0 and there is no sign of pairing at U⬎0.

Tests for pairing in the contraction V,W-models共V⫽0, U⫽W⫽0 and W⫽0, U

⬘

⫽V⫽0, respectively兲 are shown in Figs. 6 and 7. The results are in agreement with our

pertur-FIG. 5. Dependence of the ground state energy upon the number of particles with U⫽0 and V⫽W⫽0. Energy, as well as U, is in units of t. 共a兲 For U

bative calculation of Sec. 2 and with its extension for the intermediate and strong coupling limits 兩V兩ⲏt, 兩W兩ⲏt. Since the chemical potential is negative below the half-filling and positive above the half-filling, there is no pairing in the former case (W˜→0⫹) and there is a sign of pairing in the latter case (W˜⬎0), in accord with the value of the effective coupling constant W˜⫽W⫹(1/2)vV. Similarly, for W˜→0⫺ below the half-filling there is a sign of pairing (⌬⫽0) while above the half-filling there is no pairing. These results are summarized in Table I.

For larger values of the interaction parameters, the per-turbative results do not remain applicable anymore. Figure 8b shows the dependence of the parity gap⌬ on the strength of the interaction. From Fig. 8, it is understood that the W interaction introduces a ‘‘signature’’ of pairing in a similar way as the negative-U interaction does. The possibility of ‘‘contraction’’ pairing has been investigated previously in the papers.10,13

3.2. Flux quantization

Flux quantization is another signature of superconductiv-ity which is a consequence of the Meissner effect. We also tested for the periodicity of the energy versus flux

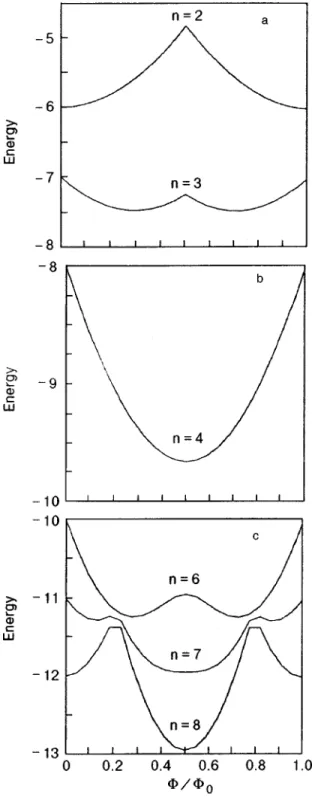
dependence with the period ⌽₁⫽hc/2e as compared to the period⌽₀⫽hc/e in the non-interacting system.27,28 Unfortu-nately, the even harmonics of⌽₀-periodic dependence of the ground state energy 共and related to it, the harmonics of the persistent current J⫽⫺⳵E/⳵⌽27,28兲 may simulate the pairing in a non-superconductive system. A small-size共mesoscopic兲 system can mask the superconducting behavior.20Flux quan-tization in Hubbard Hamiltonians was studied formerly in Refs. 29–31.

FIG. 6. Dependence of the ground state energy upon the number of particles with V⫽0 and U⫽W⫽0. Energy, as well as V, is in units of t. 共a兲, 共b兲 Both for V⬎0 and V⬍0, around the half-filling, there is a small pairing effect.

FIG. 7. Dependence of the ground state energy upon the number of particles with W⫽0 and U⫽V⫽0. Energy, as well as W, is in units of t. 共a兲, 共b兲 Both for W⬎0 and W⬍0, there is a more pronounced pairing effect below the half-filling.

TABLE I. Pairing effect for arbitrarily small values of V and W, computed by exact diagonalization of the Hamiltonian. The results presented here are in complete agreement with the perturbative calculations.

U⫽W⫽0 U⫽V⫽0 V→0⫹ V→0⫺ W→0⫹ W→0⫺ below half-filling (␮⬍0) ⌬⫽0

共no pairing兲 共pairing兲⌬⫽0 共no pairing兲⌬⫽0 共pairing兲⌬⫽0

above half-filling (␮⬎0)

⌬⫽0

共pairing兲 共no pairing兲⌬⫽0 共pairing兲⌬⫽0 共no pairing兲⌬⫽0 631

We first demonstrate the behavior of the ground state energy with respect to flux, Fig. 9. A characteristic feature of a mesoscopic system suggests that addition of one extra par-ticle to the system changes the sign of the derivative of the ground state energy with respect to magnetic flux at ⌽⫽0. That is, depending on the parity of the number of particles and on the number of sites, system can change from para-magnetic to diapara-magnetic state or vice versa. But this behav-ior is not always observed for the cubic geometry studied. Except the sign change from n⫽2 to n⫽3 and from n⫽7 to

n⫽8, no such behavior is seen. As mentioned above, how-ever, the ⌽₁-periodic component of the E(⌽) dependence begins to appear at the higher value of n共Fig. 9c兲. For both contraction parameters equal to zero, i.e., W⫽V⫽0, we ob-serve the appearance of the hc/2e-periodic component for some values of U 共Fig. 10兲. Even for positive 共repulsive兲 values of U, it is possible to see a local minimum appearing at ⌽⫽hc/2e 共Fig. 10b兲. This is in agreement with the au-thors’ previous works.13,29 But this minimum, which does not lead to an exact periodicity of the ground state energy

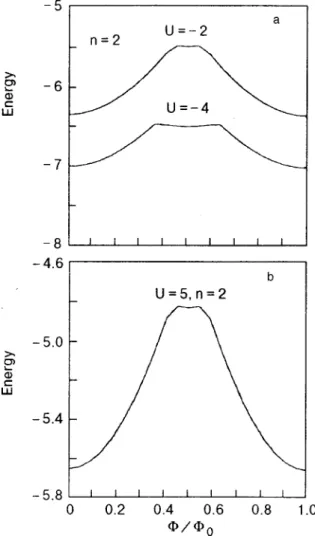
FIG. 8. Dependence of the parameter⌬ upon U for various values of W and

V below the half-filling.共⌬, U, V and W is in units of t兲.

FIG. 9. Dependence of the ground state energy共in units of t兲 upon magnetic flux. All three interaction parameters are zero, i.e., U⫽W⫽V⫽0.

with a period⌽0/2, should not be attributed to

superconduc-tivity, this is rather a characteristic behavior in mesoscopic systems.

For U⬍0 共while W⫽V⫽0兲, the expected mesoscopic behavior, that is, the change of the sign of the slope of ground state energy at ⌽⫽0, starts to reveal itself 共Fig. 11兲. But this happens at sufficiently large absolute values of 共negative兲 U. For other values of U, however, there is no such change.

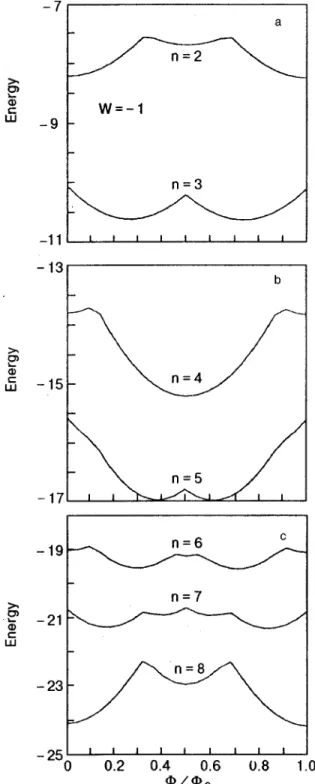
More pronounced hc/2e-periodic components are ob-served with the introduction of non-zero interaction param-eters. The role of W in the ground state energy, when both U and V are zero, is shown in Fig. 12. Meanwhile setting both U and W to zero and observing the effect of the non-zero V shows that V does not play a role as significant as the other two interaction parameters do. There is not much difference in the behavior of the ground state energy upon magnetic flux between the zero and non-zero V 共for example V⫽⫺1兲 cases.

CONCLUSIONS

We studied the peculiarity of electron conduction in sys-tems in which conduction band is derived from the atomic

shells with a small number of electrons (Ne) in an atom. Such materials may include oxygen (Ne⫽8) in the oxides, carbon (Ne⫽6) in borocarbides 共e.g., LuNi2B2C兲, hydrogen

(N_e⫽1) in some metals 共e.g., Pd–H兲. Some materials of this kind are superconductors. It was argued that the Coulomb effects within the atoms strongly influence the inter-atom wave function overlap between the atomic sites and therefore the electron hopping amplitude between the sites. The phe-nomenology of such conduction mechanism results in a novel addition, to the conventional solid state theory, i.e., Hamiltonians called the occupation-dependent-hopping 共or contraction兲 Hamiltonians, specified with the two coupling parameters V, W. We then attempted a study of supercon-ductivity in such systems within the BCS-type approach as-suming Cooper pairing of electrons. The weak-coupling limit allows the determination of the range of parameters V, W values and also of the in-site Coulomb interaction U value which show the Cooper instability. The strong-coupling limit was addressed by a numeric calculation on finite clusters using a novel algorithm 共of non-Lanczos type兲 for eigenval-ues of large sparse matrices. One of the results of this

FIG. 10. Dependence of the ground state energy upon magnetic flux. Con-traction parameters are both zero, i.e., W⫽V⫽0, only the on-site interaction parameter U is nonzero. Energy, as well as U, is in units of t.

FIG. 11. Dependence of the ground state energy upon magnetic flux. Com-paring共a兲 with Figure 9b clearly shows that the change in the parity of the number of particles for the case of negative U values introduces a sign change in the slope of E(⌽) at ⌽⫽0. Energy, as well as U, is in units of t.

633

numeric calculation was that the positive-U Hubbard model, sometimes believed to be a candidate for high-T_c supercon-ductivity, does not comply with the goal.

This work was partially supported by the Scientific and

Technical Research Council of Turkey 共TU¨BITAK兲 through the BDP program.

*E-mail: kulik@fen.bilkent.edu.tr

1

J. G. Bednorz and K. A. Muller, Z. Phys. B 64, 189共1986兲.

2_{M. K. Wu, J. R. Ashburn, C. J. Torng, P. H. Hor, R. L. Meng, L. Cao,} Z. L. Huang, Y. Q. Wang, and C. W. Chu, Phys. Rev. Lett. 58, 908

共1987兲.

3

J. Bardeen, L. N. Cooper, and J. R. Schrieffer, Phys. Rev. 108, 1175

共1957兲.

4_{M. S. Hybertsen, E. B. Stechel, M. Schlu¨ter, and D. R. Jennison, Phys.} Rev. B 41, 11068共1990兲.

5

A. K. Mahan, J. A. Annett, and R. M. Martin, Phys. Rev. 108, 1175

共1957兲.

6_{N. Nucker, J. Fink, J. C. Fugle, P. J. Durham, and W. M. Temmerman,} Phys. Rev. B 37, 5158共1998兲.

7_{P. Kuiper, G. Kruizinaga, J. Ghijsen, M. Grioni, P. J. W. Weijs, F. M.} de Groot, and G. A. Sawatsky, Phys. Rev. B 38, 6483共1988兲.

8_{J. E. Hirsch, Phys. Lett. A 134, 451共1989兲.}

9_{J. E. Hirsch and F. Marsiglio, Phys. Rev. B 39, 11515共1989兲.} 10_{J. E. Hirsch, Phys. Rev. B 48, 3327共1993兲; ibid. 48, 9815 共1993兲.} 11_{I. O. Kulik, Sov. Superconductivity: Phys. Chem. Tech. 2, 201共1989兲.} 12

I. O. Kulik, Contraction Mechanism for Pairing Interaction in Oxides

and Hydrides, in Progress in High Temperature Physics, Vol. 25,

R. Nicholsky,共Ed.兲, World Scientific, Singapore 共1990兲.

13_{H. Boyaci and I. O. Kulik, Fiz. Nizk. Temp. 24, 316共1998兲 关Low Temp.} Phys. 24, 239共1998兲兴.

14_{I. O. Kulik, Tr. J. Phys. 20, 627共1996兲.}

15_{A. A. Abrikosov, L. P. Gorkov, and I. E. Dzyaloshinsky, Methods of}

Quantum Field Theory in Statistical Physics, Dover Publications, New

York共1975兲. 16

E. Abrahams and T. Tsuneto, Phys. Rev. 152, 416共1966兲.

17_{L. P. Gorkov and G. M. Eliashberg, Z. E´ ksp. Teor. Fiz. 54, 612 共1968兲}

关Sov. Phys. JETP 27, 328 共1968兲兴.

18_{I. O. Kulik, O. Entia-Wohlman, and R. Orbach, J. Low Temp. Phys. 43,} 591共1981兲.

19

J. Callaway, D. P. Chen, and Y. Zang, Phys. Rev. 36, 2084共1987兲. 20_{E. Dagotto, Rev. Mod. Phys. 66, 763共1994兲.}

21_{K. A. Matveev and A. I. Larkin, Phys. Rev. Lett. 78, 3749共1997兲.} 22_{I. O. Kulik, Physica B 126, 280 共1984兲; Int. J. Mod. Phys. B 1, 851}

共1988兲.

23_{R. Micnas, J. Ranninger, and S. Robaszklewicz, Rev. Mod. Phys. 62, 113}

共1990兲.

24_{C. H. Pao and N. E. Bickers, Phys. Rev. Lett. 72, 1870共1994兲; D. J.} Scalapino, Phys. Rep. 250, 329共1995兲.

25

T. J. Witt, Phys. Rev. Lett. 61, 1423共1988兲; D. Esteve, J. M. Martinis, C. Urbina, M. H. Devoret, G. Collin, P. Monod, R. Ribault, and A. Percolevski, Europhys. Lett. 3, 1237共1987兲.

26_{P. L. Gammel, D. J. Bishop, G. J. Dolan, J. R. Kwo, C. A. Murray, L. F.} Schneener, and J. V. Waszczak, Phys. Rev. Lett. 59, 2592共1987兲; L. Ya. Vinnikov, L. A. Gurevich, G. A. Yemelchenko, and Yu. A. Ossipyan, Solid State Commun. 67, 253共1988兲.

27_{I. O. Kulik, Pisma Zh. E´ ksp. Teor. Fiz 11, 407 共1970兲 关JETP Lett. 11, 275}

共1970兲兴.

28

M. Buttiker, Y. Imry, and R. Landauer, Phys. Lett. A 96, 365共1983兲. 29_{A. Ferretti, I. O. Kulik, and A. Larni, Phys. Rev. B 47, 12235共1993兲.} 30_{R. M. Fye, M. J. Martins, and D. J. Scalapino, Phys. Rev. B 44, 6909}

共1991兲.

31

A. Sudbo, C. M. Varma, T. Giamarchi, E. B. Stechel, and R. T. Scalettar, Phys. Rev. Lett. 70, 978共1993兲.

This article was published in English in the original Russian journal. It was edited by R. T. Beyer.

FIG. 12. Dependence of the ground state energy upon the magnetic flux. On-site interaction parameter U and one of the contraction parameters. V, are zero. All plots correspond to the non-zero interaction parameter W⫽