IπK=1⁺ 0 States IN ¹⁶⁸Er and ¹⁷⁶Hf Nuclei

©BEYKENT UNIVERSITY

I

K=1+0 STATES IN

Er and

Hf NUCLEI

F.ERTUGRAL

, A. A. KULIEV

, E.GULIYEV

, H. YAKUT

and Z. YILDIRIM

1Physics Department, Faculty of Arts and Sciences, Sakarya University, 54100

Serdivan, Adapazarı, Turkey, ertugral@sakarya.edu.tr

2Institute of Physics, Academy of Sciences, H.Cavid avanue 33, Baku,

Azerbaijan, aguliyev@cern.ch

ABSTRACT

In this study, the properties of collective 171K = 1+0 states in doubly even

deformed 168Er and 176Hf nuclei is investigated in the framework of the

Random-Phase Approximation (RPA). Spin-spin interactions have shown that the spectroscopic 1+ states (up to energies on the order of 4 MeV) are weakly correlated and are characterized by small values of B(M1). The collective 1+ states with the largest values of B(M1) are expected in the region of energies 9-11 MeV (K=0). The structure of the 1+0 excitations and the dipole sum rule for M1 transitions are investigated.

Keywords: Hf, Er, dipole sum rule, Random-Phase Approximation (RPA),

QRPA method

ÖZET

Bu çalışmada 168Er ve 176Hf deforme çift-çift çekirdeklerin kolektif

171K = 1+0 durumu için uyarılmalarının özellikleri Kuaziparçacık Rasgele

Faz Yaklaşımı (RPA) kullanılarak hesaplandı. Spektroskobik 1+ durumlarının (4 MeV sırasındaki enerjilere kadar) spin-spin etkileşmelerine zayıf olarak bağlı olduğunu ve B(M1)'in en küçük değerleri ile karakterize edildiğini gösterdi. B(M1)'in en büyük değerli kolektif 1+ durumları 9-11 MeV enerji bölgesinde bulundu (K=0). M1 geçişleri için dipol toplam kuralı ve 1+0 uyarılmalarının yapısı araştırıldı.

1. INTRODUCTION

The study of nuclear excitations with low multipolarity, in particular collective magnetic dipole ones, gives valuable information about nuclear structure and

InK=1+0 States IN 168Er and 176Hf Nuclei

nuclear- nuclear forces at low energy. At present magnetic dipole resonances (In=1+) have been found experimentally in a wide region beginning from light spherical nuclei up to actinides . For example contrary to the well known E1 response of stable nuclei, the M1 response in the a total of 12 open-shell nuclei could only in recent years be measured through recombination of differed high- resolution probes, i.e. inelastic electron, photon and proton scattering magnetic dipole excitations in deformation nuclei has been found to give to M1 strength with the major peaks corresponding to K=0 and K=1 mode of 1+ excitations [1]. These experiments show that in heavy spherical and deformed nuclei there exists a very broad M1 resonance at energies between 7 and 11 MeV centered an energy on the order of about 44A-1/3 MeV. The remarkable features of this mode obtained from experimental results are its independence on deformation, the quenching and strong fragmentation total M1 strength in deformed [2].

In spherical nuclei, the appearance of collective 1+ states is connected with transitions between levels of the spin-orbit doublet. Recent experimental and theoretical investigation show, as a rule, that the spin part of the residual interaction in odd nuclei leads to polarization effects that influence greatly the magnetic moments and the probabilities of the allowed ¡3 transitions. These effects cause the gs factors of the nucleons in the nucleus to differ noticeably from the corresponding values for free nucleons. This is in fact equivalent to a renormalization of the single-particle matrix elements of the odd nuclei. In spherical even-even nuclei 1+ excitations are connected with particle- hole transitions between the neutron-neutron (proton-proton) levels of the spin-orbit doublets [3]. In spite of spherical nuclei in deformed nuclei the picture is more complicated, owing to the mixing of states with different j. The selection rules with respect to the l and j can be strongly violated. Besides, in axial symmetric deformed nuclei the 1+ states are split into excitations characterized by the angular momentum projection on the symmetry axis K=0 and K=1 with each of them being formed independently. Strong M1 transitions can occur in the case of A K=0 and A K=1.

In this paper, we investigated spin-vibration I nK = 1+0 excitations for

settlement nuclei at deforme region, generated by the Quasi Random Phase Approximation (QRPA), using the deformed Wood-Saxon potential, odd particle energies and wave functions

2. THEORY

2.1. HAMILTONIAN

The Random Phase Approximation (RPA) is a successful method for the describing many-body systems. In nuclear physics RPA has been extensively exploited to calculate intensities of the various nuclear reactions, decay probability of electromagnetic, beta and double beta decay transitions including ground state correlations. For the nuclei away from closed shells there appear static pairing correlations between nucleons giving rise to the energy gap in the excitation spectra. In this case one uses the quasiparticle version of RPA (QRPA). This work QRPA method is responsible investigation of InK = 1+0 spin-vibration states in deformed nuclei (150 < A < 178).

In this approximation, the model Hamiltonian of the system can be written

H = H q p + V „ (1)

H

= 2 Es (T)[a+ (T)a (T) + a+ (T)a~ (T)]

2 X T Y J ^ ^ T T ] (3) 2 i* J

where Hqp is the single quasiparticle Hamiltonian with pairing interactions, VaT takes into account isovector spin-spin interactions. Here Es are the

one-quasiparticle energies, ots(a) the quasiparticle creation and annihilation

operators and The state | s ^ is the time reversal of | s) are conjugate in time. s and t spin and izospin momentum operators, a = 2s and T = 2 t Pauli matrix for spin and izotopic spin [6].

The spectrum of collective excitations is usually found using the quasiparticle concept. The isovector spin-spin interactions that generated the 1+ states in the

deformed nuclei have the form:

VO T= 1 ZXTT'T; (T)TV(T) V = 0, ± 1 T = n, p (4) 2 T

H e r e are q=- 1 a t st at e s Xnp = Xp„ = qX a n d Xnn = Xpp =X - I n t h e

quasiparticle representation the operator Tv (T) splits up into quasiboson and

scattering terms. s

InK=1+0 States IN 168Er and 176Hf Nuclei

T

= Tq (T) + T

(t) (5)

-qp (t) = za

,(u

u

, + v

v

,) D«<

Tf

(T) = 2J

,(u

v, - u,v

+ C„.] (7)

Tv(T)

= V2e[<

I

s'> j(uv -

)[c;, + c J + J=(u

, + v ^ )

D+ + D j J

where C" ' V 2 pt±1as'pas-p c + 2 at pa t p (9) V 2 P=±1 Ds s ' = 2 Pa +s pas ' p D + = 2 Pas ' pa +s p . ( 1 0 ) p=±1 p=±1

The quantities J ^ = {S | JV | s ' ^ , JV are single-particle matrix elements of

the Pauli spin operator. p=± defines the state and the time reversal state, consequently. In the case |V|=1, the matrix elements JV | S'} in Eq.(8) are

non-zero only between the single-particle states with K=1/2. Using the expressions (6)-(7) one can write V< _JT

V = V

+ V

(11)

' JT ' JT ' JT

where V«11 generate the collective In = 1+ states in doubly even deformed

nuclei, VJT take into account the collective states-quasiparticles interactions at odd nuclei.

Supposing the generation of high lying 1+ states due to isovector spin-spin interactions, the hamiltonian of system can be written as

H

= Hqp + V

JT

In Quasi Particle Random Phase Approximation (QRPA) collective 1+ states

are considered as one-phonon excitations described by

where Q, is the phonon creation operator,

Q+=j^2(K

m- K

M (14)

| ) is the phonon vacuum which corresponds to the ground state of the even-even nucleus. The valid Q ^ ^0) = 0 for all i. The C+Q, ( Cs s, ) are

modified two-quasiparticle creation (annihilation) boson operators, i.e. W C s , Cq+q.]| ¥ „ >

=

Sq

Sq-5q,5

,

.

collective excitations wave functions and the renormalized form (9) of Cqq.

and C + provide boson commutation for Qi operators [QI, Q+ ] = Sir . The

two-quasiparticle amplitudes X^ and Yu are normalized by

2[

x

;

2

(T)

-

;

T ] =

¡¡T

C+, and Cqq, operators using the expressions (14)-(15) one can write phonon

describe.

Cq

q

,=j2

i

Cqq, = V 2 z(Xqq,Qi - Y ^ )

i

Employing the conventional procedure of RPA and solving the equations of motion

C = [(Hsqp + V^T ) , Q + ] = ® i Q

(17)

We obtain the dispersion equation for the excitation energy a>: of 1+ states.

D(a

) = 1 + x[F,

(A, ) + F

(A, )] = 0

where

E„Al L

) =

^ E T ^ T

M

E, = Es + Es, are two-quasiparticle energies of nucleons, the ( equals to

the energy of the phonon state and a , the single-particle matrix element of the spin operators. Finally, the neutron-neutron and proton-proton two quasiparticle amplitudes are given by Xand Y,

InK=1+0 States IN 168Er and 176Hf Nuclei

X = 1

=

=

yJ^MjZ(a

) E

,

a

1 cr,„,'L,

1 CTSS'LS

(20)

Y\=-

V4^Z(©,. ) ^ +®

1 cr„v'L

F

T

F n

T

Z{rn.) = 7 - + 7

^ ^ ^

( F

, - «

)

(Fl-®2Y

The function Z ( 0 ) is obtained from the normalization condition (15). Further the sum 7 denotes the summation over the states of neutron or

;;'

7 proton.

2.2. PROBABILITIES OF Ml TRANSITIONS TO COLLECTIVE 1+ STATES

The characteristic quantity for the spin-vibrational 1+ levels will be the probability of the M1 transitions. Magnetic dipol operator is given by

/ T T\ T T T

( gs - gl ) Sm - S l Jm (23)

where g l and g j are the spin and orbital gyromagnetic ratios of the free nuclei, respectively. Further, = ( s | jv | s ' ) i s the single-particle matrix

element of the angular momentum operator, n ji = | nv | t h e

single-particle matrix element of the spin operators.

Using the formula (9) and Bogolyubov canonical transformation M magnetic dipol operator is given by

M = J8-Z m

,L

,(C:

,+ C

.) (24)

The M operator are defined as phonon state by the formula (14)

M = J ] - Z m,sLss,gls, + 2 mvv'LVV'g[V'~\(Qi + Q ) (25) V i ss' vv'

where

g

= X'

+

The most characteristic quantity of state the reduced Ml transition probability, which can be written in the form.

B(M 1, 0 + ^ 1+ ) =

J ^ G

MSASG,

+2

\

The value of B(M1) for individual excitations will, as a rule, indicate the degree of collectivity of the given state. On the other hand, it is possible to draw from the sum rules only qualitative conclusions concerning the degree of collectivity of all the generated levels.

We can write the energy-weighted sum rule for M1 transition operator.

X n

=

(M

The behavior of this function enables us to assess the contribution of the different states to the sum rule and to determine the region of saturation. Equation (29) sum rule is independent from model

-SS'-JSS'Lss' (29)

X n = E E s s M l L 2

3. RESULTS AND DISCUSSION

The Nilsson single particle energies are obtained from the deformed Woods-Saxon potential. The basis contains all discrete and quasi-discrete levels in the energy region up to 3 MeV. Calculations are performed for 168Er and 176Hf

nuclei. The deformation parameters and interaction constants for these nuclei given in Table 1 are taken from Ref. [4\ and Ref. [7\, respectively. The isovector spin-spin interaction strength was chosen to be XOT = 40 / A MeV

[7\. This value allows a satisfactory description of the scissors mode

InK=1+0 States IN 168Er and 176Hf Nuclei

fragmentation in well deformed rare earth nuclei and the quadratic dependence of the summed B(M1) values on the ground states deformation parameter 5 .

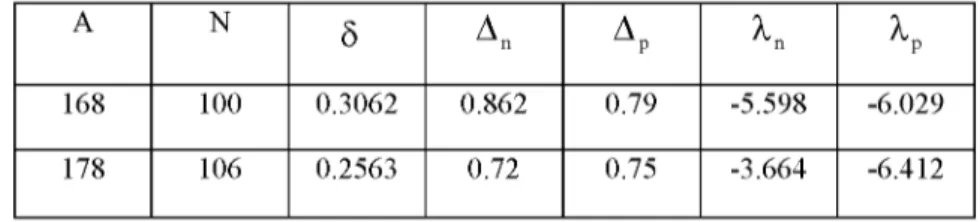
Table 1. The pair correlation parameters and the deformation parameters for 168Er and 176Hf deformed nuclei.

A N

₅

_A

n _A

P

*

* P

168 100 0.3062 0.862 0.79 -5.598 -6.029 178 106 0.2563 0.72 0.75 -3.664 -6.412

The number of calculated two-quasiparticle 1+ states turned out to be 502 for the states with K=0. We used in the calculation a scheme of single-particle levels including 294 neutron and 208 proton levels. The calculations have shown that all the 1+ states with K=0, up to an the order of 6-7 MeV, are characterized values of the probability of the M1 excitation the ground state. As a rule we have for them

B(M

1, 0 + ^ 1+0 < 1^2)

there can be as having values B(M 1,0 ^ 1) of the order of the single-particle values. Table II shows an example of spectroscopically observed low-lying 1+ states of 168Er and their interpretation. In the formed nuclei, the picture is more complicated, owing to the mixing of states with different j. The selection rules with respect to l and j can be strongly violated. Strong M1 transition can occur in the case of K = 0 . Owing to mixing with respect to j-some times between states from subshells with different l (for example of the type f7/2 ->h11/2j f5/2 ^ h9 / 2 and g7/2 ^i1 1 / 2 , etc.). Table III lists shows an example of spectroscopically observed high-lying 1+ states of 168Er and their interpretation. Table IV lists the characteristics of a number of collective 1+0 states in 176Hf. The group of strongly collective 1+ states with B(M1)>0.45 is found in the energy interval 9-11 MeV. We note that the (np) mixing is weak in low-lying 1+ states.

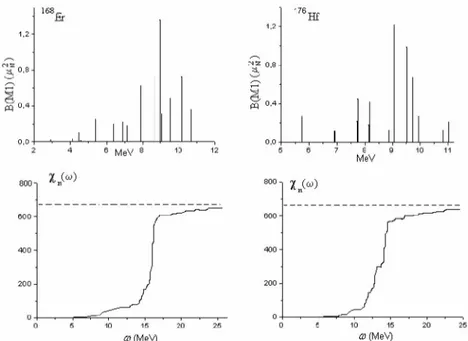
We have calculated the magnetic dipole sum rule for a number of rare-earth nuclei. The diagrams of the transition energies (n, of the values of

B(M 1,0 ^ 1) , and the sum rule for the 1+ states with K=0 in the nuclei Hf, Er are shown Figs.1. The dashed line (30) shows the single-quasiparticle estimate of the sum rule. The solid curves show the saturation function %n. The 1+ states in this region contribute about 70% to the sum rule. Here, the B(M1) value may be as large as a few single-particle units. The states of this region give the main contribution to the sum rule.

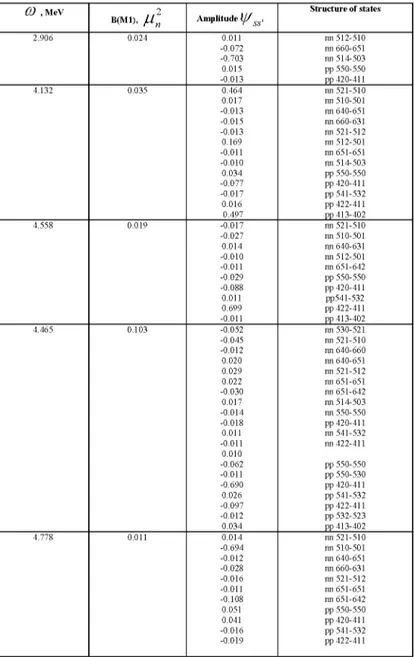
Table II. An example of spectroscopically observed low-lying I nK = 1+0 states of

168Er and their interpretation

C , MeV , , 2 Amplitude ^ s s ' Structure of states C , MeV B(M1), / Un Amplitude ^ s s ' 2.906 0.024 0.011 nn 512-510 -0.072 nn 660-651 -0.703 nn 514-503 0.015 pp 550-550 -0.013 pp 420-411 4.132 0.035 0.464 nn 521-510 0.017 nn 510-501 -0.013 nn 640-651 -0.015 nn 660-631 -0.013 nn 521-512 0.169 nn 512-501 -0.011 nn651-651 -0.010 nn 514-503 0.034 pp 550-550 -0.077 pp 420-411 -0.017 pp 541-532 0.016 pp 422-411 0.497 pp 413-402 4.558 0.019 -0.017 nn 521-510 -0.027 nn 510-501 0.014 nn 640-631 -0.010 nn 512-501 -0.011 nn 651-642 -0.029 pp 550-550 -0.088 pp 420-411 0.011 pp541-532 0.699 pp 422-411 -0.011 pp 413-402 4.465 0.103 -0.052 nn 530-521 -0.045 nn 521-510 -0.012 nn 640-660 0.020 nn 640-651 0.029 nn 521-512 0.022 nn 651-651 -0.030 nn 651-642 0.017 nn 514-503 -0.014 nn 550-550 -0.018 pp 420-411 0.011 nn 541-532 -0.011 nn 422-411 0.010 -0.062 pp 550-550 -0.011 pp 550-530 -0.690 pp 420-411 0.026 pp 541-532 -0.097 pp 422-411 -0.012 pp 532-523 0.034 pp 413-402 4.778 0.011 0.014 nn 521-510 -0.694 nn 510-501 -0.012 nn 640-651 -0.028 nn 660-631 -0.016 nn 521-512 -0.011 nn 651-651 -0.108 nn 651-642 0.051 pp 550-550 0.041 pp 420-411 -0.016 pp 541-532 -0.019 pp 422-411

InK=1+0 States IN 168Er and 176Hf Nuclei

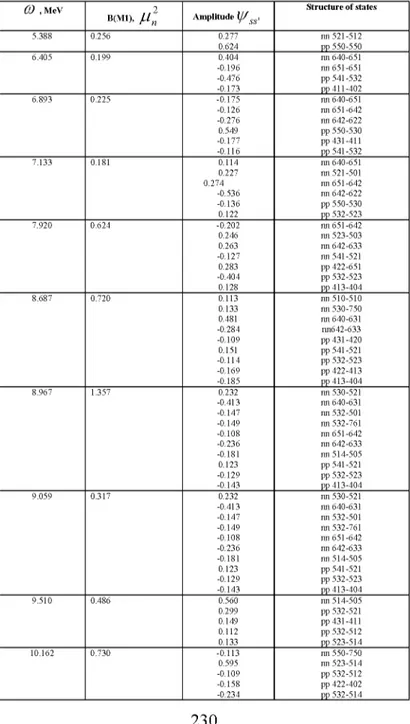
Table III. B(M1) values, energies and quasiparticle structures of high-lying I nK = 1+0 states of 168Er. CO , MeV , , 2 Amplitude Structure of states CO , MeV B(M1), /UN Amplitude 5.388 0.256 0.277 nn 521-512 0.624 pp 550-550 6.405 0.199 0.404 nn 640-651 -0.196 nn 651-651 -0.476 pp 541-532 -0.173 pp 411-402 6.893 0.225 -0.175 nn 640-651 -0.126 nn 651-642 -0.276 nn 642-622 0.549 pp 550-530 -0.177 pp 431-411 -0.116 pp 541-532 7.133 0.181 0.114 nn 640-651 0.227 nn 521-501 0.274 nn 651-642 -0.536 nn 642-622 -0.136 pp 550-530 0.122 pp 532-523 7.920 0.624 -0.202 nn 651-642 0.246 nn 523-503 0.263 nn 642-633 -0.127 nn 541-521 0.283 pp 422-651 -0.404 pp 532-523 0.128 pp 413-404 8.687 0.720 0.113 nn 510-510 0.133 nn 530-750 0.481 nn 640-631 -0.284 nn642-633 -0.109 pp 431-420 0.151 pp 541-521 -0.114 pp 532-523 -0.169 pp 422-413 -0.185 pp 413-404 8.967 1.357 0.232 nn 530-521 -0.413 nn 640-631 -0.147 nn 532-501 -0.149 nn 532-761 -0.108 nn 651-642 -0.236 nn 642-633 -0.181 nn 514-505 0.123 pp 541-521 -0.129 pp 532-523 -0.143 pp 413-404 9.059 0.317 0.232 nn 530-521 -0.413 nn 640-631 -0.147 nn 532-501 -0.149 nn 532-761 -0.108 nn 651-642 -0.236 nn 642-633 -0.181 nn 514-505 0.123 pp 541-521 -0.129 pp 532-523 -0.143 pp 413-404 9.510 0.486 0.560 nn 514-505 0.299 pp 532-521 0.149 pp 431-411 0.112 pp 532-512 0.133 pp 523-514 10.162 0.730 -0.113 nn 550-750 0.595 nn 523-514 -0.109 pp 532-512 -0.158 pp 422-402 -0.234 pp 532-514

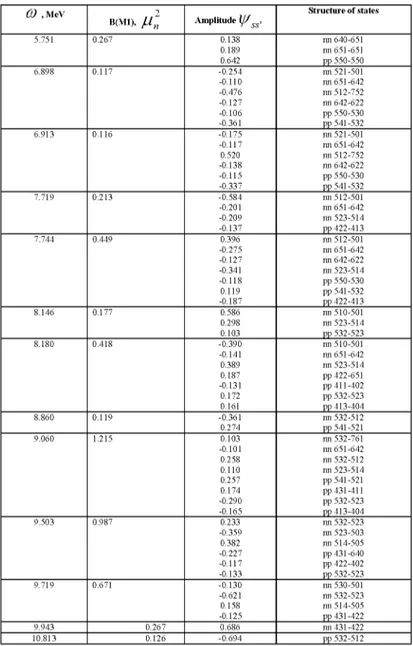
Table IV. B(M1) values, energies and quasiparticle structures of high-lying I nK = 1+0 states of 176Hf. C , MeV 2 Amplitude Structure of states C , MeV B(M1), / Un Amplitude 5.751 0.267 0.138 nn 640-651 0.189 nn 651-651 0.642 pp 550-550 6.898 0.117 -0.254 nn 521-501 -0.110 nn 651-642 -0.476 nn 512-752 -0.127 nn 642-622 -0.106 pp 550-530 -0.361 pp 541-532 6.913 0.116 -0.175 nn 521-501 -0.117 nn 651-642 0.520 nn 512-752 -0.138 nn 642-622 -0.115 pp 550-530 -0.337 pp 541-532 7.719 0.213 -0.584 nn 512-501 -0.201 nn 651-642 -0.209 nn 523-514 -0.137 pp 422-413 7.744 0.449 0.396 nn 512-501 -0.275 nn 651-642 -0.127 nn 642-622 -0.341 nn 523-514 -0.118 pp 550-530 0.119 pp 541-532 -0.187 pp 422-413 8.146 0.177 0.586 nn 510-501 0.298 nn 523-514 0.103 pp 532-523 8.180 0.418 -0.390 nn 510-501 -0.141 nn 651-642 0.389 nn 523-514 0.187 pp 422-651 -0.131 pp 411-402 0.172 pp 532-523 0.161 pp 413-404 8.860 0.119 -0.361 nn 532-512 0.274 pp 541-521 9.060 1.215 0.103 nn 532-761 -0.101 nn 651-642 0.258 nn 532-512 0.110 nn 523-514 0.257 pp 541-521 0.174 pp 431-411 -0.290 pp 532-523 -0.165 pp 413-404 9.503 0.987 0.233 nn 532-523 -0.359 nn 523-503 0.382 nn 514-505 -0.227 pp 431-640 -0.117 pp 422-402 -0.133 pp 532-523 9.719 0.671 -0.130 nn 530-501 -0.621 nn 532-523 0.158 nn 514-505 -0.125 pp 431-422 9.943 0.267 0.686 nn 431-422 10.813 0.126 -0.694 pp 532-512

InK=1+0 States IN 168Er and 176Hf Nuclei

Figure 1. Energy diagram of B(M1) values (above) and sum rule for the 1+ states K=0 in 168Er and 176Hf.

4. CONCLUSION

1) The spectroscopic 1+ states (up to energies on the order of 4 MeV) are weakly correlated and are characterized by small values of B(M1).

2) Near the neutron binding energy the 1+ states ( 0 < 7 - 9 MeV) are more collective

3) The neutron-proton mixing is weak in low-lying 1+ states.

4) The group of strongly collective 1+ states is found in the energy interval 9-11 MeV. Strong M1 transitions can occur in the case of K=0. This region contribute about 70% to the sum rule.

Acknowledgement: The author would like to acknowledge many helpful discussions with Prof. A. A. Kuliev.

REFERENCES

[1] Gabrakov, S. I., Kuliev, A. A. and Pyatov, N. I.; States In=1+ in even-even deformed nuclei, Sov. Journal of nuclear physics, Vol 1,1 (1970), 44-48.

[2] Gabrakov, S.I., Kuliev, A.A., Pyatov, N.I., Salamov, D.I. and Schulz, H.; Collective ₁₊ States in Doubly even deformed nuclei, Nuclear Phys. A182 (1972), 625-633.

[3] Bohr, A., Mottelson, B.; Nuclear Structure, Vol. 2. Benjamin, New York (1974). [4] Neumann- P. Von Cosel, Ginoccio, J.N., Bauer, H., Richter, A.; Relation between the Scissors Mode ve the Interacting Boson Model Deformation, Phys. Rev. Lett. 75, 4178, 1995.

[5] Ertugral, F., Guliyev, E., Akkaya, R. and Tutuncu, H. M.; Investigation of magnetic dipole InK=1+0 states in 150Nd and 176Hf nuclei, Nuclear science and its application, The third Eurasian Conf Tashkent, Uzbekistan (2004), p87.

[6] Soloviev, V.G.; Theory of Complex Nuclei, Pergamon Press, New York (1976). [7] Raman, S., Nestor, C.W., and Tikkanen, P.; Transition Probability From The Ground To

The First-Excited 2+ State Of Even-Even Nuclides, Atomic Data and Nuclear Data Tables