Kesirli dereceli kontrol sistemlerinde tamsayı dereceli yaklaşım metotlarının incelenmesi

(1)

Kesirli Dereceli Kontrol Sistemlerinde Tamsayı Dereceli

Yaklaşım Metotlarının İncelenmesi

Nusret Tan

1

, Ali Yüce

1

, Akın Özel

2

, Furkan Nur Deniz

1 1

Elektrik-Elektronik Mühendisliği Bölümü

İnönü Üniversitesi, Malatya

nusret.tan@inonu.edu.tr, ali.yuce@inonu.edu.tr, furkan.deniz@inonu.edu.tr 2

Teknik Bilimler MYO Elektrik Programı

Bingöl Üniversitesi, Bingöl

akozel@bingol.edu.tr

Özetçe

Son yıllarda kesirli dereceli kontrol sistemleri ile ilgili çok sayıda çalışma yapılmaktadır. Özellikle kesirli dereceli matematiğin uygulanabilmesine olanak sağlayan bugünkü teknolojik hesaplama araçlarından dolayı, önümüzdeki yıllarda bilimsel çalışmaların büyük oranda kesirli matematiğe dayalı olacağı görülmektedir. Çünkü gerçek sistemlerin

modellenmesinde kesirli matematik büyük fırsatlar

sunmaktadır. Ancak geliştirilmiş olan klasik kontrol metotlarının kesirli sistemlere uygulanma yöntemlerinden bir tanesi eşdeğer tamsayı modellerin elde edilmesidir. Bu çalışmada eşdeğer tamsayı modelleri elde etmede kullanılan metotlar özetlenmiş olup bu alanda çalışacak yeni araştırmacılara katkı sağlayacak eşdeğer tablolar elde edilmiştir. Ayrıca frekans ve zaman cevapları, kesin/gerçek cevaplar ile kıyaslamalı olarak iki farklı örnek üzerinden sunulmuştur.

1. Giriş

Son yıllarda, dinamiği kesirli dereceli türevle daha iyi ifade edilen kontrol sistemlerine yoğun bir ilginin olduğu söylenebilir [1, 2]. Bu tür kontrol sistemlerine kesirli dereceli kontrol sistemleri denilmektedir. Daha genel olarak, bir fiziksel sistemi ifade eden diferansiyel denklemlerde eğer türevin dereceleri tamsayı değil de reel herhangi bir sayı ise bu sisteme kesirli dereceli sistem denilmektedir. Kesirli dereceli sistemler söz konusu olduğunda kesirli matematik [1-3] kuralları uygulanmalıdır. Özellikle kesirli dereceli matematiğin uygulanabilmesine imkan sağlayan bugünkü teknolojik hesaplama araçlarından dolayı önümüzdeki yıllarda da bilimsel çalışmaların büyük oranda kesirli matematiğe dayalı olacağı görülmektedir. Bunun en önemli nedenlerinden bir tanesi gerçek sistemlerin modellenmesinde kesirli dereceli matematiğin büyük fırsatlar sunmasıdır [3].

Ancak klasik kontrol yöntemlerinin kesirli dereceli kontrol sistemlerine doğrudan uygulanması önünde bazı zorluklar

bulunmaktadır. Frekans tabanlı metotlar doğrudan

kullanılabilmelerine rağmen kesirli dereceli kontrol

sistemlerinde zaman cevabı hesaplamaları kolaylıkla

yapılamamaktadır. Zaman cevabı hesaplamalarında kullanılan yöntemlerden bir tanesi eşdeğer tamsayı modellerinin elde edilmesidir. Eşdeğer tamsayı modellerin elde edilmesine yönelik literatürde çok sayıda çalışma yapılmıştır. Bu

çalışmalardan bazıları CFE metodu, Oustaloup metodu, Carlson metodu, Matsuda metodu, Chareff metodu ve diğer metotlardır [4-11]. Bu çalışmada bu metotlardan bazıları özetlenmiş olup, bu alanda çalışacak yeni araştırmacılara katkı sağlayacak bazı eşdeğer tablolar elde edilmiştir.

2. Bazı Yaklaşım Yöntemleri

Bu bölümde kesirli türevin eşdeğer tamsayı yaklaşımını veren bazı metotlar özetlenmiştir.

2.1. Oustaloup Yaklaşım Metodu [6]

En iyi yaklaşımlardan biri, kutup ve sıfırların tekrarlı dağılımını kullanan Oustaloup yöntemidir. Bu yaklaşımın transfer fonksiyonu aşağıdaki gibidir.

, 1 , 1 ( ) 1 ( ) N z n v n p n s s k s      



(1)

Bu yaklaşım [ l h ] frekans aralığında geçerlidir.

Burada, Denklem (1) deki ifadenin k kazancı frekans 1 rad/s de birim kazancı verecek şekilde seçilir. Kutupların ve sıfırların sayısı bu yaklaşımın istenen performansına bağlı

olarak önceden seçilir. Düşük değerler yaklaşımı

basitleştirirken, kazanç ve fazın her ikisinin davranışlarında salınımlara yol açar. Bu salınımlar N ’nin artırılması ile azaltılabilir ama bu seferde yaklaşımda hesap işlemleri ağırlaşacaktır. Denklem (1) deki parametreler aşağıdaki gibidir. ,1 z l n   (2) , , p n z n   ; n=1,...,.N, (3) , 1 , z n p n    ; n=1,...,.N-1, (4) ( )v N h l    (5) (1 ) ( ) v N h l _    (6) 0

v durumu kesirli integrale karşılık gelir ve eşdeğeri yukarıdaki (1) nolu denklemin ters çevrilmesi ile elde edilir.

TOK 2014 Bildiri Kitabı

11-13 Eylül 2014, Kocaeli

(2)

Oustaloup yaklaşımı 1, 3, 5, 7,… gibi tamsayı derecelerde eşdeğer yaklaşımını verir. Oustaloup 1. dereceden, 3. dereceden ve 5 . dereceden yaklaşım sonuçları Tablo 1’de verilmiştir.

2.2. Matsuda Yaklaşımı Metodu [8]

( )

G s s olsun ve tamsayı eşdeğeri R s olsun. ( ) G s ’in ( )

0

 , ₁, ₂,... frekanslarında kazancı hesaplanabilir. Bu durumda Matsuda’ya göre yaklaşık tamsayı dereceli eşdeğer transfer fonksiyonu aşağıdaki gibi hesaplanır,

0 0 0 1 1 1 2 2 2 ( ) ( ) ( ) ( ) ... s G s d s d s d   _  _     _  _  (7) Bu denklemde d0( ) G j( ) ve 1( ) , 0,1, 2,... ( ) ( ) k k k k k d k d d           olur. Matsuda 1.

dereceden, 2. dereceden, 3. dereceden ve 4 . dereceden yaklaşım sonuçları Tablo 2’de verilmiştir.

2.3. Krishna Metodu [5]

Krishna metodu Denklem (8) ile ifade edilir.

1 (1 ) (1 ) (2 ) (2 ) (1 ) 1 1 2 3 2 5 ... x x x x x x              (8)

burada x s 1 kullanarak kesirli türev veya integralin tamsayı eşdeğerleri hesaplanır. s’nın birinci, ikinci, üçüncü ve dördüncü dereceden eşdeğerleri aşağıdaki denklemlerle hesaplanır. Hesaplanan Krishna 4. dereceden tamsayı eşdeğer sonuçları Tablo 3’te verilmiştir.

(1 ) (1 ) (1 ) (1 ) s s s             (9) 2 2 2 2 2 2 2 ( 3 2) ( 2 8) ( 3 2) ( 3 2) ( 2 8) ( 3 2) s s s s s                             (10) 3 2 3 3 2 2 3 2 3 2 3 2 3 3 2 2 3 2 3 2 ( 6 11 6) ( 3 6 27 54) (3 6 27 54) ( 6 11 6) ( 6 11 6) (3 6 27 54) ( 3 6 27 54) ( 6 11 6) s s s s s s s                                                             (11) 4 3 2 4 4 3 2 3 4 2 2 4 3 2 4 3 2 4 3 2 4 4 3 2 3 4 2 2 4 ( 10 35 50 24) ( 4 20 40 320 384) (6 150 864) ( 4 20 40 320 384) ( 10 35 50 24) ( 10 35 50 24) ( 4 20 40 320 384) (6 150 864) ( 4 20 s s s s s s s s                                                                         3 2 4 3 2 40 320 384)s ( 10 35 50 24)               (12) 2.4. Carlson Metodu [7]

Bu metot Newton’un iteratif metoduna dayalıdır. Uygun bir tamsayı dereceli ( )R s modeli ile yaklaşım yapılan bir kesir

dereceli integral operatörü ( ) ( ( ))a (1 / )

G s  g s  sele alalım.

( )

G s ’in eşdeğer tamsayı yaklaşımı ( )R s olsun. Bu durumda

Carlson yöntemine göre G s ve ( )( ) R s arasındaki ilişki

1 1 1 ( 1)( ( )) ( 1) ( ) ( ) ( ) ( 1)( ( )) ( 1) ( ) v n n n v n v R s v g s R s R s v R s v g s           (13)

Denklem (13) şeklindedir. Burada R s0( )1ve v1 / bir

tamsayı olmalıdır.

3. Örnekler

3.1. Örnek 1

0.5

( )

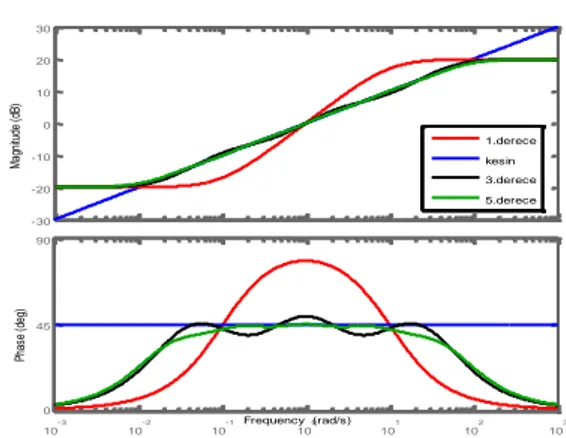
G s s ’in Oustaloup, Krishna ve Matsuda eşdeğerleri kullanılarak yaklaşık ve aynı grafik üzerine kesin Bode diyagramları Şekil 1, Şekil 2 ve Şekil 3’te çizdirilmiştir. Şekillerden görüleceği gibi Oustaloup 5. dereceden, Krishna ve Matsuda 4. dereceden tamsayı eşdeğerler gerçek sistemin Bode diyagramına yaklaşmaktadırlar.

-30 -20 -10 0 10 20 30 M ag ni tu de ( dB ) 10 -3 10 -2 10 -1 10 0 10 1 10 2 10 3 0 45 90 P ha se ( de g) Bode Diagram Frequency (rad/s) 1.derece kesin 3.derece 5.derece

Şekil 1: Oustaloup yöntemine ve gerçek/kesin duruma göre 0.5 s ’ in bode diyagramları. -30 -20 -10 0 10 20 30 M ag ni tu de ( dB ) 10 -3 10 -2 10 -1 10 0 10 1 10 2 10 3 0 30 60 P ha se ( de g) Bode Diagram Frequency (rad/s) 1.derece kesin 2.derece 3.derece 4.derece

Şekil 2: Krishna yöntemine ve gerçek/kesin duruma göre 0.5 s ’

(3)

-30 -20 -10 0 10 20 30 M ag ni tu de ( dB ) 10 -3 10 -2 10 -1 10 0 10 1 10 2 10 3 0 30 60 90 P ha se ( de g) Bode Diagram Frequency (rad/s) 1.derece kesin 2.derece 3.derece 4.derece

Şekil 3: Matsuda yöntemine ve gerçek/kesin duruma göre 0.5 s ’ in bode diyagramları. 3.2. Örnek 2 0.5 1 ( ) G s s

 ’in birim analitik basamak tepkisi 0.5

( ) 2( / )

y t  t 

dir. Şekil 4’te Oustaloup 5. dereceden, Krishna ve Matsuda 4. dereceden eşdeğer transfer fonksiyonlarının birim basamak cevapları ile analitik ifadenin birim basamak cevabı beraber verilmiştir. Gerçek sonuçla aralarındaki hatalar ise Şekil 5’te verilmiştir. Şekil 5’te de görüldüğü gibi Matsuda eşdeğer transfer fonksiyonu gerçek sistemi daha iyi takip etmektedir.

0 20 40 60 80 100 120 140 160 180 200 0 2 4 6 8 10 12 14 16 18 Unit-Step Response Krishna Oustaloup Matsuda Exact

Şekil 4: Yaklaşım metotlarının karşılaştırmalıbirim basamak cevapları.

4. Sonuçlar

Bu çalışmada kesirli dereceli sistemleri tamsayı dereceli

eşdeğer sistemlere dönüştüren yaklaşım metotları

incelenmiştir. Tablo 1’de Oustaloup yaklaşım sonuçları, Tablo 2’de Matsuda yaklaşım sonuçları verilmiştir. Örneklerde Oustaloup 5. dereceden, Krishna 4. dereceden ve Matsuda 4. dereceden eşdeğerlerin genel olarak yeterli olabileceği görülmüştür. Dolayısıyla Tablo 3’te Oustaloup 5. dereceden, Krishna 4. dereceden ve Matsuda 4. dereceden eşdeğerleri

içeren sonuçlar beraber elde edilmiştir. Bu sonuçların bu alanda yeni çalışma yapacak olan araştırmacılar için yararlı olacağı düşünülmektedir ve daha detaylı karşılaştırma çalışmalarının yapılmasına zemin oluşturacaktır.

0 20 40 60 80 100 120 140 160 180 200 -1 0 1 2 3 4 5 6 7

Yaklaşımların zamana göre hataları

t (sec) ha ta Krishna hatası Oustaloup hatası Matsuda hatası

Şekil 5: Yaklaşım yöntemlerinin birim basamak cevaplarının

hata değişim grafikleri.

Kaynakça

[1] D. Xue, Y.Q. Chen and D.P. Atherton, Feedback Control

Systems - analysis and design with MATLAB 6, London:

Springer-Verlag, 2002.

[2] C.A. Monje, Y.Q. Chen, B.M. Vinagre, D. Xue, V. Feliu,

Fractional-Order Systems and Controls: Fundamentals and Applications, Springer: London, New York, 2010.

[3] S. Das, Functional Fractional Calculus for System

Identification and Control, Springer-Verlag, Berlin,

Heidelberg, New York, 2008.

[4] B.M. Vinagre, I. Podlubny, A. Herńandez, and V. Feliu, “Some approximations of fractional order operators used in control theory and applications,” Fractional Calculus

and Applied Analysis, Cilt: 3, No: 3, s:231-248, 2000.

[5] B.T. Krishna, “Studies on fractional order differentiators and integrators: a survey,” Signal Processing, Cilt: 91, No: 3, s:386–426, 2011.

[6] A. Oustaloup, F. Levron, B. Mathieu, and F.M. Nanot, “Frequency band complex noninteger differentiator: characterization and synthesis,” IEEE Trans. on Circuit

and Systems - I: Fundamental Theory and Application,

Cilt: 47, No: 1, s:25–39, 2000.

[7] G.E. Carlson and C.A. Halijak, “Approximation of fractional capacitors (1/s)1/n by a regular Newton process,” IEEE Trans. on Circuit Theory, Cilt: 11, No: 2, s:210–213, 1964.

[8] K. Matsuda and H. Fujii, “H∞–optimized wave-absorbing

control: analytical and experimental results,” Journal of

Guidance, Control, and Dynamics, Cilt: 16, No: 6,

s:1146–1153, 1993

[9] A. Charef, H.H. Sun, Y.Y. Tsao and B. Onaral, “Fractal system as represented by singularity function,” IEEE

Trans. on Automatic Control, Cilt: 37, No: 9, s:1465–

(4)

[10] M.M. Özyetkin, C. Yeroğlu, N. Tan, and M.E. Tağluk, “Design of PI and PID controllers for fractional order time delay systems,” 9th IFAC workshop on Time Delay Systems, Prague, Czech, 2010.

[11] M. Khanra, J. Pal and K. Biswas, “Rational

Approximation of Fractional Operator – A Comparative Study”, IEEE Power, Control and Embedded Systems (ICPCES), Allahabad, India, s:1-5, 2010.

Tablo 1: Oustaloup Yaklaşım Tablosu

s

 1.derece yaklaşım 3.derece yaklaşım 5.derece yaklaşım

0.1

s

1.585 +1 +1.585 s s 3 2 3 2 1.585 30.71 26.34 1 26.34 30.71 1.585 s s s s s s       5 4 3 2 5 4 3 2 1.585 68.37 403.3 367.9 51.87 1 51.87 367.9 403.3 68.37 1.585 s s s s s s s s s s           0.2

s

2.512 1 2.512 s s   3 2 3 2 2.512 41.74 30.71 1 30.71 41.74 2.512 s s s s s s       5 4 3 2 5 4 3 2 2.512 98.83 531.7 442.3 56.87 1 56.87 442.3 531.7 98.83 2.512 s s s s s s s s s s           0.3

s

3.981 1 3.981 s s   3 2 3 2 3.981 56.75 35.8 1 35.8 56.75 3.981 s s s s s s       5 4 3 2 5 4 3 2 3.981 142.9 700.9 531.7 62.36 1 62.36 531.7 700.9 142.9 3.981 s s s s s s s s s s           0.4

s

6.31 1 6.31 s s   3 2 3 2 6.31 77.14 41.74 1 41.74 77.14 6.31 s s s s s s       5 4 3 2 5 4 3 2 6.31 206.5 924 639.3 68.37 1 68.37 639.3 924 206.5 6.31 s s s s s s s s s s           0.5

s

10 1 10 s s   3 2 3 2 10 104.9 48.67 1 48.67 104.9 10 s s s s s s       5 4 3 2 5 4 3 2 10 298.5 1218 768.5 74.97 1 74.97 768.5 1218 298.5 10 s s s s s s s s s s           0.6

s

15.85 1 15.85 s s   3 2 3 2 15.85 142.5 56.75 1 56.75 142.5 15.85 s s s s s s       5 4 3 2 5 4 3 2 15.85 431.4 1606 924 82.2 1 82.2 924 1606 431.4 15.85 s s s s s s s s s s           0.7

s

63.1 1 63.1 s s   3 2 3 2 63.1 358 89.94 1 89.94 358.4 63.1 s s s s s s       5 4 3 2 5 4 3 2 63.1 1303 3679 1606 108.4 1 108.4 1606 3679 1303 63.1 s s s s s s s s s s          

Tablo 2: Matsuda Yaklaşım Tablosu

s

 1.derece yaklaşım 2.derece yaklaşım 3.derece yaklaşım 4.derece yaklaşım

0.1

s

1.6 s + 1_{s + 1.6} 2 2 1.677 15.72 1 15.72 1.677 s s s s     3 2 3 2 1.757 49.67 41.97 1 41.97 49.67 1.757 s s s s s s       4 3 2 4 3 2 1.828 102.7 329.8 78.91 1 78.91 329.8 102.7 1.828 s s s s s s s s         0.2

s

2.566 s + 1_{s + 2.566} 2 2 2.824 20.59 1 20.59 2.824 s s s s     3 2 3 2 3.101 72.7 51.88 1 51.88 72.7 3.101 s s s s s s       4 3 2 4 3 2 3.357 161 453.9 95 1 95 453.9 161 3.357 s s s s s s s s         0.3

s

4.136 s + 1_{s + 4.136} 2 2 4.796 27.28 1 27.28 4.796 s s s s     3 2 3 2 5.526 108 65.01 1 65.01 108 5.526 s s s s s s       4 3 2 4 3 2 6.227 256.4 635 116.1 1 116.1 635 256.4 6.227 s s s s s s s s         0.4

s

6.724 s + 1_{s + 6.724} 2 2 8.266 36.75 1 36.75 8.266 s s s s     3 2 3 2 10.01 163.6 83.01 1 83.01 163.6 10.01 s s s s s s       4 3 2 4 3 2 11.74 417.1 907.9 144.6 1 144.6 907.9 417.1 11.74 s s s s s s s s         0.5

s

11.1 s + 1_{s + 11.1} 2 2 14.58 50.71 1 50.71 14.58 s s s s     3 2 3 2 18.58 254.8 108.8 1 108.8 254.8 18.58 s s s s s s       4 3 2 4 3 2 22.72 698.8 1337 185 1 185 1337 698.8 22.72 s s s s s s s s         0.6

s

18.82 s + 1_{s + 18.82} 2 2 26.67 72.57 1 72.57 26.67 s s s s     3 2 3 2 35.85 413.7 148.2 1 148.2 413.7 35.85 s s s s s s       4 3 2 4 3 2 45.73 1222 2056 246.3 1 246.3 2056 1222 45.73 s s s s s s s s         0.7

s

33.53 s + 1_{s + 33.53} 2 2 51.85 110.3 1 110.3 51.85 s s s s     3 2 3 2 73.74 717.2 215 1 215 717.2 73.74 s s s s s s       4 3 2 4 3 2 98.22 2287 3381 349.4 1 349.4 3381 2287 98.22 s s s s s s s s         0.8

s

66.13 s + 1_{s + 66.13} 2 2 113.1 187.8 1 187.8 113.1 s s s s     3 2 3 2 170.7 1401 350.1 1 350.1 1401 170.7 s s s s s s       4 3 2 4 3 2 237.8 4833 6277 557 1 557 6277 4833 237.8 s s s s s s s s         0.9

s

170.9 s + 1_{s + 170.9} 2 2 328.6 424.3 1 424.3 328.6 s s s s     3 2 3 2 528.2 3662 758.6 1 758.6 3662 528.2 s s s s s s       4 3 2 4 3 2 770 13690 15610 1182 1 1182 15610 13690 770 s s s s s s s s        

(5)

Tablo 3: Karşılaştırmalı Yaklaşım Tablosu

0.1

s

Oustaloup 5.derece yaklaşım

5 4 3 2 5 4 3 2

1.585

68.37

403.3

367.9

51.87

1

51.87

367.9

403.3

68.37

1.585 s

s



Krishna 4 .derece yaklaşım

4 3 2 4 3 2 1 1.518 21.529 44.596 18.222 18.222 44.596 21.529 1.518 s s s s s s s s        

Matsuda 4.derece yaklaşım

4 3 2 4 3 2 1.828 102.7 329.8 78.91 1 78.91 329.8 102.7 1.828 s s s s s s s s         0.2

s

5 4 3 2 5 4 3 2

2.512

98.83

531.7

442.3

56.87

1

56.87

442.3

531.7

98.83

2.512 s

s



4 3 2 4 3 2 1 2.316 29.333 56 21 21 56 29.333 2.316 s s s s s s s s        

4 3 2 4 3 2 3.357 161 453.9 95 1 95 453.9 161 3.357 s s s s s s s s         0.3

s

5 4 3 2 5 4 3 2

3.981

142.9

700.9

531.7

62.36

1

62.36

531.7

700.9

142.9

3.98 s

s



4 3 2 4 3 2 1 1 3.57 4 2.47 0.63 71.546 24.57 71.546 40.63 3.57 s s s s s s s s        

4 3 2 4 3 2

6.227

256.4

635

116.1

1

116.1

635

256.4

6.227 s

s



0.4

s

5 4 3 2 5 4 3 2

6.31

206.5

924

639.3

68.37

1

68.37

639.3

924

206.5

6.31 s

s



4 3 2 4 3 2 1 5.594 57.538 93.5 29.333 29.333 93.5 57.538 5.594 s s s s s s s s        

4 3 2 4 3 2

11.74

417.1

907.9

144.6

1

144.6

907.9

417.1

11.74 s

s



0.5

s

5 4 3 2 5 4 3 2

10

298.5 1218

768.5

74.97

1

74.97

768.5 1218

298.5

10 s

s



4 3 2 4 3 2 9 84 126 36 1 36 126 84 9 s s s s s s s s        

4 3 2 4 3 2

22.72

698.8 1337

185

1

185 1337

698.8

22.72 s

s



0.6

s

5 4 3 2 5 4 3 2

15.85

431.4 1606

924

82.2

1

82.2

924 1606

431.4

15.85 s

s



4 3 2 4 3 2 46 1 46 15.076 128.143 177.428 177.428 128.143 15.076 s s s s s s s s        

4 3 2 4 3 2

45.73 1222

2056

246.3

1

246.3 2056

1222

45.73 s

s



0.7

s

5 4 3 2 5 4 3 2

25.12

623.6 2117

1111

90.14

1

90.14 1111

2117

623.6

25.12 s

s



4 3 2 4 3 2 1 26.965 209.38 267.54 62.67 62.67 267.54 209.38 26.965 s s s s s s s s        

4 3 2 4 3 2 98.22 2287 3381 349.4 1 349.4 3381 2287 98.22 s s s s s s s s        

(6)

0.8

s

5 4 3 2 5 4 3 2

39.81

901.4 2790

1336

98.83

1

98.83 1336

2790

901.4

39.81 s

s



4 3 2 4 3 2 96 1 96 54.41 386.91 456 456 386.91 54.41 s s s s s s s s        

4 3 2 4 3 2 237.8 4833 6277 557 1 557 6277 4833 237.8 s s s s s s s s         0.9

s

5 4 3 2 5 4 3 2

63.1 1303

3679

1606

108.4

1

108.4 1606

3679

1303

63.1 s

s



4 3 2 4 3 2 1 147.04 959.64 1042.36 196 196 1042.36 959.64 147.04 s s s s s s s s        

4 3 2 4 3 2