NORTH- ttOIKAND
HYPERSOLVER: A G r a p h i c a l T o o l for C o m r n o n s e n s e S e t T h e o r y Mb'JDAT PAKKAN
Computer Engineering Department, Bo~azi~i University, 13ebek, 80815 istanbul, 7)zrkey
and
VAROL AKMAN*
Department of Computer Engineering and Informatzon Science, Bilkent University, Bilkent, 06533 Ankara, 7~rkey
Communicated by Erol Gelenbe
A B S T R A C T
This paper investigates an alternative set theory (duc to Aczel) called the Hy- persct Theory. Aczel uses a graphical representation for sets and thereby allows the representation of non-well-founded sets. A program, called ttYPERSOLVER, which can solve systems of equations defined in terms of sets in the universe of this new theory is presented. This may be a useful tool for commonscnse reasoning.
1. I N T R O D U C T I O N
Set t h e o r y has long o c c u p i e d a u n i q u e place in m a t h e m a t i c s since it al- lows v a r i o u s o t h e r b r a n c h e s of m a t h e m a t i c s to be f o r m a l l y defined w i t h i n it. T h e t h e o r y has i g n i t e d m a n y d e b a t e s o n its n a t u r e a n d a n u m b e r of different a x i o m a t i z a t i o n s were developed to formalize its u n d e r l y i n g "philosophical" p r i n c i p l e s . C o l l e c t i n g e n t i t i e s i n t o a n a b s t r a c t i o n for f u r t h e r t h o u g h t (i.e., set c o n s t r u c t i o n ) is a n i m p o r t a n t process in m a t h e m a t i c s , a n d this b r i n g s i n a s s o r t e d p r o b l e m s [5]. T h e t h e o r y h a d m a n y g r o u n d - s h a k i n g crises (like *Corresponding author. Akman's research is supported in part by the Scientific and Technical Research Council of Turkey (rI'IIBiTAK), Grant No. TBAG-992. He wishc~ to thank tile following individuals for moral support: Prof. Patrick Suppes, Stanford University, Erkan "Fin, Bilkent University, and Dr. Wlodek Zadrozny, IBM Thomas J. Watson Research Center. Preliminary versions of this paper have been presented ms [1, 2, 3, 41.
INFORM.A TION SCIENCES 85, 43- 6 l (1995) (c) Elsevier Science Inc. 1995
the discovery of the Russell's Paradox [6]) t h r o u g h o u t its history, which were nevertheless overcome by new axiomatizations.
Tile most popular of these is the Zermelo-Fraenkel axiomatization with "Choice" (ZFC). ZFC is an elegant theory which inhabits a stable place a m o n g other axiomatizations as the m a i n s t r e a m set theory. It provides a "hierarchical" framework. This hierarchy starts with only one a b s t r a c t entity, the e m p t y set (0), forms sets out of previously formed entities cu- mulatively, and is therefore called the cumulative hierarchy. T h e coherence of this hierarchy is secured by the Axiom of Foundation (FA) which for- bids infinite descending sequences of sets under the m e m b e r s h i p relation c, such as ... E a2 E al E a0 E a (thereby not allowing sets which can be constituents of themselves), and which has sometimes been regarded as a s o m e w h a t superficial limitation [6]. Sets which obey the FA are called well-founded sets.
T h e cumulative hierarchy has providcd a precise framework for the for- malization of m a n y m a t h e m a t i c a l concepts [7]. However, it m a y be asked whether the hierarchy is limiting, in the sense t h a t it might be omitting some sets one would like to have around. Cyclic sets, i.e., sets which carl be m e m b e r s of themselves, are examples of such interesting sets which are excluded in ZFC. A set like a = {a} is strictly banned in ZPC by the FA since a has no m e m b e r disjoint from itself. Such sets have in- finite descending m e m b e r s h i p sequences and are called non-well-founded sets. Non-well-founded sets have generally been neglected by the practic- ing m a t h e m a t i c i a n since the classical well-founded universe was a satisfying domain for his practical concerns. However, non-well-founded sets are use- ful in modeling various p h e n o m e n a in c o m p u t e r science, viz. concurrency, databases, artificial intelligence (AI), etc. [8].
M c C a r t h y stressed the feasibility of using set theory in AI and invited researchers to concentrate on the subject in a 1985 speech [9]. Circu- larity is an often exploited p r o p e r t y in various fields of AI, e.g., com- monsense reasoning. Rehearsing an e x a m p l e of Perlis [10], if non-profit organizations are considered as individuals, t h e n the organization of all non-profit organizations is a set. I t is conceivable t h a t this umbrella or- ganization (called N P O ) might want to be a m e m b e r of itself in order to benefit from having the status of a non-profit organization (e.g., t a x exemption). B u t this implies t h a t N P O must bc non-well-founded, i.e., N P O E N P O .
T h i s p a p e r (also see [11]) investigates an alternative set theory, due to Aczel [12], which uses a graphical representation for sets and t h e r e b y allows the representation of non-well-founded sets. A program, called HYPF_2,SOLVER, which can solve systems of equations defined in t e r m s of sets in the universe of this new t h e o r y is presented.
H Y P E R S O L V E R : A G R A P H I C A L T O O L F O R S E T T H E O R Y 45
2. H Y P E R S E T T H E O R Y
In this section w e offer, using [8] a n d [13], a brief review of the H y p e r s e t Theory, w h i c h is a n e n r i c h m e n t of the classical Z F C set theory. It is the collection of all the conventional a x i o m s of Z F C modified to be consistent with the n e w universe involving atoms, except that the F A is n o w replaced by the AFA (to be explained in the sequel). The sets in this theory are col- lections of atoms (urclements) or other sets, whose hereditary m e m b e r s h i p relation can be depicted by graphs. These sets may be well-founded or non- well-founded, i.e., m a y have an infinite descending membership sequence, in which case they are also called hypersets.
Sets can be pictured by means of directed graphs in an unambiguous manner. For example, a = {b, {c,d}} can be pictured by the graph in Figure 1. In this graph, each nonterminal node represents the set which contains the entities represented by the nodes below it. The edges of the graph stand for the hereditary membership relation such t h a t an edge from a node n t o a node rn, denoted by n --* m, mcans t h a t m is a member of n. Since b, c, and d are assumed to contain no other entities as elements (i.e., they are urelements), there are no nodes below them.
In Aczel's terminology [12], a pointed graph is a directed graph with a specific node called its point. A pointed graph is said to be accessible if for every node n, there exists a path no---*nl--* • •. ---,n from the point no to n. If this path is always unique, then the pointed graph is a tree and the point is its root. Accessible pointed graphs (apg's) will be used to "picture" sets. A decoration D for a graph is an assignment of a set to each node of the graph in such a way t h a t
]" an atom or ~, if n has no children, D ( n ) {D(m): n --* m}, otherwise. a
/
?
\
c d Fig. 1. T h e g r a p h r e p r e s e n t a t i o n of a = {b, {c, d}}.Fig. 2. The picture of the non-well-founded set ft = {.Q}.
An apg G with point n is a picture of a if there exists a decoration D(n) = a, i.e., if a is the set that decorates the top node.
An apg is called well-founded if it has no infinite paths or cycles. Mostow- ski's Collapsing Lemma states t h a t every well-founded graph has a unique decoration. As a corollary, every well-founded apg is a picture of a unique well-founded set. A non-well-founded apg can never picture a well-founded set because if a is the set which contains all tile sets pictured by tile nodes occurring in a cycle of the non-well-founded apg, then it can be seen t h a t no member of a is disjoint from a itself, violating the FA.
Aczel's Anti-Foundation Axiom (AFA) states t h a t every apg, well- founded or not, pictures a unique set, or stated in other words, every apg has a unique decoration [12, 14]. The AFA has two implications: exis- tence and uniqueness. The former assures that every apg has a decoration (which leads to the existence of non-well-founded sets besides well-founded ones) and the latter asserts that no apg h ~ more t h a n one decoration. By throwing away the FA from the ZFC (and naming the resulting sys- tem Z F C - ) and adding the AFA, we obtain the Hyperset Theory. (a.k.a. Z F C - / A F A ) .
One of the important advantages of the new theory is that, by allowing arbitrary graphs, non-well-founded sets are included. For example, the non-well-founded set ~ = {f~} is pictured by the apg in Figure 2, and by the uniqueness property of the AFA, this is the only set pictured by t h a t graph. Therefore, there is a unique set which is equal to its own singleton in the universe of hypersets.
T h e picture of a set can be unfolded into a tree picture of the same set. The tree whose nodes are the finite paths of tile apg which start from the point of the apg, whose edges are pairs of paths {n0 --~ . . . . n, no --~ . . . . n --* n~), and whose root is tile path no of length 1 is called the uT~foldin9 of t h a t apg. The unfolding of an apg always pictures any set pictured by t h a t apg. Unfolding the apg in Figure 2 results in the infinite tree in Figure 3, analogous to unfolding f~ = {f~} to ~ = {{{--.}}}.
The uniqueness property of the AFA leads to an intriguing concept of extensionality for hyI)ersets. The classical extensionality paradigm, t h a t
HYPERSOLVER: A GRAPHICAL TOOL FOR SET THEORY 47
.
Fig. 3. Unfolding R to obtain an infinite tree.
sets are equal if and only if they have the same members, works fine with well-founded sets. However, this is not of use in deciding the equality of, say, a = (1, u} and b = {l, b} because it just asserts a = b if and only if a = b [$I. However, in the universe of hypersets, a is indeed equal to b since they are depicted by the same graph.r
Aczel develops his own extensionality concept by introducing the notion of bisimulation. A bisimulation between two apg’s, Gr with point pi Gz with point ps, is a relation R 2 G1 x Gs satisfying the conditions
1. P~RPZ, 2. if nRm, then
and
l for every edge n ---f n’ of Gr, there exists an edge m + m’ of G2
such that n’Rm’,
l for every edge m -+ m’ of G2, there exists an edge n -+ n’ of Gi
such that n’Rm’.
Two apg’s Gi and Gz are said to be bisimilar if a bisimulation exists be- tween them; this means that they picture the same set. It can be concluded that a set is completely determined by any graph which pictures it. There- fore, for two sets to be different, there should be a genuine structural dif- ference between them. For instance, the graphs in Figure 4 all depict the non-well-founded set fi because their nodes can be decorated with 0‘
The AFA has interesting applications. In [S], a modeling scheme for propositions (of natural language [15, 161) is offered. In this scheme, the lTo see this [S], consider a graph G and a decoration D assigning a to a node z of G, i.e., D(z) = a. Now consider the decoration D’ exactly the same as D except that
D’(x) = b. D’ must also be a decoration for G. But by the uniqueness property of the
Fig. 4. Other graphs depicting ~. 0 P = <E,p,O> = <E,<p,O>>
{p,0}
if O0
pFig. 5. The picture of "This proposition is not expressible in eight words." t r i p l e
(P,p,i}
d e n o t e s t h a t p r o p o s i t i o n p has p r o p e r t y P if i -= 1, a n d it d o e s n o t h a v e it if i -- 0. 2 If p is t a k e n t o be, say, " T h i s p r o p o s i t i o n is n o t e x p r e s s i b l e u s i n g e i g h t w o r d s , " t h e n it c a n b e m o d e l e d b y t h e t r i p l e(E,p, O)
w h e r e E (an a t o m ) d e n o t e s t h e p r o p e r t y o f b e i n g e x p r e s s i b l e (in E n g l i s h ) using e i g h t w o r d s . I n A c z c l ' s c o n c e p t i o n , p c a n b e d e p i c t e d as in F i g u r e 5 w h e r e t h e l o n g e s t arc shows t h a t p refers t o itself.2Remember that in set theory, triples such as (x, y, z) are defined as pairs of pairs, i.e., (x, (y, z}}, and (y, z} is defined as {{y}, {y, z}}.
H Y P E R S O L V E R : A G R A P H I C A L T O O L F O R S E T T H E O R Y 49
3. S O L V I N G S Y S T E M S O F H Y P E R S E T E Q U A T I O N S
T h e AFA has an i m p o r t a n t consequence which has useful applications allowing us to assert t h a t some sets exist without having to picture t h e m with graphs. This will be motivated by the following example [12].
An equation of the form x = (0, x) in one variable x can be rewritten as x = {{0}; {0, x}}. This is equivalent to the following system of four equations in four unknowns:
= {y, z}, y = {w}, z = { ~ , z } ,
W ~--- 0.
By the AFA, this system of equations has a unique solution pictured by the g r a p h in Figure 6. Unfolding the original equation, one obtains x = <o, <o, <o,...>>>.
This result can be generalized. For any set a, the equation x = (a, x) has a unique solution x = (a, (a, ( a , . . . ) ) ) . More generally, an infinite system of equations
has a unique solution
x0 = <ao, x~>: x l = ( a l , x2),
xo -- <no, <al, <a2,...>>>, x , = <al, (a2, <a3 . . . . >>/, x2 = (a~, (a3, <a4,...//>,
Motivated by such examples, a technique to assert t h a t every system of equations has a unique solution has been developed by Aczel [12]. N a m e d the S o l u t i o n L e m m a by Barwise and E t c h e m e n d y [8], this is formulated below.
L e t ~ A be the universe of hypersets with a t o m s from a given set A. Let VA, be the universe of hypersets with a t o m s from another given set A t such t h a t A C A'. Let X be defined as A ' - A. T h e elements of X can be considered as indete~'ninates ranging over the universe ]2 A. Sets which can contain a t o m s from X in their construction are called X-sets. A s y s t e m o f
X
J
w=0
Fig. 6. The solution of the system x -~ {y,z}, y = {w}, z = {w,x}, w = 0.
equations is a set of e q u a t i o n s .
{x = ax: x • X A a~. is a n X - s e t }
for each x E X . For e x a m p l e , choosing X = { x , y , z } a n d A = { C , M } ( t h u s A ~ = {x, y, z, C, M}), we m a y consider t h e s y s t e m of e q u a t i o n s
= { c , y},
=
z = {M, x}.
( T h i s s y s t e m will be used in t h e sequel for i l l u s t r a t i v e purposes.)
A solution to a s y s t e m of e q u a t i o n s is a f a m i l y of p u r e sets b~, (sets which c a n have o n l y sets b u t no a t o m s as e l e m e n t s ) , one for each x • X , such t h a t for each x E X , bx = 7ra~. Here, rr is a substitution operation (defined below) a n d zra is t h e pure set o b t a i n e d from a by s u b s t i t u t i n g b~ for each o c c u r r e n c e of a n a t o m x in t h e c o n s t r u c t i o n of a.
T h e Substitution Lemma s t a t e s t h a t for e ~ h f a m i l y of p u r e sets b~ (x E X ) , t h e r e exists a u n i q u e o p e r a t i o n 7r which assigns a p u r e set 7ra to each X - s e t a, viz.,
7ra = {srb: b is a n X - s e t such t h a t b • a} kJ {~rx: x • a N X } . T h e Solution Lemma c a n now b e s t a t e d [12]. If a~ is a n X - s e t , t h e n t h e s y s t e m of e q u a t i o n s x = a~ (x E X ) has a u n i q u e s o l u t i o n , i.e., a u n i q u e f a m i l y of p u r e sets b~ such t h a t for each x E X , b~ = lra~.
T h i s l e m m a c a n b e s t a t e d s o m e w h a t differently [13]. L e t t i n g X a g a i n be t h e set of i n d e t e r m i n a t e s , g a f u n c t i o n from X to 2 X, a n d h a f u n c t i o n from X to A, t h e r e exists a u n i q u e f u n c t i o n f for all x E X such t h a t
H Y P E R S O ] , V E R : A G R A P H I C A L T O O L F O R S E T T H E O R Y 51 O b v i o u s l y ,
g(x)
is t h e set o f i n d e t e r m i n a t e s a n dh(x)
is t h e set of a t o m s in e a c h X - s e t a~ o f an e q u a t i o n x = a~. In t h e a b o v e e x a m p l e ,.q(x)
: {y}, : j ( y ) : z , : : { C } , h ( V ) = { C } , : c a n c o m p u t e t h e s o l u t i o nf(x)
= {C, {C, { M , x } } } ,f(y)
= {C, {M, {C; y}}},f(z)
= {M, {C, { C , z } } } , easily. 3T h i s t e c h n i q u e of soh, ing e q u a t i o n s in t h e u n i v e r s e of" h y p e r s e t s allows us t o a s s e r t t h e e x i s t e n c e of s o m e s e t s ( t h e s o l u t i o n s of t h e e q u a t i o n s ) w i t h o u t h a v i n g t o d e p i c t t h e m w i t h g r a p h s . T h i s f e a t u r e can b e of c o n s i d e r a b l e h e l p in m o d e l i n g i n f o r m a t i o n w h i c h can b e c a s t in t h e f o r m of e q u a t i o n s . A n e x a m p l e c o n c e r n i n g s i t u a t i o n t h e o r y follows.
Situation theory
is a t h e o r y o f m e a n i n g a n d i n f o r m a t i o n c o n t e n t d e v e l - o p e d b y B a r w i s e a n d P e r r y [17]. I t t r i e s to f o r m a l i z e a s e m a n t i c s for E n g l i s h in t h e w a y E n g l i s h s p e a k e r s h a n d l e i n f o r m a t i o n . Asituation
is a l i m i t e d p o r t i o n of t h e reality. A ninfon
is a n o r d e r e d list (R, a , i ) , w h e r e R is a r e l a t i o n , a is a p r o p e r s e q u e n c e of a r g u m e n t s o f R, a n d i is t h e p o l a r i t y (1 o r 0). F o r a given R a n da.
o n l y one o f t h e two infons cr = (R. a, 1) o r = (R, a~ 0) is a fact, n a m e l y t h e one w h i c h h o l d s in s o m e s i t u a t i o n s. (As a n o t a t i o n a l c o n v e n t i o n , a p o l a r i t y o f 1 is u s u a l l y d r o p p e d . )I t is g e n e r a l l y h y p o t h e s i z e d t h a t s i t u a t i o n s a r e sets o f facts a n d t h e r e f o r e c a n be m o d e l e d b y s e t s t o m a k e use o f t h e e x i s t i n g s e t - t h e o r e t i c t e c h n i q u e s . I n d e e d , t h i s was t h e a p p r o a c h B a r w i s e a n d P e r r y a d o p t e d in [17]. However, u s i n g B a r w i s e ' s
Admissible Set Theory
[7] as t h e p r i n c i p a l m a t h e m a t i c a l t o o l in t h e b e g i n n i n g led t o p r o b l e m s in t h e h a n d l i n g of c i r c u l a r s i t u a t i o n s a n d t h e y h a d to t u r n t o t h e H y p e r s e t T h e o r y [18, 19]. To d e m o n s t r a t e c i r c u l a r s i t u a t i o n s , an e x a m p l e c o n c e r n i n g c o m m o n k n o w l e d g e will now be given, viz. t h eConway paradox
[20]. T w o c a r d p l a y e r s P1 a n d P2 a r e given s o m e c a r d s such t h a t e a c h g e t s a n ace. T h u s , b o t h P1 a n d P2 k n o w t h a t t h e following is a fact:or: E i t h e r PI or P2 has a n ace.
~The Solution Lemma is an elegant r~ult, but not every system of equations has a solution. First of all, the equations have to be in the form suitable for the Solution Lemma. For example, ~ pair of equations x =
{y,z},
y = {1,x} cannot be solved since this requires the solution to be stated in terms of the indeterminate z. (Notice the a,alogy to the Diophantine equations.) As another examplc~ the equation x = 2 ~ cannot be solved because Cantor has proved in Z F C - that there is no set which contains its own power set (no matter what axioms are added to Z F C - ) [6].W h e n asked whether they knew if tile other one had an ace or not, they both would answer "no." If they are told that at least one of them has an ace and asked the above question again, first they both would answer "no." But upon hearing P1 answer "no," P2 would know t h a t P1 has an ace. Because, if P1 does not know P2 has an ace, having heard t h a t at least one of them does, it can only be becausc P1 has an ace. Obviously, Pl would reason the same way, too. So, they would conclude t h a t each has an ace. Therefore, being told t h a t at least one of them has an ace must have added some information to the situation. How can being told a fact t h a t each of them already knew increase their information? (This is the Comvay paradox.) The solution relies on the observation that initially a was known by each of them, but it was not common knowledge. Only after it became c o m m o n knowledge did it give more information.
Hence, c o m m o n knowledge can bc viewed as iterated knowledge of cr of the following form: P1 knows a, P2 knows a, P1 knows P2 knows a, P2 knows P1 knows a, and so on. This iteration can be represented by an infinite sequence of facts (where ~ is the relation "knows" and s is the situation in which the above game takes place, hence a E s):
(,~, Pl, 4 , (,~, P2, 4 , (,~, 1"1, (,~, P2, 8)), (,~, P2, (,~, P1, ~)), •. •. However, considering the system of equations
x = {(~, PI, y), (~, P2, y} },
y = ~ u {(,~, P l , y ) , (,~, P2,y)},
the Solution L c m m a asserts the existence of the unique sets s ~ and s U s' satisfying these equations, respectively, where
s ' = {(~, P1, ~ u s'), (~, g2, 8 u s')}.
Then, the fact t h a t s is common knowledge can be represented by s ', which contains just two infons and is circular. This is known as the fixed- point account of common knowledge.
4. T H E I M P L E M E N T A T I O N
HYPERSOLVER is a stand-alone program which can solve equations in the universe of hypersets b:~ making use of the Solution Lemma. It has built- in graphical capabilities for displaying the graphs depicting the equations input by the user and the solutions of these equations. HYPERSOLYER is
H Y P E R S O L V E R : A G R A P H I C A L T O O L F O R S E T T H E O R Y 53
H Y P E R S O L V E R
FILENAME:
O P T I O N S
Fig. 7. The command interface of HYPERSOLVER.
i m p l e m e n t e d o n a S P A R C s t a t i o n E L C in Lucid C o m m o n Lisp. ~lb com- m l m i c a t c w i t h t h e user a n d to d i s p l a y graphs, it makes use of t h e X V i e w W i n d o w T o o l k i t [21] b u i l t o n t h e X W i n d o w S y s t e m . T h e user interface of HYPERSOLVER, called t h e c o m m a n d interface, is s h o w n in F i g u r e 7.
4.1. F U N C T I O N A L I T Y
HYPERS[}LVER solves a s y s t e m of e q u a t i o n s in t h e u n i v e r s e of h y p e r s e t s . B y a s y s t e m of e q u a t i o n s , t h e d e f i n i t i o n in S e c t i o n 3 is m e a n t :
{ x = az: x E X a n d a~ is a n X - s e t }
for each x E X , where X is a set of i n d e t e r m i n a t e s , A is a set of a t o m s , a n d a n X - s e t is a set which c a n c o n t a i n e l e m e n t s from X . HYPERSOLVER does n o t solve s y s t e m s which are n o t of ttiis form. 4
T h e n o t a t i o n a l c o n v e n t i o n s in HYPERSOLFER are as follows. L e t t e r s A t h r o u g h L are used to r e p r e s e n t a t o m s of A, while letters M t h r o u g h Z r e p r e s e n t i n d e t e r m i n a t e s of X . T h e s y m b o l @ will be used to r e p r e s e n t t h e n o n - w e l l - f o u n d e d s i n g l e t o n ft. ( O n e - l e t t e r v a r i a b l e n a m i n g m a y seem q u i t e l i m i t i n g , b u t it is s i m p l e to a d o p t t h e p a r s e r to h a n d l e v a r i a b l e s w i t h 4Therefore, taking A = {0,1} and X = {x,y}, a system such as x = {0,1,y}, y = {x}, is a valid input for HYPERSOLVER, while the single equation 1 = {x,y, 0}, or the system x = {0, 1}, x = {x}, are not since 1 ~ X, and there should be a single equation for each x 6 X. HYPERSOLVER includes some filtering functions to detect invalid input.
7-~1 - ~i~,sai.V-Eii ...
Fig. 8. An example o u t p u t of HYPERSOLVER.
longer names.) Therefore, t h e g r a p h s of t h e solution given in Section 3 are depicted as in F i g u r e 8.
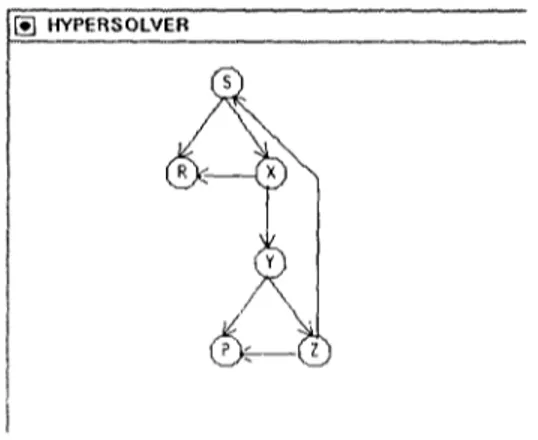
HYPERSOLVER gets its i n p u t from a file which is to be specified b y t h e user. T h e file m u s t have one e q u a t i o n per line. For example, a file consisting of t h e following lines is.a valid i n p u t file:
x = { x , Y } , Y = { A , B , Y , Z } ,
Z = {X,Y,@}.
T h e i n p u t read from t h e file is sent to t h e parser of HYPERSOLVER. T h e parser is a c h a r a c t e r - c h e c k i n g parser with a lookup table for t h e i n p u t characters. After c o n v e r t i n g t h e input into Lisp form, a t r a n s - f o r m a t i o n is applied to m a p it to a list t h a t can be processed by t h e e q u a t i o n solver. Finally, t h e input is checked to see w h e t h e r it c o n f o r m s to t h e i n p u t r e q u i r e m e n t s of HYPERSOLVER (e.g., if it contains one equa- t i o n for eazh i n d e t e r m i n a t e , if each e q u a t i o n is of t h e form x = ax, a n d
SO o n ) .
T h e equation-solving step o f tile HYPERSOLVER applies t h e Solution L e m m a to t h e i n p u t s y s t e m of equations. T h e a l t e r n a t i v e f o r m u l a t i o n m e n t i o n e d in Section 3 is used for this purpose:
f(x)
: { f ( y ) : Y e g(x)} Uh(x),
for a n y set X of i n d e t e r m i n a t e s where g is a function from X to 2 X and h is a function from X to a set A of atoms. For t h e i n p u t file above, g(X) = { X , Y } , 9(Y) = { Y , Z } , 9(Z) = { X , Y } a n d h(X) = 0,
H Y P E R S O L V E R : A G R A P H I C A L T O O L F O R S E T T H E O R Y 55
h(Y) = {A, B}, h(Z) = {@} = @. This representation scheme is suitable for recursive substitution. T h e algorithm of the equation solver performs this substitution by applying the Substitution L e m m a to each cquation of the input system. So, the solution for an indeterminate X can be found by finding the solutions of the indeterminates in g(X) recursively. For each indeterminate, a decoration is found and the solutions are expressed in t e r m s of these decorations. If the decoration for an indeterminate includes itself, then this denotes self-membership, and @ is used to signal that. For example, the decorations of the graphs for the above s y s t e m of equations are (p,q, and r are the decorations for the indeterminates X, Y, and Z, respectively):
p = { @ , { A , B , @ , { p , q,@}}}, q = {A,B,@,{{@, q},q, @}}, r = {{O,q},{A,B,@, r},@}.
To prevent duplicate substitutions which arise when an indeterminate occurs two or more times in an
X-set,
a list of already visited indetcr- m i n a t e s is maintained. Nevertheless, because of the nature of recursion, duplication m a y occur in different levels of set nesting. Therefore, a kind of filtering is applied on the o u t p u t of the solver to remove such duplicates. T h e next step is the invocation of the graph display part of the HYPER- SOLVER. This p a r t takes the solution of a system of equations produced by the equation solver as input. As the general g r a p h layout algorithm, a variant of the hierarchical layout algorithm proposed in[22]
is exploited. T h e reason to use a hierarchical layout algorithm instead of a general- p u r p o s e algorithm is t h a t most of the equations to be solved by the Solution L e m m a will be hierarchical and t h a t self-reference generally occurs for a single indeterminate. (Figure 5 is a good example of this.)T h e algorithm which has been a d a p t e d to the representation conven- tions and o u t p u t requirements of HYPERSOLVER first forms the edge list of tile solution s y s t e m which consists of pairs of nodes. This list helps to get all children of each indeterminate. T h e n the nodes corresponding to these children are distributed to the levels taking care of the relationships between pairs of nodes. A more complicated p a r t of the graph display unit is the one calculating the positions of the nodes on the screen. Tile hierarchical n a t u r e of the solution graphs is again exploited to make this calculation. T h e positions of the descendants of a node are calculated with respect to its own position, which in turn has been calculated with respect to its antecedents.
After tile calculation of the positions, the actual graph-drawing pro- cedure is activated to display first the nodes and later the edges. This
l ~
~ERSOLVER
I ®
Fig. 9. The HYPERSQLVER graph of fL
procedure pops up a large window (called the g r a p h display window, G D W ) on which all graphical information is put. T h e o u t p u t convention is such t h a t the node labels which are the decorations of the sets represented by those nodes are written inside the node boundaries. While the edges which define hereditary m e m b e r s h i p are easily drawn, care has to be taken in case of a cycle. Cycles implying self-reference are not displayed as circular edges, but are drawn in a different form. (Therefore, fl is depicted as in Figure 9.)
Cycles of one level are not much of a problem. If there exists a cycle between two nodes a and b, then the directed edge (b,a) can be drawn over the directed edge (a, b) to give a doublc arrow. However, references to higher lcvels, especially t o the root node representing the indeterminate, are problematic since a p a t h with m i n i m u m edge-crossing has to be found for aesthetic reasons. In such a case, paths walking around the g r a p h are preferred (cf. Figure 12). Edge crossings m a y be unavoidable if no such p a t h can be found. T h e solution graphs of the above example are depicted in Figure 10.
T h e displaying of the graphs depicting the input sets proceeds exactly the same way as the displaying of the solution system. For example, the
t
[~ HYPEI~SOLVERH Y P E R S O L V E R " A G R A P H I C A L T O O L F O R S E T T H E O R Y 57
~] HYPEHSOLVER
Fig. ] 1. Graphs of the input equations for the example in Subsection 4.1.
graphs of the input equations of the example system above can be found in Figure 11.
,~.2. L I M I T A T I O N S A N D O N G O I N G W O R K
HYPERSOLVER can solve any system which is in the form required by the Solution L e m m a . This requires the equations to be in the form x -= a x for each x E X . T h e systems which cannot be solved by HYPERSOLVER are those to which the Substitution L e m m a cannot be applied. Such systems have been exemplified in Section 3.
HYPERSOLVER is generally weak in i n p u t / o u t p u t operations. First of all, it has limitations on the format of the input, such as one-letter variable naming, and one equation per line in the input file with no space between the characters of the input equations. These limitations arise because of the brittleness of the parser. A more powerful parser would let HYPERSOLVER be more flexible with input, but the e x t r a features would not add to the power of the program.
T h e graph display unit is another weak p a r t of HYPERSOLVER. G r a p h drawing is a hard problem when considered for general graphs with a n y n u m b e r of nodes. Limiting the scope of the graph display problem as ex- plained above reduces the difficulties considerably, but classical problems such as minimizing the n u m b e r of edge-crossings remain. HYPERSOLVER's g r a p h display unit does not claim to know much a b o u t the graph layout problem. T h e algorithm does not work well for a r b i t r a r y graphs with no coherent node relationships. However, it works fine for the examples pre- sented so far. G r a p h - d r a w i n g problems arc addressed in [23-25], which propose generic g r a p h browsers or editors.
Future work on HYPERSOLVER will concentrate on its applications to modeling of various phenomena in AI. This m a y include, for example~ integrating HYPERSOLVER into a situation-theoretic framework [26] where the p r o g r a m m a y solve equations whose indeterminates can be unknown
[ ] HYPERSOLVER
Fig. 12. T h e gn~ph of a circular s i t u a t i o n S = (R, P, S}. (N.B. Not all t h e s t r u c t u r e is shown.)
elements of situations, or unknown situations themselves. As a simple example, if a situation S is represented by the triple <R, P, S'), meaning object P is in relation R to another situation S t, then S can bc found in t e r m s of S t by solving the equation S = <R, P, S ' / . Then, if S is a circular situation; P could also be in relation R to S itself, i.e., S = (R, P; S/. This would, for example, correspond to an actual situation S in which a person P utters the s t a t e m e n t "This is a very exciting situation." By "this situa- tion," P is surely referring to the situation which his utterance describes. Such a circular situation S would be depicted (in a s o m e w h a t compressed format) eus in Figure 12.
HYPERSOLVER's capabilities can also be exploited to model partial infor- rnation [27]. For this purpose, the objects of the universe VA (cf. Section 3) of hypersets over a set A of a t o m s can be used to model n o n p a r a m e t r i c objects, i.e., objects with complete information. T h e set X of indetermi- nates can be used to represent p a r a m e t r i c objects, i.e., objects with partial information. T h e universe of hypersets on A U X is denoted as ~2A[X], analogous to the adjunction of indeterminates in algebra. For any object a E IZA[X], the set
par(a) = {x E X: x E T C ( a ) } ,
where TC(a) denotes the transitive closure of a, is called the set of p a r a m - eters of a. If a'E VA, then par(a) = O, since a does not have any p a r a m - eters. An anchor is a fimction f with domain(f) c_ X and ran.qe(f) c VA - A which assigns sets to indeterminates. For any a E ~2A[X] and anchor f , a ( f ) is the object obtained by replacing each indeterminate
HYPERSOLVER: A G R A P H I C A L T O O L F O R S E T T H E O R Y 59
x E par(a) (q d o m a i n ( f ) by the set f ( x ) in a. This can be accomplished by
solving the resulting equations using HYPERSOLVER. 5. C O N C L U S I O N
T h e Solution L e m m a is a nice feature of the H y p e r s c t Theory. Besides its m a t h e m a t i c a l i m p o r t a n c e and elegance, it provides an interesting way of modeling various circular p h e n o m e n a [8, 28].
T h e i m p l e m e n t a t i o n presented in this paper, HYPERSOLVER, is a p r o g r a m ba.~ed on the Solution L e m m a and can be a uscful tool in areas of AI where information can be c ~ t in the form of set equations. Its simplicity, clarity, and well-defined user interface make it a practical instrument accessible for such purposes. When s u p p o r t e d by a more general parser and a b e t t e r graphical interface, it can bc one of the emerging tools in mar, hcmatical logic, along the lines of, e.g., Suppes and Sheehan's computerized set theory course [29] or Barwisc and E t c h c m e n d y ' s T a r s k i ' s World [30].
HYPERSOLVER m a y be an i m p o r t a n t utility for basic research on the use
of set t h e o r y in AI, too [31]. Such research involving conceptual innovations is urgently nc~.ded in AI, as pointed out by M c C a r t h y [32].
R E F E R E N C E S
1. V. Akman, Set theory from Zermelo to Aczel. Seminar, l)epartment of Mathemat- ics, Bilkent University, Ankara, March 10, 1992.
2. V. Akman, lIypersets and common sense. Seminar, Department of Computer Engineering, Middle East Technical University, Ankara, October 21, 1992. 3. M. Pakkan, Solving equations in tile universe of h y p e r s e t s . . M a s t e r ' s thesis,
Department of Computer Engineering and Information Science, Bilkent Univer- sity, Ankara, Turkey, 1993.
4. M. Pakkan and V. Akman, HYPERSOLVER: A graphical tool for commonsense set. theory. In Proceedings of the Ei.qhth h~ternational Symposium on Computer and Information Sciences ( I S C I S VIII), L. Grin, R. C)nvnral, and E. Gelenbe, Eds., istanbul, 1993, pp. 436-443.
5. J. IL Shoenfield, Axioms of set theory. In lIandbook of Mathematical Logic, J. Barwise, ed., North-tIolland, Amsterdam, 1977, pp. 321-344.
6. A. A. Fraenkel, Y. Bar-Hillel, and A. Levy, Foundations of Set Theory. North- Holland, Amsterdam, 1973.
7. J. Barwise, Admissible Sets and Structures. Springer-Verlag, Berlin, 1975. 8. J. Barwise and J. Etchemendy, The Liar: A n Essay on "lYuth and Circularity.
Oxh)rd University Press, NY, 1987.
9. J. McCarthy, Acceptance addre.~,~ of the International Joint Confe.rence on Ar- tificial Intelligence ( I J C A I - 8 5 ) award for rc~earch excellence, Los Angeles, CA, 1985.
10. D. Perils, Commonsense set theory. In Meta-Level Architectures and Reflec- tion, P. Mats and D. Nardi, 'Eds., Elsevier (North-IIolland), Amsterdam, 1988, pp. 87- 98.
11. M. Pakkan and V. Akman, Issues in commonsense set theory. In Proceedings of the First Turkish Symposium on Artificial Intelligence and Neural Networks, K. Oflazer, V. Akman, and U. Halici, Eds., Bilkent University, Ankara, 1992, pp. 47-52.
12. P. Aczel, Non-weU-founded sets. Number 14 in CSLI Lecturc Notes. Center for the Study of Language and Information, Stanford, CA, 5988.
13. J. Barwise and L. Moss, Hypcrsets, Mathematical Intelligencer 13(4):31-41 (1995).
54. .1. Barwise, AFA and the unification of information. In The Situation in Logic, num- ber 17 in CSLI Lecture Notes, Center for the Study of Language and Inforrnation, Stanford, CA, 1989, pp. 277-283.
15. C. McLarty, Anti-foundation and self-reference. Journal of Philosophical Logic 22:19-28 (1993).
16. D. Perlis, Languages with self-reference I: Foundations. Artificial Intelligence 25(3):301-322 (1985).
17. J. Barwise and J. Perry, Situations and Attitudes. MIT Press, Cambridge, MA, 1983.
18. J. Barwise, Situations, sets, and the axiom of foundation. In The Situation in Logic, number 17 in CSLI Lecture Notes, Center for the Study of Language and Information, Stanford, CA, 1989, pp. 577-200.
19. J. Barwise, Situated set theory. In The Situation in Logic, Center for the Study of Language and Information, Stanford, CA, 1989, Chap. 14.
20. J. Barwise, On the model theory of common knowledge. In The Situation in Logic, number 17 in CSLI Lecture Notes, Center for the Study of Language and Informa- tion, Stanford, CA, 1989, pp. 201-220.
21. D. tIeller, X V i e w Programming Manual. O'Reilly & Associates, Sebastupol, CA, 1990.
22. L . A . Rowe, M. Davis, E. Me,~singer, C. Meyer, C. Spirakis, and A. Tuan, A browser for directed graphs. Software--Practice and Experience 17(1):65-76 (1987). 23. E . R . Gansner, S. C. North, and K. P. Vo, D A G - - A program t h a t draws directed
graphs. Software--Practice and Experience 58(1l):1047-1062 (5988).
24. T. Kamazia and S. Kawai, An algorithm for drawing general undirected graphs. Information Processing Letters 31:7-15 (1989).
25. F . N . Paulisch and W. F. Tichy, EDGE: An extensible graph editor. S o f t w a r e - - Practice and Experience 20 (S 1 ) :63-88 (1990).
26. E. Tin and V. Akman, BABY-SIT: Towards a situation-theoretic computational environment. In CTtrrent Issues in Mathematical Linguistics, C. Martin-Vide, Ed., Elsevier Science B.V., Arrusterdam, 1994, pp. 299-308.
27. M . W . Mislove, L. S. Moss, and F. J. Olcs, Partial sets. In Situation Theor T and its Applications /, R. Copper, K. Mukai, and J. Perry, Eds., number 22 in CSLI Lecture Notes, Center for the Study of Language and Information, Stanford, CA, 1990, pp. 117-131.
28. L . S . Moss, Review of The Liar: A n Essay on Truth and Circularity. Bulletin of the American Mathematical Society 20(2):216-225 (1989).
29. P. Suppes and J. Sheehan, CAI course in axiomatic set theory. In University-Level Computer-Assisted Instruction at Stanford: 1968-1980, P. Suppes, Ed., Institute for Mathematical Studies in the Social Sciences, Stanford University, Stanford, CA, 1981, pp. 3--80.
30. J. Barwise and J. Etchemendy, The Language of First-Order Logic (including the Macintosh version of Tarski's World ~.0), 3rd ed. Number 23 in CSLI Lecture Notes. Center for the ,~tudy of Language and Information, Stanford, CA, 1993.
HYPERSOLVER: A G R A P H I C A L T O O L F O R S E T T H E O R Y 61
31. W. Zadrozny, Cardinalities and well orderings in a common-sense set theory. In Proceedings of the First International Conference on Principles of Knowledge Rep- resentation and Reasoning, R. J. Brachman, H. J. Levesque, and R. Reiter, Eds. Morgan Kaufmann, San Mateo, CA, 1989, pp. 486-497.
32. J. McCarthy, Artificial intelligence needs more emphasis on basic research: Presi- d e n t ' s quarterly message. A I Magazine 4:5 (1983).




![Fig. ] 1. Graphs of the input equations for the example in Subsection 4.1.](https://thumb-eu.123doks.com/thumbv2/9libnet/5788062.117667/15.648.155.482.119.245/fig-graphs-input-equations-example-subsection.webp)