Hidrojen atomunun enerji düzeylerinin belirlenmesi ve pertürbasyon uygulaması

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

HİDROJEN ATOMUNUN ENERJİ DÜZEYLERİNİN BELİRLENMESİ VE PERTÜRBASYON UYGULAMASI

Belma KIZILTOPRAK YÜKSEK LİSANS TEZİ FİZİK ANABİLİMDALI

Konya, 2009

T.C.

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

HİDROJEN ATOMUNUN ENERJİ DÜZEYLERİNİN BELİRLENMESİ VE PERTÜRBASYON UYGULAMASI

BELMA KIZILTOPRAK

YÜKSEK LİSANS TEZİ FİZİK ANABİLİM DALI

KONYA, 2009

Bu tez… / … / 2009 Tarihinde Aşağıdaki Jüri Tarafından Oybirliği / Oyçokluğu ile kabul edilmiştir.

... ...

Prof. Dr. Rıza OĞUL Y. Doç. Dr. Nuretdin EREN (Danışman) (Üye)

...

Y. Doç. Dr. Mehmet ERDOĞAN

(Üye)

ÖZET

YÜKSEK LİSANS TEZİ

HİDROJEN ATOMUNUN ENERJİ DÜZEYLERİNİN BELİRLENMESİ VE PERTÜRBASYON UYGULAMASI

Belma KIZILTOPRAK Selçuk Üniversitesi Fen Bilimleri Enstitüsü

Fizik Anabilim Dalı

Danışman: Prof. Dr. Rıza OĞUL 2009, 60 Sayfa

Jüri: Prof. Dr. Rıza OĞUL

Yrd. Doç. Dr. Nuretdin EREN Yrd. Doç. Dr. Mehmet ERDOĞAN

Schrödinger denklemi ve bu denklemin Hidrojen ve benzeri atomlara uygulanması çalışıldı. Bunu yaparken, Hidrojen atomundaki enerji kaymalarını hesaplamak için Schrödinger dalga denkleminin küresel koordinatlardaki çözümü bulundu. Daha sonra pertürbasyon teorisi ve bunun kuantum mekaniğindeki uygulamaları araştırıldı. Dejenere ve dejenere olmayan durumlar için enerji kaymalarının hesaplanması için pertürbasyon teorisi kullanıldı ve daha sonra radyal olasılık yoğunluğu dağılımları belirlendi. Zamandan bağımsız pertürbasyon teorisi kullanılarak, sonsuz potansiyel kuyusunun enerji kaymaları hesaplandı.

Anahtar Kelimeler: Schrödinger denklemi, pertürbasyon teorisi, enerji kayması

ABSTRACT

M. Sc. Thesis

DETERMINATION OF THE ENERGY LEVELS OF HYDROGEN ATOMS AND APPLICATION OF PERTURBATION THEORY

Belma KIZILTOPRAK Selcuk University

Graduate School of Natural and Applied Sciences Department of Physics

Supervisor: Prof. Dr. Rıza OĞUL 2009, 60 Pages

Jury: Prof. Dr. Rıza OĞUL

Ass. Prof. Dr. Nuretdin EREN

Ass. Prof. Dr. Mehmet ERDOĞAN

We have studied Schrödinger equation and applied the theory to Hydrogen like atoms. In doing so, we have used spherical coordinates then obtained the solution of Schrödinger equation to determine the energy levels of Hydrogen atom. Later on, we discussed the perturbation theory and its applications in quantum theory. To calculate the energy shifts for degenerate and nondegenerate states we made use of perturbation theory, and then radial probability density distributions are determined. By using time independent perturbation theory, we determined the energy shifts for infinite quantum potential well.

Key Words: Schrödinger equation, , perturbation theory, energy shifts.

ÖNSÖZ

Bu çalışma Selçuk Üniversitesi Fen Bilimleri Enstitüsüne Yüksek Lisans tezi olarak sunulmuştur. Çalışmalarım süresince bilgi ve tecrübeleri ile bana her konuda yardımcı olan danışmanım Prof. Dr. Rıza OĞUL’a ve Yrd. Doç. Dr. Mehmet ERDOĞAN’a en içten teşekkürlerimi sunarım. Ayrıca, çalışmalarım süresince manevi desteklerini hiçbir zaman esirgemeyen aileme, sonsuz saygı ve teşekkürlerimi sunarım.

Bu çalışmam sırasında beni varlığıyla motive eden canım oğlum Faik’e sonsuz sevgilerimle… Belma KIZILTOPRAK Konya, 2009 v

İÇİNDEKİLER ÖZET ABSTRACT ÖNSÖZ 1. 2. GİRİŞ...

SCHRÖDİNGER DALGA DENKLEMİ

1 3 2.1. 2.2. 2.3. 2.4. 2.4.1. 2.4.2. 2.5. 2.6. 2.7. 2.8.

Küresel Koordinatlarda Schrödinger DenklemininTemsili... Olasılık Yoğunluğu ve Yörünge Hesaplamaları... Hidrojen Atomunda Radyal Çözümler ………... Sınırlamalar ... Üst limit ... Alt limit... Ara Bölge Fonksiyonu ... Bir Dalga Fonksiyonunun Paritesi ve Parite Operatörü ... Hidrojen Atomunda Merkezcil Alan Probleminde Enerji... Hidrojen Tipi Bağlı Durum Dalga Fonksiyonları ve Olasılık Genliği.

7 16 22 24 24 25 26 34 35 37 vi

3. PERTÜRBASYON TEORİSİ ... 44

3.1.

3.2. 3.2.1.

3.2.2.

Dejenere Olmamış Durumlar İçin Zamandan Bağımsız Pertürbasyon Teorisi ... Dejenere Durumlar İçin Zamandan Bağımsız Pertürbasyon Teorisi ... Bir sonsuz kuyu potansiyelinin tüm uyarılmış durumlarının birinci dereceden enerji kaymalarının hesaplanması... Hidrojen atomunda enerji kaymalarının pertürbasyon teorisi ile hesaplanması ... 44 49 50 53 4. SONUÇLAR... 57 5. KAYNAKLAR ... 59 vii

1. GİRİŞ

Klasik fiziğin açıklayamadığı siyah cisim ışıması, fotoelektrik olay ve Compton olayı gibi fiziksel olaylar yirminci yüzyılın başlarında kuantum mekaniğinin geliştirilmesi sonucunda tam olarak açıklanabilmiştir. Kuantum fiziğinin anlaşılması ile birlikte Schrödinger mekaniği kullanılarak atomların ve moleküllerin fiziksel özellikleri daha iyi açıklanabilmiştir. Schrödinger denkleminin çözümleri genelde küresel harmonikler cinsinden verilir. Elde edilen dalga fonksiyonları kullanılarak sistemin fiziksel gözlenebilirlerinin beklenen değerleri kuantum mekaniksel olarak hesaplanır (Eisberg and Resnick 1974, Yalçın and Buget 1981).

Kuantum mekaniğinde iki potansiyelin kesin çözümü vardır. Bunlardan birisi harmonik osilatör 2

2 1

x k

U = potansiyeli, diğeri ise

r e U 2 − = Coulomb

potansiyelidir. Bu yüzden Hidrojen atomu dalga mekaniğinde temel ve önemli bir örnektir. Fakat birden fazla elektrona sahip atomların çözümlerinin zorluğundan dolayı Schrödinger denklemi yaklaşım metodları kullanılarak çözülebilmektedir. Bu sonuçlar literatürdeki sonuçlarla deney hataları içerisinde uyumlu sonuçlar vermiştir.

Hidrojen atomu için Schrödinger dalga denklemi, Coulomb potansiyeli zamandan bağımsız olduğu için değişkenlerine ayrılarak çözülmektedir(Cowan 1981). İlk olarak açılara ve yarıçapa bağlı kısımlar değişkenlerine ayrılır ve açılara bağlı kısım Küresel Harmonikler olarak adlandırılır. Küresel Harmonikleri oluşturan fonksiyon, Hidrojen atomunda elektronun sabit yarıçaplı küre yüzeyi üzerindeki harmonik hareketini temsil eder. Küresel Harmoniklerin çözümleri bulunurken, Schrödinger denklemi, değişken değiştirme işlemleri yapılarak Legendre diferansiyel denklemine dönüştürülüp bu denklemin çözümleri olan Legendre polinomları bulunur. Schrödinger denkleminin yarıçapa bağlı kısmının çözümleri de, bir asimtotik limitlerde bir de ara bölge için uygun bir fonksiyon belirlenerek

çözülmektedir. Ara bölge için Schrödinger denklemi, bazı değişken değişiklikleri yapılarak, Laguerre diferansiyel denklemine dönüştürülür ve bu denklemin çözümleri olan Laguerre polinomları bulunur (Cowan 1981, Bransden and Joachain 1989, Mandl 1992, Gros 1993, Modinos 1996).

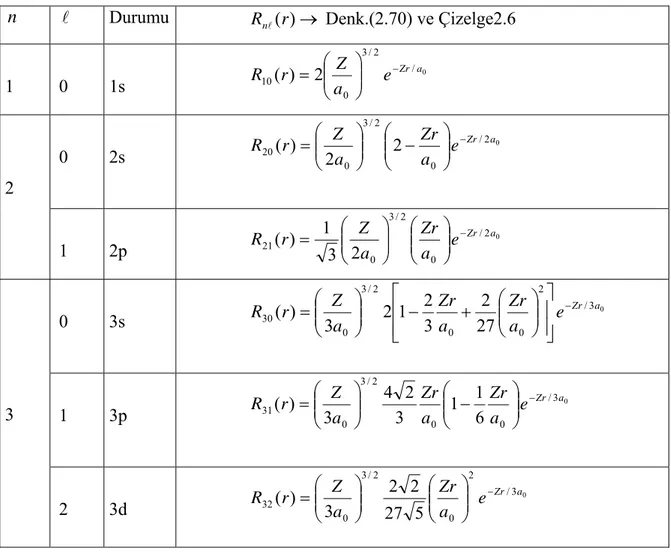
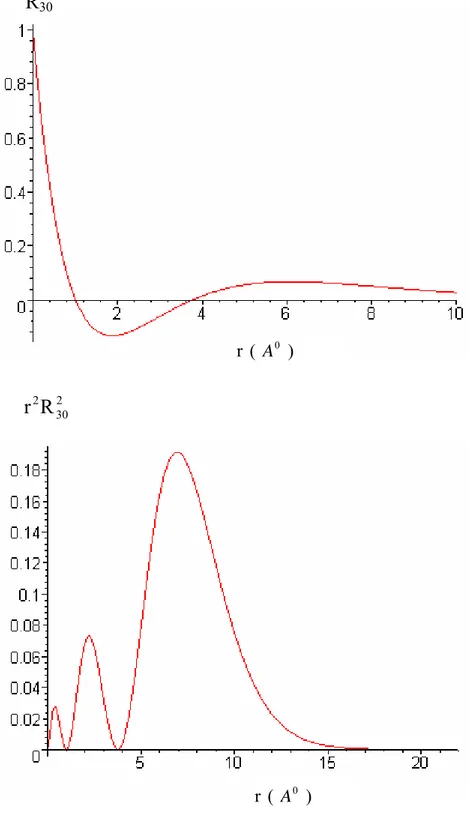
Hidrojen atomunun enerji düzeyleri, Schrödinger dalga denkleminin çözümünden elde edilmektedir(Eisberg ve Resnick 1974, Köksal ve Gümüş 1999). Hidrojen atomunun n=3ve l=0,1, 2 durumları için radyal olasılık yoğunluğunun ve radyal fonksiyonların konuma göre değişim grafikleri çizilmiştir.

Schrödinger denkleminin tam olarak çözülebildiği potansiyellerinin sayısının az olmasından dolayı hesaplamalar yaklaşım yöntemleri kullanılarak yapılır(Gasiorowicz 1996, Eugen 1998, Liboff 1998). Bu yaklaşım yöntemlerinden biri pertürbasyon teorisidir. Pertürbasyon İngilizce bir kelime olup, Türkçe karşılığı ‘rahatsız etme’ anlamına gelir. Pertürbasyon teorisi kullanılırken, mevcut potansiyellere pertürbe potansiyeller eklenerek mevcut sistem rahatsız edilir. Dolayısı ile sistemin mevcut enerji seviyelerinde ve dalga fonksiyonlarında değişimler olur. Bu değişimler, pertürbasyon potansiyelinin yeterince küçük olması durumunda pertürbasyon teorisi ile hesaplanabilmektedir. Sonsuz potansiyel kuyusu ve Hidrojen atomu için enerji kaymaları zamandan bağımsız pertürbasyon teorisi kullanılarak dejenere durumlar ve dejenere olmayan durumlar için hesaplanabilmektedir.

( )

r U

2. SCHRÖDİNGER DALGA DENKLEMİ

Kuantum mekaniği ile atomik yapılar çok iyi bir şekilde açıklanabilmektedir. Bu amaçla yapılan teorik açıklamalar deneysel gözlemlerle çok iyi uyum göstermektedir. Böylece ortaya çıkan atom modeline Dalga Modeli denir. Bu yeni model tüm atomları kapsar. Bir elektronlu Hidrojen atomunun en basit atom olması, Coulomb potansiyelinin küresel simetrik olması sebebiyle dalga modelinin en basit uygulamasını oluşturur.

Coulomb potansiyeli kartezyen koordinat sisteminde,

(

)

(

)

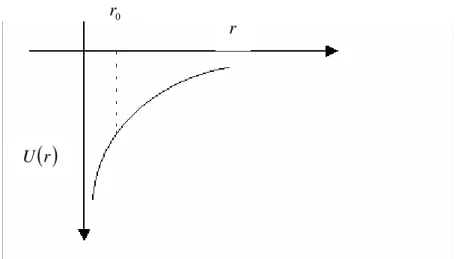
r Ze z y x Ze z y x U 0 2 2 2 2 0 2 4 4 ) , , ( πε πε + + =− − = (2.1)

şeklinde yazılır. Denk.(2.1) deki potansiyel enerjinin r’ye göre değişimi Şekil(2.1) de gösterildiği gibidir. 0 r r

( )

r U

Şekil 2.1. Coulomb potansiyel kuyusunda U(r)’nin r’ye göre değişimi

Grafikte dikkat edilmesi gereken husus Coulomb potansiyel enerjisinin hep negatif değerler alması ve r →0 iken U(r)→−∞ olmasıdır. Diğer taraftan r →∞ iken asimtotik olarak ( ) sıfıra gitmektedir. Coulomb potansiyel enerjisinin bu özelliği r’nin her doğrultusu için aynı olduğundan Şekil(2.1) küresel olarak her doğrultu için aynıdır. Bu tür potansiyellere Küresel Simetrik potansiyel denir.

) (r

U U(r)→0

Küresel simetrik bir potansiyelin uyguladığı kuvvet merkezcildir. Merkezcil bir kuvvetin en önemli özelliği ise, açısal momentumun korunumlu olmasıdır. Açısal momentum operatörü hamiltonyenle sıra değiştirme özelliğine sahip olur ve ortak özvektörlere sahiptirler (Cowan 1981).

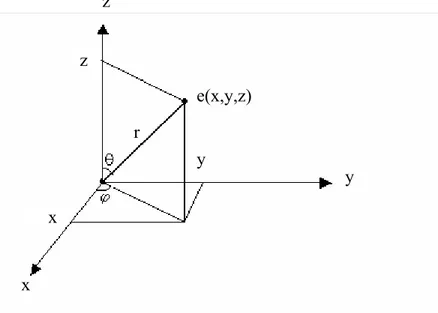
Küresel simetrinin en iyi ifade edildiği koordinat sistemi küresel koordinatlardır. Şekil (2.2) de küresel koordinatlar (r,θ,ϕ) verilmiştir. Koordinat sisteminde : r radyal uzaklık : θ kutupsal açı :

ϕ azimutal veya boylam açısı

olup, (x,y,z) kartezyen koordinatlarıyla

x z z e(x,y,z) r y y x

Şekil 2.2. Kutupsal Koordinatlarda r,θ ve ϕ

ϕ θ Cos Sin r x= (2.2) ϕ θ Sin Sin r y= (2.3) ϕ Cos r z= (2.4) şeklinde ilişkilidirler.

Elektronun Coulomb potansiyeli altındaki Schrödinger denklemi,

(

4

)

( , , ) 0 2 ) , , ( 0 2 2 2 ₌ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + ∇ ψ θ ϕ πε µ ϕ θ ψ r r Ze E r h (2.5)

olur. Coulomb potansiyeli zamandan bağımsız olduğu için Denk.(2.5) değişkenlerine ayrılarak çözülebilir. _∇2 kartezyen koordinatlarda

2 2 2 2 2 2 2 z y x ∂ ∂ + ∂ ∂ + ∂ ∂ = ∇ (2.6)

biçiminde tanımlanan bir operatördür. Denk.(2.2), (2.3) ve (2.4) kullanılarak operatörünün küresel koordinatlardaki ifadesi

2 ∇ 2 2 2 2 2 2 2 2_{( , , )} 1 1 1 ϕ θ θ θ θ θ ϕ θ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ = ∇ Sin r Sin Sin r r r r r r (2.7)

biçiminde yeniden yazılır. Denk.(2.7) deki operatör, Denk.(2.5) de yerine yazılırsa Hidrojen atomunun elektronunun Schrödinger dalga denklemi, küresel koordinatlarda

(

( )

)

0 2 1 1 1 2 2 2 2 2 2 2 2 _∂ + − = ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ µ _ψ ϕ ψ θ θ ψ θ θ θ ψ r U E Sin r Sin Sin r r r r r _h (2.8)

olur. Burada , Hidrojen atomu için Coulomb potansiyel enerjisini temsil eder ve sadece r’ye bağımlıdır. Coulomb potansiyeli (Denk. 2.1)

) (r

U

θ ve ϕ açılarından

bağımsızdır. Yani çözüm fonksiyonu ψ , simetrik olup sadece r’nin fonksiyonudur. Denk.(2.8) i değişkenlerine ayırarak çözmek için yöntemin kuralı olarak dalga fonksiyonu değişkenlerine ayrılarak yazılırsa

ψ(r,θ,ϕ)=R(r)Y(θ,ϕ) (2.9)

olur (Eisberg ve Resnick 1974, Cowan 1981). Denk.(2.9), Denk.(2.8) de yerine yazılıp tekrar düzenlendiğinde elektronun bağıl hareketinin küresel koordinatlardaki diferansiyel denklemi

(

)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ − = − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ ) ( ) , ( 1 ) ( ) , ( 1 ) , ( ) ( ) ( 2 ) , ( ) ( 1 2 2 2 2 2 2 2 2 r R Y Sin r r R Y Sin Sin r Y r R r U E Y r r R r r r ϕ ϕ θ θ θ ϕ θ θ θ θ ϕ θ µ ϕ θ h (2.10)

halini alır. Denk.(2.10), R(r)Y(θ,ϕ) ile bölünüp r ile çarpıldığında 2

(

)

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ − = − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ 2 2 2 2 2 2 ) , ( 1 ) , ( 1 ) , ( 1 ) ( 2 ) ( ) ( 1 ϕ ϕ θ θ θ ϕ θ θ θ θ ϕ θ µ Y Sin Y Sin Sin Y r U E r dr r dR r dr d r R _h (2.11)

elde edilir. Denk.(2.11) in sol tarafı radyal bileşenleri sağ tarafı ise açısal bileşenleri içermektedir. Bu denklemin,

(

r,θ,ϕ

)

bağımsız değişkenlerinin değişim sınırları içinde her değeri için doğrulanabilmesi, ancak denklemin bir sabite eşit olması ile mümkündür ve bu sabite ayırma sabiti denir. Bu sabite geçici olarak C denirse

(

E U r

)

C r dr r dR r dr d r R ⎟⎠+ − = ⎞ ⎜ ⎝ ⎛ ( ) 2 _{( )} ) ( 1 2 2 2 h µ (2.12) 6

C Y Sin Y Sin Sin Y ⎥_⎦= ⎤ ⎢ ⎣ ⎡ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ − 1 ( , ) 1₂ 2 ( ₂, ) ) , ( 1 ϕ ϕ θ θ θ ϕ θ θ θ θ ϕ θ (2.13)

olur. Açılara bağlı kısmın çözümü Y(θ,ϕ) ile gösterilir ve Küresel Harmonik adını

alır.

2.1. Küresel Koordinatlarda Schrödinger DenklemininTemsili

Hidrojen atomunda elektronun protona göre bağıl hareketine ait diferansiyel denkleminin küresel koordinatlardaki çözüm fonksiyonu olan ψ(r,θ,ϕ) nin açılara

bağlı olan kısmına Küresel harmonikler denir. Küresel harmonikler, sabit yarıçaplı bir küre yüzeyi üzerinde açıların, 0≤θ ≤π ve 0≤ϕ ≤2π aralıklarında harmonik değişimlerini temsil etmesinden dolayı Küresel Harmonik adını alır. Bu açılara bağlı olan Y(θ,ϕ) fonksiyonu, Denk.(2.13) düzenlendiğinde

) , ( ) , ( 1 ) , ( 1 2 2 2 _ϕ θ ϕ ϕ θ θ θ ϕ θ θ θ θ CY Y Sin Y Sin Sin ∂ =− ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ ∂ ∂ (2.14)

elde edilir. Bu denklem de θ ve ϕ bağımsız değişkenlerine ayrılabilir. Buna göre

) ( ) ( ) , (θ ϕ =Θθ Φ ϕ Y (2.15)

olmalıdır. Denk.(2.15), Denk.(2.14) de yerine yazıldığı zaman ve her terim ile çarpılıp, θ 2 Sin ) ( ) (θ Φ ϕ

Θ ile bölündüğünde, θ ya bağlı terimleri solda ϕ ye bağlı terimleri de sağda toplayacak şekilde düzenleme yapılırsa

2 2 2 1 1 ϕ θ θ θ θ θ ∂ Φ Φ = − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Θ Θ − CSin d d d Sin d d Sin (2.16) 7

elde edilir. Bu denklemin θ ve ϕ değişim aralıklarının her değeri için doğru olabilmesi, ancak bir sabite eşit olması ile mümkün olur. Bu sabit ile gösterilir ve Denk.(2.16) nın her iki tarafı, ayrı ayrı bu sabite eşitlenerek küresek harmonik fonksiyon çarpanları bulunur.

2 m − 2 2 1 m CSin d d Sin d d Sin ⎟− =− ⎠ ⎞ ⎜ ⎝ ⎛ Θ Θ − θ θ θ θ θ (2.17) 2 2 2 1 m d ₌₋ ∂ Φ Φ ϕ (2.18)

Denk.(2.18) in 0≤ϕ ≤2π aralığındaki normalize edilmiş çözümü

ϕ ϕ im m = Ae Φ ( ) (2.19) şeklindedir. π ϕ ϕ→ +2

olduğunda tekrar aynı noktaya geldiğine göre sınır şartı

) ( ) 2 (ϕ+ π =Φ ϕ Φ

olur . Burada Φ nin değeri yerine yazıldığında ϕ π ϕ im im Ae Ae ( +2 ) =

elde edilir. olarak alınır. Bu bağıntının sağlanabilmesi için ’nin değerlerinin 1 = ϕ im e m . ,... 3 , 2 , 1 , 0± ± ± = m

olması gerekir. Normalizasyon şartı kullanılarak A’nın değeri hesaplanırsa

∫

πΦ∗ _ϕ Φ _{ϕ ϕ} = 2 0 1 ) ( ) ( ' d m m 8

1 2 0 = − ∗

∫

π ϕ ϕ ϕ d e e A A im im 1 2 2 0 2 2 = =

∫

ϕdϕ A π A π 2 1 = A

bulunur. Denk.(2.19) un son hali ϕ π ϕ im m e 2 1 ) ( = Φ (2.20)

şekline dönüşür. Burada kuantum sayısıdır. Elde edilen m Φm(ϕ) fonksiyonları

ortanormal bir küme oluşturur. Yani,

( )

'

( )

' 2 0 m mm m ϕ ϕ dϕ δ π = Φ Φ

∫

∗ _(2.21) olur.

θ ya bağlı çarpanı belirlemek için Denk.(2.17) nin her terimi ile bölünerek yeniden düzenlendiğinde

θ 2 Sin 0 1 2 2 = Θ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ Θ θ θ θ θ θ Sin m C d d Sin d d Sin (2.22)

olur. Bu diferansiyel denklemi çözmek için

θ

ξ =Cos (2.23)

değişken değiştirmesi yapılır. Denk.(2.23) den türev alarak Denk.(2.22) nin ilk teriminin parantez dışındaki

θ Sin

1

ve dθ yerine eşdeğerleri yazıldığında ve gerekli kısaltmalar yapıldığında

0 1 2 2 2 _Θ= ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ Θ θ ξ θ ξ Sin m C d d Sin d (2.24)

elde edilir. Öte yandan

2 2_{θ =1−ξ}

Sin (2.25)

olduğundan diferansiyel denklemin son hali

(

)

0 1 1 ₂ 2 2 _Θ= ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ Θ − ξ ξ ξ ξ m C d d d d (2.26)

olur. Bu denklemde m=0, C= l_l

(

+1

)

ve Θ =P_l değişimi yapılıp, denklem yeniden düzenlendiğinde

(

1 2

)

₊

(

₊1

)

₌0 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − l _{l l Pl} d dP d d ξ ξ ξ (2.27)

olur. Burada l de yine bir kuantum sayısıdır. Denk.(2.27) deki Legendre polinomu olup normal Legendre polinomu adını alır. Denk.(2.27) de gösterilen türev işlemi yapılıp, denklem tekrar düzenlendiğinde

l P

(

)

l l _l

(

_l

)

_Pl d dP d P d 1 2 1 ₂ 2 2 _{− =− +} − ξ ξ ξ ξ (2.28)

olur. Buna Legendre diferansiyel denklemi ve çözümü olan P_l

( )

ξ fonksiyonlarına da Legendre polinomları denir. Böylece bağıl hareketin θ ya bağlı kısmının diferansiyel denklemi Legendre diferansiyel denklemine dönüştürülmüş olmaktadır.

Ancak m≠0,C=l(l+1) ve Θ )(ξ =P_lm

( )

ξ şeklinde alarak, Denk.(2.26) üzerindeki benzer işlemler tekrarlandığında

(

)

(

)

0 1 1 2 1 ₂ 2 2 2 2 ₌ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − + + − − m P_m d d d d l l l _ξ ξ ξ ξ ξ (2.29)

elde edilir. Bu denkleme de birleşik Legendre diferansiyel denklemi ve çözümü olan

( )

ξ

m

P_l fonksiyonlarına da birleşik Legendre polinomları denir. Legendre polinomları, Rodrigues formülünden başlayarak türetilir. Rodrigues formülü Legendre polinomunu, ξ ve türevlerine

_{l l} l_l

(

l l! 1 2 1 ) ( _{= ξ}2 ₋ ξ ξ d d P

)

l (2.30)

şeklinde bağlanır. Buna Rodrigues formülü denir. Görüldüğü gibi l kuantum sayısına =0,1,2,3... gibi değerler vererek karşılık gelen normal Legendre polinomları buradan belirlenebilir. Birleşik Legendre polinomları da, normal Legendre polinomlarından

( )

(

)

m m _m

( )

m d P d P ξ ξ ξ ξ l l 2 / 2 1− =

(

_l≥ m≥0

)

(2.31)

bağıntısı yardımı ile türetilir.

Denk.(2.28) ve Denk.(2.29), yeniden düzenlenerek sağ tarafları sıra ile ve olacak şekilde yazıldığında ve sol tarafları da fonksiyon (polinom) parantezine alındığında bir özdeğer denklemi görünümü alırlar. Bu işlem yapılarak Legendre operatörleri belirlenmiş olur. Legendre operatörleri özdeğer denklemlerinin her biri ilgili Legendre polinomları kümeleri tarafından sağlanır. Bu bakımdan Legendre polinomlarının her iki türü de ilgili diferansiyel denklemi sağlayan deneme fonksiyonu olarak da düşünülebilir. Denk.(2.30) ve Denk.(2.31) kullanılarak her iki tür Legendre polinomlarının

(

+

)

P

(

+

)

P ,... 3 , 2 , 1 , 0 l l l 1 ll 1 _lm =

l için tablosu Çizelge (2.1) de verilmiştir.

Rodrigues formülünden doğru türetilen Legendre polinomları normalize değildir. Dolayısıyla Çizelge(2.1) de verilen ifadeler normalize olmayan Legendre polinomlarına aittir. Legendre polinomlarının normalizasyon sabitinin genel ifadesi,

ve kuantum sayılarına bağlı olarak,

l m

( )

( )

(

)

(

)

2 / 1 2 / ! ! 2 1 2 1 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − + − = + m m N_m m m l l l l (2.32) ve

( )

₋₁(m+m)/2 _→ Faz çarpanı

ile verilir. Denk.(2.32) deki faz çarpanı terimi sadece

( )

_{m şeklinde bir işaret belirler.} ile

m

l

N P_lm

( )

ξ nin çarpımı normalize olmuş Legendre polinomlarıdır. Başka bir deyişle, normalize olmuş Θ_lm

( )

ξ fonksiyonları

( )

ξ _{m m}

( )

ξ

m N_l P_l

l =

Θ (2.33)

ya da daha açık ifadesi ile

( ) ( )

( )

(

)

(

)

( )

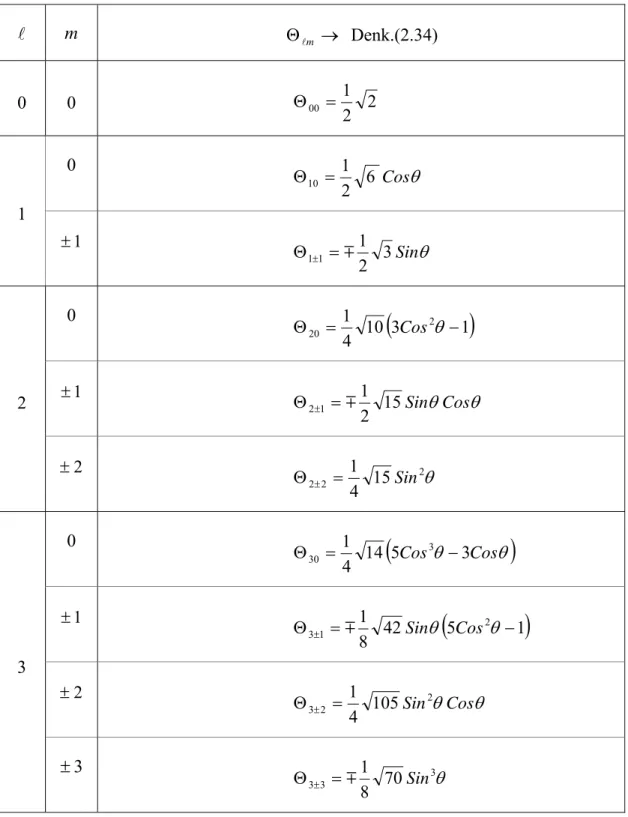
ξ ξ m m m m P m m l l l l l 1/2 2 / ! ! 2 1 2 1 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − + − = Θ + (2.34)

olur. Dolayısıyla Denk.(2.34) ün de l=0,1,2,3,.... için bir çizelgesi yapılabilir. Çizelge(2.2) de normalize Legendre polinomlarına karşılık gelen ve Denk.(2.34) de verilen Θ_lm

( )

ξ fonksiyonlarının, l=0,1,2,3,.... için açık ifadeleri verilmiştir.

Çizelge(2.2) de ’nin işaretinin, faz çarpanının işaretini nasıl belirlediği görülmektedir.

m

Çizelge 2.1. Normalize Olmamış Legendre Polinomları

l P_l(Cosθ)→ Denk.(2.30) m P_lm(Cosθ)→ Denk.(2.31)

0 P₀ =1 0 P₀₀ =1 1 θ Cos P₁ = 0 1 θ Cos P₁₀ = θ Sin P₁₁ = 2

₍

₎

1 3 2 1 2 20 = Cos θ − P 0 1 2

(

3 1

)

2 1 2 20 = Cos θ − P θ θCos Sin P₂₁=3 θ 2 22 3Sin P = 3 P

(

5Cos θ 3Cosθ

)

2 1 3 3 = − 0 1 2 3

(

)

(

)

θ θ θ θ θ θ θ 3 33 2 32 2 31 3 30 15 15 1 5 2 3 3 5 2 1 Sin P Cos Sin P Cos Sin P Cos Cos P = = − = − =

Böylece, küresel harmonikleri oluşturan fonksiyon çarpanları belirlenmiş olmaktadır. Denk.(2.20) ve Denk.(2.34), Denk.(2.15) te yerine yazılırsa

( )

( )

( )

(

)

(

)

! ( ) ! 2 1 2 1 2 1 , 2 / 1 2 / _ξ π ϕ θ ϕ m m m im m P m m e Y_{l l} l l l ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − + − = + (2.35) 13

Çizelge 2.2. Hidrojen atomunda elektrona eşlik eden dalga fonksiyonunun θ ya bağlı kısmını temsil eden normalize Legendre polinomları.

l m Θ_lm → Denk.(2.34) 0 0 2 2 1 00 = Θ 0 6 Cosθ 2 1 10 = Θ 1 1 ± _θ Sin 3 2 1 1 1 =m Θ_± 0 10

(

3 1

)

4 1 2 20 = − Θ Cos θ 1 ± 15SinθCosθ 2 1 1 2 =m Θ _± 2 2 ± 2_θ 2 2 15 4 1 Sin = Θ _± 0 14

(

5Cos θ 3Cosθ

)

4 1 3 30 = − Θ 1 ±

₍

₎

1 5 42 8 1 2 1 3 = − Θ _{± m} Sinθ Cos θ 2 ± _{3 2} 105Sin2θCosθ 4 1 = Θ _± 3 3 ± 3θ 3 3 70 8 1 Sin m = Θ _± 14

Çizelge 2.3. Küresel harmoniklerin, = 0,1,2,3, için açık ifadeleri_l l m Y_lm(θ,ϕ)→ Denk.(2.35) 0 0 Y00 = ₄1_π 0 Y _π Cosθ 4 3 10 = 1 ±1 ϕ θ π i e Sin Y_± = ± 8 3 1 1 m 0

(

3 1

)

16 5 2 2 / 1 20 ⎟ − ⎠ ⎞ ⎜ ⎝ ⎛ = θ π Cos Y ±1 _π θ θ iϕ e Cos Sin Y_± ⎟ ± ⎠ ⎞ ⎜ ⎝ ⎛ = 2 / 1 1 2 8 15 m 2 ±2 _π θ iϕ e Sin Y 2 2 2 / 1 2 2 32 15 ± ± ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 0 Y _π

(

5Cos θ 3Cosθ

)

16 7 3 2 / 1 30 ⎟ − ⎠ ⎞ ⎜ ⎝ ⎛ = ±1 _π θ

(

)

iϕ e Cos Sin Y_± ⎟ − ± ⎠ ⎞ ⎜ ⎝ ⎛ = 5 1 64 21 2 2 / 1 1 3 m ±2 _π θ θ iϕ e Cos Sin Y 2 2 2 / 1 2 3 32 105 ± ± ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 3 ±3 _π θ iϕ e Sin Y 3 3 2 / 1 3 3 64 35 ± ± ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = m

olur. Bu fonksiyon, Hidrojen atomunda elektronun, sabit yarıçaplı küre yüzeyi üzerindeki harmonik hareketlerini temsil eder. Küresel harmonik fonksiyonlar kompleks eşlenikleri ile

( )

1 ( , ) ) , ( , , θ ϕ m θ ϕ m m Y Y_l− = − ∗l (2.36)

şeklinde bağlantılıdırlar. Denk.(2.35) ile verilen küresel harmonik fonksiyonların bir çizelgesi oluşturulabilir. Çizelge(2.3) te l=0,1,2,3,....

l ≤ m

) 1

için küresel harmonikler, Denk.(2.35) de de ifade edildiği gibi normalize edilmiştir. Bu dalga fonksiyonları türetilirken, sağlamaları gereken sınır şartlarından dolayı olmak durumundadır. Herhangi bir l değerine karşın m_{→ l}(2 + farklı değer almaktadır.

2.2 Olasılık Yoğunluğu ve Yörünge Hesaplamaları

Bu kesimde, genel dalga fonksiyonunun yarıçapa bağlı olmayan kısmının, sadece θ ve ϕ açılarına bağımlılığını inceleyeceğiz. O halde bir küresel harmoniğin mutlak değer karesi, yani Ylm(θ,ϕ)2 , elektronun, söz konusu θ ve ϕ yönünde

birim hacimde bulunma olasılığını verir. Yani, θ ve ϕ ye bağlı elektron yoğunluğu

) , ( ) , ( ) , ( ) , (θ ϕ θ ϕ 2 θ ϕ θ ϕ ρ_lm = Y_lm =Y_lm Y∗lm (2.37)

ile tanımlanır. Öte yandan Denk.(2.37) deki küresel harmoniklerde Θ(θ) ve Φ(ϕ) cinsinden yazıldığında

ρ_lm(θ,ϕ)=Θ_lm(θ)Θ∗lm(θ)Φ_m(ϕ)Φ∗_m (ϕ) ρ_lm(θ,ϕ)= ρ_lm(θ)ρ_m(ϕ)

olur. Burada ise

) ( ) ( ) (ϕ ϕ ϕ ρm =Φm Φ∗m (2.38a) π ϕ ρ 2 1 ) ( = m (2.38b) 16

olan )ρ_m(ϕ , ’den bağımsız bir sabit olduğundan, m ρ_lm(θ,ϕ) grafiklerinin

şeklini )ρ_lm(θ çarpanı belirler. Yani ρ_lm(θ,ϕ) nin θ ve ϕ değişkenlerine bağlı

grafiği çizilirken grafiğe şeklini veren ρ_lm(θ) çarpanıdır. )ρm(ϕ nin etkisi sabit

olup, her ϕ açısı için 1/2π çarpanı kadardır. Buna göre

ρ_lm(θ,ϕ)=

(

1/2π

)

ρ_lm(θ) (2.39)

Şekil 2.3. Farklı ve m değerleri için kutupsal grafikler_l

olur. Buna göre her θ açısı için, ϕ den dolayı 1/2π sabit çarpanı geldiğinden yerine

) , (θ ϕ

ρ ρ(θ)grafiklerinin çizilmesi de yeterlidir. θ kutupsal açı olduğundan, herhangi ve m değerleri için _l ρ_lm(θ) nın grafiklerine kutupsal grafik denir. Böyle bir grafik Şekil (2.3) te çeşitli l ,m değerleri için gösterilmiştir. Bu şekil,

) ( ) ( ) (_{θ θ} * _θ ρ_lm =Θ_lm Θ lm (2.40)

bağıntısı ve Çizelge(2.2) kullanılarak çizilebilir. Şekil (2.3)’te gösterilen grafikler kutupsal eksen (z-ekseni) etrafında döndürüldüğünde hidrojen atomunda elektron dağılımının üç boyutlu görüntüsü elde edilir. Bu şekilde elde edilecek üç boyutlu şekil kutupsal eksene göre simetriktir. Düzlemsel ya da üç boyutlu kutupsal grafikler, yörüngeye yerleşmiş elektron bulutlarını temsil ettiğinden bunlara orbital (yörüngemsi) denir ve bunlar yörünge kuantum sayısının değerine göre spektral dil ile s( =0), p( l =1), d( =2), f( l =3),.... şeklinde kodlanır ya da söylenir. Kutupsal grafikler

o

l l

180

ϕ den bağımsız oldukları halde orbital grafikleri ϕ ’ye de bağımlıdır. Bu bağımlılık Çizelge(2.4) de verilen orbitallerin fonksiyon ifadelerinden görülebilir. Orbital grafikleri üç boyutlu olup bu tanımı ile orbital, matematiksel olarak dalga fonksiyonu anlamına gelir. Bir alt kabuğunda _l 2_l+1 tane orbital (dalga fonksiyonu) vardır. Yani m kuantum sayısının

l l l l+ − − − − + = , ( 1),...0,..., ( 1), m

olmak üzere her değerine bir orbital karşılık gelir. Dikkat edilirse burada farklı değer alır. Orbital indislemeleri dik koordinat sisteminin değişkenleri ile yapılır. İndisin anlamı küresel harmoniğin reel kısmının dik koordinat sisteminin eksenlerine göre yönelmelerini ifade eder. Bu indisler spektral harfin altına ) 1 2 ( + → l m , , , , , ,y z xy xz yz x x2,y2,z2, vb. şeklinde kodlanır. Orbitallerin fonksiyon ifadeleri

) ( 2 1 2 1 ) ( ϕ ϕ π π ϕ _e imϕ _{Cosm iSinm} m = = ± Φ ± _(2.41) 18

şeklinde elde edilir. Buradaki Cosinüslü ve Sinüslü terimler ayrı ayrı

(

ϕ ϕ ϕ im im e e m Cos = + − 2 1

₎

(2.42a)

(

ϕ ϕ ϕ im im e e i m Sin = − − 2 1

₎

(2.42b)

olduğundan m=0,±1, ±2,±3,... için Φm(ϕ) fonksiyonları çifterli yazımla reel

fonksiyonlar olarak π ϕ 2 1 ) ( 0 = Φ (2.43a) ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ = Φ_± ϕ π ϕ π ϕ Sin Cos 1 1 ) ( 1 (2.43b)

(

)

(

)

(

)

(

)

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ = − = = Φ_± ϕ ϕ π ϕ π ϕ π ϕ π ϕ Cos Sin Sin Cos Cos 2 1 2 / 1 1 2 1 2 / 1 ) ( 2 2 (2.43c)

(

)

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ − = − = = Φ_± ϕ ϕ π ϕ π ϕ θ π ϕ π ϕ 3 3 3 4 3 1 3 / 1 ) 3 4 ( 1 3 / 1 ) ( Cos Sin Sin Cos Cos Cos (2.43d) yazılır. 19

Bu ifadeler, Çizelge(2.2) de kuantum sayısının aynı değerine karşılık gelen )

(ξ

m

l

Θ ifadeleri ile çarpılarak orbitaller çizelgesi elde edilir. Çizelge(2.4) te xyz indislerinin üstlerinin toplamı kuantum sayısı nin değerini verir. _l

Küresel harmonikler atom ve molekül fiziğinde önemli bir yer tutarlar. Potansiyel fonksiyonu ne olursa olsun, parçacığın açısal konumu ve olasılığı hep bu fonksiyonlarla verilir.

Küresel harmoniklerin özelliklerinden çıkarılacak başlıca sonuçlar şu şekilde özetlenebilir:

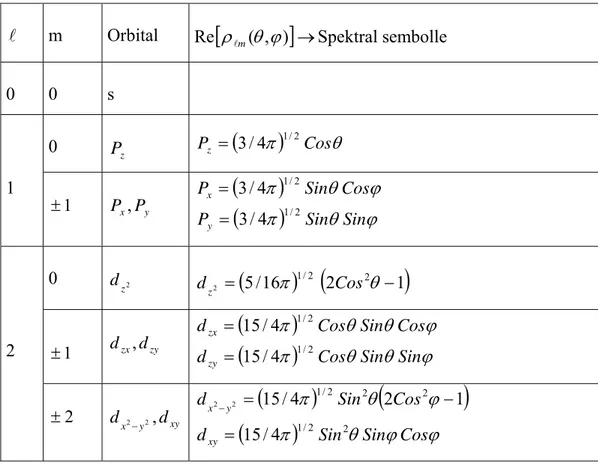
Çizelge 2.4. Orbitallerin fonksiyon ifadelerinin reel kısımları

l m Orbital Re

[

ρ_lm(θ,ϕ)

]

→Spektral sembolle

0 0 s 0 P_z Pz

(

π

)

Cosθ 2 / 1 4 / 3 = 1 1 ± P ,x Py

(

)

(

π

)

θ ϕ ϕ θ π Sin Sin P Cos Sin P y x 2 / 1 2 / 1 4 / 3 4 / 3 = = 0 d_z2 d ₂ =

(

5/16π

)

1/2

(

2Cos2θ −1

)

z 1 ± d ,zx dzy

(

)

(

π

)

θ θ ϕ ϕ θ θ π Sin Sin Cos d Cos Sin Cos d zy zx 2 / 1 2 / 1 4 / 15 4 / 15 = = 2 2 ± d_x2_−y2,d_xy

(

)

(

)

(

π

)

θ ϕ ϕ ϕ θ π Cos Sin Sin d Cos Sin d xy y x 2 2 / 1 2 2 2 / 1 4 / 15 1 2 4 / 15 2 2 = − = − 20

* indisine yörünge kuantum sayısı ve indisine magnetik kuantum sayısı denir. Atom fiziğinde kullanılan notasyona göre, =0, 1, 2, 3, ... kuantum sayılı durumlara s, p, d, f, ... yörüngeleri adı verilir.

l m

l

* Y_lm 2 olasılık yoğunluğu ϕ açısından bağımsızdır. Buna göre, verilen bir ekseni etrafında dönme simetrisi her yörünge için vardır.

z

* s yörüngelerinde (_l=0), parçacığın olasılığı (θ ve ϕ ) den bağımsız olup her yönde aynıdır. s yörüngeleri küresel simetriktir.

* Belirli bir değeri için, _l ±m durumlarında bulunma olasılıkları aynıdır.

* _{Belirli bir l değeri için, kuantum sayısı arttıkça olasılık, (}m θ =0) olan ekseninden uzaklaşıp ( ) olan

−

z θ = 90° xy-düzleminde yoğunlaşır. Klasik olarak düşünülürse, parçacık z-ekseni üzerindeyse (x= y =0) açısal momentumunun

bileşeninin sıfır olması doğaldır. Öte yandan,

x y

z xp yp

L = − xy-eksenindeki bir

yörünge L_z bileşeninin maksimum olmasını sağlar.

* Gerçekte, tek başına bir atom için, 3-boyutlu uzayda hangi yönün z ekseni olacağı belirsizdir. Ancak, bir dış etken varsa (örneğin, bir magnetik alan), bunun yönü uzayda tercihli bir doğrultu oluşturur. nin özdeğerlerine magnetik kuantum sayısı denmesinin sebebi budur.

z

L

* kuantum sayısının maksimum değeri olduğu için operatörünün maksimum özdeğeri olabilir. Oysa, operatörünün maksimum özdeğeri

dir. Bu bir çelişki gibi görünürse de, belirsizlik ilkesine göre doğrudur. Eğer, nin maksimum değeri ye eşit olsaydı, o zaman

olurdu. Yani, her üç bileşen aynı anda kesin olarak bilinmiş olurlardı. Oysa, açısal momentum operatörlerinin bileşenleri sıra değiştirme özelliğine sahip değildirler(Eisberg ve Resnick 1974, Cowan 1981, Gasiorowicz 1996, Eugen 1998).

m _l L2z 2 2 h l L2 2 ) 1 (_{l h} l + 2 z L L2 =L2_x+L2_y +L2_z 0 = = y x L L 21

2.3. Hidrojen Atomunda Radyal Çözümler

Daha önceki bölümlerde, değişkenlere ayırma yöntemi ile çözümü yapılmakta olan Schrödinger denklemi yarıçapa ve açılara bağlı kısımlarına ayrılmıştı. Denk.(2.12) kullanılarak C _{= l}l( +1)olarak yazılıp, elde edilen ifade r ile bölünüp 2 denklem yeniden düzenlendiğinde

0 ) ( )) ( ( 2 ) 1 ( 1 , 2 2 2 2 ⎥ = ⎦ ⎤ ⎢ ⎣ ⎡ − + + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ r R r U E r dr d r dr d r _h nl l l µ _(2.44)

olur. Bu denklemde ilk terim radyal kinetik enerji ile, geriye kalan tüm terimler ise E hariç, etkin potansiyel enerji ile ilgili olduğundan, denklem yeniden düzenlendiğinde

(

)

0 ) ( 2 1 ) ( 2 1 , 2 2 2 2 = ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ r R r r U E dr d r dr d r nl l l h µ µ (2.45)

olur.Buradaki Coulomb potansiyeli ile r yarıçaplı yörüngede dönmeden kaynaklanan ve ilgili açısal momentumun karesi ile orantılı olan potansiyel enerji terimlerinin toplamına etkin potansiyel denir. Yani,

(

)

2 2 . 2 1 ) ( ) ( r r U r Uet c _µ h l l + + = (2.46)

olmak üzere Denk.(2.45), yeniden yazıldığında

(

( )

)

( ) 0 2 1 , . 2 2 2 ⎥ = ⎦ ⎤ ⎢ ⎣ ⎡ _{+ −} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ r R r U E dr d r dr d r _h et nl µ (2.47)

olur. Denk.(2.44) te Coulomb potansiyel enerjisi kullanılırsa ve

l

h En

b= 2 −2µ (2.48) yer değiştirmesi yapılıp denklem 2 ile bölündüğünde

b

( ) ( ) ( )

4

( )

( )

(

1

)

( ) 0 1 2 2 2 2 2 0 2 2 2 2 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ₊ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + + + R r br br b Ze E b r b d d br r b d d nl l l h h πε µ µ (2.49) olur. Denk.(2.49) da r b = ρ

değişken değiştirmesi yapılarak ve boyutsuz bir sabit olan

n b Ze = =γ ε π µ 2 0 2 4 2 h (2.50)

ile gösterilerek, yarıçapa bağlı diferansiyel denklem çözülür. Söz konusu yer değiştirmeler yapıldığında Denk.(2.49)

(

)

0 ) ( 1 4 1 2 2 2 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + − + ρ ρ ρ γ ρ ρ ρ l l Rnl d d d d (2.51)

halini alır. Burada ρ bağımsız değişken (ara değişken), γ ise boyutsuz bir sabittir. Bu sabit baş kuantum sayısı (γ =n) olarak adlandırılır. Atomlarda daima <0 olduğundan Denk.(2.48) ile tanımlanan daima reel bir sayıdır. Bu denklem bir asimtotik limitlerde ele alınarak, bir de ara bölge için uygun bir fonksiyon belirleyerek çözülür. l n E b 23

2.4. Sınırlamalar

Denk.(2.51), birρ →∞ iken bir de ρ →0 iken ele alınarak ara değişken ρ ’nun (ρ =br olduğuna göre aynı zamanda r’nin) bu iki bölgesi için temsilci çözüm fonksiyon çarpanları bulunur. Bu işlem üç bölümde yapılır.

2.4.1. Üst limit (ρ →∞)

Bu halde elektron, hidrojen atomunun çekirdeğinden çok uzaklardadır. Üst limit bölgesinde Denk.(2.51) de paydasında ρ ve bulunan terimler sıfıra gider ve söz konusu denklem 2 ρ 0 ) ( 4 1 2 2 = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ρ ρ Rnl d d (2.52)

olur. Yani yarıçapının r→∞ olduğu bölgede yarıçapa bağlı diferansiyel denklem bu basit şekle kadar indirgenebilir. Bu denklemin çözümü ise, parantez içini sıfıra eşitleyerek bulunan operatörün, kökleri

2 1 ± = olduğundan çözüm fonksiyon 2 / ) ( ) (ρ→∞ = Sabit e±ρ Rnl

olarak bulunur. Ancak +ρ/2şeklindeki fonksiyon

e ρ →∞ için olduğundan

çözüm fonksiyon olarak kabul edilemez. Çünkü kuantum mekanik teorinin temel postülalarından birisi olan, ‘dalga fonksiyonunun sonlu olması’ ilkesine aykırıdır. Ayrıca başlangıç koşulları da öyle ayarlanabilir ki ‘integral sabiti’=1 yapılabilir. Bu durumun da yarıçapın civarındaki değerleri için çözüm fonksiyonu

∞ → l n R ∞ 24

2 /

) (ρ→∞ =e−ρ

Rnl (2.53) olmaktadır. Söz konusu bölgede fonksiyonun genel davranışı önemli olduğundan, başlangıç sabitinin bir birim olarak seçilmesinin bir sakıncası yoktur.

2.4.2. Alt limit

(

ρ →0

)

Yarıçapın çok küçük olduğu durum için ise hidrojen atomunun elektronu çekirdeğe en yakın bölgelerde düşünülmektedir. Denk.(2.51), bu alt limit bölgesi için yorumlandığında 4 1 ve ρ γ

terimleri diğer terimler yanında ihmal edilebilir. Bu halde Denk.(2.51) in son durumu

(

)

0 ) 0 ( 1 2 2 2 2 = → ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ _{+ −} + _ρ ρ ρ ρ ρ l l Rnl d d d d (2.54)

olur. Denk.(2.54) de söz konusu operatörler R_nl fonksiyonuna uygulanırsa

(

_,

)

(

₂1

)

(

_,

)

0 2 2 = + − _l l ll n n R R d d _ρ ρ ρ ρ (2.55)

olur. Bu diferansiyel denklemin çözümü ise

l l(ρ→ )0 =ρ

n

R (2.56)

olarak bilinir. Dolayısıyla yarıçapın sıfıra yakın olduğu bölgede de temsilci fonksiyon çarpanı bu son denklem ile belirlidir.

Yarıçapın çok büyük ya da çok küçük olduğu limit bölgeler için bulunan ve Denk.(2.53) ve Denk.(2.56) ile verilen fonksiyon şeklindeki ifadeler temsilci çarpanlardır. Yani gerçek Rn_l(ρ) fonksiyonu bu iki temsilci ifadeyi çarpan olarak

içermelidir. Bir de ara bölgeyi temsil etmek üzere bir ara çarpan fonksiyon f_nl(ρ) düşünülürse gerçek fonksiyon, yani 0≤ r≤∞aralığında ρ ’nun her değeri için

) ( ) (_ρ ρ/2_{ρ ρ} l l l n n e f R = − (2.57)

yazılır. Burada f_nl(ρ)öyle bir fonksiyon olmalı ki ρ →∞ ve ρ →0 limitlerinde )

(ρ l

n

f sonlu olsun. Ya da f_nl(ρ), söz konusu limitlerde R_nl(ρ)gerçek fonksiyonu sonlu tutsun.

2.5. Ara Bölge Fonksiyonu

(

fn,l(ρ)

)

Denk.(2.57) de verildiği şekli ile belirlenen fonksiyon, aralığını temsil eden Denk.(2.51) de yerine konulduğunda

∞ ≤ ≤ r 0

(

1

)

_{( ) 0} 4 1 2 , 2 / 2 2 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ _{+ − + −} + − _{ρ ρ} ρ ρ γ ρ ρ ρ ρ l l l l n f e d d d d (2.58)

olur. Buradaki operatörler, ifadeleri açık olan fonksiyon çarpanlarına, yani ye uygulanırsa Denk.(2.58) ifadesine dönüşür.

l ρ ρ/2 − e

(

)

[

2 1

]

[

(

1

)

]

_, ( ) 0 2 2 = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − + − + + γ ρ ρ ρ ρ ρ _{l l} f_nl d d d d (2.59)

Dikkat edilirse parantez dışında sadece belirlenmesi gereken fn,l(ρ)ara

bölge fonksiyonu kalmaktadır. Bu diferansiyel denklemde kuantum sayıları üzerinde aşağıdaki değişikliği yaparak denklem, standart bir diferansiyel denkleme dönüştürülür. Bunun için,

1 2 + = l j (2.60a) l l= + + = n q γ (2.60b) ) ( ) (ρ qj ρ n L f _l → (2.60c)

olsun. Söz konusu kuantum sayılarının, tanım ve değişimini kullanarak Denk.(2.59)

(

1

)

(

)

( ) 0 2 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − + + ρ ρ ρ ρ ρ q j L_qj d d j d d (2.61)

olur. Bu denklem ise birleşik Laguerre diferansiyel denklemi olarak bilinir. Denk.(2.61) in çözümü olan fonksiyonlarına birleşik Laguerre polinomları denir. ) (ρ j q L

Laguerre polinomlarının bulunmasında da Legendre polinomlarındakine benzer şekilde ve yine ilgili Rodrigues formülü yardımı ile çözüm fonksiyonlar, yani Laguerre polinomları bulunur. O halde Denk.(2.61) de j=0 alınarak

(

1

)

( ) 0 2 2 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − + ρ ρ ρ ρ ρ q L_q d d d d (2.62)

elde edilir. Denk.(2.62) Laguerre diferansiyel denklemi ve çözümü olan Lq(ρ)

fonksiyonları da normal Laguerre polinomları olarak bilinir. Normal Laguerre polinomları,

(

ρ ρ _ρ ρ ρ ₌ − e d d e L _q q q q( )

)

(2.63)

Rodrigues formülünden türetilir. Burada q, daha önce de belirtildiği gibi bir kuantum sayısıdır. O halde için Denk.(2.63) yardımı ile bir Laguerre polinomları tablosu yapılabilir. (Çizelge2.5)

,... 3 , 2 , 1 , 0 = q 27

Kuantum sayısı olduğu zaman ise çözüm fonksiyon Denk.(2.61) den belirlenmek durumundadır. Bu denklemin çözümlerine de birleşik Laguerre polinomları denir. Birleşik Laguerre polinomları, normal Laguerre polinomlarından

0 ≠ j ) ( ) (ρ j q ρ j qj L dq d L = (2.64)

formülü yardımı ile türetilir. Bu formül Laguerre polinomlarını kullanarak, yani Çizelge(2.5) te verilen ifadeleri kullanarak, birleşik Laguerre polinomları için de bir tablo yapılabileceğini göstermektedir(Çizelge (2.6)). Böylece Denk.(2.59) un çözümü olarak, fn_l(ρ)lar yerine Lqj(ρ)lar, yani birleşik Laguerre polinomları

belirlenmiş olmaktadır. Ancak θ’ya bağlı kısmı çözerken Legendre polinomlarında olduğu gibi, burada da ρ =br üzerinden yarıçapa bağlı olarak bulunan Laguerre polinomları da normalize değildir. İlgili literatürde Laguerre polinomlarının normalizasyon katsayısı n ve l kuantum sayılarına bağlı olarak

(

)

(

)

[

]

2 / 1 3 3 ! 2 ! 1 ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − − − = l l l n n n b N_n (2.65) ile verilir. Burada b , Denk.(2.48) ile tanımlanan ifade olup, Denk.(2.51) den yararlanarak 0 2 na Z b= (2.66) bulunur. Bu durumda ara değişken ρ ise

r na Z ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 0 2 ρ (2.67) olur. Burada a₀, 2 2 0 0 4 e m a = πε h (2.68) ile tanımlı Bohr yarıçapıdır(Eisberg ve Resnick 1974, Cowan 1981).

Çizelge 2.5. Kuantum sayısı j=0 için normal Laguerre polinomları q Lq(ρ)→Denk.(2.63) 0 L₀(ρ)=1 1 L₁(ρ)=−ρ+1 2 _{( )} 2 _{4 2} 2 ρ =ρ − ρ+ L 3 _{( )} 3 ₉ 2 ₁₈ 2 ₆ 3 ρ =−ρ + ρ − ρ + L

Çizelge2.6. Kuantum sayısı q=0,1,2,3, ve j≤q için birleşik Laguerre polinomları

q j Lqj(ρ)→ Denk.(2.64) ve Çizelge(2.5) 0 0 L₀₀(ρ)=1 0 L₁₀(ρ)= 1−ρ 1 _{1 ( ) 1} 11 ρ =− L 0 2 20(ρ)=2−4ρ+ρ L 1 L₂₁(ρ)=2ρ−4 2 2 L₂₂(ρ)=2 0 2 3 30(ρ)=6−18ρ+9ρ −ρ L 1 2 31(ρ)=−18+18ρ−3ρ L 2 L₃₂(ρ)=18−6ρ 3 3 L₃₃(ρ)=−6 29

Bu sonuçlara göre, hidrojen atomunun dalga fonksiyonunun yarıçapa bağlı olan kısmının, yarıçapın üst ve alt limitler arasında kalan bölgesini temsil etmekte olan )f_nl(ρ fonksiyonunun normalize şekli, normalize edilmiş birleşik Laguerre polinomlarına eşit, yani,

) ( ) (ρ n qj ρ n N L f _l = _l (2.69)

olmalıdır. O halde genel çözüm fonksiyonunun yarıçapa bağlı olan kısmının açık ifadesi

(

)

(

)

[

!

]

( ) 2 ! 1 2 ) ( /2 2 / 1 3 3 0 ρ ρ ρ ρ qj n e L n n n na Z R_l l l l − ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = (2.70)

olur. Burada, q= n+_l ve j= l2 +1 dir. Denk.(2.70) kullanılarak, ve 3 için normalize radyal dalga fonksiyonlarının tablosu yapılabilir (Çizelge2.7).

2 , 1 =

n

Kuantum mekanksel teoride bir kuantum sisteminin Schrödinger denklemini çözmek demek, sistemin içinde bulunabileceği durumları temsil eden dalga fonksiyonları ve o durumlara karşılık gelen enerjiler için ifadeler türetmek, bulmak demektir. Hidrojen atomunda merkezcil alan (Coulomb potansiyeli ile) probleminin çözümünde de aynı sonuçlara erişilmelidir. Çünkü konu, bağıl ve küresel koordinatlarda, SI birim sistemini kullanarak hidrojen atomunda merkezcil alan probleminin çözümü şeklinde ele alınmıştır. Bunu yaparken Hamiltoniyen operatörünün kinetik enerji ile ilgili terimine ait olan operatörünün küresel koordinatlardaki ifadesi kullanılmış ve zamandan bağımsız Schrödinger denklemi değişkenlerine ayırma yöntemi ile çözülmüştür. Bu çözümde hidrojen atomunun durağan enerji seviyelerinin dalga fonksiyonları, parça parça bulunmuştur. Hidrojen atomunun elektronunun zamandan bağımsız Schrödinger denkleminin, başka bir deyişle hidrojen atomunun elektronunun toplam enerjisini temsil eden, zamandan bağımsız Hamiltoniyen operatörünün (koordinata bağlı operatörün) özfonksiyonları Denk.(2.9) dan yararlanarak ve kuantum sayıları ile indisleyerek

2

∇

Çizelge 2.7. n=1,2,3 ve 0≤_l≤

(

n−1

)

için radyal dalga fonksiyonları

n _l Durumu R_nl(r)→ Denk.(2.70) ve Çizelge2.6

1 0 1s 0 / 2 / 3 0 10( ) 2 a Zr e a Z r R _⎟⎟ − ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 0 2s 0 2 / 0 2 / 3 0 20 2 2 ) ( Zr a e a Zr a Z r R _⎟⎟ − ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 2 1 2p 0 2 / 0 2 / 3 0 21 2 3 1 ) ( Zr a e a Zr a Z r R _⎟⎟ − ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 0 3s /3 0 2 0 0 2 / 3 0 30 27 2 3 2 1 2 3 ) ( Zr a e a Zr a Zr a Z r R − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 1 3p 0 3 / 0 0 2 / 3 0 31 6 1 1 3 2 4 3 ) ( Zr a e a Zr a Zr a Z r R _⎟⎟ − ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 3 2 3d 0 3 / 2 0 2 / 3 0 32 5 27 2 2 3 ) ( Zr a e a Zr a Z r R _⎟⎟ − ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ) , ( ) ( ) , , ( θ ϕ θ ϕ ψ_nlm r =R_nl r Y_lm (2.71) şeklinde yazılır. )Y_lm(θ,ϕ ve için sıra ile Denk.(2.35) de ve Denk.(2.70) de verilen ifadeleri Denk.(2.71) de yerlerine yazıldığında, hidrojen atomunun dalga fonksiyonunun en genel ifadesi

) (r R_nl

(

)

(

)

[

]

( )

( )

(

)

(

)

ϕ ρ π ξ ρ ρ ϕ θ ψ im m m m qj m n e P m m L e n n n na Z r 2 1 ) ( ! ! 2 1 2 1 ) ( ! 2 ! 1 2 ) , , ( 2 / 1 2 / 2 / 2 / 1 3 3 0 l l l l l l l l ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + − + − ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ + − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = + − (2..72)

olur. Burada q= n+_l, j= l2 +1, ρ =br, b=2Z/na₀ ve ξ =Cosθ dır. Hidrojen atomunun durağan enerji seviyeleri için dalga fonksiyonlarını veren Denk.(2.72) nin türetiminde karşılaşılan ara kuantum sayıları (q ve j ) atılarak tüm ifade, kuantum sayılarına indirgenmiş olmaktadır. Kuantum sayıları ilgili dalga fonksiyonundan ya da bu fonksiyon içindeki ilgili çarpanın sağlaması gereken sınır şartlarından kaynaklanır. Buna göre ve m kuantum sayılarının adları ve birbirleri ile olan ilişkileri

m n ,, l

l ,

n

Baş kuantum sayısı:n=1,2,3,...,∞ (2.73a)

Yörünge kuantum sayısı:_l=0,1,2,3,...,

(

n−1

)

(2.73b) Manyetik kuantumsayısı: m=−_l,....,...,0,...+_l,→

(

2_l+1

)

(2.73c)

şeklindedir. Görüldüğü gibi manyetik kuantum sayısı _{herhangi bir l değerine} karşılık tane farklı değer alır ve yörünge açısal momentum vektörü L’nin, z-yönündeki bir dış manyetik alan doğrultusu üzerindeki bileşenlerine karşılık gelirler. , m

(

2_l+1

)

z L

Kuantum sayılarının yukarıda verilen olası değerlerine göre, bir tek enerji seviyesine, çok sayıda dalga fonksiyonu yazılabilir. Bu durumdaki enerji seviyeleri dejeneredir. Bir enerji seviyesinin kaç-katlı dejenere olduğuna dejenereliğin mertebesi denir ve ile gösterilir. Denk.(2.73a,b,c) de verilen tanımlar kullanılarak dejenereliğin mertebesi, n D 2 1 0 ) 1 2 ( ... 5 3 1 ) 1 ( 2 n n D n n =

∑

+ = + + + + − = − = l l (2.74) 32

olur. Elektronun spin açısal momentumu da hesaba katıldığı zaman ve spin açısal momentumunun iki farklı değer aldığı düşünülürse, gerçek katlılık derecesi, bulduğumuz değerin iki katı olur. Yani olur. Kuantum sayılarının alabileceği değerleri kullanarak

2

2n

m n_l

ψ dalga fonksiyonları Çizelge(2.8) de olduğu gibi gösterilir(Eisberg ve Resnick 1974, Cowan 1981, Bransden ve Joachain 1989, Gros 1993).

Çizelge2.8. n=1,2 ve 3 için Hidrojen dalga fonksiyonları

n l m ψn_lm →Denk.(2.72) 1 0 0 / 0 2 / 3 0 100 1 Zr a e a Z − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = π ψ 0 0 /2 0 0 2 / 3 0 200 2 2 4 1 Zr a e a Zr a Z − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = π ψ 0 θ π ψ e Cos a Zr a Z Zr/2a0 0 2 / 3 0 210 2 4 1 − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 2 1 1 ± _θ ϕ π ψ Zr a i e Sin e a Zr a Z − ± ± ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = /2 0 0 2 / 3 0 1 21 8 1 0 0 /3 0 2 0 2 2 0 2 / 3 0 300 27 18 2 3 81 1 Zr a e a r Z a Zr a Z − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = π ψ 0 θ π ψ e Cos a Zr a Zr a Z Zr/3a0 0 0 2 / 3 0 310 6 81 2 − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 1 1 ± _θ ϕ π ψ Zr a i e Sin e a Zr a Zr a Z − ± ± ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = /3 0 0 0 2 / 3 0 1 31 6 81 1 0 _{( 1)} 6 81 1 /3 2 2 0 2 2 2 / 3 0 320 ⎟⎟ 0 − ⎠ ⎞ ⎜⎜ ⎝ ⎛ = − _θ π ψ e Cos a r Z a Z Zr a 1 ± _{θ θ} ϕ π ψ Zr a i e Cos Sin e a r Z a Z − ± ± ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = /3 0 2 0 2 2 2 / 3 0 1 32 81 1 3 2 2 ± _θ ϕ π ψ Zr a i e Sin e a r Z a Z /3 _{2 2} 2 0 2 2 2 / 3 0 2 32 0 162 1 − ± ± ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 33

2.6. Bir Fonksiyonun Paritesi ve Parite Operatörü

Bir fonksiyonun paritesi onun tek-fonksiyon mu, çift-fonksiyon mu olduğunu belirler. Matematiksel olarak tüm fonksiyonlar bu açıdan ele alındığında öncelikle, çift pariteli (simetrik) ya da tek pariteli (antisimetrik) olmak üzere kesin pariteli fonksiyonlar ve bir de bunların dışında kalan karma pariteli (asimetrik) fonksiyonlarla karşılaşılır. Çizelge(2.8) de verilen hidrojen dalga fonksiyonları kesin pariteli fonksiyonlardır. Bu fonksiyonların paritesi (tek mi ya da çift mi olduğu) parite işlemi ile anlaşılır. Üç boyutlu uzayda parite işlemi

(

r,θ,ϕ

)

noktasının orjine göre simetriği olan A′

(

r,π −θ,ϕ+π

)

noktasını bulmak demektir. Parite işleminin anlamı daha açık olarak

→ ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ + → − → → ′ → ϕ π ϕ θ π θ r r A A Yansıtma işlemi

demektir. İlgili fonksiyon çarpanlarına yansıtma işlemi uygulandığında

(

π ϕ

) ( )

m _m

( )

ϕ m + = − Φ Φ 1 (2.75)

(

π θ

) ( )

m _m

( )

θ m _l l l − = − Θ Θ ₁ + _(2.76)

( )

r R

( )

r R_nl = _nl (2.77) olur. Bu fonksiyon şeklindeki ifadeler taraf tarafa birbirleri ile çarpıldığında,

( )

2m

1 − hep çift sayı olacağından

ψ

(

r,π −θ,π +ϕ

) ( ) (

= −1lψ r,θ,ϕ

)

(2.78)

olur. P, parite operatörünü temsil etmek üzere Denk.(2.78) in sol tarafı

(

π θ π ϕ

)

ψ

(

θ ϕ

)

ψ r, − , + =P r, , (2.79)

şeklinde bir işlemin sonucudur. O halde Denk.(2.78) ve Denk.(2.79) un sağ tarafları eşit olacağından

(

θ ϕ

) ( ) (

ψ θ ϕ

)

ψ r, , 1 r, ,

P = − l (2.80)

olur. Bu da parite operatörünün özdeğer denklemidir. Parite operatörünün özdeğeri ise

(2.81)

( )

₋₁l

=

P

ile belirlidir. Buna göre hidrojen atomunun dalga fonksiyonları ψ_nlm lerden ’si çift olanlar çift pariteli (simetrik), ’si tek olanlar ise tek pariteli (antisimetrik) fonksiyonlardır. Parite işlemi açısından parite operatörünün özdeğer denklemi

l l

( )

_l

l = −1l

P (2.82)

olarak da yazılır(Eisberg ve Resnick 1974, Cowan 1981).

2.7. Hidrojen Atomunun Merkezcil Alan Problemi Çözümünde Enerji

Schrödinger denklemi çözümlerinde dalga fonksiyonu yanında belirlenmesi gereken ikinci bilinmeyen enerjidir. Denk.(2.48) ve Denk.(2.50) denklemlerinin her ikisinde de bir ara sabiti olan b bulunmaktadır. Bu iki denklem arasında yok edilip gerekli kısaltmalar yapıldığında,

b

2 2 0 2 2 ₄ 2 1 h µ πε ⎟⎟_⎠ ⎞ ⎜⎜ ⎝ ⎛ − = Ze n E_n (2.83) olur. Bohr yarıçapı a₀ ile (Denk.2.68), düzeltilmiş Bohr yarıçapı ise

µ µ πε µ m a e a ₂ 0 2 0 4 = = h (2.84)

şeklinde tanımlanır. Denk.(2.84), Denk.(2.83)’te kullanılırsa

(

)

2 2 0 0 2 2 4 n Z m a e En µ πε − = (2.85)

(

)

2 2 0 2 2 4 n Z a e E_n µ πε − = (2.86)

ifadeleri elde edilir. Burada Denk.(2.83), c ışık hızını içermeyen ve enerji düzeylerinin durgun kütle enerjisi cinsinden ifade edildiği biçimdir. Denk.(2.85) ise enerji düzeylerine görelilikten gelen düzeltmelerde kolaylık sağlaması için yazılmış biçimdir. Denk.(2.83) ifadesi

2 c µ

( )

2 2 2 2 1 n Z c E_n =− µ α (2.87) şeklinde yazılabilir. Burada α ince yapı sabitidir ve

(

c

)

e h 0 2 4πε α= (2.88)

ile ifade edilir(Eugen 1998).

Enerji ifadesi atomik birimler (a.b.) kullanılarak

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = m n Z E_{n 2} µ 2 2 (2.89) olarak bulunur.

Bir elektronlu atomlar için Schrödinger denklemini çözerek elde edilen enerji değerleri Bohr modeliyle tamamen uyuşmaktadır. Bu enerji spektrumu, deneysel spektrumla ana özellikleriyle uyuşur. Bununla birlikte, bu uygunluk tam değildir ve deneysel spektrumun ayrıntılarını açıklamak için göz önüne alınması gereken, göreli etkiler ve elektronun spininden doğan ince yapı, Lamb kayması ve çekirdek etkilerinden ileri gelen aşırı ince yapı gibi değişik düzeltmeler bulunmaktadır(Eisberg ve Resnick 1974, Cowan 1981).

n

E

2.8. Hidrojen Tipi Bağlı Durum Dalga Fonksiyonları ve Olasılık Genliği

Denk.(2.71) ile belirtilen hidrojen tipi dalga fonksiyonu ifadesi

(

)

2 , ,θ ϕ ψnlm r dr ψnm

(

r,θ,ϕ

)

ψnm

(

r,θ,ϕ

)

r drsinθ dθdϕ 2 l l ∗ = (2.90)

şeklinde yazılırsa, sistem,

(

n ,,l m

)

kuantum sayıları ile tanımlanan kararlı bir durumda iken, kutupsal koordinatlarda dr ile verilen dr hacim elemanında elektronun bulunma olasılığını gösterir.

ϕ θ θ d d dr r2 sin = m n m n m nl ψ l ψ l ψ 2 ₌ ∗ büyüklüğü olasılık yoğunluğudur. Denk.(2.39) ve Denk.(2.71) kullanılarak

(

)

( )

( )

( ) ( )

2 1

( )

2 2 2 2 2 , , , θ π ϕ θ ϕ θ ψ m n m n m n r R Y r R r l l l l l Θ = = − (2.91)

ifadesi elde edilir. Buna göre olasılık yoğunluğu Φ ye bağlı değildir.

Radyal dağılım fonksiyonu, elektronun çekirdekten r birim uzaklığında birim uzunluk başına bulunma olasılığını verir ve

( )

₂

( )

2 r R r r Pnl = nl (2.92) ile gösterilir. Denk.(2.90) θ ve ϕ açıları üzerinde integre edilir ve Denk.(2.71) kullanılırsa

( )

( )

( )

( )

r dr R r Y d d dr r R r dr r P n m n n 2 2 2 0 2 0 2 2 _{sin ,} l l l l = = π

∫

θ θ

∫

π ϕ θ ϕ (2.93)

ifadesi bulunur. Bu, doğrultudan bağımsız olarak elektronun çekirdekten r ile uzaklıkları arasında bulunma olasılığını verir. Denk.(2.93) ün sağ tarafında dr

r+ 2

r çarpanının görünmesi, r ile r+dr yarıçaplarında iki küre arasını kaplayan hacmin 2

r ile orantılı olmasındandır. Hidrojen atomu için ’in ilk üç değeri için radyal özfonksiyonu ve

n

( )

r

R_nl P_nl

( )

r radyal dağılım fonksiyonları ile birlikte Şekil (2.4) de verilmiştir.

( )

r

R_nl radyal özfonksiyonları ve P_nl

( )

r radyal dağılım fonksiyonları ile ilgili şu sonuçlar çıkarılabilir.

1) Sadece s durumları, r=0 da sıfırdan farklı radyal dalga fonksiyonlarıdırlar. Ayrıca Y₀₀ =

( )

4π −1/2, θ ve ϕ den bağımsız olduğu için Denk.(2.70) ten aşırı ince yapı kuramında önemli rol oynayan

3 3 3 2 0 2 00 (0) 4 1 ) 0 ( n a Z R_n n µ π π ψ = = (2.94)

sonucu elde edilir. Bundan başka s durumunun ψ_n00 ≅ψ_ns özfonksiyonlarının herbiri için r =0 da 0 ≠0

dr dR_n

dır. Bu garip davranış (2.1) ifadesindeki potansiyel enerjinin orijinde sonsuz olmasından dolayıdır.

2) _l≠0 halinde, Rn_l nin l

r ile orantılı olması gerçeği küçük r ler için ile artan dalga fonksiyonunu küçük kalmaya zorlar. Bu, Denk.(2.46) ile verilen etkin l