Gerotor profillerinin optimizasyonu

FEN BĐLĐMLERĐ ENSTĐTÜSÜ

GEROTOR PROFĐLLERĐNĐN OPTĐMĐZASYONU

Bekir KARAGÜL YÜKSEK LĐSANS TEZĐ MAKĐNA ANABĐLĐM DALI

ÖZET Yüksek Lisans Tezi

GEROTOR PROFĐLLERĐNĐN OPTĐMĐZASYONU

BEKĐR KARAGÜL

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Makine Anabilim Dalı

Danışman: Prof. Dr. Ziya ŞAKA 2010, 47 Sayfa

Jüri: Prof. Dr. Ziya ŞAKA Doç. Dr. Hacı SAĞLAM Yrd. Doç. Dr. Hüseyin ĐMREK

Endüstriyel hidrolik sistemlerde hem pompa hem de motor olarak kullanılan gerotorlar, akışkanları devir sayısı ile doğru orantılı olarak aktaran mekanizmalardır. Bu çalışmada episikloid esaslı gerotor profillerinin optimum olarak tasarımı amaçlanmıştır. Bunun için önce gerotor geometrisi ele alınarak profillerin denklemi parametrik olarak elde edilmiştir. Profilde oluşacak en büyük Hertz basıncını belirlemek üzere minimum eğrilik yarıçapı formüle edilmiş ve sayısal olarak bulunabileceği gösterilmiştir. Gerotor debisini bulmak için bir devirde süpürülen alan matematiksel olarak hesaplanmıştır. Değişik boyutlardaki gerotor profilleri için minimum eğrilik yarıçapı ve süpürülen alan değerleri sayısal olarak bulunmuştur. Bu değerler üç boyutlu grafiklerde gösterilerek izin verilebilecek en küçük eğrilik yarıçapına ve en büyük debiye sahip optimum gerotor profilleri belirlenmeye çalışılmıştır.

Anahtar Kelimeler: Gerotor, Episikloid, Hertz Basıncı, Minimum Eğrilik Yarıçapı, Gerotor Debisi

ABSTRACT Master Thesis

OPTIMIZATION OF GEROTOR PROFILES

BEKĐR KARAGÜL

Selçuk University Institue of the Natural and Applied Scienses Department of Mechanical Engineering

Supervisor: Prof. Dr. Ziya ŞAKA 2010, 47 Page

Jury: Prof. Dr. Ziya ŞAKA Assoc. Prof. Dr. Hacı SAĞLAM Assist. Prof. Dr. Hüseyin ĐMREK

The gerotors used as pump or motor on the industrial hydraulic systems are the mechanisms transferred fluids proportionally with the angular velocity. In this study, it is purposed optimal design of epicycloid based gerotor profiles. For this purpose, at first by considering geometry of gerotor, it is obtained equations of profile parametrically. Minimum radius of curvature has been formulated to determine maximum Hertzian stresses occured on the profile, it is shown to be able calculating numerically. In order to determine flowrate of the gerotor, the area swept in one revolution is mathematically calculated. Minimum radius of curvature and swept area values for different dimensions of gerotor profiles are found numerically. By plotting these values on the three dimensional graphics, it is tried to determine the optimal gerotor profiles having permitted minimum radius of curvature and maximum flowrate.

Key words: Gerotor, Epicycloid, Hertzian stress , minimum radius of curvature, gerotor flowrate

ÖNSÖZ

Tez çalışmam sırasında beni yönlendiren ve değerli katkılarını esirgemeyen danışman hocam Prof. Dr. Ziya ŞAKA’ya teşekkürlerimi sunarım.

Konya, 2010 Bekir KARAGÜL

ĐÇĐNDEKĐLER ÖZET………... i ABSTRACT………...……… ii ÖNSÖZ………..……… iii ĐÇĐNDEKĐLER………..iv SĐMGELER LĐSTESĐ………....v 1.GĐRĐŞ……….. 1 2. KAYNAK ARAŞTIRMASI………. 3

3. GEROTORLARIN TASARIM METOTLARI………. 5

3.1. Episikloid Esaslı Gerotorlar………. 5

3.2. Zarf Teorisi……….. 9

4. GEROTOR PROFĐLLERĐNĐN OLUŞTURULMASI………...….. 13

5. EĞRĐLĐK YARIÇAPI ANALĐZĐ………... 18

6. HERTZ BASINCI……… 23

7. GEROTOR DEBĐSĐ………...……… 26

8. OPTĐMĐZASYON……… 33

8.1 Gerotor Profilinin Optimizasyonu……….…...33

9. SONUÇ VE ÖNERĐLER………..42

9. KAYNAKLAR……….. ……….. 44

EK-1………...………... 46

EK-2………...………... 47

SĐMGELER

Simge Açıklama Birim

A Alan mm2

c Parametre

e Eksantriklik mm

E Elastisite modülü N/mm2

EE, EF Eliptik integral f, h, k Fonksiyon F Kuvvet N g Pim Yarıçapı mm H Kalınlık mm K Eğrilik 1/mm l Uzunluk mm p Ofset Mesafesi mm PH Hertz Basıncı N/mm2

r Yuvarlanan Daire Yarıçapı mm

R Temel Daire Yarıçapı mm

Re Eşdeğer Eğrilik Yarıçapı mm

Rm Profildeki Maksimum Yarıçap mm

x Kartezyen Koordinat mm

y Kartezyen Koordinat mm

z Diş Sayısı

ρ Eğrilik Yarıçapı, Kutupsal Koordinat mm

θ Kutupsal Koordinat, Açı (°)

α, β, γ, θ Açı (°)

1. GĐRĐŞ

Gerotor, bir akışkanı devir sayısı ile orantılı olarak taşıyan pozitif deplasmanlı bir pompa mekanizmasına verilen isimdir. En yaygın kullanım şekli olan hidrolik pompa özelliğinin yanı sıra hidrolik motor olarak da yaygın bir şekilde kullanılmaktadır. Ayrıca, sikloid profilli çarklar da genel olarak “gerotor” olarak adlandırılır. Bu kelime Hill (1927) tarafından “GEnerated ROTOR” ifadesinden türetilmiştir.

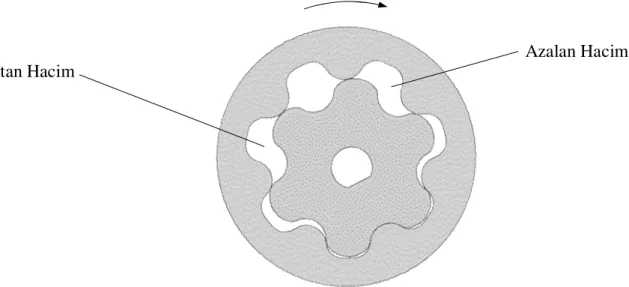
Gerotor pompa mekanizması iki elemandan oluşur: Đç rotor (rotor) ve dış rotor (çark). Đç rotorun ekseni dış rotorun eksenine göre bir miktar kaçıktır. Đç rotor motordan aldığı dönme hareketiyle dış rotoru da döndürür. Đç rotorun diş sayısı her zaman dış rotorunkinden bir diş eksiktir. (Şekil 1.1). Bu sayede dişler arasında emme ve basma hacimleri meydana gelir. Rotorlar dönmeye başladığı zaman bir tarafta artan hacim, diğer tarafta ise azalan hacim oluşur. Artan hacimde emme, azalan hacimde ise basma işlemi gerçekleşir. Eksik dişin oluşturduğu bu hacim (Şekil 1.2), her devirde pompalanan akışkanın hacmini belirler. Diş sayısı pompalanacak akışkan hacmine, hıza ve pompa gövdesine bağlı olarak değişebilir.

Şekil 1.1 Gerotor pompa mekanizması Dış Rotor

Birbirlerine göre eksantrik ve sabit merkezli rotorlar dönünce, iç ve dış rotorların dişleri arasındaki boşluk her devirde yaklaşık olarak 180° lik bir dönüşle maksimum boyuta kadar artar. (Eksik dişin hacmine eşit oluncaya kadar.) Yarım tur boyunca giderek artan boşluğa, emme ve kısmi vakumla sıvı aktarılır. Bunu takip eden 180° lik dönüş boyunca dişlerin birbiri içine girmesi ile boşluk giderek azalır ve akışkan, boşaltma kapağından çıkmaya zorlanır. Bu sırada iç ve dış rotor belli noktalarda birbiriyle sürekli temas halindedirler. (Şekil 1.2) Gerotor, hidrolik motor olarak kullanıldığı zaman ise bu olay tersine gerçekleşir.

Şekil 1.2 Đç ve dış rotor arasındaki hacim

Đç ve dış rotorun birbiriyle sürekli olarak temas etmesi sebebiyle, temas noktalarında Hertz basınçları oluşur. Basıncın şiddeti temas kuvveti ile doğru orantılı, eğrilik yarıçapı ile ters orantılıdır. Eğrilik yarıçapının artması Hertz basıncını azaltır, fakat boyutları büyütür ve debiyi azaltır. Basıncın artması aşınmayı artırır, bu da gerotorun ömrünü azaltır. Uzun ömürlü bir mekanizma için debiyi çok azaltmayacak, fakat minimum eğrilik yarıçapının makul değerlerde olmasını sağlayacak bir optimum bir çözüm bulunabilir.

Artan Hacim

2. KAYNAK ARAŞTIRMASI

Gerotorların geçmişi 1900’ lü yıllara kadar dayanmaktadır. Hill (1927), gerotorlarla ilgili ilk çalışmasını yapmış ve 1906’ dan 1921’ e kadar bütün zamanını gerotoru geliştirmek için harcamıştır. Bunlarla ilgili geometrik teoriyi geliştirmiş, gerotor kelimesini “GEnerated ROTOR” kelimelerinden türetmiş ve gerotorlarla ilgili temel patentleri almıştır.

Stryczek (1990), gerotor profillerinin oluşum mekanizmasını açıklamıştır. Episikloid ve hiposikloid esaslı gerotor profillerinin zarf teorisi yardımıyla parametrik denklemlerini elde etmiştir. Đç ve dış zarf teorisini ayrıntılı olarak açıklayarak, episikloid ve hiposikloid esaslı gerotor profillerinin nasıl elde edilebileceğini göstermiştir.

Stryczek (1993), gerotor hidrolik motor ve pompalarda kullanılan episikloid ve hiposikloid esaslı profillerin karakteristik parametrelerini ele alarak bunların hidrolik akış üzerindeki etkilerini incelemiştir. Episikloid ve hiposikloid esaslı profillerin etkilerini karşılaştırarak aralarındaki farkları belirtmiştir.

Beard, Hall ve Soedel (1991), episikloid ve hiposikloid esaslı gerotor profillerini ele alarak tasarım parametrelerine göre matematiksel denklemlerini elde etmişlerdir. Bunlara bağlı olarak debi ve sıkıştırma oranı gibi değişik çalışma karakteristikleri arasında karşılaştırma yapmışlardır.

Kwon, Kim ve Shin (2008), gerotorlarda aşınmayla ilgili çalışmalarında önce profil denklemleri yardımıyla, alttan kesmeyi önlemek için gerekli minimum eğrilik yarıçapını bulmuşlardır. Daha sonra hidrodinamik etkiyi dikkate almaksızın iç ve dış rotor arasındaki Hertz basınçlarının değişimini incelemişlerdir. Bu sonuçlara bağlı olarak yarı statik ve kuru şartlarda geçerli bir aşınma faktörü ifadesi önermişlerdir.

Maiti (1993), episikloid esaslı gerotorlarda tork karakteristiklerini mekanizmanın temel geometrisi ve kinematiği ışığında teorik olarak inceledikten sonra, bir deney seti oluşturarak deneysel sonuçlarla teorik sonuçları karşılaştırmıştır. Ani tork değişimlerini inceleyerek sürtünme ve diğer dirençlerle torktaki dalgalanmaları ve etkileşimleri araştırmıştır.

Kim, Won, Burris, Holtkamp, Gessel, Swanson ve Sawyer (2005), metal-metal temaslı eğrisel yüzeyli parçalarda Hertz basınçlarını sonlu elemanlar yöntemiyle analiz etmişler ve buldukları sonuçları deneysel sonuçlarla karşılaştırarak yorumlamışlardır.

Mimi, Bonandrini, Rottenbacher (2007), episikloid esaslı pompaların teorik performansını geometrik boyutlarının bir fonksiyonu olarak ele almışlardır. Boyutlarla ilgili üç boyutlu parametre tanımlayarak pompa performansını bunlara bağlı olarak incelemişler ve genel sonuçlar elde etmeye çalışmışlardır.

3. GEROTORLARIN TASARIM METOTLARI

Gerotor profillerinin belirlenmesi için başlıca iki yöntem mevcuttur: 1. Dış Zarf Eğrisi Metodu

2. Đç Zarf Eğrisi Metodu

Eğer dış zarf metodu tatbik edilirse, önce dış dişli şeklindeki sikloid profilli ana çark (rotor) tasarlanır. Bu şekilde tasarlanan rotor, bir dış dişli olarak iç dişli şeklindeki dış rotor yani çark ile birlikte çalışır. Gerotor olarak adlandırılan ve sistemin ana elemanını oluşturan rotorun profili sikloid eğri ailesi esaslı bir zarf eğrisidir veya onun uyarlanmış (modifiye edilmiş) formudur. Đç zarf eğrisi yöntemi dış zarf eğrisi yönteminin tersine çevrilmiş halidir.

Gerotor tasarımı yapılırken birbiri ile eş çalışan dış dişli şeklindeki rotor ve iç dişli şeklindeki çark beraberce tasarlanır. Çarkların ölçüleri ve şekli üzerinde ana çarkın profili belirleyicidir, ana çarkın (rotorun) profilinden bütün profil ortaya çıkar. Sikloid profil konstrüksiyonu için kullanılan sikloid eğrileri (episikloid veya hiposikloid) iki temel koşulu yerine getirmek zorundadır.

1. Her iki çark tam sayıda diş sayısına sahip olduğu için, profili oluşturan eğriler kapalı olmalıdır.

2. Çark profilinde girişim olmaması için eğriler kendi kendini kesmemelidir.

Bu koşulları sağlayan eğriler, dalgalı episikloidler ve dalgalı ve basit hiposikloidlerdir.

Episikloid eğrilerin kullanılması durumunda episikloid esaslı dişliler; hiposikloid eğrilerin kullanılmasıyla da hiposikloid esaslı dişliler oluşur. Sikloid esaslı dişlilerin konstrüksiyonu için ilmikli sikloidler kullanılmamalıdır, çünkü bunlar kendi kendini kesen eğrilerdir.

3.1. Episikloid Esaslı Gerotorlar

Bir dairenin bir doğru üzerinde kaymadan yuvarlanması esnasında, daire üzerindeki bir noktanın çizdiği eğriye sikloid eğrisi denir. Daire, bir doğru üzerinde

değil de başka bir dairenin dışında kaymadan yuvarlanıyorsa episikloid eğrisi, içinde kaymadan yuvarlanıyorsa hiposikloid eğrisi meydana gelir.

Gerotorların büyük çoğunluğunda episikloid esaslı profiller kullanılmaktadır. (Stryczek 1990). Bu yüzden burada bu tip gerotor profili ele alınmıştır.

Yukarıdaki birinci koşulun sağlanması için, temel daire yarıçapının yuvarlanan dairenin yarıçapına oranı tam sayı olmalıdır. Aksi halde episikloid eğrisi kapalı olmaz. (Şekil 3.1) Yuvarlanan dairenin hareket düzlemi üzerindeki herhangi bir noktanın çizdiği eğrinin genel adı da episikloiddir.

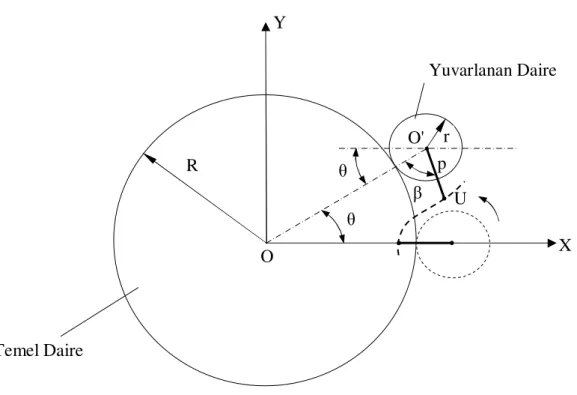
Şekil 3.1 Episikloid eğrisinin oluşumu

Şekil 3.1’ de görüldüğü gibi, R yarıçaplı temel daire üzerinde kaymadan yuvarlanan r yarıçaplı daire, kesikli çizgi ile gösterilen başlangıç konumundan itibaren şekilde görülen konuma gelmiş olsun. Kaymadan yuvarlanma şartından, yuvarlanan dairenin dönme miktarı β aşağıdaki gibi bulunur.

θ θ β R r Temel Daire Yuvarlanan Daire U X Y O O' p

Rθ = r β, β = θ r R

(3.1)

Bu dairenin hareket düzlemi üzerinde merkezden p kadar uzaklıktaki U noktasının, temel dairenin merkezindeki OXY eksen takımındaki koordinatları şu şekilde yazılabilir:

(

)

(

)

Bu ifadelerde β yerine konur ve düzenlenirse,

θ θ       + −       + = r R p r R r x 1 cos cos 1 (3.4) θ θ       + −       + = r R p r R r y 1 sin sin 1 (3.5)

şeklinde episikloid eğrisinin genel parametrik denklemleri elde edilmiş olur.

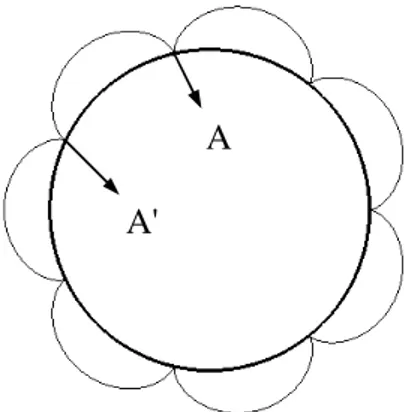
Söz konusu nokta yuvarlanan dairenin üzerinde olursa (p = r hali) klasik episikloid eğrisi oluşur. Başlangıçta, bu dairenin temel daireye temas ettiği noktada (A) ve kaymadan yuvarlanarak tekrar temas ettiği noktalarda (A', A''…) eğri, bir büküm noktasından geçer. (Şekil 3.2) Bu büküm noktalarında eğrilik yarıçapı sıfırdır ve süreksizlik oluşur. Bu yüzden bu eğri gerotor profilinin oluşturulmasında kullanılamaz.

Şekil 3.2 Klasik episikloid eğrisi A

Alınan nokta yuvarlanan dairenin dışında olursa (p > r hali) ilmikli episikloid oluşur. (Şekil 3.3) Đlmikli episikloidde eğri kendini kestiği için, yukarıdaki ikinci koşulda belirtildiği gibi profilde girişime sebep olacağından yine gerotor profillerinin oluşturulmasında kullanılamaz.

Şekil 3.3 Đlmikli episikloid

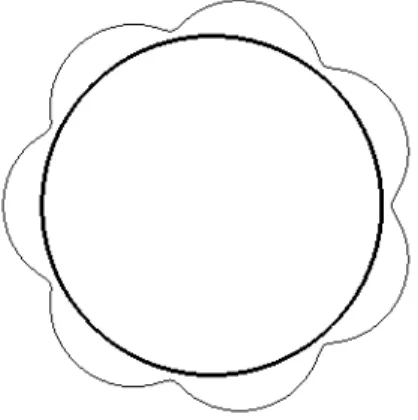
Alınan nokta yuvarlanan dairenin içinde olursa (p < r hali) dalgalı episikloid oluşur.(Şekil 3.4) Dalgalı episikloidde yukarıda belirtilen sakıncalar oluşmayacağı için, eğri gerotor profillerinin oluşturulmasında kullanılabilir.

3.2. Zarf Teorisi

Bir eğri ailesi verildiğinde her noktasında bu eğri ailesinin bir eğrisine dokunan eğri, zarf eğrisi olarak adlandırılır. Böylece zarf eğrisi eğri ailesindeki tüm eğrilere en az bir noktada teğet olmuş olur.

Bir parametreli eğri ailesi f (x,y,c) = 0 gibi bir denklemle belirlidir. Bu denklemde c değişken parametre olup her c değerinde eğri ailesinin bir eğrisi elde edilir.

Eğri ailesinde bulunan bir eğrinin herhangi bir noktasında eğimi:

y f x f dx dy ∂ ∂∂ ∂ − = (3.6) Bu denklemden 0 = ∂ ∂ + ∂ ∂ dy y f dx x f (3.7)

bağıntısı elde edilir. Bu bağıntı aynı zamanda: 0 = ∂ ∂ + ∂ ∂ dc dy y f dc dx x f (3.8)

olarak yazılabilir. Eğim denkleminden elde edilen bu ilişki eğri ailesi içinde bulunan her eğri için geçerli olacaktır. Eğer bir başka eğri (zarf eğrisi) bu eğri ailesini oluşturan bütün eğrilere teğet ise, o eğrinin de aynı bağıntıyı sağlaması gerekir.

f (x,y,c) = 0 fonksiyonunun toplam türevi:

0 = ∂ ∂ + ∂ ∂ + ∂ ∂ dc c f dy y f dx x f (3.9) veya 0 = ∂ ∂ + ∂ ∂ + ∂ ∂ c f dc dy y f dc dx x f (3.10)

olacaktır. Eğim denkleminden elde edilmiş olan bağıntı (3.8)’ de fonksiyonun toplam türevinde kullanıldığında: 0 = = ∂ ∂ c f c f (3.11)

olur. Öyle ise bu eğri ailesinin zarfı f (x, y, c) = 0 denklemini sağlaması gerektiği gibi fc=0 kısmi türevinin sıfır olmasını da sağlamalıdır. Bu iki denklemden c

parametresinin yok edilmesi ile elde edilen g (x, y) = 0 eğrisi eğri ailesinin zarfıdır. Bazı durumlarda bir eğri ailesi parametrik olarak da ifade edilebilir. Yani, eğri ailesi:

x = h (s, c) y = k (s, c)

şeklinde verilebilir. Burada s eğri parametresi, c ise eğri ailesi parametresidir. Zarf bu denklemlerden ve: 0 = ∂ ∂ ∂ ∂ − ∂ ∂ ∂ ∂ s k c h c k s h (3.12)

denkleminden c parametresinin yok edilmesi ile elde edilir (veya zarf eğrisi koordinatları c parametresine göre elde edilebilir).

Örnek 1:

f (x, y, c) = (x −c)2 + y2 −1 = 0

denklemi ile verilen eğri ailesinin zarfını bulalım. Şekil 3.5’ de gösterildiği gibi, eğri ailesi merkezi x = c, y = 0 ve yarıçapı bir birim olan dairelerdir. Her c değeri için ailenin bir eğrisi elde edilir. Denklemin c parametresine göre türevi:

fc= −2(x −c) = 0

f = 0 ve fc= 0 denklemlerinden c parametresi yok edildiğinde:

y = ± 1

elde edilir. Daire ailesinin zarfı, dairelere teğet, y = +1 ve y = −1 yatay doğrularıdır.

Örnek 2: (Söylemez 2007)

Şekil 3.6

Bir ucu duvara dayalı, bir ucu yerde duran bir merdivenin sürtünmenin az olmasından dolayı düşerken yaptığı hareketi ele alalım. (Şekil 3.6) Merdivenin farklı konumları bir eğri demetini oluşturacaktır. Bu sırada oluşturulan zarfı bulalım:

Parametrik olarak merdivenin denklemi: γ

γ sin tan l x

y=− +

γ merdiven ile yatay arasında kalan açı, l ise merdiven uzunluğudur. Bu denklemi:

f(x,y,γ)= y+xtanγ −lsinγ =0

şeklinde yazabiliriz. Denklemin γ ya göre kısmi türevi ise: 0 cos cos 1 ) , , ( = ₂ − γ = γ γ γ x y x l f

olacaktır. Bu iki denklemden x ve y için çözüm yapıldığında: γ 3 cos l x= γ 3 sin l y=

bulunur. Bu iki denklem zarf eğrisini parametrik olarak tanımlamaktadır ve zarf bu denklemlerle çizilebilir. Eğer γ parametresini bu iki denklemden yok edersek:

3 2 3 2 3 2 l y x + =

4. GEROTOR PROFĐLLERĐNĐN OLUŞTURULMASI

Gerotor tasarımı yapılırken birbiri ile eş çalışan dış dişli şeklindeki rotor ve iç dişli şeklindeki çark beraberce tasarlanır. Pratikte kullanılan gerotor pompa ve motorlarda imalat kolaylığı açısından iç dişli şeklinde düşünülen çarkın diş profili dairesel olarak düşünülür ve rotorun profili buna göre belirlenir. Dairesel profilli dişler ya gövde ile birlikte bir bütün olarak imal edilir (Şekil 4.1), ya da dairesel kesitli pimler şeklinde gövde üzerine bağlanır (Şekil 4.2). Gerotorların büyük çoğunluğu bu iki şekilde imal edilmekte ve kullanılmaktadır. Böylece dış çarkın imalatı tamamen basitleştirilmiş olmakta ve iç rotorun imalatı önem kazanmaktadır.

Şekil 4.1

Şekil 4.2

Dairesel profilli dış çark

Dış çarka ait dairesel profiller bir eğri ailesi olarak düşünülürse rotorun profili bu eğri ailesine ait zarf eğrisi olarak ortaya çıkar. Rotor profili bu dairelerin her birine bir noktada teğet olmak zorundadır. Mekanizmanın çalışması sırasında da bu durum böyledir, teğet olunan nokta sürekli yer değiştirir, fakat teğet sürekliliği devam eder.

Gerotor mekanizması çalışırken iç rotor döner ve dış rotoru da döndürür. Gerotor profilini oluşturan doğurucu eğri, Şekil 4.3 te kesikli çizgi ile gösterilen eğri olsun. Dış çarkı oluşturan dairesel profillerin iç rotora göre izafi hareketinde, merkezleri bu eğri üzerinde olmak üzere çevrede döndürüldüğü zaman dairelerin zarfı iç rotor profili olacaktır.

Şekil 4.3

Doğurucu eğri olarak Bölüm 3.1.’ de sözü edilen dalgalı episikloid eğrisi kullanılır, elde edilen profil episikloid esaslı gerotor profili olur. Dairelerin iç rotora göre izafi hareketi onun etrafında yaklaşarak ve uzaklaşarak dönmeleridir. Yani dairelerin merkezleri bu eğri üzerinde hareket ettirilerek, bunların zarfı olan eğri şeklinde rotor profili oluştuğuna göre, eğri üzerindeki her bir nokta, eğri ailesindeki bir daire merkezi koordinatı olur. Eğri denklemindeki (denklem 3.1) R/r oranı pratikte iç rotorun tamsayı olan diş sayısına eşittir. Buna göre diş sayısına z denilirse, denklem 3.4 ve 3.5’ den,

(

)

(

)θ

(

)

(

)

Buna göre dairelerin oluşturduğu eğri ailesinin denklemi, her bir dairenin yarıçapı g ise aşağıdaki gibi olur:

0 ) ( ) ( ) , , ( 2 2 2 = − − + − = x x y y g y x f θ _{e e} (4.3)

Bu denklemin yanı sıra zarf teorisine göre denklemdeki θ parametresine göre türev de sıfır olmalıdır. (Denklem 3.11)

=0 ∂ ∂ θ f 0 ) ( ) ( = ∂ ∂ − + ∂ ∂ − θ θ e e e e y y y x x x (4.4) e e x x ′ = ∂ ∂ θ ve e e y y ′ = ∂ ∂ θ denilirse, 0 ) ( ) (x−xe xe′ + y−ye ye′ = (4.5)

Denklem 4.3 ve 4.5 den ara işlemler yapılarak,

e e e e y x x x y y ′ ′ − − = − ) ( ) ( (4.6) 2 2 2 _{( )} ) ( g y x x x x x e e e e =      ′ ′ − + − (4.7) 2 2 2 ₁ ) ( g y x x x e e e =               ′ ′ + − (4.8)

Buradan x ve benzer şekilde y çözülerek zarf eğrisinin parametrik denklemleri aşağıdaki gibi elde edilir:

( )

( )

( )

( )

(

)

(

)θ

(

)

(

)θ

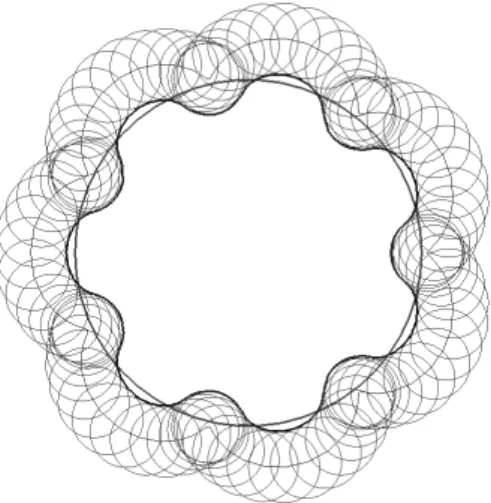
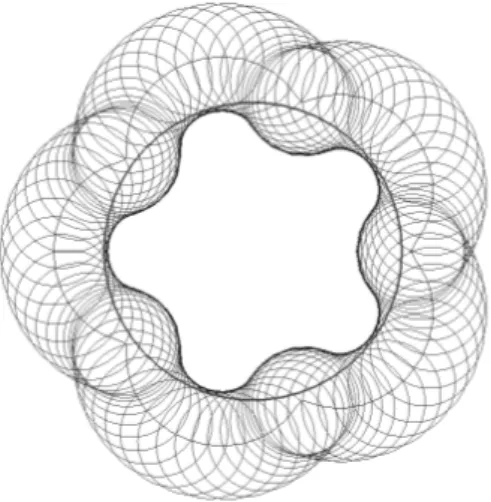
4.9 ve 4.10 denklemlerinde zarf eğrisinin dışbükey olarak elde edilmesi için ilkinde (-) işareti ve ikincisinde (+) işareti alınmalıdır. Böylece gerotor iç rotorunun profili için, zarf teorisi yardımıyla parametrik denklemler elde edilmiştir. Bu denklemler yardımıyla episikloid esaslı olmak üzere farklı boyutlara sahip tüm gerotor profilleri çizilebilir veya sayısal olarak hesaplanabilir. Bu sayısal veriler yardımıyla CNC tezgahlarında profili imal etmek mümkündür. Đki adet sayısal örnek Şekil 4.4 ve Şekil 4.5’ de görülmektedir.

5. EĞRĐLĐK YARIÇAPI ANALĐZĐ

Denklemi parametrik olarak verilen bir eğrinin herhangi bir noktasındaki eğrilik yarıçapı aşağıdaki bağıntıyla verilir. (Adams 2003)

( )

( )

[

]

Düzlemsel eğri x = x(θ) ve y = y(θ) şeklinde θ parametresi cinsinden verilmişse ( ' ) sembolü θ’ ya göre bir türevi gösterir. Bir gerotor için buradaki x ve y, gerotor profilini parametrik olarak veren denklem 4.9 ve 4.10 daki ifadelerdir. Denklemdeki türevler θ parametresine göre alınıp yerine konur ve eğrilik yarıçapı ifadesi elde edilir.

Eğrilik yarıçapının minimum ve maksimum olduğu noktalar denklem 5.1 den elde edilen eğrilik yarıçapı ifadesinin θ ya göre türevinin sıfıra eşitlenmesiyle bulunur. 0 = θ ρ d d (5.2)

Đfade oldukça uzun olduğu için Ek 1 de verilmiştir.

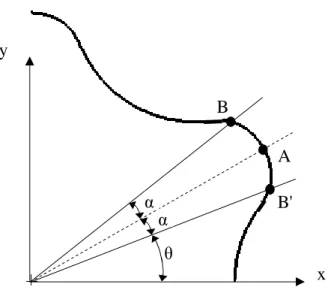
Eğrilik yarıçapının maksimum olduğu noktalar Şekil 5.1’ den de görülebileceği gibi, bir gerotor lobunun simetri ekseni üzerindeki A noktasıdır.

Minimum olduğu noktalar ise A noktasının sağında ve solunda birbirine göre simetrik olarak bulunurlar.(B ve B’ noktaları) Bu noktaların açısal konumları Denklem 5.2’ den sayısal olarak hesaplanabilir.

Şekil 5.1 Gerotor profilinde eğrilik yarıçapının minimum ve maksimum olduğu noktalar

Ek 1’ de verilen ifade oldukça uzun ve karışık olduğundan bu noktaların analitik olarak hesaplanması bir hayli zordur. Bu nedenle minimum eğrilik yarıçapı ve oluştuğu açısal konum sayısal olarak bulunmuştur. Örnek olarak, boyutları R = 35, r = 5, p = 3.7, g = 11 olan bir gerotor profilinde eğriliğin (k = 1/ρ) bir lobdaki değişimi Şekil 5.2’ de görülmektedir. Buradaki iki tepe noktası, şekildeki B ve B' noktalarına, bunlar arasındaki minimum nokta da A noktasına karşılık gelir.

Şekil 5.2: Yukarıdaki sayısal örnekte eğriliğin (1/ ρ) değişimi θ k α α B' B A θ x y

Bu sayısal değerlere göre θ = 10º açısal konumundaki B' noktasında minimum eğrilik yarıçapı yaklaşık ρmin ≈ 2.7 mm. olmaktadır. (Şekil 5.1)

Yukarıdaki sayısal örnekte, belli bir g değeri için, p parametresinin değişimi ile minimum eğrilik yarıçapının değişimi Şekil 5.3’ te görülmektedir. Değişim doğruya oldukça yakın bir parabol şeklindedir. Belli bir p değeri için, g parametresinin değişimi ile minimum eğrilik yarıçapının değişimi de Şekil 5.4’ te görülmektedir. Bu değişim oldukça doğrusaldır.

Şekil 5.3 p’nin değişimi ile minimum eğrilik yarıçapının değişimi. (R = 35, r = 5, g = 10 mm)

Şekil 5.4 g’nin değişimi ile minimum eğrilik yarıçapının değişimi. (R = 35, r = 5, p = 3.6 mm)

p ρmin

g ρmin

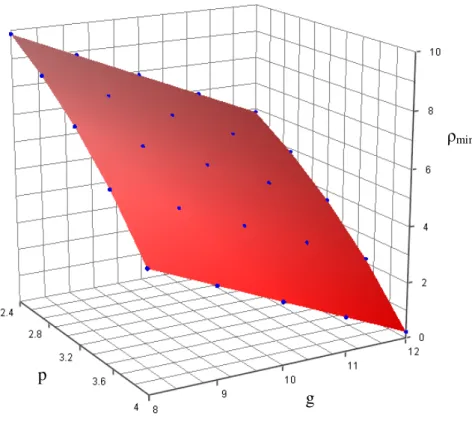
R = 35, r = 5 mm ölçüleri sabit bir gerotor profilinde, p ve g parametreleri değiştirilerek oluşan minimum eğrilik yarıçapının değişimi üç boyutlu olarak Şekil 5.5’ teki grafikte gösterilmiştir. Eğrisel yüzeyin oluşturulması için kullanılan noktalar grafikte görülmektedir. g ve p parametreleri şekilde gösterilen aralıkta değiştirilerek denklem 5.2’ den sayısal olarak bulunan ρmin değerleri şeklinde elde edilen bu

noktalar Tablo 1’ de verilmiştir.

Şekil 5.5 p ve g parametrelerinin değişimi ile ρmin’ in değişimi

Grafikte görüldüğü gibi g ve p parametrelerinin artmasıyla minimum eğrilik yarıçapı azalmaktadır.

p

g

p g ρmin 8 9.8673 9 8.8673 10 7.8673 11 6.8673 2.4 12 5.8673 8 8.8739 9 7.8739 10 6.8739 11 5.8739 2.8 12 4.8739 8 7.6494 9 6.6494 10 5.6494 11 4.6494 3.2 12 3.6494 8 6.1341 9 5.1341 10 4.1341 11 3.1341 3.6 12 2.1341 8 4.2202 9 3.2202 10 2.2202 11 1.2202 4 12 0.2202

6. HERTZ BASINCI

Herhangi bir eğrisel yüzeye sahip iki makine elemanı arasındaki teorik temas, noktasal veya çizgisel olduğu takdirde, dış kuvvetlerin etkisi altında meydana gelen şekil değiştirme sonucunda teorik temas noktası dairesel veya elips, teorik temas çizgisi ise dikdörtgen şeklini alır. Teknikte bu çeşit temaslara rulmanlarda, dişli çarklarda, sürtünme çarklarında ve kam mekanizmalarında çok rastlanır. (Kim ve ark. 2005). Temas yüzeyindeki basınçlar ve deformasyonlar Hertz teorisine göre hesaplanır. Bu teori şu kabulleri yapmaktadır:

- Temas yüzeylerinin boyutları temas eden parçaların diğer boyutlarına oranla oldukça küçüktür.

- Deformasyonlar, malzemelerin elastiklik sınırı içindedir. - Gerilme ve şekil değiştirmeler için Hooke kanunu geçerlidir. - Temas yüzeylerinde kayma gerilmesi yoktur.

Birbirine bir F kuvveti ile bastırılan eğrisel yüzeyli iki silindirik cisim arasındaki Hertz basıncı aşağıdaki bağıntı ile verilir (Akkurt 1996, Dijk 2001):

e H R H E F P π 2 = (6.1)

Burada H cisimlerin kalınlığı, E eşdeğer elastiklik modülü, Re eşdeğer eğrilik

yarıçapıdır. E ve R aşağıdaki bağıntılarla hesaplanır:

      + = 2 1 1 1 2 1 1 E E E (6.2) 2 1 1 1 1 ρ ρ + = e R (6.3)

Burada E1 ve E2 sırayla iki cismin malzemelerinin elastiklik modülü, ρ1 ve ρ2

ise temas noktasındaki eğrilik yarıçaplarıdır. Eğrilik yarıçapı; dışbükey durumda pozitif, içbükey durumda negatif olarak dikkate alınır. Gerotorlarda iç ve dış rotorun

kalınlığı her yerde aynıdır, yani bunlar silindirik olarak göz önüne alınıp Hertz basınçları denklem 6.1 deki ifade yardımıyla hesaplanmalıdır.

Gerotorlarda iç ve dış rotor sürekli olarak birbirleriyle temas halinde oldukları için temas noktalarında Hertz basınçları oluşur. Her iki rotorun da malzemeleri büyük çoğunlukla aynı olduğu için elastiklik modülleri aynıdır. Dış rotor dairesel bir kesite sahip olduğu için eğrilik yarıçapı değişmez, pim yarıçapına eşittir. Đç rotor profilinde ise, Şekil 6.1’ de görüldüğü gibi pimlerle temas halindeki profil noktalarının eğrilik yarıçapları farklı farklıdır, yani rotor profilinde eğrilik yarıçapı değişkendir. Rotora etki eden Hertz basıncı hesaplanırken en büyük değeri önemlidir, bu da denklem 6.1’ den de görülebileceği gibi Re’nin en küçük değerinde meydana

gelir. Denklem 6.3’ de ρ1 sabit olduğuna göre ρ2 nin en küçük değerinde Re minimum

olur, dolayısıyla Hertz basıncı maksimum değerini alır. Buna göre gerotor profili üzerinde eğrilik yarıçapının minimum olduğu nokta bulunarak bu noktada hesaplanacak Hertz basıncının dikkate alınması ve gerotor büyüklüğünün buna göre belirlenmesi gerekmektedir.

Şekil 6.1 Rotor profili ve pimlerin temas noktaları

Đç ve dış rotor malzemelerinin aynı olduğu düşünülerek eşdeğer elastiklik modülü E olarak alınır ve eşdeğer eğrilik yarıçapı Re denklem 6.’3 den hesaplanarak

denklem 6.1’ de yerine konulursa Hertz basıncı için aşağıdaki ifade bulunur.

min min 2 ) ( ρ π ρ g H g E F P_H = + (6.3)

7. GEROTOR DEBĐSĐ

Gerotor bir defa döndüğü zaman bir diş boşluğu kadar hacmi aktarır. Debi bu düşünceye göre hesaplanabilir. Şekil 7.1’ de görülen taralı alanın gerotor kalınlığı ile çarpımı bir devirde süpürülen teorik hacmi, bu değerin de devir sayısı ile çarpımı teorik debiyi verir. Kalınlık her yerde aynı olduğuna göre taralı alanın hesaplanması yeterlidir. Bu alan iki kısımdan oluşmaktadır. Birincisi dış rotora ait iki pim arasında kalan alan(A1), ki bu alan sabittir ve geometrik olarak kolayca hesaplanabilir. Đkincisi

gerotor profili ile pimlerin teğet dairesi arasında kalan alandır(A2), bu alan ancak bir

integral yardımı ile hesaplanabilir. Bir devirde süpürülen toplam alan bu iki alanın toplamına eşittir.

A = A1+A2 (7.1)

Şekil 7.1 Bir devirde süpürülen alan

Pimlerin teğet dairesi

A1

A2

Rg

Denklemi kutupsal olarak verilen bir eğri ile çevrili bir alanı veren integral aşağıdaki gibidir. (Adams 2003)

∫

Şekil 7.1 deki A2 alanı, Şekil 7.2 deki α açısının gördüğü daire diliminden,

denklem 7.2’ deki integralle hesaplanacak A3 alanının farkına eşittir. A3 alanı şekilde

görüldüğü gibi gerotor profilinin, iki lobunun tepe noktaları olan C ve C' arasında kalan kısmının sınırladığı alandır.

3 2 2 360 A R A =π _m α − (7.3)

Burada α açısı, C ve C' tepe noktalarını gören merkez açıdır, yani (θ2 − θ1) farkına

eşittir. Rm ise profilin en uç noktalarından geçen dairenin yarıçapıdır. (Rm=R+r+p)

(Şekil 7.2) C' C α θ2 A2 A3 θ1 Rm x

Denklem 7.2 deki ρ = ρ(θ) ifadesi gerotor profilinin kutupsal koordinatlardaki denklemidir ve aşağıdaki gibi yazılabilir.

2 2 y x + = ρ , ρ2 = x2 + y2 (7.4)

x ve y ifadeleri gerotor profilini parametrik olarak veren 4.9 ve 4.10 nolu denklemlerden yerine yazılarak, ara işlemlerden sonra aşağıdaki kutupsal profil denklemi elde edilir:

] cos ) 1 ( [ 2 cos 2 2 2 2 2 2 2 2

_θ

_θ

ρ

ρ2 ifadesi yerine konarak denklem 7.2 deki integral hesaplanırsa A3 alanı için

aşağıdaki ifade bulunur:

(

)

(

)

[

]

Denklemdeki EE ve EF, sayısal olarak hesaplanabilen E ve F tipinde eliptik integrallerdir. Bunların açık ifadeleri Ek 2 de verilmiştir.

A1 alanı Şekil 7.3 de görüldüğü gibi geometrik olarak şu şekilde

Ardışık iki pim merkezini gören γ merkez açısına sahip daire dilimi, yani şekildeki COD diliminin alanı hesaplandıktan sonra, OCF ve OGD eşit üçgenleri ile OFG üçgeninin alanları bundan çıkartılacak olursa CFGD alanı bulunmuş olur. COD daire diliminin alanından BOE daire diliminin alanını ve şekildeki gibi pim merkezinden α açısının gördüğü BCF ve GDE daire dilimleri ile yukarıdaki gibi hesaplanan CFGD alanını çıkartırsak BFGE alanını yani A1 alanını bulmuş oluruz.

Alanlar harflerle gösterilirse bu işlemler aşağıdaki gibi ifade edilebilir:

A1 = BFGE = OCD−OBE−EGD−BCF− (OCD−CFO−OGD−OGF) (7.7)

Parantez içerisindeki alanın CFGD alanı olduğu açıktır. Bütün bu alanların hesabı için gerekli olan γ, α, β açıları ve OB, BC ve OF uzunlukları gerotor geometrisinden kolayca bulunabilir. Hesaplama için kosinüs teoremi, sinüs teoremi ile üçgen ve daire ile ilgili geometrik bağıntılar kullanılmıştır.

Şekil 7.3 A1 alanı ve ilgili diğer alanlar

O C D B E F G γ α α γ' β β A2 A1

Sayısal bir örnek olarak R = 35 , r = 5, p = 3.7, g = 10 (mm) değerleri için z = 7 olur. Denklem 7.6 deki integralin sınırları, Şekil 7.3’ te profilin tepe noktaları olan B ve E noktalarına karşılık gelen merkez açılar olmak üzere θ1 = 2π/14 ve

θ2= 2π/14+2π/7 olarak yazılır. Bu sayısal değerlerle A1 ve A2 alanları aşağıdaki gibi

hesaplanmıştır:

A1 = 118.6770 mm2

A2 = 56.9404 mm2

Buna göre bir devirde süpürülen alan, A = A1 + A2 = 175.6174 mm2 olur.

Şekil 7.4 g nin değişimi ile süpürülen alanın değişimi (R = 35 , r = 5, p = 3.6 mm)

Şekil 7.5: p nin değişimi ile süpürülen alanın değişimi (R = 35 , r = 5, g = 10 mm) A

g

p A

R = 35, r = 5, g = 10 mm değerleri için p parametresinin değişimi ile süpürülen alanın değişimi Şekil 7.4’ de görülmektedir. Değişim oldukça doğrusaldır. R = 35 , r = 5, p = 3.6 mm değerleri için g parametresinin değişimi ile süpürülen alanın değişimi de Şekil 7.5’ de görülmektedir. Bu değişim doğruya oldukça yakın bir parabol şeklindedir.

R = 35, r = 5 ölçüleri sabit, p ve g ölçüleri değişken olan bir gerotor profilindeki süpürülen alanın değişimi Şekil 7.6’ daki üç boyutlu grafikte gösterilmiştir. Eğrisel yüzeyin oluşturulması için kullanılan noktalar grafikte görülmektedir. g ve p parametreleri şekilde gösterilen aralıkta değiştirilerek yukarıdaki denklemlerden sayısal olarak bulunan alan değerleri şeklinde elde edilen bu noktalar Tablo 2’ de verilmiştir. Grafikte görüldüğü gibi g’ nin artmasıyla A yaklaşık lineer olarak azalırken, p’ nin artmasıyla A artar.

Şekil 7.6 p ve g parametrelerinin değişimi ile süpürülen alanın (A) değişimi A

p

p g A 8 146.8751 9 136.4975 10 126.4458 11 116.6751 2.4 12 107.1521 8 168.2501 9 155.3673 10 142.9128 11 130.8244 2.8 12 119.0568 8 189.0155 9 173.3634 10 158.2589 11 143.6184 3.2 12 129.3814 8 209.0885 9 190.3669 10 172.3319 11 154.8728 3.6 12 137.9109 8 228.2368 9 206.0887 10 184.7896 11 164.1946 4 12 144.2025

8. OPTĐMĐZASYON

Genel bir tasarım sürecinde önce tasarım problemi tanımlanır, geliştirilir ve çözülmeye çalışılır. Böylece daha iyiyi, daha ucuza elde etme yolları aranır. Geçmişten günümüze geliştirilen optimizasyon teknikleri, birçok tasarım problemlerinin çözümünde kullanılagelmektedir. Özellikle bilgisayar teknolojisindeki gelişmelere paralel olarak bu uygulamalar çok daha kolaylaşmış ve yaygınlaşmıştır.

Optimal tasarım, mümkün tasarımların en iyisi olarak tanımlanabilir. Optimizasyon, arzulanan bir özelliğin maksimum yapılırken; arzulanmayanların minimum yapılması işlemi olarak tanımlanabilir. Genel bir optimizasyon sürecinde tasarımcı, bağımsız parametrelerin sayısal değerleri ile sabit olmayan genel kısıtlar oluşturur. Bağımsız değişkenler cinsinden tasarımın özelliklerini tanımlayan bir amaç fonksiyonu saptanır. (Börklü 2008)

Yaygın amaç fonksiyonları; maliyet, ağırlık, güvenilirlik ve üretilebilirlik gibi istekler olabilir. Amaç fonksiyonu, belirli kısıtlayıcılar tarafından sınırlandırılır. Sınırlayıcılar, fiziki kanunlar ve sınırlandırmalar veya bağımsız değişkenler üzerindeki uyumluluk şartlarından çıkmaktadır.

Genelde optimizasyon problem formülasyonunda bazı özellikler amaç fonksiyon olarak seçilirken; diğer bazı özellikler, kısıtlayıcılar konumuna dahil edilir. Kısıtlar ve amaç fonksiyonu matematiksel olarak ifade edilip, genellikle bilgisayar ortamında çeşitli yöntemlerle çözülür. Çözüm yöntemi optimizasyon probleminin lineer veya nonlineer olmasına göre farklılık ve çeşitlilik gösterir.

8.1 Gerotor Profilinin Optimizasyonu

Gerotor pompa veya motor mekanizmasının çalışması esnasında iç ve dış rotorun birbiriyle sürekli olarak temas etmesi sebebiyle, temas noktalarında Hertz basınçları oluşur. Basıncın şiddeti denklem 6.3’ de görüldüğü gibi temas kuvveti ile doğru orantılı, eğrilik yarıçapı ile ters orantılıdır. Küçük eğrilik yarıçapları, profilde sivriye yakın köşeler oluşmasına ve Hertz basıncının artmasına sebep olur. Eğrilik yarıçapının artması Hertz basıncını azaltır, fakat boyutları büyütür ve debiyi azaltır.

Ayrıca Hertz basıncının artması aşınmayı artırır (Kim ve ark. 2005), bu da gerotorun ömrünü azaltır. Uzun ömürlü bir mekanizma için debiyi azaltmayacak, fakat minimum eğrilik yarıçapının da makul değerlerde olmasını sağlayacak optimum bir çözüm bulunabilir.

Gerotor tasarımı yapılırken önce iç rotorun diş sayısı belirlenir. Bazı avantajlarından dolayı diş sayısı çoğunlukla tek sayı olarak seçilmektedir. (Dijk 2001) Dış rotorun diş sayısı da iç rotor diş sayısının bir fazlası olarak ortaya çıkar. Bundan sonraki aşama, seçilen diş sayısına bağlı olarak temel daire ve yuvarlanan daire yarıçapları R ve r nin belirlenmesidir. Bu değerler genellikle gerotor debisine ve diş sayısına bağlı olarak belirlenir ve diş sayısı değiştirilmedikçe bunların değişmesi söz konusu değildir. Bundan sonra p ve g parametrelerinin uygun olarak seçilip profilin oluşturulması gerekmektedir. Bu noktada optimizasyon problemi ortaya çıkmaktadır. Karşılaşılan en önemli kısıtlardan biri minimum eğrilik yarıçapı sınırlamasıdır. Diğer bir kısıt ise izin verilebilecek maksimum Hertz basıncı değeridir. Bu iki kısıt aslında birbirinden tamamen bağımsız değildir. Denklem 6.3’ te görüldüğü gibi maksimum Hertz basıncı (PH) değeri kullanılan malzemelere ve

çalışma basıncına bağlı olarak belirlendikten sonra profilde izin verilebilecek en küçük eğrilik yarıçapı ρmin hesaplanabilir. Fakat ifadede pim yarıçapı g’ de olduğu

için, debi de göz önünde tutularak g değeri belirlenmek zorundadır.

Profildeki en küçük eğrilik yarıçapı denklem 6.3’ ten hesaplanacak ρmin

değerinden büyük olmak zorundadır, bu ilk kısıt olarak yazılabilir.

ρ > ρmin (8.1)

Đkinci sınırlayıcı faktör, gerotorun debisidir. Debinin belli bir değerden küçük olmaması gerekir. Yukarıda 7. bölümde bulunan alan ifadesi gerotorun temel tasarım parametrelerinin (R, r, p, g) oldukça karışık bir fonksiyonudur. Sayısal bir debi değerinden bu parametreleri tahmin etmek oldukça zordur. Bu nedenle önce diş sayısı z ile R belirlenip p ve g parametreleri uygun şekilde alınarak debi hesaplanır. Arzu edilen debi değeri elde edilinceye kadar birkaç deneme yapmak gerekir. Seçilen temel boyutsal parametrelerle maksimum debi miktarının elde edilmesi bir amaç fonksiyonu olarak öne sürülebilir. Bu parametrelerin belli sayısal değerleri için

istenilen debi değeri elde edilmiş olsa bile bunun optimum bir çözüm olup olmadığını anlamak için debiyi veren alanın ve minimum eğrilik yarıçapının değişimini görmek gerekir. ρmin ve A parametrelerinin her ikisi de p ve g ye bağlı

olarak değiştikleri için değişim yüzeyi Bölüm 5 ve 7 de gösterildiği gibi üç boyutlu bir eğri olarak ortaya çıkar. Bu iki yüzeyin kesişmesi ile ortaya çıkan arakesit eğrisi optimum çözümleri verir. Debi eğrisi amaç fonksiyonunun, minimum eğrilik yarıçapı eğrisi ise kısıt fonksiyonunun değişimini göstermektedir. Dolayısıyla bu iki eğrinin arakesiti optimum çözüm eğrisi olacaktır.

Örnek olarak Şekil 5.5 ve 7.6’ daki grafiklerde sözü edilen aynı boyutsal parametrelere sahip gerotoru ele alalım. Bu iki grafiği aynı ölçekle ölçeklendirerek bir araya getirirsek Şekil 8.1’ deki grafiği elde ederiz. Yukarıdaki 8.1 denklemi bu grafikte kırmızı renkle gösterilen ρmin yüzeyinin üst kısmını ifade eder. Eğrinin

altındaki bölgede ρ < ρmin olacağı için burası uygun olmayan bölgedir. Yeşil renkle

gösterilen eğri p ve g değerlerine göre alanın değişimini göstermektedir. Đki yüzeyin arakesiti olan üç boyutlu eğri uygun çözümleri gösterir. Bu eğrinin sağ tarafında kalan noktalarda, alan, yani gerotor debisi artmasına karşın minimum eğrilik yarıçapı hızlı bir şekilde düşmektedir. Bu durum Hertz basıncının artmasına, yani gerotor ömrünün azalmasına neden olacağı için bu bölgenin uygun çözümler içermediği açıktır. Soldaki bölgede ise minimum eğrilik yarıçapı artmasına rağmen, alan yani debi azalmaktadır. Böylece arakesit eğrisi üzerindeki noktaların optimum çözümleri verdiği söylenebilir.

Şekil 8.1’ deki arakesit eğrisinin başlangıç noktası olan C noktasında sayısal olarak p = 3.05 ve g = 8 mm dir. Bu değerler için A = 181.3028 mm2 ve ρmin = 8.13

mm olarak hesaplanır. Arakesit eğrisinin bitiş noktası olan D noktasında sayısal olarak p = 2.75 ve g = 12 mm değerleri için A = 117.6523 mm2 ve ρmin = 5.01 mm

olarak hesaplanır. Eğer gerotor mekanizması bir pompa olarak kullanılacaksa, ilk çözüm alanın ve dolayısıyla debinin yüksek olması ve minimum eğrilik yarıçapının ve dolayısıyla Hertz basıncının düşük olması nedeniyle tercih edilebilir. Mekanizma bir hidrolik motor olarak kullanılacaksa ikinci çözüm debinin düşük olması nedeniyle, minimum eğrilik yarıçapının da ilk çözüme göre bir miktar küçük olması göz ardı edilerek uygun bir çözüm olarak düşünülebilir. Boyutsal parametreleri C noktasındaki gibi olan gerotor profili Şekil 8.2 de ölçekli olarak görülmektedir.

Şekil 8.1 p ve g parametrelerine göre süpürülen alanın (A) ve minimum eğrilik yarıçapının (ρmin) değişimi

Şekil 8.2 Örnek 1 de elde edilen optimum gerotor profili C D A g p ρmin

Arakesit eğrisi dışındaki çözümlere bir örnek verilecek olursa;

p = 3.6 ve g = 9 mm değerleri için A = 190.3669 mm2 ve ρmin = 5.13 mm

olarak bulunur. Burada C noktasındaki değerlere göre debi sadece % 5 artmış olmasına karşın minimum eğrilik yarıçapı ise % 36.9 oranında azalmıştır ve Hertz basıncı % 23.38 oranında artmıştır. Bu durum Hertz basıncı açısından hiç uygun bir çözüm değildir. Arakesit eğrisi dışındaki diğer noktalarda da benzer bir durumun oluşacağı görülebilir.

Şekil 8.3 p ve g parametrelerine göre süpürülen alanın (A) ve minimum eğrilik yarıçapının (ρmin) değişimi (R = 45 mm, r = 9 mm)

Đkinci bir sayısal örnek olarak R = 45 mm, r = 9 mm ve z = 5 şeklinde boyutsal parametrelere sahip olan gerotoru ele alalım. Bu gerotor için de örnek 1 deki üç boyutlu grafikleri çizip aynı ölçekle ölçeklendirerek bir araya getirirsek Şekil 8.3’ deki grafiği elde ederiz. Kırmızı renkli eğrisel yüzeyin altındaki bölge benzer

A p g E F ρmin

şekilde uygun olmayan bölgedir. Yeşil renkle gösterilen eğri p ve g değerlerine göre alanın değişimini gösterir. Burada da iki yüzeyin arakesiti olan üç boyutlu eğri uygun çözümleri gösterir. Bu eğrinin sağ tarafında kalan noktalarda, alan, yani gerotor debisi artmasına karşın minimum eğrilik yarıçapı hızlı bir şekilde düşmektedir. Sonuç olarak arakesit eğrisi üzerindeki noktaların optimum çözümleri verdiği söylenebilir.

Şekil 8.4 Örnek 2 de elde edilen optimum gerotor profili

Şekil 8.3 deki arakesit eğrisinin başlangıç noktası olan E noktasında sayısal olarak p = 6.05 ve g = 11 mm dir. Bu değerler için A = 752.9370 mm2 ve ρmin =

14.0813 mm olarak hesaplanır. Arakesit eğrisinin bitiş noktası olan F noktasında sayısal olarak p = 5.7 ve g = 15 mm değerleri için A = 575.2913 mm2 ve ρmin =

11.2172 mm olarak hesaplanır. Gerotor mekanizması bir pompa olarak kullanılacaksa, yukarıdakine benzer olarak ilk çözüm alanın ve dolayısıyla debinin yüksek olması ve ayrıca minimum eğrilik yarıçapının ve dolayısıyla Hertz basıncının

düşük olması nedeniyle tercih edilebilir. Mekanizma bir hidrolik motor olarak kullanılacaksa ikinci çözüm debinin düşük olması nedeniyle, minimum eğrilik yarıçapının da ilk çözüme göre bir miktar küçük olması göz ardı edilerek uygun bir çözüm olarak düşünülebilir. Bu örnek için boyutsal parametreleri F noktasındaki gibi olan gerotor profili Şekil 8.4’ de ölçekli olarak görülmektedir.

Arakesit eğrisi dışındaki çözümlere bir örnek olarak p = 6.8 ve g = 13 mm değerleri için A = 758.6490 mm2 ve ρmin = 9.1927 mm olarak bulunur. Burada E

noktasındaki değerlere göre debi sadece % 0.75 artmış olmasına karşın minimum eğrilik yarıçapı % 34.71 oranında azalmış ve Hertz basıncı % 12.81 oranında artmıştır. Bu durumun Hertz basıncı açısından uygun bir çözüm olmadığı açıktır. Bu örnekte de arakesit eğrisi dışındaki diğer noktalarda da benzer bir durumun oluşacağı görülebilir.

Diş sayısı daha fazla olan üçüncü bir sayısal örnek olarak R = 121 mm, r = 11 mm ve z = 11 şeklinde boyutsal parametrelere sahip gerotoru ele alalım. Bu gerotor için de örnek 1 deki üç boyutlu grafikleri çizip aynı ölçekle ölçeklendirerek bir araya getirirsek Şekil 8.5’ deki grafiği elde ederiz. Kırmızı renkli eğrisel yüzeyin altındaki bölge benzer şekilde uygun olmayan bölgedir. Yeşil renkle gösterilen eğri p ve g değerlerine göre alanın değişimini gösterir. Burada da iki yüzeyin arakesiti olan üç boyutlu eğri optimum çözümleri gösterir. Bu eğrinin sağ tarafında kalan noktalarda, alan, yani gerotor debisinin artmasına karşın minimum eğrilik yarıçapının hızlı bir şekilde düştüğü görülmektedir. Sonuç olarak arakesit eğrisi üzerindeki noktaların optimum çözümleri verdiği söylenebilir.

Şekil 8.5’ deki arakesit eğrisinin başlangıç noktası olan K noktasında sayısal olarak p = 7.2 ve g = 12 mm dir. Bu değerler için A = 1137.6358 mm2 ve ρmin =

24.6920 mm olarak hesaplanır. Arakesit eğrisinin bitiş noktası olan L noktasında sayısal olarak p = 6.6 ve g = 20 mm değerleri için A = 819.0685 mm2 ve ρmin =

18.8263 mm olarak hesaplanır. Gerotor mekanizması bir pompa olarak kullanılacaksa, yukarıdakine benzer olarak ilk çözüm alanın ve dolayısıyla debinin yüksek olması ve ayrıca minimum eğrilik yarıçapının ve dolayısıyla Hertz basıncının düşük olması nedeniyle tercih edilebilir. Mekanizma bir hidrolik motor olarak kullanılacaksa ikinci çözüm debinin düşük olması nedeniyle, minimum eğrilik

Şekil 8.5 p ve g parametrelerine göre süpürülen alanın (A) ve minimum eğrilik yarıçapının (ρmin) değişimi (R = 121 mm, r = 11 mm)

Şekil 8.6 Örnek 3 için elde edilen optimum gerotor profili A g p K L ρmin

yarıçapının da ilk çözüme göre bir miktar küçük olması göz ardı edilerek uygun bir çözüm olarak düşünülebilir.

Arakesit eğrisi dışındaki çözümlere bir örnek verilecek olursa;

p = 6 ve g = 16 mm değerleri için A = 855.2210 mm2 ve ρmin = 24.6774 mm

olarak bulunur. Burada K noktasındaki değerlere göre debi sadece % 24.82 azalmış olmasına karşın minimum eğrilik yarıçapı ise hemen hemen aynı kalmış ve Hertz basıncı bir miktar azalmıştır. Bu durum debi açısından uygun değildir. Eğrilik yarıçapı aynı kaldığına göre debinin büyük olduğu çözüm tercih edilir. Bu nokta yukarıdaki iki örnekten farklı olarak Şekil 8.5’ te de görülebileceği gibi arakesit eğrisinin solunda alınmıştır. Đlk iki örnekte olduğu gibi eğrinin sağında bir nokta alınırsa sonuç diğer örneklerdeki gibi olacaktır. Yine yukarıdaki iki sayısal örnekte de arakesit eğrisinin solunda bir nokta alınırsa bu örnekteki sonuca benzer bir sonuç elde edilmiştir. Böylece arakesit eğrisi dışındaki noktaların uygun çözümler vermediği görülmektedir.

9. SONUÇ VE ÖNERĐLER

Pozitif deplasmanlı bir pompa veya motor mekanizması olarak yaygın bir şekilde kullanılan gerotorların profilleri diğer hidrolik mekanizmalara nazaran farklılık arzeder. Bu çalışmada öncelikle zarf teorisi yardımıyla gerotor profili analitik olarak elde edilmiştir. Bu formülasyon yardımıyla profildeki minimum eğrilik yarıçapının nasıl bulunacağı gösterilmiştir. Gerotor geometrisi de göz önüne alınarak debi hesabına esas teşkil eden alan formülasyonu da yapılmıştır.

Hidrolik pompa ve motor olarak kullanılan gerotorlara ait boyutsal parametreler, esas olarak aktaracakları akışkanın hacmine göre tespit edilir. Aktarılacak akışkan hacmi yani debi belirlendikten sonra boyutsal parametreler kısıtlayıcılara bağlı olarak belirlenir. Gerotorlarda olduğu gibi birbiri ile sürekli temas halinde kalarak çalışan yüzeylerde sürekli bir aşınma sözkonusu olduğu için, sistemin uzun ömürlü olabilmesi adına bu aşınmayı oluşturan faktörleri mümkün olduğunca azaltmak gerekir. Gerotorlarda iç ve dış rotorun temas noktalarında oluşan Hertz basınçları eğrilik yarıçapıyla doğrudan ilgili olduğu için, bu basıncın azaltılabilmesi gerekir. Eğrilik yarıçapının küçük olması, Hertz basıncının artmasına ve dolayısıyla aşınmanın artmasına ve sistem ömrünün azalmasına yol açar. Eğrilik yarıçapının artması Hertz basıncının ve aşınmanın azalmasını sağlar, fakat sistemin boyutlarını büyütür ve debiyi azaltır.

Hem debinin istenilen seviyelerde olmasını sağlamak, hem de Hertz basıncının makul seviyelerde tutulmasını sağlamak için yapılan bu optimizasyon çalışmasında öncelikle gerotorun temel boyutsal parametreleri belirlenmiştir. Daha sonra gerotor profillerinin minimum eğrilik yarıçapları ve debiye esas teşkil eden alan hesapları yapılmış ve bunların değişimi üç boyutlu grafiklerde üç boyutlu yüzeyler olarak gösterilmiştir. Debi değişimini ve minimum eğrilik yarıçapı değişimini gösteren bu iki yüzeyin kesişimi ile oluşan arakesit eğrisinin optimum çözüm eğrisi olduğu belirlenmiştir.

Sonuçlar özetlenirse;

1. Bir gerotor için iki esas boyutsal parametre temel daire yarıçapı (R) ve yuvarlanan daire yarıçapı (r) dir. Bunlar belirlendikten sonra değiştirilmeleri

mümkün değildir, değiştirilebilecek iki parametre pim yarıçapı (g) ve ofset mesafesi (p) dir.

2. Profildeki minimum eğrilik yarıçapı ve debiye esas teşkil eden alan bu iki parametreye göre ortaya çıkmaktadır.

3. Gerotor debisi bir amaç fonksiyonu olarak düşünülebilir. Bunu kısıtlayan faktör ise minimum eğrilik yarıçapıdır.

4. Debinin ve minimum eğrilik yarıçapının g ve p parametrelerine göre değişimini ifade eden üç boyutlu yüzeylerin arakesit eğrisi optimum çözüm bölgesi olarak ortaya çıkmaktadır.

5. Bu arakesit eğrisi üzerinde amaca göre bir nokta seçilerek optimum gerotor profili elde edilir.

Daha ileri çalışmalarda optimal boyutları elde edilen bu profillere sahip gerotorların imal edilip, deneysel olarak debi, aşınma ve ömür açısından değerlendirilmesi düşünülebilir.

KAYNAKLAR

Hill, M. F. 1927. The Kinematics of Gerotor. Philadelphia.

Beard, J. E. 1985. Kinematic analysis of gerotor type pumps, enginees and compressors. Ph. D. Dissertaion, Purdue Univ.

Stryczek, J.,1990. Projektieren der Zykloidenverzahnungen Hydraulischer Verdrängermaschinen, Mech. Mach. Theory Vol. 25. No. 6, s. 597-610

Stryczek, J.,1992. Charakteristische Parameter Hydraulischer Verdrängermaschinen mit Zykloidenverzahnungen, Mech. Mach. Theory Vol. 28. No. 1, s. 97-112.

Kwon, S. M., Kim, M. S., Shin, J. H. 2008 Analytical wear model of a gerotor pump without hydrodynamic effect. J. of Advanced Mec. Des. Syst. and. Manufacture. Vol.2, no:2

Gamez. M., Javler, P., 2003. Contact stress in a gerotor pump, Universitat Politecnica de Catalunya, 08222 Terrassa, Spain, s. 65-71.

Tsay, C,B., Yu, C,Y.. 1989. Mathematical model for the profile of gerotor pumps. Natl Chiao Tung Univ, Hsinchu, Taiwan, s. 41-47.

Beard, J.E., Hall, A.S., Soedel, W.. 1991. Comparison of hypotrochoidal and epitrochoidal gerotors. Louisiana State Univ, Baton Rouge, LA, USA s. 133-141.

Söylemez, E., 2007. Mekanizma Tekniği. Birsen Yayınevi.

Irwin, E. 2003. What Is a Gerotor, Vian Enterprises, Inc. (http://www.vianenterprises.com/Gerotor.htm)

Adams, R.A., 2003. Calculus, Fifth Edition, Addison Wesley Longman.

Maiti, R. 1993. Torque characteristics of epitrochoid generated orbital rotary piston type hydraulic motors. Mech. Mach. Theory Vol. 28. No. 2, s. 225-231

Kim, N.H., Won, D., Burris, D., Holtkamp, B., Gessel, G.R., Swanson, P., Sawyer,W.G. 2005. Finite element analysis and experiments of metal/metal wear in oscillatory contacts. Wear, Vol. 258 s.1787–1793

Dijk, P.V., 2001. Contact Spots. ICEC Conf., s. 123-129

Mimi, G., Bonandrini, G., Rottenbacher C., 2007. Theoretical analysis of internal lobe pumps. 12th IFToMM World Congress, Besançon