Selçuk J. Appl. Math. Selçuk Journal of Vol. 8. No.2. pp. 13 - 23 , 2007 Applied Mathematics
Bending Analysis of Thick Orthotropic Sector Plates Using the Ex-tended Kantorovich Method
A. Rastgoo and H. Amirshaghaghi
Department of Mechanical Engineering, University of Tehran, Kargar shomali Ave., Tehran, Iran
e-mail:arastgo@ ut.ac.ir, h.am irshaghaghi@ m e.ut.ac.ir
Received : April 10, 2007
Summary.This study aims to demonstrate the applicability of the Extended Kantorovich Method (EKM) to obtain solution for two dimensional elasticity problems in cylindrical coordinate system. Bending of shear deformable thick orthotropic sector plates with clamped edges is considered for this purpose. Based on the first order shear deformation theory of Reissner, the governing equations of the plate in terms of deflection and rotations of the mid-plane include a system of three second-order partial differential equations (PDEs). Application of the EKM reduces the governing equation to a double set of ordi-nary differential equations (ODEs) in terms of r and . The resulting systems of ODEs are then solved iteratively until convergence is achieved. It is shown that the presented procedure can also be applied to the bending of rectangular plates by choosing sufficiently large values for inner and outer radii and small value for total angle of the sector. It is also demonstrated that the method provides suitably accurate results with very fast convergence for both sector and rectan-gular plates. Normally, four or five iterations are enough to get the final results with desired accuracy. The obtained results show good agreement with those of the commercial finite element code, ABAQUS and other published data. Key words:Extended Kantorovich Method; Bending analysis; Shear deforma-tion; Thick orthotropic sector plates.
1. Introduction
EKM was introduced by Kerr [1] to obtain approximate closed form solution for torsion of prismatic bar with rectangular cross section. Since then, it has been extensively used for various two dimensional elasticity problems in Cartesian coordinate system. For example one can refer to stress analysis of thin rectan-gular isotropic [2] and orthotropic [3] plates, bending of thick isotropic [4, 5] and
orthotropic [6] plates, eigen-value [7], vibration [8] and buckling [9,10] of rec-tangular plates. As it was discussed in other references, EKM provides solution to partial differential equations (PDEs) by reducing the PDE to a double set of ordinary differential equations (ODEs). In comparison with other numerical methods, EKM offers reasonably accurate results with minimum computational effort. Furthermore, EKM is among iterative methods with very fast conver-gence. Therefore, it would be of great interest to expand application of the method to some more problems than isotropic plates.
In this study, the method is employed to the bending of clamped shear de-formable thick orthotropic sector plates subjected to non-uniform loading. This was done after successful utilization of the method to obtain solution for bending of thin and thick isotropic sector plates [11,20]. Results show good agreement with finite element analysis.
In this study, the method is employed to the bending of clamped shear de-formable thick orthotropic sector plates subjected to non-uniform loading. This was done after successful utilization of the method to obtain solution for bending of thin and thick isotropic sector plates [11,20]. Results show good agreement with finite element analysis.
2. Analysis
2.1. Governing Equations
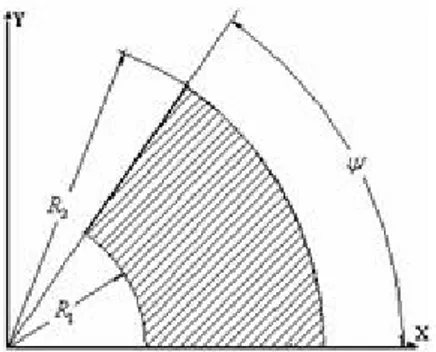
A moderately thick orthotropic annular sector plate with constant thickness , is considered. The geometry and coordinate system of the plate is shown in Figure 1.
Figure 1. Geometry of the plate
Based on the Reissner’s [12] first order shear deformation theory, the governing equations for the plate in terms of plate deflection, , and rotations around and direction and in Cartesian Coordinate system include a system of
(1) [+ +] + [1+12] + = 0 [1+ + ] − [2 +12]+ [1−12+12] − (+ )− [ (+ ) − (+ )]+ (+ )= 0 [12+12+] + [+1+ 1 +12+12] − (+ )+ (+ ) = 0
where is the applied transverse load on the upper surface of the plate and D,
D and D are plate constants defined as :
= 3 12(1−) = 3 12(1−) = 3 12
Boundary conditions for a thick clamped sector plate are:
(2) ( ) = ( ) = ( ) = 0
where (r,) is an arbitrary point on the boundary of the plate.
2.2. Solution procedure
Approximate solution to the governing PDEs (2) with appropriate boundary conditions (3) can be found with proper utilization of the EKM to convert the system (2) to a double set of ordinary differential equations (ODEs). The solution procedure will be completed by solving the obtained sets of ODEs either analytically or numerically in an iterative manner until convergence is achieved. Based on the EKM process, deflection and rotations of the plate could be considered as products of dimensionless functions of and as:
(3)
( ) = 1()1() ( ) = 2()2() ( ) = 3()3()
where () and () are unknown functions to be determined during the
(4) 1 1() ¡ 01()¢0+121()¨1() +12()(2())0 +13() ˙3() + = 0 −1 1()01() +12() ¡ 02()¢0+ 1− 222()¨2() − ¡ 1 + 1 2 ¢ 2()2()+ 1+ 2 03() ˙3() −32−23() ˙3() + = 0 −1 1() ˙1() +1+2 02() ˙2() + 32−22() ˙2()+ 1− 2 3() ¡ 03() ¢0 +123()¨3()− ¡ 1 + 1− 22 ¢ 3()3() + = 0
where 0and ˙ denotes derivation with respect to the r and nespectively. Values of are given in appendix.
To implement the boundary conditions (3) in the numerical scheme, we need to write them in terms of separable functions as:
(5) (1) = (2) = 0
(0) = () = 0 = 1 2 3
in where 1and 2 are inner and outer radii and is the total angle of the
sector plate.
Based on the general procedure of the weighted residual methods, both sides of each equation (5) should be multiplied by an appropriate weighting function of either or and after integration with respect to the same variable, or g,the first set of ODE will be obtained. For instance, 1(), 2() and 3()
are considered for the first, second and third equations, respectively. After integration with respect to gnd using integration by parts, one can obtain resulting ODE system as:
(6)
11¨1+ 1202+ 133+ 141+ 1501+ 162+ 17= 0
21¨3+ 2203+ 2302+ 243+ 252+ 261+ 27= 0
31¨2+ 3203+ 3302+ 3401+ 352+ 363+ 37= 0
where are defined in the Appendix 1 .
Repeating the same manner, this time using ()gs the weighting function and
multiplying it to the i_th equation of (7)and integrating over variable we obtain another set of ODE equations for () functions, as below:
(7) 11 1+ 12 2+ 132+ 14 1+ 15= 0 21 3+ 2+ 23 1+ 243+ 25= 0 31 2+ 32 1+ 332+ 341+ 35= 0
and are defined in the Appendix 1 too, and boundary conditions are given
() = (1() 2() 3()) () = (1() 2() 3()) Using central difference for derivatives
× −1+ × + × +1+ = 0
(8)
× −1+ × + × +1+ = 0
(9)
In equation’s (8) and (9) are three diagonal and could be solved by Thomas algorithm(TDMA).
3. Result and discussion
The procedure explained in previous section has been applied to an orthotropic plate, using: (10) 20 = = = 1010 = = 2 =5 = = 25 = 34
The plate dimension set to be 1 = 052 and =9wg. Now to start the
solution procedure we need to determine initial guesses first. Here we imple-mented equations (11) as the initial condition, which obviously do not satisfy the boundary condition.
Following functions have been implemented:
1() = (− 1)2
2() = 2 + (2) (11)
3() = (2)
Starting with equations(11) for op, new values of orp will result and iterative procedure will continue until a well converged solution is achieved. As could be seen in Fig.2 the convergence of EKM is rapid, and it could been deduced that unlike other weighted residual methods, in EKM initial guesses are arbitrary and are not necessary to satisfy the boundary data (2), which is due to iter-ative nature of EKM, where boundary conditions will be satisfied during the subsequent iterations.
Figure 2.Convergence of 1() and 1() using eqs.(11)
It should be noted that in Fig. 2, the difference between fifth and higher itera-tions were too small to be useful for graphical comparison.
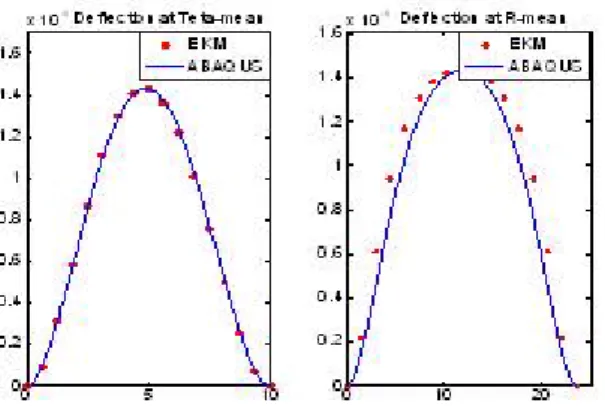
Furthermore, our literature review indicated that a great percent of previous investigations has been confined to analytical and numerical studies on deflection analysis of isotropic rectangular plates or orthotropic composite(multi-layer) plates, which could not be appropriate to validate our results[3-5,13-14]. As an alternative a deflection analysis was conducted on sector plate of equations (10), using finite element commercial software, ABAQUS, and the obtained results was compared with EKM results along &lines.These comparisons
have been done for three different plate thicknesses and results are presented in figures 3 − 5.
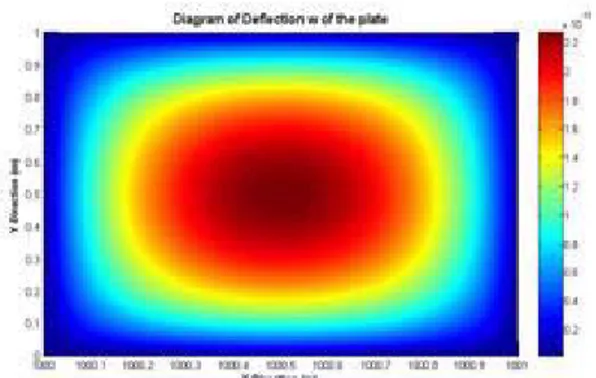
A careful look to these plots may reveal some slight deviation of EKM from those of ABAQUS, for ratios of thickness to radius () smaller than 120, which may cause due to violation of Reissner’s plate theory assumptions [12]. In addition, the method has been implemented for the particular case of isotropic rectangular plate using iso-plate properties and setting large inner and outer radiuses and proper sector angle. The obtained results are compared with Agh-dam[6] in Table 1. and deflection contours are shown in Fig. 6.
Figure 3. Comparison of plate deflection at & between EKM
and FEM for a 900 sector with 1= 052 and = 0052
Figure 4. Comparison of plate deflection at & between EKM
and FEM for a 900 sector with 1= 052 and = 052
Figure 5. Comparison of plate deflection at & between EKM
Table 1. Comparison of the results of the current work with the results of Aghdam et. al. [6] for the rectangular plate
Figure 6. Contours of displacementfor the case of rectangular plate with = 1
4.Conclusions
Bending of thick orthotropic sector plates was analyzed using the EKM. It was shown that convergence of the method is fast. The method is equally efficient for both single partial differential equation and system of equations and can easily be employed. For non-linear loading of circular plates, it is also possible to solve the resulting dual system of ordinary differential equations, (8) and (9), in a closed form manner, as it was done in [4] for the system of governing equations of laminated plates.
References
1.A. D. Kerr, An extension of the Kantorovich method, Quart Appl Math Vol 26, pp 219-229, 1968.
2.A. D.Kerr and H. Alexander, An application of the extended Kantorovich method to the stress analysis of a clamped rectangular plate, Acta Mech Vol 6, pp 180—196, 1968.
3.M. Dalaei and A.D.Kerr, Analysis of clamped rectangular orthotropic plates sub-jected to a uniform lateral load, Int J Mech Sci Vol 37, pp 527—535, 1995.
4.M.M. Aghdam, M. Shakeri and S.J. Fariborz, Solution to the Reissner plate with clamped edges, ASCE J Eng Mech Vol 122, pp 679—682, 1996.
5.S. Yuan, J. Yan and F.W. Williams, Bending analysis of Mindlin plates by extended Kantorovich method, ASCE J Eng Mech Vol 124 pp 1339—1345, 1998.
6.M.M. Aghdam and S.R. Falahatgar, Bending analysis of thick laminated plates using extended Kantorovich method, Composite Structures Vol 62 pp 279—283, 2003. 7.A.D. Kerr, An extended Kantorovich method for the solution of eigenvalue problems, Int J Solids Struct Vol 5, pp 559—572, 1969.
8.M. Dalaei and A.D. Kerr, Natural vibration analysis of clamped rectangular or-thotropic plates, J. Sounds &Vib., Vol 189 pp 399-406, 1996.
9.S. Yuan and Y. Jin, Computation of elastic buckling loads of rectangular thin plates using the extended Kantorovich method, Comp. Struct., Vol 66, pp 861-867, 1998. 10.M.Eisenberger and A. Alexandrov, Buckling loads of variable thickness thin isotropic plates, Thin Walled Structures, Vol 41, pp 871-889, 2003.
11.M.M. Aghdam and V. Erfanian, Application of Extended Kantorovich Method to bending analysis of sector plates, Proceedings of Int. Conf. on Computational Methods in Science and Engineering, pp 1-5, 2004
12.Reissner E. The effects of transverse shear deformation on bending of elastic plates, J. Applied Mechanics 1945;12:69—77.
13.E. Valot , P. Vannucci, Some exact solutions for fully orthotropic laminates, J. Composite Structures 69 (2005) 157—166
14.Two-dimensional solutions for orthotropic materials by the state space method, Composite Structures 78 (2007) 325—336
Appendix