Teknoloji Destekli Öğrenme Ortamlarında 11. Sınıf Öğrencilerinin Matematiksel Düşünme Süreçlerinin İncelenmesi

TEKNOLOJİ DESTEKLİ ÖĞRENME ORTAMLARINDA 11. SINIF

ÖĞRENCİLERİNİN MATEMATİKSEL DÜŞÜNME SÜREÇLERİNİN

İNCELENMESİ

Buğra YAĞDIRAN

YÜKSEKLİSANS TEZİ

MATEMATİK VE FEN BİLİMLERİ EĞİTİMİ ANABİLİM DALI

GAZİ ÜNİVERSİTESİ

EĞİTİM BİLİMLERİ ENSTİTÜSÜ

i

TELİF HAKKI VE TEZ FOTOKOPİ İZİN FORMU

Bu tezin tüm hakları saklıdır. Kaynak göstermek koşuluyla tezin teslim tarihinden itibaren ...(….) ay sonra tezden fotokopi çekilebilir.

YAZARIN

TEZİN

Türkçe Adı: Teknoloji Destekli Öğrenme Ortamlarında 11. Sınıf Öğrencilerinin Matematiksel Düşünme Süreçlerinin İncelenmesi

İngilizce Adı: Investıgatıon of Mathematıcal Thinking Processes of 11th Grade Students in Technology Supported Learning Environment

ii

ETİK İLKELERE UYGUNLUK BEYANI

Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu, yararlandığım tüm kaynakları kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dışındaki tüm ifadelerin şahsıma ait olduğunu beyan ederim.

Yazar Adı Soyadı: Buğra YAĞDIRAN İmza: ………..

iii

JÜRİ ONAY SAYFASI

Buğra YAĞDIRAN tarafından hazırlanan “Teknoloji Destekli Öğrenme Ortamlarında 11. Sınıf Öğrencilerinin Matematiksel Düşünme Süreçlerinin İncelenmesi” adlı tez çalışması aşağıdaki jüri tarafından oy birliği / oy çokluğu ile Gazi Üniversitesi Matematik ve Fen Bilimleri Eğitimi Anabilim Dalı’nda Yüksek Lisans tezi olarak kabul edilmiştir.

Danışman: Prof. Dr. Ziya ARGÜN ………..

(Matematik ve Fen Bilimleri Eğitimi Anabilim Dalı, Gazi Üniversitesi)

Üye: Prof. Dr. Yüksel DEDE ……….

(Matematik ve Fen Bilimleri Eğitimi Anabilim Dalı, Gazi Üniversitesi)

Üye: Yrd. Doç. Dr. Nurullah ŞİMŞEK ……….

(Matematik Öğretmenliği Anabilim Dalı, Kırıkkale Üniversitesi)

Tez Savunma Tarihi: 25/01/2018

Bu tezin Matematik ve Fen Bilimleri Eğitimi Anabilim Dalı’nda Yüksek Lisans tezi olması için şartları yerine getirdiğini onaylıyorum.

Unvan Ad Soyad

iv

v

TEŞEKKÜR

Bu çalışmanın tamamlanmasında onlarca insana teşekkür borçluyum. Çalışmanın başlangıç, süreç ve sonlandırılmasında görüş ve önerileri ile bana yardımcı olan, ilgisini ve desteğini hiçbir zaman benden esirgemeyen sayın hocam Prof. Dr. Ziya ARGÜN’e teşekkürlerimi sunarım.

Ayrıca tez çalışmam sırasında sorduğum soruları içtenlikle cevaplayan, bilgi birikimlerini benimle paylaşan ve tezimi okuma zahmetinde bulunan tüm hocalarıma ve arkadaşlarıma teşekkürü bir borç bilirim.

Tezimi detaylı bir şekilde inceleyip, verilerin kodlanma sürecinde yardımlarını esirgemeyen Sayın Araştırma Görevlisi Cansu BAKIRCI’ a teşekkür ederim.

Saygıdeğer jüri üyelerine değerli katılımlarından dolayı teşekkürlerimi sunarım.

Tüm hayatım boyunca bana verdikleri desteklerinden dolayı anneme ve babama; beni sürekli cesaretlendiren, benimle aynı heyecanları yaşayan ve her zaman yanımda olan kıymetli Ağabeyim Dr. Burak YAĞDIRAN’ a sonsuz teşekkürlerimi sunarım.

Buğra YAĞDIRAN Ankara,2018

vi

TEKNOLOJİ DESTEKLİ ÖĞRENME ORTAMLARINDA 11. SINIF

ÖĞRENCİLERİNİN MATEMATİKSEL DÜŞÜNME SÜREÇLERİNİN

İNCELENMESİ

(Yüksek Lisans Tezi)

Buğra YAĞDIRAN

GAZİ ÜNİVERSİTESİ

EĞİTİM BİLİMLERİ ENSTİTÜSÜ

Ocak,2018

ÖZ

Burton ve College (1984) nin belirtiği matematiksel düşünme işlem süreçlerine dayandırılan bu çalışmanın amacı, teknoloji destekli ortamlarda öğrencilerin matematiksel düşünme becerileri üzerindeki rolünü belirlemektir. Bu amaca ulaşabilmek için öğrencilere tablet kullanabilecekleri ve matematiksel düşünme süreçlerini gerçekleştirebilecekleri etkinlikler yöneltilmiştir. Bu yolla, (i) teknoloji kullanırken ve (ii) matematiksel durum etkinlikleri ile uğraşırken öğrencilerin matematiksel düşünme evrelerinde yaşanılan değişimler araştırılmıştır.

Bu araştırmanın deseni nitel araştırma yöntemlerinden durum çalışması araştırma yöntemidir. Araştırmanın katılımcıları, bir Anadolu Lisesinin sayısal ağırlıklı dersleri seçen 11. Sınıfta öğrenim gören 12 öğrenciden oluşmuştur. Bu çalışma, her hafta bir etkinlik uygulamak üzere 11 hafta sürmüştür. Veri toplama sürecinde iki adet görüşme, aktiviteler esnasında oluşturulan yazılı materyaller, tablet ekran kayıtları, sınıf içi video kayıtları, gözlem notları kullanılmıştır.

vii

Verilerin analizinde içerik analizi kullanılmıştır. Verilerin analizi sonucunda matematiksel düşünme evrelerinden özelleştirme evresinde teknoloji kullanımında zorluk yaşanmadığı, fakat ilerleyen evrelerde tablet kullanmakta zorlanıldığı belirlenmiştir. Bunun yanı sıra, matematiksel düşünme evrelerine göre teknoloji kullanıma amacının değiştiği belirlenmiştir. Özelleştirme ve genelleme evrelerinde düzgün şekiller çizme, örnek sayısını çoğaltmak, zaman kazanmak ve problemi daha iyi anlamak için kullanılırken; iddia etme ve ispat yapma aşamasında ise hatırlayamadıkları konuları internetten araştırmalar yaptıkları tespit edilmiştir. İddia etme ve ispat yapma evrelerinde aktif bir şekilde teknoloji kullanılmadığı belirlenmiştir. Araştırmadan elde edilen bulgular ışığında öğretmenlere, program geliştiricilere ve araştırmacılara bir takım öneriler sunulmuştur.

Anahtar Kelimeler: Matematiksel düşünme, teknoloji kullanımı. Sayfa Adedi:175

viii

INVESTIGATION OF MATHEMATICAL THINKING PROCESSES

OF 11TH GRADE STUDENTS IN TECHNOLOGY SUPPORTED

LEARNING ENVIRONMENT

(M.S. Thesis)

BUĞRA YAĞDIRAN

GAZI UNIVERSITY

GRADUATE SCHOOL OF EDUCATIONAL SCIENCES

January 2018

ABSTRACT

The aim of this work, which is based on the mathematical thinking processes of Burton and College (1984), is to determine the role of technology-based environments on students' mathematical thinking skills. In order to achieve this goal, students were able to use tablets and conduct mathematical thinking processes. In this way, we investigated the changes (if there are any) in the mathematical thinking stages of students while (i) using technology and (ii) dealing with mathematical situation activities.

This is a case study research which is the one of the qualitative research methods. Participants of the study consisted of 12 students studying in the 11th class who selected numerically weighted courses of an Anatolian Lisa. This study lasted 11 weeks to implement an activity every week. During the data collection process we used two interviews, written materials during the activities, tablet screen recordings, classroom video recordings, observation notes.

Content analysis was used in the analysis of the data. As a result of the analysis, it was determined that the mathematical thinking phase had no difficulty in using the technology

ix

in the specializing phase, but it was difficult to use the tablet in the later stages. Besides, it has been determined that the purpose of using technology is changed according to mathematical thinking stages. In specializing and generalizing stages, it is used to draw uniform shapes, to increase the number of samples, to save time and to better understand the problem; in the process of conjecturing and proving that they have been investigating the topics they cannot remember. It has been determined that technology is not actively used in the stages of conjecturing and proving. Some suggestions were presented to the teachers, program developers and researchers in the light of findings obtained from the research.

Key words: Mathematical thinking, use of technology.

Page Number: 175

x

İÇİNDEKİLER

TELİF HAKKI VE TEZ FOTOKOPİ İZİN FORMU ... i

ETİK İLKELERE UYGUNLUK BEYANI ... ii

JÜRİ ONAY SAYFASI ... iii

TEŞEKKÜR ... v

ÖZ ... vi

ABSTRACT ... viii

İÇİNDEKİLER ... x

TABLOLAR LİSTESİ ... xiii

ŞEKİLLER LİSTESİ ... xiv

BÖLÜM I ... 1

GİRİŞ ... 1

xi Sınırlılıklar ... 9 Tanımlar ... 10 Matematiksel Düşünme ... 10 Matematiksel Problem ... 10 Eğitim Teknolojisi ... 11

BÖLÜM II ... 12

İLGİLİ ARAŞTIRMALAR ... 12

Türk Müfredatında Matematiksel Düşünme ve Teknoloji Kullanımının Yeri 20

BÖLÜM III ... 24

YÖNTEM ... 24

Güvenirlik ve Geçerlik Çalışması ... 41

BÖLÜM IV ... 44

BULGULAR ... 44

xii

Özelleştirme Evresinde Eğitim TeknolojisiKullanımı ... 45

Genelleme Evresinde Eğitim Teknolojisinin Kullanımı ... 54

İddia Etme Evresinde Eğitim Teknolojisinin Kullanımı ... 60

İspat Etme (Doğrulama) Evresinde Eğitim Teknolojisi Kullanımı ... 66

Matematiksel Düşünme Evrelerini Kullanımı ... 72

“Özelleştirme” Evresinin Kullanımı ... 73

“Genelleme” Evresinin Kullanımı ... 81

“İddia Etme” Evresinin Kullanımı ... 90

“İspat Etme” Evresinin Kullanımı ... 100

BÖLÜM V ... 109

SONUÇ, TARTIŞMA ve ÖNERİLER ... 109

Sonuçlar ... 109

Teknoloji Destekli Ortamlarda Matematiksel Düşünme Evrelerindeki Eğitim Teknolojisi Kullanımına İlişkin Sonuçlar Ve Tartışmalar ... 110

Teknoloji Destekli Ortamlarda Öğrencilerin Matematiksel Düşünme Evreleri Nasıl Gerçekleştiğine İlişkin Sonuçlar Ve Tartışmalar ... 115

Öneriler ... 121

KAYNAKLAR ... 124

EKLER ... 130

EK 1. Araştırma İzin Yazısı ... 130

EK 3. Görüşme Soruları ve Kurguları ... 132

EK 4. Uygulanan Etkinliklerin Örnekleri ... 134

xiii

TABLOLAR LİSTESİ

Tablo 1. Katılımcıların Matematiksel Düşünme Süreçlerinde Bulundukları Basamaklar .. 26

Tablo 2. Matematiksel Durumların Seçilme Amaçları ... 29

Tablo 3. İlk Hazırlanan Etkinlik Örneği ... 31

Tablo 4. Pilot çalışma sonrası oluşan etkinlik örneği ... 32

Tablo 5. Etkinliklerde ki adımların amaçları ... 33

Tablo 6. Pilot çalışma öncesi hazırlanan etkinlik örneği ... 33

Tablo 7. Pilot çalışma sonrası hazırlanan etkinlik örneği ... 34

Tablo 8. Kategorileri oluşturma örneği ... 40

Tablo 9. Özelleştirme Evresinde Tablet Kullanımıyla İlgili Kodların Frekansları ... 46

Tablo 10. Genelleme Evresinde Eğitim teknolojisi Kullanımıyla İlgili Kodların Frekansları ... 55

Tablo 11. İddia Etme Evresinde Eğitim Teknolojisinin Kullanımıyla İlgili Kodların Frekansları ... 61

Tablo 12. İspat Etme Evresinde Eğitim Teknolojisi Kullanımıyla İlgili Kodların Frekansları ... 67

Tablo 13. “Özelleştirme” Evresinin Kullanımıyla İlgili Kodların Frekansları ... 74

Tablo 14. “Genelleme” Evresinin Kullanımıyla İlgili Kodların Frekansları ... 82

Tablo 15. “İddia Etme” Evresinin Kullanımıyla İlgili Kodların Frekansları ... 91

xiv

ŞEKİLLER LİSTESİ

Şekil 1. İddia etme döngüsü ... 14

Şekil 2. Özelleştirme evresinde tablet kullanım örneği ... 48

Şekil 3. Özelleştirme evresinde eğitim teknolojisini kullanmama örneği ... 53

Şekil 4. Genelleme evresinde eğitim teknolojisi kullanım örneği ... 56

Şekil 5. Genelleme evresinde eğitim teknolojisi kullanım örneği ... 58

Şekil 6. İspat yapma evresinde eğitim teknolojisi kullanım örneği ... 68

Şekil 7. İspat yapma evresinde eğitim teknolojisi kullanım örneği ... 69

Şekil 8. Özelleştirme evresini eğitim teknolojisi kullanmadan tamamlama örneği ... 76

Şekil 9. Özelleştirme evresini şekil çizmeden tamamlama örneği ... 77

Şekil 10. Özelleştirme evresinde eğitim teknolojisi kullanmadan özel örnek belirleme örneği ... 77

Şekil 11. Özelleştirme evresinde sistematik bir yol izleyerek özel örnek belirleme örneği 78 Şekil 12. Özelleştirme evresini tamamlayamama örneği ... 79

Şekil 13. Özelleştirme evresini atlama örneği ... 81

Şekil 14. Genelleme evresini sözel olarak ifade etme örneği... 84

Şekil 15. Genelleme evresini sözel olarak ifade etme örneği... 84

Şekil 16. Genelleme evresini sözel olarak ifade ederken yapılan yanlışlıklar örneği ... 85

Şekil 17. Genelleme evresini sözel olarak ifade ederken yapılan yanlışlıklar örneği ... 85

Şekil 18. Genelleme evresini sembolik olarak ifade etme örneği ... 86

Şekil 19. Genellme evresinde sembollik genelleme örneği ... 87

xv

Şekil 21. Sembolik genellemede yapılan yanlışlıklar örneği ... 87

Şekil 22. İddia etme evresini sözel olarak ifade etme örneği ... 93

Şekil 23. İddia etme evresini sözel ve sembolik olarak ifade etme örneği ... 94

Şekil 24. İddia etme evresini sözel olarak ifade edilirken sembolik olarak ifade edilememesi örneği. ... 94

Şekil 25. Sembolik olarak ifade edilebilecek iddia etme evresinin sözel olarak ifade edilemesi ... 95

Şekil 26. İddia etme evresini matematiksel olarak ifade etme örneği ... 96

Şekil 27. İddia etme evresini matematiksel olarak ifade etme örneği ... 96

Şekil 28. Matematiksel olarak ifade ettiği iddianın doğruluğunu kontrol etme örneği ... 97

Şekil 29. İddia etme evresini sembolik olarak ifade etme örneği ... 98

Şekil 30. Cebirsel olarak ispat etme örneği ... 101

Şekil 31. Cebirsel olarak ispat etmek için özel bir örnek verilme örneği ... 102

Şekil 32. Tümavarım yöntemiyle ispat yapma ... 103

Şekil 33. Doğrudan ispat yöntemi kullanılarak ispat yapma ... 104

Şekil 34. Geogebra kullanılarak ispat yapma ... 105

Şekil 35. Eğitim teknolojisi ve kağıt-kalemi eş zamanlı kullanarak ispat yapma ... 105

1

BÖLÜM I

GİRİŞ

Bulunduğumuz yüzyılda, teknoloji ve bilim baş döndürücü bir hızla ilerlemektedir. İçinde bulunduğumuz çağda çok fazla bilgiye sahip bireyler yerine bilgiyi kullanabilen, yorumlayabilen ve düşünme becerilerine sahip bireyler yetiştirmek hedeflenmektedir (Çelik, 2016). NCTM (2000) (National Council of Teachers of Mathematics) tarafından yayınlanan raporda günlük hayatta matematiği yorumlama ve kullanabilme ihtiyacı giderek arttığı ve birçok alanda matematiksel düşünme ve problem çözmeye daha çok ihtiyaç duyulduğu özellikle vurgulanmıştır. Bunun için ülkemizde 2006 yılında uygulanmaya başlayan ortaöğretim matematik dersi öğretim programında 2011 ve 2013 yıllarında düzenlemeler yapılmıştır. Yenilenen öğretim programı ile öğrencilerin matematiksel düşünme becerisini kazanma, yorumlama ve matematiğe karşı tutumlarında gelişme sağlanma, karşılaştıkları günlük yaşam problemlerinin üstesinden gelebilme, matematiği diğer disiplinler ile ilişkilendirebilmeleri hedeflenmiştir (Milli Eğitim Bakanlığı[MEB], 2011). Öğrencilerin matematiksel düşünme becerilerini kazanmış iyi bir şekilde problem çözebilen bireyler yetiştirilmesi amaçlanan programda, matematiksel kavramlara ve bu kavramlar arası ilişkilere dikkat çekilmiştir (MEB, 2013). Özellikle, matematiksel düşünme becerisi kazandırabilmek ve gerçek hayatla ilgili problemlere çözüm bulabilmek, matematik öğretiminde kazandırılması gereken temel özellikler olarak yer almıştır.

Matematiğin sadece işlem becerisi olarak görülmesi, bireyleri hesap makinesine dönüştürmekte (Alkan & Bukova, 2005) ve matematik öğretiminin temel amaçlarından olan akıl yürütme, problem çözme ve yaratıcı düşünme gibi becerilere sahip olmamasına sebep olmaktadır. Dolayısıyla yapılan araştırmalarda öğrencilere asıl zor gelen işlemsel beceriden daha ziyade programlarda yer alan matematiksel kavramlar ve bu kavramlar

2

arasındaki ilişkilerdir (Baki, 2008; Soylu & Soylu, 2006). İşlem becerisine yönelik matematik öğretiminde öğrenciler matematik ile günlük hayatı ilişkilendirememektedirler. Kişi günlük yaşamda düşünmeyi; beklenmedik bir olay, gözlem veya güçlükle karşılaştığında bu konuda aydınlanma, problemi çözme ya da beklentisine ters düşen konuda bilgilenmede kullanır (Yıldırım, 2004). Düşünme eyleminin gerçekleşebilmesi için bireyde merak ve heyecanın uyanması, gündelik hayattaki sorunların bireyleri zorlaması gerekmektedir. Bu “hal” içindeki kişi önce sorunla ilgili hipotez kurmalı ve daha sonra bu hipotezin doğruluğunu test etmelidir.

“Matematiksel düşünme” oldukça karmaşık ve ne olduğu tam olarak netleşmemiş bir kavramdır. Bu düşünme biçiminin tanımını netleştirebilmek amacıyla araştırmacılar bunun özelliklerini, işleyişini, bileşenlerini ve diğer düşünmelerden farkını belirleyebilmek için incelemelerde bulunmuşlardır. Literatür incelendiğinde araştırmacıların matematiksel düşünmenin bileşenlerini belirleyebilmek için yoğun bir çaba içerisinde bulundukları görülmektedir. Harel ve Sowder (2005) matematiksel düşünme kavramının daha kolay anlaşılabilmesi için matematiksel düşünmeyi inançlar, problem çözme yaklaşımları ve ispat etme şemaları olmak üzere üç bölüme ayırmıştır. Burton ve College (1984) matematiksel düşünme süreçlerini özelleştirme, genelleme, iddia etme ve ispatlama olmak üzere dört aşamada incelemiştir. Diğer taraftan, Alkan ve Bukova (2005) matematiksel düşünme işleyişi tahmin edebilme, örnekleme, genelleme, usa vurma, soyutlama, hipotez kurma, hipotezleri test etme, ispatlama olarak belirlenmiştir. Yıldırım (2004) da matematiksel düşünme sürecini sorunu açıklayıcı ya da giderici çözümü bulma veya oluşturma ve bulunan ya da oluşturulan çözümün doğruluğunu yoklama olarak ikiye ayırmıştır.

Yukarıdaki çalışmalarda matematiksel düşünme süreçleri benzerlik göstermektedir. Örneğin, Alkan ve Bukova (2005)’nin hipotez kurma olarak belirttiği kavram Burton ve College (1984)’nin çalışmasında iddia etme (Conjecturing) olarak ifade edilmiştir. Bu çalışmada matematiksel düşünme süreçlerinin incelenmesinin kolaylığı ve kullanışlılığı açısından Burton ve College (1984) nin belirtiği işlem süreçleri dikkate alınmıştır.

Matematiksel düşünme, problemlerin çözümünde direkt ya da dolaylı olarak matematiksel tekniklerin ve aşamaların uygulanmasıdır (Henderson vd. 2002). Bireyin çalışma alanı ve mesleği ne olursa olsun matematiksel düşünebilme yeteneğini kazanmış olması

3

gerekmektedir. Schoenfeld’e (1992) göre matematiksel düşümenin temeli, problem çözme stratejileri, matematiksel kavramaları ve tanımları etkili şekilde kullanma, matematiksel inanç ve tutuma sahip olma, matematiğe değer verme ve matematiksel işlemlere sahip olmak olarak belirtmiştir.

Öğretmen derslerde matematiksel düşünmeye önemseyip, mantıksal çıkarım yollarını ve farklı çözüm yollarını öğrencileriyle tartışıp ve sadece öğretmenin paylaştığı bilgileri tekrar etmek amacıyla yapılan ödevlerden sakınılarak matematiksel düşünme becerilerinin artırılması sağlanabilecektir(Baki, 2008). Öğrencilere problem çözme becerilerini artıracak ve düşünme becerileri kazandıracak ödevler verilmesiyle matematiksel düşünme becerilerinin artırılması sağlayacaktır. Böylece öğrencilere akıl yürütme becerilerini kullanma fırsatı verilmiş olur. Öğrencilerin matematiksel düşünmelerine önem verilmesi öğrenmeleri artırılabilecektir (Cooper, 2009). Sınıf ortamında öğrencilerin özgür düşünebileceği bir ortam ve kavramları öğrenip genel özellikleri oluşturmaya çalışırken matematiksel düşünmesini bir araç olarak kullanabileceği yaklaşımlar geliştirilmelidir (Alkan & Bukova, 2005).

Matematiksel düşünme, bireyin öğrenim derecesine ve yaşam biçimine göre değişiklik göstermektedir (Alkan & Bukova, 2005). Bunun için öğretmen dersinde bireyselleştirilmiş yaklaşımları kullanabilir. Öğretmen sınıfında öğrencilerin matematiksel düşünme seviyelerini bilerek dersini düzenlemelidir (Olkun & Toluk Uçar, 2004). Bu şekilde düzenlenen bir ders ortamında öğrencilerin düzeylerini geliştirecek bir öğrenme ortamı sağlanır.

Matematiksel düşünme becerisinin kazanılmasında etkili olan birçok faktör vardır. Bireyin matematiksel düşünmesini geliştirebilmek için problem çözmek tek başına yeterli değildir (Çelik, 2016). Teknolojinin hızlı bir şekilde ilerlediği dünyamızda kullanıldığı alanlardan birisi de eğitimdir. Teknolojik araçlar ile öğrenme sürecinde yeni yöntem ve teknikler kullanılmaya başlanmıştır. Eğitim teknolojilerinin, farklı becerilere sahip öğrencilere uygun olması, çok sayıda materyal bulunabilmesi, öğrencilerin derse ilgisini ve motivasyonun sağlanabilmesi ve zamandan tasarruf edilmesi gibi katkıları vardır (Mihalca & Miclea, 2007; Şimşek A. vd., 2008). Eğitimde teknoloji kullanımı ile bilginin görselleştirilmesi, soyut kavramları zihinde somutlaştırılması, dersi daha eğlenceli hale getirmesi gibi olumlu özelliklerinden bahsedilebilir (Baki, 2008; Tataroğlu & Erduran, 2010). Teknoloji yardımıyla öğrenci öğrenmenin merkezine geçer, öğrenmeyi

4

bireyselleştirmek ve derse karşı ilgiyi artması sağlanabilir. (MEB, 2011). Teknoloji sadece öğretimi destekleyen bir araç olarak görülmemeli, yeni öğretim, öğrenim deseni ve yaklaşımı ile eğitim sistemini etkilemektedir (Pamuk, Çakır, Ergün, Yılmaz, & Ayas, 2013). Birçok öğretmen eğitimde teknoloji kullanımının faydalı olacağını düşünmektedir (Çağıltay, Çakıroğlu, Çağıltay, & Çakıroğlu, 2001).

Öğrenme ortamında teknoloji kullanımı öğrenmeyi kolaylaştırır, zenginleştirir ve geliştirebilir (Van de Walle, Karen, & Bay-Williams, 2004). Bireysel farklılıklara göre ders işlenebilir, dönütler verilir, motive edilebilir ve her bir öğrencinin bireysel gelişimi için veri sağlanabilir. Bireyde yaşam boyu öğrenme inancı oluşturulur. Teknolojinin eğitimde sağladığı yenilikler, deneme, kontrol etme ve araştırma kolaylıklar matematiğin içeriğini, uğraş alanlarını geliştirmektedir (Baki, 2008). Bunun için Kasım 2010’da Fırsatları Artırma ve Teknolojiyi İyileştirme Hareketi (FATİH) projesi fırsat eşitliğini sağlamak amacıyla teknolojiyi öğrenme ve öğretme süreçlerinde kullanılması için tüm okullarda akıllı tahta, her öğrenciye tablet bilgisayar ve internet alt yapısı sağlanacağı duyurulmuştur. Fatih projesinin pilot uygulaması 2012 yılında başlamıştır. Bu proje ile değişen dünyaya ayak uydurabilen, donanımlı ve etkin bireyler yetiştirmek amaçlanmaktadır. Fatih projesi fırsat eşitliği ve bilişim teknolojisine erişim olanağı sağlamayı hedeflemektedir. Şu anda eğitim teknolojileri sınıflarda bulunmaktadır (Adıgüzel, Gürbulak, & Sarıçayır, 2011).

Eğitimde teknolojik destekler sağlanmasına rağmen hedeflenen amaçlara ulaşılamamıştır. Ekonomik İşbirliği ve Kalkınma Örgütü (OECD) tarafından yapılan 2016 Uluslararası Öğrenci Değerlendirme Raporu’nda (PISA) Türkiye’nin matematikte 44. sırandan 45. sıraya gerilediği sonucu yayınlandı (Özay, 2016). Türkiye’de Fatih projesi hayata geçirildiğinden itibaren uluslararası seviyelerde yapılan matematik okuryazarlığı sınavlarında gözle görülür bir değişiklik meydana gelmemiştir. Aksine matematiksel düşünme ve yorumlamada uluslararası sıralamada bir derece gerileme yaşanmıştır. Bunun nedeni teknolojinin amacına uygun şekilde kullanılmaması olduğu düşünülmektedir. Teknoloji bir okulda önemli değişiklik yaratabilir fakat tek başına yeterli değildir. Öğretmenler, öğrencilere yardım edebilecek teknoloji bilgisine sahip olup, öğrencilere rehberlik etmelidir.

Öğretim ortamında teknoloji kullanırken öğretmene büyük bir rol düşmektedir. Teknoloji kullanımının tam olarak amaçlarına ulaşılamamasının nedeni olarak öğretmenlerin

5

teknolojiyi sınıfta nasıl kullanacağını ve derse nasıl entegre edeceğini bilmemesi olarak ifade edilmektedir (Sheingold & Hadley, 1990). Bunun için öğretmenlere hizmet içi kurslar verilmeye başlanmış ve öğretmen adaylarına teknoloji kullanımı hakkında dersler verilmektedir (Adıgüzel, Gürbulak, & Sarıçayır, 2011). Teknolojik kaynaklar artırılmalı, e-içerik, video ve animasyonlara teknolojik ortamdan ulaşılabilmelidir. EBA (eğitim bilişim ağı) tarafından e-içeriklerin artırılması gerekmektedir (Pamuk, Çakır, Ergün, Yılmaz, & Ayas, 2013)

Matematik eğitiminde teknoloji 1960 lı yıllarda tartışılmaya başlanmıştır (Cedillo & Kieran, 2003). Matematik öğretiminde teknolojinin farklı rolleri vardır. Taylor (1980) de teknolojiyi matematik öğretiminde, öğretici, araç ve öğreten olarak üç rolde incelemiştir. Bilgisayar teknolojisinin matematik derslerine öğretme amacı değil de bir öğrenme aracı olarak kullanılması geleneksel öğrenme ortamını değiştirebilir ve geliştirebilir (MEB, 2011). Teknolojiyi daha çok bir araç olarak kullanılmasının öğrenme için faydalı olması beklenilmektedir.

Matematik eğitiminde teknolojinin önemli bir özelliği soyut kavramları somutlaştırmasıdır (Baki, 1996). Dolayısıyla teknoloji kullanımı ile grafik çizimleri ve hesaplamalar dışında matematik eğitimindeki problem çözme süreçlerinde de kullanılmaktadır. Öğrenci teknolojiyi problem çözen ve bilgi üreten bir araç olarak kullanabilmedir (Baki, 1996; Usta & Korkmaz, 2010). Öğrenciler teknoloji yardımıyla gündelik matematik problemler üzerine odaklanabilir ve uzun işlemlerle zaman kaybetmeyip yaratıcı düşünme ve akıl yürütme için daha fazla zaman kazanabilir.

Öğrenciler bilişim teknolojilerini; araştırma yapabileceği ve kendi bilgisini kullanabileceği bir araç olarak görmesi, matematik eğitiminde önemli değişiklikler yapacağı beklenmektedir (Papert, 1980). Öğrenciyi düşündürecek, kendi yaşam tecrübelerinden faydalanmasını sağlayacak ve bunları kullanırken teknolojiden yardım alacak şekilde etkinlikler oluşturulmalıdır. Öğretmen, öğrenmeyi kolaylaştırmak için teknoloji destekli bir ortamda öğrencinin kendi matematiksel bilgisini inşa edebileceği materyaller hazırlaması istenilmektedir. (MEB, 2011). Öğrencilere var olan bilgi doğrudan sunulmayıp, öğrencilerin matematiksel kavramlara ihtiyaç duyup çözüm için gerekli matematiksel kavramları kendileri bulmalıdır. Bu beklentinin hayata geçebilmesi için öğretmenlerin uygun ders planı ve etkinlikler düzenlemesi gerekmektedir. Teknolojinin öğrencilerin

6

öğrenmeleri üzerindeki etkilerini belirlemede, teknolojinin sınıf içi etkinliklere nasıl entegre edildiğini bilmek gerekir (Doerr & Pratt, 2008).

Öğrencinin amacı teknolojik aletleri kullanmak değildir. Çünkü matematik dersinde teknoloji kullanmanın gücü, kâğıt kalem tekniği ile bilgisayarın birleştirilmesiyle ortaya çıkacaktır (Davis & Fonger, 2014). Öğrenci teknolojiyi bir araç olarak görmeli kullanılacak yöntemlere de en az teknoloji kadar önem vermelidir (Dinçer, Şenkal , & Sezgin, 2012). Öğrenci teknoloji yardımıyla yaptığı matematiksel süreci, teknoloji kullanmadan da yapabilmelidir. Kullanılan teknoloji ile öğrenciler öğretmenin hazırladığı etkinliği tamamlarken bir yanda da etkinliğin temelindeki matematiksel anlamları bulabilirler (MEB, 2011).

Baki (1996) öğrencilerin teknolojilerden yararlanmaları için eğitimcilerin iki farklı yaklaşımla ders planı hazırlayabileceğini belirtmiştir. Birincisi, öğrenciler teknolojiyi verilen problemin çözümü için hesaplamalar veya grafik çizimi için kullanabilir. İkincisi ise teknolojinin araştırma ve deney aracı olarak kullanımına ilişkindir. Teknolojinin araştırma ve deney aracı olarak kullanılması öğrencilerin kendi bilgi ve düşüncelerini matematiğe uyarlayabilecektir (Baki, 1996). Bu şekilde hazırlanan ders planında öğrenci uzun işlemlerle zaman kaybetmeyecek, kusursuz çizilen grafikler ve şekillerle yorumlama yaparken zorlanmayacak ve gündelik hayatla ilgili problemleri teknoloji yardımıyla düşünebilecek, yorumlayacak ve çözüm önerisi üretebilecektir.

Düzenlenen ortaöğretim matematik ders programında teknolojinin bilinçli kullanımı ile öğrenci seviyeleri gözetmeksizin tüm öğrencilerin matematiksel düşünmeye ulaşabilmesi amaçlanmaktadır. (MEB, 2013). Teknolojinin bilinçli şekilde kullanımı ile matematiksel düşünmeyi becerilerinin artırılması için yapılacaklar tam olarak matematik ders programında ve bu konu ile ilgili yapılan ilgili araştırmalarda belirtilmemiştir.

Problem Durumu

Bu araştırmada, “teknoloji destekli öğrenme ortamlarının, 11. Sınıf öğrencilerin matematiksel düşünme becerileri üzerindeki rolü nasıldır?” sorusuna cevap aranacaktır. Bu problem durumu çerçevesinde aşağıda belirtilen alt problem cümlelerine cevap aranmıştır.

7

Alt Problemler

A) Teknoloji destekli ortamlarda matematiksel düşünme evrelerindeki eğitim teknolojisinin kullanımı nasıldır?

B) Teknoloji destekli ortamlarda öğrencilerin matematik durumlarında matematiksel düşünme süreçleri nasıl gerçekleşmektedir?

Araştırmanın Amacı

Bu araştırmada, teknoloji destekli ortamlarda 11. Sınıf öğrencilerin matematiksel düşünme süreçlerinin incelenmesi amaçlanmaktadır. Ortaya çıkan sonuçlardan eğitim öğretim kurumlarında görev yapan öğretmenlerin, matematik eğitimi araştırmacıların ve program geliştiricilerin faydalanması hedeflenmektedir. Böylece büyük bütçeler harcanarak eğitime entegre edilen teknolojik araçlar ile öğrencilerin matematiksel düşünme becerilerini artırabilmesi ve günümüz çağına uygun düşünebilen ve teknoloji kullanabilen bireyler yetişmesi sağlanabilir.

Araştırmanın Önemi

Toplumlar, özellikle de gelişmiş medeniyetler tarih boyunca matematiğe çok büyük ilgi göstermiştir (Merzbach & Boyer, 2011).Matematiğe gösterilen bu ilgi, matematiğin günlük yaşamdaki önemine vurgu yapmaktadır. . Günümüz dünyasında eleştirel düşünme, problem çözme ve teknoloji okur-yazarlığı gibi yeterliliklere sahip olmak gerekmektedir. Yapılan literatür taramasında teknoloji destekli öğrenme ortamlarının matematiksel düşünme becerileri üzerindeki etkileri belirten araştırmaların çok az olduğu gözlemlenmiştir. Yapılan araştırma tarzında 11. Sınıf öğrencilerin matematiksel düşünme süreçlerinin belirlenmesine yönelik çalışmalar yapılmıştır.( Arslan ve Yıldız, 2010; Keskin, Akbaba Dağ ve Altun, 2013). Bu araştırmada yapılan çalışmalardan farklı olarak eğitim teknolojisi kullanılabilen ve matematiksel düşünme süreçleri dikkate alınarak etkinlikler hazırlanmıştır. Böylece önceki araştırmalardan farklı olarak eğitim teknolojisinin

8

kullanımının matematiksel düşünme süreçlerine katkısı yönünden ilave bulgulara ulaşılmıştır.

Çağımızda bilişim teknolojisine dayalı ve daha fazla bilgisayar becerisine sahip bireyler yetiştirilmek istenmektedir. Eğitimde fırsat eşitliği gereği ve teknoloji kullanımı sağlanması için Fatih Projesi ülkemizde hayata geçirilmiştir. Fatih Projesinin amacına ulaşabilmesi için teknolojinin doğru şekilde kullanılması gerekmektedir. Bu araştırmada da fatih projesinin sınıflara sağladığı olanaklar (tablet, internet, eba, akıllı tahta vb.) kullanılarak, öğrencilerin bu kaynakları kullanma becerileri geliştirilmeye çalışılmıştır. Araştırmada öğrenciler problem çözerken tableti doğru yerde kullanımının önemli olduğunun farkına varmışlardır.

Fatih projesi kapsamında eğitim bilişim ağı geliştirilmiştir. Eğitim bilişim ağı (eba), kişinin ihtiyaç anında bilgi teknolojileri araçlarını kullanarak, etkili materyal kullanımını destekleyip teknolojinin eğitime entegrasyonunu sağlamak amacıyla oluşturulmuş bir platformdur. EBA, içeriği her geçen gün genişletilmekte öğretmen ve öğrencilerin bilgi paylaşımı yapabileceği, öğrencilere dönütler verilebileceği ve öğrencilerin teknoloji kullanımının takip edilebileceği bir ortam sağlanmaktadır. Bu proje alt yapısı ve uygulanması için yüksek bütçeler ve zaman ayrılmıştır. Yapılan bu araştırma ile harcanan maddi ve manevi emeklerin karşılığının, amaçlanan şekilde alınabilmesi için katkı sağladığı düşünülmektedir.

Her öğrencinin kendi seviyesine göre matematiksel düşünme ve problem çözme becerisine sahip olması beklenmektedir. Bu sayede gündelik hayatta karşılaştıkları sorunların üstesinden gelebileceklerdir. Matematik öğretiminde matematik işlemleri anlaşılması zor değildir, öğrencilere soruyu anlayıp yorumlama kısmı daha zor gelmektedir. Bu çalışma ile öğrencinin matematiksel yorumlamalarını artırmak için neler yapılacağı belirlenmeye çalışılmıştır. Böylece okulda öğrendiği bilgileri ilerde unutmayacak ya da hafızasında boşuna yer kaplamayacak hayatının bir yerinde kullanacaktır.

Bu çalışmada, matematik derslerinde teknoloji kullanımının ne gibi katkıları olduğu belirlenmeye çalışılıp öğrencilerin belirlenen katkılar sayesinde teknolojiyi daha işlevsel kullanmasında yardımcı olacaktır. Ayrıca teknolojinin kullanıldığı sınıflarda matematiksel düşünmeye katkılarının neler olduğu araştırılmıştır. Öğrencilerin kullandıkları teknolojilerin matematiksel alt yapısının farkında olup olmamalarının belirlenmesinin ne

9

gibi yararları olacağı hakkında literatüre katkılar sağlanması, uluslararası sınavlarda Türkiye’nin başarısının artması için teknolojinin doğru kullanımı konusuna ışık tutulması beklenmektedir. Bunun bir sonucu olarak, devlet bütçesinden büyük paralar harcanarak başlatılan Fatih projesinin amaçlarına ulaşmasında bir nebze katkı sağlanması düşünülmektedir.

Varsayımlar

Bu çalışma aşağıda verilen varsayımlar üzerine kuruludur;

Teknoloji kullanımının matematiksel düşünme becerilerine rolü bu konu üzerinde hazırlanılan etkinlikler ile belirlenebilir.

Matematiksel düşünme süreçlerinin kullanılması matematiksel durumlar ile sağlanabilir.

Sınırlılıklar

Bu araştırma,

Erzincan İline ait ilçelerden birinde bulunan bir Anadolu Lisesi’nde öğrenim gören 11. sınıf öğrenci grubu ile gerçekleştirilen 11 haftalık uygulamalarla sınırlıdır ve genellenemez.

Araştırma esnasında öğrencilerin yazılı sınavlarının başlamış olması ve hava koşulları gibi etkiler nedeniyle bazı etkinliklere eksik katılımlar gerçekleşmiş. Fakat uygulama sürecinde ki bu eksiklikler göz ardı edilerek veri analizi yapılmıştır.

Araştırma sırasında tablet ekran kayıtlarının videosu alınamadığından katılımcılardan yaptıkları işlemlerden sonra ekran resimlerini almaları istenilmiştir. Ayrıca aldıkları ekran resimlerini mail yoluyla araştırmacıya atmaları istenilmiştir.

10

Tanımlar

Matematiksel Düşünme

Matematiksel düşünme matematiksel işlem, kavram ve yöntemleri problem çözme süreçlerinde dolaylı veya doğrudan kullanmak seklinde tanımlanabilir (Henderson vd., 2002).

Matematiksel düşünme üzerinde bütün matematik eğitimcileri tarafından uzlaşılmış bir tanım henüz yoktur. Matematik eğitimi araştırmalarında matematiksel düşünmeyi açıklamaya çalışan iki farklı temel görüş bulunmaktadır. Birinci görüş matematiksel düşünmenin “soyutlama, genelleme ve ispatlar yapma” olduğu, ikinci görüş de “matematiksel kavramların gelişimi” olduğu yönündedir (Çelik, 2016).

Alkan ve Bukova (2005) matematiksel düşünmeyi “tahmin etme, genelleme, varsayımda bulunda düşünme ve ispatlama ile yeni bir bilgiye ya da kavrama ulaşması olarak ele almışlardır (Alkan & Bukova, 2005).

Matematiksel düşünmeyi normal düşünmeden ayıran farklar ise matematiksel düşünmede sonuç ve kesinlik olması gerektiğidir (Umay, 2003).

Burton ve College (1984), Matematiksel düşünme sadece matematiksel nesneler üzerinde düşünme olmadığını ve matematiksel düşünmeyi işlemler, süreçler ve dinamikler şeklinde üç başlıkta tanımlamışlardır. Bu tanımların detaylı açıklaması ilgili araştırmalar bölümünde bahsedilmektedir.

Matematiksel Problem

Problem kelimesinin anlamı “aşılması, çözülmesi veya uğraşılması gereken bir durum” anlamında kullanılmaktadır. “Matematiksel problem” ise matematiksel dilde sunulabilen, analiz edilebilen belki de matematiksel yollarla çözülebilen matematiksel durumlardır (Özsoy, 2005). Bilimsel bir konuda açık bir şekilde tasarlanan fakat hemen ulaşılamayan bir sonucu elde etmek için bilinçli bir şekilde yapılan araştırmalardır (Özsoy, 2005).

11

Eğitim Teknolojisi

Farklı bilimlerin, yöntem, araç, gereç ve değerlendirme gibi eğitimin geniş bir alanında uygulanabilen, insan gücünü en verimli şekilde kullanılmasını, ortaya çıkan sorunların çözülmesini, verimliliğin artmasını sağlayan bir sistem bütünüdür. (Güngör, 2016). Kısacası eğitim teknolojisi, öğretme süreçlerinin düzenlenmesi, hayata geçirilmesi ve geliştirilmesi sürecidir. Eğitim teknolojisi başlangıçta araç-gereç olarak görülse de günümüzde bu tanımından uzaklaşmış insan- teknoloji etkileşiminden performans teknolojilerine kadar birçok konuyu kapsayan bir disiplin haline gelmiştir (Şimşek vd., 2008).

Eğitim teknolojisinin çok genel bir tanımı vardır fakat bu araştırmada eğitim teknolojisi; dinamik matematik programları, hesap makinası kullanımı ve internetten araştırmalar yapmak olarak kabul edilmiştir. Bu çalışma boyunca eğitim teknolojisi olarak isimlendirilen yerlerde bu üç özellik kullanımından bahsedilmektedir.

12

BÖLÜM II

İLGİLİ ARAŞTIRMALAR

Matematiksel Düşünme

Matematiksel düşünme konusunda ulusal ve uluslararası düzeyde birçok çalışma (Alkan & Bukova, 2005; Arslan & Yıldız, 2010; Burton & College, 1984; Çelik, 2016; Ersoy & Başer, 2013; Harel & Sowder, 2005; Henderson vd., 2002; Keskin, Akbaba Dağ, & Altun, 2013; Umay, 2003; Yıldırım, 2004) yapılmıştır.

Burton ve College (1984), matematiksel düşünmenin tanımı belirlemek için çalışılmıştır. Matematiksel düşünme sadece matematiksel nesneler üzerinde düşünme demek değildir. Matematiksel düşünmenin kendine özgü bazı yöntemleri bulunmaktadır. Bu yöntemler, matematiksel düşünmenin işlemleri, süreçleri ve dinamikleri şeklinde üç başlıkta tanımlanmıştır. Matematiksel düşünmenin işlemleri, bireyi karşılaştığı zaman düşünmeye teşvik eden herhangi bir olay, gözlem veya fikir ile yapılabilir. Matematiksel düşünme süreçleri, özelleştirme, genelleme, iddia etme ve ispat etmedir. Bu yöntemde tümevarımsal veya tümdengelimsel bir yol izlenir. Matematiksel düşünmenin dinamikleri, durum üzerinde çalışmak, ilişkiyi anlamak ve ürünü ortaya koymak olarak belirtilmiştir. Bu süreç sarmal bir model olarak temsil edilmiştir. Bu aşamalar ve bu aşamaların özellikleri verilen kaynaklar temel alınarak aşağıda açıklanmıştır.

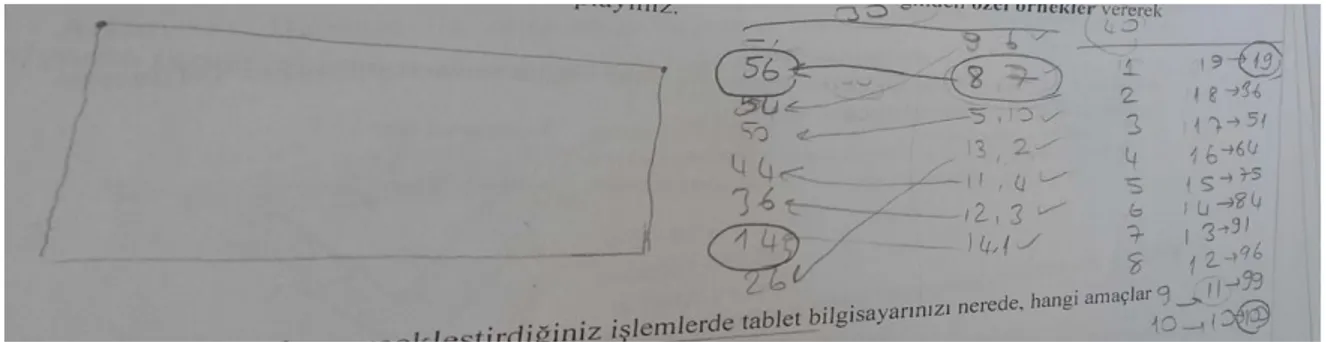
Özelleme: Bireyin bir durum veya problem hakkında sistematik veya rastgele özel örnekler vererek bu durum veya problem hakkında bir bilgiye sahip olmasıdır (Burton & College, 1984). Seçilen örnekler rastgele ve sorunun çözümü için iyi belirlenmiş olmalıdır. Soru veya problemlerle ilgili örnekler incelenmesi verilen problemin anlaşılmasını kolaylaştırır. Öğrencilerin doğal öğrenmeleri sağlanabilir ve tümevarımsal yaklaşımın kazanılmasında

13

bir başlangıç aşaması olur (Burton & College, 1984). Böylece anlaşılması zor olan bir problem daha kolay yorumlanabilir.

Genelleme: Verilen özel örnekler yardımıyla modelin tanımlanması veya düzenin ortaya çıkmasını ifade eder (Burton & College, 1984). Problemlerin geniş bir durumu hakkında örnekler yardımıyla tahminler yapılmaktadır (Mason, Burton, & Stacey, 1985). Genellemede belli sayıda örnekler çözülerek problem hakkında bir kanıya varılmaya çalışılır. Bu durum genellemenin yapılabilmesi için özelleştirmenin de yapılması gerektiğini göstermektedir. Genellemenin başlangıcında eğer ifade edilen problemler çözülemezse verilen problemle ilgili bir modelin sezilmesi gerekmektedir. Daha sonra hesaplamalar için bir çözüm bulunmuş olur ve bu hesaplama sırasında herhangi bir sıkıntı yaşanmaz (Mason, Burton, & Stacey, 1985). Oluşturulan bu temel model genellemedir. Soyutlama bilişsel yapının yeniden oluşturulması ve matematiksel yapılardan zihinsel yapıların oluşturulmasıdır (Biber & Argün, 2012). Soyutlama yardımıyla öğrenci çevresinde veya yaşantısında karşılaştığı durumları bildiği matematiksel yapılara uyarlayabilecektir. Öğrenciler verilen bir problemle ilgili sezdiği modelden yola çıkarak soyutlama yapması da beklenir. Genelleme aşamasında zorluklar yaşanıyorsa soyutlamada da sıkıntı yaşanacaktır (Alkan & Bukova, 2005). Eğer bir öğrencinin matematiksel genelleme ve soyutlama becerisi gelişirse matematiksel düşünme becerisinde de ilerleme sağlanır (Biber & Argün, 2012).

İddia Etme (Conjecturing): Yeteri kadar örnek incelendiği zaman öğrenci bir iddia da bulunabilir. İddia etme sayesinde genellemede belirlenen model araştırılır, ifade edilir ve örneklerle doğru olup olmadığı gösterilir (Burton & College, 1984). Fakat verilen modelin doğruluğu kesin olarak bilinemez. . İddianın yanlış olduğu tespit edilirse ya değişiklikler yapılır ya da yeni bir iddia ortaya koyulur (Mason, Burton, & Stacey, 1985). Mason, Burton ve Stacey (1985) iddia etmeyi döngüsel bir süreçte açıklamışlardır. İddia etme döngüsü Şekil 1 de gösterilmiştir.

14 Şekil 1. İddia etme döngüsü

Kişi iddiasını mantıklı gerekçelere dayandırıp bu iddianın doğruluğunu sezmelidir. Söylemlerinin doğru olup olmadığını belirlemek için örnekler vermelidir. Seçilen örneklerin tüm durumları kapsayacak şekilde olması gerekmektedir. Çeşitli örnekler vererek iddiayı çürütmeye çalışılsa da kişi iddiasına bu aşamada güvenmelidir. Neden doğru olduğunu veya düzeltilme gerekliyse nerelerde düzeltme yapılacağını belirlemek için yeni örnekler verilir. Eğer kişi iddiasını düzeltemiyorsa farklı bir iddia ortaya atar. İddia etmede, bu şekilde döngüsel bir süreç devam etmektedir.

İspat Etme: İddia edilen bir durumun neden olduğunu görmek kolaydır fakat niçin doğru olduğunu söylemek oldukça zordur (Mason, Burton, & Stacey, 1985). Niçin sorusuna cevap vermek tüm ifadeler için tatmin edici gerekçeyi söylemektedir. Bunun için de en önemli kriter ispat etmedir. İspat etme ve gerekçelerin denetlenmesi son derece zordur. Kişi önce kendini, daha sonra yakın arkadaşını ve en son olarak da başkalarını ikna etmelidir (Mason, Burton, & Stacey, 1985). Kişinin kendini ikna etmesi kolaydır, gerekli açıklamalar ve dayandırmalar yaptığı sürece kendini ikna etmesi için yeterlidir. Arkadaşını ikna etmeye çalışırsa kişinin doğru olduğunu düşündüğü şeyleri açık bir şekilde açıklaması yeterli olacaktır. Karşısındakini ikna etme sürecinde ise kişi her söylemini ve delilini eleştiren kişiye karşı ispatını açıklamaya çalışacaktır. Dolayısıyla kişi her söylemini eleştiren bir kişiye karşı cevap verebilecek başka kanılara dayandırabilmesi gerekmektedir. İspat etme süreci genellemelerin kişiselden evrensele ilerlemesi anlamına gelmektedir (Burton & College, 1984).

İddianın

ifade

edilmesi

iddianın

kontrol

edilmesi

Önerilen

iddiaya

güvenme

15

Yukarıdaki açıklamalardan matematiksel düşünmenin bir süreç olduğu görülmektedir. Matematiksel düşünme, günlük ve bilimsel düşünmeden farklı değildir. Matematiksel düşünme insanların günlük hayatı daha iyi anlayabilmeleri ve onlara bağlı olarak eylemler yapabilmesi için kullandığı bir araçtır (Burton & College, 1984; Çelik, 2016). Herhangi bir alana veya mesleğe özgü problemlerde de kullanılabilir. Matematiğin doğası gereği matematikle ilgili olmayan sorunlar ya da problemlerde de matematiksel düşünme kullanır. Tall (1995), çalışmada ilköğretime başlangıçlarından üniversite lisans matematiğine ve matematiksel araştırmalara kadar olan matematiksel düşünme gelişimine değinilmektedir. Çalışmada, kişinin çevresindeki nesnelerin, algılanması (perceptions of) ve eyleme (actions on) geçmesi ile matematiksel gelişimin başladığı varsayımında bulunulmuştur. Nesnelerin algılanma başarısında, Van Hiele’nin görsel-uzamsal temsilleri ile geometri ispatında artan sözlü destekler öncülük eder. Nesnelerin eylemlerindeki başarısında, aritmetik ve cebirde düşünme gerektiren kavramlar ve süreçlerin esnek sembolik temsilleri kullanır. Yapılan araştırmanın temeli, matematiksel düşünmenin bilişsel yapısı, bilişsel yapının kavramsal şekilleri kavramsal yapıyı yeniden formülüze eder ve inşa edilen formülüze kavram matematiksel bilgiyi paylaşan sistematik yapıyı parçaladığında matematiksel düşünme gelişmeye başlar. Çalışmada, matematiksel kavramların ve ispatların durumunu değiştirebileceği, matematiksel düşünmenin gelişiminde zorluklar meydana gelebileceği ve matematiksel fikrin sistematik ürününe karşı matematiksel düşünmeyi geliştirebilmek için tüm süreci öğrenme ve öğretme zorluğu vurgulanmıştır.

Ferri (2004), 15 ve 16 yaşlarındaki öğrencilerin matematiksel düşünme stillerinin yeniden oluşturulmasında öneriler verilmiştir.. Bu araştırmada farklı matematiksel düşünme stillerinin tek bir yolla gösterilmesi amaçlanmıştır. Araştırmanın sonucunda, öğretmen öğrenci anlayış ve farklılıklarına dikkat etmeden, kendi tarzı ve matematiksel düşünmelerine göre etkinlikleri düzenler. Öğretmen farklı çözüm yollarına anlayış gösterilmesi bu sorunu ortadan kaldırabilir. Öğretmenlerin bilinçli hale gelmesi, sınıf ortamında eşitliği sağlayabilmeli ve öğrencilerin kendi düşüncelerini rahatça söyleyebileceği bir ortam oluşturması öğrencilerin matematiksel düşünme potansiyellerinde gelişme sağlanacağı belirtilmiştir.

Harel ve Sowder (2005), matematiksel düşünme, matematiksel düşünme biçimi veya sadece düşünme biçiminin birbiri yerine kullandıklarının ifade etmişlerdir. Araştırmada belli bir konu veya kavrama özgü anlama biçimi ve düşünme biçimi arasında

16

gerçekleştiğini ifade etmektedir. Matematiksel düşünme kavramının anlaşılabilir olması anlama ve düşünme biçimleri arasındaki farkın ortaya koyulması ile mümkün olduğu belirtilmiştir.

Henderson vd. (2002), matematiksel düşünme için materyal geliştirme çalışmasında, organizasyonlar için en iyi online depo mekanizması geliştirmeye çalışılmış ve bilgisayar eğitiminde matematiksel düşünmeye teşvik eden materyallerin yaygınlaşmasını sağlamayı amaçlamıştır.

Alkan ve Bukova (2005), matematik öğretmen adaylarının matematiksel düşünme gelişimini ölçmeye odaklandıkları çalışmada ilk aşama olarak matematiksel düşünme gelişimini ölçme amaçlı araç geliştirmişlerdir. İkinci aşamada ise geliştirilen ölçme aracı katılımcılara uygulanmıştır. Uygulamanın sonucunda katılımcıların akademik olarak başarılı olmalarına karşılık matematiksel düşünme düzeyleri düşük, genelleme aşamasında sıkıntı çektiklerini ve dolayısıyla soyutlamada da sıkıntı yaşadıklarını, fakat en büyük sıkıntıları ispat etme aşamasında olduğu belirtilmiştir.

Bukova Güzel (2008), Yapılandırmacı öğrenme yaklaşımının matematik öğretmen adaylarının matematiksel düşünme süreçlerine olan etkisinin incelenmesi amaçlanmıştır. Araştırma bulgularında yapılandırmacı yaklaşımla işlenen bir dersin geleneksel yöntemlerle işlenen derse göre matematiksel düşünme becerisine daha fazla katkı sağladığı belirtilmiştir.

Arslan ve Yıldız (2010), 11. Sınıf öğrencilerinin matematiksel düşünmenin özelleştirme, genelleme, varsayımda bulunma ve ispatlama aşamalarıyla ilgili yaşantılarını ortaya çıkarmak amaçlanmıştır. Çalışmada özelleştirmede sıkıntı yaşamadıkları, genellemeyle ilgili olarak sayılar ve değişkenler arasındaki ilişkiyi daha çok sözel olarak ifade etmeyi tercih ettikleri, varsayımda bulunmalarda daha çok sözel olarak ifade ettikleri, ispatlamada gruplar daha çok aritmetik ya da geometrik olarak ispat etme girişimde oldukları görülmüştür.

Tataroğlu ve Erduran(2010), matematik öğretmen adaylarının matematiksel düşünme ve öğrencilerin matematiksel düşüncelerinin geliştirilmesi hakkındaki görüşlerinin incelemesi amaçlanmıştır. Araştırma bulguları, matematiksel düşünmenin bir süreç olduğu ve matematiksel durumile birlikte ele alınabileceği, matematiksel düşünme becerisi kazandırabilmesi için gündelik hayatla ilişkilendirebilmek, ön bilgilerle ilişkili etkinlikler

17

hazırlamak, açık uçlu ve öğrenciyi düşündürmeye yönelik sorular sorulması gerektiği sonuçlarına ulaşılmıştır.

Keskin, Akbaba Dağ ve Altun (2013), sekizinci ve on birinci sınıf öğrencilerinin matematiksel düşünmenin özelleştirme, genelleme, varsayımda bulunma ve ispatlama aşamalarındaki yaşadıkları farklılıkları incelenmiştir. Araştırmaya katılan öğrencilerin özelleştirme basamağında sıkıntı yaşamadıkları, genelleme ve sonrasında ki aşamalarda sırasıyla bir öncekine göre daha çok zorlandıkları gözlemlenmiştir.

Ersoy ve Başer (2013), öğretmen adaylarının matematiksel düşünme düzeylerini ölçen likert tipi bir ölçek geliştirilmek amaçlanmıştır. Çalışmada geliştirilen ölçek öğrencilerin bilişsel boyutta öğrenmelerini ölçmek amacıyla oluşturulmuştur. Geliştirilen ölçek ile matematik öğretiminde akıl yürütme, keşfetme, bilgiyi etkili kullanma, tahmin yapma, mantıksal düşünebilme gibi matematiksel düşünme becerilerini belirlenmesi sağlanmıştır. Kılıç, Tunç Pekkan, & Karatoprak (2013), Materyal kullanımının öğrencilerin matematiksel düşünme becerisine etkisinin incelenmesi amaçlanmıştır. Araştırma bulguları öğrencilerin bazı kavram yanılgıları olmalarına rağmen materyal kullanarak hem bu kavram yanılgıları giderilmesi hem de matematiğe olan ilginin artmasının sağladığı sonucuna ulaşılmıştır.

Eğitim Teknolojisi

Teknolojinin eğitime entegre edilmesiyle birlikte avantajlı ve dezavantajlı yanları belirleye bilmek için bir çok çalışma (Adıgüzel, Gürbulak, & Sarıçayır, 2011; Baki, 1996; Buchberger, 1989; Davis & Fonger, 2014; Dinçer, Şenkal , & Sezgin, 2012; Güngör, 2016; Kabaca, 2016; Pamuk, Çakır, Ergün, Yılmaz, & Ayas, 2013; Tataroğlu & Erduran, 2010; Sağlam, Altun, & Aşkar, 2009) yapılmıştır. Özellikle ülkemizde Fatih projesine geçtikten sonra konu üzerinde çalışmalarda yoğunlaşmıştır.

Van de Walle, Karen, & Bay-Williams (2004), Teknoloji terimi okul matematiğinde dijital araçlara, bilgisayarlara, hesap makinelerine, bilgisayar cebir sistemlerine, dinamik geometrik yazılımlara, internet sunum araçlarına bunun yanı sıra bu cihazlar ve araçlarla kullanılabilen genelde internet tabanlı kaynaklara işaret etmektedir. Teknoloji eğitimde kullanılan öğrenme araçlarının bir tamamlayıcısı olarak görülmelidir. Teknoloji,

18

öğrencilerin öğrenebildiği içeriğin kapsamını daha da genişletebilir ve öğrencilerin üstesinden gelebileceği problemlerin çeşitliliğini artırır. Kitapta matematik eğitiminde kullanılan teknolojik araçlar ayrıntılı bir biçimde belirtilmiştir. Matematik eğitiminde bilgisayar kullanımının çeşitli şekilleri vardır.

 Sayıları ifade etmeyi geliştirmek için bilgisayar araçları: Teknoloji kullanımda niteliksel farklılıklar vardır. Genellikle sanal manipülatifleri kullanmak, somut manipülatifleri kullanmak kadar kolaydır. Fakat bilgisayarda ki materyallerin kullanımı farklıdır. Geliştirilen bir buton yardımıyla sayılarla ilgili işlemler kolaylıkla yapılabilir. Ayrıca sembolik bağlantı kurmak kolaydır. Sayı için var olan sanal değişikliklerin çoğu bilgisayar programları ile ekranda temsilleri değiştikçe bunlar da değişir. Fakat bu işlemin somut materyallerde yapılması daha zordur. Bir başka kolaylığı ise kolay temizleme ve sınırsız materyale ulaşabilmektir. Öğrenciler sanal manipulatiflerle çalıştıklarında ekranı kolayca temizleye bilir ve yeni bir sayfa açabilir. Engelli öğrencilerin(görme, duyma bozukluğu) sayıları ya da materyalleri anlama kolaylığı sağlanabilir.

 Geometriyi geliştirmek için araçlar: Herhangi bir kısıtlama olmadan öğrencilerin çoğu bu araçları kullanabilir. Bu araçlar genel olarak somut materyallere göre daha çok avantaj sağlar. Bloklar ve karolar oluşturmada, bu blokların boyutunun büyütülmesi ya da küçütülmesi, blokların birbirine yapıştırılması, simetri doğrusuna göre yansıma yapılması, bir noktaya göre döndürme yapılması, alan ya da çevre uzunluğunun ölçülmesi, yeni bir doğru, bir doğruya paralel doğru, bir doğruya dik doğru gibi geometrik işlemlerin uygulamaları kolayca yapabilmektedir.

Teknolojinin faydası, bir öğrenme aracı olarak hizmet ettiğinde ve derslerin içine entegre edilerek öğrencilerin matematiği öğrenme imkanlarını artırdığında ortaya çıkacaktır.

Dinçer, Şenkal ve Sezgin (2012), öğretmen, öğrenci ve velilerin bilgisayar okuryazarlıkları seviyeleri incelenip Fatih projesinde öğretmen, öğrenci ve veli uyumunu artırıcı yeni yaklaşımlar önermeyi amaçlanmıştır. Öğrencilerin derslerde teknoloji kullanımına yönelik olumlu tutumları olduğu gözlemlenmiş, öğretmenlerde ise beklenen bilgi ve becerilere sahip olmadığından tam olarak amacına uygun şekilde kullanılmadığı belirlenmiş ve öğrencilere evde yardımcı olan velilerin bilgisayar okuryazarı olmaması projenin etkinliğini doğrudan etkilemekte olduğunu belirtilmiştir.

19

Çağıltay, Çakıroğlu, Çağıltay ve Çakıroğlu (2001), Türkiye’deki öğretmenlerin bilgisayarları nasıl kullandıklarını ve öğretimde bilgisayar kullanımın nasıl algılandığı ortaya koymak amaçlanmıştır. Araştırmanın sonucunda öğretmenler bilgisayar kullanımının öğretimde olumlu olacağı görüştedirler. Fakat öğretmenlerin yeteri kadar bilgisayar kullanımında bilgi sahibi olmadığı belirtilmiştir.

Hangül ve Üzel (2010), 8. Sınıf öğrencilerin matematik dersinde geometrik cisimler konusunda bilgisayar destekli öğretim yaparak öğrencilerin matematik dersine karşı tutumlarını incelemiştir. Yapılan araştırmada bilgisayar destekli ortam yapılandıramcı yaklaşımla yapılan bir öğretim programda öğrenci tutumlarını olumlu yönde etkilemiştir. Matematik dersinde anlaşılması zor olan konuların daha kolay algılanmasını ve kalıcı olmasını sağlamaktadır. Bilgisayar destekli öğretimin hem zamandan tasarruf sağladığını hem de öğretmenin işini kolaylaştığı belirtilmiştir.

Buchberger (1989), matematik derslerinde esas eğitici olarak sembolik bilgisayar yazılım sistemlerine odaklanılmıştır. Öğrencileri iki gruba ayırmış, teknolojik altında yatan matematiği bilen guruba beyaz kutu(WB), bilmeyen grubu da siyah kutu (BB) olarak isimlendirmiştir. Kişi matematiksel gerçekleri bilmeden grafik çizmek, hesaplamalar yapmak gibi uygulamalar pek fazla anlam ifade etmez. Öğrencilerin matematiğin teknoloji de nasıl entegre edilmesi gerektiğini bilmeleri gerektiği belirtilmiştir.

Davis ve Fonger (2014), taşınabilir cihazlar ve bilgisayarlarda kullanılan cebirsel semboller, ifadeler, denklem çözümleri, kesin ve yaklaşık değerleri elde edilmesini sağlayan Bilgisayar Cebir Sistemi üzerine odaklanılmıştır. Çalışmada kitaplarda ki bilgisayar cebir sistemlerini inceleyen bir ölçme aracı geliştirilmiştir ve daha sonra U.S de ki ortaöğretim matematik kitaplarına uygulanılmıştır. Çalışmanın bulgularında, öğretmen destek materyallerinde ve ders kitaplarında bilgisayarın matematik ders planı yaparken nasıl kullanacağı ile ilgili rehberlik sağlanmalı ve bilgisayar cebir sistemi ile kağıt kalem sisteminin iyi entegre edilmesiyle, bilgisayarın eğitime olan gücü tam olarak ortaya çıkacağı belirtilmiştir.

Ural (2015), Ortaokul matematik derslerinde psikomotor becerileri ile bilgi iletişim teknolojileri kullanıma yönelik hangi materyaller ve şekillerin kullanımı ve bunların kullanımına yönelik öğretmen görüşleri incelenmiştir. Çalışmanın sonuçlarında, öğretmenlerin kullandıkları bilgisayar nesneleri; Morpa ve Meb-vitamin, powerpoint, internette animasyonlar ve videolar olarak belirtilmiştir. Öğretmenlerin bilgisayar

20

kullanımında yeterliliğe sahip olmadığı, dinamik bilgisayar yazılımlarının kullanılmaması gibi olumsuz yönleri belirtilmiş. Öğretmenlerin bilgisayar kullanımında ise öğrencilerin motive etme, kalıcılık sağlama ve ilgi çekme açısından faydası olduğu belirtilmiştir.

Tatar, Kağızmanlı ve Zengin (2015), dinamik matematik yazılımı ile etkleşimli tahtanın ders içerisinde entegrasyonu sağlanıp, bu entegrasyonun öğretmen adaylarının etkileşimli tahta ile ilgili görüşlerine etkisinin incelenmesi amaçlanmıştır. Dinamik bir yazılımla etkileşimli tahtanın matematik dersine entegre edilmesiyle kavramların anlaşılması, somutlaştırma sağlanacağı, grafik ve şekil çizimlerinde kolaylaşacağı, görselleştirme ve akılda kalıcı olacağı sonucuna ulaşılmıştır.

Sağlam, Altun ve Aşkar (2009), üniversite öğrencilerinin problem çözme stratejilerini bir bilgisayar ortamında incelenmesi amaçlanmaktadır. Araştırma da bilgisayar cebir sistemine uygun olan Maple programını problem çözmede kullanımları incelenmiş. Araştırma bulguları, öğrencilerin Maple’da problem çözerken sadeleştirme, benzer problem bulma, döngüsel olmaya strateji ve araç- amaç analizinde daha çok kullanıldığı gözlemlenmiştir. Karaarslan, Boz ve Yıldırım (2013), teknolojik gelişmelerle matematik ve geometri eğitiminde ortaya çıkan farklı yaklaşımlar ve bu yaklaşımları derslerde en etkili şekilde kullanabilmek için nasıl entegre edilebileceğini belirlemek amaçlanmıştır. Çalışmanın bulgularında Türkiye’de matematik eğitiminde en sık kullanılan dinamik matematik programının Geogebra olduğu ve fatih projesi ile tüm öğrencilere ve öğretmenlere tablet bilgisayarlar sayesinde bireysel kullanmaların artması bekleniyor. Ayrıca öğretmenlere bu teknolojiyle ilgili yeterliliklerini artırması gerektiği, çağın gereklerini karşılayacak insan profilini yetiştirme açısından önem taşıdığı belirtilmiştir.

Türk Müfredatında Matematiksel Düşünme ve Teknoloji Kullanımının Yeri

Tük müfredatında 2011 ve 2013 yılında hazırlanan matematik dersi öğretim programı incelendiğinde matematiksel düşünme ve teknoloji kullanıma yönelik birçok açıklama yapılmıştır ve müfredatta ki düzeltmeler de bu iki kavram hakkında yeniliklere yer verilmiştir.

Milli eğitim programının vizyonlarından birisi de matematiksel düşünme yeteneğine sahip bireyler yetiştirilmesidir. Matematik öğrenme süreci temel matematiksel kavramların

21

kazanılmasından ziyade matematiksel düşünme, ilişkilendirme ve modelleme becerileri matematik öğrenmenin temel amaçları olarak kabul edilmiştir (MEB, 2011). Öğrencilerin matematiksel işlemler ve kavramlardan ziyade matematiksel düşünmenin öğretilmesi, problem çözme yeteneğine sahip bireyler yetiştirilmesi hedeflenmektedir. Öğrencilerin matematiksel işlemler ve kavramların ezberletilmesi matematiksel düşünme becerilerini geliştirmemektedir. Öğrenme süreçlerinde matematik kuralların ezberletilmesi yerine bu kuralları öğrencinin bulmasını sağlanması öğrencinin matematiksel düşünme becerisini geliştirir (MEB, 2011). Fakat uluslararası yapılan matematik okur yazarlığı ile ilgili sınavlarda bu uygulamaların, sıralamamızda herhangi bir gelişme sağlamadığı gözlemlenmektedir(Özay, 2016). Bunun ise öğretmenlerin matematiksel düşünme becerilerini geliştirmek için yapılacakları tam olarak bilmediklerini ve üniversite sınavına hazırlık gibi etkenlerden dolayı öğrencilere düşündürülmekten yerine kavramların ezberletildiği düşünülmektedir. Ferri(2004) de yapmış olduğu araştırma ile öğretmenlerin bilinçli hale gelmesi, sınıf ortamında eşitliği sağlayabilmeli ve öğrencilerin kendi düşüncelerini rahatça söyleyebileceği bir ortam oluşturması öğrencilerin matematiksel düşünme potansiyellerinde gelişme sağlanacağı belirtilmiştir.

Hazırlanan müfredatta matematiksel düşünmenin geliştirilebilmesi için öğrencilere uygun ortam hazırlanması gerektiği, böylece öğrencilerin matematiksel düşünme süreçlerini daha aktif bir şekilde yapabilecekleri belirtilmiştir. Öğrencilerin matematiksel düşünme süreçlerini (genelleme, varsayımda bulunma) yaşayabilmeleri için kendi aralarında tartışabilecekleri uygun ortamlar hazırlanmalıdır (MEB, 2013).

Müfredatta yapılan değişiklikler sonucunda 2013 yılında matematiksel düşünmeyi geliştirebilmek için teknolojinin de daha aktif şekilde matematik eğitiminde kullanılması gerektiği belirtilmiştir. Teknolojinin gelişmesiyle farklı problemlerle karşılaşılan günümüz dünyasında, matematiğe değer veren, matematiksel düşünme gücü gelişmiş ve problem çözme yeteneği gelişmiş bireylere daha çok ihtiyaç duyulduğu belirtilmektedir (MEB, 2013). Teknolojinin geliştiği dünyamızda karşılaşılan problemlerinde artık değiştiği ve bu problemlerin üstesinden gelebilen bireyler yetiştirebilmek için teknolojiyi kullanabilen ve matematiksel düşünme becerilerine sahip bireyler yetiştirilmesi hedeflenmiştir. Bunun için FATİH projesi; fırsat eşitliğini sağlamak, teknolojinin öğretme ve öğrenme süreçlerinde kullanmak amacıyla uygulanmaya başlamıştır. Fakat yapılan araştırmalarda öğrencilerin Fatih projesi ile teknoloji kullanımına yönelik olumlu tutumları olduğunu fakat

22

öğretmenlerin derslerde teknolojiyi nasıl kullanması gerektiğine yönelik bilgi ve becerilere sahip olmadığından fatih projesinin amaçların tam olarak gerçekleşmediği belirtilmiştir (Dinçer, Şenkal ve Sezgin, 2012). Teknoloji destekli sınıf ortamlarında dinamik matematik programları aktif olarak kullanılmadığı, sunumların veya interaktif ortama aktarılan kitapları yansıtarak teknolojinin kullanıldığı; müfredatta hedeflenen şekilde matematiksel düşünme, problem çözme, ilişkilendirme yapma gibi becerileri geliştirecek öğretim ortamı oluşmadığı gözlemlenmiştir.

Teknoloji matematik sınıflarında bir öğretme aracı olarak değil de bir öğrenme aracı olarak görülürse sahip olduğu potansiyel ile geleneksel öğrenme-öğretme ortamlarımızı geliştirebilir ve değiştirebilir (MEB, 2011). Teknolojik aletleri bir araç olarak görmek ve matematik eğitiminin içine entegre edilmelidir, bir öğretme aracı olarak görülememesi gerekmektedir. Teknolojik araçların bir hesap makinesi, bir sunum aracı olarak değil de öğrenci tarafından model kurma, yorumlama, analiz ve genelleme yapma gibi üst düzey zihinsel beceriler için kullanılmalıdır (MEB, 2011). Teknoloji destekli matematik öğretimi yapılan bir ortamları öğrenciler etkileşimli olarak kullanır, problemleri adım adım çözer, dönütler alarak yanlışlarını öğrenmelidirler. Teknoloji destekli öğrenme ortamlarında matematik öğretmenleri cevabı vermek yerine gerekli olan yerlerde dönütler vermelidir. Dolayısıyla teknolojik araçlar, öğrencinin bilgi ve becerilerini ön plana çıkaran bir köprü rolü oynar.

Matematik eğitiminde teknolojinin kullanımıyla öğrencilerin derse karşı motivasyonlarının artmasını sağlanacaktır. Bilişim teknolojisinin potansiyelinden yararlanarak tasarlanan ve geliştirilen yazılımlar yoluyla öğrenciyi öğrenmenin merkezine koymak, öğrenmeyi bireyselleştirmek ve böylece derse karşı ilgiyi artırmak mümkün görünmektedir (MEB, 2011). Teknolojik araç gereçler her öğrenme seviyesine göre uygun olduğundan bireyselleştirilmiş öğrenme ortamı oluşturulabilir ve her öğrencinin derse ilgisinin artırılması sağlanabileceği belirtilmiştir. Bilgi ve iletişim teknolojilerinin bilinçli kullanımı, teknolojinin matematik becerilerinin öğrenilmesinin yerini almasını değil; aksine, beceri seviyelerini gözetmeksizin tüm öğrencilere matematiksel düşünceyi ulaşılabilir kılmayı amaçlamaktadır (MEB, 2013). Böylece bireyselleştirilmiş olarak hazırlanan etkinlikler ile tüm öğrencilerin matematiksel düşüncelerinin geliştirilebileceği belirtilmiştir.

Öğrencilerin bilgiye ulaşmaları için öğretmen tarafından dinamik matematik programları, hesap makinası veya internetten araştırmalar yapabilecekleri etkinlikler hazırlanabilir.