Maskeli verilere dayalı parametre tahmini parameter

FEN BİLİMLERİ ENSTİTÜSÜ

MASKELİ VERİLERE DAYALI PARAMETRE TAHMİNİ

Harun KINACI YÜKSEK LİSANS TEZİ İSTATİSTİK ANABİLİM DALI

FEN BİLİMLERİ ENSTİTÜSÜ

MASKELİ VERİLERE DAYALI PARAMETRE TAHMİNİ

Harun KINACI

YÜKSEK LİSANS TEZİ İSTATİSTİK ANABİLİM DALI

Bu tez 28 / 12 / 2009 tarihinde aşağıdaki jüri tarafından oybirliği / oyçokluğu ile kabul edilmiştir.

... ... ... Doç.Dr.Coşkun KUŞ Doç.Dr.Aşır GENÇ Yrd.Doç.Dr.Hasan KÖSE (Danışman) (Üye) (Üye)

ÖZET

Yüksek Lisans Tezi

MASKELİ VERİLERE DAYALI PARAMETRE TAHMİNİ

Harun KINACI Selçuk Üniversitesi Fen Bilimleri Enstitüsü İstatistik Anabilim Dalı

Danışman: Doç.Dr. Coşkun KUŞ 2010, 67 Sayfa

Jüri: Doç.Dr. Coşkun KUŞ Doç.Dr. Aşır GENÇ

Yrd.Doç.Dr.Hasan KÖSE

Bu tez çalışmasında, iki bileşenli seri ve paralel sistemler için sistem bileşenlerinin yaşam zamanı dağılımlarının parametrelerinin maskeli verilere dayalı tahmini ele alınmıştır. Bileşenlerin yaşam zamanı dağılımlarının konum-ölçek parametreli dağılımlar ailesine ait olmaları durumunda konum parametrelerinin modifiye edilmiş en çok olabilirlik tahmin edicileri analitik olarak elde edilmiştir. Simülasyon çalışması ile lojistik dağılım için, modifiye edilmiş en çok olabilirlik tahmin edicilerinin performansları incelenmiş ve sayısal örnekler verilmiştir.

Anahtar Kelimeler: Maskeli örneklem, Seri sistemler, Paralel sistemler, En çok olabilirlik tahmin edicileri, Modifiye edilmiş en çok olabilirlik tahmin edicileri.

ABSTRACT Master Thesis

PARAMETER ESTIMATION BASED ON MASKED DATA

Harun KINACI Selçuk University

Graduate School of Natural and Applied Sciences Department of Statistics

Supervisor:Assoc.Prof.Dr Coşkun KUŞ 2010, 67 Pages

Jury: Assoc.Prof.Dr. Coşkun KUŞ

Assoc.Prof.Dr. Aşır GENÇ

Ass.Prof.Dr. Hasan KÖSE

In this thesis, it is considered that the estimation of the parameters of distributions of components for serial and parallel systems with two components based on masked data. Modified maximum likelihood estimators are obtained analitically for location parameters when the distributions of componets are belong to location-scale family. Simulation study is performed to investigate the performances of the modified maximum likelihood estimators and numerical examples are given under the logistic distribution theory.

Key Words: Masked samples, Serial system, Parallel system, Maximum likelihood estimators, Modified maximum likelihood estimators.

TEŞEKKÜR

Bu çalışma konusunu bana veren ve çalışmalarım süresince yakın ilgi ve yardımlarını hiçbir zaman esirgemeyen değerli hocam sayın Doç.Dr.Coşkun KUŞ’a, çalışmamda yardımcı olan ağabeyim ve hocam Yrd.Doç.Dr.İsmail KINACI’ya ve manevi desteğini esirgemeyen eşime teşekkürlerimi sunarım.

ÇİZELGELER DİZİNİ

Çizelge 1. ₁₂ 1 ve ₁ ₂ 2 için simülasyon sonuçları………….………48 Çizelge 2. ₁2,₂ 1 ve ₁ ₂ 2 için simülasyon sonuçları………...49 Çizelge 3. p0,₁ ₂ 1,₁ ₂ 2 için üretilen veri seti………53

Çizelge 4. ₁ ve ₂’nin ML ve MML tahmin değerleri………...53 Çizelge 5. p0 3. ,₁ ₂ 1,₁₂  için üretilen veri seti………..55 2 Çizelge 6.  ve ₁  ’nin ML ve MML tahmin değerleri………...55 ₂ Çizelge 7. ₁₂ 1 ve ₁ ₂ 2 için simülasyon sonuçları………..…...56 Çizelge 8. ₁2,₂ 1 ve ₁ ₂ 2 için simülasyon sonuçları……….…57 Çizelge 9. p0,₁ ₂ 1,₁ ₂ 2 için üretilen veri seti………60

Çizelge 10.  ve ₁  ’nin ML ve MML tahmin değerleri……….61 ₂ Çizelge 11. p0 3. ,₁ ₂ 1,₁₂  için üretilen veri seti………62 2 Çizelge 12.  ve ₁  ’nin ML ve MML tahmin değerleri……….…62 ₂

ŞEKİLLER DİZİNİ

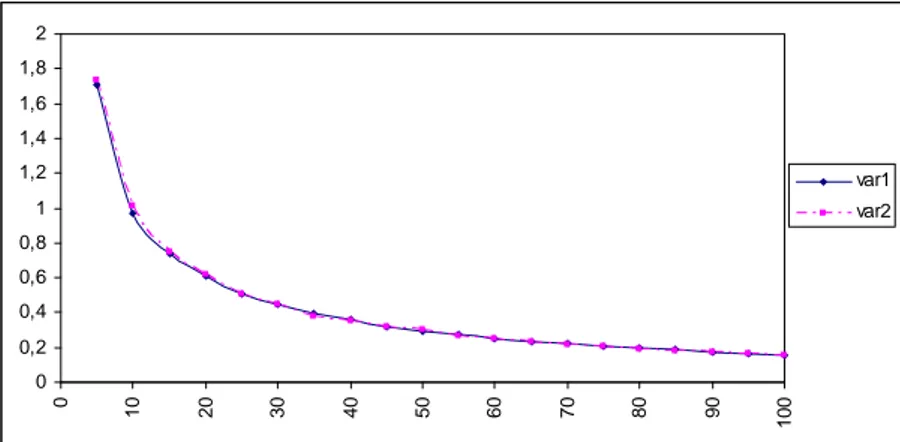
Şekil 1. p0 için  ’in değişimine göre ₁  ve ˆ₁  ’nın yanları………...…..50 ˆ₂ Şekil 2. p0 için  ’in değişimine göre ₁  ve ˆ₁  ’nın varyansları…………...…50 ˆ₂ Şekil 3. p0.3 için  ’in değişimine göre ₁  ve ˆ₁  ’nın yanları………...…51 ˆ₂ Şekil 4. p0.3 için  ’in değişimine göre ₁  ve ˆ₁  ’nın varyansları………...….51 ˆ₂ Şekil 5. p0 için n değerinin değişimine göre  ve ˆ₁  ’nın varyansları…...52 ˆ₂

Şekil 6. p0.3 için n değerinin değişimine göre  ve ˆ₁  ’nın ˆ₂

varyansları……...52

Şekil 7. Ağırlıkların grafikleri ………...54 Şekil 8. p0 için  ’in değişimine göre ₁  ve ˆ₁  ’nın yanları……….……57 ˆ₂ Şekil 9. p0 için  ’in değişimine göre ₁  ve ˆ₁  ’nın varyansları…………..….58 ˆ₂ Şekil 10. p0.3 için  ’in değişimine göre ₁  ve ˆ₁  ’nın yanları……….59 ˆ₂ Şekil 11. p0.3 için  ’in değişimine göre ₁  ve ˆ₁  ’nın varyansları……..……59 ˆ₂ Şekil 12. n değerinin değişimine göre  ve ˆ₁  ’nın varyansları……….…60 ˆ₂

İÇİNDEKİLER

1. GİRİŞ ... 1

2. TEMEL KAVRAMLAR ... 4

2.1. Sıra İstatistikleri ... 4

2.2. Konum-Ölçek Parametreli Dağılımlar Ailesi ... 8

2.2.1. Lojistik Dağılım ... 9

2.3. Taylor Açılımı... 10

2.4. Newton-Raphson Yöntemi... 11

2.5. Asimptotik Normallik ... 13

2.6. Fisher Bilgi Matrisi ... 14

2.7. En Çok Olabilirlik Tahmin Edicileri... 15

2.8. Asimptotik Güven Aralıkları ... 15

2.9. Modifiye Edilmiş Ençok Olabilirlik Tahmin Edicileri ... 16

3. MASKELİ ÖRNEKLEMLER ... 20

3.1. İki Bileşenli Seri Sistemler ... 21

3.2. İki Bileşenli Paralel Sistemler... 24

4. MASKELİ VERİLER İÇİN MML TAHMİNİ... 29

4.1. İki Bileşenli Seri Sistemler ... 29

4.2. İki Bileşenli Paralel Sistemler... 36

4.3. Maskeli Örneklemlere Dayalı Logistik Dağılımının MML Tahmin Edicileri 44 4.3.1. İki Bileşenli Seri Sistemler ... 44

4.3.2. İki Bileşenli Paralel Sistemler... 45

5. SİMÜLASYON ... 47

5.1. İki Bileşenli Seri Sistemler ... 47

5.2. İki Bileşenli Paralel Sistemler... 55

6. SONUÇ ... 63

1. GİRİŞ

İstatistik biliminin en önemli problemlerinden birisi parametre tahmini problemidir. Literatürde dağılımların parametrelerini tahmin etmek için çeşitli tahmin ediciler önerilmiştir. Bunlardan bazıları en çok olabilirlik tahmin edicileri, en küçük kareler tahmin edicileri, Bayes tahmin edicileri ve parametrik olmayan tahmin edicilerdir. Bu tahmin edicilerin, farklı durumlarda farklı kriterlere göre birbirlerine karşı üstünlükleri bulunabilir. Parametre tahmini probleminde esas amaç, içinde bulunulan durum için bilinmeyen parametrenin en iyi özelliklere sahip tahmin edicisini elde etmektir. Tahmin teorisinde alınan örnek hacmi ne kadar büyük olursa tahmin edicinin özellikleri de o kadar iyi olmaktadır yani, tahmin edici parametrenin gerçek değerine yakın sonuçlar vermektedir. Ancak çoğu durumda gerek zaman gerekse maddiyat olarak büyük hacimli örneklem elde etmek mümkün olmamaktadır. Bu sebeple elde edilen tahmin edicilerin büyük örnek hacmindeki özellikleri yerine küçük örnek hacmindeki özellikleri önem kazanmaktadır.

Uygulanmasının kolaylığı ve tahmin edicilerinin asimptotik olarak yansız ve normal dağılımlı olmasından dolayı çoğu durumda bilinmeyen parametrelerin tahmini için en çok olabilirlik tahmin edicileri kullanılmakta ve parametrelerin en çok olabilirlik tahmin edicileri elde edilmektedir. Ancak örneklemin geldiği dağılıma göre bazen bu tahmin ediciler analitik olarak elde edilememekte ve tahmin edici yerine iteratif yöntemlerle parametrenin tahmin değerleri elde edilebilmektedir. Bu gibi durumlarda parametrelerin tahmin edicilerini analitik olarak elde etmek için Tiku (1967a,1967b, 1968a, 1968b,1968c), modifiye edilmiş (asimptotik) en çok olabilirlik yöntemini önermiştir. Bu yöntemden elde edilen tahmin edicilerin asimptotik özellikleri en çok olabilirlik tahmin edicileri ile aynıdır. Modifiye edilmiş en çok olabilirlik tahmin edicisine yaklaşık MLE’ de denilmektedir (Balakrishnan ve ark. 2004 )

Güvenilirlik teorisinde genellikle, bir bileşenin veya n tane bileşenden oluşan bir sistemin yaşam zamanının dağılımının parametreleri tahmin edilmeye çalışılmaktadır. İki tane bileşenden oluşan bir sistem düşünüldüğünde bu sistemin yaşam zamanı, bileşenler seri bağlı olduğunda küçük ömürlü bileşenin, paralel bağlı ise büyük ömürlü bileşenin ömrü kadar olacaktır. Sistemin bozulmasına neden olan bileşenin gözlenemediği durumda elde edilen gözlem, maskeli gözlem olarak adlandırılmaktadır.

İncelenen maskeli örnekleme ilişkin olabilirlik fonksiyonunun yapısından dolayı örneklemin geldiği dağılımlar için parametrelerin en çok olabilirlik tahmin edicileri genellikle analitik olarak elde edilememektedir. Bu çalışmada maskeli örneklemler için parametre tahmininde modifiye edilmiş en çok olabilirlik yöntemi kullanılmış ve parametre tahmin edicileri analitik olarak elde edilmeye çalışılmıştır.

Maskeli örneklem konusu ilk önce Miyakawa (1984) tarafından ortaya atılmıştır. Çalışmasında seri bağlı iki bileşenden oluşan sistemleri incelemiş ve sistemin bozulmasına neden olan bileşenin gözlenemediği durumda bileşenlerin yaşam zamanı dağılımlarının parametrelerinin parametrik ve parametrik olmayan tahmin edicilerinin nasıl elde edileceğinden bahsetmiştir. Usher ve Hodgson (1988), sabit bozulma oranına sahip üç bileşenin seri bağlı olduğu sistemler için bileşenlerin yaşam zamanı dağılımı parametrelerinin en çok olabilirlik tahmin edicilerini elde etmişlerdir. Usher and Guess (1989), seri sistemlerdeki bileşenlerin güvenilirliklerini tahmin etmek için iteratif bir yöntem önermişler ve iki bileşen için bileşenlerin yaşam zamanlarının Weibull dağılımına sahip olması durumunda sayısal bir örnek vermişlerdir. Sarhan (2003), seri bağlı m tane bileşenden oluşan sistemleri incelemişler ve iki ve üç bileşenli sistemler için bileşenlerin yaşam zamanlarının Weibull dağılımına sahip olması durumunda yaşam zamanı dağılımlarının parametrelerinin en çok olabilirlik tahmin edicilerini analitik olarak elde etmişlerdir. Guess ve ark.(1991), seri bağlı J tane bileşenden oluşan sistemlerin bozulmasına neden olabilecek bileşenler hakkında bir önsel bilgiye sahip olunduğu durum için sistemin ve bileşenlerinin güvenilirliklerine ilişkin en çok olabilirlik tahmin edicilerini elde etmişlerdir. Sarhan ve El-Gohary (2003), yaşam zamanları Pareto

dağılımına sahip olan, birbirlerine seri bağlı J tane bileşenden oluşan sistemleri ele alarak bileşenlerin yaşam zamanı dağılımlarının parametreleri için maskeli örnekleme dayalı en çok olabilirlik ve Bayes tahmin edicilerini elde etmişlerdir. Sarhan (2004a), seri bağlı J tane bileşenden oluşan sistemler için bileşenlerin yaşam zamanı dağılımlarının maskeli örnekleme dayalı en çok olabilirlik ve Bayes tahmin edicilerini elde etmiştir. Burada sistemdeki .j bileşenin hazard fonksiyonunun

 

t t j J

h_j _j _j , 1,2,_, şeklinde olduğu varsayılmıştır. Ayrıca Sarhan (2004b), h

 

t t j j J j j j , 1,2, , 1    _{ }  

durumu için  parametresinin bilindiği varsayımı altında bileşenlerin yaşam zamanı dağılımlarının maskeli örnekleme dayalı en çok olabilirlik ve Bayes tahmin edicilerini elde etmiştir. Sarhan ve El-Bassiouny (2003), yaşam zamanları Weibull dağılımına sahip olan, birbirlerine paralel bağlı J

tane bileşenden oluşan sistemleri ele alarak bileşenlerin yaşam zamanı dağılımlarının parametreleri için maskeli örnekleme dayalı en çok olabilirlik ve Bayes tahmin edicilerini elde etmişlerdir.

Bu tez çalışmasının ikinci bölümünde, çalışmada kullanılacak temel kavramlar tanıtılmıştır. Çalışmanın üçüncü bölümünde, iki bileşenli seri ve paralel sistemler için maskeli örneklemler tanıtılmış ve maskeli örneklemlere ilişkin olabilirlik fonksiyonları verilmiştir. Dördüncü bölümde iki bileşenli seri ve paralel sistemler için, konum ölçek parametreli dağılımlar ailesinden elde edilen maskeli örnekleme dayalı, ölçek parametresi bilindiğinde konum parametreslerinin modifiye edilmiş en çok olabilirlik (MML) tahmin edicileri elde edilmiştir. Çalışmanın beşinci bölümünde ise, iki bileşenli seri bağlı sistemin bileşenlerinin, bağımsız ve aynı ölçek parametreleri lojistik dağılımdan geldiği varsayımı altında, bileşenlerin dağılımlarının konum parametreleri için elde edilen MML tahmin edicisinin küçük ve büyük örnek hacimlerindeki özellikleri farklı maskeleme olasılıkları altında simülasyon çalışması ile irdelenmiştir.

2. TEMEL KAVRAMLAR

Bu kısımda tez içerisinde kullanılacak olan sıra istatistikleri, konum ölçek parametreli dağılımlar ailesi, Taylor serileri, Newton Raphson yöntemi, Asimptotik Normallik, Fisher Bilgi Matrisi, En Çok Olabilirlik Tahmin Edicileri, Asimptotik Güven Aralıkları, Modifiye Edilmiş Ençok Olabilirlik Tahmin Edicileri gibi konular kısaca tanıtılmıştır.

2.1. Sıra İstatistikleri

n

X X

X₁, ₂,_, , F(x) dağılım fonksiyonuna sahip örnekleminin n

n n

n X X

X_1:  _2: _ _: olacak biçimde büyüklük sırasına göre dizilmesiyle elde edilen her bir X_i:n rasgele değişkeni i. sıra istatistiği olarak isimlendirilir.



n



n X X X

X_1: min ₁, ₂,_,

sıra istatistiğinin dağılım fonksiyonu,









1( ) 1: 1 1 ( ) n n F x P X x   F x (2.1) ve maks :n  n X



X₁,X₂,_,X_n



sıra istatistiğinin dağılım fonksiyonu,



:

 



( ) ( ) n

n n n

F x P X x  F x (2.2)



:





1 2



( ) , , , lerden en az tanesi

r r n n

F x P X x P X X _ X r x

₁, ₂, , lerden tam tanesi       _ 



 n r i n x i X X X P _

olur.A_i:



X₁,X₂,_,X_n lerden tami tanesi x



olması olayı olsun.A_i olayları ayrık olduğundan ,

 

( ) n n r i i i r i r F x P A P A      _{ } 











 



    n r i i n i i n F x F x C ( ) 1 ( ) (2.3)

dır. Bu ise tam olmayan beta fonksiyonudur. Yani



 





    n r i i n i i n r x C F x F x F ( ) ( ) 1 ( ) ( ) 1 0 1 (1 ) B( , 1) F x r n r t t dt r n r      



Burada B



 ,



,  1 ve   için 1





1 ₁





1 0 B  , _



x 1_x  dx

şeklinde tanımlanan Beta fonksiyonudur. X_i’ ler f x( ) dF x

 

dx

 (F x

 

in türevlenemediği noktalar hariç) olacak biçimde sürekli rasgele değişkenler ise



 _      ( ) 0 1_{(1 )} ) 1 , ( B 1 ) ( ) ( x F r n r r r _dx t t dt d r n r dx x dF x f



( )

 

1 ( )



( ) ) 1 , ( B 1 _{F x} 1 _{F x f x} r n r r n r _     (2.4) olur. Burada

 

! ( 1)!( )! ) 1 , ( B _{r nr  n} 1 _{r nr} Şeklindedir (David 1970).

Sıra istatistiklerinin olasılık yoğunluk fonksiyonları ve ortak olasılık yoğunluk fonksiyonları, kombinatorik yöntemler de kullanılarak, aşağıdaki gibi verilir (David 1970).



x X x x



A_r   _r:n  

olayı göz önüne alınsın. A_r olayının gerçeklenmesi için X₁,X₂,_,X_n

örnekleminden r 1 tane örneğin x den küçük, 1 tane örneğin ( ,x x  aralığında x] ve n r tane örneğin de x  den büyük olması gerekir. Dolayısıyla Ax _r olayı,

n r n r n r n r n r n r               _         1 1 1 1 ( ) ! ( )!( )!

farklı durumda gerçekleşebilir.

P

  

A_r P x X_r:n  xx



P



X X x X x x x X X x x



r n r n n r r r         , , _ ; ( , ]; _ , , )! ( )! 1 ( ! 1 1 1  



_{F x}

 

r _{F x x F x}



_{F x x}



n r r n r n  _{   }     ( ) ( ) ( ) 1 ( ) )! ( )! 1 ( ! 1

elde edilir. Diğer taraftan F_r(xx)F_r(x) P



x X_r:n  xx



olmak üzere

 

x x F x x F x f r r x r _       ) ( ) ( lim 0



 





x x x F x F x x F x F r n r n r n r x               ) ( 1 ) ( ) ( ) ( lim )! ( )! 1 ( ! 1 0 ) ( ) ( ) ( ) (x x F x f x x o x F       yazılırsa









_                  _x x o x x F x f x F r n r n x f x r n r x r ) ( lim ) ( 1 ) ( ) ( lim )! ( )! 1 ( ! ) ( 0 1 0



( )

 

1 ( )



( ) ) 1 , ( 1 1 x f x F x F r n r B r n r _     (2.5) bulunur (David 1970).

Özel olarak X₁,X₂,_,X_n örneklemi [0,1] aralığında düzgün dağılıma sahip olmak üzere, bu örneklemin .i sıra istatistiği Xi n_: ’in olasılık yoğunluk fonksiyonu

 

_

1

_

1





1 , 0 1 B , 1 n i i i f x x x x i n i        

olmak üzere 1 i n  için





_

_{ }











1 : 0 1 1 B , 1 B 1, 1 B , 1 1 n i i i n E X x x dx i n i i n i i n i i n             



2.2. Konum-Ölçek Parametreli Dağılımlar Ailesi

X rasgele değişkeninin dağılım fonksiyonu F_(x)ve

 

1



 

:

 





; , biliniyor



F_     F x_ F x_ F x  F (2.6)

olmak üzere ₁’e konum parametreli dağılımlar ailesi, ’ye ise konum parametresi denir. Burada  ,  parametresi için parametre uzayıdır.  parametresinin X rasgele değişkeni için konum parametresi olması için gerek ve yeter koşul X  rasgele değişkeninin dağılımının  den bağımsız olmasıdır. Yani



X x



P



X x



F



x



F



x



F(x)

P       _    

şeklindedir (Casella ve Berger, 1990).

X rasgele değişkeninin dağılım fonksiyonu F_(x) ve

 

2

 

:

 

; , biliniyor x F F x F x  F _  F        _  _{ }  _     (2.7)

olmak üzere ₂’ye ölçek parametreli dağılımlar ailesi,  ’ya ise ölçek parametresi denir. Burada  ,  parametresi için parametre uzayıdır.  parametresinin X rasgele değişkeni için ölçek parametresi olması için gerek ve yeter koşul



X

rasgele değişkeninin dağılımının  ’dan bağımsız olmasıdır. Yani



X x



F x F x F

 

x P x X P                 _      ( )



 ,







γ olmak üzere X rasgele değişkeninin dağılım fonksiyonu F ( x ) _γ

ve

 

3

   

: ; , biliniyor x F F x F x F  F          _  _{ }  _     γ γ γ γ (2.8)

olmak üzere  ’e konum ve ölçek parametreli dağılımlar ailesi, ₃ ’ye konum ve  ’ya da ölçek parametresi denir. Burada  , γ parametresi için parametre uzayıdır.

γ parametresinin X rasgele değişkeni için konum ölçek parametresi olması için gerek ve yeter koşul

  

X

rasgele değişkeninin dağılımının γ ’dan bağımsız olmasıdır. Yani









 

X x P  x P X x  F x  F    F x       _ _{     }  _       γ  

şeklindedir (Casella ve Berger, 1990).

2.2.1. Lojistik Dağılım

 ve  parametreli lojistik dağılıma sahip olan X rasgele değişkeninin olasılık yoğunluk fonksiyonu

 

2 exp , 1 exp x f x x R x       _         _ _      _{ }   (2.9)

şeklinde tanımlanır. Burada, µ konum ve _R _{ölçek parametresidir. Lojistik} dağılıma sahip olan X rasgele değişkeninin dağılım fonksiyonu

 

1 , 1 exp F x x R x         _ _   (2.10)

şeklinde elde edilir. Lojistik dağılımın beklenen değer ve varyansı sırasıyla

 

X  E ve

 

3 2 2_   X

Var şeklindedir.  ve  parametreli lojistik dağılım kısaca Lojistik



,



ile gösterilecektir. Lojistik dağılımın çarpıklık katsayısı sıfır olup E

 

X  etrafında simetriktir.

2.3. Taylor Açılımı

 

: ,

f a b R fonksiyonunun

 

a b, aralığında n. mertebeden türevi _f(n) olmak üzere

 

a,b ’nin keyfi x ve ₀ xx₀ noktaları için





( ) 0 0 0 1 ( ) ( ) ( ) ! n k k n k f x f x x x R x k  



  (2.11)

açılımına f fonksiyonunun x noktasındaki Taylor açılımı denir. Burada ₀



1



!









1

 



, 0 1 1 ) ( ( 1) _{0   0   0} 1 _{ }   n _{ } n n _ n f x x x x x n x R (2.12) şeklindedir (Shahbazov 2005). ) , ( yx f

z kapalı bir bölgede n. mertebeden sürekli ve açık bölgede



n1



.

mertebeden türevli ise bölgenin bir ( ba, ) noktası komşuluğunda iki değişkenli fonksiyonlar için Taylor açılımı

 

 



 



 



 





 





   

  

 

1 1! 1 2! 1 ! x y 2 2 xx xy yy n n x a ,y b

f ( x, y ) f a,b f a,b x a f a,b y b

f a,b x a 2 f a,b x a y b f a,b y b

f x, y f x, y x a y b R x, y n x y _{ }     _    _    _       _      _    _       (2.14) şeklindedir. Burada R , _n

     

     













1 , , , 1 , 1 ! , n n x a y b f x y f x y R x y x a y b n x y f a  x a b  y b         _    _  _   _      (2.15)

biçiminde tanımlanır ve Lagrange kalanı olarak adlandırılır (Berksoy ve Özkan 2001).

2.4. Newton-Raphson Yöntemi

 

x

f ,

 

a b, aralığında türevlenebilir bir fonksiyon olmak üzere f(x)0 denkleminin çözümü analitik olarak elde edilemediği zaman bu çözüm yaklaşık olarak,

 

a b, aralığından seçilen bir x başlangıç noktasından başlanarak, ₀

   

 

   

 

h h h h x f x f x x    1

iterasyonundan elde edilebilmektedir. Burada x_i; i.iterasyondaki değeri ifade etmektedir. x_i1x_i  olduğunda iterasyon sonlandırılır ve elde edilen x değeri _i1

 

x

f fonksiyonunun kökü olarak alınır. Bu yöntem Newton-Raphson yöntemi olarak adlandırılmaktadır.



x x1, , ,2 xk





x  olmak üzere f₁

 

x 0, f₂

 

x 0, , f_k

 

x 0 gibi k tane denklemin çözümünü bulmak için çok değişkenli Newton-Raphson yöntemi kullanılabilir. Bu durumda iterasyon formülü

 i 1  i



 

 i 1



 

 i f

J 

 _{ }

x x x f x

şeklinde olacaktır. Burada  r



₁ r , ₂ r , ,  r



k x x x  x _ , f x

 





f₁

   

x , f₂ x , ,_ f_k

 

x



 ve

 

 

 

 

 

 

 

 

 

 

1 1 1 1 2 2 2 2 1 2 1 2 k f k k k k k f f f x x x f f f J x x x f f f x x x       _{  }    _{  }    _    _          _{  }    x x x x x x x x x x       

şeklindedir. _xi1_x i _{ olduğunda iterasyon sonlandırılır ve elde edilen}

     



1 1 1



1 1 , 2 , , i i i i k x  x  x   _  x _ değerleri f₁

 

x 0, f₂

 

x 0, ,_ f_k

 

x 0 denklem sistemlerinin çözümü olarak alınır. Ugulamada genellikle _{ 10}5 _olarak alınmaktadır.

2.5. Asimptotik Normallik

 

Xn rasgele değişkenlerin bir dizisi , Z , standart normal dağılıma sahip bir rasgele değişken ve _d_{ , dağılımda yakınsamayı göstermek üzere,}

d n n n X a Z b  

olacak şekilde reel sayıların

 

a_n ve pozitif reel sayıların

 

b_n dizileri varsa,

 

X_n

dizisine asimptotik normal veya daha açık olarak “a_n ortalaması” ve “ 2 n

b varyansı” ile asimptotik normal dizisi denir ve _~



_, 2



n n n AN a b

X biçiminde gösterilir. Buradaki n

a sayısı X_n’in beklenen değeri ve 2 n

b sayısı X_n nin varyansı olmayabilir. Bu değerler sırasıyla X_n’in asimptotik ortalama ve asimptotik varyans değerleridir. (Öztürk, 2010).

2.6. Olabilirlik fonksiyonu

n

X X

X₁, ₂,..., örneklemi, olasılık (yoğunluk) fonksiyonu ( ; ),_{f x γ γR}p _olan kitleden alınan n birimlik bir örneklem olsun. Örneklemin ortak olasılık yoğunluk fonksiyonu

( ; ), n

f x γ xR

olmak üzere bu fonksiyona parametrenin bir fonksiyonu gözü ile bakıldığında

 

;

 

; , p

şeklinde tanımlanan fonksiyona X₁,X₂,...,X_n örneklemine dayalı olabilirlik fonksiyonu denir. Burada x



x x₁, , ,_{2 } x _n



ve γ 



 ₁, , ,_{2 } _n



 şeklinde olup  parametre uzayıdır. Olabilirlik fonksiyonu L γ x

 

; in logaritması alınarak

 

_{γ }log



_L

 

_{γ x};



, _{γ R}p

 (2.17)

şeklinde elde edilen fonksiyona log-olabilirlik fonksiyonu denir.

2.6. Fisher Bilgi Matrisi

Fisher bilgi matrisi









 

( ) log ; I E L E      _           _      γ γ X γ γ γ

 

 

 

 

 

 

 

 

 

2 2 2 2 1 1 2 1 2 2 2 2 2 1 2 2 2 2 2 2 1 2 p p p p p                     _{    }    _{  }                 _{  }    _{    }    γ γ γ γ γ γ γ γ γ                 (2.18)

şeklinde tanımlanır, burada L



γ X;



ve _

 

γ sırasıyla eşitlik (2.16) ve (2.17) de verilen olabilirlik ve log-olabilirlik fonksiyonlarıdır (Wu ve Kuş, 2009).

2.7. En Çok Olabilirlik Tahmin Edicileri

Olabilirlik veya log-olabilirlik fonksiyonunu maksimum yapan γ değeri

 







 



ˆ arg max L ; arg max

γ γ x _ γ (2.19)

γ nın en çok olabilirlik tahmin edicisi (MLE) olarak adlandırılır.

2.8. Asimptotik Güven Aralıkları

Eşitlik (2.19) da tanımlanan en çok olabilirlik tahmin edicisi ˆγ bazı düzgünlük şartları altında



_ˆ



d



_0, 1

 



n _{γ γ }N I _γ

olmak üzere asimptotik normaldir, burada _I1

 

_{γ , (2.18) eşitliğinde tanımlı Fisher} Bilgi Matrisidir. Fisher Bilgi matrisinin tersi ˆγ nın asiptotik varyans-kovaryans matrisi dir. Bu matrisin bilinmesi, büyük örneklemler için  ˆ ˆ₁, , ,_{2 } ˆ_n tahmin edicilerinin ayrı ayrı asimptotik varyanslarının bilinmesi anlamına gelmektedir.

 

1

I _{γ nın tutarlı bir tahmin edicisi}

 

 

 

 

 

 

 

 

 

 

1 2 2 2 2 1 1 2 1 2 2 2 1 ₂ 2 1 2 2 2 2 2 2 1 2 _ˆ p p p p p I                          _{    }    _{  }                 _{  }    _{    }    γ γ γ γ γ γ γ γ γ γ                  (2.20)

dır (Adamidis ve Loukas, 1998). Buradan ,_i i1, 2, ,_ p için ˆ_i’ya dayalı asimptotik güven aralığı

1 1 2 2 ˆ_{i ii i} ˆ_{i ii} 1 P  z _ V   z _ V               

şeklinde oluşturulabilir. Burada V_ii, (2.20) eşitliğinde verilen matrisin .i diogonal elemanıdır ve a

 

0,1 için z_a, standart normal dağılımın a. kuantilidir (Wu ve Kuş, 2009).

2.9. Modifiye Edilmiş Ençok Olabilirlik Tahmin Edicileri

En çok olabilirlik tahmin edicileri (MLE), bazı düzgünlük şartları (regularity conditions) altında asimptotik normallik gibi arzu edilen özelliklere sahip olmaktadır. Fisher bilgi matrisinin (Fisher Information Matrix) tersi, bazı düzgünlük şartları altında ML tahmin edicilerinin asimptotik dağılımının varyans-kovaryans matrisi olması nedeniyle parametrelerin asimptotik güven aralıkları ML tahmin edicilerine dayalı olarak elde edilebilmektedir. ML tahmin edicilerinin istenen özelliklere sahip olmasının yanı sıra bazı durumlarda bu tahmin edicilerin elde edilmesinde bazı sorunlar ortaya çıkabilir. Örneğin, olabilirlik fonksiyonunun parametreye göre lineer olmadığı ve birden fazla tepeli (polymodal) olması durumunda ML tahmin edicilerini elde etmek için Newton-Raphson ve EM (Expectation-Maximization) algoritması gibi bazı iteratif yöntemler kullanılmaktadır. Bu iteratif yöntemlerin uygulanmasında parametrelerin başlangıç değerlerinin seçimi birden fazla tepeli olabilirlik fonksiyonunun en büyüklenmesinde önemli rol oynamaktadır. Olabilirlik denklemlerinin gerçek çözümlerine uzak başlangıç değerleri verilmesi durumunda yukarıda bahsedilen iteratif yöntemler genel maksimum yerine yerel maksimum değerine ulaşabilir.

Sansürlü ve maskeli örneklemlere dayalı olabilirlik fonksiyonları, genellikle parametrelere göre lineer değildir. Bu sebepten iteratif yöntemlerin, istenilen çözüme ulaştırmama ihtimali göz önüne alındığında daima analitik olarak elde edilen ve ML tahmin edicileri ile aynı asimptotik özelliklere sahip olan modifiye edilmiş en çok olabilirlik tahmin edicilerinin (MMLE, Tiku 1967a, b; 1968a, b, c; 1970; 1973) önemi ortaya çıkmaktadır. Modifiye edilmiş tahmin ediciler aşağıdaki prosedür yardımıyla elde edilebilir.

Aşağıda ölçek parametresi bilindiğinde konum parametresinin modifiye edilmiş en çok olabilirlik tahmin edicisinin elde edilmesindeki prosedür verilmiştir (Tiku ve Akaya, 2004) X X₁, ₂, ,_ X_n, konum parametresi  , ölçek parametresi 

(biliniyor) olan g yoğunluklu bir kitleden alınan n birimlik bir örneklem olmak üzere bu örnekleme dayalı olabilirlik denklemi

 

_{ }

1 ln ; 1 0 n i i L g z        



x , (z_i  x_i ) / (2.21)

şeklinde yazılabilir, burada ,x i_i 1, 2, ,_{ ,} n X X₁, ₂, ,_ X_n örneklemin aldığı değerler ve x



x x₁, , ,_{2 } x_n



şeklindedir. X X₁, ₂, ,_ X_n örneklemine dayalı sıra istatistikleri de

 1  2  n

X  X _ X (2.22)

olmak üzere (2.21) eşitliği, (2.22) de verilen sıra istatistiklerine dayalı olarak

 

 

 

1 ln ; 1 0 n i i L g z        



x , z_{( )i} (x_{( )i}  ) / (2.23)

biçiminde yazılabilir, burada x_{ i} , i1, 2, ,_ n, X_{ 1} X_{ 2} _ X_{ n} sıra istatistiklerinin aldığı değerlerdir.

 i

t , .i standartlaştırılmış sıra istatistiği z_{ i} nin beklene değeri  

 

 



t_i E z_i , i1, 2, ,_ n



olmak üzere g z

 

_{ i} fonksiyonu t_{ i} civarında Taylor serisine açılıp ilk iki terimi alındığında aşağıdaki doğrusal denklik elde edilir.

 

 

 

 



   



 

 i i i i i z t g z g t z t g z z _       _{ }    (2.24)   i izi     ,



1 i n 



Burada

 

 i i z t g z z       _    , i g t

 

 i it i (2.25) dır. Eğer g(z) sınırlı bir fonksiyon ve z_{ i} beklenen değeri, t_{ i} ’ye yaklaşıyorsa,

   





lim ( _i ) ( _{i i i} ) 0

n g z    z  ,



1 i n 



(2.26)

olacaktır. (2.24) ve (2.25) den elde edilen modifiye edilmiş olabilirlik denklemi

 





* 1 ln ln 1 0 n i i i i L L z              



(2.27)

şeklinde yazılabilir. Bu eşitliği bazı çok genel şartlar altında aşağıdaki formda da yazılabilir. 0 ln ln 1 lim *                 L L n n (2.28)

(2.26) ve (2.28)’e dikkatlice bakıldığında bu iki eşitliğin birbirlerine asimptotik olarak denk olduğunu söyleyebiliriz. ’ya ait olan (2.27) denkleminin kesin çözümü MML (modified maxsimum likelihood) tahmini olarak adlandırılır.

  1 1 1 ˆ n n i i i i i x m          _  _ 

 

 ,



  n i i m 1  (2.29)

Kullanılan dağılım simetrik bir dağılım ise t_(i) t_(ni1) şeklinde yazılabilir. Bu nedenle 1    _{n i} i   ,



  n i i 1 0  , _i _ni1



1 i n 



(2.30)

dir. Simetrik bir dağılım için,  nın MML tahmin edicisi aşağıdaki sıra istatistiğinin bir lineer fonksiyonudur,

  1 1 ˆ n i i i x m    



(2.31)

ve görüldüğü üzere bu lineer fonksiyon  dan bağımsızdır. Gerçekte MML tahmin edicisi olan ˆ, asimptotik olarak ML tahmin edicisine denktir.

3. MASKELİ ÖRNEKLEMLER

m bileşenden oluşan bir sistemin yaşam zamanı X ve bozulma gerçekleştiğinde bozulmanın hangi bileşenden kaynaklandığı S ile gösterilsin. Bu durumda,

 Sistemin bozulmasına .i bileşen neden olduğunda

 

S  i

 Sistemin bozulmasına i i₁., ., , ._{2 } i_k , 1  i₁ i_{2 } i_k m bileşenlerden biri neden olduğunda



1 2, , , k



S i i _ i

olacaktır. S kümesi birden fazla elemanlı olduğunda X e maskeli rasgele değişken

denir.

Bu tezde iki bileşenli sistemler kullanılacaktır. İki bileşenden oluşan bir sistemin yaşam zamanı X ve bu bozulmanın hangi bileşenden kaynaklandığı S ile gösterilsin. Bu durumda,

 Sistemin bozulmasına 1. bileşen neden olduğunda

 

1  S

 Sistemin bozulmasına 2. bileşen neden olmuşsa

 

2  S

 Sistemin bozulmasına neden olan bileşen bilinmiyorsa

 

1,2  S

olacaktır. Sistemin bozulmasının hangi bileşenden kaynaklandığı gözlenemediğinde (maskelendiğinde, yani S 

 

1,2 durumunda) X e maskeli rasgele değişken denir.

3.1. İki Bileşenli Seri Sistemler

1i, 1, 2, ,

T i _{ : .i sistemdeki} n 1. bileşenin yaşam zamanı olmak üzere, 11, 12,..., 1n

T T T , f x₁



;₁



olasılık yoğunluk fonksiyonlu ve F x₁



;₁



dağılım fonksiyonlu bağımsız rasgele değişkenler ve T i_2i, 1, 2, ,_{ : .i sistemdeki} n 2.

bileşenin yaşam zamanı olmak üzere, T T₂₁, ₂₂,...,T ,_2n f x₂



;₂



olasılık yoğunluk fonksiyonlu F x₂



; dağılım fonksiyonlu bağımsız rasgele değişkenler olsun. ₂



Ayrıca T_1i ileT i_2i, 1, 2, ,_{ de bağımsız olsun.} n



1 2



min , , 1, 2, ,

i i i

X  T T i _ n olmak üzere yaşam süreleri



X S1, 1

 

, X S2, 2



, ,



X Sn, n



olan ve birbirinden bağımsız çalışan n tane iki

bileşenli seri sistem göz önüne alınsın.

1. Durum

 

, 1, 2, ,

i

S  j i _ n olmak üzere



X S_i, _i 

 

j



,i1, 2, ,_{ rasgele} n

değişkeninin olasılık yoğunluk fonksiyonu aşağıdaki şekilde elde edilebilir:

 



,



i i i i i

A  x  X   x x S  j şeklinde tanımlanmak üzere

 



 



 











 







 









3 3 3 , , 1 i i i i i i ji i j i i i ji i j i i j i j i j i P A P x X x x S j P x T x x T x x P x T x x P T x x F x x F x F x x                            _    _   

olarak yazılabilir. Buradan

 





 





 













 



 



, ₀ 3 0 3 , lim 1 lim 1 i i i X S i _x j i j i j i x j i j i P A f x j x F x x F x F x x x f x F x                  

elde edilir. Dolayısıyla



X S₁, ₁ 

 

j



,



X S₂, ₂ 

 

j



, ,_



X S_n, _n 

 

j



örnekleminin olabilirlik fonksiyonu



1 2



 



3

 



1 , ; n _{j i} 1 _{j i} i L   f x F_ x  



 x

şeklinde elde edilir.

2. Durum

 

1, 2 , 1, 2, ,

i

S  i _ n olmak üzere



X S_i, _i 

 

1, 2 ,



i1, 2, ,_{ rasgele} n

değişkeninin olasılık yoğunluk fonksiyonu aşağıdaki şekilde elde edilebilir:

 



, 1, 2



i i i i i

B  x  X   x x S  şeklinde tanımlanmak üzere

 



 



 







 



, 1, 2 , 1 , 2 i i i i i i i i i i i i i P B P x X x x S P x X x x S P x X x x S                  











 





 







 













 









1 2 2 1 1 2 2 1 1 1 2 2 2 1 , , 1 1 i i i i i i i i i i i i i i i i i i i i i i i i i i P x T x x T x x P x T x x T x x P x T x x P T x x P x T x x P T x x F x x F x F x x F x x F x F x x                                   _    _      _    _   

olarak yazılabilir. Buradan

 





 





 













 









 



 



 



 



, ₀ 1 1 2 0 2 2 1 0 1 2 2 1 , 1, 2 lim 1 lim 1 lim 1 1 i i i X S i _x i i i x i i i x i i i i P B f x x F x x F x F x x x F x x F x F x x x f x F x f x F x                                    

elde edilir. Dolayısıyla



X S₁, ₁ 

 

1, 2 ,





X S₂, ₂ 

 

1, 2 , ,



_



X S_n, _n 

 

1, 2



örnekleminin olabilirlik fonksiyonu



1 2





1

 



2

 



2

 



1

 





1 , ; n _i 1 _{i i} 1 _i i L   f x F x f x F x  



   x

Durum 1 ve Durum 2 göz önüne alınarak, n tane sistemin n tanesinin birinci ₁

bileşenden, n tanesinin ikinci bileşenden kaynaklandığı gözlenip, ₂ n tanesinin ₃

hangi bileşenden kaynaklandığı gözlenemediğinde



X S_i, _i



, i1, 2, ,_ n rasgele değişkeninin olasılık yoğunluk fonksiyonu aşağıdaki şekilde elde edilebilir:



X S1, 1

 

, X S2, 2



, ,



X Sn, n



örnekleminde Si 

 

1 olanlar X11,X12, , X1n1ile,

 

2 i S  olanlar 2 21, 22, , 2n X X _ X ile ve S_i 

 

1, 2 olanlar 3 31, 32, , 3n X X _ X ile gösterilmek üzere



X S₁, ₁

 

, X S₂, ₂



, ,_



X S_n, _n



örmeklemi

1 2 3

11, 12, , 1n , 21, 22, , 2n , 31, 32, , 3n

X X _ X X X _ X X X _ X

şeklinde gösterilebilir, burada n₁n₂n₃  dir. n

Durum 1 ve Durum 2 göz önüne alındığında

1

11, 12, , 1n

X X _ X

2 3

21, 22, , 2n , 31, 32, , 3n

X X _ X X X _ X örnekleminin olabilirlik fonksiyonu





 



 



 



 



 



 



 



 







1 2 3 1 2 1 1 2 1 2 2 1 2 1 1 1 3 2 3 2 3 1 3 1 , ; 1 1 1 1 n n i i i i i i n i i i i i L f x F x f x F x f x F x f x F x            







x

 



₃

 



1 1 i n j i j i j S i f x F_ x         







(3.1)

olarak elde edilir .

3.2. İki Bileşenli Paralel Sistemler

1i, 1, 2, ,

T i _{ : .i sistemdeki} n 1. bileşenin yaşam zamanı olmak üzere, 11, 12,..., 1n

fonksiyonlu bağımsız rasgele değişkenler ve T i_2i, 1, 2, ,_{ : .i sistemdeki} n 2.

bileşenin yaşam zamanı olmak üzere, T T₂₁, ₂₂,...,T ,_2n f x₂



; olasılık yoğunluk ₂



fonksiyonlu F x₂



; dağılım fonksiyonlu bağımsız rasgele değişkenler olsun. ₂



Ayrıca T_1i ileT i_2i, 1, 2, ,_{ de bağımsız olsun.} n



1 2



max , , 1, 2, ,

i i i

X  T T i _ n olmak üzere yaşam süreleri



X S1, 1

 

, X S2, 2



, ,



X Sn, n



olan ve birbirinden bağımsız çalışan n tane iki

bileşenli paralel sistem göz önüne alınsın.

1. Durum

 

, 1, 2, ,

i

S  j i _ n olmak üzere



X S_i, _i 

 

j



,i1, 2, ,_{ rasgele} n

değişkeninin olasılık yoğunluk fonksiyonu aşağıdaki şekilde elde edilebilir:

 



,



i i i i i

A  x  X x  x S  j şeklinde tanımlanmak üzere

 



 



 











 



3 3 , , i i i i i i ji i j i i i ji i j i i P A P x X x x S j P x T x x T x P x T x x P T x                     _F x_j



_i  x



F x_j

 

_{i }F x_j

 

_i

 





 





 

 

 

 

, ₀ 3 0 3 , lim lim i i i X S i _x j i j i j i x j i j i P A f x j x F x x F x F x x f x F x                  

elde edilir. Dolayısıyla



X S₁, ₁ 

 

j



,



X S₂, ₂ 

 

j



, ,_



X S_n, _n 

 

j



örnekleminin olabilirlik fonksiyonu



1 2



 

3

 

1 , ; n _{j i j i} i L   f x F_ x  



x

şeklinde elde edilir.

2. Durum

 

1, 2 , 1, 2, ,

i

S  i _ n olmak üzere



X S_i, _i 

 

1, 2 ,



i1, 2, ,_{ rasgele} n

değişkeninin olasılık yoğunluk fonksiyonu aşağıdaki şekilde elde edilebilir:

 



, 1, 2



i i i i i

B  x  X   x x S  şeklinde tanımlanmak üzere

 



 



 







 



, 1, 2 , 1 , 2 i i i i i i i i i i i i i P B P x X x x S P x X x x S P x X x x S                  











 





 







 

 





   

1 2 2 1 1 2 2 1 1 1 2 2 2 1 , , i i i i i i i i i i i i i i i i i i i i i i i i i i P x T x x T x P x T x x T x P x T x x P T x P x T x x P T x F x x F x F x F x x F x F x                           _    _   _    _

olarak yazılabilir. Buradan

 





 





 

 





   

   

   

, ₀ 1 1 2 0 2 2 1 0 1 2 2 1 , 1, 2 lim lim lim i i i X S i _x i i i x i i i x i i i i P B f x x F x x F x F x x F x x F x F x x f x F x f x F x                            

elde edilir. Dolayısıyla



X S₁, ₁ 

 

1, 2 ,





X S₂, ₂ 

 

1, 2 , ,



_



X S_n, _n 

 

1, 2



örnekleminin olabilirlik fonksiyonu



1 2





1

   

2 2

   

1



1 , ; n _{i i i i} i L   f x F x f x F x  



 x

şeklinde elde edilir.

Durum 1 ve Durum 2 göz önüne alınarak, n tane sistemin n tanesinin birinci ₁

bileşenden, n tanesinin ikinci bileşenden kaynaklandığı gözlenip, ₂ n tanesinin ₃

hangi bileşenden kaynaklandığı gözlenemediğinde



X S_i, _i



, i1, 2, ,_ n rasgele değişkeninin olasılık yoğunluk fonksiyonu aşağıdaki şekilde elde edilebilir:



X S1, 1

 

, X S2, 2



, ,



X Sn, n



örnekleminde Si 

 

1 olanlar X11,X12, , X1n1ile,

 

2 i S  olanlar 2 21, 22, , 2n X X _ X ile ve S_i 

 

1, 2 olanlar 3 31, 32, , 3n X X _ X ile gösterilmek üzere



X S₁, ₁

 

, X S₂, ₂



, ,_



X S_n, _n



örmeklemi

1 2 3

11, 12, , 1n , 21, 22, , 2n , 31, 32, , 3n

X X _ X X X _ X X X _ X

şeklinde gösterilebilir, burada n₁n₂n₃  dir. n

Durum 1 ve Durum 2 göz önüne alındığında

1

11, 12, , 1n

X X _ X

2 3

21, 22, , 2n , 31, 32, , 3n

X X _ X X X _ X örnekleminin olabilirlik fonksiyonu





   

   

   

   





1 2 3 1 2 1 1 2 1 2 2 1 2 1 1 1 3 2 3 2 3 1 3 1 , ; n n i i i i i i n i i i i i L f x F x f x F x f x F x f x F x        







x

 

₃

 

1 i n j i j i j S i f x F_ x      _{ } 







(3.2)