Pareto I Dağılımının lk Bozulma Sansürlü Örnekleme Planına Dayalı Parametrelerinin Tahmini ve Beklenen Test Süresi

(1)

Pareto I Da ılımının lk Bozulma Sansürlü Örnekleme Planına

Dayalı Parametrelerinin Tahmini ve Beklenen Test Süresi

*

Co kun KU

1

_{, Mehmet Fedai KAYA}

1

Özet: Bu çalı mada, ilk bozulma sansürlü örnekleme planı ele alınmı tır. Pareto I da ılımının parametrelerinin yeni tahmin edicileri Menon’un [8] yöntemine benzer olarak elde edilmi ve özellikleri Monte Carlo simulasyon çalı ması yapılarak incelenmi tir. Parametreler için güven aralıkları ve güven bölgeleri elde edilmi tir. Ayrıca ilk bozulma sansürlü örnekleme planına dayalı beklenen test süresi hesaplanmı ve tam örnekleme planın ki ile kar ıla tırılmı tır.

Anahtar Kelimeler: Beklenen test süresi, güven aralı ı, ilk bozulma sansürlü örnekleme planı, ortak güven bölgesi, Pareto I da ılımı.

Parameter Estimation of the Pareto I Distribution and Expected Test Time

based on First Failure-Censored Sampling Plan

Abstract: In this study, first failure-censored sampling plan is considered. Estimators of the parameters of Pareto I distribution are obtained paralel to Menon’s [8] method and their properties are investigated via Monte Carlo simulation. Confidence intervals and joint confidence regions for the parameters are given. Also expected test time is calculated based on first failure-censored sampling plan and it is compared with expected test time of complete sampling plan.

Keywords: Expected test time, confidence interval, first failure-censored sampling plan, joint confidence region, Pareto I distribution.

Giri

(

λ,β

)

I

Pareto da ılımına sahip bir X rasgele de i keninin olasılık yo unluk ve da ılım

fonksiyonları sırasıyla

( )

_x ₌_λβλ_x−(λ+1)_, _x_>_β _>₀_,_λ_>₀ f

( )

_βλ −λ − = x x F 1

eklindedir. Bu da ılım gerçekte Pearson Tip-VI da ılımının özel bir halidir. Bozulma oranı fonksiyonu

( )

_{= x}−1

x

h λ olup azalandır. Pareto I da ılımının beklenen de er ve varyansı, sırasıyla,

( )

X =λβ

(

λ−1

)

−1, λ>1 E

( )

X =β2λ

{

(

λ−1

) (

2 λ−2

)

}

−1, λ>2 Var

biçimindedir. Pareto I da ılımı aynı zaman da Lomax da ılımı olarak da bilinir.

Literatürde Pareto I da ılımının parametreleri ile ilgili istatistiksel sonuç çıkarımı hakkında bir çok makale ve kaynak kitap vardır . Bunlardan bazıları Vännman [11], Lawless [7] , Arnold ve Press [1] , Ouyang ve Wu [9], Balakrishnan ve Aggarwala [2], Soliman [10], Johnson ve ark. [5] ve Wu [12]’dur.

*

Bu makale Co kun Ku ’un doktora tezinin [6] bir kısmıdır. 1

(2)

Menon [8], Weibull da ılımının parametreleri için tam örnekleme dayalı yeni tahmin ediciler tanımlamı ve bu tahmin edicilerin özelliklerini incelemi tir. Bu çalı mada, Balasooriya [3] tarafından öne sürülen ilk bozulma sansürlü örnekleme planı ele alınmı tır. Pareto I da ılımının parametrelerinin yeni nokta tahmin edicileri Menon’un [8] yöntemine benzer olarak elde edilmi ve özellikleri Monte Carlo simulasyon çalı ması yapılarak incelenmi tir. Ayrıca parametrelerin güven aralıkları ve güven bölgeleri elde edilmi , ilk bozulma sansürlü örneklem planına dayalı beklenen test süresi hesaplanmı ve tam örneklem durumu ile kar ıla tırılmı tır.

lk Bozulma Sansürlü Örneklem

Balasooriya [3] tarafından geli tirilen ilk bozulma sansürleme modeli u ekilde tanımlanır: n hacimli k tane ba ımsız(örneklem) grup olsun. Her bir grup ilk bozulma gerçekle inceye kadar

teste tabi tutulsun. Elde edilen k hacimli örnekleme, ilk bozulma sansürlü örneklem denir. Bu tanım u ekilde de verilebilir: X1i,X2i,Κ,X_ni, i=1,2,Κ,k , sürekli F da ılım fonksiyonuna sahip

n hacimli .i örneklem ve bu .i örneklemin sıra istatistikleri i n n i n i n X X X₁_: < ₂_: <Λ < _: olmak üzere k

örneklemin de birbirinden ba ımsız olması ko ulu altında X1i:_n, i=1,2,Κ,k örneklemine ilk

bozulma sansürlü örneklem denir. Balasooriya [3], iki parametreli üstel da ılım için n hacimli k

örnekleme dayalı ilk bozulma sansürlü örnekleme planını incelemi , harcanan test zamanı bakımından ilk bozulma sansürlü örnekleme planının k×n hacimli tam örnekleme planından daha avantajlı oldu unu göstermi tir.

Pareto I Da ılımı Parametreleri çin Yeni Tahmin Ediciler

k n n

n X X

X₁1_: , ₁2_: ,Κ, ₁_: , ParetoI

(

λ,β

)

da ılıma sahip bir kitleden alınmı n hacimlik k örneklemin

birinci sıra istatistikleri olsun. A a ıdaki dönü ümü göz önüne alalım.

(

X

)

i k

Z1i:_n =λlogβ−1 1i:_n , =1,2,Κ,

Kolayca görülebilir ki i n

Z₁_: , her i=1 Κ,2, ,k için −1

n ortalamalı üstel da ılıma sahip bir rasgele

de i kendir. Böylece

( )

1

: 1 = n− Z

E i_n ve Var

( )

Z₁i_:_n = n−2 olur. Bu durumda

(

)

( )

{

( )

i

}

n i n i n i n X VarZ Var X

Z₁_: =λlogβ−1 ₁_: ₁_: =λ2 log ₁_: ifadesi kullanılarak

λ

parametresinin ilk bozulma sansürlü örnekleme dayalı bir tahmin edicisi

(

)

{

}

2 / 1 : 1 2

log

ˆ

ˆ =

− i n

X

ar

V

n

λ

(

)

{

( )

}

( )

2 / 1 2 1 : 1 1 1 2 : 1 1 2 / 1 log log 1 − = − = − ₋ − = k i i n k i i n k X X n k (1)

olarak tanımlanabilir. Burada

{

( )

i

}

n X ar Vˆ log ₁_: ,

( )

1 : 1 logX n ,

( )

2 : 1 log X n ,...,

( )

k n X₁_:

log örneklemi için örneklem varyansıdır. Yani

( )

{

}

=

(

−

)

{

( )

}

−

( )

= − = − 2 1 : 1 1 1 2 : 1 1 : 1 1 log log log ˆ k i i n k i i n i n k X k X X ar V

biçimindedir. Ayrıca ₁_: =λlog

(

β−1 ₁_:

)

( )

₁_: =λ

{

[

log

( )

₁i_:

]

−log

( )

β

}

n i n i n i n X EZ E X Z ifadesi kullanılarak β

parametresinin ilk bozulma sansürlü örnekleme dayalı bir tahmin edicisi

( )

{

}

−

( )

=exp ˆ log ₁_: ˆ−1 ˆ _λ β E Xin n =

( )

−

( )

− = 1 1 : 1 ˆ log 1 exp X nλ k k i i n (2)

olarak elde edilir. Burada

{

( )

}

( )

= − = k i i n i n k X X E 1 : 1 1 : 1 log log

ˆ _{biçimindedir ve λˆ (1)’de tanımlıdır.}

Simulasyon Çalı ması

Delphi 5 programlama dili kullanılarak, n=20, k=20,30,40,50,100,200 ,300,400 ve 500 durumları için 1000’er kez ParetoI

( )

4,2 da ılımdan örneklemler üretildi ve bu örneklemlere dayalı olarak

(3)

ekil 1. Pareto I da ılımının β parametresinin ilk bozulma sansürlü örnekleme dayalı βˆ tahmin edicisinin n=20 durumunda 1000 deneme sonucu aldı ı de erlerin Normal P-P çizitleri

(4)

ekil 2. Pareto I da ılımının λ parametresinin ilk bozulma sansürlü örnekleme dayalı λˆ tahmin edicisinin n=20 durumunda 1000 deneme sonucu aldı ı de erlerin Normal P-P çizitleri

(5)

λˆ ve βˆ tahmin edicilerinin aldı ı de erlerin histogramları ve Normal P-P çizitleri Minitab 13.1 paket programı vasıtasıyla çizdirildi. ekil 1 ve ekil 2,’de görüldü ü gibi k de eri arttıkça, λˆ ve βˆ tahmin edicilerinin aldı ı de erlerin ortalaması sırasıyla 4’e ve 2’ye yakla makta, standart sapması ve Anderson-Darling (AD) istatisti inin aldı ı de er küçülmektedir. Simulasyon sonucu olarak λˆ ve βˆ tahmin edicilerin asimptotik yansızlık, tutarlık ve asimptotik normallik özelliklerine sahip oldu u söylenebilir. Bu özelliklerin teorik olarak gösterilmesi problemi halen açıktır.

Yeni Güven Aralı ı ve Güven Bölgesi

k n n

n X X

X₁1_: , ₁2_: ,Κ, ₁_: ba ımsız ve aynı ParetoI

(

λ,β

)

da ılımından alınmı ilk bozulma sansürlü

örneklem ve ( ) ( ) ( )k

n n

n X X

X₁_:1 < ₁_:2 <Λ < ₁_: , bu örneklemin sıra istatistikleri olsun. k n n

n X X

X₁1_: , ₁2_: ,Κ, ₁_:

ba ımsız ve aynı ParetoI

(

nλ,β

)

da ılımından alınmı k birimlik tam örneklem gibi

görülebilece inden Pareto I da ılımının parametrelerinin ilk bozulma sansürlü örnekleme dayalı güven aralıkları ve güven bölgeleri a a ıdaki gibi elde edilebilir. A a ıdaki dönü üm göz önüne alınsın. ( ) _n

{

_X( )

}

_i _k Y₁_:_ni = λlogβ−1 ₁_:i_n , =1,2,Κ, Gösterilebilir ki ( ) ( ) ( )k n n n Y Y

Y₁_:1 < ₁_:2 <Λ < ₁_: , 1 ortalamalı üstel da ılıma sahip bir kitleden alınmı sıra istatistikleridir. ( )

(

)

(

( ) ( )

)

( ) ( )

(

1

)

: 1 : 1 1 : 1 2 : 1 2 1 : 1 1 1 − − = ∆ − − = ∆ = ∆ k n k n k n n n Y Y Y Y k kY Μ (3)

dönü ümü göz önüne alınsın. ∆i, i=1,2,Κ,k ba ımsız ve 1 ortalamalı üstel da ılıma sahiptir. Böylece ( ) ( )22 1 : 1 1 2 ~ 2 χ κ = ∆ = kY _n ve ( ) ( )

(

)

( ) = = − − = ∆ = k i k i k n i n i Y Y 2 1 2 2 2 1 : 1 : 1 ~ 2 2 χ ε

dir. Aynı zamanda açıktır ki ε ve κ ba ımsız rasgele de i kenlerdir. ξ ve η rasgele de i kenleri a a ıdaki gibi tanımlansın

(

)

( ) ( )

(

)

(

)

( )1 : 1 1 1 : 1 : 1 1 1 _n k i n i n Y k k Y Y k ₋ − = − = = κ ε ξ ( ) = = + = k i i n Y 1 : 1 2 κ ε η Lemma 1. ξ , F2 −k 2,2 da ılımına ve η , ( ) 2 2k

χ da ılımına sahiptir. Aynı zamanda ξ ve η ba ımsızdır (Johnson ve ark.[4]).

(6)

(

δ1,δ2

)

α

F , α sa -kuyruk olasılıklı ve δ ve ₁ δ serbestlik dereceli 2 F da ılımının yüzdeli i

ve

(

( ) ( ) ( )k

)

n n n X X X₁_:1, ₁_:2 ,Κ, ₁_: = n : 1 X olsun. Teorem 1. ( ) ( ) ( )k n n n X X

X₁1_: < ₁_:2 <Λ < ₁_: , ParetoI

(

λ,β

)

da ılımına sahip bir kitleden alınmı ilk

bozulma sansürlü örneklemin sıra istatistikleri olsun. Bu durumda verilen 0<α<1 için β parametresinin 100

(

1−

α

)

% lık bir güven aralı ı,

( − ) ( − ) − 2 2,2 2 2 , 2 2 2 1 , , , k k F F _α ϕ _α ϕ X1:n X1:n eklindedir. Burada

(

)

( )

_[

₍

₎

_]

(

−

)

+ − − − = = t k k t k X k X t k i n n 1 1 1 log log exp , 1 1: 1: 1 i n : 1 X ϕ eklinde tanımlıdır.

spat. Lemma 1’den pivot

( ) ( )

(

)

(

)

( )1 : 1 1 1 : 1 : 1 1 _n k i n i n Y k k Y Y − − = = ξ ( )

{

}

{

( )

}

(

)

{

( )i

}

n i n k i i n X k k X k X : 1 1 : 1 1 1 : 1 1 log 1 log log − − = − − − = β β β 2 , 2 2 −k

F da ılımına sahiptir. 0<α <1 için

( ) ( )

{

}

{

( )

}

(

)

{

( )

}

₍₂ ₂_,₂₎ 2 : 1 1 : 1 1 1 : 1 1 2 , 2 2 2 1 ₁ _log log log − − − = − − − ₋ < − < k i n i n k i i n k F X k k X k X F _α _α β β β olayı ( − ) < < ( − ) − 2 2,2 2 2 , 2 2 2 1 , , k k F F _α β ϕ _α ϕ X1:n X1:n

olayına denktir. Bu da ispatı tamamlar.

Bir ba ka seçenekte, β ’nın üst 100

(

1−α

)

% lık güven limiti ul bulunabilir. O zaman β ’nın üst 100

(

1−α

)

% lık güven aralı ı

(

0,ul

)

olur.

Sonuç 1. ( ) ( ) ( )k

n n

n X X

X₁_:1 < ₁_:2 <Λ < ₁_: , ParetoI

(

λ,β

)

da ılımına sahip bir kitleden alınmı ilk bozulma sansürlü örneklemin sıra istatistikleri olsun. Bu durumda verilen 0<

α

<1 için

β

parametresinin 100

(

1−

α

)

% lık üst güven limiti,

( )

(

,Fα2k−2,2

)

ϕ

X1:n

eklindedir. Burada, ϕ

(

X1:n,t

)

Teorem 1’deki gibi tanımlıdır.

( ) 2

δ α

χ , α sa -kuyruk(right-tail) olasılıklı ve δ serbestlik dereceli Ki-kare da ılımının yüzdeli i olsun. β ve λ parametrelerinin 100

(

1−α

)

% lık güven bölgesi a a ıdaki teoremle verilmi tir.

(7)

Teorem 2. ( ) ( ) ( )k n n

n X X

X₁_:1 < ₁_:2 <Λ < ₁_: , ParetoI

(

λ,β

)

da ılımına sahip bir kitleden alınmı ilk bozulma sansürlü örneklemin sıra istatistikleri olsun. Bu durumda verilen 0<α<1 için β ve λ parametrelerinin 100

(

1−α

)

% lık ortak güven bölgesi, a a ıdaki e itsizliklerin çözümünden elde edilir. ( ) ( ) ( ) ( ) ( ) ( ) < < < < = − − = − + − − − − − + k i i n k k i i n k k k X n X n F F 1 : 1 2 2 1 1 1 : 1 2 2 1 1 2 , 2 2 2 1 1 2 , 2 2 2 1 1 log 2 log 2 , , β χ λ β χ ϕ β ϕ α α α α 1:n n : 1 X X

Burada, ϕ

(

X1:n,t

)

Teorem 1’deki gibi tanımlıdır. spat. Lemma 1’den pivot

( )

{

( )

}

= − = = = k i i n k i i n n X Y 1 1: 1 1 1: log 2 2 λ β η , _{( )}2 2k

χ da ılımına sahiptir ve ξ den ba ımsızdır. 0<α<1 için ( ) ξ α( ) α α < < = − − − − − − + 1 2 , 2 2 2 1 1 2 , 2 2 2 1 1 k k F F P ve ( ) η χ ( ) α χ ₊ ₋_α < < ₋ ₋_α = 1− 2 2 1 1 2 2 1 1 k k P eklindedir. Buradan ( ) ( )

( )

(

)

( )

( ) ( ) ( ) ( )

{

}

( ) α χ β λ χ _α _α α β β β α − = < < < + − + − + < − − = − − + − = − − 1 log 2 , 1 log 1 1 log 1 log 2 2 1 1 1 1: 1 2 2 1 1 2 , 2 2 2 1 : 1 1 : 1 1 : 1 2 , 2 2 2 1 k k i i n k k n n k i i n k X n F X k k X k X F P

Bu ise a a ıdaki ifadeye denktir.

( ) ( ) ( ) ( ) ( ) ( ) < < < < = − − = − + − − − − − + k i i n k k i i n k k k X n X n F F 1 : 1 2 2 1 1 1 : 1 2 2 1 1 2 , 2 2 2 1 1 2 , 2 2 2 1 1 log 2 log 2 , , β χ λ β χ ϕ β ϕ α α α α 1:n n : 1 X X Bu da ispatı tamamlar.

(8)

Sonuç 2. ( ) ( ) ( )k n n

n X X

X₁_:1 < ₁_:2 <Λ < ₁_: , ParetoI

(

λ,β

)

da ılımına sahip bir kitleden alınmı ilk bozulma sansürlü örneklem olsun. O zaman verilen 0<α<1 için β ve λ parametrelerinin

(

1

)

%

100 −α lık ortak güven bölgesi, a a ıdaki e itsizliklerin çözümünden elde edilir.

( )

(

)

( ) ( ) ( ) ( ) < < < < = − − = − + − − − k i i n k k i i n k k X n X n F 1 : 1 2 2 2 1 1 1 : 1 2 2 2 1 1 2 , 2 2 1 1 log 2 log 2 , 0 β χ λ β χ ϕ β α α α n : 1 X

Burada ϕ

(

X1:n,t

)

, Teorem 1’deki gibi tanımlıdır. Beklenen Test Süresi

n

X X

X₁, ₂,Κ, , ParetoI

(

λ,β

)

da ılımından

n

birimlik tam örneklem olsun. Bu durumda beklenen test zamanı E

(

Xn:n

)

’dir. Xn:n rasgele de i keninin olasılık yo unluk fonksiyonu,

( )

_x ₌_n

{

₁₋_βλ_x−λ

}

−1_λβλ_x−(λ+1)

f_n n

eklindedir. Böylece

n

birimlik tam örneklemin beklenen test zamanı a a ıdaki gibidir.

(

)

₌∞

{

₋ −

}

− −( +) 0 1 1 : xn1 x x dx X E _n_n βλ λ n λβλ λ

( )

( ) − = ∞ + − − − = 1 0 1 1 1 n j j j j x d x j n n β λ λ λ _β λβ

( )

(

)

− = − − + − − = 1 0 1 1 1 1 1 n j j j j n nλβ λ (4) k n n n X X

X₁1_: , ₁2_: ,Κ, ₁_: , ParetoI

(

λ,β

)

da ılımından alınmı k birimlik birinci bozulma sansürlü

örneklem ve ( ) ( ) ( )k n n

n X X

X₁1_: < ₁_:2 <Λ < ₁_: , bu örneklemin sıra istatistikleri olsun. Bu durumda beklenen

test zamanı

(

( )k

)

:n X E ₁ dır. k n n n X X

X₁1_: , ₁2_: ,Κ, ₁_: ba ımsız ve aynı ParetoI

(

nλ,β

)

da ılımından alınmı k birimlik tam

örneklem gibi görülebilece inden (4)’den birinci bozulma sansürlü örneklem planı durumunda beklenen test zamanı a a ıda gibi elde edilir.

( )

(

)

−

( )

(

)

= − − + − − = 1 0 1 : 1 1 1 1 1 k j j k n n j j k kn X E λβ λ (5)

(9)

(4) ve (5)’den, n= k =1 Κ,2, ,30 λ =3, β =2 için ilk bozulma sansürlü örneklem planın ve tam örneklem planın beklenen test sürelerinin grafikleri yukarıdaki gibi elde edilmi tir. Grafi e dikkat edilirse ilk bozulma sansürlü örneklem planına dayalı test zamanı Pareto I da ılımının e ik(treshold) parametresine yakla maktadır. Ayrıca k arttıkça tam örnekleme dayalı test süresi

artarken, ilk bozulma sansürlü örnekleme dayalı test süresi azalmaktadır. Bu da ilk bozulma sansürlü örnekleme dayalı test planının süre bakımında ne kadar avantajlı oldu unu göstermektedir.

Uygulama

Teorem 1 ve Teorem 2’deki sonuçları örneklendirmek için ParetoI

( )

3,1 da ılımından n=5

ve k=10 durumunda ilk bozulma sansürlü örneklem üretildi. Üretilen örneklem a a ıdaki

tablodadır.

Tablo 1. Üretilen ilk bozulma sansürlü örneklem

i 1 2 3 4 5 6 7 8 9 10

i

x₁_:₅ 1.0024 1.0076 1.0214 1.0297 1.0343 1.0663 1.0813 1.0855 1.0893 1.2709 (1) ve (2) kullanılarak β ve λ parametrelerinin tahminleri sırasıyla βˆ =0.9954 ve λˆ=2.9000 olarak bulunmu tur. β parametresinin

95 %

’lik güven aralı ını elde etmek için gerekli olan yüzdelikler Minitab 13.1 paket programı kullanılarak a a ıdaki gibi elde edilmi tir.

(18,2) 39.4424 025

.

0 =

F , F0.975₍18,2₎=0.2193 ve F0.05(18,2)=19.4402

Teorem 1 ve Sonuç 1 kullanılarak β parametresinin 95%’lik güven aralıkları, sırasıyla,

(

0.9714,1.0022

)

ve

(

0,1.0020

)

olarak bulunur.

β ve λ parametrelerinin 95%’lik ortak güven bölgesini elde etmek için gerekli olan yüzdelikler Minitab 13.1 paket programı kullanılarak a a ıdaki gibi elde edilmi tir.

(18,2) 78.1835 0127 . 0 = F , F₀_.₉₈₇₃₍₁₈_,₂₎=0.1780 ve F₀_.₀₂₅₃₍₁₈_,₂₎=38.9680 ( ) 36.7027 2 20 0127 . 0 = χ ve χ₀2_.₉₈₇₃_{( )}₂₀ =8.5780

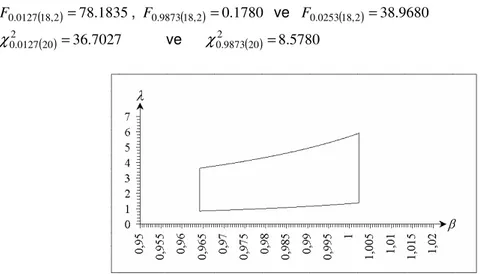
ekil 4.

β

ve

λ

parametrelerinin (6)’daki 95%’lik ortak güven bölgesi

Teorem 2 ve Sonuç 2 kullanılarak β ve λ parametrelerinin 95%’lik ortak güven bölgeleri a a ıdaki gibi elde edilir.

(10)

× × < < × × < < = = 10 1 5 : 1 10 1 5 : 1 ₂ ₅ _log 7027 . 36 log 5 2 5780 . 8 0023 . 1 9643 . 0 i i i i X X β λ β β (6) ve × × < < × × < < = = 10 1 5 : 1 10 1 5 : 1 ₂ ₅ _log 7027 . 36 log 5 2 5780 . 8 0022 . 1 0 i i i i _X X β λ β β

ekil 4’de β ve λ parametrelerinin (6)’daki 95%’lik ortak güven bölgesi görülmektedir. β büyüdükçe güven bölgesi geni lemektedir.

Kaynaklar

[1] Arnold, B.C., Press S.J., Bayesian Estimation and Prediction for Pareto Data, Journal of the American Statistical Association, 84:1079-1084 (1989).

[2] Balakrishnan N., Aggarwala R., Progressive Censoring:Theory, Methods and Applications, Boston, Birkhauser (2000).

[3] Balasooriya, U., Failure-Censored Reliability Sampling Palns for the Exponential Distribution. Journal of Statistical Computations and Simulation, 52:337-349 (1995).

[4] Johnson N.L., Kotz S., Balakrishnan N., Continuous Univariate Distributions, Vol 1, 2nd edn. New York, Wiley (1994).

[5] Johnson N.L., Kotz S., Balakrishnan N., Continuous Univariate Distributions, vol. 2, second ed., John Wiley and Sons, New York (1995).

[6] Ku , C., Bazı Ya am Zamanı Da ılımlarının Parametrelerinin Tam ve Sansürlü Verilere Dayalı Tahmini, Doktora Tezi, Selçuk Üniversitesi, Fen Bilimleri Enstitüsü (2004).

[7] Lawless J.F., Statistical Models and Methods for Lifetime Data, New York, Wiley (1982).

[8] Menon, M.V., Estimation of the Shape and Scale Parameters of The Weibull Distribution, Technometrics, 5: 175-182 (1963).

[9] Ouyang L.-Y., Wu S.-J., Prediction Intervals for an Ordered Observation From a Pareto Distribution. IEEE Transactions on Reliability, 43:264-269 (1994).

[10] Soliman A.A., Bayes Prediction in A Pareto Lifetime Model with Random Sample Sizes. The Statistician 49 51-62 (2000).

[11] Vännman K., Estimators based on Order Statistics from a Pareto Distribution, J.Amer.Stat. Assoc., 71:704-708 (1976).

[12] Wu S.-J., Estimation for the Two-Parameter Pareto Distribution under Progressive Censoring with Uniform Removals, J. Stat. Comp. Simul., 73:125-134 (2003).