İbrahim ÇERİ
Dumlupınar Üniversitesi
Lisansüstü Eğitim Öğretim ve Sınav Yönetmeliği Uyarınca Fen Bilimleri Enstitüsü Matematik Anabilim Dalında
YÜKSEK LİSANS TEZİ Olarak Hazırlanmıştır.
Danışman: Doç. Dr. Ahmet BOZ
LİNEER KESİR MERTEBELİ
DİFÜZYON DALGA DENKLEMİNİN ÇÖZÜMLERİ
İbrahim ÇERİ
Matematik, Yüksek Lisans Tezi, 2019 Tez Danışmanı: Doç. Dr. Ahmet Boz
ÖZET
Bu tezde lineer kesir mertebeli difüzyon dalga denklemlerinin bazı çözümleri incelenmiştir. Günümüzde oldukça ilgi gören kesir türev mertebeli diferansiyel denklemler sınıfından olan bu denklemlerin çözümleri de son yıllarda ilgi görmektedir.
Bu çalışma altı bölümden oluşmaktadır. İlk bölüm giriş bölümüdür. İkinci bölümünde tezin içinde kullanılacak temel kavramlar ve denklemler tanıtılmıştır. Üçüncü bölümde kesir türevli difüzyon ve difüzyon dalga denklemlerinin Petrov-Galerkin yöntemi ile kuadratik B-Spline baz fonksiyonları kullanılarak elde edilen çözümleri incelenmiştir (Esen vd., 2014). Dördüncü bölümde aynı denklemlerin B-Spline Kollokasyon yöntemiyle çözümlerinden söz edilmiştir (Esen vd., 2015). Beşinci bölümde ise kesir difüzyon denklemin serbest güç durumu için kollokasyon çözümleri ele alınmıştır (Esen vd., 2013). Son bölümde ise kesir türevli difüzyon denkleminin B-Spline kollokasyon yöntemi ile farklı bir çözümü incelenmiştir (Esen vd., 2015). Uygulanan çözüm yöntemlerine ait nümerik örnekler verilmiş ve 𝐿2 , 𝐿∞ hata normları ayrı ayrı ele alınmıştır.
Anahtar Kelimeler : Difüzyon Denklemi, Difüzyon Dalga Denklemi, Kollokasyon Yöntemi, Petrov-Galerkin Yöntemi.
SOLUTIONS OF THE LINEAR FRACTIONAL DIFFUSION WAVE EQUATION
İbrahim ÇERİ
Mathematics, M.S. Thesis, 2019 Thesis Supervisor: Assoc. Prof. Dr. Ahmet Boz
SUMMARY
In this thesis, solutions of the linear fractıonal diffusion wave equation are surveyed. The solutions of these equations, which are in the fractional differential equations category, are also popular in resent year.
This work consists of six parts. The first part is the entry part In the first part In the second part, basic concepts and equations which is going to be used in thesis are presented. In the third part, the solutions of fractional diffusion and diffusion-wave equations obtained by using Petrov-Galerkin method and Quadratic B-Spline basic functions are studied (Esen vd., 2014). In the fourth part, the solutions of the same equations with the B-Spline collocation method are mentioned (Esen vd., 2015). In the fifth part, collocational solutions of fractional diffusion for free power state are discussed (Esen vd., 2013). In the final past, a different solution of fractional diffusion equation with B-Spline collocation is analyzed. Numerical examples of applied solution methods are given and also 𝐿2 𝑎𝑛𝑑 𝐿∞ error norms are analyzed differently.
Keywords : Diffusion Equation, Diffusion-Wave Equation, Collocation method, Petrov-Galerkin Method.
TEŞEKKÜR
Bu çalışmayı hazırlama ve yüksek lisans eğitimi sürecinde bana yol gösteren, bilgi ve tecrübelerini paylaşan hocam ve danışmanım sayın Doç. Dr. Ahmet BOZ’a teşekkürlerimi sunarım. Ayrıca hayatım boyunca desteklerini esirgemeyen aileme de teşekkürü borç bilirim.
İÇİNDEKİLER Sayfa ÖZET……….……….…v SUMMARY………..vi ŞEKİLLER DİZİNİ………....x ÇİZELGELER DİZİNİ………..xi 1. GİRİŞ ………...1 2. TEMEL KAVRAMLAR……….3
2.1. Difüzyon ve Difüzyon Dalga Denklemi………...3
2.2. Sonlu Eleman Metodu…...………...4
2.2.1 Ağırlıklı kalanlar yöntemi………...5
2.2.2. Petrov-Galerkin yöntemi………...….6
2.2.3. Kollokasyon (collocation) yöntemi………...6
2.3. Gamma Fonksiyonu………..7
2.4. Mittag-Leffler Fonksiyonları………...7
3. KESİR TÜREVLİ DİFÜZYON VE DİFÜZYON DALGA DENKLEMLERİNİN PETROV-GALERKİN YÖNTEMİYLE ÇÖZÜMLERİ……….9
3.1. Giriş…...………...9
3.2. Kuadratik B-Spline Baz Fonksiyonların Petrov-Galerkin Çözümleri………....10
3.3. Başlangıç Durumu………..……16
3.4. Nümerik Örnekler………...16
3.5. Sonuç……….………..……19
4. KESİR TÜREVLİ DİFÜZYON VE DİFÜZYON DALGA DENKLEMLERİNİN B-SPLİNE KOLLOKASYON YÖNTEMİYLE ÇÖZÜMLERİ………...20
4.1. Giriş………...20
4.2. Kübik B-Spline Sonlu Eleman Kollokasyon Yöntemi………...….21
İÇİNDEKİLER (devam)
Sayfa
4.4. Nümerik Örnekler………...25
4.5. Sonuç………...……28
5. KESİR TÜREVLİ DİFÜZYON DENKLEMİNİN SERBEST GÜÇ DURUMU İÇİN NÜMERİK ÇÖZÜMÜ………...……....…29
5.1. Giriş……..….………...……...29
5.2. Kübik B-Spline Sonlu Eleman Kollokasyon Çözümleri………...….30
5.3. Başlangıç Durumu ………...31
5.4. Nümerik Örnekler………...…..33
5.5. Sonuç……….………..35
6. KESİR TÜREVLİ DİFÜZYON DENKLEMİNİN B-SPLİNE KOLLOKASYON YÖNTEMİYLE FARKLI ÇÖZÜMÜ………....36
6.1. Giriş………...……….36
6.2. Kübik B-Spline Sonlu Eleman Kollokasyon Çözümleri………..………...37
6.3. Başlangıç Durumu………...39
6.4. Nümerik Örnekler………...40
6.5. Sonuç………...…………41
7. SONUÇ………...……...42
ŞEKİLLER DİZİNİ
Şekil Sayfa 3.1. ∆t=0,00007 ve N=40 için farklı zamanlardaki 𝑢 (𝜋
2 , 𝑡) nümerik çözümler…………..17
4.1. Farklı zaman adımlarında kesir difüzyon denklemin 𝛾=0,5 ve N=40 değerleri için elde edilen nümerik sonuçlar….………...………...26 4.2. Farklı zaman adımlarında 𝛾 = 1,50 𝑣𝑒 𝑁 = 40 değerleri için kesir difüzyon dalga
denklemin nümerik sonuçlar….………..………28 5.1 Kesir difüzyon denklemin 𝛾=0,50, N=40, ∆t=0,0001, t=0,001, t=0,01, t=0,1 değerleri için elde edilen nümerik sonuçlar...………..………...…33 5.2 Kesir difüzyon denklemin 𝛾=0,75, N=40, ∆t=0,0001, t=0,001, t=0,01, t=0,1
değerleri için elde edilen nümerik sonuçlar………..…………..…….…33 6.1. t=1, t=4, t=7 ve t=10 zamanlarında 𝑎=0,50, ∆t=0,0001, N=40 değerleri için
ÇİZELGELER DİZİNİ
Çizelge Sayfa 3.1. Kesir difüzyon denklemin N=40, ∆t=0,00007, tf=0,35 değerleri için farklı
𝛾 değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması…...………...17 3.2. Kesir difüzyon denklemin 𝛾=0,50, ∆t=0,00007, 𝑡𝑓=0,35 değerleri için farklı
N değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması………..…………...18 3.3. Kesir difüzyon dalga denklemin N=40, ∆t=0,00075, tf=3,35 değerleri için farklı
𝛾 değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması……….…18 3.4. Kesir difüzyon dalga denklemin 𝛾=1,50, ∆t=0,00075, 𝑡𝑓=3,35 değerleri için farklı
N değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması…...………..…19 4.1. Kesir difüzyon denklemin N=40, ∆t=0,0007, tf=0,35 değerleri için farklı
𝛾 değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması….……….……25 4.2. Kesir difüzyon denklemin 𝛾=0,50, ∆t=0,0007, tf=0,35 değerleri için farklı
N değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması…...………..…25 4.3. Kesir difüzyon denklemin N=40, ∆t=0,0007 değerleri için farklı
𝛾 ve t değerleri için 𝐿2 𝑣𝑒 𝐿∞ hata normları………...………...26
4.4. Kesir difüzyon dalga denklemin N=40, ∆t=0,0075, tf=3,35 değerleri için
farklı 𝛾 değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması.………...27 4.5. Kesir difüzyon dalga denklemin N=40, ∆t=0,0075, tf=3,35 değerleri için
farklı N değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması………....27 4.6. Kesir difüzyon dalga denklemin N=40, ∆t=0,0075 değerleri i.in farklı
𝛾 ve t değerlerindeki L2 ve 𝐿∞ hata normları……….…..28
5.1. Farklı N değerlerine karşılık 𝛾=0,50, ∆t=0,001, tf=0,1 değerleri için
nümerik ve analitik çözümlerin karşılaştırılması ve L2 ve 𝐿∞ hata normları…...….…..34
5.2. Farklı ∆t değerlerine karşılık 𝛾=0,50, N=40 ve tf=0,1 değerleri için nümerik
ve analitik çözümlerin karşılaştırılması ve L2 ve 𝐿∞ hata normları…...………..34
5.3. Farklı N değerlerine karşılık 𝛾=0,75, ∆t=0,001 ve tf=0,1 değerleri için
nümerik ve analitik çözümlerin karşılaştırılması ve L2 ve 𝐿∞ hata normları…...…….35
6.1. 𝑎’nın farklı değerlerinde N=40, ∆t=0,0001 ve tf=0,1 değerleri için nümerik
ve analitik çözümlerin karşılaştırılması ve L2 ve 𝐿∞ hata normları…...……….….40
6.2. N’nin farklı değerlerinde 𝑎=40, ∆t=0,0001 ve tf=0,1 değerleri için nümerik
1. GİRİŞ
Son zamanlarda kesir mertebeden türevler mühendislik, fizik, kimya gibi alanlarda artarak ilgi gören bir konu haline gelmiştir. Bu alanlardaki problemler kesir türevi içeren matematiksel modeller yardımıyla başarıyla tanımlanmıştır. Aslında tam mertebeden olmayan türev ve integral alma işlemleri yeni sayılmaz. Bu konu ile ilgili hemen hemen tüm fikirlerin bulunduğu Oldham (1974) tarafından yazılmış bir eser bulunmaktadır. Ancak son birkaç yıldır birçok araştırmacı polimer bilimi gibi çeşitli uygulama alanlarına sahip kesir mertebeli türev ve integralleri daha çok kullanmaya başlamışlardır.
Kontrol teorisi (Hilfer, 2000), nakliye problemleri (Sokolov vd., 2002) tümör konusundaki çalışmalar (Iomin vd.) viskoelastik ve viskoplastik akışı (Diethelm ve Freed, 1999) alanlarındaki çalışmalar kesir mertebeden türevlerin kullanıldığı alanlardan bazılarıdır. Ayrıca Podlubny (1999) çalışmasında kesir mertebeden türevlere ait en önemli uygulamalara örnekler vermiştir. Mainardi (1995), Mainardi ve Paradisi (1997) akışkanlar mekaniğine ait problemlerle bağlantılı olarak kesir mertebeden difüzyon dalga denklemlerini incelemiştir. Kilbas vd. (2006), Ray (2007) ve Agrawal (2002) çalışmalarında çeşitli teknikler kullanarak birçok analitik çözüm incelemişlerdir. Gorenflo vd. (2002), Lynch vd.(2003), Meerschaert ve Tadjeran (2004), Langlands ve Henry (2005), Yuste ve Acedo (2005), Karatay vd.( 2011) çalışmalarında da kesir mertebeden türevlerin uygulamalı matematik konularına çeşitli uygulamaları yapmışlardır.
Kesir mertebeden türevlerin çözümü için farklı yöntemler uygulanmıştır. Örneğin Sun vd. (2011), zaman kesir mertebeli diferansiyel denklemler için yarı-analitik çözümler elde etmişlerdir. Sweilan vd. (2012), zaman kesir mertebeli diferansiyel denklemlerin çözümü için Crank-Nicolson formülasyonu yardımıyla sonlu farklar yöntemini kullanmıştır. Monami ve Odibat (2006), akışkanlar mekaniğinde ortaya çıkan lineer kesir mertebeli kısmi diferansiyel denklemlerin çözümü için Adomian ayrıştırma metodunu ve varyasyonel iterasyon metodunu kullanmıştır. Çelik ve Duman (2012), Riesz kesir türevi kullanarak kesir mertebeli difüzyon denklemini Crank-Nicolson metodu ile çözümünü incelemişlerdir. Sun vd. (2011), zaman kesir mertebeli difüzyon denklemi için yarı-analitik sonlu elemanlar yöntemi kullanmıştır. Murillo ve Yuste (2011), Caputo formunda tanımlanan kesir türevli difüzyon ve difüzyon dalga denkleminin çözümü için kapalı sonlu fark yöntemini kullanmışlardır. Sweilam vd. (2012), kesir mertebeli difüzyon denkleminin çözümü için Crank-Nicolson sonlu farklar yöntemi gibi teknikler uygulamışlardır. Tadjeran vd. (2006), kesir mertebeden difüzyon denkleminin çözümü için 2. mertebeden doğruluğa sahip nümerik yaklaşımlar kullanmışlardır. Lin ve Xu (2007), aynı
denklemin çözümü için sonlu fark yaklaşımını kullanmışlardır. Daftardar –Gejji ve Bhalekar (2008), yeni iteratif yöntemle diferansiyel dalga denklemini çözmüşlerdir. Khader (2010), kesir difüzyon denklemin çözümüne ait ve Garg ve Manohar (2010), difüzyon dalga denkleminin çözümüne ait çeşitli çalışmalar yapmışlardır. Mitkowski (2011), kesir mertebeli difüzyon denklemin nümerik çözüm algoritmalarında bazı iyileştirmeler önermiştir. Khader vd. (2011), difüzyon denklemi için benzer iyileştirme önerileri sunmuştur. Hanert (2011), konum-zaman kesir mertebeli difüzyon denkleminin çözümü için esnek nümerik algoritmalar önermiştir. Heydari vd. (2015), zaman-kesir mertebeli difüzyon dalga denklemi için Wavelets metodunu uygulamışlardır. Yuste (2006), kesir difüzyon denklemleri için ağırlıklı ortalama sonlu fark metodunu kullandı. Langlands ve Henry (2005), kesir difüzyon denkleminin çözümü için kapalı nümerik algoritmanın kararlılığını ve doğruluğunu araştırdı. Murio (2008), bir boyutlu lineer zamanlı kesir difüzyon denklemin çözümü için kapalı koşulsuz kararlı nümerik bir yöntem geliştirdi. Bunun için Caputo kesir türevini kullandı. Yuste ve Acedo (2005), adi diferansiyel denklemin çözümünde iyi bilinen ileri zaman merkezi konum metodu ile Riemann-Riouville türevinin Grünwald-Letnikov ayrıştırmasını birleştirerek kesir difüzyon denkleminin çözümünü elde etmişlerdir.
2. TEMEL KAVRAMLAR
2.1. Difüzyon ve Difüzyon Dalga Denklemi
Klasik teoride difüzyon, madde parçacıklarının yüksek yoğunluklu bir ortamdan düşük yoğunluklu bir ortama hareket etmesidir. Örneğin sıkılan parfümün havada yayılması o parfümün difüzlenmesi sebebiyledir. Aynı şekilde şekerin suda çözünmesi, moleküllerin biyolojik zarlardan geçebilmesi, kremlerin vücut içine alınabilmesi bu maddelerin difüzlenmesi sebebiyledir.
Literatürde difüzyon olayı normal ya da Fickian difüzyon olarak da adlandırılır. Normal difüzyon denmesinin sebebi bu parçacıkların normal (Gaussian) dağılım eğrisi şeklinde davranış göstermeleridir. Bu sebeple difüzyon denklemlerin çözümü olarak elde edilen fonksiyon bir Gauss fonksiyonudur.
Ancak doğada var olan bazı süreçlerde genele uymayan, yani normal olmayan dağılımlar gözlenmiştir. Yarı iletken malzemeler içindeki elektron hareketleri buna örnek olarak verilebilir. Bu durum da bize Gauss olmayan fonksiyonların varlığını ve bu fonksiyonları çözüm olarak kabul eden difüzyon denklemlerin tanımlanabileceğini ortaya koymuştur. Yeni tanımlanacak bu denklemler ise kesir difüzyon (anormal difüzyon) denklemler olacaktır. Kesirli difüzyon denklemleri likit kristaller, camlar, polimerler, protein ve biyosistemler gibi pek çok sistemin anormal davranışlarının açıklanmasında kullanılabilir.
𝑢(𝑥, 𝑡) belli bir 𝑥 ∈ 𝑅 noktasında ve t anında bir dağılımın yoğunluğunu ifade etsin. Klasik difüzyon denklemi
𝜕
𝜕𝑡𝑢(𝑥, 𝑡) = 𝜕2
𝜕𝑥2𝑢(𝑥, 𝑡)
biçimindedir. Zaman (t) ve uzay (x) değişkenlerine bağlı olarak tanımlanan 1. ve 2. mertebeden türevlerin söz konusu problemin yapısına uygun kesirli türevlerle yer değiştirmesi sonucunda ortaya çıkan yeni diferansiyel denklem artık kesirli difüzyon (anormal difüzyon) problemini ifade etmektedir (Avcı, 2013).
2.2. Sonlu Eleman Metodu
Sonlu eleman metodu (SEM), pek çok karmaşık problemin çözümü için kullanılabilen bir nümerik yöntemdir. Metot ilk kez 1956’da uçakların yapısal problemlerinin analizinde kullanılmıştır (Turner vd., 1956). Yaklaşık 10 yıl sonra farklı problem tiplerinin çözümleri için metodun potansiyeli tanınmıştır. Yıllar geçtikçe de SEM geniş bir alana hitap eden problemlerin çözümünde en iyi metodlardan biri olmuştur. Hatta SEM uygulamalı matematikçiler için aktif araştırma alanlarından biri haline gelmiştir. Metodun popüler olmasının ana nedenlerinden biri, genel bir bilgisayar programının yazılabilmesi ve herhangi bir problemin çözümü için kullanılabilmesidir.
Literatürde, üçgensel bölgeler üzerinde tanımlanmış parçalı sürekli fonksiyonların kullanımını içeren SEM’e benzer bir yaklaşımı 1943 yılında ilk kez Courant ileri sürmüştür. Günümüzde SEM’in temel fikri Turner vd. (1956) ile Argyris ve Kelsey (1954-1955)’in çalışmalarına dayanır. Sonlu eleman ismi, Clough (1960) tarafından türetilmiştir. Turner vd.’nin çalışmaları (1956), SEM’in geliştirilmesinde kilit noktalardan biri olarak görülmüş ve uçak yapısının analizi için basit sonlu elemanlar uygulamasını sunmuşlardır. Ayrıca bilgisayarların gelişmesiyle birlikte sonlu eleman metodunun uygulanması artarak ilerleme kaydetmiştir. Zienkiewicz ve Cheung (1967) metodun geniş yorumunu ve herhangi probleme uygulanmasını göstermişlerdir. SEM’in bu geniş yorumuyla, Galerkin ve en küçük kareler gibi ağırlıklı kalan yöntemleri kullanılarak türetilebilen sonlu eleman denklemleri bulunmuştur. Metot, yapı mekanikleri alanlarında geniş çapta kullanılmasının yanı sıra ısı iletimi, akış dinamiği, sızıntı akışları, elektrik ve manyetik alanlar gibi alanlarda da başarıyla uygulanmıştır. Günümüzde SEM, bilim insanlarınca ele alınan pek çok alanda popülaritesini sürdürmektedir.
SEM, diğer yöntemlerle kıyaslandığında oldukça fazla avantaja sahiptir. Düzensiz şekle sahip yapıları ve diğer yöntemlerle modellenemeyen farklı, karmaşık bölgeleri kolay bir şekilde modelleyebilir. Bunun yanında, eleman denklemleri ayrı ayrı oluşturulabildiği için farklı malzemelerden oluşan yapıları modelleyebilir. Ayrıca, sınır şartlarının değişmesi sonlu eleman modelini değiştirmediği için çok farklı sınır şartları ile birlikte kullanılabilir. Gerekli olması durumunda elemanların büyüklükleri ya da modeli değiştirilebilir (Bayraktar, 2016).
2.2.1 Ağırlıklı kalanlar yöntemi
Bir diferansiyel denklemin elde edilen yaklaşık çözümleri ile gerçek çözümleri arasındaki farkın, sıfırdan farklı bir ağırlık fonksiyonu ile çarpıldıktan sonra toplamlarının minimize edilmesine ağırlıklı kalanlar (rezidü) yaklaşımı denir. Bu yaklaşıma dayanan yöntemlere ise ağırlıklı kalanlar yöntemi denir. Bu yöntem, varyasyonel yöntemler ile kıyaslandığında daha avantajlıdır. Çünkü ağırlıklı kalanlar yöntemi sayesinde her denklemin ağırlıklı integral formu oluşturulabilir. Ağırlıklı integral form, problemin sınır şartlarından hiçbirini içermez. Dolayısıyla, ağırlık fonksiyonları seçilirken yaklaşık çözümün hem doğal hem de temel sınır şartlarını sağlayacak biçimde olmasına dikkat edilmelidir. Ağırlıklı kalanlar yöntemini anlatabilmek için V bölgesinde
𝐴(𝑢) = 𝑓 (2.1) operatör denklemi dikkate alınır. Burada A bir operatör, u bağımlı değişken ve f bağımsız değişkenlerin bir fonksiyonu olarak tanımlanır. (2.1) denklemindeki u çözümü için
𝑢𝑁 = ∑𝑁𝑗=1𝑎𝑗𝜑𝑗+ 𝜑0 (2.2)
biçiminde bir yaklaşım tanımlanır. (2.1) denkleminde (2.2) ile verilen 𝑢𝑁 yaklaşık çözümü
yerine yazıldığında 𝑓𝑁= 𝐴(𝑢𝑁) fonksiyonu elde edilir ki bu fonksiyonun f’ye eşit olma
zorunluluğu yoktur. 𝑓𝑁 𝑖𝑙𝑒 𝑓 arasındaki farka
𝑅 = 𝑓𝑁− 𝑓 = 𝐴(∑𝑁𝑗=1𝑎𝑗𝜑𝑗+ 𝜑0) − 𝐴(𝑢) ≠ 0 (2.3)
yaklaşımın kalanı denir. Burada R kalan fonksiyonu, hem 𝑎𝑗 parametresine hem de 𝜑𝑗
ifadelerinden dolayı konuma bağlıdır. 𝑎𝑗 parametrelerini tespit edebilmek için
∫ 𝜓𝑣 𝑖(𝑥, 𝑦)𝑅(𝑥, 𝑦, 𝑎)𝑑𝑥𝑑𝑦 = 0, 𝑖 = 1,2,3, … … … , 𝑁 (2.4)
integrali sıfıra eşitlenerek R kalanı sıfırlanmaya zorlanır. Burada V iki boyutlu bir bölge ve 𝜓𝑖’ler ise ağırlıklı kalan fonksiyonlarıdır. Seçilecek bu fonksiyonların kümesi lineer bağımsız
olmalıdır. Aksi takdirde (2.4) integralinden elde edilen denklemler çözülemez. Galerkin ve Petrov-Galerkin yöntemleri ağırlıklı kalanlar yönteminin bazılarıdır (Bayraktar, 2016).
2.2.2. Petrov-Galerkin yöntemi
𝜓𝑖 ağırlık fonksiyonları ile 𝜑𝑖 yaklaşım fonksiyonları 𝜑𝑖 ≠ 𝜓𝑖 olacak biçimde seçilirse
bu yöntem Petrov-Galerkin olarak isimlendirilir. A lineer bir operatör olmak üzere V bölgesinde (2.4) yaklaşımı ∑(∫ 𝜓𝑖𝐴(𝜑𝑖)𝑑𝑥𝑑𝑦)𝑎𝑖 = ∫ 𝜓𝑗[𝑓 − 𝐴(𝜑0)]𝑑𝑥𝑑𝑦 𝑉 𝑉 𝑁 𝑖=1 veya ∑ 𝐴𝑖𝑗 = 𝐹𝑖 𝑁 𝑖=1
şeklinde yazılabilir. Bu yöntemde elde edilen [𝐴𝑖𝑗] katsayılar matrisi simetrik olmayabilir. Bu
durumun matematiksel karşılığı 𝐴𝑖𝑗 ≠ 𝐴𝑗𝑖 biçimidir (Bayraktar, 2016).
2.2.3. Kollokasyon (collocation) yöntemi
Bu yöntemde V çözüm bölgesinden seçilen N adet 𝑥𝑗 = (𝑥𝑗, 𝑦𝑗) kollokasyon noktasında kalanın sıfır olması gerekir. Başka bir deyişle,
𝑅(𝑥𝑗, 𝑦𝑗, 𝑎𝑗) = 0, 𝑗 = 1,2, … . . 𝑁
olmalıdır. 𝑥𝑗 kollokasyon noktaları, denklem sisteminin iyi şartlı olmasını sağlayacak şekilde
seçilmelidir. Bu yöntemde ağırlık fonksiyonu 𝜓𝑗 = 𝛿(𝑥 − 𝑥𝑗) olur ve (2.4) denkleminde yerine
yazılırsa
∫ 𝛿(𝑥 − 𝑥𝑗)𝑅(𝑥, 𝑎𝑖)𝑑𝑥𝑑𝑦 = 0 𝑉
veya
𝑅(𝑥𝑗, 𝑎𝑗) = 0
elde edilir. Burada 𝛿(𝑥) Dirac delta fonksiyonudur ve
∫ 𝑓(𝑥)𝛿(𝑥 − 𝑥𝑗)𝑑𝑥𝑑𝑦 = 𝑓(𝑥𝑗)
𝑉
2.3. Gamma Fonksiyonu
𝛤, 𝑔𝑎𝑚𝑚𝑎 𝑓𝑜𝑛𝑘𝑠𝑖𝑦𝑜𝑛𝑢, ∀ 𝑧 ∈ 𝐶\{… . . −2, −1,0} 𝑖ç𝑖𝑛
𝛤(𝑧) = ∫ 𝑥𝑧−1𝑒−𝑥𝑑𝑥 ∞
0
şeklinde tanımlanır. Ayrıca
𝛤(𝑥) = lim 𝑛→∞ 𝑛! 𝑛𝑥 𝑥(𝑥 + 1) … … (𝑥 + 𝑛) dir.
2.4. Mittag-Leffler Fonksiyonları
Mittag-Leffler fonksiyonları (Mittag-Leffler G.) kesirli diferansiyel konusunda yaygın kullanım alanları bulan oldukça önemli bir fonksiyondur.
Üstel fonksiyon ez, tamsayı dereceden diferansiyel denklemler teorisinde çok önemli bir
rol oynar. Mittag-Leffler fonksiyonun bir parametreli genelleştirilmiş şekli
𝐸𝑎(𝑥) = ∑
𝑥𝑘
𝛤(𝑎𝑘+1)
∞
𝑘=0 (2.5)
ile Mittag-Leffler tarafından verilmiştir.
Mittag-Leffler tipi iki parametreli fonksiyona genelleştirme ise ilk olarak Agrawal ve Humbert tarafından Laplace dönüşüm tekniği kullanılarak yapılmış olup, kesirli dereceden diferansiyel hesapta önemli bir yere sahiptir.
𝐸𝛼,𝛽(𝑧) = ∑
𝑧𝑘
𝛤(𝑎𝑘+𝛽)
∞
𝑘=0 (2.6)
seri açılımı ile verilir. (2.6) denkleminden
𝐸1,1(𝑧) = ∑ 𝑧𝑘 𝛤(𝑘+1)= ∑ 𝑧𝑘 𝑘! = 𝑒 𝑧 ∞ 𝑘=0 ∞ 𝑘=0 (2.7) 𝐸1,2(𝑧) = ∑ 𝑧𝑘 𝛤(𝑘+2)= ∑ 𝑧𝑘 (𝑘+1)!= ∞ 𝑘=0 ∞ 𝑘=0 1 𝑧∑ 𝑧𝑘+1 (𝑘+1)!= ∞ 𝑘=0 𝑒𝑧−1 𝑧 (2.8)
𝐸1,3(𝑧) = ∑ 𝑧𝑘 𝛤(𝑘+3)= ∑ 𝑧𝑘 (𝑘+2)!= ∞ 𝑘=0 ∞ 𝑘=0 1 𝑧2∑ 𝑧𝑘+2 (𝑘+2)!= ∞ 𝑘=0 𝑒𝑧−1−𝑧 𝑧2 (2.9) ve en genel haliyle 𝐸1,𝑚(𝑧) = 1 𝑧𝑚−1{𝑒 𝑧− ∑ 𝑧𝑘 𝑘 ∞ 𝑘=0 } (2.10) elde edilir.
Hiperbolik sinüs, hiperbolik kosinüs, Mittag-Leffler fonksiyonun özel birer durumlarıdır.
𝐸
2,1(𝑧
2) = ∑
𝑧2𝑘 𝛤(2𝑘+1)= ∑
𝑧2𝑘 (2𝑘)!= cosh (𝑧)
∞ 𝑘=0 ∞ 𝑘=0 (2.11)𝐸
2,2(𝑧
2) = ∑
𝑧2𝑘 𝛤(2𝑘+2)= ∑
𝑧2𝑘+1 (2𝑘+1)!=
∞ 𝑘=0 ∞ 𝑘=0 sinh (𝑧) 𝑧 (2.12)3. KESİR TÜREVLİ DİFÜZYON ve DİFÜZYON DALGA
DENKLEMLERİNİN PETROV-GALERKİN YÖNTEMİYLE
ÇÖZÜMLERİ
3.1. Giriş
Kesir mertebeli kısmi diferansiyel denklemlerin çözümleri için pek çok nümerik metod mevcuttur. Yuste (2006) çalışmasında kesir mertebeli difüzyon ve kesir mertebeli difüzyon dalga denkleminin çözümü için sonlu elemanlar yöntemi kullanmıştır. Bu yöntemde kolaylık olması açısından çözüm bölgesi alt aralıklara bölünür. Böylece düğüm noktaları oluşur. Düğüm noktaları arasında da elemanlar elde edilir. Bu alt aralıklarda elde edilen çözüm genelleştirilerek denklemin çözümü haline gelir.
Bu çözüm metodu için aşağıdaki difüzyon model problemi kullanılmıştır;
𝜕𝛾𝑢 𝜕𝑡𝛾
= 𝐾
𝜕2𝑢 𝜕𝑥2 (3.1) Burada, 𝜕𝛾 𝜕𝑡𝛾𝑓(𝑡) = 1 𝛤(𝑛−𝛾)∫ (𝑡 − 𝜏) 𝑛−𝛾−1 𝑡 0 𝜕𝑛𝑓(𝜏) 𝜕𝑡𝑛 𝑑𝜏 𝑛 − 1 < 𝛾 < 𝑛 (3.2)Caputo anlamında kesir mertebeli türev belirtir (Podlubny, 1999; Kilbas vd., 2006). K genel olarak bilinen difüzyon katsayısı ve n tamsayıdır. Bu çalışma boyunca yapılacak tüm hesaplamalarda K difüzyon katsayısı 1 olarak alınacaktır. 0 < 𝛾 ≤ 1 için (3.1) denklemi kesir difüzyon denklemi veya alt difüzyon denklemi olarak adlandırılır. 1 < 𝛾 ≤ 2 için ise kesir difüzyon dalga denklemi olarak adlandırılır.
Bu çalışmada için 0 ≤ 𝑥 ≤ 𝜋 aralığında (3.1) model problemine ait sınır koşullarını
𝑢(0, 𝑡) = 0, 𝑢(𝜋, 𝑡) = 0 (3.3) ve başlangıç koşulunu
şeklinde alacağız. Difüzyon dalga denklemi için ise verilen başlangıç ve sınır koşullarına ilave olarak
𝜕𝑢(𝑥,𝑡)
𝜕𝑡 𝑙𝑡=0 = 0 (3.5)
şartı kullanılacaktır. Ele alınan model probleme ait Adomian ayrıştırma metodu ile bulunan 𝑢(𝑥, 0) = 𝐸𝛾(−𝑡𝛾)𝑠𝑖𝑛𝑥 (3.6)
tam çözümü karşılaştırma için ele alınacaktır. Burada 𝐸𝛾, Mittag Leffler fonksiyonudur. Kesir
difüzyon denkleminin sonlu elemanlar yöntemiyle çözümünü elde etmek için Quintana vd. (2011) çalışmasındaki kapalı sonlu fark yöntemiyle çözüm incelenebilir. Difüzyon denklemin çözümü için Caputo türevini 𝐿1 ayrıştırması ile ayrıştırırsak
𝜕𝛾𝑓 𝜕𝑡𝛾𝑙𝑡𝑛 = (∆𝑡)−𝛾 𝛤(2−𝛾)∑ 𝑏𝑘 𝛾[𝑓(𝑡 𝑛−𝑘) − 𝑓(𝑡𝑛−1−𝑘)] + 𝑂(∆𝑡) 𝑛−1 𝑘=0
elde edilir. Burada
𝑏𝑘𝛾= (𝑘 + 1)1−𝛾− 𝑘1−𝛾
dır ve difüzyon dalga denklemin çözümü için 𝐿2 ayrıştırması ile ayrıştırırsak 𝜕𝛾𝑓 𝜕𝑡𝛾𝑙𝑡𝑛= (∆𝑡)−𝛾 𝛤(3−𝛾)∑ 𝑏𝑘 𝛾[𝑓(𝑡 𝑛−𝑘) − 2𝑓(𝑡𝑛−1−𝑘) + 𝑓(𝑡𝑛−2−𝑘)] + 𝑂(∆𝑡) 𝑛−1 𝑘=0
elde edilir. Burada
𝑏𝑘𝛾 = (𝑘 + 1)2−𝛾− 𝑘2−𝛾 dır (Oldham ve Spanier, 1974).
3.2. Kuadratik B-Spline Petrov-Galerkin Çözümleri
(3.1) denkleminin (3.3) ile verilen sınır koşulları ve (3.4), (3.5) ile verilen başlangıç koşullarını kullanarak Petrov-Galerkin yöntemiyle çözümünü bulabilmek için ilk olarak Kuadratik B-Spline baz fonksiyonlarını tanımlayalım. Kabul edelim ki, [a,b] kapalı aralığı xm
(𝑚 = 0,1,2,3 … . . 𝑁) düğüm noktaları olmak üzere N eşit parçaya bölünsün. Bu durumda 𝑎 = 𝑥0< 𝑥1< 𝑥2… … < 𝑥𝑁= 𝑏 𝑣𝑒 ℎ = 𝑥𝑚+1− 𝑥𝑚 şeklindedir. Kuadratik B-Spline 𝜃𝑚(𝑥)
baz fonksiyonu (𝑚 = −1 (1)𝑁) 𝑥𝑚 düğüm noktalarında ve [a,b] çözüm bölgesinde
aşağıdaki gibi tanımlanır;
𝜃
𝑚(𝑥) =
1
ℎ
2{
(𝑥
𝑚+2− 𝑥)
2− 3(𝑥
𝑚+1− 𝑥)
2+ 3(𝑥
𝑚− 𝑥)
2𝑥𝜖[𝑥
𝑚−1, 𝑥
𝑚]
(𝑥
𝑚+2− 𝑥)
2− 3(𝑥
𝑚+1− 𝑥)
2𝑥𝜖[𝑥
𝑚, 𝑥
𝑚+1]
(𝑥
𝑚+2− 𝑥)
2𝑥𝜖[𝑥
𝑚+1, 𝑥
𝑚+2]
0 𝑑𝑖ğ𝑒𝑟 𝑑𝑢𝑟𝑢𝑚𝑙𝑎𝑟
(3.7) [a,b] çözüm bölgesi üzerinde {𝜃−1(𝑥), 𝜃0(𝑥), 𝜃1(𝑥) … … . 𝜃𝑁(𝑥) } Spline fonksiyonlarkümesi bir baz oluşturur. Bu yüzden 𝑈𝑁(𝑥, 𝑡) yaklaşık çözümü kuadratik B-Spline baz fonksiyonları cinsinden
𝑈𝑁(𝑥, 𝑡) = ∑𝑁𝑚=−1𝛿𝑚(𝑡)𝜃𝑚(𝑥) (3.8)
şeklinde ifade edilebilir. Burada 𝛿𝑚(𝑡) ‘ler zamana bağlı hesaplanacak parametrelerdir. Her kuadratik B-Spline fonksiyon [𝑥𝑚, 𝑥𝑚+1] aralığında ardışık 3 eleman tarafından kaplanır. Bu
çalışmada [𝑥𝑚, 𝑥𝑚+1] aralığındaki sonlu elemanlar ve 𝑥𝑚, 𝑥𝑚+1 eleman düğüm noktaları
kullanılacaktır. 𝑈𝑚 ve 𝑈′𝑚 değerleri 𝛿𝑚(𝑡) parametreleri cinsinden
𝑈𝑁(𝑥𝑚) = 𝑈𝑚 = 𝛿𝑚−1+ 𝛿𝑚
𝑈′𝑁(𝑥𝑚) = 𝑈′𝑚= ( 2
ℎ) (−𝛿𝑚−1+ 𝛿𝑚) (3.9)
şeklinde ifade edilir. [𝑥𝑚, 𝑥𝑚+1] aralığı üzerinde 𝑈𝑁(𝑥, 𝑡) nin değişimi
𝑈𝑁 = ∑𝑚+1𝑗=𝑚−1𝛿𝑗𝜃𝑗 (3.10)
ile verilir.
𝜑 ağırlık fonksiyonu 𝐿𝑚 lineer B-Spline fonksiyonları ile verilir. [a,b] aralığı üzerinde
xm düğüm noktalarındaki 𝐿𝑚 B-Spline fonksiyonları
𝐿𝑚(𝑥) = 1 ℎ{ (𝑥𝑚+1− 𝑥) − 2(𝑥𝑚− 𝑥) [𝑥𝑚−1, 𝑥𝑚], (𝑥𝑚+1− 𝑥) [𝑥𝑚, 𝑥𝑚+1] 0 𝑑𝑖ğ𝑒𝑟 𝑑𝑢𝑟𝑢𝑚𝑙𝑎𝑟 (3.11)
şeklindedir. [𝑥𝑚, 𝑥𝑚+1] aralığı üzerindeki sonlu elemanlar için yerel koordinat dönüşümü
kullanılarak lineer B-Spline şekil fonksiyonları aşağıdaki şekilde ifade edilir;
𝐿
𝑚= 1 −
𝜉
ℎ
𝐿
𝑚+1=
𝜉
ℎ
(3.12)
(3.1) denkleminde Petrov-Galerkin yöntemini uygulamadan önce (3.1) denkleminin uygun başlangıç ve sınır koşullarıyla oluşturulmuş zayıf formunu oluşturalım. Yöntemin gereği olarak (3.1) denklemindeki tüm terimleri 𝜑(𝑥) ağırlık fonksiyonu ile çarpıp [0, 𝜋] bölgesi üzerinde integralleyip bu integralin sonucunu 0’a eşitleyelim. Bu işlemler uygulandığında
∫ (𝜕𝜕𝑡𝛾𝑈𝛾 −
𝜕2𝑈
𝜕𝑥2) 𝜑𝑑𝑥 = 0
𝜋
0 (3.13)
şeklinde ifade edilir. Burada 𝜑(𝑥) ağırlık fonksiyonu 𝐿𝑚 lineer B-Spline fonksiyonu olarak alınacaktır. İntegralin içindeki yüksek mertebeden türevlerin mertebesini indirgemek için kısmi integrasyon uygulanırsa ∫ (𝜕𝜕𝑡𝛾𝑈𝛾𝜑 + 𝜕𝑈 𝜕𝑥 𝜕𝜑 𝜕𝑥) 𝑑𝑥 = 𝜑 𝜕𝑈 𝜕𝑥𝐼0 𝜋 𝜋 0 (3.14)
elde edilecektir. (3.14) ile elde edilen zayıf formun tüm problem bölgesi üzerinde özellikle [𝑥𝑚, 𝑥𝑚+1] eleman bölgesi üzerinde geçerli olduğunu düşünürsek (3.14) denklemi
∫ (𝜕𝛾𝑈 𝜕𝑡𝛾𝜑 + 𝜕𝑈 𝜕𝑥 𝜕𝜑 𝜕𝑥) 𝑑𝑥 = 𝜑 𝜕𝑈 𝜕𝑥𝐼𝑥𝑚 𝑥𝑚+1 𝑥𝑚+1 𝑥𝑚 (3.15)
şeklinde yazılır. 𝜉 = 𝑥 − 𝑥𝑚 dönüşümü kullanılarak (3.15) zayıf formu aşağıdaki hale dönüşür;
∫ (𝜕𝜕𝑡𝛾𝑈𝛾𝜑 + 𝜕𝑈 𝜕𝜉 𝜕𝜑 𝜕𝜉) 𝑑𝜉 = 𝜑 𝜕𝑈 𝜕𝜉𝐼0 ℎ ℎ 0 (3.16)
Yeni elde edilen (3.16) denklemi “e” elemanı için eleman denklemidir. Şimdi (3.7) B-Spline fonksiyonlarında gerekli dönüşümler yapılırsa
𝜃𝑚−1 𝜃𝑚 𝜃𝑚+1 = 1 ℎ2{ (ℎ − 𝜉)2 ℎ2+ 2ℎ𝜉 − 2𝜉2 𝜉2 (3.17)
haline gelir. (3.7) denkleminin (3.16)’da kullanılmasıyla
𝐴𝑒𝛿̇(𝑡) + 𝐵𝑒𝛿(𝑡) = 𝐶𝑒𝛿(𝑡) (3.18)
eşitliği elde edilir. Burada " ̇ " zamana göre 𝛾. kesir türevi belirtir. 𝐴𝑖𝑗𝑒, 𝐵
𝑖𝑗𝑒, 𝐶𝑖𝑗𝑒 ‘ler aşağıdaki
formda tanımlanmış matrislerdir.
𝐴𝑖𝑗𝑒 = ∫ 𝐿𝑖𝜃𝑗𝑑𝜉 ℎ 0 𝐵𝑖𝑗𝑒 = ∫ 𝐿′𝑖𝜃′𝑗𝑑 ℎ 0 𝜉 𝐶𝑖𝑗𝑒 = 𝐿𝑖𝜃′𝑗𝐼0ℎ
Burada 𝑖, 𝑗 = 𝑚 − 1, 𝑚, 𝑚 + 1 değerlerini alacaktır. Bu eleman matrisler aşağıdaki şekilde hesaplanır: 𝐴𝑖𝑗𝑒 = ∫ 𝐿𝑖𝜃𝑗𝑑𝜉 = ℎ 12[ 3 8 1 1 8 3] 𝐵𝑖𝑗𝑒 = ∫ 𝐿′𝑖𝜃′𝑗𝑑𝜉 = 1 ℎ[ 1 0 −1 −1 0 1 ] 𝐶𝑖𝑗𝑒 = 𝐿𝑖′𝑗𝐼0ℎ= 2 ℎ[ 1 −1 0 0 −1 1]
(3.18) denkleminden gelen veriler birleştirildiğinde
𝐴𝛿̇(𝑡) + 𝐵𝛿(𝑡) = 𝐶𝛿(𝑡) (3.19)
elde edilir. Burada 𝛿(𝑡)’ler bilinmeyen parametreler ve A, B, C’ ler (𝑁 + 2) × (𝑁 + 2) boyutlu global matrislerdir. Bu global matrislerin genelleştirilmiş m. satırları sırasıyla
𝐴: ℎ 12(1 11 11 1) 𝐵:1 ℎ(−1 1 1 − 1) 𝐶: (0 0 0 0) dır.
(0 < 𝛾 ≤ 1) kesir mertebeli difüzyon denklemi için (3.19) denklemindeki 𝛿(𝑡) zamana bağlı parametreler ve 𝛿̇(𝑡) kesir zaman türevleri Crank-Nicolson formülü ve 𝐿1 formülü
yardımıyla ayrıştırıldığında sırasıyla
𝛿𝑚 = 1 2(𝛿𝑚 𝑛 + 𝛿 𝑚𝑛+1) (3.20) ve 𝛿̇𝑚 = 𝑑𝛾𝛿 𝑑𝑡𝛾 = (∆𝑡)−𝛾 𝛤(2 − 𝛾)∑[(𝑘 + 1) 1−𝛾− 𝑘1−𝛾][𝛿 𝑚𝑛−𝑘− 𝛿𝑚𝑛−𝑘−1] 𝑛−1 𝑘=0
şeklinde ifade edilir. Bu ayrıştırmaların kullanılmasıyla 𝛿𝑚𝑛+1(𝑡) bilinmeyen parametreler
cinsinden ardışık zaman adımları için aşağıdaki tekrarlama bağıntısı elde edilir. (2 − 𝑎)𝛿𝑚−2𝑛+1 + (22 + 𝑎)𝛿 𝑚−1𝑛+1+ (22 + 𝑎)𝛿𝑚𝑛+1+ (2 − 𝑎)𝛿𝑚+1𝑛+1 = (2 + 𝑎)𝛿𝑚−2𝑛 + (22 − 𝑎)𝛿𝑚−1𝑛 + (22 − 𝑎)𝛿𝑚𝑛 + (2 + 𝑎)𝛿𝑚+1𝑛 − 2 ∑[(𝑘 + 1)1−𝛾− 𝑘1−𝛾][(𝛿𝑚−2𝑛−𝑘+1− 𝛿 𝑚−2𝑛−𝑘) + 11(𝛿𝑚−1𝑛−𝑘+1− 𝛿𝑚−1𝑛−𝑘) 𝑛 𝑘=1 +11(𝛿𝑚𝑛−𝑘+1− 𝛿𝑚𝑛−𝑘) + (𝛿𝑚+1𝑛−𝑘+1− 𝛿𝑚+1𝑛−𝑘)] (3.21) Burada 𝛼 =24(∆𝑡) 𝛾𝛤(2 − 𝛾) ℎ2 dır.
(1 < 𝛾 ≤ 2) kesir mertebeli difüzyon dalga denklemi için ise (3.18) denklemindeki 𝛿𝑚(𝑡) zamana bağlı parametreler ve 𝛿̇𝑚(𝑡) kesir zaman türevleri Crank-Nicolson ve 𝐿2
formülüyle ayrıştırılırsa sırasıyla
𝛿𝑚= 1 2(𝛿𝑚 𝑛 + 𝛿 𝑚𝑛+1) (3.22) ve 𝛿̇ =𝑑 𝛾𝛿 𝑑𝑡𝛾 = (∆𝑡)−𝛾 𝛤(3 − 𝛾)∑[(𝑘 + 1) 2−𝛾− 𝑘2−𝛾][𝛿𝑛−𝑘 𝑛−1 𝑘=0 − 2𝛿𝑚𝑛−𝑘−1+ 𝛿𝑚𝑛−𝑘−2]
elde edilir. Bu ayrıştırma ile 𝛿𝑚𝑛+1(𝑡) bilinmeyen parametrelerin hesaplanması için aşağıdaki
tekrarlama bağıntısı elde edilir.
(2 − 𝑎)𝛿𝑚−2𝑛+1+ (22 + 𝑎)𝛿 𝑚−1𝑛+1 + (22 + 𝑎)𝛿𝑚𝑛+1+ (2 − 𝑎)𝛿𝑚+1𝑛+1 = (4 + 𝑎)𝛿𝑚−2𝑛 + (44 − 𝑎)𝛿 𝑚−1𝑛 + (44 − 𝑎)𝛿𝑚𝑛 + (4 + 𝑎)𝛿𝑚+1𝑛 − 2(𝛿𝑚−2𝑛−1 + 11𝛿𝑚−1𝑛−1+ 11𝛿𝑚𝑛−1+ 𝛿𝑚+1𝑛−1) − 2 ∑𝑛𝑘=1[(𝑘 + 1)2−𝛾− 𝑘2−𝛾][(𝛿𝑚−2𝑛−𝑘+1− 2𝛿𝑚−2𝑛−𝑘 + 𝛿𝑚−2𝑛−𝑘+1) + 11(𝛿𝑚−1𝑛−𝑘+1− 2𝛿𝑚−1𝑛−𝑘 + 𝛿𝑚−1𝑛−𝑘+1) + 11(𝛿𝑚𝑛−𝑘+1− 2𝛿𝑚𝑛−𝑘+ 𝛿𝑚𝑛−𝑘+1) + (𝛿𝑚+1𝑛−𝑘+1− 2𝛿𝑚+1𝑛−𝑘 + 𝛿𝑚+1𝑛−𝑘+1) (3.23) Burada 𝛼 =24(∆𝑡) 𝛾𝛤(3 − 𝛾) ℎ2 dır.
Görülmektedir ki (3.21) ve (3.23) sistemlerinin her ikisi de 𝑁 + 2 lineer denklem ve 𝑁 + 2 (𝛿−1, … … … 𝛿𝑁)𝑇 şeklinde bilinmeyen parametreler içerir. (3.19) denklem sistemine (3.3)
3.3. Başlangıç Durumu
𝑑𝑜 = (𝛿
−1, 𝛿0, 𝛿1, … … … 𝛿𝑁−2, 𝛿𝑁−1, 𝛿𝑁)𝑇 şeklinde ifade edilen başlangıç vektörü
kuadratik spline fonksiyonlar kullanılarak yapılacak interpolasyon yardımıyla 𝑈(𝑥, 0) başlangıç koşulundan hesaplanır. Düğüm noktalarında 𝑈𝑁(𝑥𝑖, 0) = 𝑈(𝑥𝑖, 0), (𝑖 = 0, … … 𝑁) bağıntısı ile
birlikte 𝑈′𝑁(𝑥𝑁, 0) = 𝑈′(𝑥𝑁, 0) bağıntıları kullanıldığında 𝑑0 başlangıç vektörü aşağıdaki
matris formunda elde edilir;
[ 1 1 11 1 1 ⋱ ⋱ 1 1 −2 ℎ 2 ℎ] [ 𝛿−10 𝛿00 𝛿10 ⋮ ⋮ 𝛿𝑁−10 𝛿𝑁0 ] = [ 𝑈00 𝑈10 𝑈20 ⋮ ⋮ 𝑈𝑁−10 𝑈′𝑁0 ]
3.4. Nümerik Örnekler
Bu bölümde difüzyon ve difüzyon dalga problemlerinin yaklaşık çözümleri kuadratik baz fonksiyonları kullanılarak Petrov-Galerkin sonlu elemanlar metoduyla elde edildi. Bu metodun doğruluğu 𝐿2 𝑣𝑒 𝐿∞ hata normlarıyla kontrol edildi.
𝐿2= ‖𝑈𝑡𝑎𝑚− 𝑈𝑁‖2≅ √ℎ ∑|𝑈𝑗𝑡𝑎𝑚− (𝑈𝑁)𝑗| 2 𝑁 𝑗=0 𝐿∞= ‖𝑈𝑡𝑎𝑚− 𝑈𝑁‖∞≅ max 𝑗 |𝑈𝑗 𝑡𝑎𝑚− (𝑈 𝑁)𝑗|
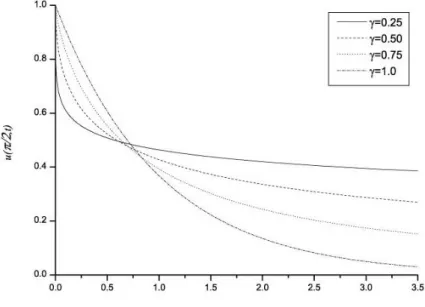
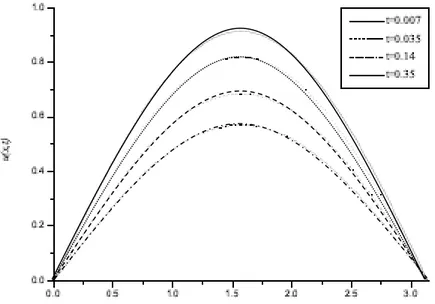
Şekil 3.1’de 𝑁 = 40 𝑣𝑒 𝛾’nın çeşitli değerleri için kesir difüzyon problemin orta noktadaki nümerik çözümleri gösterilmiştir. Nümerik ve analitik çözümler ayırt edilemeyecek şekilde birbirlerine çok benzemektedir.
Şekil 3.1. ∆t=0,00007 ve N=40 için farklı zamanlardaki 𝑢 (𝜋
2, 𝑡) nümerik çözümler.
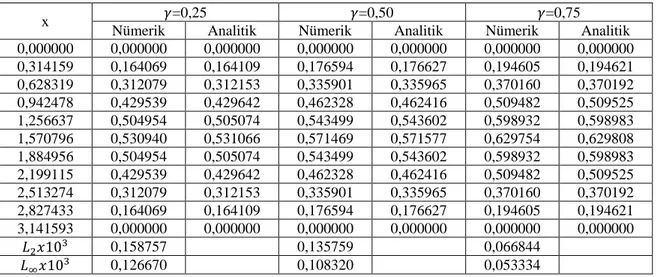
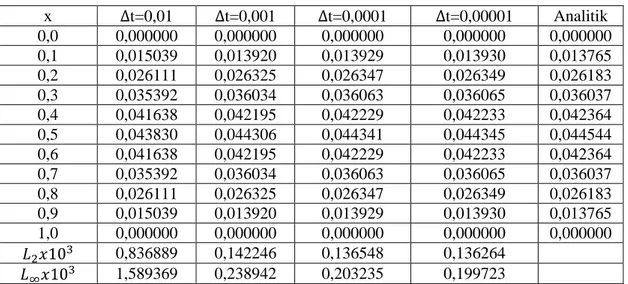
Çizelge 3.1’ de 𝛾 = 0,25 , 𝛾 = 0,50 𝑣𝑒 𝛾 = 0,75 değerleri için difüzyon denklemin nümerik ve analitik çözümlerinin karşılaştırması yapılmıştır. Çizelge 3.1’de açıkça görülüyor ki mevcut algoritma kullanılarak hesaplanan nümerik sonuçlar ile analitik sonuçlar birbiriyle uyum içindedir. Ayrıca artan 𝛾 değerlerine karşılık 𝐿2 𝑣𝑒 𝐿∞ hata normları da artmaktadır.
Çizelge 3.1. Kesir difüzyon denklemin N=40, ∆t=0,00007, tf=0,35 değerleri için farklı 𝛾
değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması.
x 𝛾=0,25 𝛾=0,50 𝛾=0,75
Nümerik Analitik Nümerik Analitik Nümerik Analitik 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,314159 0,164109 0,164109 0,176628 0,176627 0,194624 0,194621 0,628319 0,312153 0,312153 0,335966 0,335965 0,370197 0,370192 0,942478 0,429642 0,429642 0,462418 0,462416 0,509532 0,509525 1,256637 0,505075 0,505074 0,543605 0,543602 0,598991 0,598983 1,570796 0,531067 0,531066 0,571580 0,571577 0,629816 0,629808 1,884956 0,505075 0,505074 0,543605 0,543602 0,598991 0,598983 2,199115 0,429642 0,429642 0,462418 0,462416 0,509532 0,509525 2,513274 0,312153 0,312153 0,335966 0,335965 0,370197 0,370192 2,827433 0,164109 0,164109 0,176628 0,176627 0,194624 0,194621 3,141593 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 𝐿2𝑥103 0,000614 0,003551 0,010828 𝐿∞𝑥103 0,000490 0,002833 0,008639
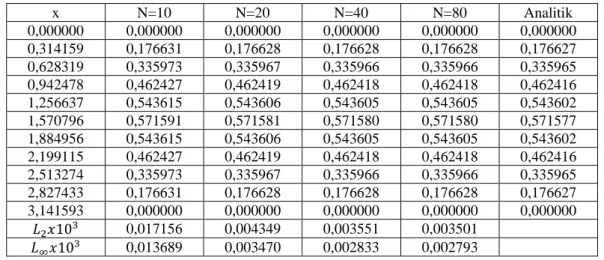
Çizelge 3.2, 𝛾 = 0,5 , ∆𝑡 = 0,00007, 𝑡𝑓 = 0,35 ve N’nin farklı değerleri için
nümerik sonuçları göstermektedir. Çizelgeden görülecektir ki, aralık sayısı (N) arttıkça 𝐿2 𝑣𝑒 𝐿∞ hata normları azalmaktadır.
Çizelge 3.2. Kesir difüzyon denklemin 𝛾=0,50, ∆t=0,00007, 𝑡𝑓=0,35 değerleri için farklı N
değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması.
x N=10 N=20 N=40 N=80 Analitik 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,314159 0,176631 0,176628 0,176628 0,176628 0,176627 0,628319 0,335973 0,335967 0,335966 0,335966 0,335965 0,942478 0,462427 0,462419 0,462418 0,462418 0,462416 1,256637 0,543615 0,543606 0,543605 0,543605 0,543602 1,570796 0,571591 0,571581 0,571580 0,571580 0,571577 1,884956 0,543615 0,543606 0,543605 0,543605 0,543602 2,199115 0,462427 0,462419 0,462418 0,462418 0,462416 2,513274 0,335973 0,335967 0,335966 0,335966 0,335965 2,827433 0,176631 0,176628 0,176628 0,176628 0,176627 3,141593 0,000000 0,000000 0,000000 0,000000 0,000000 𝐿2𝑥103 0,017156 0,004349 0,003551 0,003501 𝐿∞𝑥103 0,013689 0,003470 0,002833 0,002793
Şimdi de 1 < 𝛾 ≤ 2 difüzyon dalga denklemi için elde edilen nümerik sonuçları inceleyelim:
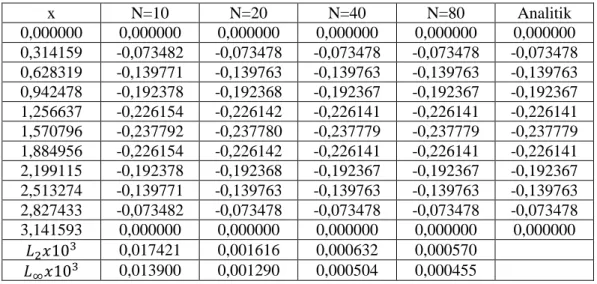
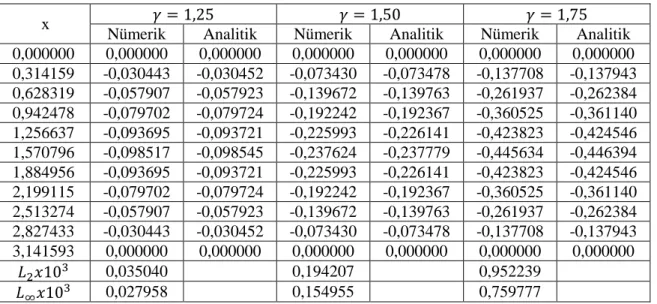
Çizelge 3.3’ te 𝛾 = 1,25 , 𝛾 = 1,50 𝑣𝑒 𝛾 = 1,75 değerleri için difüzyon dalga denklemin mevcut algoritma ile nümerik ve analitik çözümlerinin karşılaştırması yapılmıştır. Çizelgeden görülmektedir ki artan 𝛾 değerlerine karşılık 𝐿2 𝑣𝑒 𝐿∞ hata normları artmaktadır.
Çizelge 3.3. Kesir difüzyon dalga denklemin N=40, ∆t=0,00075, tf=3,35 değerleri için farklı 𝛾
değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması.
x 𝛾=1,25 𝛾=1,50 𝛾=1,75
Nümerik Analitik Nümerik Analitik Nümerik Analitik 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,314159 -0,030452 -0,030452 -0,073478 -0,073478 -0,137937 -0,137943 0,628319 -0,057923 -0,057923 -0,139763 -0,139763 -0,262371 -0,262384 0,942478 -0,079724 -0,079724 -0,192367 -0,192367 -0,361123 -0,361140 1,256637 -0,093721 -0,093721 -0,226141 -0,226141 -0,424525 -0,424546 1,570796 -0,098545 -0,098545 -0,237779 -0,237779 -0,446372 -0,446394 1,884956 -0,093721 -0,093721 -0,226141 -0,226141 -0,424525 -0,424546 2,199115 -0,079724 -0,079724 -0,192367 -0,192367 -0,361123 -0,361140 2,513274 -0,057923 -0,057923 -0,139763 -0,139763 -0,262371 -0,262384 2,827433 -0,030452 -0,030452 -0,073478 -0,073478 -0,137937 -0,137943 3,141593 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 𝐿2𝑥103 0,000081 0,000632 0,027269 𝐿∞𝑥103 0,000065 0,000504 0,021758
Çizelge 3.4 𝛾 = 1,5 , ∆𝑡 = 0,00075, 𝑡𝑓 = 3,75 ve N’nin farklı değerleri için
nümerik sonuçları göstermektedir. Çizelgeden görülecektir ki, problem alanının bölünme sayısı arttıkça, hata değerleri azalmaktadır.
Çizelge 3.4. Kesir difüzyon dalga denklemin 𝛾=1,50, ∆t=0,00075, 𝑡𝑓=3,35 değerleri için farklı
N değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması.
x N=10 N=20 N=40 N=80 Analitik 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,314159 -0,073482 -0,073478 -0,073478 -0,073478 -0,073478 0,628319 -0,139771 -0,139763 -0,139763 -0,139763 -0,139763 0,942478 -0,192378 -0,192368 -0,192367 -0,192367 -0,192367 1,256637 -0,226154 -0,226142 -0,226141 -0,226141 -0,226141 1,570796 -0,237792 -0,237780 -0,237779 -0,237779 -0,237779 1,884956 -0,226154 -0,226142 -0,226141 -0,226141 -0,226141 2,199115 -0,192378 -0,192368 -0,192367 -0,192367 -0,192367 2,513274 -0,139771 -0,139763 -0,139763 -0,139763 -0,139763 2,827433 -0,073482 -0,073478 -0,073478 -0,073478 -0,073478 3,141593 0,000000 0,000000 0,000000 0,000000 0,000000 𝐿2𝑥103 0,017421 0,001616 0,000632 0,000570 𝐿∞𝑥103 0,013900 0,001290 0,000504 0,000455
3.5. Sonuç
Bu çalışmada difüzyon ve difüzyon dalga denklemlerinin nümerik sonuçlarının hesaplanmasında Petrov-Galerkin sonlu elemanlar yöntemi başarıyla uygulanmıştır. Sunulan çizelgelerden kolayca anlaşılacaktır ki, uygulanan yöntem bu tür kesir difüzyon ve difüzyon dalga denklemlerinin nümerik sonuçlarının elde edilmesinde oldukça elverişli bir yöntemdir.
4. KESİR TÜREVLİ DİFÜZYON ve DİFÜZYON DALGA
DENKLEMLERİNİN B-SPLİNE KOLLOKASYON YÖNTEMİYLE
ÇÖZÜMLERİ
4.1. Giriş
Kesir türevli kısmi diferansiyel denklemlerin birçok çözümü mevcuttur. Fakat bu çözümler, çözümün etkinliğini azaltacak şekilde uzun çözümlerdir. Sonlu elemanlar yöntemi hem adi hem de kısmi diferansiyel denklemlerin çözümü için önemli bir yöntemdir. Bu çalışmada sonlu elemanlar yöntemi kesir mertebeden difüzyon ve difüzyon dalga denklemlerin kollokasyon çözümü için uygulanacaktır.
Bu yöntemi uygulamak için aşağıdaki difüzyon denklem kullanılacaktır;
𝜕𝛾𝑢 𝜕𝑡𝛾 = 𝐾 𝜕2𝑢 𝜕𝑥2 (4.1) Burada 𝜕𝛾 𝜕𝑡𝛾𝑓(𝑡) = 1 𝛤(𝑛−𝛾)∫ (𝑡 − 𝜏) 𝑛−𝛾−1 𝜕𝑛𝑓(𝜏) 𝜕𝑡𝑛 𝑑𝜏 𝑡 0 𝑛 − 1 < 𝛾 < 𝑛 (4.2)
Caputo anlamında kesir türevi ifade eden K difüzyon katsayısı ve n bir tamsayıdır (Podlubny, 1999 ; Kilbas vd., 2006). Bütün nümerik hesaplarda K difüzyon katsayısı “1” alınacaktır. Bu çalışmada difüzyon denklemi için (4.1) ile verilen model problemde 0 ≤ 𝑥 ≤ 𝜋 aralığında sınır koşulları
𝑢(0, 𝑡) = 0, 𝑢(𝜋, 𝑡) = 0 (4.3) ve başlangıç koşulları
𝑢(𝑥, 0) = 𝑠𝑖𝑛𝑥 (4.4)
şeklinde tanımlansın. Difüzyon dalga denklemi için ise yukarıda verilen sınır başlangıç koşullarının yanında aşağıdaki ilave başlangıç koşulu
𝜕𝑢(𝑥,𝑡)
kullanılacaktır. Her iki problem için de Adomian ayrıştırma yöntemi ile elde edilen tam çözüm (Ray, 2007)
𝑢(𝑥, 𝑡) = 𝐸𝛾(−𝑡𝛾)𝑠𝑖𝑛𝑥 (4.6)
dır. Burada 𝐸𝛾 Mittag-Leffler fonksiyonudur (Podlubny, 1999).
Kesir mertebeli difüzyon denklemin sonlu elemanlar yöntemi ile elde edilecek çözümlerinde kapalı sonlu fark metodundan faydalanılacaktır (Quintana-Murillo ve Yuste, 2011).
4.2. Kübik B-Spline Sonlu Eleman Kollokasyon Yöntemi
(4.3) sınır koşulları ve (4.4), (4.5) başlangıç koşulları yardımıyla kollokasyon sonlu elemanlar metodu ile çözüm yapmadan önce kübik B-Spline baz fonksiyonlarını tanımlayalım. [a,b] aralığının N eşit parçaya bölündüğünü ve 𝑥𝑚 (𝑚 = 0,1,2, … . . 𝑁) düğüm noktalarına sahip olduğunu düşünelim. Bu durumda 𝑎 = 𝑥0< 𝑥1< ⋯ … < 𝑥𝑁= 𝑏 𝑣𝑒 ℎ = 𝑥𝑚+1− 𝑥𝑚 olur.
[a,b] üzerinde tanımlı 𝑥𝑚 düğüm noktalarına sahip 𝜑𝑚(𝑥) kübik B-Spline baz fonksiyonları
𝜑𝑚(𝑥) = 1 ℎ2 { (𝑥 − 𝑥𝑚−2)3 𝑥𝜖[𝑥𝑚−2, 𝑥𝑚−1] ℎ3+ 3ℎ2(𝑥 − 𝑥𝑚−1) + 3ℎ(𝑥 − 𝑥𝑚−1)2− 3(𝑥 − 𝑥𝑚−1)3 𝑥𝜖[𝑥𝑚−1, 𝑥𝑚] ℎ3+ 3ℎ2(𝑥 𝑚+1− 𝑥) + 3ℎ(𝑥𝑚+1− 𝑥)2− 3(𝑥𝑚+1− 𝑥)3 𝑥𝜖[𝑥𝑚, 𝑥𝑚+1] (𝑥𝑚+2− 𝑥)3 𝑥𝜖[𝑥𝑚+1, 𝑥𝑚+2] 0 𝑑𝑖ğ𝑒𝑟 𝑑𝑢𝑟𝑢𝑚𝑙𝑎𝑟𝑑𝑎 (4.7) şeklindedir. {𝜑−1(𝑥), 𝜑0(𝑥), … … . 𝜑𝑁+1(𝑥)} spline fonksiyonlarının kümesi [𝑎, 𝑏] aralığı
üzerinde bir baz oluşturur. Bu yüzden 𝑈𝑁(𝑥, 𝑡) yaklaşık çözümü kübik B-Spline baz fonksiyonları cinsinden
𝑈𝑁(𝑥, 𝑡) = ∑𝑁+1𝑚=−1𝛿𝑚(𝑡)𝜑𝑚(𝑥) (4.8)
şeklinde yazılabilir. Burada 𝛿𝑚(𝑡) ‘ler zamana bağlı hesaplanacak parametrelerdir. Bu hesaplamalar sınır koşullarından ve kübik B-Spline kollokasyon koşullarından elde edilecektir. Her kübik B-Spline 4 eleman tarafından kapsanır. Bu yüzden [𝑥𝑚, 𝑥𝑚+1] aralığı da 4 kübik
B-Spline tarafından kapsanır. Bu denklemin çözümü için [𝑥𝑚, 𝑥𝑚+1] aralığında sonlu elemanlar ve
𝑥𝑚, 𝑥𝑚+1 düğüm noktaları tanımlanacaktır. Çözümün elde edilebilmesi için gerekli olan 𝑈𝑚,
𝑈𝑚 = 𝑈(𝑥𝑚) = 𝛿𝑚−1(𝑡) + 4𝛿𝑚(𝑡) + 𝛿𝑚+1(𝑡) 𝑈′𝑚= 𝑈′(𝑥𝑚) = 3 ℎ(−𝛿𝑚−1(𝑡) + 𝛿𝑚+1(𝑡)) (4.9) 𝑈′′𝑚= 𝑈′′(𝑥𝑚) = 6 ℎ2(𝛿𝑚−1(𝑡) − 2𝛿𝑚(𝑡) + 𝛿𝑚+1(𝑡))
[𝑥𝑚, 𝑥𝑚+1] aralığı üzerinde 𝑈𝑁(𝑥, 𝑡) yaklaşık çözümü
𝑈𝑁(𝑥, 𝑡) = ∑𝑚+2𝑗=𝑚−1𝛿𝑗(𝑡)𝜑𝑗(𝑥) (4.10)
şeklinde ifade edilir. Eğer (4.8) ve(4.9) eşitlikleri (4.1) denkleminde yerine yazılırsa aşağıdaki 1. mertebeden diferansiyel denklem sistemi elde edilmiş olur.
𝛿̇𝑚−1(𝑡) + 4𝛿̇𝑚(𝑡) + 𝛿̇𝑚+1(𝑡) − 6
ℎ2(𝛿𝑚−1(𝑡) − 2𝛿𝑚(𝑡) + 𝛿𝑚+1(𝑡)) = 0 (4.11)
Burada " ̇ " zamana göre kesir türevi ifade eder. 0 < 𝛾 ≤ 1 kesir difüzyon denklemi için eğer (4.11)’deki 𝛿𝑚(𝑡) zaman parametreleri ve 𝛿̇𝑚(𝑡) kesir zaman türevleri Crank-Nicolson ve L1
ayrıştırma formülleriyle ayrıştırıldığında
𝛿 =1 2(𝛿 𝑛+ 𝛿𝑛+1) (4.12) ve 𝛿̇ =𝑑 𝛾𝛿 𝑑𝑡𝛾 = (∆𝑡)−𝛾 𝛤(2 − 𝛾)∑[(𝑘 + 1) 1−𝛾− 𝑘1−𝛾][𝛿𝑛−𝑘− 𝛿𝑛−𝑘−1] 𝑛−1 𝑘=0
eşitlikleri elde edilir. Bu eşitlikler yardımıyla aşağıdaki tekrarlama bağıntısı elde edilir.
(1 − 𝑎)𝛿𝑚−1𝑛+1 + (4 + 2𝑎)𝛿𝑚𝑛+1+ (1 − 𝑎)𝛿𝑚+1𝑛+1
= (1 + 𝑎)𝛿𝑚−1𝑛 + (4 − 2𝑎)𝛿𝑚𝑛 + (1 + 𝑎)𝛿𝑚+1𝑛 − ∑𝑛𝑘=1[(𝑘 + 1)1−𝛾− 𝑘1−𝛾]
Burada
𝛼 =3(∆𝑡)
𝛾𝛤(2 − 𝛾)
ℎ2
dır.
1 < 𝛾 ≤ 2 kesir difüzyon dalga denklemi için (4.11)’de 𝛿𝑚(𝑡) zaman parametreleri ve
𝛿̇𝑚(𝑡) kesir zaman türevleri benzer şekilde Crank-Nicolson ve L2 ile ayrıştırıldığında
𝛿 =1 2(𝛿 𝑛+ 𝛿𝑛+1) (4.14) ve 𝛿̇ =𝑑 𝛾𝛿 𝑑𝑡𝛾 = (∆𝑡)−𝛾 𝛤(3 − 𝛾)∑[(𝑘 + 1) 2−𝛾− 𝑘2−𝛾][𝛿𝑛−𝑘− 2𝛿𝑛−𝑘−1+ 𝛿𝑛−𝑘−2] 𝑛−1 𝑘=0
eşitlikleri kullanılarak aşağıdaki tekrarlama bağıntısı elde edilir. (1 − 𝑎)𝛿𝑚−1𝑛+1 + (4 + 2𝑎)𝛿 𝑚𝑛+1+ (1 − 𝑎)𝛿𝑚+1𝑛+1 = (2 + 𝑎)𝛿𝑚−1𝑛 + (8 − 2𝑎)𝛿𝑚𝑛 + (2 + 𝑎)𝛿𝑚+1𝑛 − (𝛿𝑚−1𝑛−1 + 4𝛿𝑚𝑛−1+ 𝛿𝑚+1𝑛−1) − ∑[(𝑘 + 1)2−𝛾− 𝑘2−𝛾][(𝛿 𝑚−1𝑛−𝑘+1− 2𝛿𝑚−1𝑛−𝑘+ 𝛿𝑚−1𝑛−𝑘−1) 𝑛 𝑘=1 +4(𝛿𝑚𝑛−𝑘+1− 2𝛿𝑚𝑛−𝑘+ 𝛿𝑚𝑛−𝑘−1) + (𝛿𝑚+1𝑛−𝑘+1− 2𝛿𝑚+1𝑛−𝑘 + 𝛿𝑚+1𝑛−𝑘−1)] (4.15) Burada 𝛼 =3(∆𝑡) 𝛾𝛤(3 − 𝛾) ℎ2 dır.
(4.13) ve (4.15) denklem sistemlerinin her ikisi de N+1 lineer denklem ve (𝛿−1, … … 𝛿𝑁+1)𝑇 şeklinde N+3 bilinmeyenden oluşur. Bu sistemin çözümünü elde edebilmek
için 2 ilave şarta ihtiyaç vardır. Bu şartlar sınır koşulları yardımıyla 𝛿−1 𝑣𝑒 𝛿𝑁+1
4.3. Başlangıç Durumu
𝑑0= (𝛿
0, 𝛿1, 𝛿2, … … . 𝛿𝑁−2, 𝛿𝑁−1, 𝛿𝑁)𝑇 şeklinde tanımlı başlangıç vektörü başlangıç
ve sınır koşullarından hesaplanır. Bu durumda (4.8) yaklaşımı başlangıç koşulu yardımıyla 𝑈𝑁(𝑥, 0) = ∑𝑁+1𝑚=−1𝛿𝑚(0)𝜑𝑚(𝑥) (4.16)
şeklinde yeniden yazılabilir. Burada 𝛿𝑚(0) bilinmeyen parametredir. Nümerik çözümü başlatabilmemiz için 𝑈𝑁(𝑥, 0) yaklaşık çözümünün aşağıdaki şartları sağlaması gerekir.
𝑈𝑁(𝑥, 0) = 𝑈(𝑥𝑚, 0), 𝑚 = 0,1,2, … … 𝑁, (4.17)
(𝑈𝑁)𝑥𝑥(0,0) = 0, (𝑈𝑁)𝑥𝑥(𝜋, 0) = 0
Böylece bu koşulların kullanılmasıyla üçgensel bant matris formu
𝑊𝑑0 = 𝑏 (4.18)
şeklinde yazılabilir. Burada
𝑊 = [ 6 1 04 1 14 1 ⋱ ⋱ 1 4 0 1 6 ] ve 𝑏 = (𝑈(𝑥0, 0), 𝑈(𝑥1, 0), 𝑈(𝑥2, 0), … … … . , 𝑈(𝑥𝑁−2, 0), 𝑈(𝑥𝑁−1, 0)𝑈(𝑥𝑁, 0))𝑇 şeklindedir.
4.4. Nümerik Örnekler
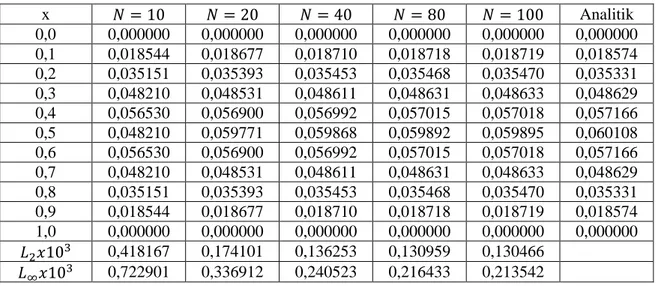
Çizelge 4.1’de 𝛾 = 0,25, 𝛾 = 0,50 𝑣𝑒 𝛾 = 0,75 değerleri için difüzyon denklemin elde edilen nümerik ve analitik sonuçlarının karşılaştırılması yapılmıştır. Çizelgeden görülmektedir ki, artan 𝛾 değerlerine karşılık 𝐿2 𝑣𝑒 𝐿∞ hata normları azalmaktadır.
Çizelge 4.1. Kesir difüzyon denklemin N=40, ∆t=0,0007, tf=0,35 değerleri için farklı 𝛾
değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması.
x 𝛾=0,25 𝛾=0,50 𝛾=0,75
Nümerik Analitik Nümerik Analitik Nümerik Analitik 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,314159 0,164069 0,164109 0,176594 0,176627 0,194605 0,194621 0,628319 0,312079 0,312153 0,335901 0,335965 0,370160 0,370192 0,942478 0,429539 0,429642 0,462328 0,462416 0,509482 0,509525 1,256637 0,504954 0,505074 0,543499 0,543602 0,598932 0,598983 1,570796 0,530940 0,531066 0,571469 0,571577 0,629754 0,629808 1,884956 0,504954 0,505074 0,543499 0,543602 0,598932 0,598983 2,199115 0,429539 0,429642 0,462328 0,462416 0,509482 0,509525 2,513274 0,312079 0,312153 0,335901 0,335965 0,370160 0,370192 2,827433 0,164069 0,164109 0,176594 0,176627 0,194605 0,194621 3,141593 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 𝐿2𝑥103 0,158757 0,135759 0,066844 𝐿∞𝑥103 0,126670 0,108320 0,053334
Çizelge 4.2’de bölgenin farklı bölünmelerine karşılık 𝛾=0,50, ∆t=0,0007 ve tf=0,35 değerleri
için nümerik sonuçlar gösterilmiştir. Açıkça görülmektedir ki, bölgenin bölünme sayısı arttıkça daha doğru sonuçlar elde edilmektedir. Bunu 𝐿2 𝑣𝑒 𝐿∞ hata norm değerlerinin azalmasından
görmekteyiz.
Çizelge 4.2. Kesir difüzyon denklemin 𝛾=0,50, ∆t=0,0007, tf=0,35 değerleri için farklı N
değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması.
x N=10 N=20 N=40 N=80 Analitik 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,314159 0,175956 0,176466 0,176594 0,176625 0,176627 0,628319 0,334689 0,335659 0,335901 0,335962 0,335965 0,942478 0,460659 0,461994 0,462328 0,462412 0,462416 1,256637 0,541537 0,543107 0,543499 0,543597 0,543602 1,570796 0,569406 0,571056 0,571469 0,571572 0,571577 1,884956 0,541537 0,543107 0,543499 0,543597 0,543602 2,199115 0,460659 0,461994 0,462328 0,462412 0,462416 2,513274 0,334689 0,335659 0,335901 0,335962 0,335965 2,827433 0,175956 0,176466 0,176594 0,176625 0,176627 3,141593 0,000000 0,000000 0,000000 0,000000 0,000000 𝐿2𝑥103 2,721007 0,652825 0,135759 0,006493 𝐿∞𝑥103 2,171049 0,520879 0,108320 0,005180
Şekil 4.1’de farklı zaman adımlarında 𝛾=0,50 ve N=40 değerleri için elde edilen nümerik sonuçlar gösterilmiştir.
Şekil 4.1. Farklı zaman adımlarında kesir difüzyon denklemin 𝛾=0,50 ve N=40 değerleri için elde edilen nümerik sonuçlar.
Çizelge 4.3’te çeşitli zaman adımlarında 𝛾 = 0,25, 𝛾 = 0,50 𝑣𝑒 𝛾 = 0,75 için 𝐿2 𝑣𝑒 𝐿∞ hata
normları gösterilmiştir.
Çizelge 4.3. Kesir difüzyon denklemin N=40, ∆t=0,0007 değerleri için farklı 𝛾 ve t değerleri için 𝐿2 𝑣𝑒 𝐿∞ hata normları.
𝑡 𝛾=0,25 𝛾=0,50 𝛾=0,75 𝐿2𝑥103 𝐿∞𝑥103 𝐿2𝑥103 𝐿∞𝑥103 𝐿2𝑥103 𝐿∞𝑥103 0,07 0,047699 0,038058 0,240770 0,192106 0,332833 0,265563 0,14 0,122036 0,097370 0,018097 0,014440 0,155756 0,124276 0,21 0,143881 0,114801 0,066579 0,053122 0,052431 0,041834 0,28 0,153593 0,122549 0,110137 0,087877 0,017091 0,013637 0,35 0,158757 0,126670 0,135759 0,108320 0,066844 0,053334
𝛾=1,25, 𝛾=1,50 ve 𝛾=1,75 değerleri için algoritma ile elde edilen kesir difüzyon dalga denklemin nümerik sonuçları ve analitik sonuçlarının karşılaştırılması Çizelge 4.4’ te verilmiştir. Artan 𝛾 değerlerine karşılık 𝐿2 𝑣𝑒 𝐿∞ hata normları artmaktadır.
Çizelge 4.4. Kesir difüzyon dalga denklemin N=40, ∆t=0,0075, tf=3,35 değerleri için farklı 𝛾
değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması ve L2 ve 𝐿∞ hata normları.
x 𝛾 = 1,25 𝛾 = 1,50 𝛾 = 1,75
Nümerik Analitik Nümerik Analitik Nümerik Analitik 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,314159 -0,030443 -0,030452 -0,073430 -0,073478 -0,137708 -0,137943 0,628319 -0,057907 -0,057923 -0,139672 -0,139763 -0,261937 -0,262384 0,942478 -0,079702 -0,079724 -0,192242 -0,192367 -0,360525 -0,361140 1,256637 -0,093695 -0,093721 -0,225993 -0,226141 -0,423823 -0,424546 1,570796 -0,098517 -0,098545 -0,237624 -0,237779 -0,445634 -0,446394 1,884956 -0,093695 -0,093721 -0,225993 -0,226141 -0,423823 -0,424546 2,199115 -0,079702 -0,079724 -0,192242 -0,192367 -0,360525 -0,361140 2,513274 -0,057907 -0,057923 -0,139672 -0,139763 -0,261937 -0,262384 2,827433 -0,030443 -0,030452 -0,073430 -0,073478 -0,137708 -0,137943 3,141593 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 𝐿2𝑥103 0,035040 0,194207 0,952239 𝐿∞𝑥103 0,027958 0,154955 0,759777
Çizelge 4.5’ te N’nin farklı değerlerine karşılık 𝛾 = 1,5, ∆𝑡 = 0,0075 𝑣𝑒 𝑡𝑓= 3,75 için elde
edilen nümerik sonuçlar verilmiştir. Çizelgede görüleceği üzere bölünme sayısı arttıkça, hata değerleri azalmaktadır.
Çizelge 4.5. Kesir difüzyon dalga denklemin N=40, ∆t=0,0075, tf=3,35 değerleri için farklı N
değerlerindeki nümerik ve analitik çözümlerin karşılaştırılması ve L2 ve 𝐿∞ hata normları.
x N=10 N=20 N=40 N=80 Analitik 0,000000 0,000000 0,000000 0,000000 0,000000 0,000000 0,314159 -0,072637 -0,073272 -0,073430 -0,073469 -0,073478 0,628319 -0,138164 -0,139372 -0,139672 -0,139746 -0,139763 0,942478 -0,190167 -0,191829 -0,192242 -0,192345 -0,192367 1,256637 -0,223554 -0,225508 -0,225993 -0,226115 -0,226141 1,570796 -0,235059 -0,237114 -0,237624 -0,237751 -0,237779 1,884956 -0,223554 -0,225508 -0,225993 -0,226115 -0,226141 2,199115 -0,190167 -0,191829 -0,192242 -0,192345 -0,192367 2,513274 -0,138164 -0,139372 -0,139672 -0,139746 -0,139763 2,827433 -0,072637 -0,073272 -0,073430 -0,073469 -0,073478 3,141593 0,000000 0,000000 0,000000 0,000000 0,000000 𝐿2𝑥103 3,408666 0,833398 0,194207 0,034703 𝐿∞𝑥103 2,719722 0,664955 0,154955 0,027689
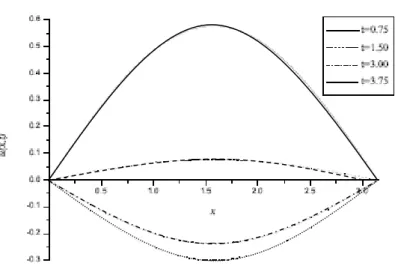
Şekil 4.2’de çeşitli zaman adımlarında 𝛾=1,50 ve N=40 değerleri için nümerik sonuçlar sunulmuştur.
Şekil 4.2. Farklı zaman adımlarında 𝛾=1,50 ve N=40 değerleri için kesir difüzyon dalga denklemin nümerik sonuçları.
Çizelge 4.6’da farklı 𝛾 𝑣𝑒 𝑡 değerlerinde 𝑁 = 40, ∆𝑡 = 0,0075 değerleri için 𝐿2 𝑣𝑒 𝐿∞ hata
normları gösterilmiştir.
Çizelge 4.6. Kesir d,füzyon dalga denklemin N=40, ∆t=0,0075 değerleri i.in farklı 𝛾 ve t değerlerindeki L2 ve 𝐿∞ hata normları.
𝑡 𝛾=1,25 𝛾=1,50 𝛾=1,75 𝐿2𝑥103 𝐿∞𝑥103 𝐿2𝑥103 𝐿∞𝑥103 𝐿2𝑥103 𝐿∞𝑥103 1,5 0,264233 0,210828 0,271215 0,216398 0,416904 0,332641 3,0 0,045250 0,036104 0,065312 0,052112 0,954343 0,761455 4,5 0,068853 0,054936 0,219035 0,174765 0,403232 0,321732 6,0 0,056669 0,045215 0,070316 0,056104 0,804592 0,641971 7,5 0,026110 0,020833 0,045078 0,035967 0,395893 0,315877
4.5. Sonuç
Difüzyon ve difüzyon dalga denklemlerinin kollokasyon yöntemiyle çözümlerine ait test problemleri incelendiğinde elde edilen nümerik sonuçların analitik sonuçlarla uyumlu olduğu görülmektedir.
5. KESİR TÜREVLİ DİFÜZYON DENKLEMİNİN SERBEST GÜÇ
DURUMU İÇİN NÜMERİK ÇÖZÜMÜ
5.1. Giriş
Metzler ve Klafter (2000 ), Balakrishman (1985) ve Wyss (1986) ile verilen serbest güç durumu için kesir difüzyon denkleminin genel formu
𝜕
𝜕𝑡𝑢(𝑥, 𝑡) = 𝐾0𝐷𝑡 1−𝛾 𝜕2
𝜕𝑥2𝑢(𝑥, 𝑡) (5.1)
şeklindedir. Burada 𝐷0 𝑡1−𝛾𝑓(𝑡) Riemann-Liouville operatörü ile tanımlanan kesir türev olup
𝐷𝑡1−𝛾𝑓(𝑡) = 1 𝛤(𝛾) 𝜕 𝜕𝑡∫ 𝑓(𝜏) (𝑡−𝜏)1−𝛾𝑑𝜏 𝑡 0 0 (5.2)
şeklindedir. Burada K difüzyon katsayısı ve 𝛾𝜖(0,1) anormal difüzyon kuvvetidir. Tüm nümerik hesaplamalarda difüzyon katsayısı “1” alınacaktır. Bu çalışmada (5.1) denkleminin 0 ≤ 𝑥 ≤ 1 sınır koşulları
𝑢(0, 𝑡) = 0, 𝑢(1, 𝑡) = 0 (5.3) şeklinde ve başlangıç koşulu
𝑢(𝑥, 0) = 𝑥(1 − 𝑥) (5.4) şeklinde olsun.
(5.1) denkleminin değişken ayrıştırma metodu ile analitik çözümü
𝑢(𝑥, 𝑡) = 8 𝜋3∑ 1 (2𝑛+1)3sin [(2𝑛 + 1)𝜋𝑥] ∞ 𝑛=0 (5.5)
dır (Yuste, 2006). Burada 𝐸𝛾 Mittag-Leffler fonksiyonudur (Podlubny, 1999).
Yapılacak nümerik çözümde, serbest güç durumu için kesir difüzyon denklemin çözümü için bir sonlu eleman algoritması elde edebilmek amacıyla Riemann-Liouville operatörünü ayrıştırırsak 𝐷𝑡1−𝛾𝑢(𝑥𝑗, 𝑡𝑛) = 𝐷𝑡 1−𝛾 𝑢𝑗𝑛 0 0 = 1 (∆𝑡)1−𝛾∑ 𝑤𝑘 1−𝛾 𝑢𝑗𝑛−𝑘+ 𝑂(∆𝑡𝑝) 𝑛 𝑘=0 (5.6)
olur (Yuste, 2006 ; Yuste ve Acedo, 2005). Burada 𝑤01−𝛾 = 1, 𝑤𝑘1−𝛾= (1 −2−𝛾 𝑘 )𝑤𝑘−1 1−𝛾 (5.7) dir.
5.2. Kübik B-Spline Sonlu Eleman Kollokasyon Çözümleri
Önceki bölümlerde kübik B-Spline fonksiyonları tanımlanmıştı.
{𝜑−1(𝑥), 𝜑0(𝑥), … … , 𝜑𝑁+1(𝑥)} kübik B-Spline fonksiyonlar kümesi [a,b] aralığında bir baz oluşturur. Böylece 𝑈𝑁(𝑥, 𝑡) yaklaşık çözümü kübik B-Spline baz fonksiyonları cinsinden
𝑈𝑁(𝑥, 𝑡) = ∑𝑁+1𝑚=−1𝛿𝑚(𝑡)𝜑𝑚(𝑥) (5.8)
şeklinde ifade edilebilir. Burada 𝛿𝑚(𝑡)’ler hesaplanacak zamana bağlı parametrelerdir. Her bir kübik B-Spline baz fonksiyonu 4 eleman tarafından kapsandığından her [𝑥𝑚, 𝑥𝑚+1] elemanı da
4 kübik B-Spline fonksiyon tarafından kapsanır. Bu problem için sonlu elemanlar [𝑥𝑚, 𝑥𝑚+1]
aralığında tanımlanır ve 𝑥𝑚, 𝑥𝑚+1 ‘ler düğüm noktaları olarak ifade edilir. 𝑈𝑚, 𝑈′𝑚, 𝑣𝑒 𝑈"𝑚’
ler 𝛿𝑚(𝑡)’ler cinsinden yazıldığında
𝑈𝑚 = 𝑈(𝑥𝑚) = 𝛿𝑚−1(𝑡) + 4𝛿𝑚(𝑡) + 𝛿𝑚+1(𝑡) 𝑈′𝑚 = 𝑈′(𝑥𝑚) = 3 ℎ(−𝛿𝑚−1(𝑡) + 𝛿𝑚+1(𝑡)) (5.9) 𝑈′′𝑚 = 𝑈′′(𝑥𝑚) = 6 ℎ2(𝛿𝑚−1(𝑡) − 2𝛿𝑚(𝑡) + 𝛿𝑚+1(𝑡))
elde edilir.. Buna göre 𝑈𝑁(𝑥, 𝑡) yaklaşık çözümü
𝑈𝑁(𝑥, 𝑡) = ∑𝑚+2𝑗=𝑚−1𝛿𝑗(𝑡)𝜑𝑗(𝑥) (5.10)
şeklinde ifade edilir.
Eğer (5.1) denkleminde (5.10) eşitliği ve (5.9) türevleri yerine yazılırsa aşağıdaki 1. mertebeden adi diferansiyel denklem sistemi elde edilir.
𝛿̇𝑚−1(𝑡) + 4𝛿̇𝑚(𝑡) + 𝛿̇𝑚+1(𝑡) − 6
Burada " ̇ " zamana göre türevi ifade etmektedir. (5.11) ifadesinde geçen 𝛿𝑚(𝑡) 𝑣𝑒 𝛿̇𝑚(𝑡)
ifadeleri Crank-Nicolson formülüyle ayrıştırılırsa.
𝛿 =1 2(𝛿 𝑛+ 𝛿𝑛+1) 𝛿̇ =𝛿𝑛+1∆𝑡−𝛿𝑛 (5.12) olur. 𝐷𝑡1−𝛾
0 Riemann-Liouville kesirli operatörünü
𝐷𝑡1−𝛾𝛿𝑛 0 = 1 ∆𝑡1−𝛾∑ 𝑤𝑘 1−𝛾 𝛿𝑛−𝑘 𝑛 𝑘=0 (5.13)
şeklinde ayrıştırırsak bilinmeyen 𝛿𝑚𝑛+1(𝑡) parametresine göre ardışık zaman adımları için
aşağıdaki tekrarlama bağıntısı elde edilir.
(1 − 𝑎)𝛿𝑚−1𝑛+1 + (4 + 2𝑎)𝛿𝑚𝑛+1+ (1 − 𝑎)𝛿𝑚+1𝑛+1 = (1 + 𝑎)𝛿𝑚−1𝑛 + (4 − 2𝑎)𝛿𝑚𝑛 + (1 + 𝑎)𝛿𝑚+1𝑛 + ∑ 𝑤𝑘 1−𝛾 [(𝛿𝑚−1𝑛+1−𝑘+ 𝛿𝑚−1𝑛−𝑘) − 2(𝛿𝑚𝑛+1−𝑘+ 𝛿𝑚𝑛−𝑘) + (𝛿𝑚+1𝑛+1−𝑘+ 𝛿𝑚+1𝑛−𝑘)] 𝑛 𝑘=1 (5.14) Burada
𝛼 =
3(∆𝑡)𝛾 ℎ2 dır.(5.14) sistemi N+1 lineer denklem ve N+3 bilinmeyenden oluşan bir sistemdir. Burada bilinmeyen parametreler (𝛿−1, … … … 𝛿𝑁+1)𝑇 şeklindedir. Bu sistemden tek bir çözüm elde
edebilmek için 2 ilave koşula ihtiyaç vardır. Bu ilave koşullar sınır koşullarının uygulanmasıyla elde edilen denklemden 𝛿−1 𝑣𝑒 𝛿𝑁+1 elimine edilir.
5.3. Başlangıç Durumu
İterasyona başlayabilmek için başlangıç zamanına ait başlangıç vektörünün hesaplanmasına ihtiyaç vardır. 𝑑0 = (𝛿
0, 𝛿1, 𝛿2, … … . 𝛿𝑁−1, 𝛿𝑁)𝑇 başlangıç vektörü başlangıç ve
𝑈𝑁(𝑥, 𝑡) = ∑ 𝛿𝑚(0)𝜑𝑚(𝑥) 𝑁+1
𝑚=−1
şeklinde tekrar yazılabilir. Burada 𝛿𝑚(0) bilinmeyen eleman parametresidir. Başlangıç koşulunu sağlayan çözüm yardımıyla aşağıdaki eşitlikler yazılabilir.
𝑈𝑁(𝑥, 0) = 𝑈(𝑥𝑚, 0), 𝑚 = 0,1,2, … … 𝑁,
(𝑈𝑁)𝑥𝑥(0,0) = −2, (𝑈𝑁)𝑥𝑥(1,0) = −2
Bu koşulların kullanılmasıyla üçgensel bant matrisi şeklinde 𝑊𝑑0= 𝑏
formu oluşturulur. Burada
𝑊 = [ 6 1 0 4 1 14 1 ⋱ ⋱ 1 4 0 1 6 ] 𝑏 = [𝑈(𝑥0, 0) + ℎ2 3 , 𝑈(𝑥1, 0), 𝑈(𝑥2, 0), … … … 𝑈(𝑥𝑁−2, 0), 𝑈(𝑥𝑁−1, 0), 𝑈(𝑥𝑁, 0) + ℎ2 3] 𝑇
dır. Bu sistemin çözülmesiyle 𝑡 = 0 zamanında eleman parametrelerinin değerleri hesaplanmış olur. Burada (5.14) tekrarlama bağıntısı yardımıyla diğer zamanlardaki sonlu eleman değerleri hesaplanmış olur.
5.4. Nümerik Örnekler
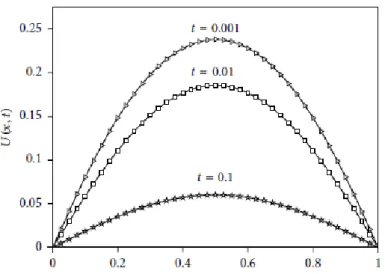
Şekil 5.1 ve şekil 5.2’de ∆t=0,0001, N=40, t=0,001, t=0,01 ve t=0,1 değerleri kullanılarak 2 farklı 𝛾 = 0,50 𝑣𝑒 𝛾 = 0,75 değeri için nümerik ve analitik sonuçlar gösterilecektir.
Şekil 5.1. Kesir difüzyon denklemin 𝛾=0,50, N=40, ∆t=0,0001, t=0,001, t=0,01 ve t=0,1 değerleri için elde edilen nümerik sonuçlar.
Şekil 5.2. Kesir difüzyon denklemin 𝛾=0,75, N=40, ∆t=0,0001, t=0,001, t=0,01 ve t=0,1 değerleri için elde edilen nümerik sonuçlar.