FEN BĠLĠMLERĠ ENSTĠTÜSÜ
PARÇACIK SÜRÜ OPTĠMĠZASYONU ALGORĠTMASININ GEZGĠN SATICI PROBLEMĠNE UYGULANMASI VE
PERFORMANSININ ĠNCELENMESĠ
MEHMET YASĠN ÖZSAĞLAM
YÜKSEK LĠSANS TEZĠ
ELEKTRONĠK VE BĠLGĠSAYAR SĠSTEMLERĠ EĞĠTĠMĠ ANA BĠLĠM DALI
T.C.
SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ
PARÇACIK SÜRÜ OPTĠMĠZASYONU ALGORĠTMASININ GEZGĠN SATICI PROBLEMĠNE UYGULANMASI VE
PERFORMANSININ ĠNCELENMESĠ
MEHMET YASĠN ÖZSAĞLAM
YÜKSEK LĠSANS TEZĠ
ELEKTRONĠK VE BĠLGĠSAYAR SĠSTEMLERĠ EĞĠTĠMĠ ANA BĠLĠM DALI
Bu tez 29.01.2009 tarihinde aĢağıdaki jüri tarafından oy birliği ile kabul edilmiĢtir.
……….. ……….. ……… Prof. Dr. Yrd. Doç. Dr. Yrd. Doç. Dr. Novruz ALLAHVERDĠ Mehmet ÇUNKAġ Fatih BAġÇĠFTÇĠ
ÖZET
Yüksek Lisans Tezi
PARÇACIK SÜRÜ OPTĠMĠZASYONU ALGORĠTMASININ GEZGĠN SATICI PROBLEMĠNE UYGULANMASI VE
PERFORMANSININ ĠNCELENMESĠ
Mehmet Yasin ÖZSAĞLAM
Selçuk Üniversitesi Fen Bilimleri Enstitüsü Elektronik ve Bilgisayar Sistemleri Eğitimi Anabilim Dalı
DanıĢman : Yrd. Doç. Dr. Mehmet ÇUNKAġ 2009, 119 Sayfa
Jüri : Prof. Dr. Novruz ALLAHVERDĠ Yrd. Doç. Dr. Mehmet ÇUNKAġ Yrd. Doç. Dr. Fatih BAġÇĠFTÇĠ
Bir çok optimizasyon tekniği doğadaki olaylardan esinlenerek geliĢtirilmiĢtir. Parçacık Sürü Optimizasyonu (PSO), kuĢ ve balık sürülerinin sosyal davranıĢlarını gözlemleyerek geliĢtirilen popülasyon temelli bir optimizasyon algoritmasıdır. Bu çalıĢmada, PSO algoritması, 8 ayrı test problemi üzerine uygulanmıĢ, Genetik Algoritmalar (GA) ve Diferansiyel Evrim Algoritmaları (DEA) ile performansı karĢılaĢtırılmıĢtır. PSO ayrıca, NP-zor sınıfına giren Gezgin Satıcı Problemi’nin (GSP) çözümü için uygulanmıĢ ve performansı Genetik Algoritma ile karĢılaĢtırılmıĢtır. GSP problemleri olarak 6 küçük boyutlu GSP, 4 orta boyutlu GSP, Türkiye haritası üzerinde il merkezleri ve ilk defa ilçe merkezleri ele alınmıĢtır.
Sürekli fonksiyonların çözümünde PSO algoritması oldukça baĢarılı sonuçlar üretmiĢtir. DEA ise GA’ ya göre iyi performans göstermesine rağmen PSO’ ya göre daha kötü sonuçlar üretmiĢtir. GSP problemlerinde ise PSO jenerasyon sayısı olarak GA’ ya göre daha iyi olmasına rağmen, ortalama yol uzunluğu olarak daha kötüdür. Sonuç olarak PSO algoritması sürekli fonksiyonların çözümünde oldukça baĢarılı bir sonuç göstermiĢtir. Ayrıca GSP çözümlerinde ise jenerasyon sayıları açısından daha iyi sayılabilir.
Anahtar Kelimeler : Parçacık Sürü Optimizasyonu, Genetik Algoritma, Diferansiyel Evrim Algoritması, Gezgin Satıcı Problemi,Optimizasyon, Yapay Zeka
ABSTRACT
MS Thesis
APPLICATĠON OF PARTICLE SWARM OPTIMISATION ALGORITHM TO TRAVELLING SALESMAN PROBLEM
AND ITS PERFORMANCE INVESTIGATION
Mehmet Yasin ÖZSAGLAM Selçuk University
Graduate School of Natural Applied Sciences Department of Electronics and Computer System Education
Supervisor : Assist. Prof. Dr. Mehmet ÇUNKAġ 2009,119 Pages
Jury : Prof. Dr. Novruz ALLAHVERDĠ Assist. Prof. Dr. Mehmet ÇUNKAġ
Assist. Prof. Dr. Fatih BAġÇĠFTÇĠ
Many of the optimisation techniques have been devoloped by the inspiration of naturel occurance events. Particle Swarm Optimization (PSO), is a population based optimization algorithm which is devoloped by the observation of bird and fish swarms social behaviors. In this study, PSO algorithm is applied on a 8 different test functions and the results are compared with Genetic Algorithms (GA) and Differantiel Evolution Algorithms (DEA). PSO specially, applied on the solution of Travelling Salesman Problem (TSP) which is catogorized as a NP-hard and also the solutions are compared with Genetic Algorithms (GA). As the TSP, problems are applied on a 6 small sized TSP, 4 medium sized TSP and province of Turkey map and the first time on the districts of Turkey.
On continuous function solutions PSO algorithm has generated a successful solutions. DEA has a successfull performance than GA but less solutions than PSO. On TSP solutions PSO has succesfull generation numbers than GA but unsuccessful by the avarage tour length. As a result PSO algorithm has a good solution on continous functions. Besides PSO can be accepted as successful in terms of generation number.
Keywords : Particle Swarm Optimization, Genetic Algorithm, Differantial Evolution Algorithm, Travelling Salesman Problem, Optimisation, Artificial Intelligance.
TEŞEKKÜR
Bu çalıĢmada bana yol gösteren danıĢman hocam Sayın Yrd. Doç. Dr. Mehmet ÇUNKAġ’ a ve bizi bu günlere getiren tüm hocalarıma, desteklerini esirgemeyen aileme ve eĢime teĢekkürlerimi sunarım.
İÇİNDEKİLER
ÖZET……… iii
ABSTRACT………. iv
TEġEKKÜR………. v
ĠÇĠNDEKĠLER……… vi
ġEKĠLLER LĠSTESĠ………... viii
TABLOLAR LĠSTESĠ………. x
SĠMGELER……….. xi
1. GĠRĠġ……… 1
1.1 Tezin Amacı ve Önemi……….. 1
1.2 Tez Organizasyonu……… 2
2. PROBLEMLER ve OPTĠMĠZASYON………... 4
2.1 Problemler……….. 4
2.2 Optimizasyon………. 6
3. GEZGĠN SATICI PROBLEMĠ……… 8
3.1 Gezgin Satıcı Probleminin Tanımı……….... 8
3.2 Gezgin Satıcı Probleminin Kesin Çözümü……… 10
4. PARÇACIK SÜRÜ OPTĠMĠZASYONU……… 13
4.1 GiriĢ……… 13
4.2 Algoritma………... 14
4.3 Algoritmanın Gezgin Satıcı Problemi için Uygulanması……….. 15
4.3.1 Yer DeğiĢtirme Operatörü………. 17
4.3.2 Algoritmanın Yeniden Düzenlenmesi……… 19
5. GENETĠK ALGORĠTMALAR……… 21
5.1 GiriĢ……… 21
5.2 Algoritma………... 23
5.3 Algoritmanın Sürekli Fonksiyonların Çözümünde Kullanılması……... 24
5.4 Genetik Algoritmanın Gezgin Satıcı Problemi için Kullanılması…….. 27
6. DĠFERANSĠYEL EVRĠM ALGORĠTMASI………... 30
6.1 GiriĢ……… 30
7. PARÇACIK SÜRÜ ALGORĠTMASININ KARġILAġTIRILMASI…….. 33
7.1 Test Fonksiyonları……….. 33
7.2 Sonuçlar……….. 34
8. GEZGĠN SATICI PROBLEMĠNĠN, PARÇACIK SÜRÜ OPTĠMĠZASYONU ĠLE ÇÖZÜMÜ……… 44
8.1 Küçük Boyutlu GSP Test Problemleri………... 44
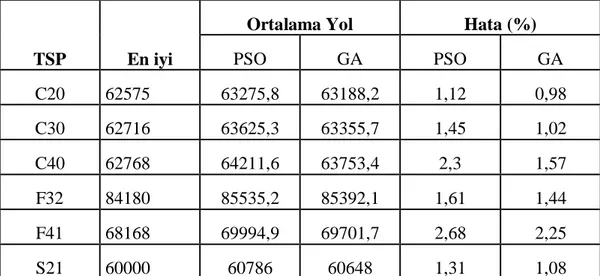
8.1.1 Küçük Boyutlu GSP Test Sonuçları………... 48
8.1.2 Küçük GSP Problemlerinin Çözümünde Parametrelerin Etkisi…. 51 8.2 Literatürde Kullanılan GSP Test Problemleri ………... 53
8.2.2 Literatürde Kullanılan GSP Test sonuçları .……….. 53
8.3 Orta Boyutlu GSP Test Problemleri ……….……… 55
8.3.1 Orta Boyutlu GSP Test Sonuçları …..………... 56
8.4 Amerika ve Türkiye Haritası Üzerinde Gezgin Satıcı Problemi……… 62 8.4.1 Amerika ġehirleri GSP Çözümü……… 62
8.4.2 Konya Ġlçeleri GSP Çözümleri ……….. 64
8.4.3 Türkiye Ġl Merkezleri GSP Çözümü ………. 66
8.4.4 Türkiye Ġlçeleri GSP Çözümleri ……… 69
9. SONUÇ ve ÖNERĠLER……… 82
KAYNAKLAR ………. 86
ŞEKİLLER LİSTESİ
ġekil 2.1 Yerel Minimum ve Global Minimum……… 7
ġekil 3.1 ABD üzerindeki 532 Ģehrin optimum yol uzunluğu………….. 9
ġekil 3.2 Örnek bir TSP çözümü………... 10
ġekil 4.1 Bireylerin Minimuma YaklaĢımı………... 14
ġekil 4.2 Parçalı Sürü Optimizasyonu AkıĢ Diyagramı……… 16
ġekil 4.3 Yer DeğiĢtirme Operatörü……….. 17
ġekil 5.1 Genetik Algoritma……….. 26
ġekil 6.1 Diferansiyel Evrim Algoritması ġeması……… 31
ġekil 7.1 F1 Fonksiyonu için Ortalama Jenerasyonlar……….. 35
ġekil 7.2 F2 Fonksiyonu için Ortalama Jenerasyonlar……….. 35
ġekil 7.3 F3 Fonksiyonu için Ortalama Jenerasyonlar……….. 36
ġekil 7.4 F4 Fonksiyonu için Ortalama Jenerasyonlar……….. 36
ġekil 7.5 F5 Fonksiyonu için Ortalama Jenerasyonlar……….. 37
ġekil 7.6 F6 Fonksiyonu için Ortalama Jenerasyonlar……….. 37
ġekil 7.7 F7 Fonksiyonu için Ortalama Jenerasyonlar………... 38
ġekil 7.8 F8 Fonksiyonu için Ortalama Jenerasyonlar……….. 38
ġekil 7.9 F1 Fonksiyonun Genetik Algoritma ile Optimizasyonu……… 39
ġekil 7.10 F1 Fonksiyonun PSO ile Optimizasyonu………... 40
ġekil 7.11 F1 Fonksiyonun DEA ile Optimizasyonu……….. 40
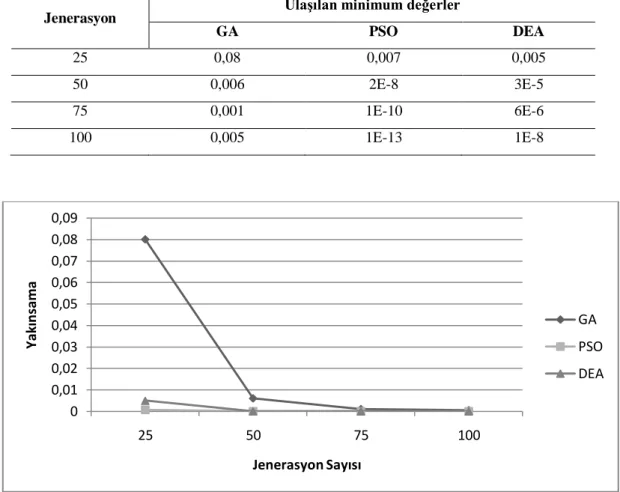
ġekil 7.12 ÇeĢitli Jenerasyonlarda Yakınsama………. 41
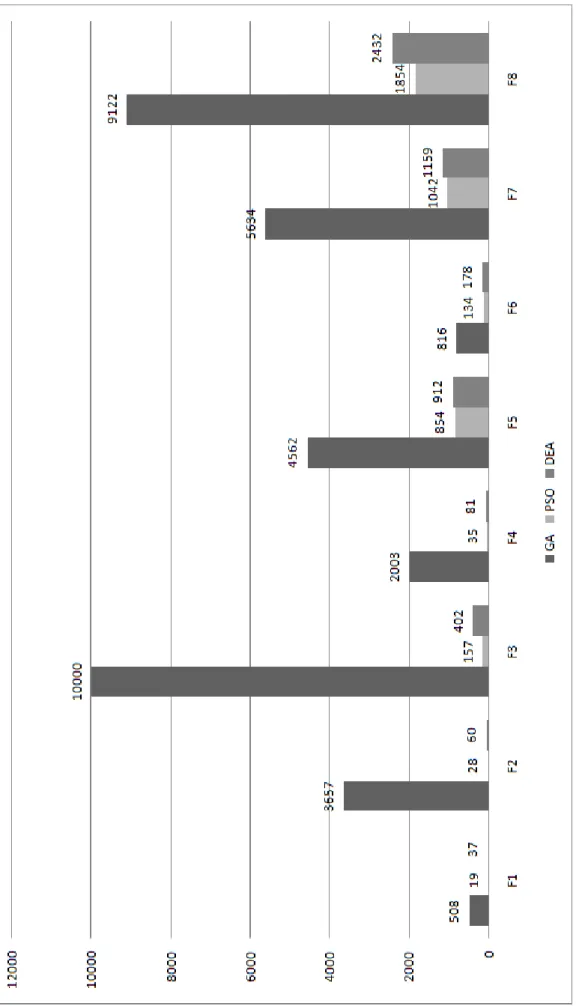
ġekil 7.13 Test Fonksiyonları Ortalama Jenerasyon Sayıları……….. 42
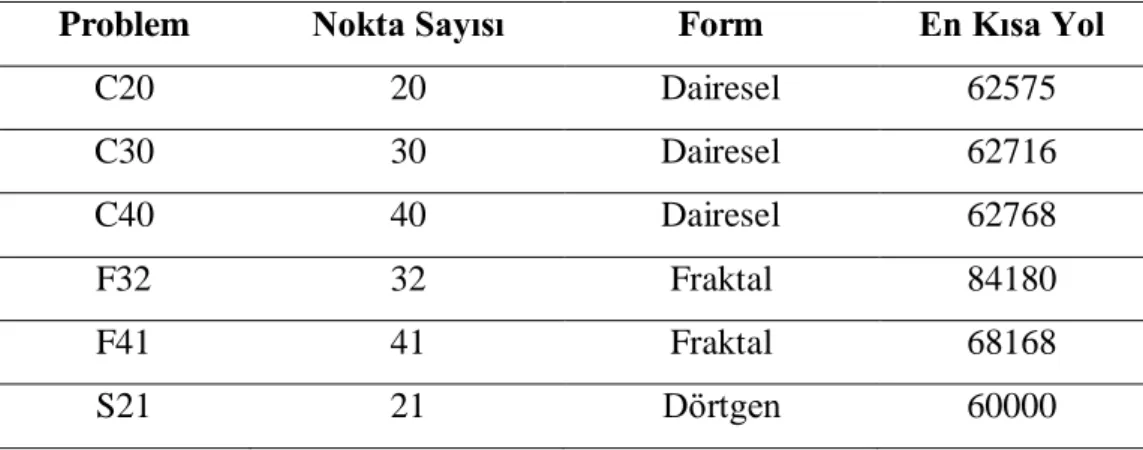
ġekil 8.1 C20 Problemi……….. 45 ġekil 8.2 C30 Problemi……….. 45 ġekil 8.3 C40 Problemi……….. 46 ġekil 8.4 F32 Problemi……….. 46 ġekil 8.5 F41 Problemi……….. 47 ġekil 8.6 S21 Problemi……….. 47
ġekil 8.7 Test Fonksiyonları Ortalama Yol Uzunlukları………... 49
ġekil 8.8 Test Fonksiyonları Ortalama Hata Değerleri………. 50
ġekil 8.9 PSO Algoritmasında Bireylerin Etkisi ………. 52
ġekil 8.10 GA Algoritmasında Bireylerin Etkisi ……….. 52
ġekil 8.11 Literatürde Kullanılan GSP Ortalama Yol Değerleri ………… 54
ġekil 8.12 Literatürde Kullanılan GSP Ortalama Hata Değerleri ……... 55
ġekil 8.13 Orta Boyutlu GSP Bulunan En Ġyi Yollar ………. 57
ġekil 8.14 Bulunan En Ġyi Yolların Ortalama Hataları ……….. 57
ġekil 8.16 Ortalama Yolların Hatası ……….. 58
ġekil 8.17 XQF131 Problemi için PSO ve GA’nın Bulduğu Minimum Yol………. 59
ġekil 8.18 XQG237 Problemi için PSO ve GA’nın Bulduğu Minimum Yol………. 59
ġekil 8.19 BCL380 Problemi Bulunan En Kısa Yollar……….. 60
ġekil 8.20 PBM436 Problemi Bulunan En Kısa Yollar………. 61
ġekil 8.21 Att532 Probleminin GA ile Bulunan En Ġyi Yolu ……… 63
ġekil 8.22 Att532 Probleminin PSO ile Bulunan En Ġyi Yolu……… 63
ġekil 8.23 Konya Haritası Üzerinde ĠĢaretlemiĢ Ġlçeler……….. 64
ġekil 8.24 PSO ve GA’nın UlaĢtığı En Kısa Yol ……….. 65
ġekil 8.25 Türkiye Ġl Merkezleri………. 67
ġekil 8.26 Türkiye Ġl Merkezleri PSO ve GA ile Bulunan en Kısa Yol……… 68
ġekil 8.27 Türkiye Ġlçe Merkezleri ……….. 70
ġekil 8.28 Türkiye Ġlçe Merkezleri GA ile Bulunan en Kısa Yol………. 71
ġekil 8.29 Türkiye Ġlçe Merkezleri PSO ile Bulunan en Kısa Yol……… 72
Ek A ġekil 1 Sürekli Fonksiyonların PSO ile Çözümü……….. 81
Ek A ġekil 2 Küçük Boyutlu GSP için GeliĢtirilen Program………. 82
Ek A ġekil 3 Orta Boyutlu GSP için GeliĢtirilen Program………. 83
Ek A ġekil 4 Konya ilçeleri GSP için GeliĢtirilen Program……… 84
Ek A ġekil 5 Türkiye Ġl Merkezlerini Kapsayan, GSP için GeliĢtirilen Program……….. 85
Ek A ġekil 6 Türkiye Ġlçe Merkezlerini Kapsayan GSP için GeliĢtirilen Program……….. 86
TABLOLAR LİSTESİ
Tablo 3.1 Sayım Tekniği ile GSP ’ lerin Çözüm Zamanları……….. 12
Tablo 4.1 Bireylerin GeliĢim Değerleri………. 14
Tablo 7.1 Parametreler için Kullanılan Değerler………... 33
Tablo 7.2 Test Fonksiyonları………. 34
Tablo 7.3 ÇeĢitli Jenerasyonlarda UlaĢılan Minimum Değerler………… 41
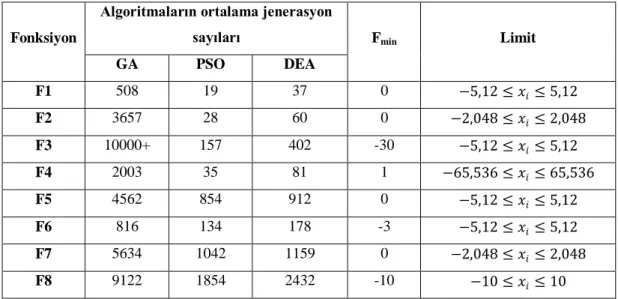
Tablo 7.4 Genel Test Sonuçları………. 43
Tablo 8.1 Küçük Boyutlu Gezgin Satıcı Test Problemleri 44 Tablo 8.2 Küçük Boyutlu GSP Test sonuçları………... 48
Tablo 8.3 Test Fonksiyonlarının Çözümünde Birey Sayının Etkisi…….. 51
Tablo 8.4 Literatürde Kullanılan ÇeĢitli GSP Test Problemleri ……….. 53
Tablo 8.5 Literatürde Kullanılan GSP Test Sonuçları……….. 54
Tablo 8.6 Orta Büyüklükteki GSP Test Problemleri……… 55
Tablo 8.7 Orta Boyutlu GSP Test Sonuçları ……… 56
Tablo 8.8 Att532 GSP Sonuçları……….. 62
Tablo 8.9 Konya Ġlçeleri Sonuçlar……… 65
Tablo 8.10 TR81 Sonuçları ……… 66
Tablo 8.11 TR81 Gerçek Koordinatlar ile Ortalama Yollar……… 66
Tablo 8.12 Türkiye Ġlçeleri GSP Çözümleri Ortalama Sonuçları………… 69
Tablo 9.1 Sürekli Test Fonksiyonları Genel Sonuçları……….. 73
Tablo 9.2 Küçük Boyutlu GSP Test Sonuçları………... 74
Tablo 9.3 Literatürde Kullanılan GSP Test Sonuçları……… 75
Tablo 9.4 Orta Boyutlu GSP Test Sonuçları……….. 75
Tablo 9.5 Türkiye 81 il merkezi GSP sonuçları……… 76
SİMGELER ve KISALTMALAR
: Toplam Ģehir sayısı
𝑑𝑖𝑗 : Ġki nokta arasındaki uzaklık
𝑓𝑡𝑝 : Tüm Ģehirler arasındaki toplam uzaklık Vid : Sürüdeki her bir bireyin hızı
W : Atalet ağırlık değeri 𝑐𝑖 : Sabit sayılar
𝑟𝑎𝑛𝑑𝑖 : 0 ile 1 arasında üretilen sabit sayılar 𝑃𝑖𝑑 : Önceki nesilde en iyi birey
𝑃𝑔𝑑 : Tüm nesillerdeki en iyi birey 𝑋𝑖𝑑 : Sürüdeki bireyler
𝑆 : Yer değiĢtirme
𝑆𝑂 : Yer değiĢtirme operatörü
𝑆𝑆 : Birden çok yer değiĢtirme operatörü
⨁ : YerdeğiĢtirme operatörlerinin sırayla uygulanması α : Bireyin önceki nesildeki bireye benzeme oranı β : Bireyin tüm nesildeki en iyi bireye yakınsama oranı 𝐶𝑅 : Çaprazlama oranı
𝐹 : Ölçekleme Değeri 𝑋𝑙𝑜𝑤 : En düĢük değerli birey 𝑋𝑖𝑔 : En yüksek değerli birey DEA : Diferansiyel evrim algoritması GA : Genetik Algoritmalar
1. GİRİŞ
1.1 Tezin Amacı ve Önemi
Matematikte, optimizasyon terimi, bir fonksiyonu minimize ya da maksimize etmek amacıyla gerçek ya da tamsayı değerlerini tanımlı bir aralıkta seçip fonksiyona yerleĢtirerek sistematik olarak bir problemi incelemek ya da çözmek iĢlemlerini ifade eder. Optimize edilecek problemin zorluğuna göre çözüm uzayı çok büyük ve karmaĢık olabilir. Bu durumda çözüm uzayında bulunan elemanların hepsini inceleyen matematiksel yöntemler yerine sezgisel yöntemlerden yararlanılmalıdır.
Son yıllarda kombinasyonel problemlerin çözülmesinde sezgisel yöntemlerin kullanımları önemli oranda artmaktadır. Jones ve diğerlerine, (2002) göre sezgisel yöntemlerin popülaritesinin 1991 yılından itibaren hızlı bir artıĢ göstermesinin nedenlerinden birincisi, bilgisayarların hesaplama gücünün iyi olması ikincisi, dönüĢtürülebilir yönünün olmasıdır. Ayrıca sezgisel yöntemlerin en büyük avantajları arasında çözüm zamanının, sayım (enumeration) yöntemine göre çok kısa olması ve her tür problem için kolay entegre edilebilmesidir. Dezavantajları ise bu yöntemlerin optimum çözümü garanti etmemesi ve iyi çözüm verebilmesi için bir çok parametrenin uygun Ģekilde ayarlanması gerekliliğidir.
Bu sezgisel yöntemlerden biri olan Parçacık Sürü Optimizasyonu (Particle Swarm Optimization, PSO), kuĢ ve balık sürülerinin iki boyutlu hareketlerinden esinlenerek ilk olarak 1995 ve 1996 yıllarında Kennedy ve Eberhart tarafından geliĢtirilmiĢtir. Parçacık Sürü Optimizasyonu (PSO) bireyler arasındaki sosyal bilgi paylaĢımını esas alır. PSO’da arama iĢlemi genetik algoritmalarda olduğu gibi popülasyondaki bireyler tarafından belirlenen nesil sayısınca yapılır. Her bireye parçacık denir ve parçacıklardan oluĢan popülasyona da sürü (swarm) denir. Her bir parçacık kendi pozisyonunu, bir önceki tecrübesinden yararlanarak bir önceki sürüdeki en iyi pozisyona doğru ayarlar. Literatürde PSO bir çok problemin optimizasyonunda baĢarı ile kullanılmıĢtır, sipariĢ miktarı belirleme, sinir ağları, akıĢ tipi çizelgeleme problemleri, güç ve voltaj kontrolü, tedarik seçimi ve sıralama problemi (Kennedy ve Eberhart 1995 ).
PSO ve Genetik Algoritmaların (GA) benzer yanları olduğu gibi, temel olarak ayrıldığı noktalarda mevcuttur. PSO ve GA her iki yöntemde problemi optimize etmek için yeni nesiller jenerasyonlar meydana getirirler. Her ikisi de popülasyon tabanlı algoritmalardır ve yeni nesillerin bir önceki nesle göre daha iyi sonuç üretmesini temel alırlar. Ġki algoritmanın birbirinden ayrıldığı temel nokta ise GA’nın yeni nesli oluĢtururken en iyi bireyi baz almamasıdır ve çeĢitli yöntemlerle bireyleri birbirleri ile çaprazlayarak, yeni nesil üretimidir. Ancak PSO’da bu durum biraz daha farklıdır, tüm bireyler en iyi bireye yaklaĢmaya çalıĢır. Bu açıdan bakıldığında PSO, GA’ya göre biraz daha aç gözlü bir algoritmadır, sonuca daha kısa sürede ulaĢmayı amaçlar. Tabi ki bu durum çözümün yerel minimuma takılmasına yol açabilir. GA ise yeni neslin oluĢturulmasında daha rastgele seçimler yaptığı için sonuca ulaĢırken yerel minimuma takılma olasılığı daha azdır. Diferansiyel Evrim Algoritması (DEA) ise basit ama güçlü popülasyon tabanlı bir algoritmadır. Popülasyon tabanlı ve mutasyon ve çaprazlama operatörlerini kullanarak hedef çözüme ulaĢmaya çalıĢan bir algoritmadır. Algoritma bir ebeveyn vektörden, bir deneme vektörü üretmek için mutasyon ve çaprazlamayı birlikte kullanır. Yeni bir yöntem olan DEA özellikle sürekli fonksiyonların çözümünde etkin bir sonuç göstermiĢtir.
Sezgisel algoritmaların kullanım alanlarını belirlemek için performanslarının ölçülmesi yararlıdır. Bu amaçla algoritmalar genellikle diğer algoritmalarla karĢılaĢtırılır. Problemin zorluğu ve özelliklerine göre algoritmaların gösterdiği performansları görmek, algoritmanın daha çok hangi problemlerin çözümünde kullanılacağını belirlemede etkilidir.
1.2 Tez Organizasyonu
Bu tezde, matematiksel metodlarla çözümü oldukça uzun olan Gezgin Satıcı Probleminin (GSP) çözümü oldukça yeni bir yöntem olan PSO ile gerçekleĢtirilmiĢtir ve GA ile performansı karĢılaĢtırılmıĢtır. Ayrıca PSO’nun sürekli fonksiyonların çözümündeki performansı GA ve DEA yöntemleri ile karĢılaĢtırılmıĢtır.
Tezin ikinci bölümünde problem çeĢitleri ve optimizasyon yöntemlerinden bahsedilmiĢtir. Üçüncü bölümde Gezgin Satıcı Probleminin niteliklerinden, çözüm yöntemlerinden bahsedilmiĢtir. Dördüncü bölümde PSO algoritması ve bu algoritmanın GSP için uyarlanması anlatılmıĢtır. BeĢinci bölümde GA iĢlem basamaklarından ve sürekli fonksiyonların çözümü için gerçek kodlu GA anlatılmıĢtır. Ayrıca GA’nın GSP için nasıl düzenlendiği anlatılmıĢtır. Altıncı bölümde DEA iĢlem basamakları anlatılmıĢtır.
Yedinci bölümde PSO, GA ve DEA yöntemlerinin 8 ayrı, sürekli fonksiyonun çözümündeki performansları ele alınmıĢtır. Sekizinci bölümde PSO ve GA algoritmalarının küçük ve orta büyüklükteki GSP problemlerinin çözümündeki performansları değerlendirilmiĢtir. Son olarak Konya ilçeleri, Türkiye il merkezleri ve Türkiye ilçelerini kapsayan GSP çözümleri yapılmıĢtır. Son bölümde ise sonuçlar ve önerilerden bahsedilmiĢtir.
2. PROBLEMLER VE OPTİMİZASYON
2.1 Problemler
Problemin çözümüne yönelik bir algoritma araĢtırılmadan önce, bu problemin, sonlu sayıda aĢamada çözülüp çözülemeyeceğini bilmek gerekir. Hesaplanabilirlik teriminin açıklaması da budur. Ġnsan veya makine tarafından gerçekleĢtirilecek bir eylemin mekanik olarak ardıĢık aĢamalar halinde yürütülebilmesi için verilen komutlara algoritma denir. Kullanılan algoritma tipine ve problemin zorluğuna göre çözüm zamanı uzayacaktır. Algoritmanın giriĢ değerlerinin boyutu veya problem boyutu, giriĢi tanımlamak için gerekli sembollerin sayısı ile bağıntılıdır.
Hesaplama teorisinde, bazı tip problemlerin çözümü için en etkili algoritmaların çalıĢma süresinin girilen verinin büyüklüğüne bir polinom cinsinden bağlı olduğu bilinmektedir (buna polinomsal zamanda çalıĢan algoritma adı verilir) ve bu tür problemler P kategorisindeki problemlerdir. Mesela verilen basamaklı bir sayının asal olup olmadığını kontrol etmek için çalıĢma süresi mertebesinde bir polinomla hesaplanabilen bir algoritma vardır. Dolayısıyla verilen bir sayının asal olup olmadığının araĢtırılması P kategorisinde bir problemdir.
Buna karĢılık bir diğer gurup problem vardır ki; bunlar için sorulan soruya, girilen verinin büyüklüğüne polinom mertebesinde bağımlı bir sürede cevap verecek bir algoritma bilinmemektedir. Fakat bu tür bazı problemler için eğer bir Ģekilde cevabı tahmin edebiliyorsak, tahminimizin doğruluğunu sınamak için veri büyüklüğüne bağlı sürelerde çalıĢacak algoritmalar vardır. Bu tür problemler, yani bir tahminin doğruluğunun kontrolü için çalıĢma süresi verinin büyüklüğüne polinom cinsinden bağımlı bir algoritma olan problemler de NP kategorisini oluĢtururlar. Örnek olarak verilen basamaklı bir sayının asal çarpanlarının neler olduğu sorusunu düĢünebiliriz. Bu sorunun cevabı için bilinen en iyi algoritmanın çalıĢma süresi sayısına bir polinom cinsinden değil de eksponansiyel fonksiyonlar cinsinden ( misali) bağımlıdır (buna üstel zamanda çalıĢan algoritma denir). Fakat bu problem için eğer bir Ģekilde cevabı tahmin edebiliyorsak tahminimizin
doğruluğunu sınamak için sayısına bağlı bir sürede çalıĢacak bir algoritma mevcuttur. Dolayısıyla verilen bir basamaklı sayının asal çarpanlarının neler olduğu sorusu NP kategorisindedir.
Bu iki kategoriden NP’nin P’yi içerdiğini görmek kolaydır. Eğer bir sorunun cevabını verinin büyüklüğüne polinom mertebesinde bağımlı sürede çalıĢacak bir algoritmayla bulabiliyorsak, bu soruya cevap olarak üretilmiĢ bir tahminin doğruluğunu da verinin büyüklüğüne polinom mertebesinde bağımlı sürede çalıĢacak bir algoritmayla kontrol edebiliriz. Bunun için verilen sorunun cevabını verecek algoritmayı çalıĢtırıp, onun verdiği cevabı kendi tahminimizle karĢılaĢtırmak yeterlidir. "P=NP?" problemi bunun tersinin de doğru olup olmadığını sorgular. Yani NP kategorisinde olup da P kategorisinde olmayan problemler var mıdır? Veya diğer bir dille asal çarpanların bulunması için polinom mertebesinde bir sürede çalıĢacak bir algoritma gerçekten yok mu? Yoksa var da biz mi bulamıyoruz? Bu alanın uzmanlarının çoğunun görüĢü bu tür algoritmaların gerçekten de var olmadıkları için bulunamadığı (yani P’nin NP’ye eĢit olmadığı) Ģeklinde ancak bu soruya kesin bir cevap verilebilmesi Ģimdilik çok zor gözüküyor.
En az her bir NP problem kadar zor olan problemlerin bulunduğu sınıfa NP-Zor (NP-hard) denir. Daha resmi bir Ģekilde,
(2.1)
Burada , L probleminin, H problemine çokterimli zamanda indirgenebildiği anlamına gelir. Bir baĢka deyiĢle, NP-Zor sınıfındaki her hangi bir problem çok terimli zamanda çözülebilirse, NP sınıfındaki bütün problemler çok terimli zamanda çözülebilir (Garey ve Johnson , 1979).
2.2 Optimizasyon
Optimizasyon; bir problemde belirli koĢullar altında mümkün olan alternatifler içinden en iyisini seçmektir. Günümüzde bir çok bilim dalı karĢılaĢtığı
problemleri optimize etmek zorundadır. Bir çok mühendislik dalında geliĢtirilen projelerde optimizasyon önemli yer tutmaktadır. Yapı-Araç Ġskeleti dinamiği'ne iliĢkin problemler sıklık ile matematiksel programlama teknikleri gerektirmektedir. Yapı-Araç Ġskeleti, manifold ile kısıtlanmıĢ bir basit diferansiyel denklem'in çözümüne ihtiyaç duyan bir yönelim olarak değerlendirilebilir.Bu durumda kısıtlar non-lineer olmayan gemotetrik çeĢitliliktedir, öneğin "bu iki nokta daima temas etmeli", "bu alan diğerine etki etmemeli" ya da "bu nokta her zaman bu eğri üzerinde olmalı" gibi. Ayrıca temas halindeki kuvvetlere iliĢkin problemler de lineer uyumluluk çatısı altında çözüldüğünden, buna da bir tür QP (Kuadratir Programlama) Problemi gözüyle bakılabilir(Avriel 2003).
Pek çok tasarım problemi de optimizasyon programları ile çözülmektedir. Bu tür uygulamalara dizayn optimizasyonu denir. Bu alanda bilinen ve büyümekte olan bir alt kol çok disiplinli dizayn optimizasyonu'dur. Bu tür, pek çok problemde kullanıĢlı olduğu gibi aynı zamanda da uzay mühendisliği sahasına uyarlanabilmektedir.
Ekonomi de matematiksel programlamaya ağır bir bağımlılık duyar. Mikroiktisat'da sık karĢılaĢılan bir problem olan marjinal fayda ve bundan kaynaklanan ikilik olan harcamaları minimize etme problemi iktisadî bir optimizasyon problemidir. Tüketiciler ve firmalar fayda/kar oranlarını maksimize etmek durumundadırlar. Ticaret teorisi de milletler arası ticari ortaklığın izahında optimizasyona sık sık baĢvurur (Nocedal ve Wright 2006).
Problemin zorluk derecesine göre çözüm uzayı büyüyebilmektedir. Bu durumda en iyiye ulaĢmak ya çok uzun zaman almakta ya da ulaĢılamamaktadır. Çözüm uzayındaki elemanların her birinin denenmesi ile yapılan eniyilemeye Sayım (enumaration) tekniği denir ve en iyiye mutlaka ulaĢılır. Fakat bu yöntem çok uzun zaman alır. Optimizasyon süresini aĢağıya çekmek için çeĢitli yöntemler geliĢtirilmiĢtir. Son zamanlarda meta-sezgisel yöntemlere dayalı algoritmalar geliĢtirilmiĢ ve uygulanmaya baĢlanmıĢtır. Sezgisel yöntemlerin dayandığı temel prensip rastgele seçimdir. Süreci iĢleyiĢi temel olarak, restgele üretilen çözüm elemanlarından en iyisini seçmek ve bu en iyi etrafında daha iyi seçimler yapmaya dayanır. Belli bir iterasyon sonunda ya en iyiye ulaĢılır yada yakın bir sonuç elde
edilir. Sezgisel yöntemlerin en büyük dezavantajlarından biri arama sürecinin yerel en iyiye takılmasıdır. Algoritmalar geliĢtirilirken bu durumları aĢmak için yeni ek süreçler eklense de genel olarak sezgisel algoritmalar yerel en iyiye takılmaktadır(ġekil 2.1).
ġekil –2.1 Yerel Minimum ve Global Minimum
ĠĢte meta-sezgisel algoritmaların yerel minimuma takılmasını önlemek için çeĢitli rastgele operatörler iĢlem basamakları içinde uygulanır. Bu operatörler, Genetik Algoritmalar için; seçim yöntemi, çaprazlama ve mutasyon olarak karĢımıza çıkar. Yeni nesillerin oluĢturulmasında kullanılan bu operatörler, algoritmayı çözüm uzayının tamamen farklı bir bölgesinde arama yapmayı sağlarken, en iyi sonuca yaklaĢmayı da hedefler. PSO için ise algoritma basamakları içinde kullandığımız, rastgele oluĢturulmuĢ sayılar, geliĢen yeni neslin, çözüm uzayının farklı bölgelerine aktarır. Arama süreci böylece çözüm uzayının farklı bölgelerinde devam eder.
Bu bölümde problem türlerinden ve bu problemlerin çözümlerinde kullanılan yöntemlerden bahsedilmiĢtir. Optimizasyon sürelerinden ve çözüm esnasında karĢılaĢılan sorunlardan bahsedilmiĢtir.
Yerel
minimum Global
3. GEZGİN SATICI PROBLEMİ
3.1 Gezgin Satıcı Probleminin Tanımı
Gezgin Satıcı Problemi (GSP) , ”Travelling Salesman Problem” (TSP) NP-Zor bir problem türüdür. Temel olarak problemin amacı bir satıcının tane Ģehri yada durağı en kısa yoldan gezmesini sağlamaktır. Bu problemin çözümü için çeĢitli algoritmalar geliĢtirilmiĢ ve süper bilgisayarlarda en iyi sonuca ulaĢılmaya çalıĢılmıĢtır (Schrijver 2005).
Problemin çözüm uzayı ;
İlk şehirde, satıcının değişik şehir arasında seçim hakkı vardır
İkinci şehirde, satıcının değişik şehir arasında seçim hakkı vardır Dolayısıyla, sonuç olarak satıcının değiĢik tur arasından seçim hakkı olacaktır. Bu, 100 Ģehirlik bir tur için bile değiĢik tur etmektedir. An itibariyle, bulunabilmiĢ en güçlü algoritma problemi en az zamanda çözebilmektedir. Yani, 100 Ģehirlik bir tur için bu adım etmektedir.
Görüldüğü gibi gezgin satıcı problemi çok olasılıklı NP - Zor bir problemdir. ÇeĢitli algoritmalar kullanılarak problemin çözümü yapılmaya çalıĢılmıĢtır. Bugüne kadar çözülen en büyük gezgin satıcı problemi 24,978 noktalıdır ve Ġsveç'te yerleĢimi olan her nokta için çözülmüĢtür. Bu çözüm, Intel Xeon 2.8 ghz bir iĢlemcinin 92 yılına denk bir sürede yapılmıĢtır (öte yandan, 96 bilgisayarlı bir ağ üzerinde çözüldüğünden çözülmesi 3 yıl sürmüĢtür). ġu anda çözülmeye çalıĢılan en büyük problem Dünya üzerinde kayıtlı yerleĢim olan her nokta için en kısa yolun ne olduğudur. Bu problem 1.904.711 Ģehir içermektedir.
Gezgin satıcı problemi üzerine, dünya haritası üzerinde çeĢitli ülkelerin Ģehirleri için çözümler yapılmaktadır. Bir çok üniversite yeni algoritmalar geliĢtirerek optimizasyon zamanını azaltmaya ve en iyi sonuca ulaĢmaya
çalıĢmaktadır. AĢağıda ġekil 3.1’de ABD üzerindeki 532 Ģehre ait çözüm yer almaktadır.
ġekil 3.1 ABD üzerindeki 532 Ģehrin optimum yol uzunluğu (tsp.gatech.edu adresinden alınmıĢtır.)
Gezgin satıcı problemi sezgisel optimizasyon metotlarının en iyiye yaklaĢma için test aracı haline gelmiĢtir (Garey ve Johnsan 1979). Simetrik GSP, A Ģehrinden B Ģehrine olan uzaklık ile B’den A’ya olan uzaklığı eĢit kabul eder fakat Asimetrik GSP ise uzaklıkları farklı kabul eder (Freisleben ve Merz 1996). Asimetrik ve simetrik GSP’nin bu yüzden farklı durum uzayı mevcuttur. Simetrik GSP iki Ģehir arasındaki, karĢılıklı uzaklığı aynı kabul ettiği için çözüm uzayı yarıya düĢecektir. Fakat algoritma tüm adımları kontrol edeceği için optimizasyon zamanı değiĢmeyecektir. GSP’nin öneminin bu kadar artmasındaki temel faktör birçok bilimsel araĢtırmada, mühendislikte ve biyo-enformasyon alanında kullanılmasıdır ( Tsai ve diğerleri 2004 ). Kullanım alanlarını sıralarsak,
1. Araç rotası tayin etme (Clarke ve Wright 1964),
3. Entegre devre tasarımı (Kirkpatrick ve diğerleri 1983), 4. Fiziki harita problemleri (Alizadeh ve diğerleri,1993)
5. Genetik bilimler için filo-genetik ağaç yapılandırması problemi (Korostensky ve Gonnet 2000).
Durum uzayının oldukça büyük olmasından dolayı GSP sezgisel yöntemlerle geliĢtirilen algoritmalarla çözülebilmiĢtir. Problemde bulunan nokta sayısı çok az dahi olsa problemin çözümünde sayım tekniğinin kullanılması oldukça uzun zaman alacaktır. ġekil 3.2’de 10 Ģehirli bir GSP’nin çözümünde kullanılan ihtimalleri görülmektedir.
ġekil 3.2 Örnek bir TSP çözümü
3.2 Gezgin Satıcı Probleminin Kesin Çözümü
GSP’nin çözüm uzayının, problemdeki nokta sayısına bağlı olarak çok büyük olmasından dolayı, sezgisel yöntemler her zaman kesin sonucu vermemektedir. Simetrik bir GSP’nin çözümünde iki Ģehir arasındaki mesafe kuĢbakıĢı mesafe yani
Öklit mesafesidir. Pisagor teoremiyle hesaplanır. Hesaplamada kullanılan matematiksel formül çok karmaĢık olmamasına karĢın, iĢlem basamaklarının sayısı çok fazla olduğu için çözüm süresi önemli bir zaman almaktadır. Problemin çözümünde kullanılan formüller aĢağıda verilmiĢtir.
Problemin çözümünde bilinen iki nokta (x1,y1) ve (x2,y2) arasındaki uzaklık, aĢağıdaki formülle bulunur;
𝑓𝑝 = (𝑥1− 𝑥2)2+ (𝑦
1− 𝑦2)2 (3.1) Problemdeki tüm Ģehirlerin (noktaların) (n), koordinatları biliniyorsa (xi,yi) bu durumda toplam yol uzunluğu Ģu Ģekilde hesaplanır;
𝑓𝑡𝑝 = 𝑖=1𝑛−1 (𝑥𝑖− 𝑥𝑖+1)2+ (𝑦𝑖 − 𝑦𝑖+1)2+ (𝑥𝑛 − 𝑥1)2+ (𝑦𝑛 − 𝑦1)2 (3.2) Herhangi bir GSP problemi’nin kesin çözümü için, sayım tekniği (enumaration) kullanılmak zorundadır. Sezgisel yöntemler çözüm uzayının çok büyük olması ve arama sürecinde yerel optimuma takılmalarından dolayı, her zaman kesin çözüme ulaĢamamaktadırlar. Ancak küçük ölçekli GSP problemlerinin çözümünde tam sonuca ulaĢıldığı görülmüĢtür. Sayım tekniği ise her olasılığı denediği için kesin sonuca ulaĢmaktadır ama çözüm zamanı sezgisel yöntemlere göre çok uzun sürmektedir. ÇeĢitli üniversitelerde yapılan çalıĢmalarla sayım tekniği yöntemi kullanılmakta, çözümler süper bilgisayarlardan oluĢan ağlarda yapılmaktadır. Hesaplanan en iyi çözümler sezgisel yöntemlerle kıyaslanmaktadır.
N Ģehirli Asimetrik bir GSP’nin çözümü için (n-1)! ihtimal bulunmaktadır bu yüzden az noktalı GSP problemlerinin çözümü sayım tekniği ile kolayca bulunabilir. Saniyede 1010 ihtimali hesaplayabilen bir bilgisayar için, 10 Ģehirli GSP sorusunun çözümü, (10-1)!/1010
saniye olacaktır. Bu da yaklaĢık olarak 3,6.10-5 saniye olacaktır. Simetrik GSP’nin çözümünde ihtimal sayısı, n Ģehirli bir problem için (n-1)!/2 olduğu için yarı yarıya azalmaktadır. ġehir sayısı arttıkça çözüm süreleri uzamaktadır. Saniyede 1010
ihtimali deneyen bir bilgisayarın çeĢitli sayılarda sehirlerden oluĢan GSP problemlerini çözüm süreleri Tablo 3.1 de gösterilmiĢtir.
Tablo 3.1 Sayım Tekniği ile GSP’lerin Çözüm Zamanları ġehir
Sayısı
Gerekli Süre
Saniye Dakika Saat Gün
10 1,8E-5 0,3E-6 ~0 ~0
11 1,8E-4 0,3E-5 ~0 ~0
12 1,9E-3 0,4E-4 ~0 ~0
13 0,2E-1 0,3E-2 0,5E-4 ~0
15 4,3 0,7E-1 0,1E-1 ~0
20 6E+6 1E+5 1,6E+3 70
25 3,1E+12 5,1E+11 8,6E+9 3,5E+8
30 4,4E+20 7,3E+19 1,2E+17 5,1E+15
GSP’nin çözümünde sayım (enumaration) tekniğinin kullanılması uzun zaman almaktadır. Süper bilgisayarlarla bile bu süre çok fazla olmaktadır. O yüzden bu problemin çözümünde sezgisel yöntemleri kullanmak çözüm zamanı açısından yararlı olacaktır.
4. PARÇACIK SÜRÜ OPTİMİZASYONU
4.1 Giriş
Parçacık Sürü Optimizasyonu (PSO) , (Particle Swarm Optimization) , popülasyon tabanlı , sürü zekası (swarm intelligance) esasına dayalı bir optimizasyon yöntemidir. Bu yöntem Kennedy ve Eberhart tarafından 1995-1996 yıllarında geliĢtirilmiĢtir (Kennedy ve Eberhart 1995). Yöntem doğadaki bütün canlılarda bulunan sosyal zeka, temeline dayanmaktadır. Ġnsanların konuĢarak bilgiyi paylaĢması gibi, kuĢların yön tayin etmelerinde birbirlerinden yararlanmaları, balık sürülerinin hareketlerini ortak bir kararla almaları sosyal bir zekanın varlığına kanıttır.
PSO’da bulunan bireylerin (parçaların), her birinin ayrı bir hızı vardır. Her nesilde bireyler kendi hızlarını, en iyi bireye göre yenilerler. Böylece yeni nesil, bir öncekine göre daha iyi duruma gelir. Tüm bireyler en iyi bireye yaklaĢırken, kullanılan rastgele operatörler sayesinde, bir sonraki nesilde, bir önceki neslin en iyisini geçebilirler. ĠĢte nesiller arasındaki bu hızlı iyileĢme PSO’nun sonuca hızla yaklaĢmasını sağlamaktadır. ġekil 4.1’de ve Tablo 4.1’de , 3 bireyli bir popülasyonun, 𝑓 𝑥, 𝑦, 𝑧 = 𝑥2+ 𝑦2+ 𝑧2 fonksiyonunun minimuma yaklaĢırken, bireylerin geliĢimi gösterilmiĢtir.
PSO’da popülasyonu oluĢturan bireyler parçacık olarak adlandırılır, her bir parçanın durum uzayında hareket ettiği varsayılır ve her parça potansiyel çözümü taĢır. Her parça en iyi durumu hatırlayabilir ve parçacıklar kendi arasında bilgi alıĢveriĢinde bulunabilirler(Wang ve diğerleri 2003). Literatürde PSO bir çok problemin optimizasyonunda baĢarı ile kullanılmıĢtır,
1. SipariĢ miktarı belirleme,
2. Sinir ağları,
3. AkıĢ tipi çizelgeleme problemleri, güç ve voltaj kontrolü,
Tablo 4.1 Bireylerin GeliĢim Değerleri
1. Birey 2. Birey 3. Birey
1. Nesil 4,25 3,16 3,83
2. Nesil 3,44 2,46 2,03
3. Nesil 1,25 1,59 1,44
4. Nesil 0,7 0,86 0,89
5. Nesil 0,12 0,16 0,08
ġekil 4.1 Bireylerin Minimuma YaklaĢımı
4.2 Algoritma
PSO’da her bir parçacığın kendine ait bir hızı vardır ve bu hız parçacığı diğer parçalardan aldığı bilgilerle optimum sonuca doğru hızlandırır. Her bir jenerasyonda bu hız önceki en iyi sonuçlardan da faydalanarak yeniden hesaplanır. Bu sayede popülasyonda bulunan bireyler giderek daha iyi pozisyona gelirler. Algoritmayı adımları Ģu Ģekildedir;
4,25 3,16 3,83 3,44 2,46 2,03 1,25 1,59 1,44 0,7 0,86 0,89 0,12 0,16 0,08 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 0 1 2 3 4 Sı fı ra Y ak la şı m Bireyler 1. nesil 2. Nesil 3. Nesil 4. Nesil 5. Nesil
1.Popülasyonun oluşturulması; parçacıklar, rastgele üretilen baĢlangıç pozisyonları
ve hızları ile birlikte oluĢturulur.
2.Uygunluk değerlerinin hesaplanması ; popülasyon içindeki tüm bireylerin
uygunluk değerleri hesaplanır.
3. En iyi üyenin bulunması; her jenerasyonda bütün bireyler bir önceki
jenerasyondada bulunan en iyi (pbest) ile karĢılaĢtırılır. Eğer daha iyi birey varsa yer değiĢtirilir.
4. Global en iyinin bulunması ; jenerasyondaki en iyi değer global en iyi değerden
daha iyi ise yer değiĢtirilir.
5. Pozisyon ve hızların yenilenmesi ;
id id id id gd id id id id V X X X P rand c X P rand c V W V * 1* 1*( ) 2* 2*( )
Burada Xid pozisyon ve Vid hız değerlerini verirken, rand1 ve rand2 değerleri, 0 ile 1 arasında, rastgele üretilmiĢ sayılardır. W ise atalet ağırlık değeridir. Burada c1 ve c2 değerleri sabit değerlerdir ve genellikle 2 ye yakın bir değer kabul edilirler.
6.Durdurma kriteri sağlanıncaya kadar adımları tekrar et. Durdurma kriteri
sağlanıncaya kadar adım 2-5 tekrar et.
Algoritma ġekil 4.2’de akıĢ diyagramı gösterilmiĢtir.
4.3 Algoritmanın Gezgin Satıcı Problemi için Uyarlanması
PSO, 1995 yılından bu yana bir çok problemin çözümünde oldukça baĢarılı bir Ģekilde kullanılmıĢtır ve bu alanda bir çok çalıĢma yapılmıĢtır. Fakat ayrık problemlerin çözümü için hala yeni bir alandır, özellikle PSO’nun gezgin satıcı problemine uygulanması yeni bir araĢtırma yönüdür (Wang ve diğerleri 2003).
Gezgin satıcı probleminin yapısı gereği bir çok meta-sezgisel algoritma bu problemin çözümü için yeniden düzenlenmektedir (SHI ve diğerleri 2004). Yeniden
(4.1) (4.2)
düzenlenen algoritmalar çoğu zaman algoritmaya fazladan yük getirdiği için bu problemin çözümünde performans kaybına uğramaktadırlar (Tagawa ve diğerleri 1998). PSO yönteminin gezgin satıcı problemine uygulanması için temel adımlar aĢağıdaki baĢlıklarda ele alınmıĢtır.
ġekil 4.2 Parçalı Sürü Optimizasyonu AkıĢ Diyagramı Başlangıç popülasyonunu, hızları ve
pozisyonları oluştur.
Sürüdeki bütün parçaların uygunluk değerini hesapla.
Her iterasyonda tüm bireyleri önceki iterasyonun en iyisi ile karşılaştır. Daha
iyi ise yerdeğiştir.
En iyi değerleri kendi arasında karşılaştır ve en iyi olanı global en iyi
olarak ata
Hız ve pozisyon değerlerini yenile.
Durdurma kriteri
4.3.1 Yer Değiştirme Operatörü
Bu operatör PSO’nun gezgin satıcı problemine uygulanması için çok büyük öneme sahiptir çünkü PSO matematiksel fonksiyonların optimizasyonunda kullanılmak için geliĢtirilmiĢtir. GSP’de ise durum değiĢmekte ve çözüm uzayını Ģehirler arasındaki uzaklıklar belirlemektedir. Yer değiĢtirme operatörü, N adet noktadan oluĢan bir GSP probleminde aĢağıdaki gibi tanımlanabilir;
𝑆 = (𝑎 𝑖), 𝑖 = 1. . 𝑛
𝑆𝑂(𝑖1, 𝑖2) (4.3) Formülde 𝑎𝑖1 noktası ile 𝑎𝑖2 noktalarının yer değiĢtirmesini ifade eder. Formül aĢağıdaki gibi ifade edilir.
𝑆′ = 𝑆 + 𝑆𝑂(𝑖
1, 𝑖2) (4.4) N noktalı S kümesinde hangi elemanların aralarında yer değiĢtireceğini göstermektedir dolayısıyla buradaki’+’iĢareti yeni bir anlam kazanmaktadır.
Yukarıdaki operatörü örnekle açıklayalım;
S = ( 1, 3, 5, 2, 4) çözümüne SO(1,2) operatörünü uygularsak;
S’= S + SO(1,2) = (1, 3, 5, 2, 4) + (1,2) = (3, 1, 5, 2, 4) olarak bulunur. Yoldaki değiĢim ġekil 4.3 deki gibi olacaktır.
Bir çok yer değiĢtirme operatörü , sırayla bir çözüm kümesine yani noktalar arasındaki yola uygulanabilir;
𝑆𝑆 = (𝑆𝑂1, 𝑆𝑂2, 𝑆𝑂3, … , 𝑆𝑂𝑛) 𝑆′ = 𝑆𝑆 = 𝑆 + 𝑆𝑂
1, 𝑆𝑂2, 𝑆𝑂3, … , 𝑆𝑂𝑛 = 𝑆 + 𝑆𝑂1 + 𝑆𝑂2 … … . 𝑆𝑂𝑛) Operatörler sırası ile yola uygulanır ve yeni çözüm elde edilir. Aynı Ģekilde yer değiĢtirme öbekleri, sırası ile çözüme uygulanabilir.
𝑆𝑆′ = 𝑆𝑆
1 ⨁ 𝑆𝑆2 Bunu bir örnekle açıklarsak;
Elimizde bulunan A ve B çözümlerine ait temel yer değiĢtirme operatörünü Ģu Ģekilde ifade edebiliriz.
𝑆𝑆 = 𝐴 − 𝐵
Burada’-’iĢareti B çözümündeki noktaları sağdan sola doğru A çözümüne benzetmeyi ifade eder.
𝐴 = 𝐵 + 𝑆𝑆
B çözümünün yer değiĢtirme operatörü aĢağıdaki adımlarla oluĢturulur; A : (1, 2, 3, 4, 5)
B : (2, 3, 1, 5, 4) Ģeklinde iki adet çözümümüz bulunsun.
1. A(1) = B(3) dolayısıyla ilk operatör SO(1,3) Ģeklinde oluĢacaktır.
B’= B + SO(1,3) iĢlemini uyguladığımızda yeni B’çözümü aĢağıdaki gibi olur; B’: (1, 3, 2, 5, 4 )
2. A(2) = B’’(3) dolayısıyla ilk operatör SO(2,3) Ģeklinde oluĢacaktır.
B’’: (1, 2, 3, 5, 4)
3. A(3) = B’’(3) dolayısıyla ilk operatör SO(3,3) Ģeklinde oluĢacaktır. Bu durumda her iki çözümde de noktalar yer değiĢtirmeyecektir.
B’’’= B + SO(3,3) iĢlemini uyguladığımızda yeni B’’’çözümü aĢağıdaki gibi olur;
B’’’: (1, 2, 3, 5, 4)
4. A(4) = B’’’’(5) dolayısıyla ilk operatör SO(4,5) Ģeklinde oluĢacaktır.
B’’’’= B + SO(4,5) iĢlemini uyguladığımızda yeni B’’’’çözümü aĢağıdaki gibi olur;
B’’’’: (1, 2, 3, 4, 5)
Görüldüğü gibi B çözümü oluĢturulan yer değiĢtirme operatörleri ile A çözümüne yaklaĢmıĢ oldu. B çözümü için oluĢturulan operatörleri aĢağıdaki gibi ifade edilebilir;
𝑆𝑆 = 𝐴 − 𝐵 = (𝑆𝑂 1,3 , 𝑆𝑂 2,3 , 𝑆𝑂 3,3 , 𝑆𝑂 4,5 )
4.3.2 Algoritmanın Yeniden Düzenlenmesi
Yer değiĢtirme operatörleri, PSO’da bulunan parçacıkların hızını hesaplamak için kullanılan formül için yeniden düzenlendiğinde;
𝑉𝑖𝑑 = 𝑉𝑖𝑑⨁𝛼∗(𝑃
𝑖𝑑 − 𝑋𝑖𝑑)⨁𝛽∗ 𝑃𝑔𝑑 − 𝑋𝑔𝑑 burada 𝛼, 𝛽 𝜖 [0,1] (4.5) α ve β değiĢkenleri 0 ve 1 arasında rastgele oluĢturur yada sabit bir değer atanabilir. Bu değerler bireyin bir önceki bireye ve popülasyondaki en iyi bireye benzeme oranını belirler. 𝛼∗(𝑃
𝑖𝑑 − 𝑋𝑖𝑑) iĢleminde α , 𝑋𝑖𝑑 çözümünün 𝑃𝑖𝑑 çözümüne ne kadar benzeyeceğini belirler ve en fazla çözümde bulunan noktaların sayısı kadar olabilir. β değiĢkeni aynı Ģekilde 𝛽∗ 𝑃
𝑔𝑑 − 𝑋𝑔𝑑 iĢlemini etkiler. Algoritma gezgin satıcı problemi için aĢağıdaki adımlarla yeniden tanımlanabilir;
1. Popülasyondaki parçacık sayısı kadar çözüm üret ve her parçacık için hız yerine
geçecek yer değiĢtirme öbeği üret.
2. Bütün parçalar için Xid, çözümlerinin X’id yenide hesapla;
2-1. Pid ve Xid değerlerinin farkının hesaplanması 𝐴 = 𝑃𝑖𝑑 − 𝑋𝑖𝑑 , bu iĢlem bireyin bir önceki en iyiye (Pid) benzemesini sağlar.
2-2. Pgd ve Xid değerlerinin farkının hesaplanması 𝐴 = 𝑃𝑔𝑑 − 𝑋𝑖𝑑 , bu iĢlem bireyin global en iyiye (Pgd) benzemesini sağlar.
2-3. Yeni hızın hesaplanması; 𝑉𝑖𝑑 = 𝑉𝑖𝑑⨁𝛼∗(𝑃
𝑖𝑑 − 𝑋𝑖𝑑)⨁𝛽∗ 𝑃𝑔𝑑 − 𝑋𝑔𝑑 (4.6) 2-4. Yeni parçacığın (çözümün) hesaplanması;
𝑋𝑖𝑑 = 𝑋𝑖𝑑 + 𝑉𝑖𝑑 (4.7) Bu iĢlem yeni bireyin yeni oluĢturulan hıza benzemesini sağlar.
2-5. Yeni Pid değeri daha iyi ise eski değer ile yer değiĢtir. 3. Ġterasyondaki Pgd değeri daha iyi ise eski değer ile yer değiĢtir. 4. Ġstenen Ģart sağlandıysa algoritmayı bitir.
Bu bölümde PSO algoritması ve algoritmanın GSP’ye uygulanması anlatılmıĢtır. GSP kendine has özellikleri olan bir problem türü olduğu için, optimizasyon algoritmalarının bu probleme uyarlanması gereklidir. Ek operatörlerin tanımlanması ile PSO algoritması GSP’ye uygun olarak düzenlenmiĢtir.
5. GENETİK ALGORİTMALAR
5.1 Giriş
Doğada gözlemlenen evrimsel sürece benzer bir Ģekilde çalıĢan arama ve eniyileme yöntemidir. KarmaĢık çok boyutlu arama uzayında en iyinin hayatta kalması ilkesine göre genel en iyi çözümü arar.
Genetik algoritmaların temel ilkeleri ilk kez Michigan Üniversitesi'nde John Holland tarafından ortaya atılmıĢtır. Holland 1975 yılında yaptığı çalıĢmaları “Adaptation in Natural and Artificial Systems” adlı kitabında bir araya getirmiĢtir. Ġlk olarak Holland evrim yasalarını genetik algoritmalar içinde eniyileme problemleri için kullanmıĢtır. (Goldberg 1989)
Genetik algoritmalar problemlere tek bir çözüm üretmek yerine farklı çözümlerden oluĢan bir çözüm kümesi üretir (Albayrak 2008). Böylelikle, arama uzayında aynı anda birçok nokta değerlendirilmekte ve sonuçta genel çözüme ulaĢma olasılığı yükselmektedir. Çözüm kümesindeki çözümler birbirinden tamamen bağımsızdır. Her biri çok boyutlu uzay üzerinde bir vektördür.
Genetik algoritmalar problemlerin çözümü için evrimsel süreci bilgisayar ortamında taklit ederler. Diğer eniyileme yöntemlerinde olduğu gibi çözüm için tek bir yapının geliĢtirilmesi yerine, böyle yapılardan meydana gelen bir küme oluĢtururlar. Problem için olası pek çok çözümü temsil eden bu küme genetik algoritma terminolojisinde popülasyon adını alır. Popülasyondaki vektör, kromozom veya birey adı verilen sayı dizilerinden oluĢur. Birey içindeki her bir elemana gen adı verilir. Popülasyondaki bireyler evrimsel süreç içinde genetik algoritma iĢlemcileri tarafından belirlenirler.
Problemin bireyler içindeki gösterimi problemden probleme değiĢiklik gösterir. Genetik algoritmaların problemin çözümündeki baĢarısına karar vermedeki en önemli faktör, problemin çözümünü temsil eden bireylerin gösterimidir. Nüfus içindeki her bireyin problem için çözüm olup olmayacağına karar veren bir uygunluk
fonksiyonu vardır. Uygunluk fonksiyonundan dönen değere göre yüksek değere sahip olan bireylere, nüfustaki diğer bireyler ile çoğalmaları için fırsat verilir. Bu bireyler çaprazlama iĢlemi sonunda çocuk adı verilen yeni bireyler üretirler. Çocuk kendisini meydana getiren ebeveynlerin (anne, baba) özelliklerini taĢır. Yeni bireyler üretilirken düĢük uygunluk değerine sahip bireyler daha az seçileceğinden bu bireyler bir süre sonra nüfus dıĢında bırakılırlar. Yeni nüfus, bir önceki nüfusta yer alan uygunluğu yüksek bireylerin bir araya gelip çoğalmalarıyla oluĢur. Aynı zamanda bu nüfus önceki nüfusun uygunluğu yüksek bireylerinin sahip olduğu özelliklerin büyük bir kısmını içerir. Böylelikle, pek çok nesil aracılığıyla iyi özellikler nüfus içersinde yayılırlar ve genetik iĢlemler aracılığıyla da diğer iyi özelliklerle birleĢirler. Uygunluk değeri yüksek olan ne kadar çok birey bir araya gelip, yeni bireyler oluĢturursa arama uzayı içerisinde o kadar iyi bir çalıĢma alanı elde edilir. Probleme ait en iyi çözümün bulunabilmesi için;
Bireylerin gösterimi doğru bir Ģekilde yapılmalı,
Uygunluk fonksiyonu etkin bir Ģekilde oluĢturulmalı,
Doğru genetik iĢlemciler seçilmeli.
Bu durumda çözüm kümesi problem için bir noktada birleĢecektir. Genetik algoritmalar, diğer eniyileme yöntemleri kullanılırken büyük zorluklarla karĢılaĢılan, oldukça büyük arama uzayına sahip problemlerin çözümünde baĢarı göstermektedir. Bir problemin bütünsel en iyi çözümünü bulmak için garanti vermezler. Ancak problemlere makul bir süre içinde, kabul edilebilir, iyi çözümler bulurlar. Genetik algoritmaların asıl amacı, hiçbir çözüm tekniği bulunmayan problemlere çözüm aramaktır. Kendilerine has çözüm teknikleri olan özel problemlerin çözümü için mutlak sonucun hızı ve kesinliği açısından genetik algoritmalar kullanılmazlar (ÇunkaĢ 2004). Genetik algoritmalar ancak;
Arama uzayının büyük ve karmaĢık olduğu,
Mevcut bilgiyle sınırlı arama uzayında çözümün zor olduğu,
Problemin belirli bir matematiksel modelle ifade edilemediği,
Geleneksel eniyileme yöntemlerinden istenen sonucun alınmadığı alanlarda etkili ve kullanıĢlıdır.
Genetik algoritmalar parametre ve sistem tanılama, kontrol sistemleri, robot uygulamaları, görüntü ve ses tanıma, mühendislik tasarımları, planlama, yapay zeka uygulamaları, uzman sistemler, fonksiyon ve kombinasyonel eniyileme problemleri ağ tasarım problemleri, yol bulma problemleri, sosyal ve ekonomik planlama problemleri için diğer eniyileme yöntemlerinin yanında baĢarılı sonuçlar vermektedir.
Diğer Yöntemlerden Farkı
1. Genetik algoritmalar problemlerin çözümünü parametrelerin değerleriyle değil, kodlarıyla arar. Parametreler kodlanabildiği sürece çözüm üretilebilir. Bu sebeple genetik algoritmalar ne yaptığı konusunda bilgi içermez, nasıl yaptığını bilir.
2. Genetik algoritmalar aramaya tek bir noktadan değil, noktalar kümesinden baĢlar. Bu nedenle çoğunlukla yerel en iyi çözümde sıkıĢıp kalmazlar.
3. Genetik algoritmalar türev yerine uygunluk fonksiyonunun değerini kullanır. Bu değerin kullanılması ayrıca yardımcı bir bilginin kullanılmasını gerektirmez.
4. Genetik algoritmalar gerekli kuralları değil olasılıklı kuralları kullanır.
5.2 Algoritma
Genetik Algoritmaların uygulanması aĢağıdaki basamaklardaki gibi özetlenebilir.
1. Olası çözümlerin kodlandığı bir çözüm grubu oluşturulur ; (çözüm grubu,
biyolojideki benzerliği nedeniyle, toplum (populasyon), çözümlerin kodları da kromozom olarak tanımlanır). Toplumda bulunacak birey sayısı için bir standart yoktur, problemin türüne göre bu sayı değiĢebilir. Toplum rasgele oluĢturulur. OluĢturulan bireyler problemin türüne göre çeĢitli yöntemlerle kodlanmalıdır.
2. Her kromozomun uygunluk değeri hesaplanır. Popülasyondaki bireylerin
baĢarısı çoğu zaman bu fonksiyonun verimli olmasına bağlıdır. EĢleme havuzu oluĢturulurken uygunluk değerleri baz alınır ve çeĢitli seçim yöntemleri kullanılır.
3. Seçilen kromozomları eşleyerek yeniden kopyalama ve değiştirme uygulanır.
EĢleĢme havuzunda bulunan bireylerin çaprazlanması ve yeni bireylerin mutasyona uğraması bu aĢamada yapılır. Mutasyon toplumda çeĢitliliğe neden olur ve problem sonucunun yerel minimuma takılmasını önler.
4. Yeni nesil bireylerin ebeveyn bireylerle yer değiştirmesi. Bu yöntemle
popülasyonun sabit büyüklükte kalması sağlanır.
5. Tüm kromozomların uygunluk değerleri tekrar hesaplanır. Ebeveynlerle yer
değiĢtiren yeni nesil kromozomlarla birlikte uygunluk değerleri tekrar hesaplanır.
6. Belli bir nesil sayısına kadar döngü devam eder. Popülasyonun uygunluk
değerleri tekrar hesaplanır, 2. adımdan itibaren iĢlemler tekrar edilir.
7. Son olarak üretilen nesiller içinden en uygun değere sahip olan birey çözüm
olarak kabul edilir.
ġekil 5.1 de algoritmanın akıĢ diyagramı gösterilmiĢtir.
5.3 Algoritmanın Sürekli Fonksiyonların Çözümünde Kullanılması
Ġkili (Binary) kodlu GA’lar bir çok problemin çözümünde baĢarı ile kullanılmıĢtır. Bu yöntemin pek çok avantajı olmasına rağmen, programa çok fazla ek yük getirdiği için çözüm zamanı uzamaktadır ( Adewuya 1996). Bu durumda özellikle gerçek değerli matematiksel fonksiyonların çözümü için farklı genetik operatörlerin kullanılması gereklidir. Sürekli fonksiyonların çözümünde, özellikle çaprazlama ve mutasyon operatörlerinde değiĢikliğe gidilmek zorundadır.(Wright 1991). Bu tür problemlerin çözümü için geliĢtirilen algoritmalara Gerçek Kodlu Genetik Algoritmalar denir.
Gerçek kodlu genetik algoritmalar temel olarak aynı algoritmayı kullanmasına karĢın, çaprazlama ve mutasyon operatörlerinde değiĢiklikler vardır.
Çaprazlama operatörü seçilen iki bireyin genlerinin yani fonksiyonun değiĢkenlerin çeĢitli formlarda çaprazlanması ile gerçekleĢtirilir;
Birey1 = [x1.1, x1.2, x1.3, ……, x1.n] Birey2 = [x2.1, x2.2, x2.3, ……, x2.n]
Birey1 ve Birey2’den seçilen iki kromozom Radcliff’e göre Ģu formülle çaprazlanır;
𝑃𝑦𝑒𝑛𝑖 = 𝛽𝑥1.𝑥 + (1 − 𝛽)𝑥2.𝑥 (5.1) Bu Ģekilde çaprazlanan kromozomlar yeni bireylere aktarılır. Burada β değer 0 ile 1 arasında rastgele seçilen bir sayıdır. Böylece her iki ebeveynden de belirli oranlarda gen transferi yapılmıĢ olur.
Burada seçim yönteminin yanı sıra, daha iyi olan bireylerin genlerinin çaprazlanmasında β değerlerinin yüksek tutulması daha iyi sonuçlar verecektir. YaklaĢma hızı buna bağlı olarak artacaktır fakat yerel optimuma takılma olasılığı da artacaktır.
Gerçek kodlu GA’larda mutasyon iĢlemi ise rastgele seçilen bireylerin aynı kromozomlarının yer değiĢtirmesi ile gerçekleĢtirilir;
Birey1 = [x1.1, x1.2, x1.3, ……, x1.n]
Birey2 = [x2.1, x2.2, x2.3, ……, x2.n]
Mutasyon oranı kadar, ebeveyn bireylerden seçilen kromozomlar birbirleri ile yer değiĢtirilir. Böylece bireylerin genleri rastgele Ģekilde seçilir ve arama belli bir yerel optimumda takılıp kalmaz.
ġekil 5.1 Genetik Algoritma Başlangıç bireylerinin üretilmesi Çaprazlanacak bireylerin seçilmesi Çaprazlama Mutasyon Bireylerin uygunluk değerlerinin hesaplanması İstenen şartlar var mı? Sonuç
5.4 Genetik Algoritmanın Gezgin Satıcı Problemi için Kullanılması
Gezgin satıcı probleminde, satıcı her Ģehri en kısa yoldan dolaĢmak zorundadır. Satıcının dolaĢması gereken Ģehir sayısını 10 olarak kabul edersek ve her Ģehri “0” dan baĢlayarak kodlayalım.
1.Popülasyonun oluşturulması;
TSP için popülasyondaki her birey Ģehirler arasındaki güzergahtır. Popülasyondaki bireylerin sıralanıĢı sırayla hangi Ģehirlere gideceğinin sırasını belirtir. Satıcının gittiği Ģehre tekrar gitmemesi gerekir. Popülasyon üyelerinin aĢağıdaki gibi oluĢturabilir;
9340182576 8420975361 0459763281 7310428956
2.Uygunluk değerlerinin hesaplanması ve seçim;
Bireyleri oluĢturan sayıların her biri bir Ģehri ifade ettiğinden her bir bireyin uygunluk değeri hesaplanırken aĢağıdaki formül kullanılır.
2 2 j i j i ijx
x
y
y
d
(5.2)Uygunluk değerleri hesaplandıktan sonra eĢleme havuzunun oluĢturulması için bireyler turnuva , rulet tekeri ve elitizim gibi çeĢitli yöntemlerle seçilirler.
3.Çaprazlama ;
Çaprazlama iĢleminde eĢleme havuzundan seçilen iki birey kendi aralarında gen değiĢimde bulunurlar. Burada 2. ve 3. bireyin rasgele seçildiğini ve çaprazlama noktasını da 6 olarak kabuledelim.
Çaprazlama öncesi durum Çaprazlama sonrası durum
8420975361 8420973281
0459763281 0459765361
Çaprazlama sonrasında oluĢan yeni bireylerde aynı güzergahların tekrar ettiği durumlar olabiliyor. Bu durumu ortadan kaldırmak için standartlaĢtırma iĢlemi uygulanır. StandartlaĢtırma iĢleminde kromozom içinde takrar eden ilk Ģehir ziyaret edilmeyen en küçük numaralı Ģehir ile değiĢtirilir.
Standartlaştırma öncesi Standartlaştırma sonrası
8420973281 5460973281
0459765361 0429785361
4.Mutasyon ;
Mutasyon iĢlemi gezgin satıcı problemine uygun olması açısından, rasgele seçilen iki genin yerdeğiĢtirmesi ile gerçekleĢtirilir.
Mutasyon öncesi Mutasyon sonrası
5.Durdurma Kriteri;
Durdurma kriteri iterasyon sayısı yada problemin baĢında belirlenen bir değerin altında oluncaya kadar 2 ve 4. adımlar devam tekrar edilir. Algoritmanın sonunda en iyi birey çözüm olarak kabul edilir.
Bu bölümde GA’nın iĢlem basamakları anlatılmıĢtır. Gerçek kodlu GA iĢlem basamaklarından ve GA’nın GSP’ye uygulanması anlatılmıĢtır.
6. DİFERANSİYEL EVRİM ALGORİTMASI
6.1 Giriş
Gerçek parametreleri optimizasyon, bilimde, mühendislikte ve iĢ ortamlarında karĢılaĢılan pratik problemlerin önemli ve geniĢ sınıfını oluĢturmaktadır. Zor optimizasyon problemleriyle karĢılaĢıldığında genellikle ilk yapılması gereken probleme özel sezgisel bir yaklaĢım tekniğini belirlemek olacaktır.
Diferansiyel evrim algoritması tipik bir poülasyon tabanlı geliĢim algoritmasıdır. Mutasyon ve çaprazlama operatörlerini kullanarak hedef çözüme ulaĢmaya çalıĢır. Algoritma bir ebeveyn vektörden, bir deneme vektörü üretmek için mutasyon ve çaprazlamayı birlikte kullanır (Karaboğa 2004).
6.2 Algoritma
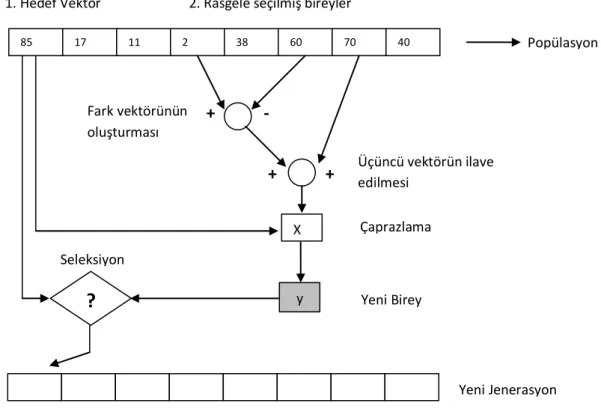
Popülasyon tabanlı diğer algoritmalarda olduğu gibi Diferansiyel Evrim Algoritmasında da ilk önce baĢlangıç popülasyonu oluĢturulur. Popülasyon sayısı NP >= 4 olmak zorundadır. Popülasyon içinden rasgele seçilen 2 bireyin önce fark vektörü oluĢturulur. Fark vektörü rasgele seçilmiĢ üçüncü bir bireyle toplanır. Toplanan birey ebeveyn olarak seçilen bireyle çaprazlanır eğer oluĢan yeni birey ebeveyn bireyden daha iyi ise yer değiĢtirilir (Karaboğa ve Ökdem 2004).
BaĢlangıç parametreleri olan CR ve F değerleri kullanıcı tarafından belirlenir. CR olasılığı temsil ettiği için 0 ile 1 arasında değerler almaktadır. F bir ölçekleme faktörüdür, iĢlem süreci içinde rasgele üretilen Randj [0,1] CR’den küçükse veya eĢitse yeni parametre, rasgele seçilmiĢ üç parametrenin doğrusal kombinasyonu olacaktır.
Algoritmanın çalıĢması ġekil 6.1’de verilmiĢtir.
ġekil 6.1 Diferansiyel Evrim Algoritması ġeması
1. Başlangıç popülasyonu ve kontrol parametrelerinin tanımlanması;
NP>=4 , F є (0,1+) , CR є [0,1] ve parametre sınırları belirlenir xlow , xhigh. CR ve F değerleri kullanıcı tarafından belirlenir.
2. Başlangıç popülasyonunun oluşturuması;
] 1 , 0 [ ] 1 , 0 [ , 0 ), ..., 2 , 1 ( ), ..., 2 , 1 ( ]. 1 , 0 [ : , , 0 j lo j hi j j lo j G j i rand G D j NP i x x rand X x D j NP i 85 17 11 2 38 60 70 40 Popülasyon + - + + X y?
Fark vektörünün oluşturması1. Hedef Vektör 2. Rasgele seçilmiş bireyler
Üçüncü vektörün ilave edilmesi Çaprazlama Yeni Birey Seleksiyon Yeni Jenerasyon
Burada D popülasyon üyelerinin boyutunu ifade ederken, G ise 0 olarak atandığı için bireyin ilk parametresini ifade eder.
3.Mutasyon ve Çaprazlama; ) ( ) ] 1 , 0 [ ( ) .( , ) ( }, ,..., 2 , 1 { ) ( }, ,...., 2 , 1 { , , , , , 2 , , 1 , , 3 , 1 , , 3 2 1 3 2 1 durumlarda diger X j j CR rand eger x x F x u D j seçim rasgele D j seçim rasgele i r r r NP r r r G i j rand j G r j G r j G r j g j i rand 4.Seçim
Yeni bireyin uygunluk değeri hedef vektör olarak seçilen ebeveynin uygunluk değerinden daha iyi ise yeni birey ebeveyn il yer değiĢtirir.
diger x x f u f eger u x G i G i G i G i G i , , 1 , 1 , 1 , ) (5. Durdurma kriteri sağlanıyorsa sonucu göster değilse 3 ve 4. adımları tekrarla
Bu bölümde DEA’nın iĢlem basamakları anlatılmıĢtır. Sürekli fonksiyonların karĢılaĢtırılması esnasında bu algoritma da kullanılacaktır.
7. PARÇACIK SÜRÜ OPTİMİZASYONU ALGORİTMASININ KARŞILAŞTIRILMASI
Sezgisel algoritmaların performanslarının ölçmenin temel yöntemlerinden biri de algoritmanın performansını diğer algoritmaların performansları ile karĢılaĢtırmaktır (Özsağlam ve ÇunkaĢ 2008). Bu bölümde Parçacık Sürü Algoritması (PSO), Genetik Algoritma (GA) ve Diferansiyel Evrim Algoritması(DEA) ile karĢılaĢtırıldı. KarĢılaĢtırma kriteri olarak ortalama jenerasyon değerleri ele alınmıĢtır.
7.1 Test fonksiyonları
Bu bölümde Parçacık Sürü Optimizasyonu sürekli fonksiyonların çözümünde kullanıldı. PSO, Genetik Algoritma(Gerçek Kodlu) ve Diferansiyel Evrim Algoritması (DEA) ile karĢılaĢtırıldı. Test fonksiyonlarında amaç algoritmaların minimum sonucu bulmasıdır. De Jong tarafından önerilen F1, F2, F3 ve F4 test fonksiyonları bir çok araĢtırmada, optimizasyon algoritmalarının performanlarının değerlendirilmesinde kullanılmıĢtır. F5, F6, F7 ve F8 test fonksiyonları ise Toksarı’nın (2007) çalıĢmasından alınmıĢtır. Test aĢamasında kullanılan algoritma parametreleri Tablo 7.1 de gösterilmiĢtir.
Tablo 7.1 Parametreler için Kullanılan Değerler
PSO GA DEA
Populasyon Sayısı:100
Atalet ağırlık değeri(W)=0,99
Ölçeklendirme faktörleri (C1 ve C2)=1,99 Populasyon Sayısı:100 Çaprazlama oranı=0,8 Mutasyon oranı=0,02 Populasyon Sayısı:100 Kombinasyon oranı(CR)=0,8 Ölçeklendirme faktörü (F)=0,8
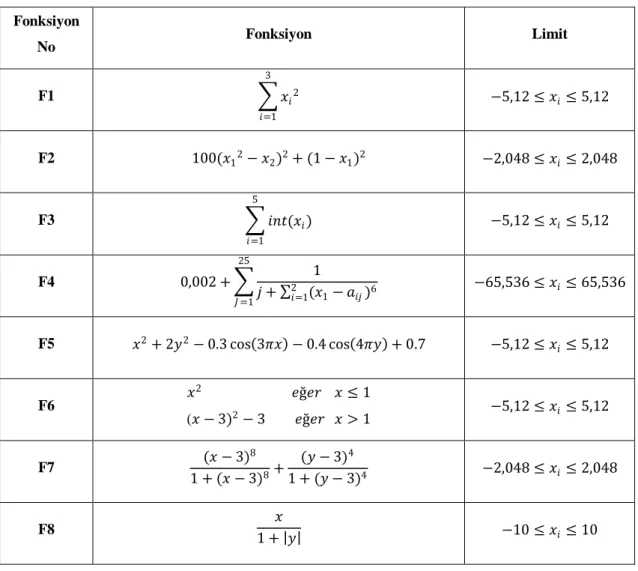
Tablo 7.2 Test Fonksiyonları Fonksiyon No Fonksiyon Limit F1 𝑥𝑖2 3 𝑖=1 −5,12 ≤ 𝑥𝑖 ≤ 5,12 F2 100(𝑥12− 𝑥2)2+ (1 − 𝑥1)2 −2,048 ≤ 𝑥𝑖 ≤ 2,048 F3 𝑖𝑛𝑡(𝑥𝑖) 5 𝑖=1 −5,12 ≤ 𝑥𝑖 ≤ 5,12 F4 0,002 + 1 𝑗 + (𝑥2𝑖=1 1− 𝑎𝑖𝑗)6 25 𝐽 =1 −65,536 ≤ 𝑥𝑖 ≤ 65,536 F5 𝑥2+ 2𝑦2− 0.3 cos 3𝜋𝑥 − 0.4 cos 4𝜋𝑦 + 0.7 −5,12 ≤ 𝑥𝑖 ≤ 5,12 F6 𝑥 2 𝑒ğ𝑒𝑟 𝑥 ≤ 1 (𝑥 − 3)2− 3 𝑒ğ𝑒𝑟 𝑥 > 1 −5,12 ≤ 𝑥𝑖 ≤ 5,12 F7 (𝑥 − 3) 8 1 + (𝑥 − 3)8+ (𝑦 − 3)4 1 + (𝑦 − 3)4 −2,048 ≤ 𝑥𝑖 ≤ 2,048 F8 1 + 𝑦 𝑥 −10 ≤ 𝑥𝑖 ≤ 10 7.2 Sonuçlar
Sonuçlar alınırken, program 50 defa çalıĢtırıldı, algoritmaların optimum sonuca ulaĢtıkları jenerasyon sayılarının ortalamaları alındı. Algoritmalar jenerasyon sayıları ile kıyaslandı. AĢağıdaki grafiklerde her bir fonksiyon için ortalama jenerasyon sayıları gösterilmiĢtir. Test fonksiyonları 2.4 Ghz çift çekirdekli iĢlemci ve 2048 Mb RAM’a sahip bilgisayar üzerinde çalıĢtırılmıĢtır.
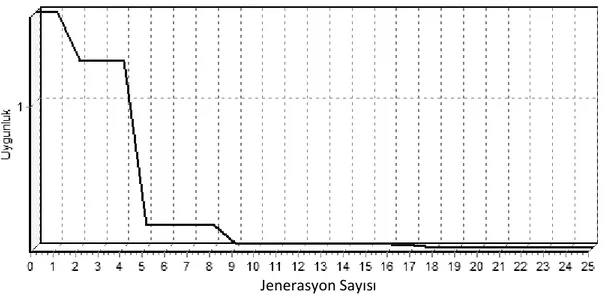
Sonuçlar alınırken yakınsama oranı göz önüne alındı. Bazı fonksiyonlarda algoritmalar istenilen jenerasyon zamanında en iyi sonuca ulaĢamadı. Bu durumlar
için 10000 jenerasyon sınır kabul edildi. Ortalama jenerasyonlar, program optimum değere 0,001 yaklaĢtığı zaman alındı.
F1 fonksiyonu için; GA, PSO ve DEA’ya göre kötü bir performans elde etmiĢtir (ġekil 7.1).
ġekil 7.1 F1 Fonksiyonu için Ortalama Jenerasyonlar
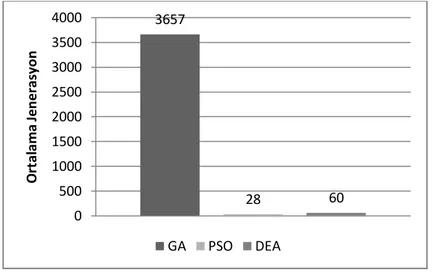
F2 fonksiyonu için; GA yine PSO ve DEA’ya göre kötü bir performans elde etmiĢtir. PSO ve DEA birbirlerine yakın bir sonuç elde etmiĢlerdir (ġekil 7.2).
ġekil 7.2 F2 Fonksiyonu için Ortalama Jenerasyonlar
F3 fonksiyonu için; GA 10000 jenerasyonu geçmesine rağmen sonuca ulaĢamamıĢtır bu yüzden 10000+ Ģeklinde gösterilmiĢtir. GA; PSO ve DEA’ya göre
508 19 37 0 100 200 300 400 500 600 O rt al am a Jen era syo n GA PSO DEA 3657 28 60 0 500 1000 1500 2000 2500 3000 3500 4000 O rt al am a Jen e ra syo n GA PSO DEA
oldukça kötü bir performans elde etmiĢtir. PSO ve DEA birbirlerine yakın bir sonuç elde etmiĢlerdir (ġekil 7.3).
ġekil 7.3 F3 Fonksiyonu için Ortalama Jenerasyonlar
F4 fonksiyonunda PSO ve DEA oldukça kısa jenerasyon sayılarında en iyiye ulaĢmıĢlardır. (ġekil 7.4)
ġekil 7.4 F4 Fonksiyonu için Ortalama Jenerasyonlar 10000+ 157 402 0 2000 4000 6000 8000 10000 12000 O rt al am a Jen era syo n GA PSO DEA 2003 35 81 0 500 1000 1500 2000 2500 O rt al am a Jen e ra syo n GA PSO DEA