Cayley ağacı üzerinde p-adik Ising-Vannimenus ve p-adik Lamda-modellerinin p-adik Gibbs ölçümleri ve faz geçişleri

T.C.

SELÇUK ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ

CAYLEY AĞACI ÜZERĠNDE p-ADĠK ISING-VANNIMENUS VE p-ADĠK 

-MODELLERĠNĠN p-ADĠK GIBBS ÖLÇÜMLERĠ VE FAZ GEÇĠġLERĠ

Mutlay DOĞAN DOKTORA TEZĠ Matematik Anabilim Dalı

Temmuz-2015 KONYA Her Hakkı Saklıdır

TEZ BĠLDĠRĠMĠ

Bu tezdeki bütün bilgilerin etik davranıĢ ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalıĢmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.

DECLARATION PAGE

I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.

Mutlay DOĞAN Tarih: 24/07/2015

ÖZET

DOKTORA TEZĠ

CAYLEY AĞACI ÜZERĠNDE p-ADĠK ISING-VANNIMENUS VE p-ADĠK  -MODELLERĠNĠN p-ADĠK GIBBS ÖLÇÜMLERĠ VE FAZ GEÇĠġLERĠ

Mutlay DOĞAN

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı

DanıĢman: Doç. Dr. Yıldıray KESKĠN

Ġkinci DanıĢman: Prof. Dr. Farrukh MUKHAMEDOV 2015, 90 Sayfa

Jüri

Prof. Dr. DurmuĢ BOZKURT Prof. Dr. Hasan AKIN Doç. Dr. Yıldıray KESKĠN Doç. Dr. Bünyamin AYDIN Yrd. Doç. Dr. Kemal USLU

Bu tezimizde iki dallı Cayley ağacı üzerinde p-adik analiz yöntemlerini kullanarak; p-adik Ising-Vannimenus ve p-adik -modelleri için genelleĢtirilmiĢ p-adik quasi Gibbs ölçümlerinin varlığını ve faz

geçiĢinin olup olmadığını inceledik. Öncelikle her iki modelimiz için iki dallı Cayley ağacı üzerinde p-adik katsayılı dinamik sistemler elde ettik. Bu dinamik sistemlerin sabit noktalarını bulmak için, yapmıĢ olduğumuz dönüĢümlerle bu dinamik sistemleri, üçüncü dereceden p-adik katsayılı polinom denklemlerine indirgedik. Bundan sonra, genelleĢtirilmiĢ p-adik quasi Gibbs ölçümlerinin varlığını, bu polinomların köklerinin varlığına ve genelleĢtirilmiĢ p-adik quasi Gibbs ölçümlerinide bu p-adik katsayılı polinomların köklerinin ölçümüne indirgemiĢ olduk. Her iki model için aĢikar olmayan köklerin varlığını gösterdik ve dolayısıyla genelleĢtirilmiĢ p-adik quasi Gibbs ölçümlerinin var olduğunu gördük. p-adik Ising-Vannimenus model için elde ettiğimiz p-adik katsayılı polinomun üç tane kökünün olduğunu ve bu köklerden birinin ölçümünün sınırlı, diğer ikisinin ölçümünün de sınırsız olduğunu ispatladık. Bu da bize

p-adik Ising-Vannimenus model için faz geçiĢinin varlığını gösterdi. Ayrıca sınırsız olan ölçümlerin

oranını inceledik ve oranı bir olarak elde ettik. Bu sonuçta bize bu ölçümlerin aynı hızla sonsuza gittiğini gösterdi. p-adik -modelde ise model için elde ettiğimiz p-adik katsayılı üçüncü derece polinomun

 _p ve  1

p olmak üzere iki durumda en az iki kökünün olduğunu dolayısıyla genelleĢtirilmiĢ p-adik quasi Gibbs ölçümünün varlığını gösterdik. Ölçümlerin varlığının ispatından sonra her iki;  p ve

1

 

p durumlarında faz geçiĢinin olup olmadığını ispatlamak için bu ölçümlerin sınırlı olup olmadıklarına baktık. Ġncelememiz sonucunda  p durumunda faz geçiĢinin olduğunu,  p1 durumunda ise güçlü faz geçiĢinin olduğunu gördük. Elde ettiğimiz bu sonuçlar bugüne kadar bu modellerle ilgili yapılan çalıĢmalardan daha genel sonuçlardır. Bu nedenle bu sonuçlar tezimize orijinallik kazandırmıĢtır.

Anahtar Kelimeler: Cayley Ağacı, Faz GeçiĢi, p-adik quasi Gibbs ölçümü, p-adik

ABSTRACT Ph.D THESIS

p-ADIC GIBBS MEASURES AND PHASE TRANSITIONS OF p-ADĠC

ISING-VANNIMENUS AND p-ADĠC -MODELS ON THE CAYLEY TREE Mutlay DOĞAN

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY

DOCTOR OF PHILOSOPHY IN MATHEMATICS

Advisor: Assoc. Prof. Dr. Yıldıray KESKĠN Co-Advisor: Prof. Dr. Farrukh MUKHAMEDOV

2015, 90 Pages Jury

Prof. Dr. DurmuĢ BOZKURT Prof. Dr. Hasan AKIN Assoc. Prof. Dr. Yıldıray KESKĠN Assoc. Prof. Dr. Bünyamin AYDIN

Assist. Prof. Dr. Kemal USLU

In this thesis, we have investigated the existence of the generalized p-adic quasi Gibbs measures and phase transitions for the p-adic Ising-Vannimenus and p-adic -model by using p-adic analysis

methods on the Cayley tree of order two. First, we obtained the dynamic systems with p-adic coefficients for both models on the Cayley tree of order two. And then by using appropriate transformations, we have reduced these dynamic systems to the third degree polynomials with p-adic coefficients to find the fixed points of these dynamic systems. Our problem has been reduced to problem of the existence of roots of these polynomials and the measurement of the roots of these polynomials with p-adic coefficients. For both models, we have proved that there exist three non-trivial solutions, which imply the existence of adic quasi Gibbs measure, hence the existence of the generalized adic quasi Gibbs measures for both p-adic Ising-Vannimenus and p-p-adic -models. Third degree polynomials with p-adic coefficients have

three non-trivial solutions and the measurement of one root is bounded and the measurements of other two roots are unbounded for p-adic Ising-Vannimenus model. So, this fact proves that phase transition occurs for p-adic Ising-Vannimenus model. We have also checked the rate of unbounded measures for Ising-Vannimenus model that goes to infinity in the same rate. However, for p-adic -model, we have

shown that at least two non-trivial solutions of third degree polynomials with p-adic coefficients exist in both cases  _p and  1

p which means the generalized p-adic quasi Gibbs measures exist for the model. After the proving existence of the measurements in both cases  _p,  1

p , we have investigated the existence of the phase transitions and proved that there exists phase transition in both cases  _p,  1

p . However in the case  p 1, we have proved that there exists strong phase transition. We obtained more general results than the previous results about these models. These results make this thesis distinct.

Keywords: Cayley Tree, Phase Transition, p-adic quasi Gibbs measures, p-adic

ÖNSÖZ

Öncelikle, doktora çalıĢmamda her türlü desteği ve fedakarlığı esirgemeyen kıymetli eĢim ve çocuklarıma; her türlü yardım ve yol göstericiliği hiç eksik etmeyen çok değerli hocam Prof. Dr. Hasan AKIN bey’e; Selçuk Üniversitesindeki çok değerli hocalarıma ve ikinci danıĢmanım Prof. Dr. Farrukh MUKHAMEDOV’a gönülden teĢekkür ediyor, Ģükranlarımı sunuyorum.

YapmıĢ olduğum bu çalıĢma ve daha sonra yapacağım çalıĢmalarımla ülkeme ve bilim dünyasına katkıda bulunmayı, kararlılıkla bu yoldan ayrılmamayı hedeflemekteyim. Bu duygu ve düĢüncelerle hep çalıĢmayı yüce yaratıcıdan niyaz ediyorum.

“İlim ilim bilmektir, ilim kendin bilmektir, sen kendin bilmezsen, bu nice okumaktır.”

Yunus EMRE

Mutlay DOĞAN KONYA-2015

ĠÇĠNDEKĠLER ÖZET ... iv ABSTRACT ... iv ÖNSÖZ ... v ĠÇĠNDEKĠLER ... vi BÖLÜM 1 ... 8 1 GĠRĠġ ... 8 2 KAYNAK ARAġTIRMASI ... 10 BÖLÜM 3 ... 14

3 GEREKLĠ TANIM VE TEOREMLER ... 14

3.1 p-Adik Sayıların ĠnĢası

 

_p ... 14

3.1.1 Rasyonel sayıların tamlanıĢı ... 14

3.1.2 Normlu cisimler ... 16

3.1.3 Normlu cisimlerin tamlanıĢlarının inĢası ... 23

3.1.4 p-adik sayılar cismi ( p) ... 25

3.1.5 Rasyonel sayıların p-adik açılımı ... 32

3.1.6 Hensel lemması ve denklikler ... 33

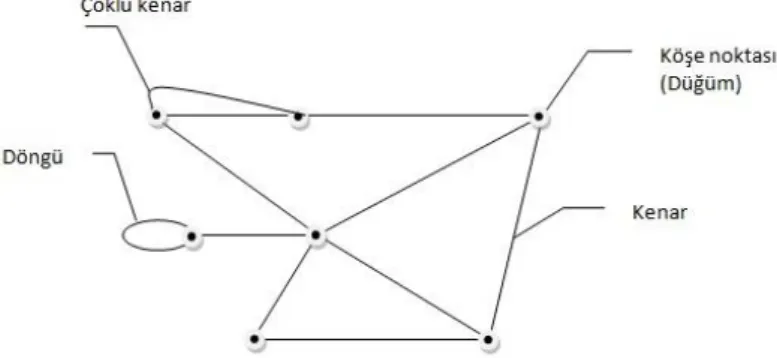
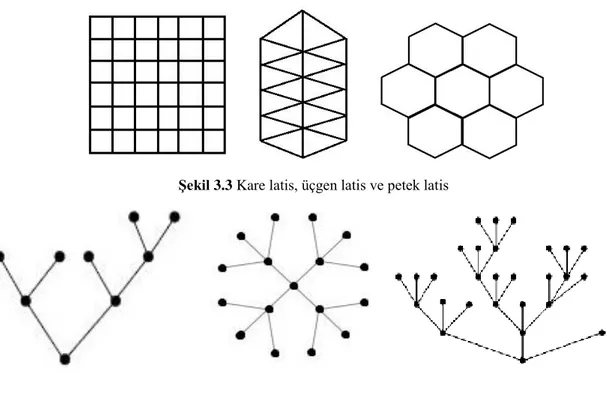
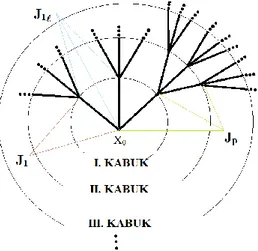
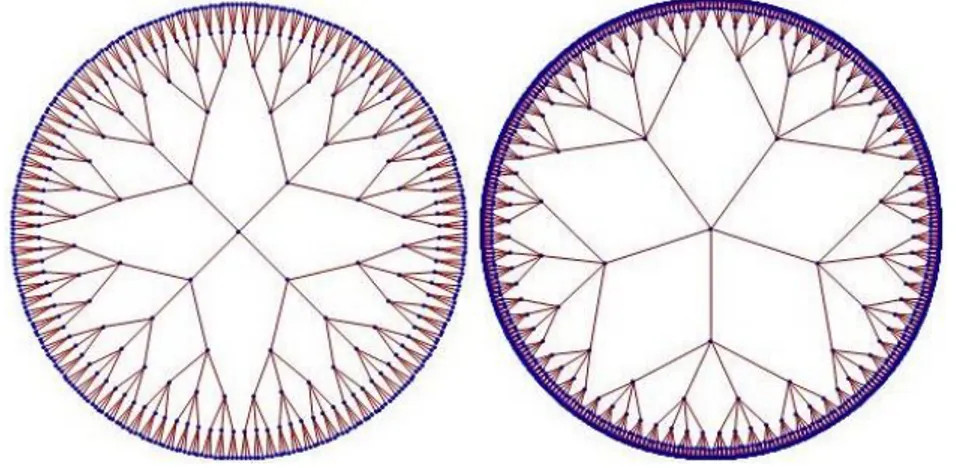
3.2 Ising modeli ... 37 3.3 Graf (Çizge) ... 38 3.4 Latis (Örgü) modeli ... 38 3.5 Spin ... 39 3.6 Konfigürasyon ... 40 3.7 Cayley ağacı ... 40

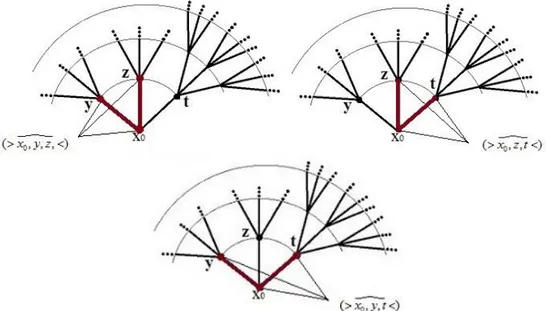
3.7.1 Cayley ağacı üzerindeki komĢuluklar ... 42

4 CAYLEY AĞACI ÜZERĠNDE p-ADĠK ISING-VANNIMENUS MODELĠN

p-ADĠK GIBBS ÖLÇÜMLERĠ VE FAZ GEÇĠġĠ ... 44

4.1 Önhazırlıklar ... 44

4.1.1 p-adik sayılar ... 44

4.1.2 p-adik ölçüm ... 46

4.1.3 Cayley Ağacı ... 47

4.2 p-Adik Ising-Vannimenus Model ve Bu Modelin p-adik Gibbs Ölçümleri . 47 4.2.1 p-adik quasi Gibbs ölçümlerinin varlığı ... 54

4.2.2 Faz geçiĢi ... 61

BÖLÜM 5 ... 66

5 CAYLEY AĞACI ÜZERĠNDE p-ADĠK -MODELĠNĠN FAZ GEÇĠġĠ ... 66

5.1 p-Adik -Model ve Bu Modelin p-adik Gibbs Ölçümleri ... 66

5.2 p-adik quasi Gibbs ölçümlerinin varlığı ... 71

5.2.1  _p durumu ... 71 5.2.2  _p 1 durumu... 76 5.3 Faz GeçiĢi ... 79 5.3.1  _p durumu ... 81 5.3.2  _p 1 durumu... 82 6 SONUÇLAR ... 86 KAYNAKLAR ... 87 ÖZGEÇMĠġ ... 90

BÖLÜM 1 1 GĠRĠġ

Bu doktara tezinde, p-adik analiz yöntemlerini kullanarak, Cayley ağacı (Bethe örgüsü) üzerinde Ising-Vannimenus ve -model için Gibbs ölçümleri ve faz geçiĢlerini inceledik. Bunun içinde tezin ikinci bölümünde bu konuyla ilgili kaynak araĢtırması, üçüncü bölümde de p-adik analiz ve Cayley ağacı ile ilgili temel tanım, teorem ve önermeleri verdik.

Cayley ağacı üzerinde Ising-Vannimenus modelinin Gibbs ölçümünün varlığı, yapılan (Georgii 1988) çalıĢmasındaki yaklaĢımlar kullanılarak reel durumda (Ganikhodjaev ve ark 2011) tarafından incelenmiĢtir. Yapılan bu çalıĢmaya benzer Ģekilde tezimizin dördüncü bölümünde, Cayley ağacı üzerinde Ising-Vannimenus modeli, p-adik durumda inceledik (Vannimenus 1981). Cayley ağacını yapılan [bkz. (Ostilli 2012)] bu çalıĢmadaki gibi verimli bir Ģekilde kullanarak, Ising-Vannimenus modelin daha detaylı incelemesini yaptık. Örgü sistemindeki en önemli problem, verilen Hamiltonyene göre sonsuz boyutlu Gibbs ölçümünü tanımlama zorluğudur. Genellikle bu tür problemlerin tam analiz edilebilmesi oldukça zordur [bkz. (Georgii 1988, Rozikov 2013)]. Bu sebeble önce ele aldığımız modele göre konfigürasyonumuzun Hamiltonyenini yazdık. Daha sonra elde ettiğimiz Hamiltonyenin p-adik olasılık ölçümünü bulduk. Bu ölçümden elde edilen sabit yinelemeli rekorans denklemlerinin Kolmogorov uyumluluk Ģartını sağladığını Teorem 4.2.0.3’te ispatladık. Bu da bize modelimiz için sonsuz boyutlu p-adik olasılık ölçümünü, sonlu boyutlu bir ölçümle yapabileceğimizi gösterdi. Daha sonra (4.37)’de elde ettiğimiz dinamik sistemin p-adik quasi Gibbs ölçümüne baktık. Bu ölçümün varlığını daha kolay inceleyebilmek için, bu dinamik sistem üzerinde bazı dönüĢümler uygulayarak bu dinamik denklemi (4.49)’daki üçüncü dereceden p-adik katsayılı polinom denklemine indirgedik. Bundan sonra p-adik quasi Gibbs ölçümünün varlığı, elde ettiğimiz bu p-adik katsayılı polinomun köklerinin varlığına dönüĢtü. YapmıĢ olduğumuz iĢlemler neticesinde üçüncü dereceden p-adik katsayılı polinom denkleminin x₀ _p ve x x₁, ₂ _{p p} olmak üzere üç tane kökü olduğunu ispatladık. Buda bize p-adik quasi Gibbs ölçümlerinin varlığını gösterdi.

Daha sonra elde ettiğimiz bu ölçümler için Ising-Vannimenus modelin faz geçiĢini inceledik. Faz geçiĢinin varlığı; biri sınırlı diğeri sınırsız olmak üzere en az iki tane p-adik quasi Gibbs ölçümünün varlığı anlamına gelmektedir. YapmıĢ olduğumuz iĢlemler neticesinde (4.83) ve (4.84) sonuçlarını elde ettik. Bu da bize biri sınırlı diğer

ikisi sınırsız olan en az iki tane p-adik quasi Gibbs ölçümün varlığını gösterdi. Dolayısıyla faz geçiĢinin varlığını ispatlamıĢ olduk. Daha sonra elde edilen sınırsız p-adik quasi Gibbs ölçümlerinin oranının (4.85)’te bir olduğunu ispatladık. Bu da bize sınırsız olan p-adik quasi Gibbs ölçümlerinin aynı hızla ilerlediğini gösterdi.

Tezimizin beĢinci bölümünde ise, (Khamraev 2004, Khamraev ve Mukhamedov 2004) çalıĢmaları ile baĢlatılan -model üzerindeki araĢtırmalara devam ettik. Bahsedilen bu çalıĢmalarda iki dallı Cayley ağacı üzerindeki -modelle ilgili sadece Gibbs ölçümünün tekliği çalıĢılmıĢtır. Yakın zamanda bu çalıĢmalardaki yazarlardan biri tarafından faz geçişi ve güçlü faz geçişi olmak üzere iki tip faz geçiĢi tanımlanmıĢtır (Mukhamedov 2012). (Mukhamedov 2012, Mukhamedov ve Akin 2013) çalıĢmalarında eğer ,p q ’yu böler ise q2 olmak üzere q1-durumlu Potts modeller için güçlü faz geçiĢinin varlığı ispatlanmıĢtır. Eğer q1 alınırsa q1 modeli Ising modele dönüĢür. Ayrıca yapılan (Khakimov 2014A, 2014B) çalıĢmalarda Potts model için faz geçişinin olduğu gösterilmiĢtir. Dolayısıyla doğal olarak Ģu soruyu sorabiliriz: Potts modellerden farklı modeller içinde faz geçişi var mıdır? Tezimizin beĢinci bölümünde bu soruya cevap aradık.

Bu cevap için beĢinci bölümde, -model için genelleĢtirilmiĢ p-adik quasi Gibbs ölçümünü inĢa ettik. Bu tür ölçümlerin varlığı, etkileĢim fonksiyonlarından elde edilen denklemlerin Kolmogorov uyumluluk Ģartını sağlamasına bağlıdır. Daha sonra  parametresine göre  p ve  _p 1 durumlarını inceledik. Bu iki durumda da

genelleştirilmiş p-adik quasi Gibbs ölçümlerinin varlığını ispatladık. Son olarak tezimizin ana sonuçlarından biri olan; iki dallı Cayley ağacı üzerinde ele aldığımız  -model için  _p ve  _p 1 durumlarında faz geçişinin varlığını gösterdik. Ayrıca

1

p

  durumunda güçlü faz geçişinin olduğunu ispatladık. Bu da tezimiz için önemli bir yeniliktir. Elde ettiğimiz bu sonuç Ģimdiye kadar yapılan (Mukhamedov 2012, Khakimov 2014A) çalıĢmaları da kapsayan en genel sonuçtur.

Tezimizdeki tüm iĢlemlerde p-adik analiz yöntemlerini kullandık. Dolayısıyla elde ettiğimiz sonuçlar reel durumda geçersizdir.

2 KAYNAK ARAġTIRMASI

p-adik sayılar ilk olarak Alman matematikçi K. Hensel tarafından ortaya atılmıĢtır. YaklaĢık bir asır sonra p-adik sayılar pür matematiğin önemli bir ilgi alanı haline gelmiĢtir. Bunun yanında teorik fizikteki birçok uygulaması yapılan (Arefeva ve ark 1991, Khrennikov 1997, Rozikov 1998, Khrennikov 2003, 2004, Ganikhodjaev ve Rozikov 2009) gibi çalıĢmalarda gösterilmiĢtir. Yapılan (Arefeva ve ark 1991) çalıĢmada olduğu gibi, fizikte ki bir çok p-adik model Kolmogorov aksiyomları olarak bilinen sıradan olasılık teorileriyle tanımlanamaz. Dolayısıyla yapılan (Khrennikov 1994, 1996) bu çalıĢmalarda yeni p-adik olasılık modelleri araĢtırılmıĢtır. Bu olasılık modeller, _p cismi üzerinde değerler aldığından dolayı Kolmogorovyen değildir.

Ganikhodjaev ve arkadaĢları tarafından yapılan (Ganikhodjaev 1998, Ganikhodjaev ve ark 2011) bu çalıĢmalarda, p-adik değerli stokastik yöntem teorisi ve non-ArĢimediyen değerli olasılık dağılımlarına sahip, daha genel non-ArĢimediyen cisimler geliĢtirilmiĢtir. Kolmogorov teoreminin non-ArĢimediyen benzerliği, sonlu boyutlu olasılık dağılımları kullanılarak, stokastik yöntemlerin daha geniĢ sınıflandırılmasına olanak sağlamıĢtır.

Bilindiği üzere istatiksel mekanik teorisi, olasılık ve stokastik yöntemler teorisi üzerinde durmaktadır. Çünkü non-ArĢimediyen durumunda kullanılan olasılık ve stokastik yöntemler teorisi, p-adik olasılık teorisinde istatiksel mekanik problemlerinin çalıĢılmasını ve daha da geliĢtirilmesini sağlamıĢtır.

Gibbs ölçümlerinin ana problemlerinden birisi verilen bir Hamiltonyen’e göre sonlu boyutlu Gibbs ölçümlerini tanımlama zorluğudur. Bununla birlikte, özel Hamiltonyenler için Gibbs ölçümlerinin tam analizi genelde zor bir problemdir. Eğer verilen bir Hamiltonyen’e göre biri sınırlı diğeri sınırsız olan iki tane Gibbs ölçümü varsa o halde bu model için faz geçişi vardır denir. k2 boyutlu Cayley ağacında Ising model için faz geçiĢinin varlığı Katsura ve Takisawa tarafından gösterilmiĢtir (Katsura ve Takizawa 1974). Bu çalıĢmalardan sonra, Ising modelin analizi Cayley ağacı üzerinde birçok yönde geliĢtirilmiĢtir [bkz. (Khrennikov 1997)].

Ġstatiksel mekanikte en çok çalıĢılan modellerden biri, geniĢ bir uygulama alanı olan Ising modeldir [bkz. (Baxter 1982, Wu 1982)]. Cayley ağacı üzerinde tanımlanan Ising modelle ilgili yapılan (Vannimenus 1981) çalıĢmada en yakın komĢuluklar arasındaki etkileĢim ele alınmıĢ ve bu modelin faz diyagramı tanımlanmıĢtır. Bunun yanında bu tür modeller istatiksel mekaniğin her çeĢit modellerini gösterecek

zenginliktedir. Bahsedilen bu modelle ilgili birçok çalıĢma yapılmıĢtır (Mariz ve ark 1985, Ohanyan ve ark 2007, Ostilli ve ark 2008). Fakat yapılan bu çalıĢmalardaki çoğu sonuçlar nümerik olarak elde edilmiĢtir. Cayley ağacı üzerinde bahsedilen Ising-Vannimenus modelinin Gibbs ölçümü, yapılan (Georgii 1988) çalıĢmadaki yaklaĢım kullanılarak (Ganikhodjaev ve ark 2011) tarafından reel durumda yapılmıĢtır. Bizde bu tez çalıĢmamızın dördüncü bölümünde benzer Ģekilde, Cayley ağacı üzerinde Ising-Vannimenus modeli, p-adik durumda inceledik (Ising-Vannimenus 1981). Tezimizde [bkz. (Ostilli 2012)] çalıĢmasında olduğu gibi, Cayley ağacını verimli bir Ģekilde kullanarak Ising-Vannimenus modelin daha detaylı incelemesini yaptık. Örgü sistemindeki en önemli problem, verilen Hamiltonyene göre sonsuz boyutlu Gibbs ölçümünü tanımlama zorluğudur. Genellikle bu tür problemlerin tam analiz edilebilmesi oldukça zordur [bkz. (Georgii 1988, Rozikov 2013)].

Ising-Vannimenus modelin Gibbs ölçümünün p-adik durumda incelenmesi gibi bu tür p-adik yaklaĢımlarla, p-adik sayılar kuantum fiziğindeki modellerde kullanılmıĢ ve bu modeller p-adik olasılık ölçümü olarak adlandırılmıĢtır. Fizikte, bilinen Kolmogorov olasılık teorisiyle tanımlanamayan birçok model vardır [bkz. (Koblitz 1977, Marinary ve Parisi 1988, Vladimirov ve ark 1994, Khrennikov 1997)]. Bu nedenle Khrennikov ve Besser yapmıĢ oldukları (Khrennikov 1996, Besser ve Deninger 1999, Khrennikov ve ark 1999, Khrennikov 2004) bu çalıĢmalarda p-adik olasılık modelleri incelemiĢlerdir. Yapılan bu (van Rooji 1978, Khrennikov 2003, Ludkovsky 2005) çalıĢmalarda p-adik ölçüm teorisi kullanılarak _p cismi üzerinde non-ArĢimediyen değerli yeni olasılık dağılımları tanımlanmıĢtır. Özellikle Kolmogorov teoreminin non-ArĢimediyen benzerliği ispatlanmıĢ [bkz. (Ganikhodjaev 1998)] ve bu benzerlik bize sonlu boyutlu olasılık dağılımları kullanarak sonsuz boyutlu olasılık dağılımlarını bulmamızı sağlamıĢtır (Freund, P.G.O. ve ark., 1987). (Ganikhodzhaev ve ark 2002, Khamraev ve Mukhamedov 2004, Mukhamedov 2004, Mukhamedov 2013, Mukhamedov ve Akin 2013) yapmıĢ oldukları bu çalıĢmalarda iki dallı Cayley ağacı üzerinde en yakın komĢulukların etkileĢimini ele alarak, yeni bir p-adik olasılık teorisi yaklaĢımıyla p-adik Ising ve Potts modellerinin Gibbs ölçümlerini incelemiĢlerdir. Muhamedov yapmıĢ olduğu (Mukhamedov 2010, 2014) bu çalıĢmalarda q+1 durumlu Potts modeller ile p-adik quasi Gibbs ölçümü olarak adlandırılan yeni bir p-adik ölçüm tanımlamıĢtır. Bu tür ölçümler (Khamraev ve Mukhamedov 2004, Mukhamedov 2004) çalıĢmalarında ele alınan Gibbs ölçümlerinden tamamıyla farklıdır. Son zamanlarda

Khakimov yapmıĢ olduğu (Khakimov 2013, 2014B) bu çalıĢmalarda iki dallı Cayley ağacı üzerinde p-adik Ising modellerde en yakın komĢulukların etkileĢimi için p-adik quasi Gibbs ölçümlerini araĢtırmıĢtır. Bu tür modeller sadece birinci seviyede ki etkileĢimleri içerir. Bu yönüylede (Vannimenus 1981) çalıĢmasındaki ölçümden farklıdır.

Bu tezimizde, (Vannimenus 1981) çalıĢmasındaki modelin p-adik benzerliğini, Cayley ağacı üzerindeki en yakın ve bir sonraki en yakın komĢuluklar arasındaki etkileĢimleri ele alarak inceledik. Bu modeli p-adik Ising-Vannimenus model olarak adlandırdık. Bu modelimiz, (Khakimov 2014B) çalıĢmasındaki modelden daha kapsamlıdır. Tezimizde bu modelin Gibbs ölçümünü bulmak için yeni bir ölçüm teorisi ile çalıĢtık. Yani; etkileĢim fonksiyonları ile yeni bir p-adik quasi Gibbs ölçümü tanımladık. p-adik durumda güçlü faz geçişi ve faz geçişi gibi değiĢik türden faz geçiĢleri vardır [bkz. (Mukhamedov 2013, 2014)]. Burada faz geçiĢi ile aĢikar olmayan, biri sınırlı diğeri sınırsız olan en az iki tane p-adik quasi Gibbs ölçümünün varlığı ifade edilmektedir. p-adik olasılık ölçümünde, reel durumdaki ölçümden faklı olarak, olasılık ölçümünün sınırsız olabileceği yapılan (van Rooji 1978) çalıĢmada gösterilmiĢtir. Faz geçiĢinin varlığı, Khakimov tarafından yapılmıĢ olan (Khakimov 2013, 2014B) bu çalıĢmalarda vurgulanmıĢtır. Biz de tezimizin dördüncü bölümündeki ana sonuçları bulmak için, elde ettiğimiz denklemlerde benzer Ģekilde p-adik analiz yöntemlerini kullanarak p-adik quasi Gibbs ölçümünlerinin varlığını gösterdik.

Yapılan (Rozikov 1998, Mukhamedov 2004) bu çalıĢmalarda istatiksel mekanikte en çok kullanılan modellerden biri olan iki dallı Cayley ağacı üzerinde  -model incelenmiĢtir. Tezimizin beĢinci bölümünde -modeli p-adik durumda daha detaylı olarak inceledik. Standart birçok fiziksel niceliklerin analitik çözümleri bulunamamasına karĢın, iki dallı Cayley ağacı (örgü) gibi değiĢik örgüler kullanılarak analitik çözümleri bulunamayan birçok modelin faz geçiĢlerinin incelenmesiyle tam olarak hesaplaması yapılabilmektedir (Rozikov 2013). Diğer taraftan tam çözümlü modellerin çalıĢılması, istatiksel mekanikte de bu tür modellerin kullanılması yönünde ilgi uyandırmıĢtır (Baxter 1982). Yapılan (van Rooji 1978, Khrennikov ve ark 1999, Ostilli 2012) bu çalıĢmalarda p-adik olasılık ölçümleri inĢa edilmiĢtir. Bu tür yaklaĢımlarla, kuantum fiziğinde ki, Kolmogorov olasılık teorisi ile çözülemeyen bazı modellerin olasılık ölçümlerinin yapılması sağlanmıĢtır [bkz. (Koblitz 1977, Marinary ve Parisi 1988, Vladimirov ve ark 1994, Khrennikov 1997)]. Bu nedenle yapılan (Khrennikov 1996, Besser ve Deninger 1999, Khrennikov 2004) bu çalıĢmalarda p-adik

olasılık modelleri araĢtırılmıĢtır. (Khrennikov 2003, Ludkovsky 2005, Khrennikov 2007) çalıĢmalarında p-adik ölçüm teorisi kullanılarak p-adik ve non-ArĢimediyen teoride yeni yöntemler geliĢtirilmiĢtir. (Mukhamedov ve Rozikov 2005, Mukhamedov 2010, Gandolfo ve ark 2012) çalıĢmalarında p-adik istatiksel mekanikte, yeni p-adik olasılık teorisi ve p-adik ölçüm yöntemleri geliĢtirmiĢlerdir.

Tezimizin beĢinci bölümünde, Khamraev ve Mukhamedov tarafından baĢlatılan

-model ile ilgili (Khamraev 2004, Khamraev ve Mukhamedov 2004) çalıĢmaları daha detaylı ve genel bir Ģekilde incelemeye benzer yöntemleri kullanarak devam ettik.

BÖLÜM 3

3 GEREKLĠ TANIM VE TEOREMLER

Bu bölümde tezimizde kullanacağımız gerekli tanım ve teoremleri detaya girmeksizin vereceğiz. Reel sayılar ve p-adik sayılar kümesi, rasyonel sayılar kümesinin tamlanıĢından elde edilen iki kümedir. Bu sayılar herhangi iki rasyonel sayı arasındaki mesafenin bulunuĢunda kullanılır. Öklid normu herhangi bir reel sayının orijine olan uzaklığını, sonsuzdaki

 

 _ mutlak değer olarak ifade eder. Eğer bilinen mutlak

 

_ değerde sonsuz yerine herhangi bir p asal sayısı alınırsa, bu mutlak değere p-adik metrik denir ve  _p ile gösterilir. p-adik metriğin en önemli özelliği güçlü üçgen eşitsizliği

olarak bilinen max



,



p p p

xy  x y eĢitsizliği sağlamasıdır. p-adik metrik yardımıyla rasyonel sayıların ikinci tip tamlanıĢı olan _p p-adik sayılar cismi inĢa edilir.

3.1 p-Adik Sayıların ĠnĢası

 

_p

Reel sayıların inĢasında olduğu gibi _p cismi de rasyonel sayıların belirli bir norma göre tamlanıĢından elde edilmiĢtir. Bu norm p asal sayılarına dayandırılmakta ve reel sayılarda bilinen Öklid normundan farklılıklar göstermektedir. Bu durumda ’nun tamlanıĢı olan ve _p kümelerinin her ikiside birer normlu tam cisimdir. Bu kavramları (3.1.2)’de detaylı bir Ģekilde açıklayacağız. Ġlk olarak (3.1.1)’de tamlanıĢ prosedürünü reel durumdakine benzer Ģekilde uyguladık







. (3.1.3)’te de herhangi bir normlu cisim üzerinde genellemesini yapacağız.

3.1.1 Rasyonel sayıların tamlanıĢı

Reel sayılar, rasyonel sayıların tamlanıĢından elde edilmiĢtir. Bu prosedür tüm metrik uzaylara uygulanabilir. M boĢtan farklı bir küme ve d M: M  

 

0 Ģeklinde tanımlanan d fonksiyonu;

1) ( , )d x y 0; ( , )d x y   0 x y 2) ( , )d x y d y x( , ),x y, M

3) ( , )d x y d x z( , )d z y( , ),x y z, , M

bu üç özelliği sağlarsa, d fonksiyonuna M kümesi üzerinde bir metrik ve



M d ,



ikilisine de metrik uzay denir.

Cauchy Dizisi: (M d bir metrik uzay ve ( ), ) r ’de bu uzayda bir dizi olsun. Verilen n

herhangi bir 0 için her m n, N( ) olduğunda ( , )d r r_{m n}  olacak Ģekilde bir N( ) sayısı varsa ( )r dizisine Cauchy dizisi denir. n M kümesindeki her ( )r Cauchy dizisi n

yakınsak ise yani r_n  r M ise (_{M d metrik uzayına tam metrik uzay denir.} , )

Teorem 3.1.1.1 (Katok 2007) Eğer (M d tam metrik uzay değil ise o halde öyle bir , ) (M d metrik uzayı vardır ki aĢağıda ki özellikleri sağlar. , )

1) M tamdır.

2) M M ’ye izometrik olan bir , M₀ altkümesi içerir.

3) M₀ , M ’de yoğundur. Yani M ’deki her bir nokta M₀ için bir limit noktasıdır. Bu teoremin ispatı M ’nin tamlanıĢının inĢasına ve M üzerinde tanımlanan

( , ) lim ( _n, _n)

n

d A B d a b



 (3.1)

d metriğine dayanmaktadır. Bu metrik, M ’deki A

 

 

a_n , B

 

 

b_n denklik sınıflarının kümeleri arasındaki uzaklığı ifade etmektedir. Bu yapının elemanları M ’de bulunan iki tane

 

xn ve

 

yn Cauchy dizilerinin denklik sınıflarıdır. Yani;

( , ) 0

n n n n

x  y d x y  . M  için rasyonel sayılarda bilinen Öklid metriği

1 2 1 2

( , )

d r r  r r (3.2) Ģeklinde tanımlanmıĢtır. Bu uzaklık, mutlak değer olarak bildiğimiz, rasyonel sayılar kümesindeki herhangi iki noktanın Öklid normuna göre birbirine olan uzaklığıdır. Yani sayı doğrusu üzerindeki herhangi iki nokta arasındaki uzaklıktır. Reel sayıları oluĢturan rasyonel sayıların tamlanıĢının daha basit tanımı kesirli sayılar üzerinde kurulmuĢtur. Herhangi bir rasyonel sayı, sonsuz ondalık kesirler olarak yazılabilir ve bu sonsuz ondalık kesirler peryodiktir. Diğer taraftan her bir ondalık kesirli sayı, sayı doğrusu üzerinde bir nokta belirtir. O halde bu sonsuz ondalık kesirlerle reel sayıları tanımlamak mümkündür. Her bir pozitif reel sayı

10 k k k m a a    



(3.3) Ģeklinde ondalık kesir toplamı Ģeklinde yazılabilir. Burada m bir tamsayı ve



0,1, 2,3, 4,5, 6, 7,8,9



k

a  . Bu gösterim tüm kn için a_k 0 olmak üzere tektir. Rasyonel sayılarda limiti olmayan Cauchy dizisini inĢa etmek oldukça kolaydır. Örneğin; 0,1; 0,1011; 0,10110111; 0,1011011101111;... gibi.

Diğer taraftan rasyonel sayılar kümesi üzerindeki her bir Cauchy dizisinin her bir denklik sınıfı, (3.3) serisinin kısmi toplamları olarak gösterilebilir. Bilinen Öklid metriğine göre reel sayılar tamdır. Reel sayıların sonsuz ondalık kesirlerle inĢası ile Öklid metriğine göre tamlanıĢ prosedürleri aynıdır. Herhangi bir a reel sayısının t

tabanında gösterimi;





; 1, 2,3,..., 1 k k k k m a a t a t    



  (3.4) Ģeklinde genelleĢtirilebilir. Burada t ve t2 dir. t nin k. kuvveti azalarak ’a gider. Pratik olarak tamlanıĢ farklı yöntemlerle elde edilebilir.

Tanım 3.1.1.2 ( , )M d bir metrik uzay olsun ve  pozitif reel sayıları göstersin. r  yarıçaplı aM merkezli açık yuvar; B a r( , )



xM d a x: ( , )r



ve r  yarıçaplı aM merkezli kapalı yuvar; B a r( , )



xM d a x: ( , )r



Ģeklinde gösterilir. Eğer her xM için B a r( , )M açık yuvarı mevcut ise x ’i içeren

AM’ye açıktır denir. Eğer M A açık ise AM’ye kapalıdır denir.

Önerme 3.1.1.3 (Katok 2007) M tam metrik uzay ve X M olsun. XMkapalı ise o halde X tamdır. Yani; X tamdır X Mise.

Örnek 3.1.1.4 ( , )a b açık aralığının Öklid metriğine göre tamlanıĢı

 

a b kapalı , aralığıdır. Yani

 

a b,  .

3.1.2 Normlu cisimler

Rasyonel ve reel sayılar, cisim olarak adlandırılan özel cebirsel yapılardır. Bir F cismi, toplam ve çarpım iĢlemlerine göre aĢağıdaki temel özellikleri;

1) a b, F a b,   b a (Toplamaya göre değiĢmeli) 2) a b c, , F a,     (b c) (a b) c (BirleĢme özelliği)

3) 0 F öyle ki  a F için 0 a a (Toplamaya göre birim eleman) 4)  a F için  0 F öyle ki a  ( a) 0 (Toplamaya göre ters eleman) 5) a b, F a b,   b a (Çarpmaya göre değiĢmeli)

6) a b c, , F a b c,     ( ) (a b c) (Çarpmaya göre birleĢme özelliği)

7) 1 F  öyle ki  a F*  F

 

0 için 1 a a (Çarpmaya göre birim eleman) 8)  a F* için a1F* öyle ki a a 1 1 (Çarpmaya göre ters eleman) 9) a b c, , F a b c,      ( ) (a b) (a c) (Toplama üzerine dağılma özelliği)

sağlayan bir kümedir. Sadece bir iĢleme göre ilk dört özelliği sağlayan cebirsel yapıya abelyen (değişmeli) grup denir. Buna göre F cismi toplamaya göre değiĢmeli bir gruptur. *

F , F cisminin çarpımsal grubudur. Bir cebirsel yapı ilk altı özelliği ve 9. özelliği sağlarsa bu yapıya değiĢmeli halka denir.

Tanım 3.1.2.1 F bir cisim olmak üzere, F cismi üzerinde  :F  

 

0 bir fonksiyon olsun. Eğer bu fonksiyon;

1) x   0 x 

2) xy  x y ,x y, F

3) xy  x  y ,x y, F (Üçgen eĢitsizliği)

Ģartlarını sağlıyor ise bu fonksiyona, F ’de bir norm denir.



F, 



ikilisine normlu uzay denir. Eğer x 0 ve her x0 için x 1 ise bu norma aşikar norm denir. Her

n için

defa

1 1 1 ... 1

n

n     (3.5) olur. n tane bir sayısının toplamına karĢılık gelen doğal sayıyı n ile gösteririz.

Önerme 3.1.2.2 (Katok 2007) Her ,x yF için aĢağıdaki önermeler sağlanır. 1) 1   1 1 2) x  x 3) xy  x  y 4) x y x  y 5) x x , y 0 y  y  6) n   n; n

Tanım 3.1.2.3

 

an , F cisminde bir dizi olsun.

1) Eğer n  için a_n C eĢitsizliğini sağlayacak Ģekilde bir C0 sabiti varsa,

 

a_n dizisine sınırlı dizi denir.

2) Eğer lim _n 0

n a  ise. Yani  0 için N vardır öyle ki n N için

3) Eğer  0 için N vardır ki n m, N için a_na_m  ise

 

a_n dizisine bir Cauchy dizisi denir. Yani;

,

lim _{n m} 0

n m a a  ise.

4) Eğer lim _n 0

n a a  ise

 

an dizisi a’ya yakınsaktır denir. Yani 0

için N vardır öyle ki  n N için a_n a .

Tanıma göre null (sıfır) dizileri sıfıra yakınsar. Buna göre üçgen eĢitsizliğinden dolayı her yakınsak dizi bir Cauchy dizisidir. Bunun ispatını basitçe aĢağıdaki Ģekilde gösterebiliriz.

Farzedelim ki lim n

na a olsun. Her n m, N için an a ₂ ve am a ₂

ise

2 2

n m n m n m

a a  a   a a a  a   a a a    olur. O halde (a_n) dizisi bir Cauchy dizisidir. Özellikle her sıfır (null) dizisi bir Cauchy dizisidir. Cauchy dizileri için aĢağıdaki özellikler verilebilir.

1) Her Cauchy dizisi sınırlıdır.

2)

 

a_n bir Cauchy dizisi ve



n n n₁, ₂, ₃,...



artan bir pozitif tamsayı dizisi olsun. Eğer

1, 2, 3,...

n n n

a a a altdizisi bir sıfır dizisi ise o halde

 

a_n dizisinin kendiside sıfır dizisidir.

3) Eğer

 

a_n ve

 

b_n sıfır dizisi ise o halde



a_nb_n



diziside bir sıfır dizisidir. 4) Eğer

 

a_n sıfır dizisi ve

 

b_n diziside sınırlı ise o halde



a b_n _n



dizisi bir sıfır

dizisidir.

AĢağıdaki önerme basit fakat çok kullanıĢlı bir sonuçtur. Önerme 3.1.2.4 (Katok 2007) Eğer lim n 0

nx  ise o halde x 1 dir.

Ġspat: x 1 olsun. xn  x olduğundan limn 0

 

n

n x olur. Yani; lim 0 n

nx  dır.

Aksine, eğer x 1 ise o halde tüm pozitif n ’ler için xn 1 elde edilir ve bu da

lim 0

 

n

n x olduğunu gösterir. Bu da lim 0 n

nx  olma Ģartımızla çeliĢir.

Tanım 3.1.2.5 Eğer herhangi bir

 

an dizisi, d metriğine göre Cauchy dizisi iken 1 d 2

metrikler denir. Eğer ₁ ve ₂ normları aynı metriği (uzaklığı) veriyorsa o halde bu iki norm denktir,





1 2

  .

Önerme 3.1.2.6 (Katok 2007) ₁ ve

2

 , F cismi üzerinde iki norm olsun. Eğer

2 1 ,

x  x   x F (3.6) olacak Ģekilde herhangi bir pozitif  reel sayısı var ise bu iki norm denktir,

1 2

  .

Ġspat: Farzedelim ki ₁ ₂ olsun. Eğer x0 yada x1 ise (3.6)’nın herhangi bir

 için sağlandığı açıktır.

Eğer ₁ aĢikâr değil, yani x0 _{ya da x 1} ise o halde öyle bir aF seçelim ki a₁ 1 ve a₁0 olsun. a yerine 1

a yazalım. Buradan da a11 alalım ve 2 1 log log a a   olarak tanımlayalım.

Normların denk olduğunu göz önüne alırsak a ₂ 1 dir. O halde her iki logaritmada negatiftir ve  0 dır. ġimdi bu  ’nın (3.6)’yı sağladığını gösterelim. Ġlk olarak bir xFalalım ve x₁1 olsun. AĢağıdaki

1 1 : , , r m S r m n x a n   _    _   (3.7)

kümesini ele alalım. S kümesinde ki koĢula göre mn olduğuna dikkat edelim. Bu durumda her rS için x₁m  a₁n olduğundan

1 1 m n x a  dir. O halde 1 2 olduğundan 2 1 m n x a  olur. Buradan da 2 2 m n x  a ve x ₂r  a ₂. x ₂ ve x₁’in

yerlerini değiĢtirerek aynı iĢlemleri yaparsak;

2 2 : , , r m S r m n x a n   _    _   (3.8)

elde ederiz. (3.7) ve (3.8) kümelerindeki eĢitsizliklerin her iki tarafının logaritmasını alır ve elimizdeki tüm logaritmaların negatifliğini gözönünde bulundurursak, bu eĢitsizlikler

1 2 1 2 log log , log log a a r r x x   (3.9) Ģeklinde yazılabilir. Buradan da

1 2 1 2 log log log log a a x  x (3.10)

olmak durumundadır. Aksi durumda bu iki sayı arasında bir r _{rasyonel sayısı olabilir}

ve (3.9) durumundaki Ģartlardan sadece birisini sağlar. O halde

2 2 1 1 log log log log x a x  a  (3.11)

olur ve böylece ispat tamamlanmıĢ oldu.

ġimdi rasyonel sayılar

 

kümesi üzerindeki tüm normların  mutlak değer normuna denk olduğunu söyleyebiliriz.

Önerme 3.1.2.7 (Katok 2007) Eğer 1 ise o halde x  x,0 ’da bir

normdur. Bu durumda    dir.

Ġspat: Farzedelim ki  1 olsun. Normun ilk iki özelliğinin sağlandığı açıktır. Burada sadece üçgen eĢitsizliğinin sağlanıp sağlanmadığına bakacağız. Farzedelim ki y  x

olsun. O halde ( ) (1 ) (1 ) (1 ) y x y x y x x y y x x x y x _x                      (3.12)

Ġlk eĢitsizlik t1 için t t durumundan gelir. Örneğin 2, 1 2

t   olsun. O halde

22 dir. Ġkinci eĢitsizlikte 0 t 1 için t t durumundan gelir. Örneğin;

1 1

,

2 2

t    olsun. O halde 22 olduğundan 1 1 2

2  dir. Diğer taraftan eğer 1 ise üçgen eĢitsizliği sağlanmaz. Örneğin 1 1  2 1 1 2. Ostrowski teoreminden dolayı Önerme 3.1.2.7, ’da ki tüm normların mutlak değer  normuna denk olduğunu gösterir.

Tanım 3.1.2.8 Eğer bir norm





maks ,

xy  x y

(3.13) eĢitsizliğini sağlarsa bu norma non-Arşimediyen norm denir. Aksi halde norm Arşimediyen normdur.

Not 3.1.2.9 Normun non-ArĢimediyen özelliği, maks



x , y



 x  y olduğundan üçgen eĢitsizliğini sağlar. Bu özelliğe güçlü üçgen eşitsizliği denir. Non-ArĢimediyen normu ile elde edilen metriğe ultra metrik denir. Bilinen uzaklık fonksiyonundaki

( , ) ( , ) ( , )

d x z d x y d y z üçgen eĢitsizliği yerine non-ArĢimediyen normda güçlü üçgen eĢitsizliği d x z( , )maks



d x y d y z( , ), ( , )



kullanılır. Bu metrik uzaya ultra metrik uzay denir.

AĢağıdaki önerme bir normun non-ArĢimediyen olması için gerekli Ģartları verir. Önerme 3.1.2.10 (Katok 2007) AĢağıdaki iki durum birbirine denktir:

1)  non-ArĢimediyendir. 2)  n için n 1.

Ġspat: (1)(2): Bu iddiayı tümevarımla ispatlayacağız. Ġlk olarak n1 için 1  1 1 dir. k n 1 için k 1 olduğunu varsayalım. Buradan da n 1 olduğunu gösterelim.

1 1

n  k  ve 1 1 olduğundan n    n 1 1 maks



n1 , 1



1 elde edilir. O halde her n için n 1 olur.  n n olduğundan her n içinde n 1

olur. (2)(1):





0 0 0 ( ) ( 1) maks , n n n _{n k n k} k n k k k n _n k n k k n n x y x y x y x y k k x y n x y               _{ }  _{ }         _{  }







(3.14)

O halde her n için n 1 maks{ , }

xy  n x y elde edilir. n  iken

maks{ , }

xy  x y olur. Çünkü burada n k

   

  bir tamsayı ve lim 1 1

n

n n  dir.

Bu önerme ArĢimediyen ve non-ArĢimediyen normlar arasındaki farkı anlamamızı sağlar. Bu durumda tekrar edecek olursak; verilen ,x yF x, 0 için

n x  y eĢitsizliğini sağlayan herhangi bir pozitif n tamsayısı var ise bu norma  ArĢimediyen norm denir. Bunu göstermek için ,x yF olmak üzere y  x alırız. O halde ArĢimediyen norm özelliği öyle bir pozitif n tamsayısının varlığını gösterir ki

1

y n

x

bir pozitif n tamsayısı vardır ki n 1 dir. O halde k  iken n k   dur ve bazı k ’lar için n k y

x

 olur ve n xk  y ArĢimediyen özelliği sağlanır. Yani;





sup n n:    (3.15) olur. (3.15)’in sağlandığı, Önerme 3.1.2.10 ile gösterilebilir.

Önerme 3.1.2.11 (Katok 2007) F cismi non-ArĢimediyen bir cisim olmak üzere; eğer ,

a xF için x a a eĢitsizliği sağlanıyor ise o halde x  a .

Ġspat: Güçlü üçgen eĢitsizliğinden x    x a a maks



x a , a



 a olur. Diğer taraftan a    a x x maks



x a , x



olur. Eğer xa  x ise a  x a dır. Buda x a a Ģartı ile çeliĢir. O halde x a x ve a  x . Böylece x  a

olduğu ispatlanmıĢ oldu.

Not 3.1.2.12 Yukarıda ki önermeyi aĢağıdaki Ģekilde de ifade edebiliriz: ,a bF ve

 ’da F cismi üzerinde bir non-ArĢimediyen norm olsun. O halde .

a  b   a b a (3.16) Bu durum geometrik olarak Ģu Ģekilde ifade edilebilir; ultrametrik uzaydaki her üçgen ikizkenardır ve taban uzunluğu eĢ olan kenarların uzunluğunu geçmez.

Önerme 3.1.2.13 (Katok 2007) Eğer bir norm

 

 non-ArĢimediyen norm ise bir





( , ) :

B a r  x x a r açık yuvarının F cismindeki her noktası bu yuvarın merkezidir. Yani; eğer bB a r( , ) ise B b r( , )B a r( , ) dir. Aynı durum kapalı yuvar içinde geçerlidir.

Ġspat: xB b r( , ) olsun. Kabulümüzden, a b _p r, bx_p r olur ve güçlü üçgen eĢitsizliğinden;





( ) ( ) maks ,

p p p p

ax  a b  b x  a b bx r

olarak elde edilir. Buradan da B b r( , )B a r( , ) olur. b için ab_p r olduğundan ( , )

bB a r aynı Ģekilde aB b r( , ) olur. O halde B a r( , )B b r( , ) elde edilir ve böylece her iki yuvarında aynı olduğu ispatlanmıĢ olur.

AĢağıda ki önerme ile iki denk normun ya Arşimediyen yada non-Arşimediyen olduğunu gösterdik.

Önerme 3.1.2.14 (Katok 2007) Bir F cismi üzerindeki iki denk normun



₁ ₂



her ikiside ya ArĢimediyendir yada non-ArĢimediyendir.

Ġspat: Eğer ₁ ₂ ise o halde her x tamsayısı için x₁ 1 ve x ₂ 1 dir. Ġlk olarak bunu ispatlamak için farzedelim ki

1 1

x  ve

2 1

x  olsun. O halde n  iken

1

n

x   ve

2 0

n

x  olur. Buda

 

xn dizisinin ₁ normuna göre Cauchy olmadığını

2

 normuna göre ise Cauchy olduğunu gösterir. Buda normların denkliğiyle çeliĢir. O halde Önerme 3.1.2.10’dan her iki norm ya Arşimediyen ya da non-Arşimediyendir.

3.1.3 Normlu cisimlerin tamlanıĢlarının inĢası

Bu bölüme; bir  ’a göre tam olup olmadığı bilinmeyen keyfi bir F cismi alarak baĢlayacağız. Bu F cismini de içeren bir F cismini inĢa edeceğiz ve bu cismi F ’nin normundan elde edilen bir normla tamlayacağız. Burada F ’yi tam normlu bir cisim olarak elde edeceğiz. Cauchy dizileri toplanabilir, çıkarılabilir ve çarpılabilirdir.



F, 



normlu uzaydaki tüm Cauchy dizilerinin kümesini

 

F ile gösterelim.



F, 



uzayı değiĢmeli bir halkadır. Bu halkanın toplamaya ve çarpmaya göre sırasıyla birim elemanlarının; 0



0, 0, 0,...



, 1



1,1,1,...



toplamı ve çarpımları birer dizidir.

 

F , Cauchy dizileri kümesinin bir cisim olmadığı açıktır. Çünkü

 

F ’nin



1, 0, 0,... 0,1, 0,...





0 (3.17) (3.17)’de verilen bir sıfır böleni gibi sıfır bölenleri vardır. Her aF için



, , ,...



a  a a a sabit dizisi bir Cauchy dizisidir ve bu dizi

 

F ’dedir. O halde

 

F , F ’ye izomorf olan bir alt halka içerir. Özel olarak P tüm sıfır (null) dizilerinin kümesi olsun. P ,

 

F ’nin bir altkümesidir. O halde P ,

 

F ’de bir idealdir. Yani her p P

ve aF için a p P olan bir alt halkadır. Eğer

 

a_n ve

 

bn P ’de ise



anbn



P.

Eğer

 

an P ve

 

bn dizisi de sınırlı ise



a bn n



P.

 

F  F P olarak alalım. F elemanları



F, 



normlu uzaydaki Cauchy dizilerinin denklik sınıflarıdır. Eğer ele alınan herhangi iki Cauchy dizisinin fark dizisi olan c_n a_n b_n (0, 0, 0,...) dizisi sıfır dizisi ise bu iki Cauchy dizisi birbirine denktir.



, , ,...



farklı denklik sınıflarına aittir.

 

a_n Cauchy dizisinin denklik sınıflarının kümesini

 

 

an ile gösterelim. O halde

 

(an) F dir. BudaFF olduğunu gösterir.

Teorem 3.1.3.1 (Katok 2007) F bir cisimdir.

Ġspat: Eğer

 

an A ve

 

bn B ise o halde A B (anbn) ve A B (a bn n)

Ģeklinde ki toplam ve çarpım dizileri de değiĢmeli birer halkadır. Burada

 

0 toplamaya göre birim eleman ve

 

1 çarpmaya göre birim elemandır. ġimdi F ’nin bir cisim olduğunu ispatlayalım. A , F ’de sıfır denklik sınıfından farklı A P (0) bir denklik sınıfı olmak üzere;

 

a_n A ’da bir Cauchy dizisi olsun.

 

a_n dizisi sıfır dizisinden farklı olduğundan öyle iki tane pozitif c ve pozitif N tamsayısı vardır ki a   c, n N için

 

0, 11 1 ise , ise n n n N a n N a         _  (3.18)

olarak yeni bir

 

a_n dizisi tanımlayalım. Ġddia ediyoruz ki

 

a_n bir Cauchy dizisidir. Eğer her ,n mN ise o zaman 0 _m* _n* 1 1 m n 2 _{m n}

m n m n a a a a c a a a a a a          

olur ve

 

a_n dizisi Cauchy dizisi olduğundan iddia elde edilmiĢ olur.

 

a_n ’ın denklik

sınıfını 1

A ile gösterelim. O halde

 

 

*

N-1 tane

0,..., 0 ,1,1,1,...

n n

a a  _ _

  Cauchy dizisinin sağ

tarafı sıfır dizisinden 1 kadar yani

1 tane ( 1) 1,..., 1, 0, 0, 0,... N          

kadar fark eder. O halde

1

(1)

A A   dir. Buda F ’nin cisim olduğunu ispatlar. ġimdi  normu F ’den F ’ye geniĢleteceğiz.

Tanım 3.1.3.2

 

a_n , A ’da herhangi bir Cauchy dizisi ve  A F olmak üzere lim _n

n

A a



 olur.

Öncelikle buradaki norm iyi tanımlı olup, limitinin varlığını ve A ’daki herhangi bir

 

a_n Cauchy dizisine bağlı olmadığını göstermeliyiz. a_n  a_m  a_na_m

gösterir. Reel sayılar kümesi tam olduğundan tanımlanan lim _n

n a vardır. ġimdi farklı

bir

 

a_n A dizisi alalım. Aynı eĢitsizlikten; 0 lim _{n n} lim _{n n} 0

n a a n a a

 

    

olur. O halde lim _n lim _n

n a n a



 olur.

Önerme 3.1.3.3 (Katok 2007)  , F ’de bir normdur.

Ġspat: Tanım 3.1.2.1’deki üç özelliğin sağlandığını göstermeliyiz.

1) Eğer A

 

0 ise o halde

 

a_n bir sıfır dizisidir. Dolayısıyla A 0 olur. Eğer

 

0

A ve A

 

 

a_n ise o zaman her nN için a_n  c 0 Ģartını sağlayan

c ve N pozitif sayıları vardır. Böylece A 0 dır.

2) A

 

 

a_n ve B

 

 

b_n iki tane dizi kümesi olmak üzere, limitin özelliğinden

lim _{n n} lim _{n n} lim _n lim _n

n n n n

AB a b a b a b A B

   

     elde edilir.

3) Benzer bir yolla;

lim n n lim( n n ) lim n lim n

n n n n

A B a b a b a b A B

   

         elde edilir.

Yani; F ’deki Cauchy ve sıfır dizileri  ’a göre sınırlıdır.

Teorem 3.1.3.4 (Katok 2007)  ’a göre F tamdır ve F , F ’de yoğun bir altkümedir. Önerme 3.1.3.5 (Katok 2007) Eğer lim( n)

n A a   , lim( )_n n B b 

 ise o halde aĢağıdaki; lim( _{n n}) n A B a b     ve lim( _{n n}) n A B a b     olur.

3.1.4 p-adik sayılar cismi ( _p)

Mutlak değer

 

 rasyonel sayılar cismi üzerinde bir normdur. d x y( , ) x y

metriği sayı doğrusu üzerinde iki nokta arasındaki uzaklığı (Öklid mesafesi) ifade eder. Bu norma göre rasyonel sayılar kümesinin tamlanıĢı reel sayılar cismidir. Yani

 dir.

ġimdi kendimize Ģu soruyu soralım: Rasyonel sayılar arasındaki uzaklığı sadece Öklid metriğiyle mi bulabiliriz? Rasyonel sayılar arasındaki uzaklığı bulabilmek için acaba baĢka yol var mıdır? Bu sorunun cevabı bize baĢka bir yolunda varlığını gösterir.

AĢağıda vereceğimiz yeni yapı; rasyonel sayılar arasındaki uzaklığı ölçmenin baĢka bir yolununda olduğunu gösterir. p bir asal sayı olsun.

ord ( ) 0 p x k k k x p x p      _{ } 



 (3.19) ve

'i bölen asal sayısının en yüksek kuvveti,

eğer , , , 0 ise dir

p p p x p x ord x _a x a b b ord a ord b b      _{   }  (3.20)

olarak verilsin. ġimdi (3.19) ve (3.20) ifadelerini kullanarak; eğer 0 ise 0 eğer 0 ise p ord x p p x x x   _      (3.21)

elde ederiz. Bu (3.21) normunu _p:  Ģeklinde bir dönüĢüm olarak tanımlayalım. Bu norma rasyonel sayılar üzerinde p-adik norm denir.

Not 3.1.4.1 Bu norm

 

_p sadece



pn,n





 

0 ayrık değerler kümesinde değer alır.

Not 3.1.4.2 Eğer a b,  ise o halde a b(modpn) a b_p 1_n p

    olur. Çünkü

(mod n)

ab p ise a b  p tn dir. Buradan da _p n 1_n

p

a b p t

p

    elde edilir. Önerme 3.1.4.3 (Katok 2007) Yukarıda tanımlanan

 

_p p-adik norm ’da bir non-ArĢimediyen normdur. Yani; xy_p maks



x_p, y _p



dir.

Ġspat: ord ( )_p x m x p n  ve ord ( )p y s y p t

 birer rasyonel sayı olmak üzere Tanım 3.1.2.1’deki

1. özellik: x_p   0 x 0 olduğu açıktır.

2. özellik: ord (p xy)ord ( ) ord ( )p x  p y olduğundan;

ord ( )p x ord ( )p y ord ( )p x ord ( )p y

p p p p p p m t m t x y p p p p x y n s n s      elde edilir.

3. özellik: Eğer x0 ya da y0 ise 3. özelliğin sağlandığı aĢikardır.

, 0 x y olsun ve x a, y c b d   alalım. O halde x y ad bc bd    ve

ord ( ) ord ( ) ord ( )

min{(ord ( ), ord ( )) ord ( ) ord ( )} min(ord ord , ord ord )

min(ord , ord ) p p p p p p p p p p p p p x y ad bc bd ad bc b d a b c d x y            olur. O halde

ord ( ) ord ord

maks ( , ) maks ( , )

p x y px py

p p p p p

xy  p   p p  x y  x  y olur.

Buda _p normunun güçlü üçgen eşitsizliğini sağladığını gösterir. O halde; _p normu, non-Arşimediyen normdur.

Not 3.1.4.4 Eğer p₁  p₂ birbirinden farklı iki asal sayı ise 1 p  normu, 2 p  normuna

denk değildir. Gerçekten herhangi bir

 

1 2 n n p x p     

  dizisi için xn p10 dır. Fakat 2

n p

x   dur. Yani; n  iken 1 1 1 1 2 0; n n n p n p p x p p     fakat n  iken 2 2 1 2 2 . n n n p n p p x p p

    O halde bu p-adik normlar denk değildir.

ġimdi p p-adik sayılar cismini tanımlayabiliriz. p sabit bir asal sayı olsun. p’yi ’nun (3.21) normuna göre tamlanıĢı olarak tanımlayabiliriz. Tanım 3.1.3.2’ye

göre p -adik norm p’ye geniĢletilebilir; yani  p. Her x p için

: p _p

g x  x ve f x:   f x( ) olmak üzere eğer ( )g x  f x( ) ise g ’ye f ’nin

p’ye geniĢlemesi denir.



p,p



p-adik norm uzayı tamdır. p’ye p -adik sayılar

cismi denir. _p’nin elemanları p -adik normun geniĢlemesine göre ’daki Cauchy dizilerinin denklik sınıflarıdır. Daha önce ifade edildiği gibi rasyonel sayılar ( ) sabit Cauchy dizilerinin denklik sınıflarından oluĢan _p p-adik sayılar cisminin bir alt cismi olarak tanımlanabilir.

p

a için

 

a_n dizisi a ile gösterilen rasyonel sayıların sabit bir Cauchy dizisi olsun. O halde tanıma göre n

n n k

a a p

 





olarak yazıldığı için lim _n

p _n p

a a



 (3.22) olur. ’daki değerler ile _p’de aynı değerleri alan

 

p

kümesi yani



pn,n





 

0 Öklid metriği ile yeterince farklı bir durum oluĢturur.

p

 normları ’dan ’ye geniĢletildiğinde tüm negatif değerleri alabilir. AĢağıdaki seriyi ele alalım.   i m için 0< d_m p ve 0 d_i p olmak üzere

2 1 0 1 2 1 ... ... k m m k m m k m d d d d p d p d p p p             



(3.23) serisinin kısmi toplamları bir Cauchy dizisi oluĢturur. Çünkü her 0 olmak üzere öyle bir N seçebiliriz ki N p  ve k  n N için 1 maks( ) k n k i i i i N i i i i _p n i k m m p n p d p d p d p d p p          







(3.24)

olur. O halde (3.23)’te verilen her bir seri, _p’nin bir elemanını tanımlar. Bu durumun tersi de doğrudur. ġimdi ’daki Cauchy dizilerinin her bir denklik sınıfının kanonik formunun tek olduğunu gösterelim.

Bu kanonik formun inĢası için aĢağıdaki lemmayı vermemiz gerekmektedir. Lemma 3.1.4.5 (Katok 2007) 



0,1, 2,...,pi1



olmak üzere, eğer x ve x_p 1

ise o halde her bir i için i p

x p

_{ } 

olacak Ģekilde sadece ve sadece birtek  vardır.

Ġspat: x a b

 olsun öyleki

 

a b, 1 dir. x_p 1 olduğundan p , b’yi bölmez ve b ile

i

p birbirine göre asaldır. O halde m ve n gibi iki tane tamsayı bulabiliriz ki 1 (mod )

i

mb np  p olur.   a m olsun. O halde; 1 1 p p p p i i i p p p a a x am mb b b mb np n p p             

olur. Son olarak i

p

x p

_{ } 

olmak üzere 0 ile p arasında bir tam sayı elde etmek i için güçlü üçgen eĢitsizliğini kullanarak  tamsayısına p ’nin herhangi bir katını i ekleyebiliriz ve hala x_p  pi eĢitsizliği sağlanır.

Örnek: 10 21

x ve p5 olsun.



10, 21



1 dir. Buradan 1

5 5 10 2 5 5 1 21 21     

olduğundan



5, 21



1. m1 ve n1 alırsak 1 21 1 5 1 (mod 5)    olur. O halde 5 1 0(mod 5)