T.C.
SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
ÖZEL CEBİRSEL GRAFLAR
AYŞE JÜLİDE AKZEYBEK
YÜKSEK LİSANS TEZİ
MATEMATİK Anabilim Dalı
Kasım-2013 KONYA Her Hakkı Saklıdır
II
TEZ BİLDİRİMİ
Bu tezdeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.
DECLARATION PAGE
I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.
AYŞE JÜLİDE AKZEYBEK
III ÖZET
YÜKSEK LİSANS TEZİ ÖZEL CEBİRSEL GRAFLAR
AYŞE JÜLİDE AKZEYBEK
Selçuk Üniversitesi Fen Bilimleri Enstitüsü MATEMATİK Anabilim Dalı
Danışman: Prof. Dr. Ahmet Sinan ÇEVİK 2013, 58 Sayfa
Jüri
Prof. Dr. Ahmet Sinan ÇEVİK
Doç. Dr. A. Dilek MADEN (GÜNGÖR) Yrd. Doç. Dr. Eylem GÜZEL KARPUZ
Bu çalışmada grup, monoid, yarı grup, serbest çarpım ve direkt çarpım sunuşları genel anlamıyla verilmiştir. Bu sunuşları kullanarak tezin temel konusu olan Gröbner-Shirshov tabanı kullanarak oluşturulan grafların şekilleri çizilip grafların parametre değerleri hesaplanmıştır.
Bu tez üç bölümden oluşmaktadır.
Birinci bölümde, tez çalışmasının sonraki bölümlerinde kullanılacak olan grup, monoid, yarı grup, serbest ve direkt çarpım yapılarının genel sunuşları verilmiştir. Bir metot olan yeniden yazma sistemi üzerinde sunuşu verilen cebirsel yapıların tam olma durumu incelenmiştir. Ayrıca grafların temel tanım ve özellikleri verilmiştir.
İkinci bölümde, bir metot olarak kullanılan Gröbner-Shirshov tabanı incelenmiştir. Birinci bölümde bahsedilen yeniden yazma sistemi ile Gröbner-Shirshov tabanı karşılaştırılmıştır. Bunun üzerine sunuşu verilen monoid ve grup yapılarının tabanları incelenmiştir.
Üçüncü bölümde, Gröbner-Shirshov taban özelliği kullanılarak oluşturulan yeni graf tanımı verilmiştir. Bu graf tanımının şekli çizilip graf parametre değerleri hesaplanmıştır.
Anahtar Kelimeler: Grup, monoid, sunuş, serbest çarpım, direkt çarpım,
IV
ABSTRACT
MS THESIS
SPECIAL TYPE OF ALGEBRAIC GRAPHS
AYŞE JÜLİDE AKZEYBEK
THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELÇUK UNIVERSITY
THE DEGREE OF MASTER OF SCIENCE IN MATHEMATICS
Advisor: Prof. Dr. Ahmet Sinan ÇEVİK 2013, 58 Pages
Jury
Advisor Prof. Dr. Ahmet Sinan ÇEVİK Assoc. Prof. Dr. A. Dilek MADEN (GÜNGÖR) Assist. Prof. Dr. Eylem GÜZEL KARPUZ
In this work, each of the presentation of groups, monoids, semigroups, free and direct products has been given. Also, by using these presentations, graphs constructed by Gröbner-Shirshov base have been defined and then calculated some parameters of these graphs.
This thesis consists of three chapters.
In the first chapter, the general presentations of group, monoid, semigroup, free and direct products have been presented which will be used for the remaining chapters of this thesis. Also, on the presentation of given algebraic structure has been investigated whether or not completeness property holds by using rewriting system. After that, the main definition and characteristic of graphs have been given.
In the second chapter, it has been studied a method (Gröbner-Shirshov bases) which searches roughly reducible monomials of relations. Moreover, it searches the correspondence between terminology in systems and bases.
In the third cahapter, new graph definition has been given by using Gröbner-Shirshov bases. Besides, by drawing graphs, some spectral parameters have been calculated.
Keywords: Group, monoid, presentation, free product, direct product, rewriting
V ÖNSÖZ
Tezimi hazırlamakla geçirdiğim çalışma sürecinde beni deneyim ve bilgileriyle yönlendiren, değerli zamanını ayırıp ilgisini esirgemeyen değerli hocam ve danışmanım Prof. Dr. Ahmet Sinan ÇEVİK’ e en içten teşekkürlerimi sunarım.
Tezimde ve yaptığımız çalışmalarda benimle bilgilerini paylaşan Yrd. Doç. Dr. Eylem KARPUZ’a ve öğrenim hayatım boyunca emeği geçen tüm hocalarıma teşekkür ederim.
Yaşamımın her anında maddi ve manevi olarak beni destekleyen, beni bugünlere getiren sevgili annem, babam ve bu süreçteki sıkıntılı günlerimin vazgeçilmez dostu canım kardeşime teşekkürlerle…
KONYA-2013 AYŞE JÜLİDE AKZEYBEK
VI ÖZET ... iii ABSTRACT ... iv ÖNSÖZ ... v İÇİNDEKİLER ... vi SİMGELER ... viii ŞEKİL LİSTESİ ... x
ÇİZELGE LİSTESİ ...xi
1. TEMEL BİLGİLER ... 1 1.1 Giriş ... 1 1.2 Serbest Grup ... 2 1.3 Sunuşlar ... 4 1.3.1 Grup Sunuşları ... 4 1.3.2 Monoid Sunuşları ... 6
1.3.3 Yarı Grup Sunuşlar ... 7
1.3.4 Serbest Çarpım Sunuşları ... 8
1.3.5 Direkt Çarpım Sunuşları... 9
1.4 Yeniden Yazma Sistemi ... 10
1.4.1 Pozitif Yeniden Yazma Sistemine Giriş ... 11
1.4.2 Bir [X;R] Sunuşu için Yeniden Yazma Sisteminin Tam Olduğunun gösterilmesi ... 13
1.4.3 Knuth-Bendix Algoritması ... 17
1.5 Temel Graf Bilgileri ... 19
2. ÖZEL AFİN WEYL GRUPLARI ÜZERİNDEKİ GRÖBNER-SHİRSHOV TABANI ... 21
2.1 Afin Weyl Grup için Yeniden Yazma Sistemi ile Değişmeli Olmayan Gröbner-Shirshov Tabanının Karşılaştırılması ... 27
3. GRUPLAR ÜZERİNDE GRÖBNER-SHİRSHOV TABANI KULLANILARAK OLUŞTURULAN GRAF TABANI ... 36
3.1 İki Üreteçli Çarpım Grupları ... 37
VII
3.1.2 İki Üreteçli Direkt Çarpım Grupları ... 39
3.2 Üç Üreteçli Çarpım Grupları ... 42
3.2.1 Üç Üreteçli Serbest Çapım Grupları ... 42
3.2.2 Üç Üreteçli Serbest-Direkt Çarpım Grupları ... 43
3.2.3 Üç Üreteçli Direkt-Serbest Çarpım Grupları ... 45
3.3 Dört Üreteçli Çarpım Grupları ... 47
3.3.1 Dört Üreteçli Serbest Çarpım Grupları ... 47
3.3.2 Dört Üreteçli Serbest-Direkt-Serbest Çarpım Grupları ... 48
3.4 Gröbner-Shirshov Tabanlı Grafın Genel Grafının Çizilip Tanımlanması ... 51
4. SONUÇ ve DEĞERLENDİRME ... 54
5.KAYNAKLAR ... 55
ÖZGEÇMİŞ... 58
VIII SİMGELER VE KISALTMALAR
Simgeler Açıklamalar
( ) kelimesinin başlangıç harfi ( ) kelimesinin bitiş harfi 1 boş kelime
( ) kelimesinin uzunluğu
( ) kelimesindeki herhangi bir harfinin uzunluğu ≈ serbest olarak iki kelimenin eşitliği
[ ] kelimesinin denklik sınıfı
( ) kümesi üzerindeki serbest (free) grup
| | kümesinin eleman sayısı
℘ grup sunuşu
≈℘ ve kelimeleri ℘ bağlı olarak denktir
[ ]℘ ℘ sunuşuna bağlı olarak kelimesindeki denklik sınıfları [1]℘ ℘ sunuşuna bağlı grubun birimi
(℘) ℘ sunuşun temsil ettiği grup normal kapanış
ℤ mertebeli sonlu devirli grup
∗ ve iki grup olmak üzere, iki grubun serbest çarpımı × ve iki grup olmak üzere, iki grubun direkt çarpımı □ ispatın sonuna eklenir
↔∗ tarafından üretilen Thue kongrüanstır ̅ nin başlangıç kelimesi
yi içeren Gröbner-Shirshov tabanı
∗ kümesinin serbest çarpımından elde edilen kelimelerin
kümesidir
IX
Γ(V( )) grubunun, Γ grafının köşe kümesi Γ(E( )) grubunun, Γ grafının kenar kümesi
deg ( ) köşe derecesi
( , ) ve köşelerinin birbirine uzaklığı ( ) dışmerkezlilik
Δ( ) grubunun grafının maksimum köşe derecesi ( ) grubunun grafının minimum köşe derecesi
( ) grubunun grafının çapı ( ) grubunun grafının yarıçapı
ℎ( ) grubunun grafının girth sayısı
( ) grubunun grafınınkromatik sayısı ( ) grubunun grafının klik sayısı
( ) derece sıralanması ( ) düzensizlik indeksi ( ) baskınlık sayısı
X ŞEKİL LİSTESİ
Şekil Numarası Şekil Adı Sayfa
Şekil 3.1 Γ( ) grafı 38 Şekil 3.2 Γ( ) grafı 40 Şekil 3.3 Γ( ) grafı 43 Şekil 3.4 Γ( ) grafı 44 Şekil 3.5 Γ( ) grafı 46 Şekil 3.6 Γ( ) grafı 48 Şekil 3.7 Γ( ) grafı 49 Şekil 3.8 Γ( ) grafı 51
XI ÇİZELGE LİSTESİ
Çizelge Numarası Çizelge Adı
Çizelge 2.1 Yeniden yazma sistemi ile Gröbner-Shirshov taban terimlerinin karşılaştırılması
1. TEMEL BİLGİLER
1.1 GİRİŞ
Bu tezin birinci bölümünde, tezimiz için genel anlamda gerekli olan bazı yapılar tanıtılarak, bunların tezde nasıl uygulanacağı vurgulanmıştır.
İncelenen materyaller anlamında en temel öğe serbest gruplar olup, bu özel grup yapısı grup sunuşları, yeniden yazma sistemi ve dolayısıyla Gröbner-Shirshov tabanı hakkındaki konuları ve sonuçları kavrayabilmek için, bilinmesi gereken kavramdır. Bununla birlikte, yine tezimiz içinde verilen sonuçlar ile doğrudan ilişkili olacak ve yine sonuçları örneklendirecek diğer önemli bir yapı ise graf teori olacağından, ayrı bir alt bölüm olarak bu matematiksel kavrama da birinci bölüm içerisinde değinilecektir. Tezimizin son bölümünde, Gröbner-Shirshov tabanının tanımı ve özelliğinden oluşturulan, yeni bir graf üzerinde çalışılmıştır. Aslında graf teorinin ilk temelleri ünlü matematikçi Leonhard Euler (1707-1783) tarafından atılmıştır. Euler, Köningsberg şehrini iki adaya ve iki kara parçasına ayıran Pregel nehrinin üzerine kurulan yedi köprünün, herhangi bir köprüden yola çıkarak ve her bir köprüden yalnız bir kez geçerek tüm şehri dolaşabilmenin mümkün olmadığını, grafla modelleme yaparak ispatlamıştır. Daha sonra birçok matematikçinin yaptığı çalışmalarla, graf teori günlük hayatta karşılaşılan problemlere uygulanmıştır. Ancak biz burada spektral graf ile cebir bilgilerimizi birleştirerek, tarafımızdan genel bir graf elde edip grafın parametrelerini hesaplama işlemi ile ilgileneceğiz. Kısaca, sunuşu verilen bir yarı grubun, monoidin ya da grubun, verilen yeni graf tanımına göre grafının çizilmesi ve bu grafın, maksimum ve minimum dereceleri, çap ve yarıçap sayıları, girth, kromatik, klik sayıları, derece
sıralaması (DS), düzensizlik indeksi ve baskınlık sayısı olan parametrelerinin hesaplanmasından oluşmaktadır.
Bu bölüm içerisinde kullanılan temel kavramlar için (Book,1987), (Cohen, 1998), (Lyndon,1977), (Rotman,1988), (Haynes,1998), (Henning, 2000), (Gross, 2004) gibi kaynaklara bakılabilir.
1.2 Serbest Grup
X boş olmayan bir küme olsun. Bu küme ile ⟷ ( ∈ ) eşlemesinden
yararlanarak kümesini tanımlayalım ve ± = ∪ olsun. Burada ±
kümesinin her bir elemanına harf adı verilir. Ayrıca ∈ ℕ, ∈ , = ±1 ve 1 ≤ ≤ olmak üzere,
… (1.1) ifadesine üzerinde bir kelime denir ve ile gösterilir. kelimesinin başlangıç harfi
( ) ile gösterilip, burada ( ) = dir. Benzer şekilde bitiş harfi ( ) ile gösterilip, (1.1) deki kelimenin bitiş harfi ( )= dir. Özel olarak = 0 ise boş kelime elde edilir ve ile gösterilir. (1.1) deki gibi boş olmayan bir kelime ( > 0) için her = +1 oluyorsa kelimesine pozitif kelime denir. Ayrıca (1.1) deki kelimesinin
tersi … kelimesi olarak tanımlanır ve olarak gösterilir.
(1.1) de verilen kelimesinin uzunluğu, içindeki harflerin sayısı olarak tanımlanır, ayrıca kelimesindeki herhangi bir harfinin uzunluğu da ∑ | | olarak hesaplanır ve bunlar sırasıyla ( ) veya ( ) ile gösterilir.
kümesi üzerinde verilen iki kelime ve olsun. ve kelimelerinin çarpımını, kelimesinin arkasına kelimesini getirip yan yana yazarak elde ederiz ve bu çarpım ile ifade edilir. Verilen bu çarpım altında kelimeler üzerinde aşağıdaki şekilde işlemler tanımlanabilir.
( ) = ±1 olmak üzere, herhangi bir kelime içinde çiftleri varsa, bu çiftler silinir. Yapılan bu işleme indirgeme işlemi denir.
( ) = ±1 olmak üzere, herhangi bir kelimeye şeklindeki ters harf çiftleri eklenebilir. Bu işleme de kelime üzerinde ekleme işlemi denir.
kümesi üzerindeki iki kelime ve olsun. Eğer bu kelimelerden biri diğerine yukarıdaki ( ) ve ( ) işlemlerinin sonlu sayıdaki uygulamasıyla elde ediliyorsa, bu iki kelimeye serbest olarak eşit denir ve bu ≈ ile gösterilir. Aslında ≈ olarak gösterilen serbest olarak eşitlik, bir denklik bağıntısıdır. Dolayısıyla herhangi bir kelimesini içeren serbest denklik sınıfı [ ] ile gösterilir. Eğer kümesi üzerindeki tüm kelimelerin serbest denklik sınıflarının kümesi ( ) ile gösterirsek,
( ) üzerindeki çarpma işlemi
[ ][ ]= [ ] (1.2) olarak tanımlanır ve bu çarpma işlemi iyi tanımlıdır. Bu çarpma işlemi altında ( ) bir grup oluşturur ve oluşan bu gruba kümesi üzerindeki serbest grup denir.
kümesi üzerinde alınan , ve kelimeleri için = eşitliği varsa bu durumda kelimesine kelimesinin alt kelimesi denir. kümesi üzerindeki bir kelime ( ∈ , = ±1) harf çiftini içermiyorsa bu kelimeye indirgenmiş
kelime denir.
Aşağıdaki sonuç, grup sunuşlarının oluşturulmasında önemli bir yer teşkil etmektedir.
Teorem 1.2.1 (Normal Form Teoremi) (Cohen, 1989): Her bir denklik sınıfı tek bir
indirgenmiş kelime içerir.
Teorem 1.2.2 (Evrensel Dönüşüm Özelliği) (Cohen, 1989 ve Johnson, 1990):
herhangi bir grup ve : → bir dönüşüm olsun. Bu durumda
: ( ) →
biçiminde tanımlanan ve dönüşümünün genişlemesi olan bir tek grup
homomorfizması vardır.
1.3 Sunuşlar
Birleştirilmiş grup ve yarı grup teoride önemli bir yere sahip olan sunuşlar, birçok cebirsel problemin çözümünde kolaylık sağlamaktadır. Tezin bu alt bölümünde diğer bölümlere hazırlık sağlaması açısından öncelikle grup, monoid, yarı grup, serbest çarpım ve direkt çarpım sunuşları verilecektir.
1.3.1. Grup Sunuşları
Tanım 1.3.1.1: bir küme ve Υ, kümesi üzerindeki kelimelerin bir kümesi olsun. Bu durumda;
℘ =< ; >
ikilisine grup sunuşu denir. Burada e üreteç, Υ e de bağıntı kümesi denir.
Bu ℘ sunuşunda verilen kümesinin kelimeleri üzerinde, 1.2 Bölüm’de ( ) ve ( ) maddeleri olarak verdiğimiz ekleme ve sadeleştirme işlemlerine ilave olarak aşağıdaki işlemleri de kullanarak bir grup tanımlayabiliriz. Bu işlemler için kümesi
üzerinde bir kelime, ∈ ℕ, ∈ , = ±1 ve 1 ≤ ≤ olmak üzere,
= …
olsun.
(i) kelimesi, ( ∈ , = ±1) şeklinde bir alt kelime içeriyorsa bu alt kelimeyi sileriz.
(ii) kelimesi içinde herhangi bir yere ( ∈ , = ±1) alt kelimesini ekleriz.
kümesi üzerinde herhangi iki kelime ve olsun. Eğer kelimesinden
kelimesini elde etmeyi sağlayan yukarıdaki (i) ve (ii) deki işlemlerin sonlu bir zinciri var ise ve kelimelerine ℘ sunuşuna bağlı olarak denk kelimeler denir ve bu denklik
~℘
ile gösterilir. Buradaki ′′~℘ ′′ bağıntısı kümesindeki bütün kelimelerin kümesi
üzerinde bir denklik bağıntısıdır. kelimesini içeren denklik sınıfını [ ]℘ ile gösterelim. Bu denklik sınıfı üzerindeki çarpma işlemi;
[ ]℘[ ]℘= [ ]℘
biçiminde tanımlanır. Bu çarpma işlemi altında tüm denklik sınıflarının kümesi bir grup olur ve (℘) ile gösterilir.
Eğer herhangi bir grubu için, ≅ (℘) ise grubu ℘ ile sunuluyor ya da tanımlanıyor denir.
Sonuç 1.3.1.2: (i) (℘) grubunun yapısı ( ) serbest grubunun yapısındadır.
(ii) Her ∈ için [ ] ∈ (℘) ve aynı zamanda [ ] ∈ ( ) dir. Ayrıca kümesi, {[ ]: ∈ } normal kapanış kümesi olmak üzere aşağıdaki teorem elde edilir.
Teorem 1.3.1.3: (℘) ≅ ( ) .
İspat: ℘ sunuşu ile tanımlanan (℘) grubu ve kümesi için,
: → (℘) öyle ki ( ) = [ ]℘
dönüşümü tanımlayalım. Bu dönüşümün iyi tanımlı olduğunu gösterelim:
, ∈ ve = olsun. Bu durumda [ ]℘= [ ]℘ yani ( ) = ( )
olduğundan iyi tanımlıdır.
Teorem 1.2.2’deki Evrensel Dönüşüm özelliğinden , : ( ) → (℘) öyle ki [ ] = [ ]℘
homomorfizması vardır. , ∈ ve [ ] = [ ] olsun. O zaman,
[ ]℘ = [ ]℘ ise =
olduğundan birebirdir.
Sonuç 1.3.1.2 yardımıyla nin örten olduğu açıktır. O halde bir
izomorfizmadır. Ayrıca,
ç = { ∈ ( ): [ ] = 1 (℘)}
ve [ ] = [ ]℘= 1 (℘) olduğundan,
ç =
dir. Böylece Birinci İzomorfizma Teoremine göre,
(℘) ≅ ( )
olur. □
Uyarı 1.3.1.4: Teorem 1.3.1.3’e göre, ∈ olmak üzere, [ ] elemanlarının ( ) grubunu ürettiği gerçeğinden, [ ]℘ = [ ] yazarak, [ ]℘ nin (℘) yi ürettiği sonucu elde edilir.
℘ =< ; > sunuşu bir grubunu temsil etsin. Eğer ve kümelerinin her ikisi de sonlu sayıda eleman içeriyorsa, ye sonlu sunuşludur denir.
Teorem 1.3.1.5: Her grup sunuşa sahiptir ve her sonlu grubun sunuşu da sonludur.
Serbest grupların sunuşu sonlu olduğu halde, kendileri sonsuz mertebelidir. Diğer bir deyişle, herhangi bir kümesi üzerinde tanımlı serbest grubun sunuşu
℘=< ; > şeklindedir. Doğal olarak, tek bir elemanı tarafından üretilen sonsuz mertebeli devirli grubun sunuşu ℘=< ; > şeklindedir.
Örnek 1.3.1.6: ℤ kümesi ′′ + ′′ işlemine göre 1 sayısı (elemanı) tarafından üretilen sonsuz mertebeli devirli grup olduğundan, (ℤ, +) grubu, aslında boyutu (rankı) 1 olan serbest gruptur.
1.3.2 Monoid Sunuşları
bir monoid ve da bu monoidin üreteç kümesi olmak üzere kümesi kümesindeki elemanlarla oluşturulan en az bir uzunluklu kelimelerin kümesi olmak üzere, monoidler için tanımlanan kelimeler
∗ = ∪ {1}
kümesinden alınır.
Tanım 1.3.2.1: boştan farklı bir küme (üreteç kümesi) ve ⊆ ∗× ∗ olacak şekilde
bir alt kümesi olsun. Bu durumda bağıntı kelimelerinin kümesi olarak adlandırılıp, ℘ =< ; >
ikilisine bir monoid sunuşu denir. Gruplarda olduğu gibi ve kümelerinin her ikisi de sonlu ise ℘ sunuşu da sonludur.
Aşağıdaki verilecek teoremde ve bir sonraki alt bölümde değinilecek yarı grup sunuşlarında oldukça önemli bir yer tutan ‘kongrüans’ terimi aşağıdaki şekilde açıklanabilir:
bir monoid ( bir yarı grup) ve , üzerindeki (veya ) bir denklik
bağıntısı olsun. Her , , ∈ (veya ) için , ∈ ⇒ ( , ) ∈ oluyorsa
bağıntısına bir sağ kongrüans bağıntısı denir. Benzer olarak, her , , ∈ için, , ∈ ⇒ ( , ) ∈ oluyor ise bu bağıntısına bir sol kongrüans bağıntısı denir. Eğer bağıntısı hem sağ hem de sol kongrüans oluyor ise bu bağıntısına kongrüans
bağıntısı denir. Başka bir şekilde, her = 1,2 ve alınacak her ( , ) ∈ ikilisi için,
şartı sağlanıyorsa bağıntısına kongrüans bağıntısı denir.
Teorem 1.3.2.2: bir monoid, da için bir üreteç kümesi ve , ∗ kümesi üzerinde bağıntı kümesini içeren en küçük kongrüans olsun. Bu durumda
≅ ∗
dir.
Teorem 1.3.2.2 nin ispatı, Teorem 1.3.1.3 ün ispatına benzer olarak yapılabilir.
1.3.3 Yarı Grup Sunuşları
Yarı gruplar ve bunların sunuşları, grup ve monoid cebirsel yapılarına göre çalışılması daha zor yapılardır. Yarı grup sunuşlarında genel olarak iki tip problem vardır. Birincisi verilen bir yarı grubun sunuşunu bulmak, diğeri ise verilen bir sunuş tarafından temsil edilen yarı grubu bulmaktır. Bu yarı grubun belirlenmesinden sonra bu yarı grubun birçok cebirsel özelliğe sahip olup olmaması da yarı grup teoride çalışılan önemli bir konudur.
boştan farklı bir küme (üreteç kümesi) ve ⊆ × kümesi, , ∈ için ( , ) ∈ (ki bu genellikle = şeklinde gösterilir) elemanlarından oluşan bir
bağıntı kümesi olsun. Bu durumda = { , , … , } ve = { = , … , = }
için,
℘ = [ ; ] = [ , … , ; = , … , = ]
ikilisine bir yarı grup sunuşu denilir. Eğer kümesi sonlu ise, ℘ sunuşunun temsil ettiği yarı grup sonlu üreteçlidir. ve kümelerinin her ikisi de sonlu ise ℘ sunuşunun temsil ettiği yarı gruba sonlu sunumludur denir.
℘ = [ ; ] bir yarı grup sunuşu ve , ∈ olsun. Eğer , ∈ ve
( , ) ∈ (ya da ( , ) ∈ ) için = ve = oluyorsa, kelimesi
kelimesinden elde ediliyor denir. Ayrıca ve kelimeleri arasında, , , … , ∈
olmak üzere, = , , … , = şeklinde sonlu bir dizi varsa (ki burada her bir , den bağıntısı ile elde edilir), = bağıntısı bağıntısının (veya alternatif olarak ℘ sunuşunun ) bir sonucudur denir.
Herhangi bir kelimesinin ℘ sunuşuna bağlı olarak denklik sınıfı [ ]℘ biçimindedir.
Teorem 1.3.3.1: bir yarı grup, kümesi kümesi için bir üreteç kümesi ve ,
≅
dir.
Teorem 1.3.3.3 ün ispatı, Teorem 1.3.1.3 ün ispatına benzer olarak yapılabilir.
Teorem 1.3.3.2: ℘ = [ ; ] bir yarı grup sunuşu ve ≅ ise bu sunuşun temsil ettiği yarı grup olsun. , ∈ için, = bağıntısının içinde sağlanması için gerek ve yeter koşul onun ℘ in bir sonucu olmasıdır.
Örnek 1.3.3.3: [ ; = ] sunuşunun temsil ettiği yarı grup { } ile üretilen tekil yarı gruptur.
1.3.4 Serbest Çarpım Grubunun Sunuşu
Birleştirilmiş Grup teori konusunun temeli serbest gruplara dayanmaktadır. Biçim ve özellik olarak da serbest gruplara en yakın gruplar, alınacak herhangi iki grubun serbest çarpımıdır. Çünkü bir serbest grup, sonsuz devirli grupların serbest çarpımıdır (Rotman, 1988). Son bölümde serbest çarpım yine karşımıza çıkacaktır. Bu yüzden aşağıdaki teoremlerle serbest çarpım grubunu kısaca inceleyeceğiz.
Tanım 1.3.4.1: Sırasıyla < ℎ , … , ℎ ; , … , > ve < , … , ; , … , > sunuşlarının temsil ettiği ve grupları için,
℘ ∗ =< ℎ , … , ℎ , , … , ; , … , , , … , >
sunuşunun temsil ettiği = ∗ grubuna, ve gruplarının serbest çarpımı denir. Buradaki ve gruplarına ise grubunun çarpanları denir. Ayrıca grubunun üreteçleri, ve nın üreteçlerinden, bağıntıları ise bu grupların bağıntılarının ayrık birleşiminden oluşur.
Örnek 1.3.4.2: < , ; , > sunuşunun temsil ettiği grup, aslında bir elemanı ile üretilen 3 mertebeli devirli grup ile yine bir elemanıyla üretilen 4 mertebeli devirli grubun serbest çarpımıdır.
= ∗ olmak üzere, ℎ ∈ ve ∈ ( = 1, 2, … , ) için
ℎ … ℎ ∈ formundaki elemana grubunda bir kelime denir. Ayrıca bu
şekildeki bir ifade de her bir ℎ ≠ 1 ve ≠ 1 oluyorsa, bu kelimeye indirgenmiş
kelime denir.
Teorem 1.3.4.3 (Normal Form Teoremi) (Miller III): ∗ serbest çarpımının her
Buradaki teklik ifadesiyle serbest çarpım grubundan alınan ℎ … ℎ ve ℎ ′ ′ … ℎ ′ ′ ∈ biçimindeki herhangi iki kelime için,
ℎ … ℎ = ℎ ′ ′ … ℎ ′ ′
oluyorsa, = ve her ℎ , ℎ′ ∈ , , ′ ∈ için ℎ = ℎ′ ve = ′ olma durumu kastedilmektedir.
Teorem 1.3.4.4 (Serbest Çarpımların Karakterizasyonu) (Miller III): G grubunun
ve alt gruplarının serbest çarpım olması için gerekli ve yeterli koşul aşağıdaki iki şartın sağlanmasıdır.
(i) ve alt grupları grubunu üretir, dolayısıyla nin her elemanı
ℎ … ℎ formundadır .
(ii) = ℎ … ℎ ve = 1 ise ℎ = 1 ya da = 1 dır.
Tanım 1.3.4.1 de belirtildiği gibi bir serbest çarpım grubunun sunuşunun bağıntı kümesinde, bu serbest çarpım grubunun her iki çarpanının da üreteç elemanlarıyla oluşturulan bağıntı bulunmaz.
1.3.5 Direkt Çarpım Grubunun Sunuşu
ve gibi herhangi iki grup verilsin. ve grupları üzerindeki işlemler yardımıyla = × direkt çarpım kümesi üzerinde yeni bir işlem tanımlayarak, kümesinin bu işlem altında bir grup olduğunu söyleyip bu grubun sunuşunu vereceğiz.
ve çarpma işlemi altında tanımlı iki grup olsun. ( , ), ( ′, ′) ∈ herhangi iki eleman ise, bunların çarpımını
( , )( ′, ′) = ( ′, ′) (1.3)
( , ′ ∈ , , ′ ∈ ) olarak tanımlayalım. Bu çarpımdaki ′ bileşeni grubundaki işleme göre, ′ bileşeni grubundaki işleme göre hesaplanmıştır.
kümesi (1.3) ile tanımlanan işleme göre bir gruptur. Bu gruba ve gruplarının direkt çarpım grubu denir ve × ile gösterilir. ve gruplarının her ikisinin de değişmeli olması halinde grubunun da değişmeli olacağı açıktır. Sonuç olarak direkt çarpımdan dolayı
| | = | || | şeklindedir.
Teorem 1.3.5.1 (Johnson, 1990): ve grupları sırasıyla
sunuşlarıyla verilsin. ∩ = ∅ olmak üzere, ve gruplarının direkt çarpımı olan
= × grubunun sunuşu
℘ =< , ; , , >
şeklinde tanımlanır. Burada bağıntı kümesi {[ , ] = : ∈ , ∈ } olarak
tanımlanır.
Örnek 1.3.5.2: Teorem 1.3.5.1 e göre, ℤ × ℤ direkt çarpım grubunun sunuşu ℤ =< ; > ve ℤ =< ; >
olmak üzere,
ℤ × ℤ =< , ; , , [ , ] > biçiminde elde edilir.
1.4 Yeniden Yazma (Rewriting) Sistemi
Bir metot olarak yeniden yazma sisteminin kullanım alanları, sembolik cebir, otomata teori, yüksek seviye program dilleri, program verileri ve yapay zeka şeklinde özetlenebilir. Yani bu yapı her ne kadar matematiğin cebirsel kısmında çalışılan bir konu olsa da anlamı aynı, fakat dili farklı olan değişik başlıklar altında örnek verdiğimiz gibi birçok bilim dalında da bulunmaktadır. Bize genel olarak, eşitlikler verildiğinde eşitlikleri türeterek onların sonuçlarını verilen çeşitli denklemleri sağlaması için kullanacağız. Aslında bize verilen sistemi belli kurallar çerçevesinde başka yapılara dönüştüreceğiz, yani bize verileni yeniden yazacağız. Bu yüzden, yeniden yazma uygun denklemler kullanıldığında çok güçlü bir metottur.
Yönlendirilmiş (sırası belirlenmiş) denklemlere yeniden yazma kuralları adı verilir. Verilen eşitlikler sırası belirlendikten sonra eşitliğin karşısındaki denklem yerine kullanılır. Yeniden yazma teorisinin merkezi normal form çevresindedir. Hesaplama, yeniden yazmanın normal formunu içerir. Yeniden yazmaya eşit konular her zaman aynı normal formu oluşturduğunda kurallar kümesine tam (convergent, complete) denilebilir ve denklik kontrolü için kullanılabilir.
Yeniden yazma sisteminin birçok çeşidi bulunmaktadır. Bunlar; pozitif (string)
yeniden yazma, konu (term) yeniden yazma, graf (graph) yeniden yazma, durum (conditional) yeniden yazma sistemleri, ...vb. Biz bunlardan sadece pozitif yeniden
1.4.1 Pozitif (String) Yeniden Yazma Sistemine Giriş
Yeniden yazma sistemi, özellikle monoid ve yarı grupların sunuşundaki kelimelerin (bağıntıların) indirgenir olup olmadığını öğrenmek için temel bir metottur. Ayrıca ikinci bölümde benzer bir metot olan Gröbner-Shirshov tabanı ile karşılaştırma yapabilmemizi sağlaması için önemli bir metottur. Monoid ve yarı grup yapıları gruplara göre biraz daha genel oldukları için bu cebirsel yapılar üzerinde tanımlanacak kelimenin (bağıntının) indirgenir olabilmesi ve gruplara göre başka özelliklerin de aranmasını gerektirmektedir. Örneğin, gruplarda elemanların temsilci kümesini (aslında, her bir denklik sınıfı tek bir indirgenmiş kelime içerdiğinden bu temsilci kümesindeki elemanlar indirgenmiş kelimelerdir) oluşturarak verilen bir kelimenin bu kümedeki grubun birimine eşit olup olmadığı araştırılıyordu. Ancak monoidlerde, bu temsilci kümesini oluşturabilmek için verilen bir kelimenin indirgendiği tek bir kelime bulmamız gerekmektedir. Şimdi de bunları daha ayrıntılı inceleyebilmek için temel tanımları verelim.
Sonlu bir alfabesi için, ∗ bu alfabedeki harflerden oluşan bütün kelimelerin kümesi ve boş kelime olsun. üzerinde ki yeniden yazma kuralı aslında ( , ) ∈ ∗×
∗ şeklindeki sıralı çiftlerdir. Bu kural ( → ) biçiminde gösterilir. Buradaki kelimesi
sol yan (left hand side), kelimesi ise sağ yan (right hand side) diye adlandırılır.
Yeniden yazma sistemi üzerindeki yeniden yazma kurallarının bir kümesidir ve bu sistem ile gösterilir. ∗ kümesindeki kelimeler arasındaki bu bağıntı
(→ ) (1.4) için aşağıdaki kural tanımlanır:
üzerinde ki pozitif kelimeler (string) ve olmak üzere, → olması için gerek ve yeter koşul
, ∈ ∗ ve ( → ) ∈ için = ve =
olmasıdır.
Tanım 1.4.1.1: Bir ∈ ∗ kelimesi için → olacak şekilde bir ∈ ∗ kelimesi
varsa bu kelimesine indirgenir (reducible) kelime denir. Aksi durumda ise (yani
→ olacak biçimde bir kelimesi yoksa) bu kelimesine indirgenemez
(irreducible) kelime denir.
Önerme 1.4.1.2 (Book, 1987): Tanımlanan (1.4) deki bağıntının yansımalı (reflexive),
geçişmeli (transitive) kapanışı olan →∗ kuralı, aslında tarafından üretilen bir
indirgeme bağıntısıdır.
Tanım 1.4.1.3: , ∈ ∗ için kelimesi indirgenemez olsun. Buna göre →∗
Tanım 1.4.1.4: Tanımlanan (1.4) deki bağıntının yansımalı, simetrik ve geçişmeli
kapanışıdır, bunu da ↔∗ ile gösterelim, tarafından üretilen bir Thue kongruanstır (Book, 1987). Bir ∈ ∗ kelimesi için nin kongruans sınıfı { ∈ ∗| →∗ } olup,
bu denklik sınıfı [ ] ile gösterilir. Ayrıca, ∗ ↔∗ bağıntısı bütün kongruans
sınıflarının kümesini gösterir. ve kelimelerinin kongruans sınıflarının çarpımı
[ ] [ ] = [ ]
şeklindedir. Bu çarpma işlemi birleşme özelliğini sağlar ve [ ] birim elemanıdır. Böylece ∗ ↔∗ bağıntısı bir monoiddir ve [ ; ] çifti bir monoid sunuşudur. Bu
sunuştaki üreteç kümesi sonlu ise bu monoide sonlu üreteçli monoid, hem hem de sonlu ise ozaman bu monoide sonlu sunumlu monoid denir.
Yeniden yazma sistemleri üzerinde aşağıdaki sonuç önemlidir:
Önerme 1.4.1.5: Aynı alfabe üzerindeki iki yeniden yazma sistemi eğer aynı Thue
kongruansını üretirlerse, bu iki yeniden yazma sistemi denktir.
Bir yeniden yazma sistemi için en önemli konu, verilen ↔∗ bağıntısının
sağlanıp sağlanmadığının kontrol edilmesidir. Yani bu iki kelimenin belli bir kural altında birbirine denk olup olmamasının incelenmesidir.
Tanım1.4.1.6: yeniden yazma sistemi olsun. Bu durumda, I) sistemi için kelimeler arasında
1 →R 2 → 3 → …
şeklinde sonsuz bir zincir yoksa, bu yeniden yazma sistemine Noetherian ya da sona
ermiş (terminating) denir.
(II) sisteminden alınacak bütün , , ∈ ∗ kelimeleri için,
↔∗ ve ↔∗ iken ↔∗ ve ↔∗
olacak şekilde bir ∈ ∗ kelimesi varsa, bu yeniden yazma sistemine elmas kuralı
(confluent) denir.
Tanım 1.4.1.6 ya ek olarak, verilen bir sistemden yeni özellikler de türetilebilir.
Tanım 1.4.1.7: Hem sona ermiş hem de elmas kuralının özelliklerini sağlayan yeniden
yazma sistemine tam yeniden yazma sistemi denir.
Uyarı 1.4.1.8: sona ermiş yeniden yazma sistemi ise her ( ; ) kongruans sınıfı bir indirgenemeyen kelime içerir. Varsayalım ki, sona ermiş olsun. Bu durumda nin tam yeniden yazma sistemi olması için gerek ve yeter koşul ( ; ) nin her kongruans
sınıfının tam olarak bir indirgenemez kelime içermesidir. Bu yüzden tam yeniden yazma sistemi her bir kongruans sınıfı için tek bir normal forma sahiptir.
1.4.2 Bir [ ; ] Sunuşu İçin Yeniden Yazma Sisteminin Tam Olduğunun
Gösterilmesi
Bir [ ; ] sunuşunun yeniden yazma sisteminin tam olduğunu göstermek için iki adım kullanılır:
1.ADIM: Öncelikle bu sistemin sona ermiş olduğu gösterilir.
Bunun için ∗ daki kelimeler arasında bir indirgeme sıralaması olması gerekir. Yani verilen sunuştaki her bir = bağıntısı için eğer > ise bu > sıralaması bu sunuş için uygundur. Diğer bir deyişle, bütün ve kelimeleri için → kuralı > sıralamasını sağlar. Yeniden yazma sisteminde kullanılan birkaç tipte indirgeme sıralaması vardır. , ∈ ∗ olmak üzere, bu sıralamaları aşağıdaki gibi
tanımlayabiliriz.
1) Uzunluk Sıralaması (L): Harf sayısı fazla olan kelime daha büyüktür. Yani,
> ⇒ | | > | | şeklindedir.
2) Ağırlık Sıralaması (W): in her bir elemanı pozitif bir sayı ile belirtilir. Bir
kelimenin ağırlığı ise bu kelimedeki harflerin belirttiği sayıların toplamıdır ve herhangi bir kelimesi için bu kelimenin ağırlığı ( ) ile gösterilir. Gösterim olarak,
> ⇔ ( ) > ( )
biçimindedir.
3) Soldan Sözlük Sıralama (LL): Bu sıralama içindeki harflerin kendi aralarında
sıralanmasıyla uygulanır. Örneğin, alfabedeki … harflerinin < < < ⋯ şeklinde sıralanması gibi. Herhangi iki kelimeyi sıralamak için ise soldan başlayarak her iki kelimenin harfleri karşılaştırılır. İlk farklı olan harflerden hangisinin harfi sıralamada daha büyükse, o kelime daha büyüktür. Örneğin, = { , , , … } ve sıralama < <
< ⋯ olsun. ∗ dan = ve = şeklinde iki kelime alalım ve bu iki
kelimeyi karşılaştırdığımızda ilk olarak beşinci harfleri farklıdır ve < olduğu için de > olur. Benzer olarak kelimeler arasında sağdan sözlük sıralama (LR) da yapılabilir.
4) Uzunluk ve Soldan Sözlük Sıralama (LLL): Burada > olması için gerek ve yeter koşul ya | |> | | olması ya da | | = | | ise > olmasıdır. Örneğin iki
olmasına rağmen > dir. Benzer olarak, kelimeler arasında uzunluk ve sağdan sözlük sıralaması da (LRR) uygulanabilir.
2. ADIM: Bu yeniden yazma sisteminin elmas kuralını sağladığı gösterilir.
Bunun için ise bütün krtik çiftlerin (critical pairs) çözülebilmesi gerekir. Buradaki kritik çift ile anlatılmak istenen; , , , ve kelimeleri ∗ da olmak üzere
= ve = ( boş kelimeden farklı ) bağıntılarından elde edilen { , } kelime çiftleridir. Bu { , } kritik çiftlerin indirgenebilir olması demek ise,
→∗ ve →∗
olacak şekilde bir ∈ ∗ kelimesinin elde edilebilir olmasıdır.
Örnek 1.4.2.1: Aşağıda verilen dört yeniden yazma kuralının oluşturduğu yeniden
yazma sisteminin elmas kuralına sahip olduğunu gösterelim. Verilen bu yeniden yazma kuralları
→ , → , → ( ) , ( ) →
olmak üzere, bunların sol yanlarına bakalım ve çakışan bütün kelimeleri ele alalım. Bu
çakışan kelimelerden elde edilen {( ) , }, { , ( ) }, { , ( ) },
{ ( ) , } kritik çiftlerinin indirgenebilir olduğunu gösterelim.
( ) = ( ) ( ) = ( )
( ) ( ) ( ) ( ) ( ) ( ) = ( ) ( ) ( )
Sonuç olarak verilen yeniden yazma sistemi elmas kuralına sahiptir.
Örnek 1.4.2.2: ℘ = [ , , ; = , = ,
= , = , = , = , =
, = ] sunuşundaki üreteçlerinin indisleri arasındaki sıralama
3 > 2 > 1 ise üreteçler arasındaki sıralama > > şeklindedir. Bu sunuştaki üreteç kümesi ve bağıntı kümesi sonlu olmasına rağmen bu sunuşun temsil ettiği
Chinese monoid sonsuzdur. Genel olarak bu tipteki Chinese monoidin sunuşu,
℘ = [ , , ; = = ]
indisler arası sıralama ise ≥ ≥ dır. Biz özel durum olan = 3 için Chinese monoidin tam yeniden yazma sistemine sahip olduğunu göstereceğiz (Güzel, 2010).
İlk olarak, → , → , → , →
, → , → , → , →
kurallarındaki kelimeler arasında tek bir indirgeme söz konusu olduğundan ve aşağıda gösterdiğimiz gibi kelimeleri sonlu sayıda adımla bulduğumuzdan sona ermiş olma özelliğini de sağlamış olur. Bu yeniden yazma kurallarının sol yanlarına bakalım ve çakışan bütün kelimeleri ele alalım. Elde edilen,
{ , }, { , }, { , },
{ , }, { , }, { , },
{ , }, { , }, { , }, { ,
}, { , }
kritik çiftlerinin elmas kuralına sahip olduğunu yani her birinin tek bir kelimeye indirgendiğini gösterelim.
Sonuç olarak, Chinese monoidin sona ermiş olma ve elmas kurallarının her ikisini birden sağladığından tam yeniden yazma sistemine sahip olduğunu söyleyebiliriz.
1.4.3 Knuth- Bendix Algoritması
Knuth-Bendix algoritması, verilen bir sunuşun bağıntı kümesindeki eşitlikleri elmas kuralını sağlayan yeniden yazma sistemine dönüştüren bir algoritmadır. Eğer bu algoritma başarı ile sonuçlanırsa (yani bağıntı kümesindeki eşitlikler elmas kuralını sağlayan yeniden yazma sistemine dönüştürülürse), verilen sunuşun temsil ettiği grup için tam yeniden yazma sistemine sahiptir diyebiliriz. Bu algoritmayı aşağıdaki örnek üzerinde inceleyelim.
Örnek 1.4.3.1: Herhangi bir grubu için
< , ; = = ( ) = 1 >
sunuşu verilsin. Bu sunuştaki üreteç kümesi ve bağıntı kümesi sonlu olmasına (yani sunuşun sonlu sunumlu olması) rağmen bu sunuşun temsil ettiği grup sonsuzdur. Genel olarak bu tipteki yani
< , ; = = ( ) = 1 >
biçimindeki sunuşlar için, eğer 1 + 1 + 1 > 1 ise, sunuşun temsil ettiği grup sonludur (Rotman,1988). Bu grubun elemanları için bir kanonik form oluşturamıyoruz. Ancak bu durum, grubun tam olduğu anlamına gelmez. Onun için bizde,
(1) → 1, (2) → 1, (3) ( ) → 1,
yeniden yazma kurallarını kullanarak, çakışan bütün kelimelerden oluşan kritik çiftlerin indirgenebilir olması için yeni yeniden yazma kuralları bulmalıyız. İlk olarak, (1), (3) kurallarının sol yanlarındaki çakışan elemanı için kelimesini göz önüne alalım. Bu kelimeye (1) ve (3) teki indirgeme işlemlerini uygulayarak = eşitliği, buradan da
kuralı elde edilir. (Knuth-Bendix algoritmasında = kuralı şeklinde gösterilir.) Benzer olarak, kelimesi için de (2) ve (3) kullanılarak
(5) → ,
kuralı elde edilir. Bir sonraki adım olarak (3) kuralı kaldırılır ve (1) ile (5) teki
elemanının çakışmasıyla oluşan kelimesinden
(6) → ,
kuralı elde edilir. Daha sonra (4) ve (5) kuralları kaldırılır. Son olarak da kelimesine (5) ile (1) kuralları uygulanarak
(7) →
kuralı oluşturulur. Sonuç olarak,
(1) → 1,
(2) → 1,
(6) → ,
(7) →
yeniden yazma kurallarının oluşturduğu yeniden yazma sistemi elmas kuralını sağlamış
olur. Bunu aşağıdaki şekilde kontrol edelim. Öncelikle, { , }, { ,
}, { , }, { , } kritik çiftlerini elde edilmiştir. Şimdi kritik
çiftlerin elmas kuralına sahip olduğunu gösterelim.
olduğundan (yani (1), (2), (6) ve (7) kurallarının sol yanlarındaki çakışan bütün kelimelerin oluşturduğu kritik çiftler tek bir kelimeye indirgendiğinden) algoritma başarıyla sonuçlanmıştır. Dolayısıyla da
< , ; = = ( ) = 1 >
sunuşunun temsil ettiği grup için tam bir sisteme sahiptir.
1.5 Temel Graf Bilgileri
Çalışmamızın bu bölümünde, graf teoride kullanılan temel graf tanımları verilmiştir ve bu tanımlanan materyallere (Buckley 1990), (Hartsfield 1998) gibi kaynaklardan ulaşılabilir. Tezimizin üçüncü bölümünde bu tanımlardan yararlanılarak hesaplamalar ve genel sonuçlar elde edilmiştir. Γ grafı, basit ve yönlendirilmemiş graf olmak üzere;
Γ = ( (Γ), (Γ)) grafı, köşeler denilen boş olmayan bir (Γ) sonlu objeler kümesi ile birlikte, nin farklı köşe çiftlerinin düzensiz sıralanışı olan bir (Γ) (boş olabilir) kenarlar kümesidir. Bir graftaki başlangıç ve bitiş köşeleri aynı olan kenara
bukle (loop) denir.
Bir grafta en az bir kenar yönlü ise, bu grafa yönlü (directed) aksi halde yönsüz
veya yönlendirilmemiş (undirected) graf denir.
Bir Γ grafının herhangi iki köşesi arasında birden fazla kenar varsa bu kenarlara çok katlı kenar, bu tür graflara çok katlı (multiple) graf denir. Çok katlı ve bukle içermeyen graflara basit (simple) graf denir.
Bir Γ grafında kenarı ve köşelerini birleştiriyorsa, = ( , ) biçiminde gösterilir. ve köşelerine komşu köşeler (adjacent vertices) denir.
Bir Γ grafının her köşe çiftinin arasında en az bir tane yol varsa Γ grafına birleştirilmiş veya bağlantılı (connected) graf denir.
Bir köşeden farklı bir köşeye varışta kullanılan her köşe bir kez kullanılıyorsa bu yürüyüşe yol (path) denir. köşeli bir yolda kenar sayısı − 1 dir. Bir köşeden farklı bir köşeye varışta kullanılan kenar sayısına yolun uzunluğu (length of path) denir.
Bir Γ grafında ve gibi iki köşe arasındaki yollar içinde minimum uzunluğu olanın uzunluğuna; ve nin uzaklığı (distance) denir ve ( , ) biçiminde gösterilir.
Bir Γ grafında herhangi bir ∈ derecesi (degree), o köşenin komşu olduğu köşelerin sayısıdır ve ( ) ile gösterilir.
Tüm köşeleri birbirinden farklı ve köşe sayısı ≥ 3 olan kapalı bir yürüyüşe
devir (cycle) denir.
sayıda köşeye sahip bir Γ grafının tüm köşeleri birbiri ile komşu ise bu grafa
tam (complete) graf denir ve ile gösterilir.
Tanım 1.5.1: Γ ve Γ herhangi iki graf olmak üzere; Γ ( ) ⊂ Γ ( ) ve Γ ( ) ⊂ Γ ( ) ise Γ grafına Γ grafının alt grafı (subgraph) denir ve Γ ⊂ Γ şeklinde gösterilir.
2. ÖZEL AFİN WEYL GRUPLAR ÜZERİNDEKİ GRÖBNER-SHİRSHOV TABANI
Bu bölüm içinde verilen temel bilgilere (Bokut, 2001), (Newman, 1942), (Shirshov, 1962), (Buchberger, 1970 ve 1982) gibi kaynaklardan ulaşılabilir.
1.4 Bölümde incelediğimiz yeniden yazma sisteminin, Gröbner-Shirshov taban ile karşılaştırılarak Afin Weyl grubu üzerinde incelenmesi, bu bölümün ana temasıdır. Gröbner-Shirshov taban bir metot olarak kullanılmakla beraber, tabanı incelenen yapının lineer sıralı olması gerekmektedir. Bu yüzden, öncelikle lineer sıralı küme tanımlanıp, sonrasında Gröbner–Shirshov tabanının tekil (sıfıra indirgenebilmesi) olduğunun gösterilmesi esas adımlardır. Bu bölüm içindeki işleyiş bu şekilde olacaktır.
Lineer sıralıların kümesi, bu küme üzerindeki ekleme (plus) bağıntısıdır. Kısmi
sıralama bağıntısına, karşılaştırma özelliği eklenince lineer sıralı (veya tam sıralı) küme elde edilir. Kısaca, " ≤ " bağıntısı kümesi üzerinde tam sıralı olması için aşağıdaki özellikleri sağlamalıdır:
(1) Yansıma: ≤ , ∀ ∈ .
(2) Ters Simetri: ≤ ve ≤ , = dir.
(3) Geçişme: ≤ ve ≤ ise ≤ dir.
(4) Karşılaştırma (trichotamy kuralı): Herhangi , ∈ için ≤ ve ≤ olmalıdır.
kümesi lineer sıralı küme olsun. cisim ve < >, üzerinde serbest (free) birleşik (associative) cebir olduğundan, daki üreteçler tam sıralı kümesindeki harflerden oluşmaktadır.
∗, kümesinin serbest çarpımındaki harflerden oluşan monomiyallerin
(kelimeler) kümesidir. Yani tarafından üretilen ∗ a serbest monoid de denilmektedir. Bu ∗ içinde monomiyallere uzunluk ve sözlük sıralaması uygulanır. Bu da iki monomiyalin önce uzunluk sonra da sözlük sıralaması olarak karşılaştırılması demektir.
bir polinom olmak üzere; ∈ < > , ∗ içinde monomiyallerin lineer
toplamıdır.
∈ < > içinde ki herhangi polinom sonlu birçok monomiyal içerdiğinden ve uzunluk-sözlük sıralaması tam sıralı olduğundan, herhangi ∈ < > polinomu
baş (leading) monomiyal içerir. polinomunun baş monomiyali ̅ şeklinde gösterilmektedir. ̅, polinomu içinde katsayısı 1 olan monik polinomdur.
< > cebirinden, ve gibi iki monik polinomu alalım. Buna göre, iki çeşit
bileşen (compositions) olan kesişim ve içeren bileşeninin belirsizliğini (ambiguity of the
intersection and inclusion) tanımlayalım.
(i) bir monomiyal ve , ∈ ∗ olsun. Bu durumda | ̅| + | ̅| > | | için,
= ̅ = ̅ şeklindeyse, o zaman ( , ) = − polinomu ve
polinomlarına ve monomiyaline göre kesişim bileşeni olarak adlandırılır. Buradaki monomiyaline kesişimin belirsizliği adı verilir.
(ii) , ∈ ∗ için = ̅ = ̅ ise, bu durumda ( , ) = ̅ − ̅ polinomu
ve polinomlarına ve monomiyaline göre içeren bileşenleri olarak adlandırılır. Buradaki monomiyaline içerenin belirsizliği adı verilir.
( , ) = − , içinde nin (ELW) baş monomiyallerin eleminasyonu adı verilir. ( , ) bileşeninin tekil bağıntıları ⊂ < > adı verilebilmesi için
( , ) = ∑ , ∈ , ∈ , , ∈ ∗ ve < olmalıdır. Özellikle,
eğer ( , ) , nin ELW ı sıfıra giderse o zaman ( , ) tekil bağıntıdır, denir. Bu durum,
( , ) ≡ 0 ( , )
ile gösterilir.
Gröbner-Shirshov tabanı, < > cebirinin alt kümesi olması için polinomların herhangi bileşenleri den e tekil bağıntılı olmalıdır.
< ; > cebiri üreteçleri ile bağıntılarından oluşmaktadır. ile ideal üretilerek < > cebirininin çarpan (factor) cebirini oluşturur.
Lemma 2.1 (Bileşen Elmas Lemma): nin Gröbner-Shirshov tabanı olması için
gerek ve yeter koşul nin indirgenen kelimelerinin kümesinin
{ ∈ ∗| ≠ ̅ , ∀ ∈ }
< ; > cebirinin lineer tabanını içermesidir.
< > cebirininin alt kümesi Gröbner-Shirshov tabanı değilse, ye nin polinomlarının bütün tekil olmayan bileşenlerini ekleyebiliriz. yi içeren Gröbner-Shirshov tabanı elde edebilmek için bu metot uygulamasına devam edilir. Bu metoda Buchberger-Shirshov algoritması adı verilir.
Gröbner-Shirshov tabanının indirgenir olabilmesi için ∈ , \ { − monomiyal} nin lineer kombinasyonu olmalıdır.
Not olarak, herhangi < > cebirinin ideali tek indirgenen Gröbner-Shirshov tabanına sahiptir. Eğer yarı grup bağıntılarının
{ − ; , ∈ ∗}
kümesiyse, herhangi tekil olmayan bileşen sunuşu ile aynı yapıya sahip olacaktır. Sonuç olarak, kümesi yarı grup bağıntılarını içerir.
= < ; > yarı grup sunuşu olsun. Buna göre ⊂ < > ve Gröbner-Shirshov tabanını bulabiliriz. kümesi ya bağlı değildir ve yarı grup bağıntılarını içerir. kümesine, yarı grup sunuşunun Gröbner-Shirshov tabanı denir. =< ; > yarı grup cebirinin Gröbner-Shirshov tabanıyla aynıdır. Aynı terminoloji, herhangi grup sunuşu içinde geçerlidir. Bunun anlamı,
= 1, = 1, ∈ formunun bütün tekil grup bağıntılarının sunuşlarınıda
içerir.
Uyarı 2.2: Bu bölüm boyunca, herhangi ve monik polinomlarının kesişim bileşeni,
∩ ve içeren bileşeni, ∪ şeklinde gösterilmiştir.
Örnek 2.3: : = [ , , ; = , = ,
= , = , = , = , =
, = ]
şeklindeki Chinese monoidin sunuşunu ele alalım. Bu sunuşun temsil ettiği monoidinin Gröbner-Shirshov tabanının
= { − , − , − , − ,
− , − , − ,
− }
olduğunu gösterelim.
Öncelikle, üreteçler arasındaki sıralamayı > > şeklinde kabul edelim. Üreteçler arasında verilen sıralamaya göre monomiyallerin iki-yanlı polinomlarını belirleyelim: (1) 3 2 1− 2 3 1 (2) 3 1 2− 2 3 1 (3) 2 1 1− 1 2 1 (4) − (5) 3 1 1− 1 3 1 (6) 2 2 1− 2 1 2 (7) − (8) −
Şimdi de kesişim belirsizliklerini ( , ) modülüne göre tekil olduğu yani sıfıra indirgendiğini gösterelim. (2) ∩ (3): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ − + ≡ − + ≡ − + ≡ 0 (2) ∩ (6): = − , = = , = 3 1 2 2 1, ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ − + ≡ 0 (4) ∩ (6): = − , = − , = 3 2 2 1, ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ 0
(4) ∩ (3): = − , = − , = 3 2 2 1 1, ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ 0 (7) ∩ (3): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ 0 (7) ∩ (6): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ 0 (1) ∩ (3): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ 0
(8) ∩ (5): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + ≡ 0 (7) ∩ (1): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + ≡ 0 (8) ∩ (2): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ − + ≡ 0 (6) ∩ (3): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + ≡ 0 Sonuç olarak, = { − , − , − , − , − , − , − , −
} kümesi monoidi için bir Gröbner-Shirshov tabandır. Ele alınan monoidi dikkatlice incelediğimiz de bu monoidin Gröbner-Shirshov tabanının aslında 1.4.2.2
Örnekte verilen tam yeniden yazma sistemine sahip olan monoid ile aynı yapıda olduğu görülür. Bunu da her bir eşleşen (match) polinomların sıfıra indirgendiğini göstererek gerçekleştirmiş olduk. Buradan acaba bir cebirsel yapının tam yeniden yazma sistemiyle Gröbner-Shirshov tabanının aynı olup olmadığı sorusu aklımıza gelir. Bu iki metodun karşılaştırıldığı tabloyu şekildeki gibi verebiliriz:
Çizelge 2.1
2.1 Afin Weyl Grup için Yeniden Yazma Sistemi ile Gröbner-Shirshov Tabanının Karşılaştırılması
Grup, monoid, ve yarı grup yapıları için yeniden yazma sistemi polinom cebirinde Gröbner-Shirshov taban teorisinin özel durumu olduğu bilinmektedir. Bu yüzden 1.4 Bölüm de bahsettiğimiz yeniden yazma sistemi ile Gröbner-Shirshov tabanı aynı yapı üzerinde çalışılarak bu özel durumu sağlandığı örneklenecektir. Bunu göz önüne alarak daha önce yapılan bir çalışmada (Çevik ve ark., 2010) özel uygulama olarak ( ≥ 2) tipindeki Afin Weyl grupları incelenmiştir. Ancak çalışmadaki metodu daha ayrıntılı olarak görebilmek için ( ≥ 2) üzerinde bu Gröbner-Shirshov tabanını incelemiş bulunmaktayız. Bu çalışma birleştirilmiş grup teori ile halka teori arasında farklı sonlu gruplar üzerine geçiş çalışması olarak da düşünülebilir.
Yapılan işlemlerde ele alınan grup, monoid veya yarı grup gibi cebirsel yapılar, sistem ve tabanı sağlamıyorsa, bunu sağlamasına yardımcı olabilecek algoritmalar kullanmak gerekmektedir. Bunlar; yeniden yazma sistemi için Knuth-Bendix iken, Gröbner-Shirshov tabanı için de Buchberger-Shirshov algoritmasıdır. Bunun yanı sıra literatür de yeniden yazma sisteminden Gröbner-Shirshov tabanlarına geçiş konusu
i) yeniden yazma
sistemi
i) Gröbner-Shirshov
taban
ii) kural ii) iki-yanlı polinom
iii) kelime iii) monomiyal
iv) indirgeme iv) indirgeme
v) sol yan v) baş monomiyal
vi) alt kelime vi) alt monomiyal
vii) sağ yan vii) arta kalan
viii)çakışan viii)eşleşen
ix) kritik çift ix) S-polinom
x) çözüm x) sıfıra indirgeme
xi) kritik çift
indirgemesi
xi) S-polinom
indirgemesi
xii) tam yeniden
yazma sistemi
xii) Gröbner-Shirshov
hakkında yeterli çalışma bulunmamaktadır. Bu incelenen çalışmada Afin Weyl grubunun ( ≥ 2) tipi için sistemden tabana geçişi göz önünde bulundurup aşağıdaki sonuç ispatlanmıştır.
Teorem (Ana teorem) 2.1.1 (Çevik ve ark., 2010): ( ≥ 2) tipindeki Afin Weyl grubu tam yeniden yazma sistemine ve Gröbner-Shirshov tabanına sahiptir.
Ayrıca Afine Weyl grubu indirgenemez Coxeter gruptur (1.4.3 Bölümde Coxeter grubun özel durumu için indirgenebilmesini sağlayan örnek vermiştik). için, < , , … , ; = 1 (1 ≤ ≤ + 1),
= (1 ≤ ≤ ),
= (1 ≤ < − 1 < + 1
( , ) ≠ 1, ( + 1) = > (2.1)
Lemma 2.1.2: bir küme olmak üzere, ∗ ile tarafından üretilen bütün kelimelerin serbest monoidlerini içeren kümeyi gösterelim. üzerindeki yeniden yazma sisteminin sona ermiş olması için gerek ve yeter koşul ile uyumlu olan ∗ üstünde indirgeme sıralaması olmalıdır.
Afin Weyl grubunun tam yeniden yazma sistemine sahip olması için Knuth-Bendix uygulaması gerekmektedir. Tabi ki kuralları belirlerken de bizim için üreteçlerin uzunluk-sözlük sıralaması önem kazanmaktadır.
Sonsuz grup için örnekleme yapmadan önce sayılabilir bir durum için yapılan örneklemesini inceleyelim. Bu yüzden = 2 için Afin Weyl grubunun
< , , ; = 1 (1 ≤ ≤ 3), = , = ,
= >
sunuşunu göz önüne alalım. Buradaki sunuş aslında (2.1) deki sunuştan yararlanarak oluşturulmuştur. Grup için tanımlanan bağıntılar yeniden yazma sisteminin kurallarını oluşturur. Bu gerçeğin ışığında için yeniden yazma kuralları kümesi,
{ = 1 (1 ≤ ≤ 3), = , = , = } (2.2)
şeklindedir. Üreteçlerinin uzunluk-sözlük sıralaması > > biçiminde kabul edilmiştir. Öncelikle yeniden yazma sistemi için sona ermiş olma özelliğini kontrol etmeliyiz. Sonrasında da üreteçler arasındaki > > indirgeme sıralamasını kullanarak sistemin için elmas kuralını sağlamış olduğunu göstermeliyiz. Buna ek olarak nin elmas kural özelliği için (2.2) deki kelimelerin çakışanlarını bulup yeniden çözmeliyiz. Elde edilen
{ , }, { , }, { , }, { , },
{ , }, { , }, { , }, { , }, { , }, { , },
{ , }, { , },{ , },
{ , }
kritik çiftlerinin elmas kuralına sahip olduğunu ve her birinin tek bir kelimeye indirgendiğini gösterelim:
Burada, Afin Weyl grubunun sona ermiş olma ve elmas kuralı özelliklerini sağladığını göstermiş olduk. Ayrıca hesaplamaya alternatif olarak, birkaç bilgisayar program paketi (mesela GAP) çakışan kelimelerin tek bir kelimeye indirgenip indirgenmediğini hesaplamada kullanılabilmektedir. Ancak yapılan bu çalışmada herhangi bir program kullanılmamıştır.
Sonuç 2.1.3 : Afin Weyl grubu tam yeniden yazma sistemine sahiptir.
= 2 için uyguladığımız yukarıdaki tüm işlemleri, aslında tümevarım gibi düşünerek ≥ 2 değerleri için de hesaplayabiliriz. Bu yüzden Teorem 2.1.1 in ispatı yapılmış olup, bu bize Afin Weyl grubunun tam yeniden yazma sistemine sahip olduğunu gösterecektir.
Afin Weyl grubunun üreteçleri , , , … , den oluşmaktadır. (2.1) deki bağıntılardan yararlanılarak, = 2 için Afin Weyl grubunun Gröbner-Shirshov tabanı incelenmiştir.
(2.2) kümesindeki bütün eşleşen monomiyalleri göz önünde bulundurarak, için kritik çiftlerin analizini yapabiliriz veya basit olarak, için uzunluk-sözlük sıralaması da kullanılarak yeniden yazma sisteminde olduğu gibi bir bilgisayar paket programları (mesela GAP gibi) tarafından da kontrol edilebilmektedir. Ancak biz bu çalışmada böyle bir program kullanmadık. Şimdi, Teorem 2.1.1 i göz önünde bulundurarak elde edilen sonucu inceleyelim.
Sonuç 2.1.4 : Afin Weyl grubu Gröbner-Shirshov tabanına sahiptir.
= 2 için, Afin Weyl grubunun, (2.1) deki bağıntılara göre üreteçlerinin sıralaması > > şeklindedir. Bu sıralamaya göre Sonuç 2.1.4 ü inceleyelim. O zaman, Afin Weyl grubunun iki-yanlı polinomları,
(1) − 1, (2) − 1, (3) − 1, (4) − , (5) − , (6) −
şeklindedir. Burada bulduğumuz, (1), (2), (3), (4),(5) ve (6) iki-yanlı polinomları (2.1)
deki Afin Weyl grubu için verilen bağıntılarda indisine 2 değeri verilerek Afin Weyl grubu elde edilmektedir. Şimdi de Gröbner-Shirshov tabanlarının tekil olduğunu
göstermemiz gerekmektedir. Öncelikle, monomiyallerin kesişen ve içeren
belirsizliklerini tabloda gösterip bunların tabanlarının tekil olduğunu gösterelim: Çizelge 2.2 ∩ : belirsiz lik yeni poli nom (1)∩(4) Tekil (4)∩(1) Tekil (1)∩(6) Tekil (6)∩(1) Tekil
(1)∩(1) Tekil (2)∩(2) Tekil (3)∩(3) Tekil (4)∩(4) Tekil (5)∩(5) Tekil (6)∩(6) Tekil (5)∩(2) Tekil (2)∩(5) Tekil (4)∩(6) Tekil (6)∩(4) Tekil
Çizelge 2.2 den yararlanarak, kesişen belirsizliklerin tekil olduğunu
ispatlayalım. O zaman, (1) ∩ (4): = 12− 1, = − , = , ( , ) = ( − 1) − ( − ) = 12 2 1− 2 1− 1 2 2 1+ 1 2 1 2 = − 2 1+ 1 2 1 2 ≡ − + ≡ − + ≡ 0 (4) ∩ (1): = − , = − 1, = , ( , ) = ( − ) − ( − 1) = − − + = − + ≡ − + ≡ − + ≡ 0 (1) ∩ (6): = − 1, = − , = , ( , ) = ( − 1) − ( − ) = − − + ≡ − + ≡ − + ≡ 0
(6) ∩ (1): = − , = − 1, = , ( , ) = ( − ) − ( − 1) = − − + = − + ≡ − + ≡ − + ≡ 0 (1) ∩ (1): = − 1, = − 1, = , ( , ) = ( − 1) − ( − 1) = − − + ≡ 0 (2) ∩ (2): = − 1, = − 1, = , ( , ) = ( − 1) − ( − 1) = − − + ≡ 0 (3) ∩ (3): = − 1, = − 1, = , ( , ) = ( − 1) − ( − 1) = − − + ≡ 0 (4) ∩ (4): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + ≡ − + ≡ 0
(5) ∩ (5): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ 0 (6) ∩ (6): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ 0 (5) ∩ (2): = − , = − 1, = , ( , ) = ( − ) − ( − 1) = − − + = − + ≡ − + ≡ − + ≡ 0 (2) ∩ (5): = − 1, = − , = , ( , ) = ( − 1) − ( − ) = − − + = − + ≡ − + ≡ 0
(4) ∩ (6): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ − + ≡ − + ≡ 0 (6) ∩ (4): = − , = − , = , ( , ) = ( − ) − ( − ) = − − + = − + ≡ − + ≡ − + ≡ − + ≡ 0 Tüm bu işlemlerden sonra { − 1, − 1, − 1, − , − , − }
kümesinin, Afin Weyl grubu için bir Gröbner-Shirshov tabanı olduğu ortaya çıkmış olacaktır.
Sonuç olarak, Afin Weyl grubunu = 2 için yapılan işlemler, tümevarım şeklinde düşünüldüğünde, Teorem 2.1.1 in ispatı tamamlanmış olacaktır.
3. GRUPLAR ÜZERİNDE GRÖBNER-SHİRSHOV TABANI KULLANARAK OLUŞTURULAN GRAF
Bu bölümde Gröbner-Shirhov tabanının özelliklerini kullanarak
tanımlayacağımız grafın özellikleri, şekiller yardımıyla hesaplanacaktır. Çizilen grafın köşeleri etiketlenerek, graf parametrelerinden olan maximum ve minumum derece (maximum and minimum degree), çap (diameter), yarıçap (radian), girth, kromatik (chromatic), klik (clique), derece sıralaması (degree sequence, DS), düzensizlik indeksi (irregularity index, MWB) ve baskınlık (domination) sayıları bulunmuştur.
Şimdi, yeni grafın tanımını ve bu bölüm için bize yardımcı olacak parametre tanımlarını verelim. Buna göre, köşe ve E kenar kümesini göstermek üzere, bir Γ = Γ(V, E) grafını göz önüne alalım.
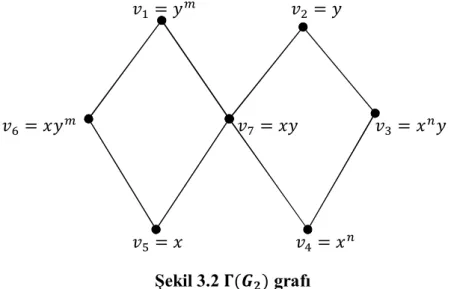
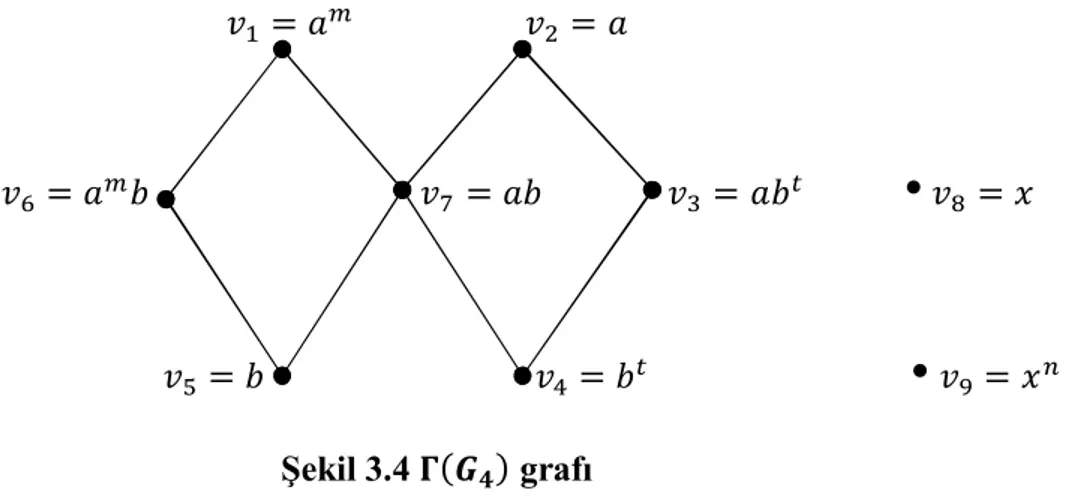
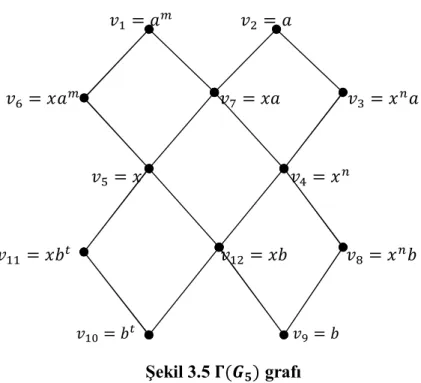
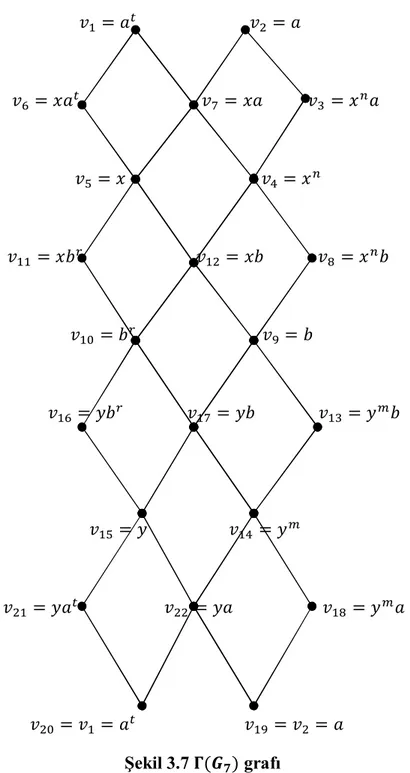
Tanım 3.1: Grubun sunuşu ℘ =< ; > olmak üzere, köşe kümesi V = {grubun sunuşundaki üreteçler, bağıntıların baş monomiyalleri, eşleşen monomiyaller} ve kenar kümesi E = ↔ ⟺ 1 ş ş , 2) ∃ ∈ ∗: = = , , ∈ 3) → ∶ }
olacak şekildeki Γ = Γ(V, E) grafını tanımlayalım.
Şimdi özelliklerini inceleyeceğimiz bazı graf parametrelerinin tanımlarını verelim. Bunun için, Γ yı yönlendirilmemiş basit bir graf alalım.
Tanım 3.2 (Buckley ve Harary, 1990): i) Bir Γ grafının köşe derecelerinin en büyüğünü veren köşeye maksimum dereceli köşe denir ve ∆(Γ) ile gösterilir.
ii) Bir Γ grafında köşe derecelerinin en küçüğünü veren köşeye minimum dereceli köşe denir ve (Γ) grafın minimum köşe derecesini gösterir.
iii) Dış merkezlilik (eccentricity), her köşenin diğer köşelere olan uzaklıklarının en
büyük değeridir ve ( ) şeklinde gösterilir. En büyük dış merkezlilik değerine de çap denir ve (Γ) şeklinde gösterilir. En küçük dış merkezlilik değerine de yarıçap denir ve (Γ) şeklinde gösterilir.