Bazı lineer olmayan fark denklem sistemlerinin çözümlerinin periyodikliği

T.C.

SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ

BAZI LİNEER OLMAYAN FARK DENKLEM SİSTEMLERİNİN

ÇÖZÜMLERİNİN PERİYODİKLİĞİ Vural DENİZ

YÜKSEK LİSANS TEZİ Matematik Anabilim Dalını

Şubat-2019 KONYA Her Hakkı Saklıdır

TEZ KABUL VE ONAYI

Vural DENİZ tarafından hazırlanan “Bazı Lineer Olmayan Fark Denklem Sistemlerinin Çözümlerinin Periyodikliği” adlı tez çalışması 26.02.2019 tarihinde aşağıdaki jüri tarafından oy birliği ile Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı’nda YÜKSEK LİSANS tezi olarak kabul edilmiştir.

Jüri Üyeleri İmza

Başkan

Prof. Dr. Özkan ÖCALAN ………..

Danışman

Doç. Dr. Kemal USLU ………..

Üye

Dr. Öğr. Üyesi Haldun Alpaslan PEKER ………..

Yukarıdaki sonucu onaylarım.

Prof. Dr. Mustafa YILMAZ FBE Müdürü

TEZ BİLDİRİMİ

Bu tezdeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde edildiğini ve tez yazım kurallarına uygun olarak hazırlanan bu çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf yapıldığını bildiririm.

DECLARATION PAGE

I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.

Vural DENİZ 26.02.2019

iv

ÖZET

YÜKSEK LİSANS TEZİ

BAZI LİNEER OLMAYAN FARK DENKLEM SİSTEMLERİNİN ÇÖZÜMLERİNİN PERİYODİKLİĞİ

Vural DENİZ

Selçuk Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dalı

Danışman: Doç. Dr. Kemal USLU 2019, 83 Sayfa

Jüri

Danışman: Doç. Dr. Kemal USLU Prof. Dr. Özkan ÖCALAN

Dr. Öğr. Üyesi Haldun Alpaslan PEKER

Bu çalışmada bazı lineer olmayan fark denklem sistemleri araştırılmış, bu sistemlerin çözümlerinin periyodik davranışları incelenmiştir. Ayrıca bu sistemlerin çözümleri başlangıç şartlarına bağlı olarak elde edilmiştir.

Anahtar Kelimeler: Lineer olmayan fark denklem sistemleri, çözümlerin periyodu, rasyonel fark denklem sistemleri.

v

ABSTRACT MS THESIS

THE PERIODICITY OF SOLUTIONS OF SOME NON-LINEAR DIFFERENCE EQATION SYSTEMS

Vural DENİZ

THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCE OF SELCUK UNIVERSITY

THE DEGREE OF MASTER OF SCIENCE MATHEMATICS

Advisor: Assoc. Prof. Dr. Kemal USLU 2019, 83 Pages

Jury

Advisor: Assoc. Prof. Dr. Kemal USLU Prof. Dr. Özkan ÖCALAN

Assist. Prof. Dr. Haldun Alpaslan PEKER

In this study, some of non-linear difference equation systems are investigated, periodic behaviors of solutions of these systems are investigated. Also the solutions of these systems are obtained by initial conditions.

Keywords: Non-linear difference equation systems, the period of solutions, system of the rational difference equation.

vi

ÖNSÖZ

Bu çalışma Selçuk Üniversitesi Fen Fakültesi Matematik Ana Bilim Dalı Öğretim Üyesi Doç. Dr. Kemal USLU danışmalığında hazırlanarak Selçuk Üniversitesi Fen Bilimleri Enstitüsü’ ne Yüksek Lisans Tezi olarak sunulmuştur.

Çalışmalarım boyunca değerli yardım ve desteklerini esirgemeyen danışman hocam Doç. Dr. Kemal USLU’ ya, maddi ve manevi destekleriyle beni hiçbir zaman yalnız bırakmayan çok değerli eşime ve aileme teşekkürü bir borç bilirim.

Vural DENİZ KONYA-2019

vii İÇİNDEKİLER ÖZET ... iv ABSTRACT ...v ÖNSÖZ ... vi İÇİNDEKİLER ... vii 1. GİRİŞ ...1

2.FARK DENKLEM SİSTEMLERİ İLE İLGİLİ YAPILMIŞ ÇALIŞMALAR ...3

3.FARK DENKLEMLERİ ...9

4. BAZI LİNEER OLMAYAN FARK DENKLEM SİSTEMLERİNİN ÇÖZÜMLERİNİN PERİYODİKLİĞİ ... 15

4.1. (4.1) FARK DENKLEM SİSTEMİNİN PERİYODİKLİĞİ ... 18

4.2. (4.2) FARK DENKLEM SİSTEMİNİN PERİYODİKLİĞİ ... 22

4.3. (4.3) FARK DENKLEM SİSTEMİNİN PERİYODİKLİĞİ ... 29

4.4. (4.4) FARK DENKLEM SİSTEMİNİN PERİYODİKLİĞİ ... 34

4.5. (4.5) FARK DENKLEM SİSTEMİNİN PERİYODİKLİĞİ ... 43

4.6. (4.6) FARK DENKLEM SİSTEMİNİN PERİYODİKLİĞİ ... 49

4.7. (4.7) FARK DENKLEM SİSTEMİNİN PERİYODİKLİĞİ ... 61

4.8. (4.8) FARK DENKLEM SİSTEMİNİN PERİYODİKLİĞİ ... 63

5. NÜMERİK ÖRNEKLER VE ŞEKİLLERİ ... 75

5.1. Nümerik Örneklerden Elde Edilen Sonuçlar ... 79

6. SONUÇLAR VE ÖNERİLER ... 80

6.1. Sonuçlar ... 80

6.2. Öneriler ... 80

KAYNAKLAR ... 81

viii SİMGELER VE KISALTMALAR

Simgeler

ℝ : Reel sayılar ℕ : Doğal sayılar

ℝ ℝ : İki boyutlu reel sayılar kümesi ∀ : Her ∃ : En az < : Küçük > : Büyük ≤ : Küçük eşit ≥ : Büyük eşit = : Eşit ≠ : Eşit değil

1. GİRİŞ

Fark denklem, bir ya da daha çok değişkenli bir fonksiyonun sonlu farklar ile bağımsız değişkenleri arasındaki cebirsel bir bağıntıdır. Diferansiyel denklemlere benzerlik göstermesine rağmen inceleme süreci yönünden diferansiyel denklemlerden daha yenidir. Diferansiyel denklemlerin temeli doğada kopukluğun olmadığı varsayımına dayanmaktadır. Birçok olayın matematiksel modeli, sürekli değişim oranları arasındaki denklemler ile ifade ediliyordu. Fakat 20. yüzyılın başlarında radyasyondaki quanta ile biyolojide genetik olaylardaki gelişmeler tüm doğa olaylarının süreklilik terimlerinin ile ifade edilemeyeceğini göstermiştir. Bu nedenle diferansiyel denklemlerde görülen süreksizlik halleri, fark denklemleri kullanılarak kaldırılmak istenmiştir.

Diferansiyel denklemlerin bazı başlangıç değer problemleri için kapalı formda çözümleri yoktur ya da çözümleri bulmak çok zor olabilir. Böyle durumlarda nümerik yöntemlerle çözümlere ulaşılmaya çalışılır. Bu yöntemlerden birisi de fark denklemlerdir. Fark denklemler yapısı itibariyle temel aritmetik işlemlere dayandığı için problemin çözümünde kolaylık sağlar.

Günümüzde birçok alanda uygulanan fark denklemleri daha çok, ekonomide arz talep dengesi hesabında, ekonomik dalgalanmalar ile fiyat değişim problemlerinde, işsizlik oranları hesabında, kuşaklar arasında genetik başkalaşım ilişkisinde, spektrum analizinde filtre dizaynı gibi alanlarda yaygın olarak kullanılmaktadır.

Son yıllarda fark denklemleri ile fark denklem sistemlerinin davranışları ve özellikle de periyodikliği, kararlılığı, sınırlılığı ve salınımlılığı ile ilgili birçok çalışma yapılmaktadır. Biz de bu çalışmamızda, bazı fark denklem sistemleri tanımlayarak bu sistemlerin çözümlerinin davranışlarını inceleyeceğiz.

Bu tez çalışmasında; 1 1 1 n n n n n n A B p s r q q r         , 1 1 1 1 1 ( ) n n n n n n n n n Cr s r q A q s r q r            , 1 n n n n A r s r q     , 1 1 1 1 1 ( ) 2 , 0 n n n n n n n n n n n Cr s r q A D s n s r q r p r              

1 1 1 1 2 2 n n n n n n A B p s r q q r            , 2 2 2 1 1 1 1 1 ( ) n n n n n n n n n Cr s r q A q s r q r               , 1 1 1 1 n n n n A r s r q        , 2 2 2 1 1 1 1 1 1 1 ( ) 2 _{n n n n} n n n n n n n Cr s r q A D s s r q r p r                   , n 0 1 2 2 2 3 3 n n n n n n A B p s r q q r            , 3 3 3 1 2 2 2 1 ( ) n n n n n n n n n Cr s r q A q s r q r               1 2 2 2 n n n n A r s r q        , 3 3 3 1 2 2 2 1 2 2 ( ) 2 _{n n n n} n n n n n n n Cr s r q A D s s r q r p r                   ,n 0

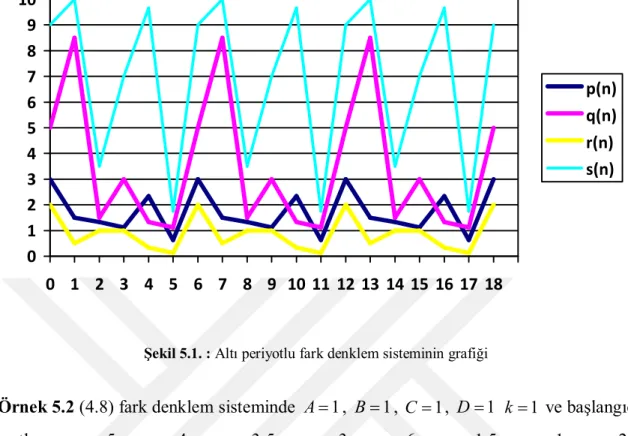
fark denklem sistemlerinin A 1, B 1, C 1, D 1 olduğu durumda periyodikliği incelenerek sonrasında aynı denklemlerin A B C D , , , ℝ-

 

0 parametrelerine bağlı olduğu durumlarda periyodikliği incelendi. Sonra bu sistemin genel hali olan

1 ( 1) ( 1) n n k n k n k n k n k A B p s r q q r              , ( 1) ( 1) ( 1) 1 ( ) n n k n k n k n n k n k n k n k Cr s r q A q s r q r                  , 1 n n k n k n k A r s r q        , ( 1) ( 1) ( 1) 1 1 ( ) 2 n n k n k n k n n k n k n k n n k n k Cr s r q A D s s r q r p r                      , n 0

rasyonel fark denklem sistemi ele alınarak bu sistemin de çözümlerinin A 1, B 1,

1

C  , D 1 olduğu durumda ve A B C D , , , ℝ-

 

0 parametrelerine bağlı olduğu durumlarda periyodikliği ayrıca incelenmiştir.

Son olarak da bu fark denklem sistemleri için nümerik örnekler ve bu örneklerin grafikleri verilmiştir.

2.FARK DENKLEM SİSTEMLERİ İLE İLGİLİ YAPILMIŞ ÇALIŞMALAR

Fark denklemleriyle ilgili son yıllarda çok sayıda çalışma bulunmaktadır. Fark denklemlerinin davranışları ve fark denklem sistemlerinin özellikle periyodikliğiyle ilgili literatürde son yıllarda yapılmış olan bazı çalışmalara göz atalım:

Çınar (2004) çalışmasında, 1 1 1 1 n n n n x x x x       , n 0

fark denkleminin çözümlerini ve bu çözümlerin lokal asimptotik kararlılığını incelemiştir.

Dehghan ve ark. (2006) çalışmalarında,

1 3 n n k n k A B x x x      fark denkleminin, , (0, ) A B   ; 3 2 3k 1, k ,..., 0 (0, ) x x x  

    olmak üzere çözümlerinin k periyotlu olduğunu

göstermişlerdir.

Taşkara ve ark. (2011) çalışmalarında;

k ℕ, x k 1,xk,...ℝ başlangıç şartları olmak üzere

( 1) 1 ( 1) n n n k n n n k p x x x q x         ,

fark denkleminin periyodikliğini incelemişler ve (k 1) periyotlu olduğunu göstermişlerdir.

Schinas (1997) çalışmasında, 1 1 1 n n n x x x   

 ,n 0,1,... Lyness fark denkleminin çözümlerinin periyodikliğini kullanarak;





1 1 1 1 , , 0, 0, n n n n n n ay A bx A x y n A x y           





1 1 1 1 , , 0, 0, n n n n n n n n a y A b x A x y n A x y           













1 1 1 1 max , max , , , 0, 0, n n n n n n n n a y A b x A x y n A x y         

fark denklem sistemlerini incelemiştir. Sonrasında fark denklem sistemlerinin denge noktalarını, denklemlerin katsayılarının a,b pozitif sabit sayılar olması veya

   

a_n , b_n pozitif sayıların periyodik dizisi olması durumlarda katsayılara ve denklemin genel terimlerine bağlı olarak elde etmiştir.

Grove ve ark. (2001) çalışmalarında,

a , b, c ve d reel sayılar ve x y keyfi reel sayılar olmak üzere; ₀, ₀

1 n n n a b x x y    , n 1 n n c d y x y    , n 0,1,...

fark denklem sisteminin, çözümlerinin davranışlarını araştırmışlardır.

Clark ve Kulenović (2002) çalışmalarında,

a , b, c ve d pozitif sayılar ve x y başlangıç şartları negatif olmayan sayılar olmak ₀, ₀ üzere;

1 n n n x x a cy    , 1 n n n y y b dx    , n  için 0

fark denklem sisteminin asimptotik davranışlarını ve sistemin çözümlerinin global asimptotik kararlılık özelliklerini incelemişlerdir.

Kulenovic ve Nurkanovic (2003) çalışmalarında,

A ve B katsayıları

_

0, 

_

aralığında reel sayılar ve başlangıç şartları x y negatif ₀, ₀ olmayan keyfi sayılar olmak üzere,

1 1 n n n n y x Ax y    , 1 1 n n n n x y By x    ,

fark denklem sisteminin çözümlerinin global kararlılığını incelemişlerdir.

Çınar (2004) çalışmasında, 1 1 1 1 1 , n n n n n n y x y y x y      

fark denklem sistemini inceleyerek çözümlerinin dört periyotlu olduğunu elde etmiştir.

Çınar ve Yalçınkaya (2004) çalışmalarında,

1 1 1 1 1 1 1 1 1 , , n n n n n n n x y z z x y x         

fark denklem sisteminin pozitif çözümlerinin periyodikliğini inceleyerek

 

xn ,

 

zn

çözümlerinin üç periyotlu,

 

y_n çözümlerinin ise on iki periyotlu olduğunu göstermişlerdir.

Camouzis ve Papaschinopoulos (2004) çalışmalarında,

1 1 , 1 1 , 0 n n n n n m n m x y x y n y x         

fark denklem sisteminin pozitif çözümlerinin davranışlarını incelemişlerdir.

Kulenovic ve Nurkanovic (2005) çalışmalarında,

, , , ,

a b c d e ve f, 0,







aralığında keyfi seçilen reel sayılar ve başlangıç şartları

0, 0, 0

x y z negatif olmayan keyfi sayılar olmak üzere,

1 , 1 , 1 , 0,1, 2,... n n n n n n n n n a x c y e z x y z n b y d z f x             

fark denklem sistemin çözümlerinin global kararlılığını incelemişlerdir.

Özban (2006) çalışmasında;

tüm başlangıç şartları ve parametreler pozitif olmak üzere,

1 1 , 1 1 , 0 n n n n n k n m n m k x y x y n y x y           

fark denklem sisteminin bütün pozitif çözümlerinin periyodikliğini incelemiştir.

Iricanin ve Stevic (2006) çalışmalarında;

(2) (3) (1) (1) (2) ( ) 1 (3) 1 (4) 1 (2) 1 1 1 1 1 1 , , ... , k n n n n n n n n n x x x x x x x x x             (2) (3) (3) (4) (1) (2) (1) 1 (2) 1 ( ) 1 1 (4) 1 (5) 1 (3) 2 2 2 1 1 1 , , ... , k n n n n n n n n n n n n x x x x x x x x x k x x x                   ℕ

Papaschinopoulos ve ark. (2007) çalışmalarında;

, , ( 1, 2,..., )

i i

a b i k pozitif sabitler , k 3 tamsayı ve bütün başlangıç şartları pozitif olmak üzere, 1 1 ( ) ( 1) , ( 1) k k k k a x n b x n x _ n     1 1 1 2 ( ) ( 1) , ( 1) k a x n b x n x n     . . . 1 1 1 2 ( ) ( 1) , ( 1) i i i i i a x n b x n x n         i3, 4,...,k

denklem sisteminin çözümlerinin davranışlarını incelemişlerdir.

Şimşek ve ark. (2009) çalışmalarında;

A katsayısı ve x y başlangıç şartları ₀, ₀

_

0, 

_

aralığında reel sayılar olmak üzere,

1 max , n n n n y A x x x     _{ }   , ₁ max , n n n n x A y y y     _{ }   , n 0

fark denklem sisteminin çözümlerini incelemişlerdir.

Köse ve ark. (2010) çalışmalarında;

1 1 1 1 , n , 0,1, 2,... n n n n n Bx A x y n y x y        ve x_1,x y₀, _1,y A B₀, ,  ℝ-

 

0

Kılıklı (2011) tez çalışmasında; 1 1 1 1 ( 1) , , n , 0,1, 2,... n n n n k n k n n k Bx A B x y z n y z y x             ve A B , ℝ-

 

0

denklem sisteminin çözümlerinin periyodikliğini incelemiştir.

Emre (2014) tez çalışmasında;

1 1 1 1 3 2 2 2 2 , , , 0 n n n n n n n n n n Ay B B A x y z n y z z z x y               

fark denklem sisteminin A B , ℝ

 

0 durumunda çözümlerinin periyodikliğini incelemiştir.

Uslu ve Esen (2015) çalışmalarında;

1 1 1 1 1 1 1 2 1 , , n , 0 n n n n n n n n n Ax A B A x y z n y z x x y y               

lineer olmayan fark denklem sisteminin A B , ℝ

_{ }

0 durumunda çözümlerinin periyodikliğini incelemiştir.

Uslu ve Uğurlu (2016) çalışmalarında;





1 1 1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 , , n , 0 n n n n n n n n n n n n n n x x y z n x y z x x y x x y x y                         

3.FARK DENKLEMLERİ

Bu bölümde fark denklemleri ile ilgili literatürde yer alan bazı genel tanımlara ve teoremlere yer verilecektir.

Tanım 3.1. n ℕ bağımsız değişken ve x bilinmeyen fonksiyon olmak üzere;

( , ( ), ( 1),..., ( )) 0

F n x n x n x n k _{ (3.1)}

eşitliğine bir fark denklemi denir (Bereketoğlu ve Kutay, 2012).

Tanım 3.2. Bir fark denkleminde bilinmeyen fonksiyonun mevcut en büyük ve en

küçük argümentlerinin farkına o denklemin mertebesi (basamağı) denir (Bereketoğlu ve Kutay, 2012).

Tanım 3.3. a n a n₁( ), ₂( ),...,a n , katsayıları ile _k( ) g n , ( ) nn₀ için tanımlı reel değerli fonksiyonlar ve [ , )n₀  

_

n n₀, ₀1,n₀2,...

_

üzerinde a n  olmak üzere _k( ) 0

1

( ) ( ) ( 1) ... _k( ) ( ) ( )

x nk a n x n k   a n x n g n

(3.2)

biçimindeki bir denkleme k yıncı basamaktan lineer fark denklem denir. Bu denklem, ( ) 0

g n  olduğu zaman homojen fark denklemi, aksi durumda homojen olmayan fark

denklemi olarak adlandırılır. Buna göre k yıncı basamaktan bir lineer homojen fark denklem

1

( ) ( ) ( 1) ... k( ) ( ) 0

x nk a n x n k   a n x n 

(3.3)

şeklinde ifade edilir. Ayrıca, bütün a n katsayıları _i( ) a n_i( )a_i şeklinde sabitse, (3.2) denklemine sabit katsayılı, aksi halde değişken katsayılı fark denklem denir (Bereketoğlu ve Kutay, 2012).

Her nn₀ için

1 1( ) 2 2( ) ... r r( ) 0

c f n c f n  c f n 

(3.4)

olacak biçimde hepsi birden sıfır olmayan c c₁, ₂,...,c sabitleri var ise, bu durumda _r



f n f n1( ), 2( ),...,f nr( )



cümlesine [ , )n  üzerinde lineer bağımlıdır denir. (3.4) eşitliği 0

her nn₀için sadece ve sadece c₁ c₂ ...c_r  durumunda sağlanıyorsa, 0



f n f n1( ), 2( ),...,f nr( )



cümlesine [ , )n  üzerinde lineer bağımsızdır denir 0

(Bereketoğlu ve Kutay, 2012).

Teorem 3.1. I reel sayıların herhangi bir alt aralığı olmak üzere, f I:   sürekli I I

diferansiyellenebilen bir fonksiyon olmak üzere  x_1,x₀ başlangıç şartları için I

1 ( , 1) 0

n n n

x_  f x x _ n (3.5) denklemi bir tek

 

_{n 1}

n

x _ çözümüne sahiptir (Elaydi, 1995).

Tanım 3.5. Eğer xnoktası için f x x( , )x ise x’e (3.5) denkleminin denge noktası denir (Elaydi, 1995).

Tanım 3.6. Eğer  n 0için x_1,x₀ iken J x_n olacak şekilde bir J J I alt aralığı varsa, bu aralığa (3.5) denkleminin değişmez aralığı denir (Elaydi, 1995).

Tanım 3.7. x, (3.5) denkleminin denge noktası olmak üzere:

 Eğer x_1,x₀ olmak üzere her J  0 için, x₀x  x_1x  iken her

0

n  için, x_nx  olacak şekilde bir  0 sayısı varsa, xdenge noktası kararlıdır,

 Eğer x denge noktası kararlı ve x_1,x₀ iken J lim _n

nx x olacak şekilde,

0 1

x x  x x  şartını sağlayan   sayısı varsa, 0 x denge noktası

lokal asimptotik kararlıdır,  Eğer her x_1,x₀ iken J lim _n

 Eğer xdenge noktası kararlı ve çekim noktası ise, x denge noktası global asimptotik kararlıdır,

 Eğer x denge noktası kararlı değil ise, kararsızdır,

 Eğer x_1,x₀ iken J x₀x  x₁x  ve bazı N  1 sayıları için

N

x x r olacak şekilde bir r 0 sayısı varsa, x denge noktasına repeller denir

(Elaydi, 1995).

Tanım 3.8. Eğer

_{ }

x_n dizisi için p, x_{n p} x_n eşitliğini sağlayan en küçük pozitif tamsayı olmak üzere,

_{ }

x_n dizisi p periyotludur denir (Elaydi, 1995).

Tanım 3.9. Eğer

_{ }

x_n dizisinde sonlu sayıda terim hariç tutulduğunda, geriye kalan sonsuz sayıdaki terim için p, x_{n p} x_n eşitliğini sağlayan en küçük pozitif tamsayı olmak üzere,

_{ }

x_n dizisine er geç p periyotludur denir (Elaydi, 1995).

Tanım 3.10. (3.5) denkleminde, f x x( ,_{n n1}) fonksiyonunu f u v şeklinde alırsak; ( , )

( , )x f r u x    ve ( , )x f s v x    olmak üzere; 1 1 n n n y _ ry sy _ (3.6) denklemi elde edilir. Bu denkleme (3.5) denkleminin x denge noktası civarındaki lineer denklemi denir.

(3.6) denkleminin karakteristik denklemi ise;

2 _{r s 0}

    (3.7) şeklindedir (Elaydi, 1995) .

Teorem 3.2.(Lineer Kararlılık Teoremi)

a. Eğer (3.7) denkleminin her iki kökü de mutlak değerce 1’den küçük ise, x

b. Eğer (3.7) denkleminin köklerinden en az biri mutlak değerce 1’den büyük ise, xdenge noktası kararsızdır.

c. Eğer (3.7) denkleminin her iki kökünün de mutlak değerce 1’den küçük olması için gerek ve yeter şart r   1 s 2 olmasıdır. Bu durumda, x

denge noktası lokal asimptotik kararlıdır.

d. Eğer (3.7) denkleminin her iki kökünün de mutlak değerce 1’ den büyük olması için gerek ve yeter şartlar s 1 ve r  1 s olmasıdır. Bu durumda,

x denge noktası repellerdir. e. Her x_1,x₀ için eğer I lim _n

nx x ise; o zaman x denge noktası global

çekimlidir denir.

f. Eğer x denge noktası kararlı ve global çekimli ise x’e global asimptotik kararlıdır denir.

g. Eğer (3.7) denkleminin, bir kökünün mutlak değerce 1’den büyük, diğer kökünün mutlak değerce 1’den küçük olması için gerek ve yeter şartlar

2

4 0

r  s ve r  1 s olmasıdır. Bu durumda, x denge noktası kararsızdır

(Chatterjee ve ark., 2003).

Tanım 3.11.

 

_{n 1}

n

x _ dizisinde her n için Px_n Q olacak şekilde P ve Q pozitif

sayıları varsa

 

_{n 1}

n

x _ dizisine sınırlıdır denir (Elaydi, 1995).

Tanım 3.12. 1 1 1 2 1 3 ( , , ) ( , , ) ( , , ) n n n n n n n n n n n n x f x y z y f x y z z f x y z       (3.8)

fark denklem sistemi verilsin. Eğer x y z (3.9) şartları sağlarsa, , , ( , , )x y z I1I2I3

noktası (3.8) denklem sisteminin denge noktası olarak adlandırılır

1 2 3 ( , , ) , , , ( ) ( , ) x x y z y x y z z x f f f y z    (3.9) (Nasri ve ark., 2005).

Tanım 3.13.   0 için ( ,x₀ y₀,z₀) ( , , ) x y z  iken (( ,x y z_{0 0}, ₀)I₁I₂I₃)

0 n

  için ( ,x y_{n n},z_n) ( , , ) x y z 

olacak şekilde  0 mevcut ise (3.8) sisteminin denge noktası olan ( , , )x y z kararlıdır

denir. Aksi halde, kararsızdır (Nasri ve ark., 2005).

Tanım 3.14. Eğer (3.8) sisteminin denge noktası kararlı ve ( ,x y z_{0 0}, ₀)I₁I₂I₃ için

0 0 0

( ,x y ,z ) ( , , ) x y z 

olacak şekilde   varsa ve 0 lim ( ,_{n n}, _n) ( , , ) 0

n x y z  x y z 

ise (3.8) sisteminin denge noktası asimptotik kararlıdır (Nasri ve ark., 2005) .

Tanım 3.15. Eğer (3.8) sisteminin denge noktası kararlı ve ( ,x y z0 0, 0)I1I2I3 için

lim ( ,_{n n}, _n) ( , , ) 0

x x y z  x y z 

ise (3.8) sisteminin denge noktası olan ( , , )x y z global asimptotik kararlıdır denir (Nasri

ve ark., 2005).

Teorem 3.3. (3.8) denklem sisteminin ( , , )x y z denge noktasında jakobiyen matrisi

1 1 1 ( , , ) ( , , ) ( , , ) 2 2 2 ( , , ) ( , , ) ( , , ) 3 3 3 ( , , ) ( , , ) ( , , ) , , ( ) x y z x y z x y z x y z x y z x y z x y z x y z x y z df df df dx dy dz df df df x y z dx dy dz df df df dx dy dz J                          _{     }                        

olup, bu jakobiyen matrisinin karakteristik polinomu





( ) det ( , , ) 0

P   J x y z I 

ile verilsin.

Bu polinomda aşağıdaki eşitlikler doğrudur;

 P( ) nın köklerinden en az biri 1 den büyükse denge noktası ( , , )x y z

kararsızdır (Nasri ve ark., 2005).

4. BAZI LİNEER OLMAYAN FARK DENKLEM SİSTEMLERİNİN ÇÖZÜMLERİNİN PERİYODİKLİĞİ

Bu bölümde elde edilen sonuçlar Kılıklı (2011), Emre (2014) ve Hanedar’ın (2014) çalışmalarındaki yöntemlerden yararlanılarak elde edilmiş olup ilk kez ele alınan orijinal sonuçlardır.

Sekiz alt bölümden oluşan bu bölümde ilk olarak,

0, 1, 0, 1, 0, 1, 0 (0, ) p q_ q r_ r s_ s   ve p₀ r s₀, _i q_ir q_i, _i r i_i,  



1, 0



olmak üzere, 1 1 1 1 1 n n n n n n p s r q q r         , 1 1 1 1 1 ( ) 1 n n n n n n n n n r s r q q s r q r            , 1 1 n n n n r s r q     , 1 1 1 1 1 ( ) 2 n n n n 1 n n n n n n n r s r q s s r q r p r              (4.1)

lineer olmayan fark denklem sisteminin çözümünün periyodikliği incelenmiştir.

Sonrasında (4.1) sisteminde A B C D ℝ, , , 

 

0 parametreleri kullanılarak yazılan,

1 1 1 n n n n n n A B p s r q q r         , 1 1 1 1 1 ( ) n n n n n n n n n Cr s r q A q s r q r            , 1 n n n n A r s r q     , 1 1 1 1 1 ( ) 2 _{n n n n} n n n n n n n Cr s r q A D s s r q r p r              (4.2)

lineer olmayan fark denklem sisteminin çözümünün periyodikliği incelenmiştir.

Benzer şekilde (4.3) bölümünde,

1, 0, 2, 1, 0, 2, 1, ,0 2, 1, 0 (0, ) p_ p q_ q_ q r_ r_ r s_ s_ s   , s_i q_i r q_i, _i r i_i,   



2, 1, 0



ve





, 1, 0 i i p r i  olmak üzere;

1 1 1 1 2 2 1 1 n n n n n n p s r q q r            , 2 2 2 1 1 1 1 1 ( ) 1 _{n n n n} n n n n n r s r q q s r q r               , 1 1 1 1 1 n n n n r s r q        , 2 2 2 1 1 1 1 1 1 1 ( ) 2 _{n n n n} 1 n n n n n n n r s r q s s r q r p r                   (4.3)

lineer olmayan fark denklem sisteminin çözümünün periyodikliği incelenmiştir.

Sonrasında (4.3) sisteminde A B C D ℝ, , , 

 

0 parametreleri kullanılarak yazılan,

1 1 1 1 2 2 n n n n n n A B p s r q q r            , 2 2 2 1 1 1 1 1 ( ) n n n n n n n n n Cr s r q A q s r q r               , 1 1 1 1 n n n n A r s r q        , 2 2 2 1 1 1 1 1 1 1 ( ) 2 _{n n n n} n n n n n n n Cr s r q A D s s r q r p r                   (4.4)

lineer olmayan fark denklem sisteminin çözümünün periyodikliği incelenmiştir.

Çalışmanın (4.5) bölümünde, 2, 1, 0, 3, 2, 1, 0, 3, 2, 1, ,0 3, 2, 1, 0 (0, ) p_ p_ p q_ q_ q_ q r_ r_ r_ r s_ s_ s_ s   , p_i r i_i,   

_

2, 1, 0

_

ve





, , 3, 2, 1, 0 i i i i i s q r q r i    olmak üzere; 1 2 2 2 3 3 1 1 n n n n n n p s r q q r            , 3 3 3 1 2 2 2 1 ( ) 1 _{n n n n} n n n n n r s r q q s r q r               , 1 2 2 2 1 n n n n r s r q        , 3 3 3 1 2 2 2 1 2 2 ( ) 2 _{n n n n} 1 n n n n n n n r s r q s s r q r p r                   (4.5)

lineer olmayan fark denklem sisteminin çözümünün periyodikliği incelenmiştir.

(4.6) bölümünde ise (4.5) sisteminde A B C D ℝ, , , 

 

0 parametreleri kullanılarak yazılan, 1 2 2 2 3 3 n n n n n n A B p s r q q r            , 3 3 3 1 2 2 2 1 ( ) n n n n n n n n n Cr s r q A q s r q r               1 2 2 2 n n n n A r s r q        , 3 3 3 1 2 2 2 1 2 2 ( ) 2 _{n n n n} n n n n n n n Cr s r q A D s s r q r p r                   (4.6)

lineer olmayan fark denklem sisteminin çözümünün periyodikliği incelenmiştir.

Sonrasında önceki altı bölümde incelenen sistemlerin periyotlarının belirli bir düzen içerinde olduğu göz önüne alınarak bu sistemlerin genel hali olan;

1 1 0 1 1 0 1 1 0 1 1 0 , ,..., , , , ,..., , , , ,..., , , , ,..., , (0, ) k k k k k k k k p_ p_{ } p_ p q_{ } q_ q_ q r_{ } r_ r_ r s_{ } s_ s_ s   ve





, , 1,..., 0 i i p r i k  k , s_i q_i r q_i, _i r i_i,    

_

k 1, k,..., 0

_

, k ℕ olmak üzere; 1 ( 1) ( 1) 1 1 n n k n k n k n k n k p s r q q r              , ( 1) ( 1) ( 1) 1 1 ( ) 1 n n k n k n k n n k n k n k n r s r q q s r q r                  1 1 n n k n k n k r s r q        , ( 1) ( 1) ( 1) 1 1 ( ) 2 n n k n k n k 1 n n k n k n k n n k n k r s r q s s r q r p r                      (4.7)

lineer olmayan fark denklem sisteminin çözümünün periyodikliği incelenmiştir.

Son olarak (4.7) sisteminde A B C D ℝ, , , 

 

0 parametreleri kullanılarak yazılan,

1 ( 1) ( 1) n n k n k n k n k n k A B p s r q q r              , ( 1) ( 1) ( 1) 1 ( ) n n k n k n k n n k n k n k n k Cr s r q A q s r q r                  , 1 n n k n k n k A r s r q        , ( 1) ( 1) ( 1) 1 ( ) 2 n n k n k n k n n k n k n k n k n k n k Cr s r q A D s s r q r p r                      (4.8)

4.1. (4.1) FARK DENKLEM SİSTEMİNİN PERİYODİKLİĞİ Bu bölümde; 0, 1, 0, 1, 0, 1, 0 (0, ) p q_ q r_ r s_ s   ve p₀ r s₀, _i q_ir q_i, _i r i_i,  

_

1, 0

_

olmak üzere; 1 1 1 1 1 n n n n n n p s r q q r         , 1 1 1 1 1 ( ) 1 _{n n n n} n n n n n r s r q q s r q r            , 1 1 n n n n r s r q     , 1 1 1 1 1 ( ) 2 _{n n n n} 1 n n n n n n n r s r q s s r q r p r              (4.1)

lineer olmayan fark denklem sisteminin çözümlerinin periyodikliği incelenmiştir.

Öncelikle sistemde bulunan denklemlerin iyi tanımlı olup olmadıklarına bakalım. p q₀, _1,q r₀, _1, ,r s_{0 1},s₀(0, ) , p₀ r₀, s_i q_ir q_i, _i r i_i,  

_

1, 0

_

ve

0, 1, 0, 1, ,0 1, 0

p q_ q r_ r s_ s herhangi pozitif başlangıç şartları olmak üzere (4.1) denkleminde n 0 alırsak; 1 0 0 0 1 1 1 1 p s r q q r      , 0 1 1 1 1 0 0 0 1 ( ) 1 r s r q q s r q r           , 1 0 0 0 1 r s r q    , 0 1 1 1 1 0 0 0 1 0 0 ( ) 2 r s r q 1 s s r q r p r            

eşitlikleri elde edilir. Sonraki her adımlarda indisler birer arttırılır ve bir önceki adımlarda elde edilen sonuçları yerine koyarak gerekli sadeleştirmeleri yaparsak aşağıdaki eşitlikler elde edilir;

2 0 0 1 1 1 0 0 0 0 1 1 1 p p r s r q q r q r          , 1 0 0 0 2 0 0 1 1 1 0 0 ( ) 1 r s r q 1 q p r s r q r r          , 2 0 0 1 1 1 1 r p r s r q      , 1 0 0 0 2 0 0 1 1 1 1 1 0 1 1 0 ( ) 2 1 1 2( ) r s r q s p r q r s r q r p r r                1 3 1 1 1 1 1 1 0 1 1 1 1 1 ( ) r p p r q r q r r s r q                , 3 1 1 _{1 1 1} 0 0 0 1 1 q p r s r q r q_ r_         ,

3 1 1 1 1 1 r p r q_ r_     , 3 1 1 ₁ 0 0 _{1 1} 0 0 0 0 0 1 2 2( ) s p r q r s r q q r r q_ r_             0 4 0 0 0 1 0 0 0 0 0 1 1 ( ) r p r q r r s r q q r         , 4 0 0 1 1 1 0 0 0 0 1 1 1 q s r q q r q r p r          , 4 0 0 1 r q r   , 0 1 1 1 4 1 1 1 1 1 0 0 0 0 0 0 1 ( ) 2 2 1 ( ) ( ) r s r q s s r q q r q r q r p r r                   1 5 1 1 1 0 1 1 1 0 0 0 1 1 ( ) r p r q r r s r q s r q              , 1 5 1 1 1 1 1 1 0 1 1 1 1 1 ( ) r q q r q r p r r s r q                , 1 5 1 1 0 1 1 1 1 ( ) r r q r r s r q          , 1 0 0 0 1 5 1 1 1 1 1 1 0 0 1 1 1 0 ( ) 2 2 1 1 ( ) r s r q r s q r q r p r r r s r q r                    0 6 0 0 0 0 1 0 0 0 1 1 1 1 ( ) r p r p r p r s r q s r q           , 0 6 0 0 0 0 0 0 1( 0 0 0) r q q r r q r q r s r q          , 0 6 0 1( 0 0 0) r r r r s r q     , 0 6 0 0 0 0 0 0 0 0 0 1 0 0 0 1 2 1 2 ( ) r s q r r q r s r q s r s r q r             

Bu şekilde işleme devam edersek, p0 r0, si qir qi, i r ii,  



1, 0



olduğundan hiçbir adımda rasyonel ifadelerin paydasının sıfır olmadığı görülmektedir. Elde edilen tüm ifadeler p q₀, _1,q r₀, _1, ,r s_{0 1},s₀ başlangıç şartlarına bağlı olarak yazılabilmektedir. Başlangıç şartları ne olursa olsun bu durum değişmeyeceği için sistemdeki bütün denklemler iyi tanımlıdır. O halde aşağıdaki teoremi verebiliriz.

Teorem 4.1.1. p q0, 1,q r0, 1, ,r s0 1,s0(0, ) ve p0 r0, si qir qi, i r ii,  



1, 0



olmak üzere, (4.1) denklem sisteminin çözümü



p q r s_n, _n, ,_{n n}



olsun. Bu durumda (4.1) denklem sisteminin çözümleri periyodiktir ve periyodu altıdır.

İspat: (4.1) fark denklem sisteminde her bir adımda n yerine (n+1) yazarak iterasyon

yöntemi uygularsak aşağıdaki eşitlikler elde edilir;

1 1 1 1 1 n n n n n n p s r q q r         , 1 1 1 1 1 ( ) 1 n n n n n n n n n r s r q q s r q r            , 1 1 n n n n r s r q     , 1 1 1 1 1 ( ) 2 _{n n n n} 1 n n n n n n n r s r q s s r q r p r              2 1 1 1 1 1 1 n n n n n n n n n n p p r s r q q r q r              , 1 2 1 1 1 ( ) 1 n n n n 1 n n n n n n n n r s r q q p r s r q r r               , 2 1 1 1 1 n n n n n n r p r s r q          , 1 2 1 1 1 1 1 1 1 ( ) 2 1 1 2( ) n n n n n n n n n n n n n n n n r s r q s p r q r s r q r p r r                       1 3 1 1 1 1 1 1 1 1 1 1 1 ( ) n n n n n n n n n n n n r p p r q r q r r s r q                     , 3 1 1 1 1 1 1 1 n n n n n n n n n q p r s r q r q r               , 3 1 1 1 1 1 n n n n n r p r q r          , 3 1 1 1 1 1 1 2 2( ) n n n n n n n n n n n n n s p r q r s r q q r r q r                  

4 1 1 1 ( ) n n n n n n n n n n n r p r q r r s r q q r           , 4 1 1 1 1 1 1 n n n n n n n n n n q s r q q r q r p r              , 4 1 n n n r q r    , 1 1 1 4 1 1 1 1 1 1 ( ) 2 2 1 ( ) ( ) n n n n n n n n n n n n n n n n n r s r q s s r q q r q r q r p r r                         1 5 1 1 1 1 1 1 1 1 ( ) n n n n n n n n n n n n r p r q r r s r q s r q                  , 1 5 1 1 1 1 1 1 1 1 1 1 1 ( ) n n n n n n n n n n n n r q q r q r p r r s r q                     , 1 5 1 1 1 1 1 1 ( ) n n n n n n n n r r q r r s r q             , 1 1 5 1 1 1 1 1 1 1 1 1 ( ) 2 2 1 1 ( ) n n n n n n n n n n n n n n n n n n r s r q r s q r q r p r r r s r q r                          6 1 1 1 1 1 ( ) n n n n n n n n n n n n n r p r p r p r s r q s r q                , 6 1( ) n n n n n n n n n n n n r q q r r q r q r s r q            , 6 1( ) n n n n n n n r r r r s r q       , 6 1 1 2 1 2 ( ) n n n n n n n n n n n n n n n n r s q r r q r s r q s r s r q r                

4.2. (4.2) FARK DENKLEM SİSTEMİNİN PERİYODİKLİĞİ Bu bölümde, 0, 1, 0, 1, ,0 1, 0 (0, ) p q_ q r r s_{ } s   ,p₀r s₀, _iq_ir q_i, _ir i_i,  

_

1,0

_

ve A B C D ℝ, , , 

 

0 olmak üzere, 1 1 1 n n n n n n A B p s r q q r         , 1 1 1 1 1 ( ) n n n n n n n n n Cr s r q A q s r q r            , 1 n n n n A r s r q     , 1 1 1 1 1 ( ) 2 n n n n n n n n n n n Cr s r q A D s s r q r p r              (4.2)

lineer olmayan fark denklem sisteminin çözümlerinin periyodikliği incelenmiştir.

Öncelikle sistemde bulunan denklemlerin iyi tanımlı olup olmadıklarına bakalım. (4.2) fark denklem sistemi (4.1) sisteminin A B C D, , , parametrelerine bağlı

şekildeki ifade edilmiş hali olduğundan, (4.1) sistemindeki denklemler iyi tanımlı ve

, , ,

A B C D ℝ

 

0 olduğu için (4.2) sistemindeki denklemler de iyi tanımlıdır. O halde aşağıdaki teoremleri verebiliriz.

Teorem 4.2.1. p q₀, _1,q r₀, _1, ,r s_{0 1},s₀(0, ) , p₀ r₀, s_i q_ir q_i, _i r i_i,  



1, 0



ve , , ,

A B C D ℝ

 

0 olmak üzere, (4.2) denklem sisteminin çözümü

_

p q r s_n, _n, ,_{n n}

_

olsun. Bu durumda (4.2) denklem sisteminin çözümlerinin altı periyotlu olması için gerek ve yeter şart BDC olmasıdır.

İspat: Yukarıda belirtilen başlangıç şartları altında (4.2) denklem sisteminin

çözümlerinin altı periyotlu olduğunu varsayalım. Bu durumda (4.2) denklem sisteminde iterasyon yöntemi kullanılarak aşağıdaki eşitlikler yazılabilir.

1 1 1 n n n n n n A B p s r q q r         , 1 1 1 1 1 ( ) n n n n n n n n n Cr s r q A q s r q r            , 1 n n n n A r s r q     , 1 1 1 1 1 ( ) 2 _{n n n n} n n n n n n n Cr s r q A D s s r q r p r              2 1 1 1 ( _{n n}) n n n n n n n n A p r A B B p s r q q r D q r              , 1 2 1 1 1 ( ) ( ) n n n n n n n n n n n n Cr s r q A p r A AC q s r q r D r               , 2 1 1 1 ( _{n n}) n n n n A p r A r s r q D          , 1 1 1 2 1 1 1 1 1 ( ) 2 ( ) ( ) n n n n n n n n n n n n n n n n Cr s r q A p r D q r A D AC s s r q r p r D r B                      1 1 1 3 1 1 1 1 1 1 1 ( ) ( ) ( ) n n n n n n n n n n n n A p r B AB Br p D q r D q r Cr s r q                     , 1 1 3 1 1 1 ( ) ( ) ( ) n n n n n n n n n A p r AC AB q C s r q D r D q r               , 1 1 3 1 1 ( ) ( ) n n n n n A p r AB r D D q r          , 1 1 3 1 1 1 2 ( ) ( ) 2 ( ) ( ) ( ) n n n n n n n n n n n n n A p r AC D q r AB D q r s C s r q D r B D q r B                   4 1 ( ) ( ) ( ) n n n n n n n n n n n Br Br AB AB p D q r Cr s r q D q r AC           , 4 ( 1 1 1) ( ) ( ) n n n n n n n n n n AB AB CD q C s r q D q r D q r p r              , 4 ( ) n n n AB r D q r    , 1 1 1 1 1 4 1 1 1 1 ( ) ( ) 2 2 ( ) ( ) ( ) n n n n n n n n n n n n n n n n n D q r CDr s r q AB AB CD s C s r q D q r B D q r p r Br                        

1 1 5 1 1 1 1 1 ( ) ( ) ( ) n n n n n n n n n n n n Br ABr AB B p D q r AC CDr s r q C s r q                  , 1 1 1 5 1 1 1 1 1 1 1 ( ) ( ) ( ) n n n n n n n n n n n n ABr CD q r AB CD q D q r p r CDr s r q B                     , 1 5 1 1 1 1 1 ( ) ( ) n n n n n n n n ABr AB r D q r CDr s r q             , 1 1 1 1 5 1 1 1 1 1 1 1 ( ) 2 ( ) 2 ( ) ( ) n n n n n n n n n n n n n n n n n n CDr s r q ABr CD q r AB CD ACD s D q r p r Br CDr s r q B Br                          6 1 1 1 1 ( ) ( ) ( ) n n n n n n n n n n n n n ABr B Br B p r Bp p CDr s r q C s r q CD CD CD                , 6 1 ( ) ( ) ( ) n n n n n n n n n n n n n ABr CD q r Br CD q r B DC CD q r q CDr s r q B CD B DC B B           _  _      , 6 1( ) n n n n n n n ABr Br r CDr s r q CD       , 6 1 1 2 ( ) ( ) 2 2 2 ( ) ( ) n n n n n n n n n n n n n n n n n ABr CD q r ACD s CDr s r q B Br Br CD DC B CD DC q r s r q r s CD B B CD B B                  _  _   

bulunur. Sistemin altı periyotlu olabilmesi için son eşitliklerden BDC olacağı açıktır.

Teoremin yeter şartının ispatı için (4.2) denklem sisteminde BDCalarak sistemimizin altı periyotlu olduğunu göstermeliyiz. (4.2) denklem sisteminde BDC

olsun; 1 1 1 n n n n n n A DC p s r q q r         , 1 1 1 1 1 ( ) n n n n n n n n n Cr s r q A q s r q r            , 1 n n n n A r s r q     , 1 1 1 1 1 ( ) 2 _{n n n n} n n n n n n n Cr s r q A D s s r q r p r              2 ( _{n n}) n n n A p r DC p D q r      , 2 ( _{n n}) n n A p r AC q D r     , 2 ( _{n n}) n A p r r D    , 1 1 2 2 ( _{n n}) _{n n} n n A p r AC q r s D r C        