INVESTIGATION
OF EFFECTS OF CROSS-SECTIONS
ON THE
RAY-EFFECT DISTORTIONS
S. SAÖLAM1
Abstract
In this study, a wellknown numerieal method has been used to solve neutron transport equation and the ray-effeet anomaly observed on the results of the method hase been introdueed. To examine the effeets of eross-seetions on the ray-effeet, two Benehmark problems have been ehosen as test problems. Then, two dimensional transport code, TWOTRAN-1I has been exeeuted for these problems for84-816 approximations. Finally, by eomparing all the results with eaeh other, the effeets of eross-seetions have been examined in detail.
1. INTRODUCTION
The main problem of reactor physics is determination of neutron distribution in a system; such as nuclear core. This is important because of the evaluation of different nuclear reactions. To determine distribution of neutrons, the process of neutron transport is investigated [1-2]. The neutron transport is given by neutron transport equation which states a mathematical balance on the physical production and losses of particles (Eg.l and Eg.2).
~ ~ ~ ~ ~ L ~(r ,E,Q, t) =Q(r ,E,Qt) (1) ~ 1 a ~ ~ ~CO ~ ~ ~ L=--Q.v+Li(rE)- J dQ'J dE'Ls(r,E'~E,Q'~Q) v at 4rr o ~CO ~
- X(E)f dQ J dE'v(E')L f(r ,E') (2)
41t o
in nuclear reactor design and analysis, the solution of transport equation plays an important role. This solution consists of complete distribution of particles throughout the space, energy, direction of motion and time portions of the problem. However, it is very difficult to solve this equation, exeept for simple problems sinee it has an integro -differential form with seven variables. Other faetors have also an effeet complieating the solution, sueh as eomplex energy dependenee of eross-seetions and geometrical arrangement of materials used in the reaetoT. Therefore, the neutron transport equation together with the appropriate boundary conditions is solved usually by numerical solution methods. These methods may be probabilistie methods (i.e. Monte Carlo) or deterministie methods (i.e. PN
-spherieal harmonies expansion method and SN -diserete ordinates method [3-4]).
S. Saglam
2. METHOD AND RAY-EFFECT
Discrete Ordinates Method, SN, that is the main subject of this study is one of the important deterministie solution methods of neutron transport equation. The method is straightforward and widely used in transport ca1culations. in the method, a set of diserete directions (or ordinates) for angular variable is chosen and transport equation is evaluated for these directions by suitable averaging processes. The choice of these ordinates is not arbitrary; it seeks to satisfy some conditions [1,2], for example: they must satisfy certain mechanical integration requirements. The derivatives appearing in the equation are replaeed by a corresponding discrete representation by us ing finite difference techniques (i.e. forward difference, diamond difference ete.) and the integrals in the equation are replaced by numerical integration schemes (i.e. standard Gauss quadratures: Gauss - Legendre quadrature (Eg. 3) and Gauss - Chebyshev quadrature (EgA».
+1 n J F(x)dx =
L
wj F(xj )(3) -1 I=O -1 1 J ~F(X)dx=fw.F(X.)(4) -1 ~1-
X2 I=O ii
Where Wjare cal1edas the weights of the quadratures.
in this study, the angularflux is expanded in a series of Legendre polynomials [4]as,
00 n
<i>=
L
(ln +1)L
R~<i>~ (5)n=O k=O
and the expansion coefficients are given by, +1 ir
<i>~= J d~ J d<pR~ <1>/2n (6)
-1 o
The integral given above, according to the Gauss-Legendrequadrature consideration is approximated by the sum [4],
Where, <Pm is defined in TWOTRAN-II code as,
-1( 2 2 112 (8)
<Pm = tan l-~m-~m) /Y1m , Y1m>O
And, the total source is given as S ..glJm by the sum of,
IGM iseT n k k
(SS)gijm=(Scartersource)gijm= h=! n=O
L
L
(2n+1)0'snh--+gk=OL
R mmNnhij.. IGM O
(FS)gijm=(Fissionsource)gijm=Xgh=!L VO'fuNOhij(ll)
IQAN n k k
(IS)gjjm=(hihomogeneous source) gijm= n=OL (2n+1)k=OL Rnm Qngij
Where,
IGM: number of groups used, ISCT: scattering order,
IQAN: distributed sources anisotropy order.
A1though the SNmethod has some advantages to solve transport equation, sometimes for some regions having strong absorbers and localized neutron sources some unexpected problems have been met; such as ray-effect. The ray-effect distortions that plague the method are anomalous ripples that appear in the scalar flux in two or three dimensional problems. These nonphysical bumps can be confused with physical ones, especiaIly in deep penetration applications [4-5]. Nowadays, several remedies for eliminating or mitigating that problem have been proposed. it seems that the practical remedy for the ray-effect is to increase the order of SNmethod (the number of directions). hi general when this is done, the frequency of oscillations becomes higher and the magnitude becomes smaIler. However, while substantial improvement results, ray-effects tend to be remarkably persistent even for high order SNapproximations [2,6].
3. RESUL TS OF THE STUDY
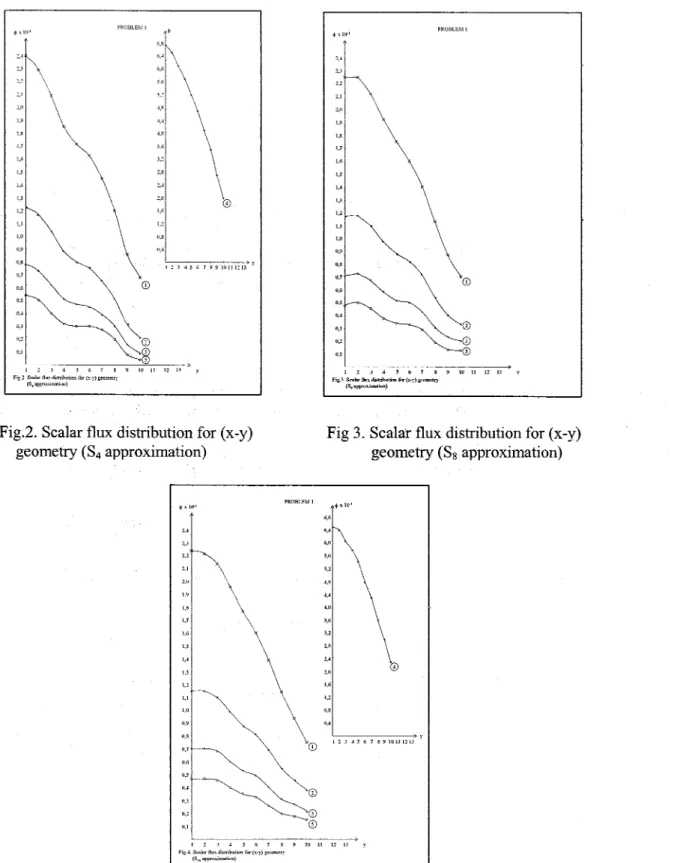
In this study, to demonstrate the effects of cross-sections on the ray-effect, one of important two dimensional transport codes, TWüTRAN-II has been chosen and executed for two test problems. Problem 1 is a wellknown benehmark problem given in (x-y) two dimensional cartesian geometry [7]. hi this problem there is a flat isotropic source at the left bottom comer of a square region. The boundary conditions are given as reflective on the bottom and the left sides, and vaeuum on the top and the right sides of the region (Fig. 1).
S. Saglam
Vacuum Boundary
Reflective Boundary
Fig.1: Sample problem in (x-y) geometry (Problem 1)
The parameters of problem 1 have been given in tab1e 1. First, the code has been executed for this problem and distributions of sca1ai flux have been observed for S4 - SI6 approximations. The ray-effect distortions in theflux have been·examined by changing the value s of scattering cross-section for each SN approximation (Fig2-4). Then, problem 1 has been adapted to cy1indrica1 geometry (problem 2) and the effectof scattering cross-section on the ray-effect distortions has been examined in the simi1ar way. Theparameters of the problem 1, given in tab1e 1, are a1so valid for the second problem, and the boundary conditions are taken to be the same. The results of problem 2 are demonstrated in figures (Fig.5-7). Lt =1.0 For böth of problems L f= 0.0 S=1.0La LsCase . 0.00.500.25 0.7510.501.042 , 0.75 0.25 . 3 1.0 0.05
Table 1: Problem parameters for sample propJems
Accordingto the figuresobtained from problem 1, the case 4 which represents the scattering medium, is the best of all cases. it does not exhibit any ray-effect as expected [8,9]. Among the other cases, case 1 seems better than the others. If we compare all SN approximations use d in case 1, we observe that the S4 approximation gives ray-effect. But, as the order of SN approximations is getting higher a considerable mitigation is obtained. Because, in the 10w order SN approaches, such as S4, the number of characteristic discrete directions allowed for partide streaming is restricted. Consequently, streaming contributions to the flux at a given position in the medium are limited to contributions from those characteristic directions in which source are visible. On the other hand, although the graph
MM
=
(ISN)*
(ISN+2)/8 Where,MM: number of directions per octant ISN: order of SN approximation
Besides, the cas e 5 which is a purely absorbing medium, is the worst of all cases as expected. in such medium a poor value of scalar flux is obtained no matter how many discrete directions are used.
Except for the magnitude of flux, this conelusion mentioned above is also valid for (r-z) cylindrical geometry (for problem 2) as seen in the figures, Fig.5, Fig.6 and Fig.7.
4. CONCLUSION
in this study, we tried to observe the ray-effect distortions depend upon the values of scattering and absorption cross-sections, by using two benehmark problems. We chose the best and the worst cases of all used in the study. We use d different SNapproximations, such as S4, S8, Sio, SI6 for each case as seen in the figures. By comparing these figures obtained from two problems we tried to make a conclusion about "the best" and "the worst" cases. But, the study mentioned here has not been completed yet. This artiele may be the first chapter of the whole study. For further study, we are planning to examine different boundary conditions for these problems. Af ter completed all the examinations we planned, we will try some remedies to eliminate or strongly mitigate the ray-effect.
in this study, for the iteration count comparisons, no acceleration method was used to speed up convergence. This work has been operated by linux computer system.
Acknowledgments
The author is grateful to Istanbul Technical University staff for computer support. References
[1] R.D.O'dell and R.E.Alcouffe, Transport Calculations for nuclear analysis: Theory and guidelines for
effeetive use of transport eodes, Los Alamos Lab.Report, LA-I0983, (1987).
[2] E.E.Lewis and W.F.Miller Jr., Computational Methods of Neutron Transport, John Wiley and Sons Publ.,
(1984).
[3] J.H.Mathews, Numerical Methods for Mathematics, Science and Engineering, Prentiee Hall Inl. Ine.,
(1992).
[4] K.D.Lathrop and F.W. Brinkley, TWOTRAN-II: An Interfaeed Exportable Version of the Twotrans Code
for Two Dimensional Transport, Los Alamos Scientific Lab.Report, (1973).
[5] lE.Morel, T.A.Wareing, R.B.Lowrie, and D.K.Parsons, Analysis of Ray-Effeet Mitigation Teehniques,
Nucl.Sci.Eng., 144, (2003), i.
[6] V.Khromov, E.Kryuehh, G.Tikhomirov, L. Coneharov and, V.Kondakov, Nucl.Sci.Eng., 121, (1995), 264.
[7] E.M.Gelbard, Benehmark Problem S-Al, Argonne Code Center Benchmark Problem Book, ANL-7416,
Suppl. 1, Argonne National Lab, (1972).
[8] T.Noh, w.P. MilIer Jr., and lE. Morel, Nucl.Sci.Eng., 123, (1996), 38.
S, Saglam <!lxio·' 6,8 "',<10"' I,S i,' I,' l,i i,l i,o O,, 0,_ 0,1 O,, 0,5 0,4 0,2 0,1 i 2 3 " 5 6 7 8 9 Fig.2_S""l:irllu:>i:di:l1ribuiionlbr(x_y)goomeirr (S.appro:Ym3tion) I,' 1,2 0"1 0,4 ;y 1234S61g91o-111213 . --> 1213 2,3 2,1 2,U I,' 1,1 I,' 1,-1,2 1,1 1,0 O,, O,, 0,1 ",' O,, O,, 0,1 ---> i 2 3 .• 5 6 7 8 9 LO IL 12 13
Fig,3. 8ciilor~" dililribalim liir(x·y)1:<omdiy (S.approximalion)
Fig.2. Scalarflux distribution for (x-y) geometry (S4 approximation)
<1>"Ht'
Fig 3. Scalar flux distribution for (x-y) geometry (Ss approximation) ',' 2,4 2,2 2,1 2,(1 1,9 I,' 1,1 I,' I,' I,' 1,3 \,2 0,2 11,1
o
o
:1 " 5 6 7 Fig ...i.SL"h"tluxdi,iribuiioiiliir(x·y)gcoineiry (S"upp",xiniatjun)PROlllEM2 <ji~10-' 7,2 rp ~10-' ,i)) 1,2 0,8 0,.1 12345(18911)11> •. O,~ 0,2 i 2 3 .• 5 6 7 8 9 Fig.5.S<.-aOirilu"dii;lribuiionlhr(r..z)geomell)' (S~approxirnation)
Fig.5. Scalar flux distribution for (r-z) geometry (S4 approximation) ~ xlti·, .1,2 ',0 '," 3,6 3,.1 ,. 3,11 2,8 2,6 2,' 2,2 2,0I," 1,0 I,' 1,2"O 0,8/
"
~ 'Ci) U,r. O,' u,i i 2 3 .1 5 6 7 Fig.7.:>Cal:irlhi"di<iribuiionliir(r-z)gcolOl.1r) (S"apprmÜinati"n) 3,2 i 2 3 .i s 6 1 8 Fig.6. ScabrOu",d;"trib~tioiili)r(r'z) i:<.~>llli:lry{S,approximiition)
Fig.6. Scalar flux distribution for (r-z) geometry (Ss approximation)
Fig.7. Scalar flux distribution for (r-z) geometry (S16approximation)
S. Saglam
Keywords
Neutron transport equation Discrete Ordinates Method Gauss-Legendre quadrature Ray-effect distortions Benchmark problems
List of Tables
Table i. Problem parameters for samp1e problems
List of Figures Fig.i. Fig.2. Fig.3. FigA. Fig.5. Fig.6. Fig.7.
Sample problem in (x-y) geometry (Problem 1)
Scalar flux distribution for (x-y) geometry (S4 approximation) Scalar flux distribution for (x-y) geometry (S8 approximation) Scalar flux distribution for (x-y) geometry (S16approximation) Scalar flux distribution for (r-z) geometry (S4apporximation)
Scalar flux distribution for (r-z) geometry (S8 apporximation) Scalar flux distribution for (r-z) geometry (S16apporximation)