FEN BİLİMLERİ ENSTİTÜSÜ
GRAVİTENİN BAZI JEODEZİK PROBLEMLERDE KULLANIMI
Evren ÇANKAYA TONGUR YÜKSEK LİSANS TEZİ HARİTA MÜHENDİSLİĞİ JEODEZİ ANABİLİM DALI
i ÖZET Yüksek Lisans Tezi
GRAVİTENİN BAZI JEODEZİK PROBLEMLERDE KULLANIMI
Evren ÇANKAYA TONGUR
Selçuk Üniversitesi Fen Bilimleri Enstitüsü Harita Mühendisliği Jeodezi Anabilim Dalı
Danışman: Yrd.Doç.Dr. Bayram TURGUT 2010, 53 sayfa
Jüri: Yrd.Doç.Dr. Bayram TURGUT Doç.Dr. Galip OTURANÇ Yrd.Doç.Dr. Aydın ÜSTÜN
Jeodezinin amacı, yeryuvarının çekim alanını belirlemektir. Yeryuvarının şeklinin belirlenmesinde esas olan jeoidin bulunmasıdır. Jeoidi belirlemek için gravite değerinin bilinmesi gerekir. Gravite, çekim kuvvetinin ve merkezkaç kuvvetinin bileşkesi olan top-lam kuvvettir. Bu çalışmada gravitenin temel ilkelerinden, indirgeme ve ölçme yöntemle-rinden bahsedilmiştir. Jeodezide gravitenin en önemli uygulama alanları açıklanmıştır. Uygulama olarak Konya, Karaman, Niğde ve Aksaray illerinin kuşatan bir bölgede enlem, boylam ve deniz yüksekliği bilinen noktalarda EGM08 modeli kullanılarak gravite değer-leri belirlenmiştir. Bulunan gravite değerine boşlukta gravite ve Bouguer indirgemesi ya-pıldıktan sonra grid enterpolasyonu yapılarak grid bölgesinde tekrar boşlukta gravite anomalilerine dönüş yapılmış ve haritalandırılmıştır.
Anahtar Kelimeler: Jeoit, Gravite, Gravite indirgemeleri, Gravite ölçme yön-temleri, Bouguer indirgemesi, Boşlukta gravite indirgemesi.
ii
ABSTRACT Master Thesis
GRAVITY USE SOME GEODESIC PROBLEMS Evren ÇANKAYA TONGUR
Selçuk University
Graduate School of Natural and Applied Sciences Department of Geodesy
Supervisor: Yrd.Doç. Dr. Bayram TURGUT 2010, 53 Pages
Jury: Yrd.Doç.Dr. Bayram TURGUT Doç.Dr. Galip OTURANÇ Yrd.Doç.Dr. Aydın ÜSTÜN
Aim of Geodesy is to determine the gravity of earth in order to determine the shape of the earth, mathematical earth, geodesy, should be known. For Geoid total force of the gravity and centrifugal force joining should be found. In this study, measurement techniques of gravity force is examined and necessary reduction techniques are explained. In Geodesy, most important appliation of gravity is explained. Application as Konya, Karaman, Niğde and Aksaray in the surrounding area, latitude, longitude and height of the sea at points of known gravity values were determined using the EGM08 model. Bougner gravity values and the reduction of gravity in a space after the interpolation grid to grid in back and in space has been converted to gravity anomalies have been mapped.
Key words: Geoid, Gravity, Gravity reduction, Gravity measurement methods, Bouguer reduction, Free air reduction.
iii ÖNSÖ Z
Tezin hazırlanması sırasında bana destek olan danışmanım Yrd.Doç.Dr. Bayram TURGUT’a, yardımlarını esirgemeyen Yrd.Doç.Dr. Aydın ÜSTÜN’e ve hep yanım-da olan çok değerli eşim Vahit TONGUR’a teşekkürlerimi sunarım.
iv İÇİNDEKİLER ÖZET ... i ABSTRACT ... ii ÖNSÖZ ... iii ŞEKİL LİSTESİ ... vi
ÇİZELGE LİSTESİ ... viii
1.GİRİŞ ... 1
2. GRAVİTENİN TEMEL İLKELERİ ... 3
2.1. Newton Kanunu ... 3
2.2. Potansiyel Kuramının Temelleri ... 4
2.3. Fiziksel Yeryüzü ve Yüzeyler... 5
2.4. Jeoit ve Elipsoit ... 6
3. GRAVİTE ... 9
3.1. Gerçek Gravite ve Bileşenleri... 9
3.2. Seviye Yüzeyleri ...12
3.3. Yükseklik Kavramı...13
3.4. Normal Gravite ...16
4. GRAVİTE İNDİRGEMESİ ...19
4.1. Gravite Ölçülerine Yapılan Düzeltmeler ...19
4.1.1. Sürüklenme düzeltmesi ...19
4.1.2. Enlem etkisi düzeltmesi ...20
4.1.3. Yükseklik (Kot) etkisi ve düzeltmesi...20
4.1.3.1. Boşlukta gravite indirgemesi ...21
4.1.3.2. Bouguer indirgemesi ...22
4.1.4. Arazi düzeltmesi ...23
4.1.5. İzostatik etki ve düzeltmesi ...24
v
5. GRAVİTE ÖLÇÜM YÖNTEMLERİ...27
5.1. Yersel Yöntemler ...27
5.1.1. Mutlak gravitenin ölçülmesi...27
5.1.1.1. Sarkaç yardımıyla mutlak gravitenin ölçülmesi ...28
5.1.1.2. Düşen cisim yardımıyla mutlak gravitenin ölçülmesi...29
5.1.2. Bağıl gravitenin ölçülmesi ...29
5.1.2.1 Sarkaç yöntemi...29
5.1.2.2 Burulma terazisi ...30
5.1.2.3 Gravimetre ...31
5.2. Uzaysal Yöntemler ...35
6. JEODEZİDE GRAVİTENİN UYGULAMA ALANLARI ...36
6.1. Stokes İntegrasyonu ...36
6.2. Çekül Sapması Bileşenleri ...38
6.3. Yükseklik Sistemleri ...39
7. SAYISAL UYGULAMA...42
7.1. Sayısal Uygulama Alanı ...42
7.2. GMT (Generic Mapping Tools) ...42
7.3. Gravite ve Anomalilerin Hesaplanması...43
8. SONUÇ ve ÖNERİLER...50
vi ŞEK İL LİS TES İ
Şekil 2.1: Gravitasyon kuvveti ...3
Şekil 2.2: Çekim kuvveti...4
Şekil 2.3: Referans elipsoidi ve jeoit arasındaki farklılıklar ... 7
Şekil 2.4: Referans yüzeyler...7
Şekil 2.5: Ortalama yeryuvarı elipsoidi ... 8
Şekil 3.1: Merkezkaç kuvvet ...9
Şekil 3.2: Gravite vektörü ... 11
Şekil 3.3: Seviye yüzeyleri ve çekül eğrileri... 12
Şekil 3.4: Nivo yüzeyleri ve çekül eğrileri... 13
Şekil 3.5: Jeoit yüksekliği ... 14
Şekil 3.6: Jeoit, kuasi-jeoit ve elipsoit ... 15
Şekil 3.7: Jeopotansiyel ve sferopotansiyel yüzeyler ... 17
Şekil 3.8: Jeopotansiyel ve sferopotansiyel yüzeyler ... 18
Şekil 4.2: Enlem etkisi ... 20
Şekil 4.3: Boşlukta gravite etkisi... 21
Şekil 4.4: Bouguer etkisi... 22
Şekil 4.5: Arazi etkisi... 24
Şekil 4.6: Pratt-Hayford sistemi ... 25
Şekil 5.1: Sarkaç yöntemi ... 28
Şekil 5.2: Serbest düşme yöntemi... 29
Şekil 5.3: Gravimetre... 31
Şekil 5.4: Gravimetre... 32
vii
Şekil 5.6: Kararsız denge durumu ... 33
Şekil 5.7: Worden gravimetresi... 34
Şekil 5.8: Lacoste-Romberg gravimetresi... 34
Şekil 5.9: CHAMP, GRACE ve GOCE uyduları... 35
Şekil 6.1: Çekül sapması... 38
Şekil 6.2: Geometrik nivelman... 40
Şekil 7.1: Ölçü noktalarında boşlukta gravite anomali haritası ... 45
Şekil 7.2: Grid noktalarında Bouguer anomali haritası ... 46
viii Çİ ZELG E L İST ESİ
Çizelge 3.1: Gravite sembolleri... 18 Çizelge 4.1: Türkiyenin yer aldığı enlemlere ait enlem indirgemesi
katsayıları ... 20 Çizelge 4.2: Boşlukta gravite indirgemesi katsayıları ... 21
1. GİRİŞ
Jeodezi kısaca yeryüzünün ölçülmesi ve referans alınan yüzeye yani hesap yapı-lan yüzeye izdüşürülmesidir. Amaç çekim ayapı-lanlarını hesaplamak ve parametreler yar-dımıyla ortalama yer elipsoidi belirlemektir. Yeryuvarının ölçmesi “geometrik kısmını”, çekim alanlarıysa “fiziksel kısmını” oluşturur. Yeryuvarının şeklini, fiziksel yeryüzü ve matematiksel yeryüzü olmak üzere iki kavramda düşünebiliriz. Fiziksel yeryüzünün kar-maşık yapıya sahip olması sebebiyle matematiksel ifadesi imkansızdır (Yerci,1999). Öl-çülerin değerlendirilmesi ve hesaplanması için basit yüzeyler kullanılır. Fiziksel yeryüzü-nün kara kısmı konum ve yükseklik belirlenerek oluşturulur. Fiziksel yeryüzüyeryüzü-nün deniz-lerde kalan kısmıysa yaklaşık bir nivo yüzeyidir. Bunun karaların altından da devam ettiği düşünülürse jeoit elde edilir. Bu da matematiksel yeryüzüdür. Yeryuvarının şeklinin belir-lenmesinde esas olan jeoidin bulunmasıdır. Jeoidi belirlemek için gravite değerinin bilin-mesi gerekir. Gravite, çekim kuvvetinin ve merkezkaç kuvvetinin bileşkesi olan toplam kuvvettir (Turgut, 1996).
Yeryüzünde ölçülen gerçek gravite değeri ile hesaplanan gravite değeri doğrudan karşılaştırılamaz. Deniz yüzeyine indirgemesi gerekir. Fiziksel yeryüzünde ölçülen gravite üzerindeki etkiler kaldırılarak gravite değerini hesaplamış oluruz. Gravite ölçüm yöntem-leri yersel(mutlak ve bağıl yöntem ) ve uzaysal yöntem olarak ikiye ayrılır. Türkiye Temel Gravite Ağı’nda (TUTGA-99), mutlak ve bağıl ölçüm yöntemleri kullanılmıştır.
Gravite ölçüleri jeodezik, jeolojik ve mühendislik amaçlı çalışmalarda kulla-nılmaktadır. Jeodezide gravite ölçüleri her alanda kullakulla-nılmaktadır. En önemli uygu-lama alanları; Stokes integrasyou, çekül sapması bileşenlerinin hesabı ve yükseklik sistemlerinde potansiyel farkının hesaplanmasıdır.
Bu çalışmada, graviteyle ilgili kavramlar belirtilmiş olup uygulama kısmı ile ilgili sonuçlar sunulmaktadır. Sayısal uygulama Konya, Karaman, Niğde ve Aksaray illerinin kuşatan bir bölgede enlem, boylam ve deniz yüksekliği bilinen noktalarda EGM08 modeli kullanılarak gravite değerleri belirlenmiştir. Uygulama sırasıyla aşağıdaki adımlardan oluşmuştur.
Noktalardaki gravite değerlerinin hesaplanması
Noktalardaki boşlukta gravite anomali değerlerinin hesaplanması Noktalardaki Basit Bouguer anomali değerlerinin hesaplanması 3 ́ lık aralıklarla grid oluşturulması
Her grid noktasındaki Basit Bouguer anomalilerinin hesaplanması Her grid noktasında Basit Bouguer anomaliden boşlukta gravite
2. GRAVİT EN İN T EM EL İ LK EL ERİ
2.1. Newton Kanunu
Gravite, temeli Newton Kanunu’ndan oluşan çekim kuvvetidir. Newton’un bi-rinci kanunu çekim kuvvetinin büyüklüğü, doğrultusu ve yönü hakkında bilgi verir. F çekim kuvveti, m ve mgibi iki kütlenin bir biri üzerine uyguladığı kuvvet olup, kütle-lerin çarpımıyla doğru, aralarındaki uzaklığın karesiyle ters orantılıdır.
Şekil 2.1: Gravitasyon kuvveti
2 r m m k F (2.1) k: Gravitasyon sabiti = 6.6710-8 cm-3/gr.sn
Newton’un ikinci kanununda ise; F çekim kuvveti, meydana getirdiği hareketin ivmesiyle kütlenin çarpımına eşittir.
a m F (2.2a) 2 r m k a (2.2b)
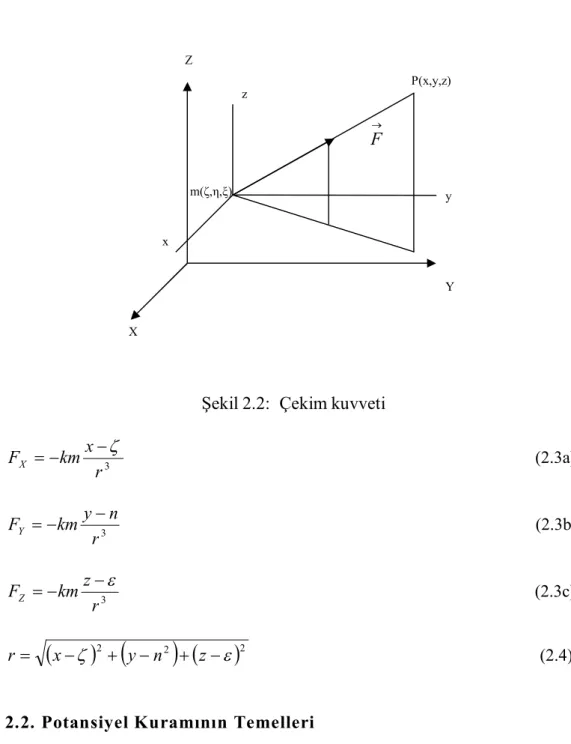
Bir X,Y,Z koordinat sistemi alınırsa ve m, çeken kütlenin koordinatlarına ζ, n, ε;çekilen nokta koordinatlarına da x y z denirse kuvvet büyüklüğü F olan
F vektörü-nün bileşenleri aşağıdaki gibidir.
Şekil 2.2: Çekim kuvveti
3 r x km FX (2.3a) 3 r n y km FY (2.3b) 3 r z km FZ (2.3c)
2
2
2 x y n z r (2.4)2.2. Potansiyel Kuramının Temelleri
Gravite ve manyetik alanın temeli potansiyeldir. Bir kütlenin oluşturduğu çekim alanı büyüklüğünü hesaplamak için potansiyellerin göz önüne alınan noktada türevleri alınır (Sanver ve İşseven, 2007).
Bir nokta kütlenin m0=1 birim kütleli A (x y z) noktasına etki ettiği F çekim
kuvvetinin bileşenleri;
x
r km Fx 3 , 3 ( y) r km Fy ,
z
r km Fz 3 ‘dir. (2.5) X P(x,y,z) F Y Z z x y m(ζ,η,ξ)İlk olarak Lagrange 1773 yılında bu üç bileşenin bir V(x,y,z) fonksiyonunun kısmi türevleri olduğunu belirlemiş ve Gauss’da bu V fonksiyonunu potansiyel olarak adlandırmıştır (Erden, 1979). r m k V (2.6)
skaler fonksiyonunun x y z’ye göre kısmi türevleri;
3 r x km x V Fx x V (2.7a) 3 r y km y V Fy y V (2.7b) 3 r z km z V Fz z V (2.7c) V fonksiyonu m kütleli bir nokta kitlenin m0=1 birim kütleli A(x,y,z) noktası
çe-kim potansiyelidir. Potansiyel birim kitleyi sonsuzda belli bir konuma getirmek için yapılır. V gradV k z V j y V i x V F (2.8)
2.3. Fiziksel Yeryüzü ve Yüzeyler
Yeryuvarı karmaşık bir yapıdadır. Yeryuvarının şekli denilince fiziksel yeryü-zü, elipsoit, jeoit, küre ve düzlem yüzeyler akla gelir. Jeodezik uygulamalarda üç te-mel referans yüzeyi kullanılır. Bunlar; fiziksel yeryüzü, dönel elipsoit ve jeoittir.
Fiziksel yeryüzü, yeryuvarı kütlesinin katı veya sıvı kısmının atmosfer ile olan sınırıdır. Girinti ve çıkıntılarından dolayı düzgün bir yüzey değildir. Bu nedenle bu yüzey, matematiksel olarak açıklanamaz.
Yeryuvarı yüzeyindeki parametrelerin hesaplanması için matematiksel bir refe-ransa ihtiyacımız vardır. Referans yüzeyi olarak alınacak yüzeyin nivo yüzeyi (durgun
su yüzeyi) ve kapalı bir fonksiyonla hesabı yapılacak bir yüzey olmalıdır. En uygun referans dönel elipsoittir.
Dönel elipsoit, elipsin küçük ekseni etrafında döndürüldüğünde meydana gelir. 1909 Hayford elipsoidi Uluslararası Jeodezi ve Jeofizik Birliği (IUGG) kongresinde Uluslararası Elipsoit olarak kabul edilmiştir (Bilgin, 1974). Diğer bir referans elipsoidi GRS80 elipsoididir. GRS80 elipsoidi bir eşpotansiyelli yüzeydir.Yapmış olduğumuz sayısal uygulamada GRS80 referans elipsoidi için formüller kullanılarak değerler elde edilmiştir.
2.4. Jeoit ve Elipsoit
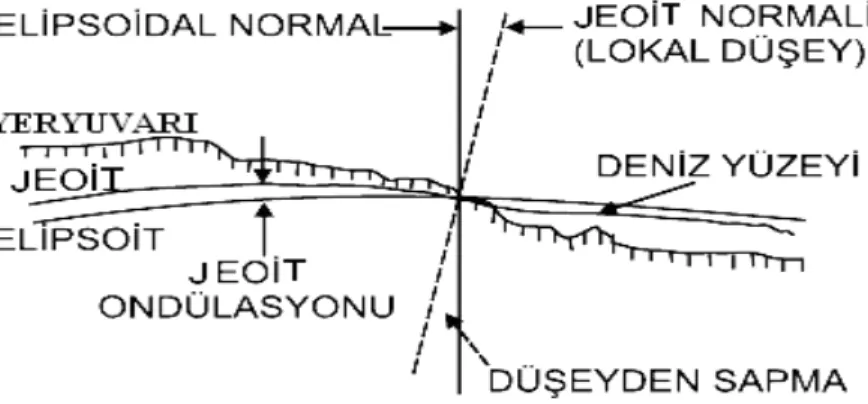
Durgun her su yüzeyi yani nivo yüzeyi ağırlık kuvvetine diktir. Akıntıların, gel git olayının, rüzgarın etkisinde olmayan deniz yüzeyinin, karaların altından devam ettirilerek bulunacak olan yüzey dünyanın matematiksel şekli olarak alınabilir. Bu yü-zeyde J.B.Listing JEOİT adını vermiştir (Ulusoy,1977).
Ortalama deniz yüzeyindeki kütleleri kaldırırsak kısa mesafede eşit yükseklik-teki noktalar düz çizgi şekilde görülür. Uzak mesafelerde ise çizgi eğri şeklindedir. Yeryüzü kapalı bir şekil olarak düşünüldüğünde bu çizgiler her bakışta değişik yön-lerdedir. Yüzeyleri normalleri yardımıyla incelendiğinde bu doğrultuların ağırlık kuv-vetinin doğrultuları olduğu görülür. Ağırlık kuvveti ise çekim ve merkezkaç kuvveti-nin bileşkesidir. Böylece jeoidin denklemi ağırlık kuvveti ve potansiyeliyle açıklana-bilir. Jeoidin eğriliği ise sürekli bir fonksiyon şeklinde olmadığından hesap yüzeyi ola-rak en yakın basit yüzeyler kullanılır. Dönel elipsoit yeryüzünü yaklaşık olaola-rak belirtir. Potansiyeli eşit olan noktaların oluşturduğu yüzeye eşpotansiyelli yüzey veya nivo yüzeyi denir. Jeoit, sıfır yüksekliğine sahip bir nivo yüzeyidir. Bir eş potansiyel yüzeyi olan sferoit yüzeyi ortalama deniz seviyesini gösterir.
Şekil 2.3: Referans elipsoidi ve jeoit arasındaki farklılıklar
Potansiyeli eşit olan yüzeyleri normal olarak kesen eğriler tam doğru olmayıp hafifçe eğridirler. Bunlar çekül eğrileridir ve serbestçe sallandırılan bir çekülün ipiyle çakıştığında çekül doğrultusu elde edilir. Ağırlık kuvvetinin doğrultusunu çekül ile gösterildiğinde elipsoidin normalleri ile çekül doğrultularının çakışmadığı görülür. Oluşan fark çekül sapmasıdır (θ). Çekül sapmaları kullanılan referans yüzeylerine gö-re değişir. Referans olarak seçilen elipsoide bağlı olan çekül sapmasına “Bağıl Çekül Sapmaları”, ortalama yeryuvarı elipsoidine göre bulunan çekül sapmalarına “Mutlak Çekül Sapmaları” denir (Gürkan, 1979).
Şekil 2.4: Referans yüzeyler
Şekilde görüldüğü üzere P1 noktasında çekül doğrultusu ile elipsoit normali
ça-kışık olduğu için çekül sapmaları sıfırdır. P2 de çakışma dolayısıyla, θ çekül sapması
değiştirerek daha uygun elipsoitlerin bulunması, yeryuvarı ölçmesinde temel prob-lemdir. Bu nedenle, bir bölgeye en iyi uyan elipsoit ve ortalama yeryuvarı elipsoidi kavramları ortaya çıkmaktadır. Ortalama yeryuvarı elipsoidi dünyayı hacim olarak en iyi belirten elipsoittir. Yüksekliklerin belirtilmesinde ise esas yüzey olarak jeoit yüze-yinden yararlanılır (Kurt, 1998).
3. GRAVİT E
3.1. Gerçek Gravite ve Bileşenleri
Yeryüzünde cisme etki eden kuvvet olan kitlesel çekim kuvveti ile merkezkaç kuvvetinin bileşkesi olan toplam kuvvet gravite denir.
Şekil 3.1: Merkezkaç kuvvet
Bir birim kitle üzerindeki merkezkaç kuvvet ƒ, yeryuvarının kendi ekseni etra-fında dönüşünün açısal hızı ω ve kitlenin dönme ekseninden uzaklığı
2 2 y x p (3.1) olmak üzere f=ω2p (3.2)
ile bellidir. Bu kuvvete ait
f vektörü
x, y,0
p
vektörü ile aynı doğrultuda olup
2 , 2 ,0
2 y x p f (3.3) şeklindedir.Merkezkaç kuvvet aynı zamanda
2 2
2 2 1 y x (3.4)şeklinde bir potansiyel de üretilebilir.
z y x grad f , , (3.5)
Gravitenin W potansiyeli, çekim kuvvetinin V potansiyeli ile merkezkaç kuvve-tinin Ф potansiyelinin toplamına eşittir. Yani;
v y x dv k V z y x W W 2 2 2 2 1 , , (3.6) olup integral tüm yeryuvarını kapsamaktadır. Türevi2 2 2 2 2 2 2 2 z y x (3.7) eşitliğini verir. Eğer bu, V için olan Poisson denklemi ile ele alınırsa W gravite potansiyeli için 2 2 4 W k (3.8) olan genelleştirilmiş Poisson denklemi elde edilir.
z W y W x W gradW g , , (3.9)
Yerin gravite alanında; yoğunluğun sabit olduğu ve kütlenin bulunmadığı yer-lerde Laplace denklemi, kütlenin bulunduğu yeryer-lerde ise Poisson denklemi geçerlidir.
Herhangi bir noktada gravite potansiyeli W, belirlenebiliyorsa yeryuvarının gravite alanı biliniyor demektir. Gravite potansiyelinin belirlemek için V’nin bulun-ması gerekir. Yer çekim potansiyeli,
max 2 0 sin sin cos 1 , , n n n m nm nm nm n P m S m C r a r GM r V (3.10)şeklinde sonlu küresel harmonik serilerle gösterilir. (Rapp , 1997) ,λ,r : Sırasıyla jeosentrik enlem, boylam ve yarıçap
nmax : Küresel harmonik açınımın maksimum derecesi
GM : Newton’nun evrensel çekim sabiti ve yeryuvaranın kütlesi çarpımı a : Ekvatoral yarıçap
nm nm S
C , : Tam normalleştirilmiş küresel harmonik katsayılar
nm
P : Tam normalleştirilmiş birinci tür Legendre fonksiyonudur.
Şekil 3.2: Gravite vektörü
Yeryüzünde bir noktaya kitle çekim kuvveti
F ve yerin kendi ekseni etrafında sabit ve açısal hızı ile dönmesinden dolayı merkezkaç kuvveti etki eder. Yeryuvarının ağırlık kuvveti
g ’nin doğrultusuna çekül doğrultusu denir. Boyutu gal ile ölçülür. (1 gal=1cm/sn2). g’nin sayısal değeri yaklaşık olarak ekvatorda 978 gal, kutup-larda 983 gal’dir.
3.2. Seviye Yüzeyleri
Potansiyelinin sabit olduğu yüzeylere eşpotansiyel yüzeyler olup, eşpotansiyelli yüzeylerin normali de gravite vektörüdür. Tüm eşpotansiyelli yüzeyleri normal olarak kesen eğrilere çekül eğrileri denir.
Şekil 3.3: Seviye yüzeyleri ve çekül eğrileri
Bir P noktasındaki çekül eğrisinin uzunluğu jeoit yüzünden itibaren yüksekliği deniz yüzeyinden olan ortometrik yüksekliktir.
dW=-gdH (3.11)
g değeri hiçbir zaman sıfır olmayacağından, dW de sabit olduğundan dH da sıfır olamaz. Yani nivo yüzeyleri kesişmezler. Nivo yüzeylerinin her noktasında potansiyel değeri sabit olduğundan bunlara eş potansiyelli yüzeyler de denilir. Ayrıca g değişken olduğu için dH da değişken olur. Çarpımları sabit olduğundan nivo yüzeyleri de bir-birlerine paralel değildir.
Şekil 3.4: Nivo yüzeyleri ve çekül eğrileri
Jeodezik ölçüler seviye yüzeyleri ve çekül eğrilerine göre yapılır. Burada amaç yeryuvarındaki gravite alanına ait seviye yüzeylerinin belirlemektir.
3.3. Yükseklik Kavramı
Yükseklik noktanın konumun belirtir. Bir noktanın yüksekliği çekül eğrisi bo-yunca uzanan mesafedir. Yeryüzündeki bir noktadan sarkıtılan çekül eğrisinin jeoide değdiği nokta ile fiziksel yeryüzündeki nokta arasındaki çekül eğrisi boyuna yükseklik denir. Bir noktanın yüksekliğinin bulunması için referans yüzeyinin belirlenmesi ge-rekir (Turgut,1996).
Jeopotansiyel sayı (c), yeryüzündeki bir noktadan geçen nivo yüzeyinin potan-siyeli wp ile jeoidin potansiyeli wo kgalmetre birimindeki farktır.
Jeopotansiyel sayı;
nokta jeoid o W gdh W c (3.12)dh diferansiyel yükseklik farkı, g gerçek gravitedir. Jeopotansiyel sayı (c) ve G ortalama gravite olmak üzere yükseklik;
G c
Yükseklik (3.13)
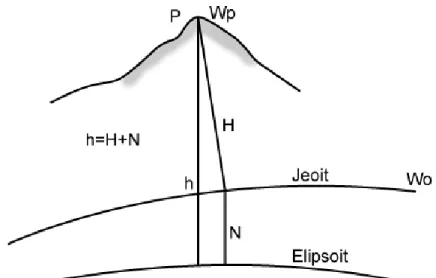
Elipsoidal yükseklik, yeryüzündeki bir noktadan elipsoide inilen uzunluktur. Gravite alanından bağımsız olup geometrik olarak kullanılan bir büyüklüktür.
Şekil 3.5: Jeoit yüksekliği
Elipsoit yükseklikleri ile jeoit yükseklikleri arasındaki ilişki ise;
N=h-H (3.14) Jeoit ile elipsoit arasındaki N uzaklığına jeoit yüksekliği veya jeoit ondülasyonu
denir. Elipsoidal yüksekliklerden ortometrik yüksekliklere geçiş için N jeoit yüksekli-ği kullanılır.
Bunun yanı sıra; jeoidin dışındaki kitlelerin yoğunluğunun bilinmesi ya da bazı kabuller yapılması zorunluluğu olduğundan Molodensky 1945’te farklı br yaklaşım önermiştir (Kartal,1998).
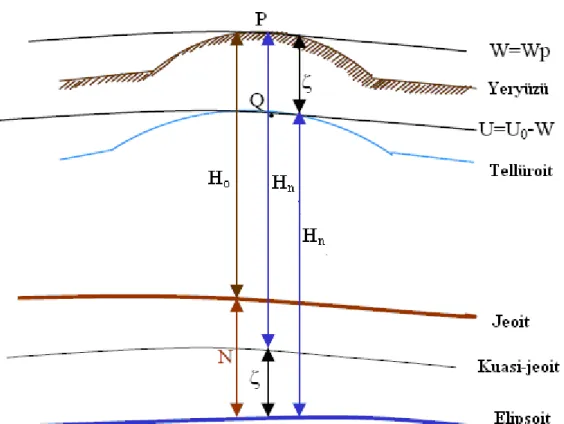
Şekil 3.6: Jeoit, kuasi-jeoit ve elipsoit Hn : Normal yükseklik
Ho : Ortometrik yükseklik
ζ : Yükseklik anomalisi
P noktasının çekül eğrisi boyunca jeoide uzaklığı ortometrik yükseklik, normal çekül eğrisi boyunca uzaklığı normal yüksekliktir. Geometrik yükseklik (h) ve ortometrik yükseklik (H) yerine normal yükseklik Hn ve jeoit ondülasyonu N yerine
yükseklik anomalisi konarak,
Hn
h (3.15) ile belirlenir (Gürkan,1984).
UQ=WP olacak şekilde bir yüzey düşünülürse bu yüzeye tellüroit denir.
Elipso-itten tellüroide kadar olan düşey uzaklık Hn normal yüksekliktir. Buna karşılık
geo-metrik yükseklik h, elipsoitten yeryüzüne kadar olan düşey uzaklıktır. Bu iki yüksek-lik arasındaki fark N=h – H jeoit ondülasyonuna karşılık gelen;
h Hn (3.16) yükseklik anomalisidir.
Yükseklik sistemleri birbirinden gravite değerinin seçimine bağlı olarak farklı-lık gösterirler ve kullanılan referans elipsoidine bağlıdırlar.
Ortometrik yükseklikler deniz düzeyinden yani jeoit yüzeyden olan doğal yük-sekliklerdir. Noktanın coğrafi enlemine ve gravite değerine bağlıdır. Dinamik yüksek-likler, jeopotansiyel sayılar g ağırlık değerine bölündüğünde elde edilen yükseklik di-namik yüksekliktir. Didi-namik yüksekliğin herhangi bir geometrik anlamı yoktur. Ok-yanuslarda jeoit ile çakışan ve karada farklılık gösteren yüzey Kuasi-jeoit olup normal yüksekliklerin (Molodensky) başlangıç yüzeyidir.
3.4. Normal Gravite
Gerçek gravite alanına benzer, matematiksel temelleri kolay olan normal gravite alanı tanımlanır.
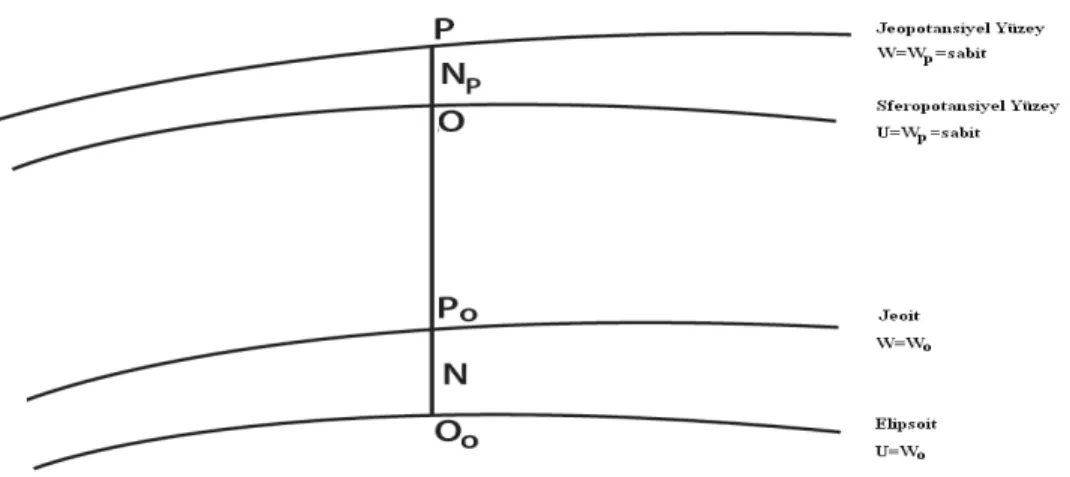
Jeoide karşılık oluşan yüzey sferoit olup U=U0=sabitdir. Bu bir dönel
elipsoitdir. Birbirinin karşılığı olan bir jeop ile bir sferopun farklı geometrisi olmasına karşın üzerindeki jeopotansiyel sayılar aynıdır (Turgut, 1996).
Şekil 3.7: Jeopotansiyel ve sferopotansiyel yüzeyler
Normal gravite alanının potansiyel fonksiyonu u=u(x,y,z); bir sferopun denkle-mi u(x,y,z)=u=sabit; gerçek gravite vektörü
g den hem büyüklük hem de doğrultu bakımından farklı olan normal gravite vektörü
z U y U x U gradU , , (3.17)
olur. Yeryüzünün gerçek gravite alanına ilişkin her büyüklüğe karşılık normal gravite alanında da büyüklük vardır. Normal gravite alanı; her türlü matematik işlem olabildiğince basit ve kapalı ifadelerde yapılabilmelidir.
Yeraltında yoğunlukların değişik olmasından dolayı jeoit yüzeyi sferoitten fark-lıdır. Sferoit (dönme elipsoidi) bir elipsin küçük ekseni boyunca kesilip bu eksen bo-yunca 360 döndürülmesiyle elde edilir. Sferoit yüzeyi kıtalarda jeoidin altından, ok-0 yanuslarda ise üstünden geçer. Jeoit ile sferoit yükseklik farkının ve jeoit normali ile
sferoit normali arasındaki çekül kapsamının bilinmesiyle birinden diğeri hesaplanabilir. Gerçek gravite alanının normal alanından sapmaları oldukça küçüktür.
Yeryu-varının gravite alanını “normal” ve geriye kalanı “bozucu” alana ayırmak hesapları ko-laylaştırır.
Wp≠Up
Çizelge 3.1 Gravite sembolleri
Bir P noktasına ait gerçek ve normal gravite vektörlerinin büyüklük farkı;
δg = gp – γp (3.19)
δg gravite bozukluğudur.
Bir P noktasındaki gerçek gravite vektörünün büyüklüğü ile bu noktadan geçen jeopun karşılığı sferop üzerinde P’nin izdüşümü olan θ noktasındaki normal gravite vektörünün büyüklüğü farkı;
Δg= gp - γθ (3.20)
olarak bulunur. Δg gravite anomalisidir.
Gravite anomalileri yer altı jeolojisindeki yoğunluk farkından ileri gelir.
Şekil 3.8: Jeopotansiyel ve sferopotansiyel yüzeyler
g gravite anomalisi; P noktasındaki gp
gerçek gravite vektörü (jeoit yüzeyi-ne dik) ve Q noktasındaki Q
normal gravite vektörü (sferoit yüzeyine dik) arasındaki farktır.
Gravite Vektörü Gravite
Potansiyeli Büyüklük Doğrultu
Gerçek Gravite Alanı W g Ф, Λ
Normal Gravite Alanı U γ φ ,λ Bozucu Gravite Alanı T δg, Δg θ, ά, ή, ξ
Sferoit Yüzeyi Jeoit Yüzeyi
g
p g gx gz Q .
.
4. GRAVİT E İ NDİ RGEM ES İ
Topografik kitlelerden dolayı yeryüzünde ölçülen gerçek gravite (g) ile elipsoit yüzeyine ait normal gravite (γ) değeriyle karşılaştıramayacağından gerçek gravitenin deniz yüzeyine indirgenmesi gerekir.
Şekil 4.1: Gravite indirgemesi
4.1. Gravite Ölçülerine Yapılan Düzeltmeler 1. Sürüklenme düzeltmesi
2. Enlem etkisi düzeltmesi
3. Yükseklik (kot) etkisi düzeltmesi a. Serbest hava indirgemesi b. Bouguer indirgemesi 4. Arazi düzeltmesi
5. İzostasi etkisi ve düzeltmesi
4.1.1. Sürüklenme düzeltmesi
Gravite aletlerinin zamanla yaylarında oluşan hatadır. Bu hatanın düzeltilmesi için ölçmelere başlanmadan önce gravite aleti bir baz noktasında kurulmalı, ölçmeler yapıldıktan sonra tekrar aynı baz noktasında ölçüm yapılmalıdır. İki baz noktası ara-sındaki fark diğer ölçü noktalarına dağıtılır.
4.1.2. Enlem etkisi düzeltmesi
Yerkürenin şeklinden kaynaklanır. Baz noktasının enlem değeri belirlenir. Di-ğer noktaların enlem düzeltmesi bu deDi-ğere göre hesaplanır. Kuzey yarımkürede bulu-nan noktalar için düzeltme eksi, güneyinde bulubulu-nan ölçü noktaları için artı işaretli-dir(Erden,1979).
Şekil 4.2: Enlem etkisi
Çizelge 4.1 Türkiyenin yer aldığı enlemlere ait enlem indirgemesi katsayıları
Φ 0.8122 sin2Φ 36 0.7727 mGal/km 37 0.7809 mGal/km 38 0.7883 mGal/km 39 0.7946 mGal/km 40 0.8000 mGal/km 41 0.8044 mGal/km 42 0.8079 mGal/km
4.1.3. Yükseklik (Kot) etkisi ve düzeltmesi
Değişik yükseklikte olan ölçü noktalarının referans yüzeyine indirgenmeleri ge-rekir. Bu referans yüzeyine datum denir. Datum bir noktanın konumunu belirlemek için alınan referans yüzeyidir. Koordinatlar için alınan yüzey yatay datum,
yükseklik-ler için alınan yüzey düşey datumdur. İndirgenen noktalar eş yükseklikte olacağından ölçü değerine yükseklik farkından gelen bir düzeltme yapılır. Yükseklik düzeltmesi iki kısımda incelenir.
4.1.3.1. Boşlukta gravite indirgemesi
Sadece yükseklikten kaynaklanan etkilerin giderildiği düzeltme şeklidir. Her ölçü noktasının yükseklik değerinin bilinmesi gerekir. Boşlukta gravite anomalileri küçüktür ve topografyaya bağlıdırlar.
Şekil 6.3’te olduğu gibi P0 ile Ph noktaları arasındaki gravite değerlerinin farkı
boşlukta gravite etkisini verir. Deniz düzeyinin üzerinde hiç kütle yokmuş gibi kabul edilir.
Şekil 4.3: Boşlukta gravite etkisi
Çizelge 4.2: Boşlukta gravite indirgemesi katsayıları Enlem Derece Gradyen (m gal/m)
30 0.30866
35 0.30863
40 0.30859
Türkiye için boşlukta gravite düzeltmesi katsayının 0.3086 olarak alınır. Boşlukta gravite indirgemesi;
h H F h h 0.3086 (4.1) 4.1.3.2. Bouguer indirgemesi
Şekil 4.4: Bouguer etkisi
Jeoit ile fiziksel yeryüzü arasındaki kitleler graviteye etki eder. Yumuşak deği-şimli anomalilerdir. Jeoidin dışında kalan kitlelerin tümüyle kaldırılması amacıyla bir Bouguer plakası kullanılır. Ph noktasından geçen nivo yüzeyi ile jeoit arasındaki kütle
gravite değerlerine etki eder.
AB = 2πkρh (4.2) AB = 0.04191 ρh (4.3) ρ = 2.67 g/cm3 ve h metre olmak üzere,
AB = 0.1119 h mgal (4.4)
Plakanın kaldırılması demek ölçülen gravitenin çıkarılması demektir. Bu indir-gemeden sonra, boşlukta gravite indirgemesiyle jeoite (Po ) indirilmesi gerekir.
h F h g (4.5) h F h g ~ 0.3086h mgal (4.6) Jeoitde Bouguer gravitesi;
gB = g – AB +F (4.7) gB = g – 0.1119 h + 0.3086h = g + 0.1967h (4.8) g: gravite
AB: Bouguer plakası
F: Boşlukta gravite indirgemesi gB: Bouguer gravitesi
Bouguer anomalisi, Bouguer gravitesi jeoidin yüzeyine indirildiğinden, elipsoi-din yüzündeki gravite γ’nin çıkarılmasıyla bulunur.
gB gB (4.9)
4.1.4. Arazi düzeltmesi
Ölçü noktasının etrafındaki saha engebeli ise, ölçülen gravite değeri için ayrıca topografik düzeltme yapmak gerekir. Bouguer düzeltmesi yaparken plaka varmış ka-bul ederek ve düzeltme değeri negatif olduğundan ölçü değerinden çıkarılmıştı. Topografik düzeltme ise yine kütle varmış kabul ederek önceden çıkartılan düzeltme değeri kadar pozitif olarak P noktasındaki ölçü değerine ilave edilir. Böylece Bouguer düzeltmesi ile ölçü değerinden çıkarılan etkisi arazi düzeltmesi ile ilave edilirse birbi-rini götürür. P noktasından geçen nivo yüzeyinin üstündeki ve altındaki kitlenin etki-sinden ileri gelen düzeltme yapılmış olur.
Şekil 4.5: Arazi etkisi
Arazi düzeltmesi miktarı genellikle azdır. 3000m yükseklikteki dağlarda arazi düzeltmesi yalnızca 50mgal’dir (Erden, 1979).
gB = g-AB + At + F (4.10)
Ölçülen gravite değerine boşlukta gravite indirgemesi ve bouguer indirgemesi yaptıktan sonra elde edilen değere arazi düzeltmeside eklenerek olgunlaştırılmış Bouguer gravitesi bulunur.
4.1.5. İzostatik etki ve düzeltmesi
Yüksek dağ kütlelerinin ve yoğunlukları farklı parçaların arasındaki çekim kuvvetinin beklenenden az olmasıyla oluşan denge durumudur. İzostatik anomaliler küçüktür ve topografyadan bağımsızdırlar. Günümüzde Pratt ve Airy kuramları yaygın olarak kullanılmaktadır.
Pratt-Hayford Sistemi (Denge Teorisi) de kütleleri kolonlar şeklinde düşünül-düğünde derinliği belli yerde dengede dururlar. Denge yüzeyinin altında yoğunluk ay-nı olur. Denge yüzeyinin üstünde ise yoğunluğu büyük olan yerler küçük olan kolon-ları, yoğunluğu küçük olan yerler büyük kolonları oluşturur.
P
Şekil 4.6: Pratt-Hayford sistemi
Airy-Heiskanen sistemi ( Lokal Yüzme)’de kolonlar aynı yoğunlukta olup kütleler değişiktir.
Şekil 4.7: Airy-Heiskanen sistemi
İzostatik indirgemeler sonucu elde edilen gravite; gI ile gösterilirse;
gI = g-At +Ac+F (6.17)
Toplam indirgeme;
go = g-FB+At+Ac+F (6.18)
4.1.6. Dolaylı etki
Gravite indirgemeleri jeoidi değişikliğe uğratır buna dolaylı etki denir. Gravite indirgemesiyle bulunan değerler ile Stokes formülüyle hesaplanan değerler kojeoit
yüksekliğidir. Jeoit yüksekliğinden farklıdır. Her gravite indirgemesi farklı bir jeoide karşılık gelir. Bouguer anomalilerinde dolaylı etki çok büyük olduğundan jeoidin be-lirlenmesinde kullanılmaz. İzostatik anomalilerde dolaylı etki küçüktür (Heiskanen ve Moritz, 1967).
5. GRAVİT E ÖLÇ ÜM YÖNTEM L ER İ
Gravite ölçümünde kullanılan yöntemler genel olarak yersel ve uzaysal olarak iki bölümde incelenebilir.
Yersel Yöntemler
1. Mutlak gravite ölçümü 2. Bağıl gravite ölçümü Uzaysal Yöntemler
5.1. Yersel Yöntemler
5.1.1. Mutlak gravitenin ölçülmesi
Mutlak gravite ölçmeleri yalnızca karada yapılır. Ölçme doğruluğu en yüksek olan FG5 aletidir. Bir cismin boşlukta serbest düşüşü gözlenir. Üç düşme yol uzunlu-ğu ve süreler ölçülür. Mutlak gravite ölçümü bir sarkaç yardımıyla veya serbest düş-me, simetrik serbest hareket prensiplerine göre çalışan aletlerle yapılır. Genelde mut-lak gravite ölçerler ağır ve büyüktürler. Bu aletlerin pahalı olmaları, ölçümlerin zaman alması, ölçülerin getirilen düzeltmelerin hesabının uzun olması gibi nedenlerden dola-yı mutlak gravite ölçüsü yerine göreli gravite ölçüleri yapılır. Bu yöntemde hem yol hem de zaman değerlerinin ölçülmesi gerekir.
5.1.1.1. Sarkaç yardımıyla mutlak gravitenin ölçülmesi
Bu yöntemde özel duyarlı sarkaçlar kullanılarak salınımları gözlenir.
Şekil 5.1: Sarkaç yöntemi
L x mg mg F sin (5.1) 2 2 t x m F (5.2)
x değeri basit harmonik hareketle;
g L
T 2 (5.3)
olur. L, sarkacın uzunluğu olup periyodu aynı olan eşdeğer basit bir sarkacın uzunluğuna eşittir. Buradan yerçekimi ivmesi;
2 2 4 T L g (5.4) olur.
5.1.1.2. Düşen cisim yardımıyla mutlak gravitenin ölçülmesi
Düşen cismin hızının zamanla değişimini ölçülerek doğrudan yerçekim ivmesi hesabına dayalı bir yöntemdir.
Şekil 5.2: Serbest düşme yöntemi
2 1
2 1 2 1 1 2 2 t t t t t S t S g (5.5)t1, t2 zamanları ve S1 S2 düşüş yolu çok duyarlı olarak geliştirilmiş optik
sistem-lerle ölçülerek gravitenin mutlak değeri bulunabilir.
5.1.2. Bağıl gravitenin ölçülmesi
Bağıl gravite ölçüleriyle iki nokta arasındaki gravite farkı belirlenir. Bağıl gravite ölçerlerin ayarlanmaları gerekir. Sıfır noktaları zamana bağlı olarak değişir. Bu yöntemde yol ve zaman değerlerinden sadece birini ölçmek yeterlidir. Bağıl gravitenin ölçülmesinde kullanılan aletler sarkaç, burulma terazisi, gravimetrelerdir.
5.1.2.1 Sarkaç yöntemi
Sarkaç yöntemi belli bir noktadaki gravite değeri biliniyorsa diğer noktadaki gravite değeri sarkaç yardımıyla bulunabilir. Ölçmeler uzun zaman aldığı için
kulla-nılmamaktadır. A noktasındaki gA gravite değeri biliniyorsa, B noktasındaki gB gravite
değeri sarkaç yardımıyla bulunabilir.
Sarkaç önce A noktasına konularak salınımların periyodu ölçülüp ortalaması alınırsa (5.1) formülüne göre;
2 2 4 A A T L g (5.6) olur. Aynı aletle B noktasında ölçü yapılır.
2 2 4 B B T L g (5.7) İki formülün taraf tarafa oranlanması ile;
2 B A A B T T g g (5.8) bulunur. Sarkaç ile yapılan ölçüler uzun zaman gerektirdiği için gravite etütlerinde kullanılmamaktadır. Biri Kandilli (İstanbul) gözlem evinde olmak üzere Türkiye’de 8 adet sarkaç baz istasyonu vardır (Erden, 1979).
5.1.2.2 Burulma terazisi
R. Eötvös tarafından geliştirilen burulma terazisi ile, gravite potansiyelinin tü-revleri bulunur ve eş potansiyel yüzeyin eğriliği hesaplanabilmektedir.
Hesaplanan büyüklükler yz xz W z y W W z x W 2 2 , (5.9a) yy xx W y W W x W 2 2 2 2 , (5.9b) xy W y x W 2 dir. (5.9c) Bunlardan Wxz ve Wyz gravitenin yatay gradyanlarıdır. Toplam yatay gradyan
2 2
g wxz wyz
Gravitenin yatay gradyanı ve potansiyel yüzeyin eğrilikleri her noktada belli olur. Bunların anomali haritaları çizilerek değerlendirme yapılır. Burulma terazisinde de bir noktada ölçü almak uzun zaman gerektirdiğinden bugün gravite projeksiyon etütlerinde gravimetre aletleri kullanılmaktadır (www.mta.gov.tr).
5.1.2.3 Gravimetre
Gravimetre ile iki noktaya ait çekim ivmeleri arasındaki fark ölçülür. Kolay ta-şınır ve hızlı ölçü yapılır. Gravimetreler bir kütle üzerine etki eden kuvveti yay veya burulma telindeki elastik gerilmelerle denge durumuna getirme yoluyla ölçü yapan aletlerdir.
Gravimetrelerde denge durumu, kararlı ve kararlı olmayan olarak ikiye ayrılır. Gravimetreler çekim ivmesi nedeniyle yay ucuna asılan kütleye etki eden gravite kuvveti belli bir oranla yayı gerer ve yay boyunun değişimine neden olur (www.mta.gov.tr).
Yaydaki gerilme ile yerçekimi ivmesi arasında; k mg x (5.11) bağıntısı vardır. Şekil 5.4: Gravimetre g deki değişim Δg, z deki değişim Δz kadar olursa;
2 2 4 T z g
Kütlenin dönme momenti Mm (g, φ) ve yayın dönme momenti Mf (τ, φ) ise
(τ=yay sabiti), toplam moment M=Mm-Mf olur.
Denge halinde M=0 dolayısıyla Mm=Mf olur.
Eğer 0
M
ise denge durumu kararlıdır. Askania, Nörgaard, Hartley, Gulf vb. gravimetreleri kararlı denge durumunda olan aletlerdir.
Şekil 5.5: Kararlı denge durumu Eğer 0 M
ise denge durumu kararsızdır. Thyssen, LaCoste-Romberg, Worden, World-Wide vb. gravimetreleri kararsız denge durumunda olan aletlerdir.
Şekil 5.6: Kararsız denge durumu
En çok kullanılan gravimetreler LaCoste-Romberg, Worden, World-Wide vb. gravimetreleridir.
Şekil 5.7: Worden gravimetresi
.
5.2. Uzaysal Yöntemler
Gps ile elde edilen elipsoidal yüksekliklerin ortometrik yüksekliklere dönüştü-rülmesi için ortalama deniz yüzeyi olan jeoit kullanılır. Jeodezik amaçlı uygulamalar-da gravimetrik yöntemle belirlenen jeoit istenilen doğruluğu vermeyebilir. Bunun için lokal bölgede ortometrik yüksekliği bilinen noktaların aynı zamanda elipsoidal yük-seklikleri belirlenerek bir model oluşturulabilir. Böyle bir model için gravite alanı be-lirleme amaçlı uydulardan alınan veriler kullanılarak bulunan değerlerle sonuçlar kar-şılaştırılır. Gravite alanı belirlemede kullanılan yakın yer uyduları CHAMP, GOCE ve GRACE‘dır. Bu kapsamda gerçekleştirilen ilk uydu 2000 tarihinde CHAMP (Challenging Mini-Satellite Payload for Geophysical Research and Application) olup, 2002 tarihinde yörüngeye giren GRACE (Gravity Recovery and Climate Experiment) ve 2006 tarihinde GOCE (The Gravity Field and Steady-State Ocean Circulation Explorer)’dur (http://science.nasa.gov).
CHAMP ve GOCE gravite alanının belirlenmesinde ve GRACE ise bunun ya-nında zamana bağlı değişimleride göstermektedir (Karslıoğlu, 2005; Üstün, 2006).
CHAMP uydusu; manyetik, atmosferik ve graviteyle ilgili veriler sunmaktadır. GRACE uydusundan alınan verilerle elde edilen statik gravite alanın çözünürlüğü di-ğerlerine göre yüksek olup önemli derecede katkı sağlamaktadır. GOCE uydusu ile global gravite alanı çözünürlüğünün artırılması amaçlanmıştır (Üstün, 2006).
Şekil 5.9: CHAMP, GRACE ve GOCE uyduları
Yerin uzaydan gravite alanının belirlenmesine önemli rol oynayan bu uydular CHAMP, GRACE, GOCE yörünge belirleme işlemini GPS ile gerçekleşmektedir.
6. JEODE ZİD E GRAV İ TEN İN UYG UL AM A ALANL AR I
Yeryuvarındaki gerçek gravite alanının bilinmesi için çok sayıda ölçüye ihtiyaç vardır. Bugünün imkanları ile çok sayıda ölçü almak yetersiz kalkmaktadır. Bu ve benzeri nedenlerle gerçek gravite alanına bir yaklaşım olmak üzere matematiksel te-melleri kolay bir normal gravite alanı tanımlanır. Gravite ölçülerine etki eden bozucu etmenlerin hesaplanıp ölçülen değerlerin düzeltilmesi gerekir. Günümüzde uydular yardımıyla çok sayıda gravite verisi elde edilmektedir. Bunun sayesinde çözümdeki doğruluklar artmıştır.
Gravitenin genel olarak kullanıldığı alanlar;
1. Ölçülen değerlerin jeoitden, referans yüzeyi olan dönel elipsoide indirgenmesinde, 2. Astro-Jeodezik çekül sapmalarının sıklaştırılması ve Astronomik koordinat-lardan jeodezik koordinatlara geçmede,
3. Jeopotansiyel sayının belirlenmesinde 4. Gravimetrik jeoidin belirlenmesinde 5. Yükseklik sistemlerinde kullanılır.
Gravitenin en önemli uygulamaları; Stokes integrasyou, Çekül sapması bileşen-lerinin hesabı ve yükseklik sistemlerinde potansiyel farkının hesaplanmasıdır.
6.1. Stokes İntegrasyonu
. Stokes formülünün kullanılması, jeoit üzerindeki her nokta için verilen gravite anomalilerinden bir potansiyelin hesaplanmasıyla ilgilidir (Sideris, 1994). Yeryüzünde ölçülen gerçek gravite, elipsoit yüzeyine ait normal gravite değeri birbiriyle doğrudan karşılaştırılamayacağından gerçek gravite değerinin jeoide indirgenmesi gerekir. Jeoit dışındaki topografik kitleler tümüyle kaldırılır.
G gS d R N 4 (6.1) N: Jeoit YüksekliğiR: Yeryuvarı ortalama yarıçapı
G: Yeryüzü üzerindeki gravite için ortalama bir değer S
: Stokes fonksiyonuΔg : Gravite farkı dσ : Yüzey elemanı
Stokes fonksiyonu, yeryuvarını kapsayan gravite verilerinden gravimetrik yön-temle jeoit belirlenmesini sağlar jeoit yüzeyi oluşturulacak bölgelerde seçilen nokta-larda ölçmeler yapılır. Gerekli düzeltmeler yapıldıktan sonra gravimetrik değerler he-saplanır. Stokes fonksiyonuyla ölçümler yapılan noktanın jeoit yükseklikleri hehe-saplanır. Stokes fonksiyonunun çözülmesi için kalıp ve ıskara yöntemleri kullanılır. Ka-lıp yönteminde iç daireler ve yarıçaplarıyla bir bölümlendirme oluşturulur. Bu altlık aynı ölçekli bir gravite haritasının üstüne konur ve aynı anda merkezi harita üstündeki hesap noktası ile çakışacak şekilde yerleştirilir. Iskara çizgileri yönteminde ise dik-dörtgen şeklinde bölmeler oluşturulur. Standart büyüklükteki bölmelerden bulunacak ortalama anomaliler bilgisayarda hesaplanır.
6.2. Çekül Sapması Bileşenleri
Şekil 6.1: Çekül sapması
Gerçek ve normal gravite alanlarına ait gravite vektörlerinin doğrultuları farkı-na çekül sapması denir. Çekül sapması jeodezik ölçülerin elipsoit yüzeyine indirgen-mesinde ve jeoit modellemede kullanılır. Astro-jeodezik yöntemde, astronomik koor-dinatlar ve jeodezik koorkoor-dinatlarla hesaplanır. Gravimetrik yöntemde, gravite anoma-lileri kullanılarak stokes integralinden hesaplanır. Çekül sapmasını bileşenlerine ayı-rırsak; doğu-batı bileşeni için (η) ve kuzey-güney bileşeni içinse (ξ) kullanılır.
Çekül eğrisinin doğrultusu η’nin coğrafik koordinatları astronomik olarak belir-lenebilir.
Astronomik koordinatlar Φ, Λ , jeoit normali n Coğrafik koordinatlar φ , λ , elipsoit normali n
ξ = Φ – φ (6.2) η= (Λ - λ)CosΦ (6.3) Up=UQ – γN (6.4) olduğundan; Wp=Up+Tp = UQ = γN + T (6.5) Wp = UQ = W0olduğundan; N= T/γ (6.6) bulunur ( Gürkan, 1979).
Jeoit ondülasyonu ile bozucu potansiyel arasındaki bağlantı “Bruns Formü-lü”dür.
Çekül sapmalarının hesaplama yöntemleri konumlarına göre adlandırırlırlar. – Astrojeodezik çekül sapması
– Gravimetrik çekül sapması
– Topografik –izostatik çekül sapması
Astrojeodezik çekül sapması: Hesaplama işleminde astronomik ve jeodezik ve-riler kullanılır. Ortalama yer elipsoidi referans elipsoidi olarak alınır.
Gravimetrik çekül sapması: Çekül sapması bileşenlerinin gravite ölçülerinden yararlanarak hesaplanmasıdır. Bunun için;
d Cos Sin d ds G g 4 1 (6.7)Vening Meinesz integralleri kullanılır.
G: yeryüzü için ortalama bir gravite değeridir. τ: Tüm yeryüzü
dτ: Yüzey elemanı
ψ: Yüzey elemanının bulunan noktaya olan küresel uzaklığı α: Azimut
Vening Meinesz fonksiyonu, Stokes fonksiyonunun ψ’ya göre türevidir
Topografik –izostatik çekül sapması: Topografik haritalardan elde edilen değer-lere göre hesaplanır. Elde edilen yoğunluklara ilişkin varsayımlar yapılır.
6.3. Yükseklik Sistemleri
Bir noktanın yüksekliğinin bulunması için referans alınan yüzeyinin belirlen-mesi gerekir. Yeryuvarının homojen bir yapıda olmamasından dolayı, farklı yollarla yapılacak aynı nokta yükseklikleri de farklı olur.
Bu bize nivelman sonuçlarının yola bağlı olduğunu gösterir. Noktaların yük-seklikleri belirtilirken sadece yükseklik farklarını ölçmek yeterli olmayıp, yol boyun-ca gravite değerlerinin de ölçülmesi gerekir.
Şekil 6.2: Geometrik nivelman
δH yükseklik farkını ölçmek için A ve B noktaları arasındaki noktalara miralar
düşey olarak tutulup arada bir yere nivo kurulur. A ve B arasındaki nivelmandan bu-lunan yükseklik farkının toplamı HA ve HB deki yükseklik farkına eşit olmayacaktır.
Nivelmanın verdiği δn miktarları seviye yüzeylerinin paralel olmaması nedeniyle
HB’deki δHB miktarında farklıdır. W potansiyelindeki artma miktarı δW ile gösterilerek,
δW = -g′δHB
g, nivonın bulunduğu yerdeki gravite
g′: B’den geçen çekül eğrisi üzerindeki δHB deki gravite
n n B g g H (6.8) δW = -gδn (6.9)
B A A B W gdn W (6.10)Potansiyel farklar nivelman sonuçlarının gravite ölçüleriyle birleştirilmesinden doğar.
l 1
l 2
Bölüm 3.3’te bahsedildiği üzere, yükseklik sistemleri birbirinden gravite değe-rinin seçimine bağlı olarak farklılık gösterirler.
45 o o g G Sabit o d g c H Yükseklik Dinamik (6.11) G=gp + 0,0424H Yay parçası boyunca g ağırlık değerlerinin ortalamasıdır, (Helmert)
m o g c H Yükseklik Ortalama (6.12) G=γm = Çekül eğrisi boyunca olan ortalama gravite değerleri , (Molodensky)
m n c H Yükseklik Normal (6.13) Yada;
2 2 sin 2 1 1 a H a H f m f G n n o (6.14)gp , P yeryüzü noktasında ölçülen gravite; γ , Elipsoit üzerinde normal gravite;
φ, Jeodezik enlem; γ45, φ=45o için normal gravite ; f, Basıklık ‘dır.
kM ab m 2 (6.15)
Ω, Yerin açısal dönme hızı; a,b Elipsoidin büyük ve küçük yarı eksenleri kM : Newton çekim sabiti ile yerin kitlesinin çarpımıdır
7. SAYISAL U YGUL AM A
7.1. Sayısal Uygulama Alanı
Uygulama Konya, Karaman, Niğde, Aksaray illerini kuşatan bir bölgede 37<φ<39,5 ve 31<λ<34,5 enlem ve boylama sahip, deniz seviyesinden yüksekliği bi-linen 2682 noktada gerçekleştirilmiştir.
Uygulama sırasıyla aşağıdaki adımlardan oluşmuştur. Noktalardaki gravite değerlerinin hesaplanması
Noktalardaki boşlukta gravite anomali değerlerinin hesaplanması Noktalardaki Basit Bouguer anomali değerlerinin hesaplanması 3 ́ lık aralıklarla grid oluşturulması
Her grid noktasındaki Basit Bouguer anomalilerinin hesaplanması Her grid noktasında Basit Bouguer anomaliden boşlukta gravite
anoma-lilerine geri dönülmesi
7.2. GMT (Generic Mapping Tools)
Uygulamada gridleme, grid üzerinde dayanak noktalarına göre (ölçülmüş nok-talar) yükseklik hesabı ve haritaların çiziminde GMT programından faydalanılmıştır. Bu yazılım veri değerlendirme, filtreleme, iki üç boyutlu verilere dayalı matematiksel işlemleri gerçekleştirebilen, hacim ve trend yüzeyi hesaplayabilen zengin bir çeşitliliği sunmaktadır. Sadece belirli bir uygulamaya yönelik olmayan bu yazılımın çeşitliliği kullanıcıların da müdahalede bulunabilmelerinden kaynaklanır. Açık kaynak kodu olan işletim sistemi LINUX’da olduğu gibi ihtiyaç duyulduğunda kullanıcı programa ilave yazılımlar ekleyebilmektedir. Her ne kadar UNIX üzerinde geliştirilse de diğer ortamlarda da rahatlıkla kullanılabilmektedir. Bu çalışma da LINUX üzerinde gerçek-leştirilmiştir.
7.3. Gravite ve Anomalilerin Hesaplanması
7.1 başlığındaki belirtilen noktalarda EGM08 modeli kullanılarak gravite değer-leri (||
g ||) elde edilmiştir.
Gravite değerleri yer şekline göre değişim gösterebilmektedir. Ölçüm yapılan noktanın konumuna, örneğin deniz seviyesinden yüksekliğine bağlı olarak hesaplanan gravite değerleri değişebilmektedir. Yeryüzünün biçimi ile ilgili olan bu etkilerin he-sap edilip, bulunan gravite değerlerine eklenmesi veya çıkarılması gerekmektedir.
Genellikle küçük farklarla ve düzgün bir değişim gösteren gravite verileri üze-rindeki bu etkilerin giderilmesi sağlık bir değerlendirmeyi amaçlamakta ve yanlış yo-rumlamayı engellemektedir.
Bu sebeplerden dolayı gravite verileri üzerinde bazı düzeltmelerin yapılması zorunludur.
Uygulamada kullanılan ölçü noktalarının değişik yükseklikte olmalarından do-layı ölçüler arasında yükseklikle ilgili bir ayrım olur. Bundan dodo-layı hesaplanan gravite ölçülerinin datum adı verilen düzeye indirgenmesi gerekir. Bu indirgemeyle, ölçü noktaları eş yükseklikte alınmış gibi olur ve her gravite değerine ölçü noktasının datumdan olan yükseklik farkı ile orantılı bir düzeltme yapılır. Bu düzeltmeye yüksek-lik düzeltmesi denir.
Bu çalışmada hesap edilen gravite değerleri üzerinde yükseklik düzeltmesi adı altında boşlukta gravite indirgemesi ve Bouguer indirgemesi uygulanmıştır.
Deniz seviyesinden yukarıya doğru çıkıldıkça gravite değerinde bir azalma olur. Bu etkinin giderilmesi için ölçü noktası ile deniz seviyesi arasında kütlenin bulunma-dığı varsayılır. Ölçü noktaları aynı seviyede olmayacağı için ölçü noktalarını aynı se-viyeye indirgemek gerekir. Bu indirgemeye boşlukta gravite indirgemesi denir.
Eldeki mevcut ve hesaplanmış veriler C++ ortamında geliştirilmiş fanomol isimli yazılımla boşlukta gravite indirgemesine dahil edilmiş olup sonuçlar bir dosya-da tutulmuştur.
Boşlukta gravite indirgemesi, indirgeme düzeyi ile ölçü noktaları arasındaki kütlenin bulunmadığı varsayılarak yapılmıştır. Ancak iki düzey arasında kalan kütle-nin yoğunluğu düşünüldüğünde kütleden kaynaklanan gravite etkisikütle-nin de giderilmesi gerekmektedir. Kütleden kaynaklanan bu düzeltmeye Bouguer indirgemesi denir.
Jeoit ile fiziksel yeryüzü arasındaki kitleler graviteyi etkilediğinden jeoit dışın-da kalan kitlelerin kaldırılması için Bouguer indirgemesi yapılması gerekir.Her nokta-da hesaplanan boşlukta gravite anomali ve yükseklik değerleri yine C++ ortamınnokta-da ge-liştirilen bir yazlımla,
Δgb = ΔFA – 0.1119h (7.1)
formülünde yerine yazılarak Bouguer anomali değerleri hesaplanmıştır.
Yüzey enterpolasyonu için GMT yazılımı kullanılarak Surface komutu ile 2682 nokta 3 ́ lık arayla gridlendirilerek 3621 nokta oluşturulmuştur. Boşlukta gravite ano-mali değerlerini haritalamak için daha önce hesaplanan boşlukta gravite anoano-mali de-ğerleri grid noktalarında yeniden hesaplanarak Şekil 7.1’deki harita elde edilmiştir.Bu işlem için GMT resmi sitesi http://gmt.soest.hawaii.edu/ adresindeki örnek bir script dosyası seçilerek, bash kabuk programlama ile toplu işlem dosyası oluşturulmuş ve boşlukta gravite anomali değerleri harita üzerinde gösterilmiştir.
Şekil 7.1: Ölçü noktalarında boşlukta gravite anomali haritası
Aynı komut yapısında boşlukta gravite değerleri yerine Bouguer gravite anoma-li değerleri yazılarak işlem tekrar edildiğinde grid noktalarında Bouguer gravite ano-mali değerleri hesaplanmış olur. Grid alanında Bouguer gravite anoano-mali değerlerine ait harita ise Şekil 7.2’deki gibidir.
Şekil 7.2: Grid noktalarında Bouguer anomali haritası
İki harita arasındaki farktan da görüldüğü üzere jeoit ile fiziksel yeryüzü ara-sındaki kitleler kaldırıldığında Şekil 7.2’deki gibi gravite yoğunluğunun olduğu bölge-ler çok daha belirgin bir şekilde karşımıza çıkmaktadır. Bouguer gravite anomali hari-taları MTA başta olmak üzere birçok kuruluş maden, petrol ve buna benzer yer altı kaynakların tespitinde kullanmaktadırlar.
Bouguer anomali değerleri hesaplandıktan sonra grid noktalarındaki anomali değerlerinin jeoit hesaplarında kullanılabilmesi için düzenli bir anomali değerleri elde edilmesi gerekmektedir. Bu nedenle grid noktalarındaki bouguer anomali değerlerini hesap düzeyine çekmek için tekrar boşlukta gravite anomali değerlerine geçiş yapıl-mıştır.
Grid noktalarında Bouguer anomali değerlerinden tekrar boşlukta gravite ano-mali değerlerine geri dönülebilmesi için grid noktalarında yükseklik değerleri hesap edilmiştir. Ölçülmüş yükseklik değerleri GMT yazılımı içerisindeki surface komutu ile 3 lık grid bölgelerinde yükseklik enterpolasyonu yapılmıştır. Elde edilen yüksek-lik değerleri ve grid noktalarındaki bouguer anomali değerleri C++ ortamında gelişti-rilen bir yazılımla,
ΔFA = Δgb + 0.1119h (7.2)
formülünde yerine yazılarak her grid noktasındaki boşlukta gravite anomali değerleri hesaplanmıştır.
Grid noktalarındaki boşlukta gravite anomali değerleri GMT yazılımı yardımıy-la Şekil 7.3’teki gibi harita oluşturulmuştur.
Şekil 7.3: Grid noktalarında Bouguer’den boşlukta gravite anomaliye geçiş Uygulamada yüzey enterpolasyonu olarak multikuadrik enterpolasyon yönte-miyle GMT içerisinde bulunan surface komutu kullanılarak elde edilen enterpolasyon kıyaslamaya çalışılmıştır.
Bunun için Bildirici vd.(2008)’de ele alınan radyal bazlı multikuadrik fonksiyon kul-lanılmıştır.
n i i i i x x y y c z 1 2 2 2 (7.3)Burada n ölçülmüş nokta sayısı (dayanak noktaları) xi ve yi bu noktaların
koor-dinatlarını, x ve y ise grid noktaların koordinatlarını ci ise ağırlık katsayılarını
Formülü uygulayabilmek için bilinmeyenlerin bulunması gereklidir. Öncelikle Δ2 hesabı için yine Bildirici vd.(2008)’de kullanılan eşitlikten yararlanılmıştır.
n i n j j i j i x y y x n n 1 1 2 2 2 1 1 (7.4)Enterpolasyon için geliştirilen kodlamada Δ2 hesabı için C++ ortamında yazılan fonksiyon 2.018005 sonucunu vermiştir.
ci ağırlık katsayılarını bulabilmek için dayanak noktalarından oluşan doğrusal
denklemin çözülmesi gerekmektedir.
2682 26822682 3 26823 2 26822 1 26821 2682 2682 22682 3 23 2 22 1 21 1 2682 12682 3 13 2 12 1 11 1 c a c a c a c a z c a c a c a c a z c a c a c a c a z (7.5)
Böyle bir doğrusal denklem sistemi matris yöntemleriyle çözüme ulaştırılmak istenirse matrisin elemanlarını oluşturan aij değerlerinin bilinmesi gerekmektedir.
Bil-dirici vd. (2008)’de bu değerler aşağıdaki formülden elde edilmiştir.
2
2 2 i j i j ij x x y y a (7.6)z=Ac ise c=A-1z (7.7)
c katsayılarının bulunabilmesi için A matrisinin tersini almak gereklidir. Bunun için Gauss Eleminasyon yöntemi, Gauss-Jordan yöntemi ve LU(ayrıştırma, Cholesky) yöntemleri denenmiştir. Ancak matrisin boyutunun çok büyük olması (2682x2682) matrisin kondisyonunun bozulmasına doğal olarak da çözüme ulaşılmasına engel ol-muştur. Matrisi kararlı hale getirmek için tam pivotlama yapılarak yukarıdaki yöntem-lerin denenmesine rağmen doğrusal denklemin çözümüne ulaşılamamıştır. Bu nedenle surface kullanılarak elde edilen değerler kıyaslanamamıştır.
8. SONUÇ ve ÖNER İL ER
Gravite ölçüleri jeodezik, jeolojik ve mühendislik amaçlı çalışmalarda kulla-nılmaktadır. Jeodezide gravite ölçüleri her alanda kullakulla-nılmaktadır. En önemli uygu-lama alanları; Stokes integrasyou, çekül sapması bileşenlerinin hesabı ve yükseklik sistemlerinde potansiyel farkının hesaplanmasıdır. Jeoloji alanında ise gravite değerle-ri ele alınıp değişimledeğerle-ri incelenerek yeraltında bu değişimlere sebep olan kütle dağılışı bulunmaya çalışılır.
Yeryüzünde ölçülen gerçek gravite değeri ile hesaplanan gravite değeri doğru-dan karşılaştırılamaz. Deniz yüzeyine indirgemesi gerekir. Fiziksel yeryüzünde ölçü-len gravite üzerindeki etkiler kaldırılarak gravite değeri hesaplanır. İndirgeme yöntem-lerinin neler olduğuna kısa değinilmiştir. Bu yöntemlerinden birisi de yükseklik (kot) düzeltmesidir.
Bu çalışmada; Konya, Karaman, Niğde, Aksaray illerini kuşatan bir bölgede 37<φ<39,5 ve 31<λ<34,5 enlem ve boylama sahip, deniz seviyesinden yüksekliği bi-linen 2682 nokta üzerinden EGM08 modeli kullanılarak gravite değerleri bulunmuş ve yükseklik düzeltmesi uygulanmıştır. Deniz seviyesinden yukarıya doğru çıkıldıkça gravite değerinde bir azalma olur. Bu etkinin giderilmesi için ölçü noktası ile deniz seviyesi arasında kütlenin bulunmadığı varsayılır. Ölçü noktaları aynı seviyede olma-yacağı için ölçü noktalarını aynı seviyeye indirgemek gerekir. 2682 nokta için boşluk-ta gravite indirgemesi yapılarak ölçü nokboşluk-taları aynı seviyeye getirilmiştir. Boşlukboşluk-ta gravite indirgemesinde ölçü noktalarıyla indirgeme seviyesi arasında hesaba katılma-yan kütlelerin yoğunluğu düşünüldüğünde kütleden kaynaklanan gravite etkisinin de giderilmesi gerekmektedir. Yine tüm noktalar için bouguer indirgemesi yapılarak ölçü noktalarıyla indirgeme seviyesi arasındaki kütlelerin graviteye etkisi kaldırılmıştır. Belirtilen enlem ve boylam bölgeleri içerisinde GMT yazılımı yardımıyla 3 lık grid enterpolasyonu yapılarak bölgenin bouguer anomali haritası çıkartılmıştır. Grid nokta-larındaki anomali değerlerinin jeoit hesaplarında kullanılabilmesi için düzenli bir anomali değerleri elde edilmesi gerekmektedir. Bu nedenle grid noktalarındaki bouguer anomali değerlerini hesap düzeyine çekmek için tekrar boşlukta gravite
ano-mali değerlerine geçiş yapılmıştır. Bouguer indirgemesi yapılmadan önceki boşlukta gravite anomali değerleriyle bouguer anomali değerlerinden tekrar boşlukta gravite anomali değerlerine yükseltilmiş sonuçlar arasında çok küçük farklılıkların olması beklenir. Bouguer indirgemesi yapılmadan önceki boşlukta gravite anomali haritası ile bouguer anomali değerlerinden hesap düzeyine çekilmiş boşlukta gravite anomali de-ğerlerine ait haritaya bakıldığında beklendiği gibi anomali değerleri arasında çok kü-çük farklılıkların olduğu gözlenmiştir. Bu durum doğru sonucun elde edildiğini gös-termektedir.
Enterpolasyon, dayanak noktalarınki ölçme değerlerinden, ölçülmeyen nokta-lardaki ölçü büyüklüklerinin kestirimdir. Çok çeşitli enterpolasyon yöntemleri mev-cuttur. Bu çalışmada enterpolasyon yöntemlerden birisi olan multikuadrik yüzey enterpolasyonu kullanılarak GMT ile elde edilen grid anomali değerleri kıyaslanmaya çalışılmıştır. Bu yöntemde ölçülmüş yükseklik değerlerden (dayanak noktalarından) grid noktalarındaki yükseklik değerleri bulunurken radyal bazlı fonksiyon kullanılmış-tır. Bu fonksiyondaki her nokta için sabit olan c katsayısının hesabında 2682 denk-lemden oluşan bir lineer denklem sisteminin çözümü gerekmektedir. Bu denklem sis-teminin çözümü için elde edilen matris Gauss Eleminasyon, Gauss-Jordan ve LU(ayrıştırma, Cholesky) yöntemleri ile çözülmeye çalışılmıştır. Ancak matrisin kon-disyonunun bozulması nedeniyle çözüme ulaşılamamıştır. 32 bitlik bir işletim siste-minde C++ ortamında yazılan kodlamada kullanılan çift duyarlıklı sayı değişkeni ile matris işlemindeki her adımda köşegen eleman sıfıra yakınsayarak gittiğinden matri-sin satır ve sütun işlemleri henüz bitmeden köşegen elemanı sıfır değerini almıştır. Aynı işlem genişletilmiş çift duyarlıklı sayı değişkeni ile denendiğinde matris işlemle-rinin 3 adım daha ilerlediği görülmüş ancak sonuca ulaşılamamıştır. Bu büyüklükteki bir matris parçalanarak işlendiğinde muhtemel bir çözüme ulaşılabilir ancak değerle-rin çok hassas olmasından dolayı sonuçların doğruluğu tartışılmalıdır.