İlköğretim matematik öğretmen adaylarının analitik geometri alan dilini kullanma becerileri ve tutumlarının incelenmesi

İLKÖĞRETİM MATEMATİK ÖĞRETMEN ADAYLARININ ANALİTİK GEOMETRİ ALAN DİLİNİ KULLANMA BECERİLERİ VE

TUTUMLARININ İNCELENMESİ

BÜŞRA NUR PAZARBAŞI

YÜKSEK LİSANS TEZİ

İLKÖĞRETİM MATEMATİK EĞİTİMİ ANABİLİM DALI

GAZİ ÜNİVERSİTESİ

EĞİTİM BİLİMLERİ ENSTİTÜSÜ

i

TELİF HAKKI ve TEZ FOTOKOPİ İZİN FORMU

Bu tezin tüm hakları saklıdır. Kaynak göstermek koşuluyla tezin teslim tarihinden itibaren on iki (12) ay sonra tezden fotokopi çekilebilir.

YAZARIN Adı : Büşra Nur Soyadı : Pazarbaşı

Bölümü : İlköğretim Matematik Eğitimi İmza :……….

Teslim tarihi : 08 / 04 / 2015

TEZİN

Adı: İlköğretim Matematik Öğretmen Adaylarının Analitik Geometri Alan Dilini Kullanma Becerileri ve Tutumlarının İncelenmesi

İngilizce Adı: An Inquiry Into The Attidues Of The Prospective Primary Education Math Teachers Towards Analytical Geometry And Their Field Language Skills

ii

ETİK İLKELERE UYGUNLUK BEYANI

Tez yazma sürecinde bilimsel ve etik ilkelere uyduğumu, yararlandığım tüm kaynakları kaynak gösterme ilkelerine uygun olarak kaynakçada belirttiğimi ve bu bölümler dışındaki tüm ifadelerin şahsıma ait olduğunu beyan ederim.

Yazar Adı Soyadı: Büşra Nur Pazarbaşı İmza: ..………..

iii

JÜRİ ONAY SAYFASI

Büşra Nur Pazarbaşı tarafından hazırlanan “İlköğretim Matematik Öğretmen Adaylarının Analitik Geometri Alan Dilini Kullanma Becerileri ve Tutumlarının İncelenmesi” adlı tez çalışması aşağıdaki jüri tarafından oy birliği / oy çokluğu ile Gazi Üniversitesi Eğitim Bilimleri Enstitüsü İlköğretim Matematik Eğitimi Anabilim Dalı’nda Yüksek Lisans tezi olarak kabul edilmiştir.

Danışman: Yrd. Doç. Dr. Hasan ES

İlköğretim Matematik Eğimi Ana Bilim Dalı, Gazi Üniversitesi ……… Başkan: Prof. Dr. Cengiz ÇİNAR

İlköğretim Matematik Eğimi Ana Bilim Dalı, Gazi Üniversitesi ………… Üye: Yrd. Doç. Dr. Hasan Hüseyin SAYAN

Elektrik Elektronik Müh. ABD (Teknoloji Fakültesi) , Gazi Üniversitesi ..……….. Tez Savunma Tarihi: 08 / 04 / 2015

Bu tezin İlköğretim Matematik Eğitimi Anabilim Dalı’nda Yüksek Lisans tezi olması için şartları yerine getirdiğini onaylıyorum.

Eğitim Bilimleri Enstitüsü Müdürü

iv

v

TEŞEKKÜR

Matematiğin bilimsel ilerlemede beşeri ilimler için önemli bir kaynak olması, üretmek ve keşfetmek için matematiksel düşünmenin öneminin yadsınamaz gerçeği, muasır medeniyetler seviyesine çıkma arzuları, zihinlerimize “matematikten daha fazla nasıl yararlanabiliriz?” sorusunu yerleştirmiştir. Bu sebeple dikkatler, matematiğin içeriğine, matematiği yarının bilim insanı olacak genç nesillere öğretecek olan öğretmen adaylarının matematik bilgisine ve bu eğitim öğretim sürecine yöneltilmiştir. Bu amaçla Türkiye’de yıllardır birçok önemli araştırma yapılmış ve bu araştırmaların önderliğinde öğretim programı zaman zaman köklü değişiklere uğramış, bu vesile ile öğretmen adaylarının öğretme bilgi ve becerisi artırılmıştır.

İlköğretim matematik öğretmen adaylarının analitik geometri alan dilini kullanma becerileri ve tutumlarının incelenmesi amacı ile gerçekleştirilen bu çalışma pek çok kişinin katkıları ile ortaya çıkmıştır.

Araştırmaya başladığım andan itibaren, yoğun iş temposuna rağmen destek ve fikirlerini benden esirgemeyerek akademik yardımları ile bana yol gösteren değerli danışmanım ve hocam Yrd. Doç. Dr. Hasan Es’e, araştırmamın bazı aşamalarında fikirleri ile bana destek olan Sayın Ar. Gör. Nejla Çalık’a teşekkürü bir borç bilirim.

Araştırmanın yapılması esnasında maddi manevi destekleri ile sürekli yanımda duran ve bugünlere gelmem için büyük emek sarf ederek başarımın asıl mimarı olan anne ve babama, çalışmam süresince destekleri ve sabrı için eşime ve çalışmamda emeği geçen herkese sonsuz saygı ve teşekkürlerimi sunarım.

Büşra Nur Pazarbaşı Ankara - 2015

vi

İLKÖĞRETİM MATEMATİK ÖĞRETMEN ADAYLARININ

ANALİTİK GEOMETRİ ALAN DİLİNİ KULLANMA BECERİLERİ

VE TUTUMLARININ İNCELENMESİ

(YÜKSEK LİSANS TEZİ)

BÜŞRA NUR PAZARBAŞI

GAZİ ÜNİVERSİTESİ

EĞİTİM BİLİMLERİ ENSTİTÜSÜ

NİSAN, 2015

ÖZ

Bu araştırmanın amacı, ilköğretim matematik öğretmen adaylarının analitik geometri alan dilini kullanma becerileri ve tutumlarının incelenmesidir. Böylece, ilerleyen yıllarda gidecekleri orta ve yükseköğretime temel olacak ön bilgilerle genç nesilleri çekirdekten yetiştirme görevi verilen ilköğretim matematik öğretmen adaylarının analitik geometrinin dolayısı ile matematiğin kendine has bir dilinin olduğu gerçeğini kabul etmeleri, bu dili bilmelerinin ve doğru kullanmalarının önemi vurgulanmıştır. Araştırma, pilot ve asıl uygulama olmak üzere iki basamakta gerçekleştirilmiştir. Pilot uygulama, 2012-2013 eğitim öğretim yılı güz döneminde Gazi Üniversitesi Eğitim Fakültesinde öğrenim gören 295 ilköğretim matematik öğretmen adayı ile yürütülmüştür. Asıl uygulamanın dolayısı ile araştırmanın örneklemini, 2012-2013 eğitim öğretim yılında Türkiye’nin yedi fiziki bölgesindeki bünyesinde ilköğretim matematik öğretmenliği bulunduran üniversiteler arasından rastgele seçilmiş yedi devlet üniversitesinde ilköğretim matematik öğretmenliği bölümü 4. sınıf öğrencisi olan, 350 öğretmen adayı oluşturmaktadır. Araştırmanın modeli tarama modelidir. Ölçme aracı olarak araştırmacı tarafından üç uzman görüşü alınarak geliştirilen içeriğinde açık uçlu sorularla çoktan seçmeli soruların bulunduğu Analitik Geometri Alan Bilgisi Beceri Testi ile öğretmen adaylarının Analitik Geometri Alan Dilini

vii

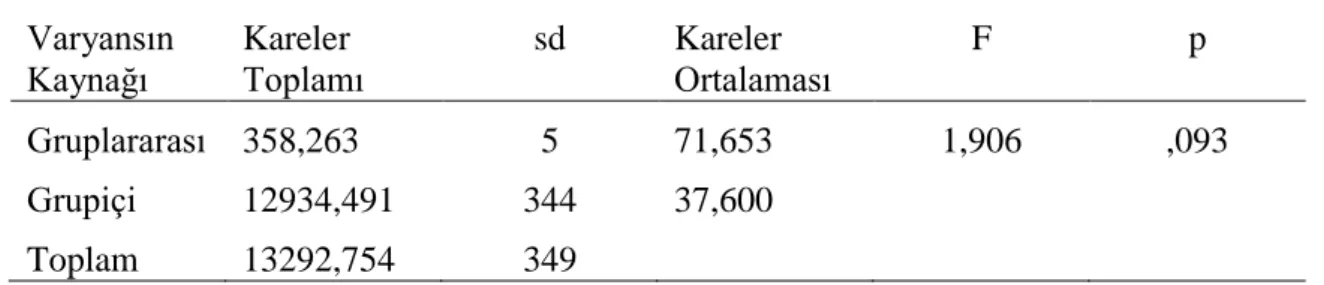
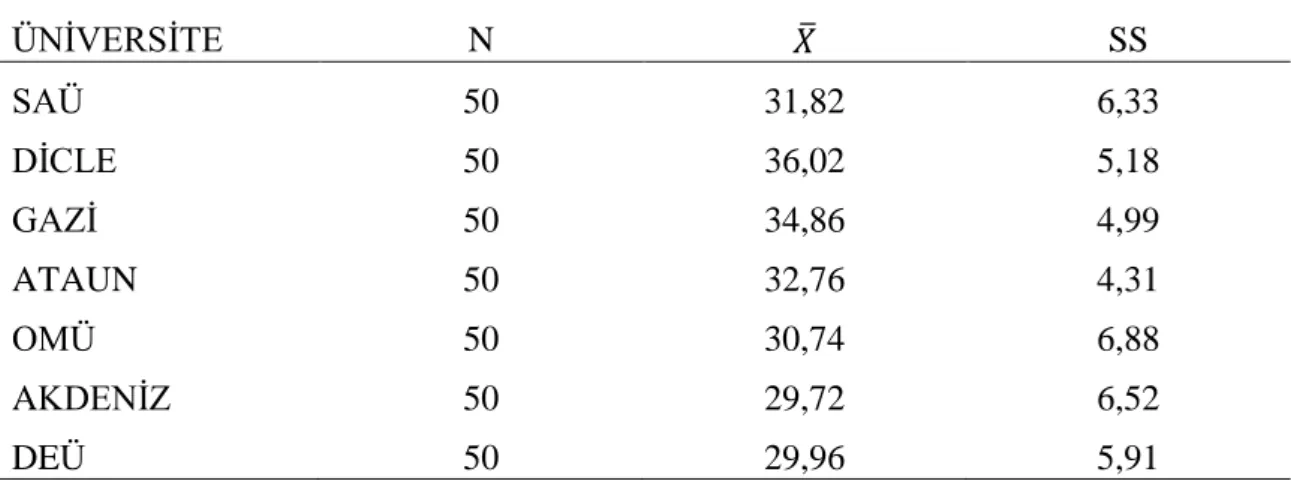
Kullanmalarına Yönelik Tutum Ölçeği kullanılmıştır. Burada kullanılan sorular öğretmen adaylarının analitik geometri alan bilgisine hâkimiyetlerini ölçmeyi esas alırken, geçerlik ve güvenirlik analizi yapılan tutum ölçeği ile öğretmen adaylarının analitik geometriye karşı tutumlarının ölçülmesi amaçlanmıştır. Uygulanan test ve ölçekten elde edilen veriler SPSS paket programına işlenmiş ve verilerin analizi esnasında tek faktörlü varyans analizi (ANOVA), t-testi ve başarıyla tutum arasındaki ilişkinin incelenmesi amacıyla korelâsyon analizi yapılmıştır. Yapılan analizler sonucunda elde edilen bulgular incelendiğinde, öğretmen adaylarının analitik geometriye yönelik tutum ve başarıları cinsiyet, mezun olduğu ortaöğretim kurumu, öğretim şekli ve yaş değişkenlerine göre anlamlı bir fark göstermemiştir. Ancak çalışma değişkenine göre anlamlı farklar gözlemlenmiştir. Bulgulara göre öğretmen adaylarından meslekleri ile ilgili herhangi bir kurumda çalışmış olanların analitik geometriye yönelik tutumlarının daha olumlu, analitik geometri alan dili başarılarının daha yüksek olduğu tespit edilmiştir. Bulgulara göre öğretmen adaylarının tutumları öğrenim gördükleri üniversiteye göre değişmemekte fakat alan dili başarıları öğrenim gördükleri üniversitelere bağlı olarak anlamlı bir değişiklik göstermektedir. Buna göre Dicle ve Gazi Üniversitelerinin puan ortalamaları, Akdeniz ve Dokuz Eylül Üniversitelerinin puan ortalamalarından anlamlı derecede daha yüksek iken Dicle Üniversitesinin puan ortalaması ise Sakarya ve On Dokuz Mayıs Üniversitelerinin puan ortalamalarından anlamlı derecede daha yüksektir. Atatürk Üniversitesi ile diğer üniversiteler arasında anlamlı bir fark bulunamamıştır.

Bilim Kodu:

Anahtar Kelimeler: Analitik geometri alan dili, matematik, tutum. Sayfa Adedi: 77

viii

AN INQUIRY INTO THE ATTIDUES OF THE PROSPECTIVE

PRIMARY EDUCATION MATH TEACHERS TOWARDS

ANALYTICAL GEOMETRY AND THEIR FIELD LANGUAGE

SKILLS

(Ph. D. THESIS)

BÜŞRA NUR PAZARBAŞI

GAZI UNIVERSITY

GRADUATE SCHOOL OF EDUCATIONAL SCIENCES

APRIL, 2015

ABSTRACT

The purpose of this study is inquiring the prospective primary education math teachers’ skills of using analytic geometry field language and their attitudes. Thus, it emphasizes that the prospective primary education math teachers’ who are given responsibility in training young generation with introductory information that will be base in high school and university where they will study in the future, accepting the real of math’s having a special language and the importance of knowing this language and using accurately. This study is realized into 2 steps: pilot and real practice. Pilot practice is carried out with 295 prospective primary education math teachers who have studied in the Education Faculty of Gazi University in the first term of 2012-2013 academic years. 350 prospective primary math teachers who are chosen randomly between universities of 7 regions in Turkey that have primary math teachers at 4. grade from sample of the study because of main practice. The modal of the study is review modal. As a scale tool; Analytic Geometry Field Knowledge Skill Test that is developed by researcher who takes views from 3 experts and includes open-ended and multiple choice tests and Attitude Scale intended to prospective teachers’ using Analytic Geometry Field Language are used. While used questions aim to measure dominance to field language of prospective teachers, attitude test that validity and

ix

reliability are analyzed aims to measure prospective teachers’ attitudes toward analytic geometry. Applied test and datas obtained from the scale are entered SPSS programme and ANOVA, t-test and correlation analysis is done for the purpose of inquiring relation between success and attitude during the analysing data. When the findings obtained from the result of analysis are inquired, the success and attitudes toward analytic geometry of prospective teachers don’t have significant differences in terms of sexes, graduated from secondary education, style of education and age. However; significant differences are observed according to studying variable. According to the findings; it shows that the attitudes of prospective teachers who have studied institutions about their profession are more positive and their analytic geometry field language success are better. According to the findings the attitudes toward analytic geometry of prospective teachers don’t have significant differences in terms of their university which are still educated but success toward analytic geometry of prospective teachers has significant differences. With reference to this, Dicle and Gazi University's average scores are higher than Akdeniz and Dokuz Eylül Universities with a significant difference. And Dicle University's average score is higher than Sakarya and On Dokuz Mayıs Universities with a significant difference. Ataturk University has not significant differences with and the other Universities.

Science Code:

Key Words: Analytical geometry field language, mathematics, attitude. Page Number: 77

x

İÇİNDEKİLER

TELİF HAKKI ve TEZ FOTOKOPİ İZİN FORMU ... i

ETİK İLKELERE UYGUNLUK BEYANI ... ii

JÜRİ ONAY SAYFASI ... iii

TEŞEKKÜR ... v

ÖZ ... vi

ABSTRACT ... viii

İÇİNDEKİLER ... x

TABLOLAR LİSTESİ... xiv

SİMGELER ve KISALTMALAR LİSTESİ ... xvi

BÖLÜM 1 ... 1 GİRİŞ ... 1 1.1. Problem Durumu... 1 1.2. Araştırmanın Amacı ... 3 1.3. Araştırmanın Önemi ... 4 1.4. Araştırmanın Sınırlılıkları ... 5 1.5. Araştırmanın Varsayımları ... 5 1.6. Tanımlar ... 6 BÖLÜM 2 ... 7 KAVRAMSAL ÇERÇEVE ... 7

xi

2.1.1. Matematik Nedir?... 7

2.1.2. Matematiğin Ögeleri ... 8

2.1.3. Analitik Geometri Nedir? ... 9

2.1.4. Analitik Geometrinin Önemi ... 10

2.1.5. Matematik Öğretiminde Öğretmenin Rolü ... 10

2.1.6. Lider Öğretmenin Özellikleri ... 12

2.2. Dil ve Alan Dili... 13

2.2.1. Dil Nedir? ... 13

2.2.2. Matematik Alan Dili ve Önemi... 14

2.3. Tutum ... 16

2.3.1. Tutum Nedir? ... 16

2.3.2. Tutumun Ögeleri ... 17

2.3.3. Tutumun Özellikleri ... 18

2.3.4. Tutumun Ölçülmesi ve Tutum Ölçekleri ... 18

2.3.5. Tutum ve Davranış İlişkisi ... 20

2.3.6. Matematiğe Yönelik Tutum, Korku ve Kaygı ... 21

2.4. İlgili Araştırmalar ... 22

2.4.1. Alan Dilini Kullanma ile İlgili Yapılan Araştırmalar ... 22

2.4.2. Tutum Konusunda Yapılan Araştırmalar ... 26

2.4.3. Analitik Geometri ile İlgili Araştırmalar ... 29

BÖLÜM 3 ... 33

YÖNTEM... 33

3.1. Araştırmanın Modeli... 33

3.2. Evren ve Örneklem ... 34

3.3. Veri Toplama Araçları... 36

xii

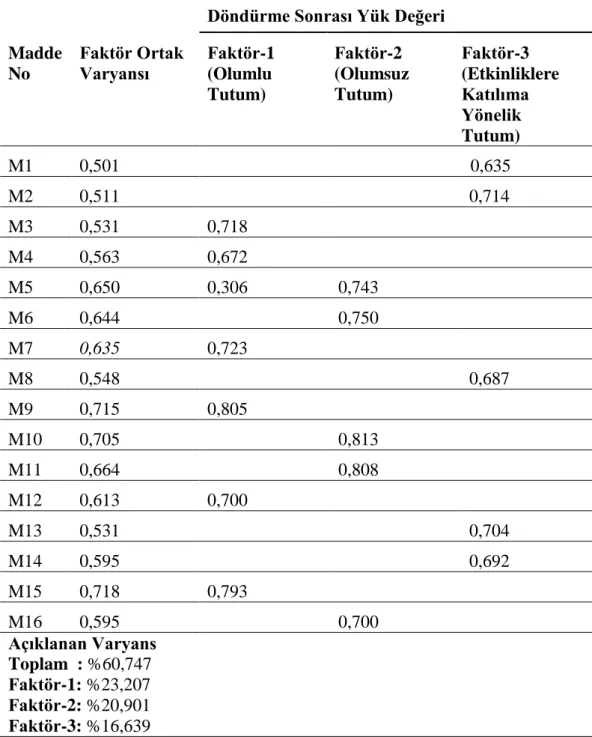
3.3.2. Analitik Geometri Alan Diline Yönelik Tutum Ölçeği... 37

3.4. Verilerin Toplanması ... 40

3.5. Verilerin Analizi ... 40

BÖLÜM 4 ... 41

BULGULAR VE YORUM ... 41

4.1. Birinci Alt Probleme İlişkin Bulgular ve Yorum ... 41

4.1.1. Analitik Geometri Alan Dili Başarısının Cinsiyet Değişkenine Göre Dağılımına İlişkin Bulgular ... 41

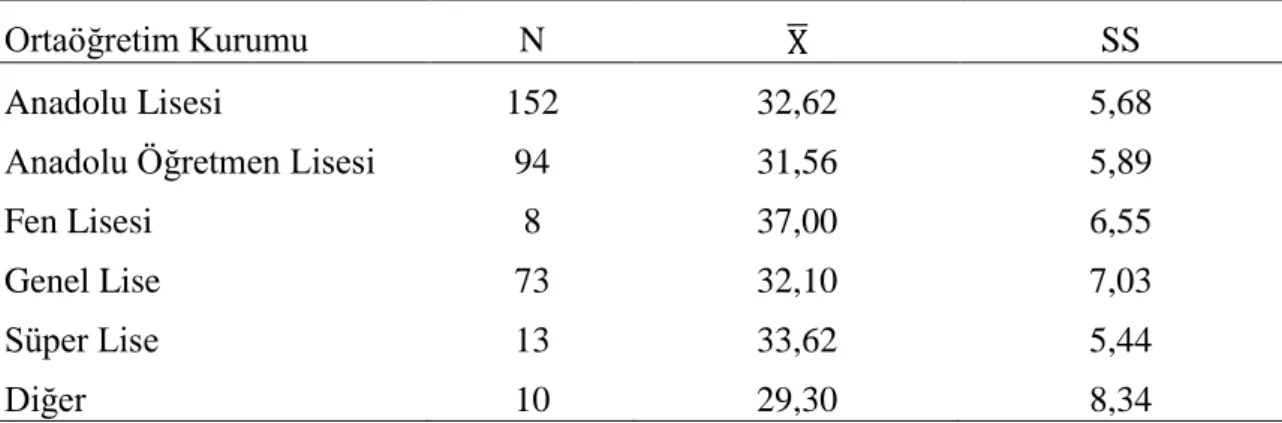
4.1.2. Analitik Geometri Alan Dili Başarısının Mezun Olunan Ortaöğretim Kurumu Değişkenine Göre Dağılımına İlişkin Bulgular ... 42

4.1.3. Analitik Geometri Alan Dili Başarısının Adayların Öğretim Şekli Değişkenine Göre Dağılımına İlişkin Bulgular ... 43

4.1.4. Analitik Geometri Alan Dili Başarısının Adayların Yaş Değişkenine Göre Dağılımına İlişkin Bulgular ... 44

4.1.5. Analitik Geometri Alan Dili Başarısının Adayların Alanlarıyla İlgili Herhangi Bir Yerde Çalışma Değişkenine Göre Dağılımına İlişkin Bulgular ... 45

4.1.6. Analitik Geometri Alan Dili Başarısının Öğretmen Adaylarının Öğrenim Gördüğü Üniversite Değişkenine Göre Dağılımına İlişkin Bulgular ... 46

4.2. İkinci Alt Probleme İlişkin Bulgular ve Yorum ... 47

4.2.1. Analitik Geometri Alan Diline Yönelik Tutumun Cinsiyete Göre Dağılımına İlişkin Bulgular ... 48

4.2.2. Analitik Geometri Alan Diline Yönelik Tutumun Mezun Olunan Ortaöğretim Kurumu Değişkenine Göre Dağılımına İlişkin Bulgular... 48

4.2.3. Analitik Geometri Alan Diline Yönelik Tutumun Adayların Öğretim Şekli Değişkenine Göre Dağılımına İlişkin Bulgular ... 50

4.2.4. Analitik Geometri Alan Diline Yönelik Tutumun Adayların Yaş Değişkenine Göre Dağılımına İlişkin Bulgular ... 50

xiii

4.2.5. Analitik Geometri Alan Diline Yönelik Tutumun Adayların Alanlarıyla İlgili Herhangi Bir Yerde Çalışma Değişkenine Göre Dağılımına İlişkin Bulgular

... 52

4.2.6. Analitik Geometri Alan Diline Yönelik Tutumun Öğretmen Adaylarının Öğrenim Gördüğü Üniversite Değişkenine Göre Dağılımına İlişkin Bulgular... 53

4.3. Üçüncü Alt Probleme İlişkin Bulgular ve Yorum ... 54

BÖLÜM 5 ... 57

SONUÇ VE ÖNERİLER ... 57

5.1. Sonuçlar... 57

5.1.1. Öğretmen Adaylarının Analitik Geometri Alan Dili Başarıları ... 57

5.1.2. Öğretmen Adaylarının Analitik Geometri Alan Diline Yönelik Tutumları 58 5.1.3. Öğretmen Adaylarının Analitik Geometri Alan Diline Yönelik Tutum ve Başarıları Arasındaki İlişki ... 59

5.2. Öneriler ... 59

KAYNAKLAR ... 63

ÖZGEÇMİŞ... 71

EKLER... 73

EK I : Kişisel Bilgi Formu & Analitik Geometri Alan Diline Yönelik Tutum Ölçeği ... 73

xiv

TABLOLAR LİSTESİ

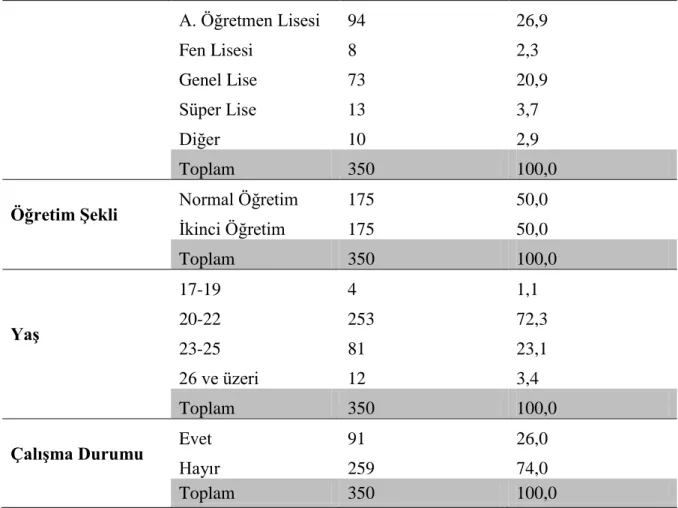
Tablo 1. 5‘li Likert Tipi Ölçek Örneği...1 Tablo 2. Araştırmaya Katılan İlköğretim Matematik Öğretmen Adaylarının Demografik Bilgileri...2 Tablo 3. Analitik Geometri Alan Bilgisi Beceri Testi’nin Puanlanması...3 Tablo 4. Analitik Geometri Alan Diline Yönelik Tutum Ölçeği Faktör Analizi (Dönüştürülmüş Temel Bileşenler Analizi) Sonuçları...4 Tablo 5. Analitik Geometri Alan Diline Yönelik Tutum Ölçeği’nin Puanlanması...5 Tablo 6. Öğretmen Adaylarının Test Puanlarının Cinsiyet Değişkenine Göre T-Testi Sonuçları...6 Tablo 7. Öğretmen Adaylarının Mezun Olunan Ortaöğretim Kurumuna Göre Analitik Geometri Alan Bilgisi Beceri Testi Betimsel İstatistikleri...7 Tablo 8. Öğretmen Adaylarının Test Puanlarının Mezun Olunan Ortaöğretim Kurumu Değişkenine Göre ANOVA Sonuçları...8 Tablo 9. Öğretmen Adaylarının Test Puanlarının Öğretim Şekli Değişkenine Göre T-Testi Sonuçları...9 Tablo 10. Öğretmen Adaylarının Yaş Değişkenine Göre Analitik Geometri Alan Bilgisi Beceri Testi Betimsel İstatistikleri...10 Tablo 11. Öğretmen Adaylarını Test Puanlarının Yaş Değişkenine Göre ANOVA Sonuçları...11 Tablo 12. Öğretmen Adaylarının Test Puanlarının Alanları ile İlgili Herhangi Bir Yerde Çalışma Değişkenine Göre T- Testi Sonuçları...12

xv

Tablo 13. Öğretmen Adaylarının Üniversite Değişkenine Göre Analitik Geometri Alan Bilgisi Beceri Testi Betimsel İstatistikleri...13 Tablo 14. Öğretmen Adaylarının Test Puanlarının Üniversite Değişkenine Göre ANOVA Sonuçları...14 Tablo 15. Öğretmen Adaylarının Ölçek Puanlarının Cinsiyet Değişkenine Göre T- Testi Sonuçları...15 Tablo 16. Öğretmen Adaylarının Ölçek Puanlarının Mezun Olunan Ortaöğretim Kurumu Değişkenine Göre Betimsel İstatistikleri...16 Tablo 17. Öğretmen Adaylarının Ölçek Puanlarının Mezun Olunan Ortaöğretim Kurumu Değişkenine Göre ANOVA Sonuçları...17 Tablo 18. Öğretmen Adaylarının Ölçek Puanlarının Öğretim Şekli Değişkenine Göre T-Testi Sonuçları...18 Tablo 19. Öğretmen Adaylarının Analitik Geometri Alan Diline Yönelik Tutumlarının Yaş Değişkenine Göre Betimsel İstatistikleri...19 Tablo 20. Öğretmen Adaylarının Ölçek Puanlarının Yaş Değişkenine Göre ANOVA Sonuçları...20 Tablo 21. Öğretmen Adaylarının Ölçek Puanlarının Alanları İle İlgili Herhangi Bir Yerde Çalışma Değişkenine Göre T-Testi Sonuçları...21 Tablo 22. Öğretmen Adaylarının Ölçek Puanlarının Üniversite Değişkenine Göre Betimsel İstatistikleri...22 Tablo 23. Öğretmen Adaylarının Ölçek Puanlarının Üniversite Değişkenine Göre ANOVA Sonuçları...23 Tablo 24. Öğretmen Adaylarının Başarı ve Tutumları Arasındaki İlişki...24

xvi

SİMGELER ve KISALTMALAR LİSTESİ

N Örneklem Listesi

Ortalama

SS Standart Sapma

sd Serbestlik Derecesi

t Regresyon Katsayısının Anlamlılığına İlişkin T-Testi Sonucu

p Anlamlılık Düzeyi

ANOVA Tek Faktörlü Varyans Analizi

F Varyans Oranı

r Korelasyon Katsayısı

r2 Açıklanan Varyans

SAÜ Sakarya Üniversitesi DİCLE Dicle Üniversitesi GAZİ Gazi Üniversitesi ATAUN Atatürk Üniversitesi

OMÜ On Dokuz Mayıs Üniversitesi AKDENİZ Akdeniz Üniversitesi

1

BÖLÜM 1

GİRİŞ

Öğretmenleri iyi yetiştirilmemiş toplumların gelecekleri tehlike altındadır. Bu sebeple ülkemizde ve dünyada bu konunun üzerinde önemle durulmuş ve konuya ilişkin çok sayıda araştırma yapılmıştır. Bu bölümde, yapılacak araştırmaya yönelik problem durumu, araştırmanın amacı, araştırmanın önemi, araştırmanın sınırlılıkları, varsayımları ve araştırma sırasında kullanılacak terimlere yer verilmiştir.

1.1. Problem Durumu

Birçok insan için matematik, hayatını zehir eden derslerden, içine korku salan sınavlardan ve okulu bitirir bitirmez kurtulacağı büyük bir kâbustan ibarettir. Bazıları içinse matematik, hayatı anlamanın ve sevmenin bir yolu olabilmiştir (Sertöz, 2000). Dönmez (2002)’ye göre matematik bilimi ciddi bir iştir fakat aynı zamanda aslında asık yüzlü ve korku duyulan bir disiplin olmayıp, tersine yaşam gibi eğlenceli, neşeli ve insanı dinlendiren bir uğraş alanıdır. Matematik öğretiminin, eğitim sürecindeki önemi ve bireyin yaşamındaki gereksinimlerine katkısı hiç azalmadan sürmektedir. Bireyin aldığı matematik eğitimi, onun sosyal ve ekonomik yaşamını, teknolojiye ve bilime yapacağı katkılarını doğrudan etkilemektedir (Küçükyörü, 2006). Bu bağlamda bakıldığında, etkili matematik öğretimi bireylerin sadece okulda aldıkları eğitimi değil yaşamsal faaliyetlerini de doğrudan ilgilendirmekte ve bu sebeple hayati önem taşımaktadır.

Geometriyi cebir aracılığıyla işleyen matematiğin verimli bir dalı olan analitik geometri, soyut kavramları ve soyut düşünmeyi içeren bir dal olması sebebiyle öğrencilerin anlamakta güçlük çektikleri konulardan biridir. Analitik geometride, geometri, şeklin

2

gözlenmesinden kurtularak nicelikler düzeni halini alırken cebire yaklaşmış, yani geometri cebirin egemenliğine girmiştir, dolayısıyla daha da soyutlaşmıştır (Gözen, 2001). Matematikte çok önemli bir yer tutmasına rağmen, öğrenciler analitik geometriyi öğrenmede büyük sıkıntılarla karşılaşmaktadır. Analitik geometri dersi, öğrenciler tarafından zor anlaşılan, öğretmenler tarafından ise somutlaştırılması zor olan bir ders gibi görülmektedir. Bu noktada öğretmen ve öğrencilerin birbirini anlaması, analitik geometri dersinin anlamlandırılması açısından hayati öneme sahiptir. Bu sebeple, matematik derslerinde öğretmen ve öğrenci arasında matematiksel ilkelere uygun bir iletişimin gerçekleşmesi şarttır. Derslerde anadilin iyi kullanılmasının yanı sıra kendisine özgü bir dili olan matematiğin aracılığıyla iletişim kurabilmek de oldukça önemlidir.

Öğretmenlerin ilköğretimin ilk yıllarından itibaren derslerde kullanmakta oldukları matematiksel alan dilinin, öğrenimlerinin en son kademesine kadar olan süreçte kavramların oluşumuna etkisi oldukça fazladır. Öğretmenlerin ihmal ederek kısa sürede doğru olarak kullanmadıkları alan dili, zaman içerisinde sağlıksız bir iletişime neden olacak ve uzun sürede de öğrencilerin matematiksel kavramları inşasında aksaklıklar meydana getirecektir. Doğru kullanımı halinde ise öğrencilerin matematiksel düşünme ve matematiksel güçlerinde büyük bir gelişme sağlanacaktır (Yeşildere, 2007).

Matematik öğretmenlerinin matematiğe yönelik bilgilerinin geliştirilmesinin yanı sıra, öğretmenlik becerilerinin gelişmesi yönünde de çalışmaların yapılması gerekmektedir. Matematikle ilgili kavram ve bilgileri edinmenin ve matematiksel düşünmeye ulaşmanın temel öğelerinden biri; alana ait dilin doğru kullanımıdır. Dil kullanımı, tanıtılan kavramları öğrencilerin doğru ve eksiksiz anlamasında önemli rol oynamaktadır (Lansdell, 1999). Alan dili kavramlar arasındaki ilişkiyi güçlendirir, kavramların daha doğru ve yerinde kullanılmasını sağlar (Köroğlu, Yavuz ve Ertem, 2003).

Birçok nedenden dolayı kişiler, herhangi bir yemeği, bir politikacıyı, bir şehri, bir dersi veya bir öğretmenin ders anlatış şeklini beğenmeyebilir. Bu gibi durumlarda, örneğin, o yemeği yememek, beğenmediği politikacının partisine oy vermemek, o dersten ya da öğretmenden nefret etmek gibi değişik tutumlar sergileyebilirler. Tutumlar bilişsel, duyuşsal ve davranışsal tepkileri içerebilir. Tutumlar doğrudan gözlenebilen özellikler değildir fakat tutumlar davranışı etkilediğinden, davranışlardan çıkarsama yaparak kişilerin tutumları hakkında bilgi sahibi olunabilir. Tutum hakkında bilgi sahibi olmak da bireylerin davranışları hakkında yordama olasılığını ortaya çıkarmaktadır. Tutumları etkileyen birçok faktör vardır fakat güçlü tutumların değişmesi oldukça zordur (Kağıtçıbaşı, 1999). Bu

3

sebeple bir konu hakkında oluşan ön yargıları yıkmak ve tutumları değiştirmeye çaba harcamak yerine ön yargısız ve doğru tutumlar oluşturularak başlangıç yapmış olmak tercih sebebidir.

Öğretmen adaylarının mesleklerine ve mesleki alan bilgisine yönelik tutumları onların gelecekte nasıl birer öğretmen olacaklarının belirlenmesinde etkin rol oynamaktadır. Aynı şekilde öğretmen adaylarının kendi alanlarına yönelik tutumları da onların mesleki çalışmalarında belirleyici olacaktır. Öğretmen tutumlarının öğrencilerin tutum ve davranışlarını da büyük ölçüde etkilediği düşünülecek olursa, analitik geometri öğretimine yönelik öğretmen tutumlarının öğrenci başarısı ve tutumlarını etkilemesi kaçınılmazdır. Eğitim süreci içerisinde tutumlar değişmektedir. Öğretmen adaylarının da eğitim süresince analitik geometrinin öğretimine yönelik tutumlarının değişim yönü, öğretim sırasındaki davranışları etkileyecektir.

Bu sebeple, analitik geometri öğretiminin gerekçelerini öğrencilere açıklayacak olan matematik öğretmenlerinin, eğitim fakültelerindeki öğrenim süreçleri ve alan bilgisi ile mesleki tutumları üzerinde dikkatle durmak gerekmektedir. Battista (1986)’nın “öğretmen eğitimi sırasında öğretmen adaylarının edindikleri olumsuz tutumların hem kendi matematik öğrenmelerini hem de daha sonra matematiği öğretmedeki etkin yöntemler kullanabilmelerini sınırlamaktadır” görüşü öğretmen adaylarının analitik geometri öğretimine yönelik tutumlarının bilinmesinin önemini ortaya koymaktadır (Battissa'dan aktaran Doğan, 2004).

Bu çalışmada analitik geometri dersinin incelenmesinin nedeni; analitik geometri eğitiminin matematik başta olmak üzere pek çok çalışma alanını yakından ilgilendiren, kendine has bir dilinin ve kavramlarının olduğu gerekçesi ile analitik geometri alan dilinin öğretmen adayları ve hayatlarının ileri safhalarında pek çok yerde bu dili kullanacak öğrenciler tarafından çok iyi bilinmeleri ve doğru kullanılmaları gerektiğinin vurgulanmasıdır.

1.2. Araştırmanın Amacı

Bu araştırmanın amacı, ilköğretim matematik öğretmen adaylarının analitik geometri alan dilini kullanma becerileri ve tutumlarının incelenmesidir. Böylece, ilerleyen yıllarda gidecekleri orta ve yükseköğretime temel olacak ön bilgilerle genç nesilleri çekirdekten yetiştirme görevi verilen ilköğretim matematik öğretmen adaylarının analitik geometrinin

4

dolayısı ile matematiğin kendine has bir dilinin olduğu gerçeğini ne derece kabullendikleri, bu dili özümseyerek mesleklerinde kullanılır hale getirip getirmedikleri araştırılmış, bu dili bilmelerinin ve doğru kullanmalarının önemi vurgulanmıştır.

Bu amacın gerçekleştirilebilmesi için aşağıdaki alt problemlere yanıt aranmıştır: 1) İlköğretim matematik öğretmen adaylarının analitik geometri alan dili başarısı,

a. Cinsiyet

b. Mezun olunan ortaöğretim kurumu c. Öğretim şekli

d. Yaş

e. Alanları ile ilgili herhangi bir kurumda çalışıp çalışmama durumu

f. Hâlihazırda öğrenim gördükleri yüksek öğretim kurumuna göre anlamlı bir fark göstermekte midir?

2) İlköğretim matematik öğretmen adaylarının analitik geometri alan diline yönelik tutumları,

a. Cinsiyet

b. Mezun olunan ortaöğretim kurumu c. Öğretim şekli

d. Yaş

e. Alanları ile ilgili herhangi bir kurumda çalışıp çalışmama durumu

f. Hâlihazırda öğrenim gördükleri yüksek öğretim kurumuna göre anlamlı bir fark göstermekte midir?

3) İlköğretim matematik öğretmen adaylarının analitik geometri alan diline yönelik tutumları ve başarıları arasında anlamlı bir ilişki var mıdır?

1.3. Araştırmanın Önemi

Türkiye’deki araştırmalar incelendiğinde öğretmen adaylarının mesleki alan dilini kullanma becerileri ve tutumları konusunda yapılmış yeteri kadar araştırma bulunmamaktadır. Bu sebeple, yapılan bu araştırma matematik öğretmen adaylarının

5

mesleklerine yönelik tutum ve becerileri konusunda ilerleyen zamanlarda yapılacak olan çalışmalara yol gösterici olabilmesi açısından önemlidir.

Ülkemizde olduğu gibi değişik dünya ülkelerinde de analitik geometri alan dili konusunda yapılmış araştırma sayısı yok denecek kadar azdır. Dolayısıyla, bu çalışma, küreselleşen dünya sistemi göz önüne alındığında yabancı araştırmacılar için de bir kaynak niteliğinde olacaktır.

Bilindiği gibi bu araştırmada, ülkemizin yedi bölgesinden rastgele seçilmiş yedi devlet üniversitesinde ilköğretim matematik öğretmen adayı olarak öğrenim gören öğrencilerin analitik geometri alan dili kullanımlarındaki beceri ve tutumları arasındaki ilişki incelenmiş, coğrafi bir kıyaslama yapılmıştır. Bu açıdan düşünüldüğünde araştırma, ülkemiz üniversitelerinin bölgelere göre eğitim öğretim durumlarının analizi için bir örnek niteliğindedir.

1.4. Araştırmanın Sınırlılıkları

1) Araştırma zaman açısından 2012-2013 eğitim öğretim yılı ile sınırlıdır.

2) Araştırma, ekonomik zorluklar, zaman sınırlılığı, ulaşım zorluğu ve uygulama ile ilgili sıkıntılar sebebiyle; örneklem açısından Türkiye’de rastgele seçilen yedi devlet üniversitesinin ilköğretim matematik öğretmenliği programında öğrenim gören 4. sınıf öğrencileri ile sınırlı tutulmuştur.

3) Araştırma, öğrencilerin “Analitik Geometri Alan Diline Yönelik Tutum Ölçeği” ve “Analitik Geometri Alan Bilgisi Beceri Testi”nden elde edilen puanları ile sınırlandırılmıştır.

1.5. Araştırmanın Varsayımları

1) Araştırmanın örneklemi evreni temsil etmektedir.

2) Öğrenciler, araştırma sorularına samimi cevaplar vermişlerdir.

3) Kullanılan yöntem, ölçek ve testler araştırmanın amacına ve konusuna uygundur. 4) Araştırma sonucunda elde edilen veriler araştırmayı destekler niteliktedir.

6

5) Analitik geometri alan bilgisi beceri testindeki sorulara yanlış verilen cevaplar o konuda doğru bilgi sahibi olunmadığını ve boş bırakılarak herhangi bir cevap verilmeyen sorular ise konu hakkında herhangi bir şey bilinmediğini ifade etmektedir.

1.6. Tanımlar

Araştırmada kullanılacak olan terimler aşağıda tanımlanmıştır.

Eğitim: Bireyde kendi yaşantısı yoluyla kalıcı istendik davranış değişikliği meydana getirme sürecidir.

Öğretim: Eğitimin okulda planlı ve programlı yürütülen kısımdır.

Öğrenme: Kişinin çevre ile etkileyişimi sonucunda meydana gelen kalıcı davranış değişiklikleridir.

Öğretme: Öğrenmeyi kılavuzlama faaliyetidir.

Tutum: Belirli nesne, durum, kavram ya da değer, insanlara karşı öğrenilmiş, olumlu ya da olumsuz tepkide bulunma eğilimidir (Tezbaşaran, 1997).

Matematik Alan Dili: Matematiksel beceriler arasındaki ilişkiyi basitten karmaşığa doğru düzenleyen matematiğin kendine has dilidir (Collins Browning, 2009).

Analitik Geometri: Geometrik çalışmaya cebrik analizi uygulayan ve cebrik problemlerin çözümü için geometrik kavramlardan faydalanan bir matematik dalıdır (Brannan, Esplen ve Gray, 2002).

7

BÖLÜM 2

KAVRAMSAL ÇERÇEVE

2.1. Matematik ve Analitik Geometri

2.1.1. Matematik Nedir?

Hızla küreselleşen dünyamızda genellikle öğrenciler tarafından sevilmeyen, korkulan, zor olmakla tasvir edilen soyut bir disiplin olan matematiğin pek çok disiplinde önemi gittikçe artmaktadır. Bu bağlamda, “matematik nedir, ne değildir?” sorusunun yanıtını bilmek ve temelden kavramak; kavram yanılgılarını, korku, endişe, telaş gibi hisleri ve yanlış şartlanmayı önleyecektir.

Türk Dil Kurumu (1983)’na göre matematik; biçim, sayı ve çoklukların yapılarını özelliklerini ve aralarındaki bağlantıları mantık yoluyla inceleyen, aritmetik, cebir, geometri gibi dallara ayrına bilim dalıdır (Türk Dil Kurumu'ndan aktaran Çiftçi 2005). Matematik, insanlık tarihinin bilinen en eski bilimlerinden biridir. Çok eskiden sayı ve şekillerin ilmi olarak tanımlanan matematiği geçen zaman içinde gösterdiği gelişim ve değişim sebebi ile birkaç cümle ile tanımlamak mümkün değildir. Galileo Galilei'nin tabiat matematik dilinde yazılmıştır demesi de bu tanımlamanın mümkün olmadığını kanıtlar niteliktedir (Ülger, 2003).

Matematik soyut bir bilim olduğundan toplum matematiği doğrudan kullanmaz, dolaylı yoldan kullanır (Nesin,1989). Marketten ya da manavdan alışveriş yaparken kullandığımız parasal hesaplar, araba kullanırken kullandığımız vücut dili, herhangi bir alet çalarken ortaya çıkan analitik düşünme aslında farkında olmadan dolaylı yoldan matematiği hayatımızın her evresine yerleştirmektir.

8

Matematiğin konusunu sayılar, şekiller, fonksiyonlar, kümeler, uzaylar gibi soyut kavramlarla bunların arasında kurulan bağlantılar oluşturur. Matematikçi bu kavram ve tanımların yapı ve özelliklerini inceler, ilgili genelleme ve ispatlara ulaşır (Alkan ve Altun, 1998). Matematiğe matematikçi gözüyle baktığımızda günlük hayatta kullanılan matematikten çok daha karmaşık yapılar görmemiz, bu bağlamda çok yönlü düşünmemiz, sürekli “acaba?” ve “neden?” sorularını sormamız da bu sebepledir.

Matematik, Antik Yunanca “matesis-ben bilirim” anlamına gelen kelimeden türetilmiş olup bu terim yerine Osmanlı İmparatorluğunda “Riyazet-toy taylara başkaldırma eğitimi” kelimesinden türetilmiş “riyaziye” kelimesi kullanılmıştır.

Karaçay (2001)’e göre; matematiğin farklı tanımlarına bakıldığında; aynı zamanda işlevlerini de belirten şu noktalara ulaşabilir: Matematik insanlığın ortak dili, bilimidir. Bilimin vazgeçilmez aracı ve sanattır. Nitekim kâinat bir matematikçi gözüyle incelendiğinde evrendeki eşsiz uyum ve güzelliğin aslında matematikten ibaret olduğu apaçık görülmektedir.

Baykul 1994'te katıldığı, Türk Eğitim Derneği 12. Öğretim Toplantısında matematiğin ardışık soyutlama ve genellemelerle geliştirilen yapı ve bağıntılardan oluşan ve mantıksal düşünmeyi geliştiren bir sistem olduğunu ifade etmiştir. Baykul (2005)’a göre matematik bütün insanlığın kullandığı sembollere dayanan bir dildir ve fiziksel sistemlerden farklı olarak zihinseldir, kokusu, sertliği rengi yoktur, duyu organlarıyla gözlenmez ancak akıl yoluyla kavranır. Matematiğin bazılarınca ‘zor’ olarak tasvir edilmesi de bu özelliğinden ileri gelir.

2.1.2. Matematiğin Ögeleri

Matematiğin ögelerini; mantık, sezgi, çözümleme, yapı kurma, genellik, bireysellik ve estetik olarak sıralayan Alkan ve Altun (1998)’a göre matematik, soyut ve somut olmak üzere ikiye ayrılır. Somut matematik dendiğinde pratik hesaplamalar, problem çözme ve ölçme yaparken kullanılan matematik akla gelirken soyut matematik, matematiğin kendine has iç tartışma ve çatışmalarının yer aldığı matematiktir. Bu matematiği pür matematik olarak isimlendirilir. Teoremlerin ispatı, sayı sistemlerinin kurulması, yeni matematiksel yapıların oluşumu ve iç dinamiklerinin açıklanması bu bağlamda değerlendirilir. Soyut matematiğin hayatla ilişkisi zamanla oluşur ve gelişimi sadece insan zihninin merakını giderme ve gerçeği bulma uğraşına dayanır.

9

Orta ve yükseköğretim kademelerinde pür matematik pek çok disipline ayrılarak incelenir. Bunlardan yükseköğretim kademesinde gösterilen bazı kollar; cebire giriş, soyut cebir, soyut matematik, lineer cebir, analitik geometri analiz, elementer sayı kuramları, diferansiyel denklemler ve istatistiktir.

2.1.3. Analitik Geometri Nedir?

Bilindiği gibi bütün disiplinler ve bilimler insan ihtiyacının karşılanamadığı durumlarda, yani ihtiyaç duyulduğunda, bir gereksinim dâhilinde ortaya atılmış ve geliştirilmiştir. Hooper (1961)’a göre geometrik şekillerin oluşumu ve geometri biliminin doğması da Nil Nehri kenarında yaşayan Mısır halkının yüzlerce yıl önce nehrin taşması sonucu tarla sınırlarının değişmesi ile yeniden ve yeniden sınırları çizmek zorunda kalışları ile doğrudan ilişkilidir. Zamanla, yine gereksinimler dâhilinde, geometri ve cebrin birleşmesi ve yardımlaşması ile pratik ve kuramsal değerleri olan yeni bilim dallarından biri daha insanlığın faydasına sunulmuştur. Bu bilim dalı, ünlü Fransız düşünür Rene Descartes tarafından 1637’de icat edilen analitik geometriden başkası değildir (Hogben, 1942). Analitik Geometri, koordinat sistemi adı verilen bir sistemde yerleştirilmiş, geometrik şekillerin yeri ve boyutları hakkında açıklamalarda bulunan, bunun için de cebirsel denklemleri kullanan bir matematik dalıdır. On yedinci yüzyılda gelişmeye başlayan analitik geometri, “kartezyen geometri-koordinat geometri” olarak da isimlendirilmektedir. Analitik geometrinin matematiğe ve diğer disiplinler ve bilimlere en büyük katkısı, kuşkusuz, bir cebirsel denklemi geometrik bir şekille ilişkilendirmede kullanılmasıdır. Temeli, geometrik temsili bulunan noktaları reel sayılarla bağlantılandırarak koordinat sisteminde yerleştirmeye dayanmaktadır. Bu sebeple analitik geometri, fen bilimleri ve endüstri alanları başta olmak üzere birçok alanda yaygın bir şekilde faydalanılan matematiğin alt bilim dallarından biridir.

Analitik geometri, Öklid geometrisinde ölçmeye imkân tanınmayan, noktalar, doğrular ve düzlemler arasındaki ilişkileri açıklamayı hedefler. Düzlemsel şekillerin incelenmesine yönelik kısmı “düzlem analitik geometri” olarak adlandırılırken, cisimler ve uzay eğrilerini kapsayan kısmı da “uzay analitik geometri” olarak isimlendirilir (Altun, 2004).

10 2.1.4. Analitik Geometrinin Önemi

Günlük yaşantılarımızda her an gereksinim duyduğumuz sayma, zamanı tanımlama, alışverişte hesap işlemleri, tartma, ölçme, biçme, basit grafik ve şemaları yorumlama, aritmetik işlemler gibi pek çok konu aslında matematiğin temelini oluşturan kavramlardır. Bu bağlamdan bakıldığında endüstriden teknolojiye kadar birçok medeniyet harikası var olmasını matematiğe borçludur (Işık ve Bekdemir, 1998).

Geometri, şekiller arasında ve şekiller içinde desenler ile değişmez ilkeler bulma etkinliklerini içermektedir (Olkun ve Toluk, 2003). Geometriye dair temel içerikler en basit şekille başlar, noktadan doğruya; doğru parçalarına, ışınlara, eğrilere, iki boyutlu ve üç boyutlu düzlemlere doğru genişler. Nokta, çıkış noktasıdır (Sheffıeld, Cruikshank ve Douglas, 2005). Analitik geometrinin noktalardan doğması modern matematiğin pek çok branşının en temel araçlarından biri olmasını sağlamaktadır.

Matematiğin diğer alt dalları gibi analitik geometri de kendine has bir dil ve gösterime sahiptir. Öklid geometrisinde ulaşılamayan ilişkiler analitik geometri sayesinde kolayca tanımlanabilir, analiz edilebilir ve bir sonuca bağlanabilir.

Bireylerin eleştirel düşünme becerilerini etkin bir şekilde kullanması, etkili sorular sorması, ön yargısız ve eleştiriye açık desteklenmiş düşünceler geliştirmesi ve yanlışlarını kolayca kabul edip çok yönlü fikirler üretebilmesi için ilk olarak konunun özünü bilmeleri gerekmektedir. Konunun özü, bahsi geçen bilimin kendine has alan dilinin temelden bilinmesi ile kavranır ki bu, analitik geometri dersinin öğrenme-öğretme sürecinde de diğer bilimlerde olduğu gibi önemli bir yere sahiptir.

2.1.5. Matematik Öğretiminde Öğretmenin Rolü

Eğitim Terimleri Sözlüğü (Oğuzkan, 1974)’nde öğretmen, ‘resmî ya da özel bir eğitim kurumunda çocukların, gençlerin ya da yetişkinlerin istenilen öğrenme yaşantıları kazanmalarına kılavuzluk etmek ve yön vermekle görevlendirilmiş, bilgi, görgü ve yaşantısı ile belli dal ve alanlarda başkalarının yetişme ve gelişmesine yardım eden, öğretmenlik mesleğinin gerektirdiği öğrenimi bitirerek ya da yeterlikleri kazanarak öğretmenlik yapma yetkisini elde etmiş olan, bir bilim dalını, bir sanatı, bir tekniği veya belli bir bilgiyi öğretmeyi kendisine meslek edinmiş kimsedir’ şeklinde tanımlanır.

11

Öğretmenleri kaliteli yetiştirilmiş ülkelerde, kaliteli eğitim-öğretim, kaliteli öğrenci ve dolayısıyla gelişmiş teknolojiler ve küreselleşen dünyaya kolay uyum sağlayan gelişmiş bir ülke kurulması hedeflenir. İçinde bulunduğumuz 21. yüzyılın geçtiğimiz asırlara göre en belirgin özelliği ‘Bilgi Çağı’ olmasıdır. Baştürk ve Yücel (2004)’e göre öğrenmeyi öğrenme, sinerji ve bilgi okuryazarlığı, öğretmen eğitiminde kısa ve uzun vadeli hedefler için kalitenin önemli göstergeleri sayılmaktadır. Bilim ve teknolojinin, toplumun aydınlar kesimine has olma özelliğinden kurtulup halk tabakasına inmesi, böylelikle toplum olarak “bilgi toplumu” olma süreci içerisinde en önemli rol şüphesiz öğretmene düşmektedir. Özer (1998), bu sebeple "bireylerin sürece uyum aşamasında düşünme yollarını bilip uygulayabilme, sorun çözebilme, araştırma yapabilme, bilgiyi yaratıcı bir şekilde kullanabilme, bilgi ve teknoloji üretebilme niteliklerine sahip olması elzemdir" diye düşünür (Özer'den aktaran Adıgüzel, 2008).

Karagözoğlu (1987), eğitim sisteminin çarklarının düzgün çalışmasında üç temel ögenin öğretmen, öğrenci ve eğitim programları olduğunu savunur. Eğitimin etkili ve hedeflenen düzeyde olması bu ögeler arasındaki uyumla doğrudan ilişkilidir. Bu ögelerden en önemlisi öğretimi etkilemede diğer ikisinden daha güçlü olan öğretmen ögesidir. Eğitim sistemindeki başarı, sistemi işletecek olan öğretmenin özellikleri ile doğduran bağlantılıdır (Karagözoğlu'ndan aktaran Oktar ve Bulduk, 1995).

Öğretmen, öğrenci, sınıfın fiziki koşulları, eğitim programı,öğrencilerin ekonomik durumu, okulun imkanları gibi birçok etken matematik öğretimini önemli ölçüde etkiler. Ancak bu etkenlerden en önemlisinin öğretmen olduğu yadsınamaz bir gerçektir. Bu sepeble matematik öğretiminde en önemli görev öğretmenlere düşmektedir. Çakmak (2004)’e göre, süreci aktifleştirmek, öğrenciyi sürecin parçası haline getirmek, öğrenciye yol göstermek gibi vazifeleri yerine getirirken, öğretmen;

o Çeşitli öğretim yöntem ve tekniklerini bir arada kullanabilir, o Problem çözmeye dayalı, keşfetme odaklı çalışmalar yaptırabilir,

o Öğretim etkinliklerine öğrencilerin grup olarak aktif bir şekilde katılımını sağlayabilir,

o Akran değerlendirmesine fırsat tanıyabilir,

o Öğrencilerin proje ve performanslarını sınıf ya da okul düzeyinde sunmalarını isteyebilir,

12

o Okulun imkanları dahilinde çeşitli ders materyalleri kullanarak dersin işlenişini zenginleştirebilir (Çakmak'tan aktaran Akyıldız, 2013).

Geleneksel ve modern eğitim yaklaşımlarına bakıldığında hepsinde az ya da çok öğretmenin önemi üzerinde durulmaktadır. Geleneksel yöntemlerde öğretmen, bilgiyi öğretici konumunda katışıksız tek lider iken; modern yaklaşımlarda daha çok, bilgiyi öğrenmede yol gösteren, rehberlik eden konumunda yer almaktadır. Ancak her iki yaklaşımda da öğretmensiz bir eğitim öğretim sürecinden bahsedilmemektedir.

Eğitim fakültelerinde eğitim gören öğretmen adaylarının okuduğu matematik müfredatı ile dersin işlenişi konularınının daha fazla ayrıntı içermesi gerektiğine değinen Baki (1996), adayların aldıkları eğitim disiplinini mezun olduktan sonra gittikleri yerde uygulayacağına inanmaktadır. Bu sebeple, adayların matematik bilgi birikimlerinin yanı sıra eğitimcilikleri de önemle üzerinde durulması gereken hassas konulardan biridir.

Bahsi geçenlerin hepsinden anlaşıldığı üzere, matematik öğretimi için öğretmen öz yeterlilikleri ön plandadır. Yüksek öğreniminde iyi bir eğitim almış; bilgi, beceri ve donanımı güçlü öğretmenler, matematik öğretiminde daha idealist ve kararlı tutumlar sergileyecektir. Öğretmen adaylarının eğitim seviyesi ne kadar etkili ve kaliteli ise yetiştirecekleri neslin, dolayısı ile ülkenin, bilgi ve teknolojisi ile kalitesi de bu oranda artacaktır.

2.1.6. Lider Öğretmenin Özellikleri

Modern eğitim sistemlerinde öğretmenin yolda yürüten değil yolu tarif eden, rehber olduğundan bahsedilir. İnsanlığın geleceğe hazırlanmasını sağlayan öğretmenlerin yetiştirdikleri talebelerinin, kendilerine güvenmeleri, yeterli zeka kapasitesine sahip bireyler olduklarını hissetmeleri ve “nasıl?” değil “neden?” öğrenmeleri gerektiğini farketmeleri gerekir bunun için de geleceğe imza atmak isteyen ülkeler, sıradışı ve lider öğretmenlere gereksinim duymaktadır.

Upham (2001)'a göre “sıra dışı” öğretmen;

1. Planlara uymada ve gün içindeki değişiklere uyum sağlamada esneklik gösterir,

2. Hiperaktif görünür, gün içindeki koşuşturmalara rağmen yorulmaz ve kendi heyecan duyduğu gibi öğrencilere de bunu aşılayacak coşku ve enerjiye sahiptir,

13

4. Dersin içeriğine hakimdir, sürekli öğrenir, alanındaki yenilikleri takip eder, 5. Sağlıklı bir mizah anlayışına sahiptir, zira mizah gerilimleri yumuşatır, 6. Her tür farklılığa ve çeşitliliğe karşı hoşgörülü ve toleranslıdır,

7. Sadece öğrencilere değil diğer öğretmen ve velilere de rehber ve destekleyicidir,

8. Rol modeli olarak araştırma, yaratıcı düşünme ve yeni öğretme yolları bulma konusunda meraklıdır, böylece öğrencilerini cesaretlendirir,

9. Öğrencilerine ihtiyacı olduğunda yardımcı olur, kararlıdır,

10. Sınıftaki kısıtlı kaynaklara yaratıcı çözümler bulur, orijinal fikirleri vardır, 11. Öğrencinin güven ve saygısını kazanmakta ustadır,

12. Öğrencilerle ilişki kurabilme yeteneği vardır ki bu sayılan özellikleri arasında aslında en önemlisidir (Upham'dan aktaran Çeküç, 2008).

2.2. Dil ve Alan Dili

2.2.1. Dil Nedir?

En basit şekliyle dil bir iletişim aracıdır. Özmermer (2008)’e göre doğumla başlayan ve ölüme kadar süregelen iletişim sürecinin bu önemli organı dil ile ilgili pek çok filozof, dilbilimci, sosyolog ve psikolog değişik tanımlarda bulunmuştur. Bu tanımlardan bazılarına aşağıda yer verilmiştir:

Dil, insanlar arasında anlaşmayı sağlayan doğal bir öge, kendine özgü kuralları olan ve sadece bu kurallar içerisinde değişip gelişen canlı bir varlık, temeli tarihin bilinmeyen dönemlerinde atılmış bir gizli anlaşmalar düzeni, seslerden örülmüş toplumsal bir kurumdur (Ergin, 2008).

Banguoğlu (2007)’na göre dil, insanların meramını anlatmak üzere kullandıkları bir sesli işaretler sistemidir. Elle, başla, göz ve kaşla çeşitli işaretler yaparak bazı duygu düşünce ve isteklerimizi anlatabiliriz fakat en etkili anlatma aracı dildir.

Konrot (1991)’a göre bireyler arası iletişimde temel amaç bireyin zihninde düzenlediği mesajı karşısındaki bireyin zihnine aynen ya da benzeri şekilde iletmektir. Bu süreçte rol oynayacak doğrudan bir kaynak, bir bağlantı noktası yoktur. Söz gelimi, yanımızda

14

bulunan birinin kafatasına dokunduğumuzda zihninden geçenleri kendi zihnimize aktarmak mümkün değildir. Bu yüzden bu aktarımı yapacak öyle bir araç gerekir ki mesajı alan ve veren tarafından aynı şekilde paylaşılmalı, aynı anlam çağrıştırılmalı ve çözümlenmelidir. Dil bütün bu sistemi tek başına temsil eden temel bir araç, bir koddur ( Kontrot'tan aktaran Topbaş ve diğerleri, 1998).

Gencan (1966)’a göre dil, ulusal varlığın temeli, düşüncenin yani geniş manasıyla iç benliğimizin aynasıdır.

Kavcar (1988) ise dili şöyle tanımlar: “Dil, milli kültürün temel ögelerinin başında yer alan ve insanları birbirine yaklaştıran toplumun düşünme aracı, toplumu gelişigüzel insan topluluğu olmaktan çıkarıp millet haline getiren en önemli ögelerden biridir”.

"Dil, onu konuşanların his, düşünce ve hayal dünyalarına yön verir" diyen Kaplan (2002)’e göre bir milletin dünya görüşü dilinin sahip olduğu kelime haznesi kadardır.

Akıl ve düşünme yetisi, varlıklar içinde sadece insana has bir özellik olduğundan düşünmenin temelini oluşturan en önemli özellik, dil, insan için bulunmaz bir fırsattır (Damarlı Oçak, 2007).

2.2.2. Matematik Alan Dili ve Önemi

Damarlı Oçak (2007)’a göre çocuklar okula başladıklarında hayata dair bütün bilgileri sistemli, planlı ve düzenli olarak öğrenmeye başlar. Çocuğun sahip olduğu dilsel beceri, tanımadığı bu ortam içinde onu başarıya götürecek ilk basamaktır. Çocuğun eğitim müfredatı kapsamında almak zorunda olduğu matematik, türkçe, sosyal bilgiler ve fen bilimleri gibi derslerdeki başarısı, dinlemesi ve okuduğunu anlamasıyla doğrudan ilişkilidir (Damarlı Oçak'tan aktaran Akyıldız, 2013).

Davis ve Hersh (1989)’a göre, dili kullanmakla dile getirmek arasında ince bir fark vardır. Örneğin; “4/3πr3_{”sembolik bir ifadedir. Edebi karşılığı “dört bölü üç pi r küp” olan bu} ifadenin yalın anlamı “4/3, pi sayısı ve r’nin küpünün çarpımıdır”. Matematiksel anlamı ise “yarıçapı r olan bir kürenin hacmidir”. Bu ifadeye, “bir kürenin hacmi, yarıçapının küpüyle doğru orantılıdır” ya da “bir kürenin hacmi ile yarıçapının küpü arasındaki oran, sabit bir sayıdır ve bu sayı 4/3π’dir” gibi başka matematiksel anlamlar da atfedilebilir. Görüldüğü üzere, simgesel bir ifadeye birçok matematiksel anlam yüklenebilmektedir. Matematikte bir sembolik ifadenin ona yüklenen bütün matematiksel anlamları algılamadan öğrencinin

15

öğrenme süreci tam olarak gerçekleşmiş olamaz (Davis ve Hersh'ten aktaran Aydın ve Yeşilyurt, 2007).

Her bilimin kendine has bir alan dili olduğu gerçeğinden hareketle matematiksel alan dilinin bilinmesi ve problem çözümünde ifade aracı olarak kullanılması, bireyin matematik başarısının artmasını sağlayacaktır. Dolayısı ile dil ve öğrenme arasında bir doğru orantı olduğundan söz etmek, yanlış olmayacaktır.

Çok eski zamanlardan günümüze uzanan, köklü bir geçmişe sahip, matematik alan dili fikrinin yeniliğini savunmak yanlış olacaktır. Nitekim, matematik diline Galileo’nun doğa hakkındaki kitabında rastladığımız gibi başka birkaç matematikçi de “matematiğin dili” adlı birkaç kitap yayınlamış ve alana ait dilin yabancı diller kategorisinde değerlendirilip ekstra emek ve çaba ile öğrenilmesi gerektiğini belirtmişlerdir (Gray, 2004).

“Matematik bir dildir ve matemamatik metnini okumak orijinal dilinde Tolstoy’un Anna Karanina’sını okumak gibidir” diyen Lindgren (1999) ve “matematik ilköğretim öğretmenlerinden üniversite profesörlerine kadar saygı duyulması gereken bir dildir” diyen Renne (2004) bu matematikçilere örnek gösterilebilir (Lindgren ve Renne'den aktaran Owens, 2006).

Matematiğin diğer dillerdeki gibi söz dizimi, anlamsal yapı ve fonksiyonları olmasına rağmen, doğal diller ile arasında 3 büyük farklılık söz konusudur:

 Kimse bu dilin konuşmacısı değildir.

 Matematik kendi başına bir dil değildir, bir dilin yanında kendine has sembollerle kullanılır.

 Okur yazarı olmadan bu dilin akıcı olması mümkün değildir.

Matematiksel ifadelerin yazınsal dilde sembolik yoğunluklarının fazla olması dolayısıyla matematiksel dilin, uluslar arası bir dil olduğu iddiası gündemdedir. Fakat matematikçiler, matematiksel konuşmaları içinde kendi anadillerini kullanırlar. Bu da matematiğin iletişim kanalı içerisinde bireylerin kendi anadillerini de kullandığını gösterir. Dolayısıyla matematik, doğal bir dil olmaktan çıkar ve doğal dillerde olduğu gibi sözel olarak değil yazılı olarak ifade edilir (Gray, 2004).

Çalıkoğlu Bali (2002), pek çok bilim dalı gibi matematiğin de kendine ait bir sözcük dağarcığı olduğunu savunur. Kelime haznesinde günlük hayatta kullanılan sözcüklerin yanı sıra matematiğin uzmanlık alanına dahil olan terimler de yer almaktadır. Matematik

16

öğretiminde her yeni kavram, yeni sözcükler ve yeni düşünceler demektir. Bu yüzden matematik öğretiminde özellikle öğretmenlerin matematiksel ifadeleri doğru ve eksiksiz kullanmaları gerekmektedir.

Bilindiği üzere, matematik semboller yardımıyla öğrencilere aktarılır. Öğrenciler bu sebeple bu sembolik dili öğrenmek ve anlamlarını bilerek doğru yerde doğru şekilde kullanmak zorundadır (Çalıkoğlu Bali, 2002). Matematiğin bu sembolik doğası yönüyle öğrenciler matematiği algılama, yorumlama ve analiz edip yansıtmada güçlük çekmektedirler. Öğrencilerin bu güçlükleri çekmesini önlemenin temelinde verilen matematiksel bir ifadeyi, problemi ya da sembolü nasıl algıladığını doğru bilmek yatar. Öğrenciler karşılaştıkları durumları matematiksel dile dönüştürmekte ya da yorumlamakta konuya karşı ilgisizlik, bilgiyi tam kavrayamama ya da yanlış yorumlama durumları yüzünden zorluk yaşamaktadırlar ( Doğan ve Güner, 2012).

Matematiksel dilin oluşmasında öğretmen rolü yadsınamaz bir gerçeklikte önemlidir. Çünkü öğrenciler matematiğin temellerini öğretmenlerinin onlara sağladığı deneyimlerle atarlar. Öğrencilerin matematiksel anlayışlarının şekillenmesinde ilk sırada okulda karşılaştıkları öğretimler gelir (Aksu, Demir ve Sümer, 1998). Tüm bu sebepler dikkate alındığında matematik öğretmen adaylarının, alan dilini iyi kavramış olmaları, öğretmen olduklarında öğrencilerine dili doğru aktarmalarını sağlayacaktır.

Owens (2006)’a göre öğrencilerin matematiksel potansiyellerinin hedeflenen seviyeye ulaşması için matematiksel kelimelerinin geliştirilmesi gereklidir. Başarı için çok önemli olan bu kelime aşinalığı, direkt olarak, öğrencilerin kavramsal anlamalarıyla bağlantılıdır. Öğretmen, sınıfta uygun matematiksel kelimelerin kullanımını desteklemeli ve öğrencilerin matematiksel iletişimini sağlamak için gayret göstermelidir (Owens'tan aktaran Akyıldız, 2013).

2.3. Tutum

2.3.1. Tutum Nedir?

17

Katz (1967) tutumu, “bireyin sahip olduğu değerler dizgesine bağlı olarak bir simgeyi, bir nesneyi, bir kişiyi veya dünyayı iyi ya da kötü, yararlı ya da zararlı yönleriyle algıladığı bir ön düşünce biçimidir” şeklinde tanımlar (Katz'dan aktaran Tavşancıl, 2002).

Smith (1968)’e göre tutum, “bir bireye atfedilen ve onun bir psikolojik obje ile ilgili düşünce, duygu ve davranışlarını düzenli bir biçimde oluşturan bir yönelme işlemidir” (Smith'ten aktaran Kağıtçıbaşı, 1999).

Yenilmez ve Özabacı (2003), tutumu; “bireyler genelikle çevrelerinde oluşan olaylara belirli anlamlar yüklerler, bu anlamları kazanılmış bireysel deneyimler olarak dışa yansıtırlar ve bu yansıtma sonucunda inanç ve yaklaşımlarını şekillendirirler, işte bu inanç ve yaklaşımların hepsinin ortak adı tutumdur” şeklinde açıklar.

Tüm bu tanımlardan yola çıkarak tutum, “belirli koşullarda etkileşimler sonucu ortaya çıkan çeşitli duygusal yaşantıların zihinlerde organize edilmiş düşünsel yapıları oluşturması ve bu sayede tepkisel bir yapılanmanın meydana gelmesi” olarak özetlenebilir (Pehlivan, 1997).

2.3.2. Tutumun Ögeleri

M. Sheriff ve C. W. Sheriff’in 1969’da yazdıkları “Sosyal Psikoloji” adlı kitabından aktaran Tolan, İsen ve Batmaz (1985)’a göre; tutumun özellikleri şunlardır:

 Tutumlar doğuştan getirilen özellikler değildir, sonradan kazanılır.

 Tutumlar geçici düşünsel durumlar değildir, ortaya çıktıktan sonra az ya da çok belirli bir süre zarfında devam ederler.

 Tutumlar bireyle nesneler arasındaki ilişkilere bir kararlılık ve düzenlilik kazandırırlar.

 İnsan ve nesne ilişkilerinde özellikle tutumlar aracılığıyla bir etkilenme, güdülenme süreci ortaya çıkar.

 Tutumun oluşması ve biçimlenmesi için birbiriyle karşılaştırılabilir birçok ögenin bir arada bulunması zorunludur.

 Genel olarak kişisel tutumların oluşmasıyla ilgili ilkeler, toplumsal tutumların oluşmasına da uyarlanabilir (Tolan, İsen ve Batmaz'dan aktaran Pehlivan, 1997).

18

Şimşek (2002)’in Katz ve Stotland (1954)’ten aktardığına göre tutum, içinde pozitif ve negatif etkileri barındıran 3 başlık altnda incelenmektedir. Bu ögeler aşağıda açıklanmıştır:

 Bilişsel Öge: Kişinin tutum konusundaki inançlarıdır. Buna örnek olarak matematiği zayıf bir öğrencinin “öğretmen düşük not verdi” inancına sahip olması gösterilebilir (Yıldız, 2006).

 Duyuşsal Öge: Kişinin duygusal tepkileridir. Pozitif ve negatif etkiler içeren duyuşsal ögeler derecesine göre tutumları farklılaştırabilir (Köklü, 1995). Matematiği seven dolayısıyla olumlu bir tutum sergileyen bir öğrencinin derse istekli davranması, derse katılımı, mutlu ve huzurlu bir şekilde ders saatinde sınıfta bulunması örnek olarak gösterilebilecekken, olumsuz tutum sahibi bir öğrencinin ise tam tersine ilgisiz, mutsuz ve ders esanasında huzursuz olup arkadaşlarına da engel olması örnek gösterilebilir (Yıldız, 2006).

 Davranışsal Öge: Kişinin hareketleridir. Yıldız (2006), bu durumu, "olumlu tutum sahibi bir öğrenci ödevlerini titizlikle yaparken olumsuz tutum sahibi örneci ise ödev yapmamanın yanısıra derse devamsızlık gösterir ya da sınıfa geç gelir" şeklinde örneklendirir (Yıldız ve Köklü'den aktaran Akyıldız, 2013).

2.3.3. Tutumun Özellikleri

Güç derecesi, karmaşıklık, diğer tutumlarla ilişki ve merkezcilik, ögeler arası tutarlılık ve tutumlar arası tutarlılık olarak özetlenebilir (Kağıtçıbaşı, 1999).

2.3.4. Tutumun Ölçülmesi ve Tutum Ölçekleri

Bireylerin tutumlarını, boyunu ya da saç rengini ölçer gibi doğrudan gözlemlemek ve ölçmek imkansızdır. Tutumlar, dolaylı olarak, davranışlar yoluyla ölçülebildiğinden bu ölçmede kullanılan davranış, sorulara verilen cevaplar ya da konu hakkında yürütülen fikir belirtme işlemleri gibi sözel davranışlardır. Bu amaçla geliştirilen ölçme tekniklerinin başlıcaları arasında tutum ölçekleri gelmektedir (Çetin, 2003).

Tavşancıl (2002)’a göre bu ölçekler test maddelerine benzeyen cümlelerden oluaşn tutum cümlelerinden meydana gelir. Bu maddelerin; süreklilik, tek boyutluluk, doğrusallık ve eşit aralıklar ile üretebilirlik ilkelerine uygunluğu ölçüsünde geçerli olacağı söylenebilir.

19

Süreklilik: Tutum ölçeklerinde bir ölçeğin birbirine zıt iki ucu arasındaki çeşitli derecelerin sonsuz ölçüde birbirini izleyen küçük birimlere ayrılması halinde bile sürekliliğinin korunacağı varsayılır. Bu da en azından bu değişkenin eşit aralıklı ölçekle ölçülmesini gerektirir.

Tek boyutluluk: Ölçek maddesinin tek bir özelliği ölçmesini öngörür.

Doğrusallık ve eşit aralıklar: Ölçülen özelliğin bir doğru biçiminde ve eşit birimlerden oluşan aralıklarla ölçülmesidir.

Üretilebilirlik: Ölçekten elde edilen bilgiye dayanılarak yeni bilgilere ulaşılabilmesidir (Tavşancıl'dan aktaran Akyıldız, 2013).

Araştırmalar incelendiğinde kullanılan başlıca tutum ölçekleri arasında; Bogardus’un toplumsal uzaklık ölçeği, Thurstone’un eşit görünümlü aralıklar ölçeği, Likert’in dereceleme toplamlarıyla ölçekleme tekniği, Guttman’ın birikimli ölçekleme tekniği, Osgood’un duygusal anlam ölçeği, Leeds ölçeği, Minnesota öğretmen tutum envanteri ve Evans ölçeği sayılabilir.

Yapılan araştırmada Likert tipi ölçek kullanıldığından aşağıda ayrıntılı bir şekilde anlatılmıştır. Diğer ölçeklerin ayrıntıları için Tavşancıl (2002) ve Köklü (1995) incelenebilir.

2.3.4.1. Likert Tipi Tutum Ölçeği

1932’de Rensis Likert tarafından geliştirilen Likert tipi tutum ölçeği bir şahsın tek bir objeye karşı gösterdiği tutuma ilişkili olarak hazırlanmış cümle dizisinden meydana gelmektedir. 2 tip cümle yapısı gözlenen ölçekte, birinci tip; ilgi objesine karşı olumlu tutumu ifade eden onaylama cümlelelerinden meydana gelirken, ikinci tip ise olumsuz tutumu sergileyen onaylama cümlelerinden oluşmaktadır. Likert tipi ölçeklerde bu iki tip cümle serisi yaklaşık olarak aynı sayıda üretilmeye çalışılmaktadır (Köklü,1995).

Ölçeğin en çok kullanılan çeşitlerinde ölçeğin uygulanacağı bireye sunulan cümleler için 3, 5 ya da 7 seçenekten oluşan onay cümleleri yer alır. Ancak bunlardan en yaygın ve kullanım kolaylığı açısından en pratik olanı 5’li ölçeklerdir. Aşağıda 1. ve 2. tip cümleleri içeren 5’li Likert tipi ölçeğe uygun bir örneğe yer verilmiştir.

20 Tablo 1. 5'li Likert Tipi Ölçek Örneği

Kesinlikle Katılıyorum Katılıyorum Emin Değilim Katılmıyorum Kesinlikle Katılmıyorum Matematik dersini severim Matematik dersinden hoşlanmam

Özgüven (1994)’e göre Likert tipi tutum ölçeği uygulanan birey benimsediği ifadeleri işaretlemek yerine verilen bir ifadeye ne ölçüde katıldığını derecelerle belirlemektedir (Özgüven'den aktaran Tavşancıl, 2002). Ölçekte bulunan her bir derece belli bir puana sahip olup ölçek puanı bu derece puanlarının toplanmasıyla elde edilir.

2.3.5. Tutum ve Davranış İlişkisi

Tavşancıl (2002)’a göre birçok psikolojik değişken gibi tutum da doğrudan gözlenemeyen kuramsal ve gizli değişkenlerden oluşan ve varlığı sadece sözlü ve davranışsal belirteçlerle saptanan değişkenlerdendir. “Kişi davranışlarının tutumları tarafından belirlendiği” görüşü yapılan araştırmalar sonucu doğruluğunu kaybetmiş ve yerini “tutum ve davranış arasında tutarlılık olduğu” fikrine bırakmıştır.

Tutum ve davranışlar formal ve informal eğitim sonucu oluşmaktadır. İnsanların tutumları biliniyorsa davranışları hakkında fikir yürütülebilir ancak tersi her zaman için doğru olmayabilir (Akyıldız, 2013).

Son zamanlarda yapılan araştırmalar incelendiğinde tutum ve davranış arasında sıkı bir bağ olduğu görülmüştür. Buna göre;

 Tutum kuvvetliyse,

 Tutum bireyin şahsi yaşantısına dayalıysa,

21

 Tutumun sık sık kendini ortaya koyma şansı varsa tutumun bilişsel yönü ile davranış arasındaki ilişki ortaya çıkar. Bu dört koşuldan biri yada birkaçı eksik ise tutum davranış arasındaki ilişki aksar (Cüceloğlu, 2012).

2.3.6. Matematiğe Yönelik Tutum, Korku ve Kaygı

Neale (1969), matematiği sevme ya da sevmeme, matematiksel aktivitelerle uğraşma ya da onlardan kaçma eğilimi, kişinin matematikte iyi ya da kötü olacağı inancı ve matematiğin faydalı ya da faydasız olduğu fikirlerinin toplamına matematiğe yönelik tutum olarak bakmaktadır (Neale'den aktaran Akgün, 2002).

Ülkemizde ve dünya genelinde pek çok öğrenci matematiğin zor olduğu ve dolayısıyla matematiği başaramayacağını düşünerek kaygı duyar, dolayısıyla derse karşı olumsuz tutum geliştirir. İlköğretimde başlayıp yıllarla birlikte artarak devam eden bu olumsuz tutum geliştirme sonucunda öğrenciler kendilerine güvensizlik besler ve matematiği öğrenecek kadar zeki olmadıklarını, matematiğin uğraş alanları içine girmediğini düşünürler (Baykul, 2002).

Eğitim sürecinin başında oluşacak aksamaların önüne geçilmesi ve bu aksaklıkların sürüp gitmesinin engellenmesi maksadıyla öncelikle sorun tanısının doğru konulması gerekmektedir. Bloom (1998), bir öğrencinin belli bir üniteyi iyi öğrenebilmesi için bu öğrencinin öğrenilecek yeni üniteye açık ve istekli olması gerektiğini savunurken Ertem ve Alkan (2004), öğrencilerin matematik dersindeki başarılarında matematiği sevme derecelerinin ve matematiğe karşı tutumlarının etken olduğu görüşünde hemfikirdirler. Matematik kaygısı, Tobias (1993)’a göre bireyin okul ya da günlük yaşamda karşısına çıkan matematiksel problemlerin çözümü esnasında sayılarla işlem yapmak zorunda kaldığında kişide oluşan duygusal gerilim şeklinde ifade edilebilir (Tobias'tan aktaran Yenilmez ve Özabacı, 2003).

Oktay (2003)’la Ali Nesin’in yaptığı söyleşide “Neden korku ve matematik?” sorusuna Ali Nesin, “matematiğin zor ve eğlenceli yanının bir arada olduğu” cevabını vermiştir. İnsan bilmediğinden korkar, dolayısıyla matematik insan zihninde “bilinmeyen” hükmünde yer işgal ettiğinden korkulacak bir alandır. İnsanlar en az düşünerek, kolay yoldan yaşamayı zora tercih ettiğinden, matematiksel düşünmekten kaçınır ve olacaklar hakkında kaygı duyarlar. Ayrıca matematik bilgi ve süreklilik ister. Söz gelimi İnkılap Tarihi dersini