Quantum-statistical properties of a Raman-type model

(1)

Quantum-statistical

properties

of

a Raman-type

model

Alexander

S.

Shumovsky* and

B.

Tanatar

Department ofPhysics, Bilkent University, Bilkent, 06599Ankara, Turkey (Received 10May 1993;revised manuscript received 21 July 1993)

Amodel describing three boson fields with the decay ofRayleigh mode into the Stokes and vibra-tion (phonon) modes is examined. The problem of exact eigenvalues and eigenstates is reduced to the calculation ofzeros ofnew orthogonal polynomials defined in terms ofdi8'erence and difFerential equations. The instability of the spectrum ofeigenvalues is established. The quantum-statistical properties are investigated for various initial conditions. The possibility ofusing the correlation Ra-man spectroscopy to measure the quantum-statistical properties of the vibration mode is discussed. PACS number(s): 42.50.

—

p, 42.65.

—

k, 32.80.Bx

I. INTRODUCTION

Raman scattering is known as an important method of spectroscopy of rnolecules and solids

[1].

The standard measurements

of

frequency and angular distribution of scattered light give us very important information about the linear properties of vibration (phonon) modes. A more detailed picture would arise from the measurement

of

quantum distribution function or ofhigher-order cor-relation functions

of

phonons.

It

should be emphasized that this distribution can

dier

markedly from the Bose-Einstein distribution for bosons even at equilibrium with a given temperature

T[2].

An essential physical quan-tity that may be measured by the methods of correlation spectroscopy [3]is the degree ofcoherence ofsecond-order for the scattered light. However, it is necessary to know how the statistical properties

of

scattered light are re-lated to the statistical properties of the vibration mode. The recent progress in quantum optics permits us to discuss the possibility ofusing the nonclassical states

of

light as the pumping field in a Raman scattering pro-cess.

It

is interesting

to

compare the changes in statisti-cal properties of scattered light with the changes in the pumping field at agiven state of the vibration mode.

Tosolve these problems it isnecessary

to

examine afull quantum model of the Raman scattering. The simplest model ofsuch type is described by the Hamiltonian _[4]

H

=

era"a

+

wsasas

+

wi,btbt

+

p(bt

asa

t

+

a

asb),

where at and a+~ are the creation operators for the Rayleigh and Stokes modes, respectively, with the cor-responding frequencies w and ug, bt is the creation oper-ator for the vibration mode with frequency up, and p is the coupling constant. We restrict our consideration

to

the Stokes process only because we will examine the case oflow intensity initial Geld. We note that the same form of the Hamiltonian is usually employed in the theory of parametric optical processes [5—

8].

*Permanent address: Bogolubov Laboratory of Theoretical Physics, 3INR, Dubna, Moscow Region, Russia.

The change of operators

at

and a by e numbers, cor-responding

to

the classical amplitudes

of

an intense laser field, [9] leads

to

an eB'ective bilinear boson Hamiltonian. In this case the problem can be solved exactly [10]with the aid

of

Bogolubov canonical transformation

11 .

But

of course, it is impossible

to

speak about the quantum-statistical properties of the Rayleigh field in such an ap-proach.

Another type of effective Hamiltonian is connected with an analogy in mathematical formulation

of

Raman scattering process and of the interaction of a set

of

two-or three-level atoms with the resonant radiation Gelds [12—

15].

This problem is also solved exactly in the single atom case

[16].

The model systems associated with the Hamiltonian

_{of Eq. (1)}

have been examined using various techniques, such as numerical solution [17,

18],

operator linearization method

[19],

and the short-time approxima-tion [20]. The Heisenberg dynamical equations have been solved exactly [21]by applying some iterative procedure. The existence of simple conservation laws can also be used to construct the exact solution in the Schrodinger picture [2, 22,

23].

The exact eigenvalues

of Eq. (1)

can be expressed in terms ofnew orthogonal polynomials [2, 22] which are reduced to the Hermite polynomials in some special case.

In the present paper we use the exact solution of the problem with the Hamiltonian

_{of Eq. (1)}

in the Schrodinger representation [2, 22] in order

to

examine the quantum-statistical properties of scattered light and its dependence on the properties of Rayleigh Geld and phonons.

The organization ofthis paper is as follows. In

Sec.

II

we present the details ofour exact solution of the trilin-ear boson Hamiltonian for the Raman-type model. We discuss the structure of the eigenvalue spectrum and the corresponding eigenstates, and their asymptotic behav-ior. We then describe in

Sec.

III

the dynamics of the Raman-type model considered for di8'erent preparations

of

the photon and phonon initial

state.

In

Sec.

IVwe ex-hibit our numerical results of the dynamical problem for various initial photon and phonon distributions. Discus-sion ofour results in connection with other approaches and experiments is given. Finally, we conclude with a

(2)

4736 ALEXANDER S.SHUMOVSKY AND

B.

TANATAR brief summary stressing the physical significance ofour

calculations. A'+'i Kn

—

j)(j+

1)(m+

j+

1)l"

II. EIGENVALUES

AND

EIGENSTATES

In this section we investigate the eigenvalue spectrum and eigenstates

of

the Hamiltonian of

_{Eq. (1)}

with the assumption of the exact resonance condition

(2)

It

follows from the boson commutation relations that the Hamiltonian depicted in

Eq. (1)

has the following inte-grals of motion:

ata

₊

a&as

—

const,

ata

₊

b~b

=

_const,

which express the Manley-Rowe relations in nonlinear op-tics

_[1].

From these two conservation laws we construct the following operator:

N

=

ata+

(a~+ay

+

btb)/2 such that [N, H]

= 0,

(4) which describes the number of collective excitations in the system. Thus, we can consider the eigenfunctions of

N

~(y(n))

~@(n))

as the eigenstates ofHamiltonian given by

Eq. (1)

corre-sponding

to

the nth excited state

H~y(n)) @(n)~@(n))

with the eigenvalue

E(

~.

_It

follows from the definition

of Eq.

(4) that ~g(

))

should be chosen in the following

form:

~@"

₎

=

)

A(")~n

—

j,

m+

j)

for all n

j=O with

j=O

where ~k, I,p) isthe direct product ofcorresponding

num-ber states for Rayleigh, Stokes, and vibration modes. Then, for any n the eigenvalues

E(

~ are determined _by

the equation

=*'"'A,

'"'-A,

'"'

K

-j+1)j(

+j)l"

(»)

This recursion relation will be represented by the equiv-alent expression

(i2)

defining the new orthogonal polynomials

P

(x),

which have been previously introduced [22, 23] for m

=

0. Here

(("),

=

((")

_[(n

—

_j

₎

_j

_(m

₊

_j

_{+ 1)]'~',}

q

")

=

(n

—

j

+

1)

j(m+

j)

.

Then instead of

_{Eq. (8),}

we obtain

P()(

₎ 0

which is the equation for the eigenvalues ofHamiltonian given in

Eq.

(1).

For any fixed n this equation has

n+

1

real

roots.

In addition

to

the difFerence equation given in

_{Eq. (12),}

the orthogonal polynomials P~ can bedefined also by the diB'erential equation [23] OF O

O'l

~F'(2:,

_t)

=

+t

~

n(m+1)

—

t,

~

(tF),

Ot Ot Ot2)

where the generating function has the form

pic

F(x,

t)

=

)

Pk(x)

—,.

The polynomials P~

(z)

in turn can be expressed in terms of the Bernoulli polynomials B&+ _(n) in the following way: 2

P(n))

(n, ) L=O where

detX("~

=

O,

where

X(

) _is _{the real symmetric}

_(n+1)

_x

_(n+1)

_matrix

with elements and

V_(,",

+i

=

4'+'(n)%'+'(n)

A _p

=

& [(n

—

n+

1)n(m+ n)]'i

,

0

In the above expression we have

x(")

=

(Z(")

~n

~bm)/p

ifP=o.

+1

otherwise.

(io)

With the help of the above relations, we obtain for the coeflicients ofthe eigenfunctions given in

Eq.

(7)

The recursion relation between the coefficients of wave function of

Eq.

(7)has the form,

(3)

where

x;

is any solution of

Eq.

(8) [or of the equivalent

Eq. (13)]

and

E;„nw+m~b

p—x

„nur+mwb —

p[n

+nn

m]

(15)

The coefficient AI)

(x,

) is deterinined from the normal-ization condition

)

lA.

(x;)l

=

1 for all

x;,

i

=

1,2,

. . .

,

n+1.

j=O

For small n, the coefficients given by

Eq. (14)

as well as the eigenvalues

E{

~ can be calculated analytically. We

list a few of those in Table

I.

One can observe from

_{Eq. (13)}

that the roots

(x.

(~)

₎

are ordered symmetrically with respect

to

zero (we have enumerated the roots starting from the maximum value). The value

x(")

=

0isthe root

_{of Eq. (13)}

for even n only.

It

means that forn

=

2k,inthe spectrum ofeigenenergies

E{

~ there exists a central line with energy Ek+~{2k)

—

—2k'+

mug, while for n

=

2k

+

1such a line is absent in the spectrum.

Using the Hadainard criterion [24],it is not difficult

to

show that the maximum root has the following

asymp-totic

behavior

n'~',

n-+

c,

m &&n

m ~ _n, _m —

_{+oo, n(&m}

It

follows &omthe symmetry of roots that

x;„=

—

x

Thus, the minimum eigenvalue has the asymptotic behav-ior

From

Eq. (15)

we observe that for any fixed w, wb, and

p it is possible to find no such that for any n

)

no, the value of

E;„becomes

negative. In other words, we have instability ofeigenvalues

of

the Hamiltonian given in eq.

(1)

with respect

to

the number

of

photons in the Rayleigh mode, whereas they are stable relative

to

the number of excitations in the vibration mode.

It

is not surprising

to

find such an instability for the system with a cubic nonlinearity. Similar results occur for the system describing the decay

of

a mode

of

Bose fields _{into p modes with p}

)

2 [2,22]. The possible phys-ical reasons for such an instability have been discussed in detail in Ref. [22].

III. DYNAMICAL

BEHAVIOR

If

we know the set of eigenvalues and eigenfunctions for any n and _{m, the} time dependent wave function is represented by

n,m.=O l=].

where the index I enumerates the roots of

Eq.

(8) and coeKcients C& are determined by the initial conditions.

We have suppressed the dependence on m of the eigen-values E& and the coe%cients A-& in the expansion of

) determined by the relations of

Eqs. (13)

and

_(14).

TABLE

I.

List ofthe orthogonal polynomials P& (x),zeros ofthese polynomials, the

eigenval-ues E'

',

and the coeKcients for eigenstates A& for n

=

0,1,and 2, and fixed

I,

.

n=0

P(o)( ₎ xj

—

0 (o)

P,

("(x) =

*'

—

(m+»

xi

=

V'm

+ 1,

x2

=

—

V'm

₊

1

Ei

(i)

=

cu

+

m~b

+

pV'm

+

1

Ao'(a)

_(x,

₎

=

~,

i _A,(i)

'

_(xi)

=

—

'

E2(1)

=

(u

+

m(ub

—yam

+

1 &.(1)

(*

)

=

~

1 &i'(1)

(*z)

=

—

~

P,

'"(*)

=*'

—

*(4

+6)

xi

—

v4m+6,

x2

=0,

Ei

=

2~

+

m~b

+

pv4m

+

6 E2

= 2~+

mu)b p(2)( ₎

(

~pi

)~&2 p(2)( ) xs

=

—

+4m+

6 p(2)( ₎ (~+2) it'2 p(2)( ₎ (

~+i

)i&2 ),(2)( ₎ ₍~+2

₎

~&2

(4)

B.

TANATAR Taking into account of the explicit form of the eigenvalues

where

_(xI

₎

are the solutions of

Eq.

(13),

symmetric rel-ative

to

x~ ~

=

_0,_we obtain for the wave function

Let us now discuss the possible choice ofinitial condi-tions. We shall consider the case when the Stokes mode is initially in the vacuum state l0)

g.

Let the initial states of Rayleigh _{lR) and vibration} lV) modes be deffned by the expansions

)

—i(nw+m~g)t

)

~(~)

i'm& —tl@(~)₎ n,m=O

(-4)

=

(&(t)l&l&(t)).

(18)

We shall consider the first- and second-order correlation functions for the Rayleigh and Stokes photons in the sys-tem. For the mean number ofRayleigh photons we get

oo n+1

( t y

~

-

₍

(~)*~(~)

—ip(x'„"'—~I"')t

n,m=o k,l=1

Then the time dependent average ofany dynamical vari-able A of the system under consideration is determined by I&)

=

)

~-lm)s.

m=o n+1 ~(n)p(n) Pngm ) lm

jl

_otherwise

_.

l=1 (23) The distribution for the Rayleigh mode will be chosen by the following _{cases: (a)}

a

number state with a given n

(b)

a

coherent state with parameter n

n

exp (

—

l~l'/2)

nI

Then the coefficients ( I in

Eq. (17)

are determined by

the equations

atria,

s

t

=

a,~a,

o—

(20)

For the mean squared intensities we obtain

((

t )2)

)

-

)

-

~(n)e~(n),

~(~I"I ~I"I)t

n,m=o k,l=l

Then, according

to

the Manley-Rowe relations (cf.

Sec. I)

we have for the Stokes photons

and

_(c)

a squeezed vacuum state with parameters p and

(

)n/2

II-(0),

n!IM

(2p)

where

_{H (x)}

is the Hermite polynomial of order

n.

For the vibrational mode, we shall examine the following pos-sibilities: (a) anumber state with a given m

gm'

—

~mm' )

x)

j=o

((

t )2)

)

-

)

-

( ( )*(

(")

—*'~( ',

"'

—,

'"')t

(21)

and (b) a squeezed vacuum state with parameters pv and

&v

~-(0)

gm'pv

(2ILtv) n,m=o k,l=l

x

_jkm _jim~

j=o

(22) for the Rayleigh and Stokes photons, respectively.

It

fol-lows from the relations

_{of Eqs. (19)}

—(22) that the expec-tation values of number and square number of photons in both modes are independent of the mode frequencies. In other words, their dynamics isdetermined by the cou-pling constant

p.

This isalso the case for any expectation value of the type

Relating to our choice of the initial states of the Rayleigh and vibrational modes, we make the following remarks. The coherent and squeezed states of photon initial states correspond

to

the idea of application of a nonclassical light inthe Raman scattering process.

It

also enables us

to

examine the dependence of statistical prop-erties of scattered light both on the type ofinitial state ofphotons and that of the vibrational mode (phonons). Use of asqueezed vacuum state forthe vibrational mode, on the other hand, corresponds to the phonons ofa po-laritonlike system for which the number distribution is given by a squeezed state at zero temperature [2].

((c'c)")t

P 1)2)~~~

where c is defined

to

be the operator corresponding

to

Rayleigh, Stokes, or phonon mode. Thus, the statistical properties of scattered light are independent of the mode frequencies. The real magnitudes of expectation values are provided by the symmetry

of

solutions

of Eq.

(13).

IV. RESULTS

AND

DISCUSSION

The mean values for the number ofphotons and their variances are normalized with respect

to

the initial num-ber ofRayleigh mode photons at t

=

0,

(ata)o,

viz.

(5)

Stokes mode, we assu

t

ere are no inc}a

t

h

, we assume a vacuum

d' _b

s

ses wit increasin n

is g n number

of

photo ons

ib io od d d

fixed

dn.

Form

)p

e an ecreases with' h increasing m

at

n, the deviati

em w en n

=

2 for which we have

a)«g(ata)

In

F'

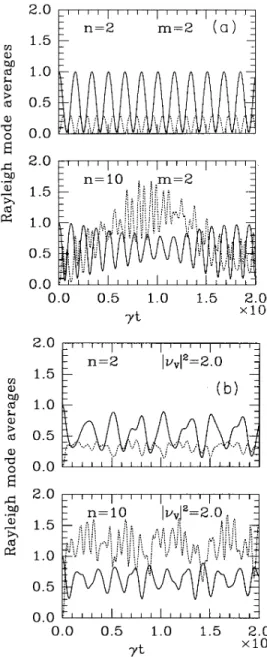
Fig. 1,

we show the norm

b

t t

t}1 0 photons depicted

I,

=

_{p onons, in}

_Fig.

_1(a).

For the

2.

0

1. 5—

I I I i I I I I i I I I I

Il=2

IT1=2 I

(a)

2.

0 I'''

I

1.

0

0.

5

o

2.

0

1. 5—

1.

0

0.

5 n=10

I ~ II I'If ~I ~ ~ ~I ~I~ I I I~I I I I~ ~I I I ~~I I I~ ~I I111 I~I~ I liI~ 11I~ Il It II I~ I ~ I~ ~ ~_Ill IIIIII l,ss I I I i,lS (ITl= II tl ~IiiC~ ~I~III Il IIII~I ~~ ~11II I s~~I'lit' h ~illII I I~ ~~~ss s~ ~~ii IIIIIII ~ I~I ~ II I I I~I I~~I~ ,tiit ,~lit'i~ ~I~I I I I I ~I 'I~ I I I I I

1.

5

2.

0

tg

1.

5

4 N ~I ~I ~~I ~ ~ ~~I~IiI ~e'I ~~~ ~ ~~~ ~ ~~ I I ~ I~~ cx

=0.

5

I I J I I I I

a =2.

0

~ ~ ~t~ ~~ ~ ~tttt Its ~ ~I I ~Itlt II~Il~I)~ ff"' ~~₎ttI'~It~~I~I~~~ ~I~~ ~II~

(a)

=

IIII(

I|IIlt

Iil I I I I ( I I I I I I I IIl

=

2

~ ~ ~1tl ~~~ HIli~I Is ti»tlt~I~s~ ~I~ ~t ~IIII~ti~tie~ I~I ~I ~~~II ~ I~I~~I~~I~ ~~~I~~~ ~~~ IJ ~ I~s~I~ s, ~,~~s'r~

0.

0

'

0.

0

0.

5

I I I I ~ I I

1.

0

1.

5

I

~vl'=Z.

o

2, 0

x10

0.

5

00

I

«I

I

««

I

«

0.

0

1.

0

2.

0

I I I I

3.

0

4.

0

5.

0 x1Q

I I I I

2.

0

1

0

I

2.

I I I I I j I I I i I I I

0. n=10

I~ I~II I~ ~~~ ~ ,~Ii , '~IiI~ ~ ~I II~ ~~ ~I ~I ~I ~ ~II~I~ I ~I~ ~~ I ~ I~ I I I ~~I ~~ ~~ ~~ ~ st II~ I~~ I r~s' I',~ ~S' I~~~II I I~II I I~~~ ~IIII I~III ~I~~ ~ ~,Isr ~~ IS~ ~~Itt ~~ ~ ~ I I I ',~i I II I I~ I I I ~III ~~ I~~ IIII ~I I» ~II I ~I ~I~ ~~I I I ~~I~I ~~I I~ ~~ ~II~ tII ~ I~ ~ ~I I 1 I I II I I I I~ ~~I ~ItII I I ~I II ~I I I ~~ I~ I~ r P ~lr~ tI ~~ I tl ~~ I I '~~~ ~tts IeI

0.

5

M (0

1.

0

Q

0.

5

(0

.0

',

,

i.

. . I ~ ~ ~ ~ ~ II ~~~~ ~~~ ~T ~ ~t~ I~I

j

I~II IIi~~

2.

0

1. 5—

M tg

1. 0,

—

Q

0.

5

Q

00

I I I I I I I I I I I I I I I I I

a=0.

5

lvv

=2.

0

2.

0

tg

1.

5

1.

0

I I I I I I I I I I I I I I I I I

a=2.

0

1~vi

=2.

0 I''I'

I I ~ ~ ~~ I~I~ti I~~II~ Ii~I~ II ~III~ IS

~

~ I ~ ~ ) I~~,r~ I~ ~ It~ ~I~I ~ III s y~ ~~ s~ ~ ~ ~ i~~III~ ~Is\I~ I ,s~'~I tt ii II It ~l II ~I I,~ II ~~~ ~I%II~~~ItI~ ~4i~ ~ I r 14~I ~I I'S altl ~~ I I I l I I II II I I I I I I I I I

0.

0

' '

0.

0

I I I I I I I I I II I I I I I I I

0.

5

1.

0

1

5

2.

0 yt

x1Q

FIG.

1.

Thee imetime dependence of th

(o

ons a a)q (solid line an

average h t ' d b lo ₎

hoo

di

h i~vi'

=

2O. in t e squeezed state vacuum state.

s, e tokes mode is initially in the

0.

5

I I I I I I II II II I I I I I I I

0.

0

1.

0

2.

0

3.

0 yt

I I I I I I

4.

0

5.

0 x1Q

FIG.

2. Samearne asas Fag.1for the Ra

oh t

tt

c aracterizedh by a o.

=

iia

yin

( ) d

=

2 (1o

ho o 'thi vvl

=

2.

(6)

B.

TANATAR

(ata)q

—

(2[(m+

1)

cosO

t+

_(m+

_2)]

+

(m+ 1)(2m+

3)sin

0

2m,

+3

'

=

1+

cos

(2p~mt),

(24)

((ata) )t

—

(4[(m

+

1)cos

0 t

+

(m,

+

2)]

+

(m,

+

1)(2m

+

3)sinzO

2m+

3

1.

2

—

[cos

(2p~mt)

+

1]

+

—sin

_(2p~mt),

2 (25) where

0 =

p[2(2m

+

3)]

~,

so that 1

vq(ata)

—

(ata)q

—

—[1

+

cos

(2p~mt)]

2 (26)

a

qualitative change in the behavior of statistics of scat-tered light in comparison with the case ofphonons in the number

state.

This qualitative di6'erence can be used for experimental observation ofsqueezing of the vibrational Similar time dependent behavior for m

))

n was also

ob-tained by Drobny and

Jex

[25].Increasing n at fixed m implies an increase in the number ofterms with diR'erent frequencies in the sums of

Eqs. (19)

arid

(21).

Therefore,

it

is not surprising to observe the collapse-revival pat-terns as in the Jaynes-Cummings model [26,27].We note

that

in Ref.[25] such time dependent behavior was ex-amined only for the coherent initial state of the Rayleigh mode.

When the phonons are initially in the squeezed vac-uum state [depicted in

Fig. 1(b)]

we also have change in the type ofnumber distribution in time, but in contrast

to

the previous case the increase of n at fixed mean num-ber ofphonons (btb)o

—

lvvl leads

to

the almost super-Poissonian state for both the Rayleigh and Stokes pho-tons. _{As lvvl} becomes larger for fixed n, we also observe achiefly super-Poissonian

state.

In other words, we have

2.

0 a=0.

5

lvv

=2.

0

1. 5—

1. 0—

0.

5

0

P

0 2-0

n=2.

0

lvv

'=2.

0

1. 5—

o I I I I I I I I I I I I I I I I I I

4.

0

=— I I I I I I

(a)

3.

0

:

2.

0

1.

0

~i ~~~~ ~~~~~ ~~ I~I~~I I~~ ~ ~~ ~ t~ \~~ ~ ~~~II~i $ I ~ ~ I~~II ~II ~~ I II ~~I I~I ~~&~II~ ~I It~ I ~ ~I ~~ I~\I,~I&~~~ I ~& I~I~ ~I~~ ~ II ~ ~IIg ~ ~I' ~I~~ II~ ~ &~~~ ~ ~~ ~~ ~I I~~ II ~~ P, ~IP t I I II III I~~I~ ~I ~ I tltI~I~~ ~II II~ ~~gI~~I~ ~ II~ ~'~'~I I~'~~ I' I''I~'~.I,~ ~I ~~ I&'I' »ll~I~ ~~ I III~ I lVII~~ ~ ~ ~~ Il~ ~I~I ~ ~I~ & ~II & ~II ~ ~~ ~ ~~I ~ ~I I ~~I I ~II~ ~I~~ ~~ ~I I~~I ~,I, ItI, I I I I I I ~~I~ I&~~ I~I I~I~ ~g ~~ I* I ~~ ~ &I~ &~ ~ ~ I ~ ~~~~~~ ~~II~~~~&lt I~~~~~ ~ ~ 'i&I''~I'~i ~~I~ ~ ~I ~ ~ ~I ~~

5.

0

4.

0

3.

0

2.

0

1.

0

' ~I I I I I I I I I I I I I I I I I I I I I I I I IIl IIl I ~ I ,&?, I Iil I I h&»~II I~l&i&&iI~I ~I~~I~lt~I ~II I~~I ~ ~I I~ ~ ~I ~ ~I~

I I I &I I&I I II I~I I I~II~~V ~ II&I~ I~I~I

LVIIt ti~ ~I»I~Ig ~~IItl&I~I&I~II&l~II&~II~~~~ ~I~I~ \~ II~~~~IVII~~~~\ ~\I ~I I~&~~ ~~I~\~I I I I I II~I I I~~~I~I~I IIgII ~~ ~ ~I I I

~ ~ I»~I~~I gI~I II I I~I~~III~ ~&\~ ~II~~ ~I~II I& I~ &I»I

~~I~ ~ ~ IItI&I~ ~I III~~~I~III II&~ ~ ~ll~ ~I &j~I~I~ I~ ~ ~III~~

II IIII IIII~II» III~~~I~I I ~~I8'~~Ill~ ~ ~~I I II ~I I~ I~I~II ~I~~I ~I~~&I~ IgI~tt1~Il ~tl ~I~ ~I~,IlV~ iIt(~,~»,I& '~gI,™LI~ II.~,' ~ I I\ ~I

iv)'=2. 0

0.

0

0.

0

1.

0

2.

0

3.

0

4.

0

5.

0

x1Q

7t,

5.

0

I I I I I I I I I I I I I I I I I I

4

p =

lvl'=0 5

lvv

'=2

0

3.

0

2.

0

1.

0 o

0.

0

I I I ~ ~~ ~~ ~ I'I&I~ t ~~~ ~ ~~ ~~I tt I~g I~ ~~~ ~ g ~~I~ ~ ~ ~ ~ ~ ~ lg ~I II ~ ~ I ~I I~ i tl ~ ~I ~~ ~ ~8~ ~~ ~ ~ ~~ &~~'~I'& I'~ I~ I ~ ~ ' ll&i II'~I~ ~ ~~ '~~' ~ »V~~ I ~ ~ V ~&~ ~ ~ ~ ~~ ~ ~~ ~ &I ~ ~ ~~~~ ~&'~t I~ ~~~ ~~~ I,'ll ~ ~ + I I~ ~» I \ I I I I I I I I I I I I I I I I I I I I I I I I I tg

1.

0

III~I ~ , 'IPIi~&~IP~ ~~»I~Ie~i&~~~ ~~ t&I~V~~ » lg I I~~~~itI~II~I~ ~~ I~I~ I ~t~ t~II&l&&&I Il fIi t '(g

4.

0

3.

0

I ~~I L»~ I I ~ LL~ ~I~~I ltlg ~I ~ & ~ I~~~~I~~g&~~~~ ~gl I~I 4I ~ ~ ~ ~ ~~ ~I I~~ ~~~I~~II~ ~I&~I L8

. .&&tt Igg»~ &~~~t&Z.~ ~~~I~~~~~~~~~~~'II~~~ ~'~I~~~~~ ~~~~~ ~I~~~~~W

~I ~I~ IV ~~ ~~&

0.

5

'

2.

0

='-'

lvl'=2.

0 lvvl'=2.

0

0.

0 '''''I'

I'

'I'''

I

0.

0

1.

0

2»0

3.

0

4.

0

5.

0 x10

7t

FIG.

3.

The time dependence of the (normalized) aver-age number of photons (alas)t, (solid line) and the vari-ance vz(asas) (dotted line) for the Stokes mode initially in the coherent state characterized by n

=

0.5 (upper) and n

=

2.0 (lower) photons and in the squeezed state phonons with lvvl

=

2.

1.

0

:

0

-I I I I I

»»

I I I I I I

»»

I I I I

I-0.

0

1.

0

2.

0

3.

0

4.

0

5.

0 x10

FIG.

4. Same as Fig.1 for the Rayleigh mode initially in the squeezed state characterized by (a) lvl

=

0.5(upper) and

~vl

=

2 (lower) photons and m

=

2phonons; (b) lvl

=

0.5

(upper) and lvl

=

2 (lower) photons and in the squeezed

(7)

mode.

It

ispossible

to

see from

Fig.

1the collapse-revival phe-nomenon occurring for initially squeezed phonon

states.

Qualitatively similar time dependent behavior is ob-served for the Stokes mode averages. The number oscil-lations for the Stokes photons have the mirror symmetry relative to the Rayleigh mode because

of

the Manley-Rowe law [given in

Eq.

(4)] while the oscillations of the variance in number

of

photons strictly coincide with the corresponding Rayleigh mode variance. Such a mirror symmetry is

a

general property

of

asystem independent

of

the initial

state.

The dynamics

of

the system in initial coherent state

of

the Rayleigh mode is presented in Figs.2 and 3 for the Rayleigh and Stokes modes, respectively. When the mean number of initial Rayleigh photons

(ata)o

—

]n] is small enough the distribution remains Poissonian for

t

)

0, as the number ofphonons in the vibrational mode m increases. On the other hand, as ]n~ increases for

a

fixed m,

a

super-Poissonian statistics for the Rayleigh photons is observed. Similar conclusions may be drawn for the Stokes photons, although the oscillations in the variance do not coincide with those for Rayleigh pho-tons, in this case.

If

the vibration mode is initially in a squeezed

state,

the response of the system is qualita-tively similar [see

Fig. 2(b)].

In

Fig.

3 we show only the dynamics of the Stokes mode when the vibration mode phonons are initially in the squeezed state, since the case with phonons inthe number state has amirror symmetry

to

the ones shown in

Fig.

2, similar

to

the discussion of

Fig.

1.

Finally, we show the time dependence

of

the Rayleigh mode fluctuations in

Fig.

4, when the initial state of Rayleigh photons is a squeezed

state.

The main result we obtain &om these 6.gures is that the sub-Poissonian distribution is absent here, in contrast

to

the previous cases.

As for a brief summary, we list below some

of

the main conclusions

of

this work.

(I)

The collapse-revival phenomenon is the property

of

the model under consideration, independent of the type of the initial state used

to

prepare the system (for the Rayleigh mode in the number state, it can be observed for n

)

2).

(2) The sub-Poissonian statistics is seen

to

be obeyed for the number and coherent initial state of the Rayleigh mode, but not for the squeezed vacuum

state.

(3)

The behavior of the scattered light in the number state di8'ers qualitatively depending on the initial state of the vibration mode.

In connection with the last result, we note that the number states of the vibration mode may be considered as a state

of

harmonic phonons

at

zero temperature while the squeezed vacuum state corresponds

to

the correlated phonons due

to

some mechanism of interaction [2]. We can assume the number ofinitial phonons (ormean num-ber)

to

be given. Then, the change in initial intensity of the Rayleigh mode and the observation

of

the correspond-ing change in the Mandel's factor

vt(ctc)

—

(ctc),

(c

c),

would allow us to find the type of phonon distribution present in the system.

ACKNO%'LED G MENTS

A.

S.

acknowledges the hospitality

of

the Physics De-partment

at

Bilkent University during his stay. A.

S.

also would like to thank Professors

C.

Bowden,

R.

Bullough,

S.

Carusotto,

F.

Persico, and

V.

Rupasov for fruitful dis-cussions.

[1]

Y.

R.

Shen, The Principles of Nonlinear Optics (Wiley, New York, 1984).

[2] A. S.Shumovsky, in Modern Nonlinear Optics, Part 2, edited by M.W. Evans (Wiley, New York, 1993).

[3]

B.

Crosignani, P. Di Porto, and M. Bertolotti, Statisti cal Properties of Scattered Light (Academic, New York, 1975).

[4] D.

F.

Walls, Z.Phys.

237,

224 (1970).

[5]

B.

R. Mollow and

R.

J.

Glauber, Phys. Rev.

160,

1076 (1967).

[6]

R.

Graham, Z. Phys.

211,

469 (1968).

[7]

F.

Persico and G.Vetri, Phys. Rev. A

12,

2083 (1975).

[8]

K.

J.

McNeil and C. W.Gardiner, Phys. Rev. A28, 1560

(1983).

[9]W.

J.

Mielniczuk, Opt. Acta 26, 1115 (1979). [10] H. P.Yuen, Phys. Rev. A

18,

2226 (1976).

[11]N. N. Bogolubov,

J.

Phys. (Moscow)

11,

23 (1947). [12] G.P.Agarval and S. S.Iha, Z.Phys.

B

25, 391(1979). [13]V.

I.

Rupasov and V.

I.

Y'udson, Zh. Eksp. Teor. Fiz.

87,

1617 (1984)[Sov. Phys.

JETP 60,

927 (1984)]. [14]A.S.Shumovsky,

R.

Tana's, and Tran Quang, Opt.

Com-mun. 64,45 (1987).

[15]A. S. Shumovsky and Tran Quang, in Interaction of

Electromagnetic Field with Condensed Matter, edited by N. N. Bogolubov, A. S.Shumovsky, and V.

I.

Yukalov (World Scientific, Singapore, 1990).

[16]C. C. Gerry and

J.

H. Eberly, Phys. Rev. A 42, 6805 (1990).

[17]D.

F.

Walls and C.

T.

Tindle,

J.

Phys. A 5, 534 (1972). [18]

J.

Mostowski and

K.

Rzazewski, Phys. Lett. 66A, 275

(1978).

[19]

J.

Katriel and D.G.Hammer,

3.

Phys. A

14,

1211

(1981).

[20] P.Szlachetka, S.Kielich,

3.

Perina, and V.Perinova, Opt. Acta 27, 1609 (1980).

[21]S.Carusotto, Phys. Rev. A 40,1848

(1989).

[22] Yu. Orlov,

I.

Pavlotsky, A.Shumovsky, V.Suslin, and V. Vedenyapin, Int.

3.

Mod. Phys.

B.

(to be published) [23] Yu. N. Orlov and V.V.Vedenyapin, Mod. Phys. Lett.

B

(to be published).

[24]

R.

Bellman, Introduction to Matrix Analysis (McGraw-Hill, New York, 1960).

[25] G.Drobny and

I.

Jex,Phys. Rev. A 46, 499 (1992). [26] H.

I.

Yoo and

J.

H. Eberly, Phys. Rep.

118,

239

(1985).

[27] Fam Le Kien and A.S.Shumovsky, Int.

J.

Mod. Phys.

B