Polynomially solvable cases of multifacility distance constraints on cyclic networks

(1)

(2)

CYCLIC NETWORKS

A THESIS

SUBMITTED TO THE DEPARTMENT OF INDUSTRIAL ENGINEERING

AND THE INSTITUTE OF ENGINEERING AND SCIENCES OF BILKENT UNIVERSITY

IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF

MASTER OF SCIENCE

By

Naile Giilcan Ye§ilk6kgen

July, 1993

(3)

5^,35 /Лг/

(4)

I certify that I have read this thesis and that in my opinion it is fully adequate, in scope and in quality, as a thesis for the degree of Master of Science.

Assoc. Prof. Barbaros Q. Tansel(Principal Advisor)

I certify that I have read this thesis and that ij;w;цy opinion it is fully adequate, f i \

in scope and in quality, as a t h e ^ for the_^egree of Master of Science.

I certify that I have read this thesis and that in my opinion it is fully adequate, in scope and in quality, as a thesis for the degree of Master of Science.

As^uCTPro|.>Mr Gemal Dinger

Approved for the Institute of Engineering and Sciences:

’rof. M ehm ^t^aray

(5)

ABSTRACT

POLYNOMIALLY SOLVABLE CASES OF MULTIFACILITY

DISTANCE CONSTRAINTS ON CYCLIC NETWORKS

Naile Giilcan Ye§ilk6kgen

M.S. in Industrial Engineering

Supervisor: Assoc. Prof. Barbaros Q. Tansel

July, 1993

Distance Constraints Problem is to locate one or more new facilities on a network so that the distances between new and existing facilities as well as between pairs of new facilities do not exceed given upper bounds. The prob lem is AfV-Complete on cyclic networks and polynomially solvable on trees. Although theory for tree networks is well-developed, there is virtually no the ory for cyclic networks. In this thesis, we identify a special class of instances for which we develop theory and algorithms that are applicable to any metric space defining the location space. We require that the interaction between new facilities has a tree structure. The method is based on successive appli cations of EXPANSION and INTERSECTION operations defined on subsets of the location space. Application of this method to general networks yields strongly polynomial algorithms. Finally, we give an algorithm that constructs an e-optimal solution to a related minimax problem.

Key words: Distance Constraints, Network Location, Minimax Problem with Mutual Communication.

(6)

GENEL SERIMLERDE ÇOKTESISLI UZAKLIK KISITLARI

PROBLEMİNİN POLİNOM ZAMANDA ÇÖZÜLEBİLİR

DURUMLARI

Naile Gülcan Yeşilkökçen

Endüstri Mühendisliği Bölümü Yüksek Lisans

Tez Yöneticisi: Doç. Dr. Barbaros Ç. Tansel

Temmuz, 1993

Uzaklık Kısıtları Problemi, bir serim üzerinde bir yada daha fazla yeni tesisi, yeni tesislerle varolan tesisler arasındaki ve yeni tesis çiftleri arasındaki uzaklıklar belli üst değerleri geçmeyecek biçimde yerleştirme problemidir. Prob lemin genel serimlerde A^'P-Zor/u^îi ağaç serimlerde ise polinom zamanda çözü- lebilirliği bilinmektedir. Ağaç serimler için geliştirilmiş temel kuramlar ol masına karşın, genel serimlerde geliştirilmiş hiçbir kuram ve algoritma bu lunmamaktadır. Bu tez çalışmasında, biz uzaklık kısıtlarının yeni tesisler arasındaki ilişkilerin ağaç serimi biçiminde olduğu özel bir sınıfını çözen ve yerleşim uzayı olarak alınan herhangi bir metrik uzaya uygulanabilen bir yöntem sunuyoruz. Yöntem, yerleşim uzayının alt kümelerinde tanımlanmış GENİŞ LETME ve KESİŞTİRME işlemlerini temel almaktadır. Bu yöntemin genel serimlerde uygulaması polinom zamanlı algoritmalar verir. Son olarak, ilgili bir enküçük-enbüyük problemine e-eniyi çözüm üreten bir algoritma veriyoruz.

Anahtar Kelimeler: Uzaklık Kısıtları, Serim Yerleşimi, Enküçük-enbüyük Problemi.

(7)

(8)

I am indebted to Associate Professor Barbaros Tansel for his invaluable guidance, encouragement and above all, for the enthusiasm which he inspired on me during this study.

I am grateful to every individual of my family whose love and support have always been with me in spite of the distances that kept us apart.

I would like to extend my thanks to Ogan Ocah for his love, patience and encouragement especially at times of despair and hardship. My special thanks are due to my former and present ofBcemates Ash Sencer Erdem, Pınar Keskinocak, Mehmet Özkan and Sibel Salman for their interest and encour agement in every step of this study.

(9)

INTRODUCTION

1.1 Introduction and Overview

A location problem, in its most general form is to determine locations of several new facilities in a given location space so as to provide goods and services to existing facilities and/or to each other under one or multiple criteria, and possibly subject to a set of constraints. The typical measure for the quality of service is some function of distances between facilities.

Depending on the location space, distance function, objective criteria, num ber of new facilities to be located, type of interaction between facilities, pres ence of uncertainty in several parameters of the problem, and possibly some other factors, different types of location problems can be characterized. In a recent survey of Brandeau and Chiu [1], over 50 representative problems on lo cation theory are provided with their formulations and relations to each other. There is also an extensive bibliography of location literature by Domschke and Drexl [5].

Network location problems occur when the location space is a network. A road network, a river network, an air transport network or a network of ship ping lanes may constitute the network of interest. In most of the network

(15)

location problems, the new facilities are idealized as points and may be lo cated anywhere on the network. Constraints may be imposed on the problem so that the new facilities are within specified distances of existing facilities and other new facilities as well. A comprehensive survey by Tansel, Francis, and Lowe [17, 18] provides a review of network location problems with spe cific emphasis on work which deals directly with the network of interest and exploits the structure of the network. In part I of the survey, the p-center and p-median problems are considered and in part II, several network location problems including multifacility minimax and minisum problems with mutual communication, distance constraints, multifacility, and path location problems on tree networks are reviewed. A rather recent survey by Labbe, Peeters, and Thisse [11] discusses median and center problems, economic models of location as well as the discrete location models of network location problems.

In this thesis, we work on Distance Constraints which requires locating several new facilities on a network so that they are within specified distances of existing facilities and within specified distances of one another. Although the theory for tree networks is well developed and efficient algorithms exist, there is virtually no theory and algorithms on general networks regarding the distance constraints. Here, we go one step forward and provide algorithms of polynomial complexity which solves distance constraints problem on general networks for a special structure of the interaction between new facilities. We also consider the Multifacility Minimax Problem with Mutual Communication in the context of distance constraints. We now provide an overview of the thesis.

CHAPTER 1. INTRODUCTION 2

In the remainder of Chapter 1, we first define our terminology and give formal definitions of embedded networks and distances with their properties. Next we define Distance Constraints Problem on networks. We also introduce Multifacility Minimax Problem with Mutual Communication which is also called m-Center Problem with Mutual Communication in the literature. We give an equivalent formulation of the problem in terms of distance constraints.

(16)

and related minimax problem. Since almost all of the related literature we are aware of deals with these problems on tree networks, we provide an overview of existing theory and algorithms on tree networks. We also cite some of the characteristics of those problems on trees which may provide a partial answer to the question of why tree networks are more tractable than general (cyclic.) networks.

Our main results are provided in Chapter 3. Here, we deviate from the network context and approach the problem from a different perspective. We provide a new method to solve distance constraints defined in any metric space. The basic idea is to apply EXPANSION a,nd INTERSECTION opeT&tions de fined on subsets of the location space. For a special structure of interaction between new facilities, this approach leads to exact algorithms for determining the consistency or inconsistency of distance constraints and for finding a feasi ble solution if it exists. We also consider a broader problem of characterizing the set of all feasible solutions for all new facilities, by defining a region of feasibility for each new facility. This problem has not been addressed in the literature except for the single facility case. The algorithms we provide here are applicable to any metric space with differences arising only in algorithmic details.

In Chapter 4, we apply our approach to network spaces and construct strongly polynomial algorithms to determine the consistency or inconsistency of distance constraints and to find a feasible location vector if it exists. We also construct the regions of feasibility.

In Chapter 5, we provide an equivalent formulation of Multifacility Minimax Problem with Mutual Communication in terms of distance constraints with parametric distance bounds. We give a polynomial algorithm to construct an t — optimal solution for fixed e that relies on a bisection search on the optimal objective value. Each trial in the search requires solving a set of distance constraints with fixed distance bounds.

In Chapter 6, we give a summary of the report and we pose unresolved questions on the problems discussed. We also give directions for future research.

(17)

CHAPTER 1. INTRODUCTION

1.2 Networks, Embedding, and Distance

Before defining the problems in consideration we develop our terminology. Throughout the thesis we may also give other definitions as necessary. Note that, we use graph, node and arc interchangeably with network, vertex and edge respectively. Basic definitions of networks, embedding and distance pro vided here are due to Bearing, Francis and Lowe [4].

Given a set of n distinct vertices, V = {i^i,..., I'n} which is a subset of a given infinite set and a set of undirected edges consisting of unordered pairs of distinct vertices, an undirected network or graph ^ is a pair (V,S) with a length function that assigns a positive real number to each edge (i/,·, i/j). An embedding oi Q = (V,5) in some space <S is a set (7 in such that

G = U{[t;,·, Uj] : € S} where is the image of the unit interval

under a one-to-one mapping T{j : [0,1] S', with T,j(0) = u,· and T',_;(l) = vj with vi,...,Vn being distinct points in S representing respectively. Define V = {vi, ...Un} and E = {[u,·, Vj] : (i/,·, Vj) € S}. V is the vertex set of G and E is the edge set of G.

For a point Xin [u,, Vj] there exists a unique A in [0,1] such that Tij{\) = x. If we denote the inverse of T,_, by A,j then A,j(x) = A if and only if Tij{\) = x. A point X in [u,-,Uj] defines two subarcs [u,-,x] = {y ■■ Tii( a) = y for some o; € [0,A,j(x)]} and [x,Vj] = {y : Tij{a) = y for some o: € [Aij(x),l]}. If x = 7ij(A), then the lengths of [u,-,x] and [x,Uj] are defined as A/,j and (1 — \ ) U j respectively. Figure 1.1 illustrates the idea.

A subset of G is connected if there do not exist two disjoint subsets A and B o[ G such that A intersects Q, B intersects Q, and Q C A U B. A path joining xi E G and X2 € (7 is a minimal connected subset of G containing Xi and X2- The length of a path is equal to the sum of the lengths of all edges

or subedges on this path. Network G is connected if and only if every pair of vertices is joined by a path. A network whose any two distinct points are joined by a single path is called a free, denoted T.

(18)

Figure 1.1: Illustration of the 1-1 Mapping from [0,1] onto an Edge

For any two points x , y E G, define d(x, y) to be the length of a shortest path, denoted P{x,y), connecting x and y. d{x,y) is appropriately called the distance between x and y since the function d(·,·) has the well-known properties of nonnegativity, symmetry and triangle inequality of a metric. That is, Vx,i/ G G :

(1) d{x,y) > 0 ,d ( x ,x ) = 0 (Nonnegativity)

(2) d{x,y) = d{y,x) (Symmetry)

(3) d(x, y) < d(x, z) + d{z, y) Vz e G (Triangle Inequality)

Hence, G together with distance d constitutes a well-defined metric space. We should also note that from the compactness of an embedded edge, G is compact and d(x, y) as a function of x and for fixed y is continuous.

The distance between a given point of G and a variable point along an edge of G, has the following property :

T h e o re m 1.1 Let y be a fixed point on G. Let A G [0,1] with Tpq{X) = x G [vp,Vq] G E. Then d(Tp,(A),j/) is a function of \ which is continuous, piecewise linear concave with at most two pieces.

P ro o f : From the definition of distance we have d{x,y) = d{Tpq{\),y) - min{A/p, -|- d{vp,y),{l — X)lpq + d(u,,?/)}. Let a = Xlpq and define fl'p(a) —

(19)

a+d{vp,y),gg{a) = {Ipg - a)+d{vq,y), and g{a) = d{x,y) = mm{gp{a),gg{a)}. gp(a) is a linear function with slope +1 and gq{a) is a linear function with slope — 1. This implies that g{ct) = d(x, y) is a piecewise linear concave function with

at most two pieces. □

Figure 1.2 illustrates the possible shapes of y(a) = d{x,y) with x being a variable point on [up, u,] 6 E and у being a fixed point on G.

CHAPTER 1. INTRODUCTION 6

d(x,y) d(x,y) d(x,y)

Фі>у)= ^i+d(v, y) d<Vp.y}= .y, ¡м+Фч >y) diVq.y)

Figure 1.2: Possible Shapes of d{x^y)

1.3 Distance Constraints and m-Center Prob

lem with Mutual Communication

Distance constraints arise when new facilities should not be located too far from existing facilities as well as from other new facilities. For example, consider emergency service units such as fire stations, ambulances, and police patrol ve hicles. In order to avoid fatalities, damage to human life and excessive property losses, it may be appropriate to require service units to be within a specified driving time of any point in the region they serve. Distance constraints ensure the service units reach the emergencies within specified critical response times. In military scenarios, response units may be required not to be too far from

(20)

their supply bases and from each other in order to reinforce other units if a need arises.

Another important factor that justifies the consideration of distance con straints is that the analysis of these constraints facilitates the analysis of mini max type location problems since some of these problems can be reformulated in the form of distance constraints with parametric bounds.

Let G be the network of interest. Existing facilities are defined by the nodes of the network and new facilities are to be located anywhere on the network satisfying the given distance constraints. We denote by G”* the m- fold Cartesian product of G by itself and denote any location vector in G”* by X — ..., Xfn)·

The Single Facility Distance Constraints Problem, abbreviated as DC{1), is to find a point x in G, if it exists, such that

d(x,Vi) < Ci, ¿ = l,...,n

where c,· are known nonnegative constants.

The Multifacility Distance Constraints, DC{m), is to find a location vector X = (xi,...,Xm) G G”*, if it exists, such that

d{xj,Vi) < Cji , 1 < i < I < i < n d{xj,Xk) < bjk , I < j < k < m

where Cj,·, bjk are known nonnegative constants, some of which may be infinity. Clearly, if any one of the bounds cji, bjk is oo then that particular constraint has no effect on the solution of distance constraints. Hence we may omit such constraints from the formulation. Let Ic = {(i, i) · Cji < 00} and Ib = {(i, k) : bjk < 00}. Note that Ic is a subset of { l,...,m } x { ! ,...,n} and Ib is a subset

of {(i? k) : I < j < k < 7n}. Then we rewrite the distance constraints (DC) as follows:

d{^Xj,vf^ — Oj* , (^,^) G Ic

d(^Xj,Xk^ — i ^

{DC.\) (DC.2)

(21)

CHAPTER 1. INTRODUCTION

This time Cji, bjk are known nonnegative finite constants. Note that DC{m) includes DC{\) as a special case.

From now on we will not distinguish between single and multifacility dis tance constraints, we will only use DC to indicate the distance constraints in general. DC is said to be consistent if there exists a solution vector X =

{xi, such that (DCA) and {DC.2) are satisfied. Otherwise DC

is inconsistent. Determining the consistency or inconsistency of DC is known to be AfV-Complete for arbitrary networks [12].

A problem related to DC is the Multifacility Minimax Problem with Mutual Communication. The original form of the unconstrained problem is as follows;

Given nonnegative weights wji, Vjk for all index pairs

Min f { X )

w h e re /(X ) = m<ix{fi{X), f2{X)}

w ith /i(X ) = max Wjid{xj,Vi)

l<j<my l<*<n

M X ) = , max Vjkd{xj,Xk)

Xl5 XjYi G

This problem can be reformulated in terms of distance constraints eis fol lows:

Min 2

subject to

d{xj,Vi) < z/wji , (j,i) e Ic d{xj,xk) < zfvjk , {hk) € Ib

Xli ···! Xm € G

where wji, vjk are the positive constants for the given index pairs. The problem is to find points xi,...,Xm G G for which maximum distance between specified pairs of facilities is as small as possible.

(22)

EXISTING THEORY FOR

TREE NETWORKS

2.1 Convexity on Tree Networks

Most of the network location problems are well-solved when the network is a tree whereas a substantial computational effort is required when the network is cyclic. Part of the answer to the question why tree networks are more tractable than cyclic ones comes from the convexity results on trees. Yet convexity does not provide a full answer because some of the well-known nonconvex functions like the p-center and p-median problems are efficiently solved on tree networks whereas no polynomial order algorithms are known to exist to solve them on arbitrary networks.

The convexity discussion presented here is due to Dearing, Francis and Lowe [4]. The convexity results given in the paper have important applications for the four problems we describe next. First let us specify the total cost function g and minimax function h defined on G'^. For X = (a:i, ...,x,n) € G"^

»(A') M X )

V'm

¿-i ■

(23)

CHAPTER 2. EXISTING THEORY FOR TREE NETWORKS 10

where Wji and Vjk are known nonnegative constants.

Upper bounds on the distances between new and existing facilities as well as between pairs of new facilities can be imposed. Those bounds are named as distance constraints (DC) and are introduced in Chapter 1. Let the feasible set of solutions to DC be

s = [X £ : X satisfies DCA and DC.2).

Clearly if 5” ^ 0 then DC is consistent, otherwise DC is inconsistent. We have two unconstrained multifacility problems:

mmxgc?'" minxeGm !7(A·) MAO ( F I ) (F2)

(P I) is called the Minisum (or m-Median) Problem with Mutual Commu nication and (P2) is called the Minimax (or m-Center) Problem with Mutual Communication. The constrained versions of these problems are as follows:

minxes g(X) minxes h(X)

where S is the feasible set of DC defined above.

( C - P \ ) (C - P2)

Given nonnegative weights Vjk·, the functions g and h are convex, also the feasible set S of solutions to DC is a convex subset of in a well- defined sense (explained in the next subsection) if and only if the underlying network is a tree. Hence the problems P I, P2, C — PI, C — P2 are convex optimization problems on convex feasible regions for all data choices if and only if the network is a tree. This implies the following important result for tree networks.

(24)

2.1.1 C o n v ex ity o f D ista n ce

In order to address the question of convexity of functions g and h, the following distance functions are considered first.

f i ( x : a) = d{x, a) , x 6 G, a is a fixed point in G /2(2:1, X2) - d(xi,X2) , {x\ , X 2 ) € G ‘^

Let us first define the basic notation and give the definitions of convex sets and convex functions on a network. For details refer to [4]. For every Y = ( j / i , i / m) , Z = € G^ and for all 0 < A < 1 we define Lx{X) = { X e G^ : d{yi,Xi) + d(xi,Zi) = d(x,-,x.) = \d(yi,Zi), 1 <

i < m}. Then the line segment in G’^ is defined as L(Y, Z) = Uo<a<i1'a(F, Z).

For m = 1, L(y, z) is simply the union of all shortest paths connecting y and z in G. Any subset S of G’" is said to be convex if for every Y , Ze S L(Y, Z) C S.

If 5* is a convex subset of G'" and / is a real valued function with domain G'^ and range then / is said to be convex on S if given any Y, Z 6 S, f ( X ) < ^ f ( Y ) + (1 ~ for every X G L\{ Y ,Z ) and every 0 < A < 1.

In the proof of convexity of the functions / 1 and /2 the following lemma, which we provide without proof, is used. The reader is referred to [4] for the proof.

L em m a 2.1 Let w, y, z be any three points of a tree. Then, for all points x

in L{y,z), X e L{w,7y)U L{w,z). □

Now, we have the following lemma which shows that / 1 is a convex function on trees.

L em m a 2.2 Let a be any fixed point in G. Then the function fi{ x : a) is

convex on G if and only if G is a tree. Q

P ro o f : Assume f i{ x : a) is convex. Suppose G is not a tree. Then there (ixists a cycle G of shortest length in G. Let I be the length of the cycle.

(25)

We can choose points x, y, z and a in C such that d{a,x) = d{y,z) = d{a,y) = d{x,y) = d{z,a) = d{x,z) = Then fi{x : a) = ^ > \fx{y : a) + \ f i { z : a) = ^ which provides a contradiction to the assumption that f i ( x : a) is convex. Hence G is a tree.

Suppose the network is a tree. Then we have to show that Vx 6 L\{y,z) and 0 < A < 1

f i{ x : a) < \ f i { y : a) + (1 - X)fi{z : a) (2.1) or equivalently,

d{x,a) < \d{y,a) + (1 — X)d{z,a). (2.2)

For A = 0 and A = I, X = z and x = y so the inequality holds. Assume now

0 < A < 1. From the definition of L\{y,z) we have

d{y,z) = d{y,x) + d{x,z)

and

_ d{x,z) _ d{x,y)

d{y,z) d{y,z)'

So we can rewrite the inequality (2.2) as follows:

(2.3)

(2.4)

(2.5) d{x, a)d{y, z) < d{x, z)d{y, a) + d{x, y)d(z, a).

X G L{y,z) and Lemma 2.1 implies x 6 L{y,a) U L{z,a). Without loss of generality we can assume x G L{z,a). Then

d(a, x) + d{x, z) = d(a, z).

Then we have

(2.6)

d{x,a)d{y,z) = d{x,a)[d{y,x) + d{x,z)] = d(x,a)d{y,x) + d{x,a)d{x,z)

< d{x, a)d{y, x) + [d(a;, n) + d{y, a)]d(a:, z)

= [d(a, z) - d{x, z)]d{y, x·) + [d(x, rj) + d(j/, a)]d(x, z) = d{a,z)d{y,x) + d{y,a)d{x,z).

The first equality comes from (2.3), the inequality is a consequence of the triangle inequality and the next equality is a consequence of (2.6). Hence we have proven (2.5) which is equivalent to (2.2), so /i(x : a) is convex. □

(26)

We now give the convexity result for /2.

L em m a 2.3 /2 is convex on if and only if G is a tree. □

The necessity simply follows from the analysis, if /2(^:1, X2) is convex on G^

then for any fixed X2, /2(^1 : X2) is convex and hence f\{ x ; a) is convex which

implies G is a tree by Lemma 2.2. The sufficiency part is proved considering the two cases and uses Lemma 2.1 and some properties of convex sets. The proof is technical but not too difficult, so we omit it and refer the reader to [4] for details.

2.1.2 Im p lica tio n s o f C o n v ex ity o f D ista n c e

Having proved the convexity of distance on tree networks, it is easy to show that the functions h and g are convex. ^ is a function of sum of distances multiplied by positive constants. Multiplication of a convex function with a positive constant is also convex. So g is convex on trees. Similarly h is the maximum of a set of convex functions. It is also well known that max of a set of convex functions is also convex. Hence, h is convex on trees. This analysis imply that (P I) and (P2) are convex optimization problems on trees. Hence a local minimum to (P I) and (P2) is a global minimum.

With convexity of distance functions from Lemmas 2.2 and 2.3, and with the property that intersection of convex sets is convex and level sets of convex functions are also convex, we can conclude that the feasible set S of DC is also convex. Convexity of the set S and convexity of functions g and h imply that the constrained problems (C — P I) and {C — P2) are convex optimization problems on convex sets when the network is a tree. Hence a local optimum to these problems is a global optimum.

(27)

2.2 Distance Constraints on Tree Networks

Distance constraints are first defined by Dearing, Francis, and Lowe [4] in their work which is discussed in the previous section. They establish that the feasible set of distance constraints is convex if and only if the underlying network is a tree. Francis, Lowe, and Ratliff [8] developed the theory for distance constraints on tree networks. They give necessary and sufficient conditions for DC to be consistent, and also they provide algorithms that find a feasible solution whenever one exists.

2.2.1 S in gle F acility C ase

Recall that the distance constraints for a single new facility is as follows: Given c,· > 0 Vi, find X in T such that

d{x, Vi) < Ci , i ^ I (DC{\))

Francis, Lowe, and Ratliff [8] show that there exists a feasible solution X £ T to distance constraints if and only if the conditions d(vi,Vj) < Ci + Cj are satisfied 1 < i < i < n. If we define N{a,r) = {x G T : d(x,a) < r,·} to be the neighborhood around a center a with radius r, then we can have an equivalent formulation of distance constraints in terms of neighborhoods N{v{, c,·) centered at Vi with radius c,. To satisfy the i-th constraints of D(7(l), a feasible solution X E T must be in the neighborhood defined by that constraint, that is x 6 N(vi, Ci). So X must be in every neighborhood defined by all of the constraints. This implies that x must be in the intersection of all neighborhoods. Therefore the intersection of all neighborhoods define the set of all feasible solutions. Let S — nr=i N{vi,Ci). If 6' = 0 then DC is inconsistent else it is consistent. We should note here that the above results also hold for arbitrary networks and in general for arbitrary metric spaces. However, other results obtained for trees are not valid for arbitrary networks.

(28)

due to Horn [10] states that intersection of subtrees of a tree is nonempty if and only if every pairwise intersection is nonempty. From this result it follows that the intersection of two neighborhoods A^(u,-,c,·) and N{vj,Cj) defined on a tree is nonempty if and only if the distance between two vertices (centers) of these neighborhoods is less than the sum of their radii, that is if and only if the condition d(vi, Vi) < Ci + Cj is satisfied. Based on these properties, necessary and sufficient conditions follow:

P r o p e r ty 2.1 DC(1) is consistent if and only ifd{vi,Vj) < Ci +Cj, 1 < i <

j < n. □

This property provides a basis for the Sequential Intersection Procedure {SI P) developed in [8] to construct the feasible set of solutions to DC^ by intersecting neighborhoods pair at a time in an arbitrary order.

The intersection of two neighborhoods N{a,r) and N{a',r'), whenever nonempty, is a neighborhood N{d, ?“) with unique center a, and radius f. N{d, f) is termed the Composite Neighborhood Representation of N{a,r) and N{a',r'). Three cases may occur regarding the intersection :

Case 1 : d { a ,a ') + r < r' (i.e. N{a^r) C N{a\r')) Case 2 : d{a,a') + 7·' < r {i.e. N{a',i'') C N{a,r))

Case 3 : otherwise

Depending on the cases described above, the computation of d and f is as follows:

a = <

a if Case 1 occurs

a' if Case 2 occurs

the point in L{a,a') for which if Case 3 occurs d{a, a) = |[d(a, a') + r - r'j

r if Case 1 occurs

?· = < 7·' if Case 2 occurs

(29)

Then we have the following property.

P r o p e r ty 2.2 Given a, r defined above, N(a,r)r\N(a',T') = N{d, f) whenever

r > 0. □

If f < 0 we define N(d, f) = 0. Starting with arbitrary two neighborhoods, in each step S I P produces a composite neighborhood representation of two neighborhoods, discards the two old ones, inserts the new representation, and repeats the procedure with the new list of neighborhoods. The list size is de creased by one at each step. Hence, at the final step S I P produces a composite neighborhood representation of all neighborhoods N{v{, c,), i = I , ..., n in n — 1 steps. Therefore the computational complexity of S I P is 0{n). From the analysis of S I P , we have the following property.

P r o p e r ty 2.3 If N{vi,Ci) / 0 then there exists a neighborhood N{a,r)

with center a and radius r such that N{a,r) = n"=i K{vi,Ci). □

Analysis of the computation of d and f for composite neighborhood rep resentation leads to the observation that d does not change by reducing each neighborhood by e, and f is reduced by e. From this observation next property follows:

P r o p e r ty 2.4 If N{a, r) = f |”-i N{vi, c,·) theii N{a, r — e) — flL i N{vi, Ci — e) for e < r.

Property 2.4 enables a sensitivity analysis on the bounds of distances.

2.2.2 M u ltifa cility C ase

(30)

d { x j , X k ) < bjk, U , k ) e l B

(DCA) (DC.2)

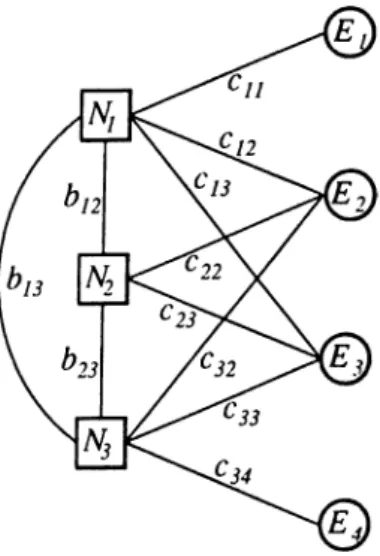
The necessary and sufficient conditions for consistency of DC are provided in [8] in terms of n (n — l)/2 inequalities named Separation Conditions (SC). In order to define these conditions, an auxiliary network (which we call Linkage Network {LN) throughout the thesis) is constructed by using the sets Ic and Ib- For each existing facility i, there exists a node E{, I < i < n, associated

with this existing facility, and for each new facility j there exists a node Nj, 1 < i :^ ^ ) associated with this new facility. Two nodes Nj and £',· are joined by an undirected arc of length Cji for each (j,i) G Ic·, and two nodes Nj, Nk are joined by an undirected arc of length bjk for each (j, k) 6 Ib· The node set

of L N is { N i , N m } U {Ei,...,En} and arc set of L N is {(Nj,Ei) : (j,i) G Ic} U {{Nj,Nk) : (j,k) G Ib}· Figure 2.1 below provides an example for the network LN.

Figure 2.1: Example of a Linkage Network (LN)

It is reasonable to assume that L N is connected, otherwise each compo nent of L N can be handled independent of other components. That is, DC decomposes into as many independent subproblems as there are components in LN.

(31)

Let £(Ep, Eg) be the length of a shortest path between Ep and Eg on LN. Then the following theorem of [8] is the most fundamental result regarding the consistency of D C .

T h e o re m 2.1 (Separation Conditions (SC)) DC is consistent if and only if

d{vi, Vj) < C{Ei, Ej) for 1 < i < y < n. □

We note here that for single new facility S C are just those conditions d(vi,Vj) < c,· + Cj, 1 < i < j < n which we have stated in the context of neighborhood intersections. The necessity part of the theorem is proved by a repeated application of the triangle inequality. Hence it is applicable to general networks. The sufficiency of 5'C' is proved by means of an algorithm called Se quential Location Procedure (SLP) which constructs a feasible solution if one exists or concludes that DC is inconsistent. This implication is not extendible to general networks. Figure 2.2 below provides an example to failure of suf ficiency of S C even on a simple cycle of 3 nodes. Although the separation conditions are satisfied DC is inconsistent.

(LN)

d(x,v,)^l d(Vg,v^ ^ L ( E ,J E 2)='2 d(x,v^ ^ 1 diVg.Vj) < <L(Ei£ 3)=2 diXyV^}^! d(v2,Vj} ^ JL(E2Ei

(DC) (SC)

Sufficiency of S C also fails when new facilities are restricted to nodes of the network. A simple example is provided in Figure 2.3 below.

The following string model represents how S L P works. Imagine that the tree is represented by appropriately inscribing straight line segments on a board such that each line segment represents an arc. At each vertex y,· strings of length Cji are fastened for each new facility such that (j,i) € la- At each step a tip vertex is chosen and all the strings fastened at that vertex are pulled tight on

(32)

d(x,v,) ^1

d(x,v^ ^ 1 d(Vj.V2) < L ( EiJE2)=2

(DC) (SC)

Figure 2.3: Failure of Sufficiency of S C for Node Restricted DC

the edge towards the adjacent vertex. If all strings reach that vertex then they are engaged there and the tip vertex, just processed, together with its incident edge is removed from the board. The procedure is repeated with the resulting tree. If at some step, some of the strings do not reach the adjacent vertex, the shortest one is selected. The point on the edge where the endpoint of the shortest string reaches is the location of the new facility it is associated with. Those strings that are pulled from the chosen tip are engaged at that point. Then all the strings left at the nonprocessed nodes that are related to the newly located new facility are pulled towards the point where the new facility is just located. This provides a feasibility check for the present location of that new facility. If all the strings reach then the location is feasible and all the strings related to this new facility are removed from the board. However, if at least one of the strings do not reach then the algorithm terminates infeasible. New strings are engaged to the point of location of this new facility for those unplaced new facilities that are related to the current new facility. The algorithm continues in this manner treating each placed new facility like an existing facility, until either all new facilities are placed or the the current tree reduces to a point. In the latter case all unplaced new facilities are located at that point.

If the separation conditions hold S L P described above always finds a feasi ble location vector in 0[in{rn + n)) time and it is also proven in [8] that S L P is a best algorithm for determining consistency of DC.

Tansel, Francis and Lowe [15] provide extensions of the results obtained in [8]. They characterize uniquely located new facilities by means of binding separation conditions.

(33)

CHAPTER 2. EXISTING THEORY FOR TREE NE TWORKS 20

A separation condition holding at equality is called binding. Let P{Ei, Ej) be a path in LN. P{Ei,Ej) is said to be a tight path if C{Ei,Ej) = d{vi,Vj). We say new facility k is uniquely located if its location point is the same in all feasible solutions to DC. The following property relates uniquely located new facilities and tight paths to each other.

P r o p e r ty 2.5 New facility k is uniquely located if and only if Nk is on at least

one tight path in LN . □

An immediate corollary to this property suggests that DC has a unique feasible solution if and only if every new facility node lies on at least one tight path.

Another result, enabling to locate new facilities on tight paths without using S L P is provided with the next property.

P r o p e r ty 2 .6 The nodes representing new and existing facilities in a tight path P{Ei, Ej), occur with the same ordering mid spacing in the path as do the corresponding locations in P{vi,Vj) on the tree. Also all facilities on the tight

path are uniquely located. □

A sketch of the proof of this property can be given by a string analogue of the problem. Assume buttons representing new and existing facilities on the tight path P(Ei, Ej) are placed on the corresponding nodes of the tree and the string path of length C{Ei,Ej) is pulled tight from E, to Ej on the tree, the length of the string path exactly matches d(u,, V j ) in T, since the corresponding separation condition is binding.

(34)

2.3 Minimax Problem with Mutual Commu

nication

The theory of separation conditions developed in Section 2.2 can be applied to Multifacility Minimax Problem with Mutual Communication defined below:

MinA-eG·" f ( X )

w h e re/(X ) = max { /i( X ) ,/2(X)}

w ith /i(X ) = max {wjid(xj,Vi) : (j,i) e Ic} f2(X) = max {vjkd{xj,xk) : (j,k) e Ib}

All weights wji, vjk are positive real numbers.

The problem is first defined in [4] in the presence of distance constraints and it is also established that the function / is convex on tree networks. The problem is shown to be AfV-Havd by Kolen [1 2] on general networks. The equivalent version of the problem in terms of distance constraints is solved in [8]. An equivalent formulation of the problem which we denote by P M M C is as follows:

{ P M M C ) Min z

subject to

d{xj,Vi) < z/wji , (j,i) e Ic d(xj,xk) < z/vjk , { j , k ) e l B

X 6

Let z* be the minimum z such that constraint set of P M M C has a feasible solution. Existence of z* is guaranteed due to continuity and compactness considerations and due to consistency of DC for sufficiently large z.

Given z, we can construct an auxiliary network which is the linkage network LN{z) as dependent on z in a similar manner as described in Section 2.2. The edge lengths on LN{z) are the corresponding reciprocal weights l/vüji or Ijvjk multiplied by z. Let Cz{Ei,Ej) be the length of a shortest path in LN{z). Then C~{Ei,Ej) = zC\{Ei, Ej) where C\{Ei,Ej) is the length of a shortest

(35)

path in L N {1) with 2; taken to be unity. If we define n,j = Ci{Ei, Ej) then we

have Cz(Ei, Ej) = znij. Note that riij is just the sum of the reciprocal weights on the path P(Ei,Ej) of LN (l). Hence the separation conditions

d(u,·, Vj) < C~{Ei, Ej) , I < i < j < n (2.7)

are equivalent to

d(vi, Vj) < ZTiij , I < i < j < n (2.8)

Then from (2.8) we have z > d{vi,Vj)/nij, I < i < j < n. So minimum feasible z is found by taking z* = maxi<,<j<„{d(v,,u_,)/n,j}. Once z* is computed, a feasible location vector can be constructed by applying S L P to constraints

d{xj,Vi) < z*fwji , \ < j < n d(xj,Xk) < z*/vjk , 1 < i < ^ < m

Complexity of solving P M M C is determined by the complexity of finding z* which requires finding all shortest path distances in LN{\). Using Dijkstra’s shortest path algorithm once for each £'-node, z* can be calculated in 0 (n(m + n)^) time which dominates complexity of SLP.

An implication of tight paths discussed in Section 2.2 for P M M C is that new facilities on the tight paths are located uniquely without using S L P and the rest of the new facilities can be located by S L P operating on a smaller set of distance constraints.

2.3.1 D ista n c e C on strain ed

P M M C

on Tree N etw ork s

Erkut, Francis and Tamir [7] considers P M M C on tree networks in the pres ence of distance constraints. From the analysis in the previous sections it is easy to find the equivalent formulation of the problem as:

(36)

{C - P M M C ) Min Z subject to d(xj ,v,·) < z / w j i _{> ( i}_>0 _{€ Ic} d{xj, < _{x / v j k} _> _{i h k )} e Ib d{xj ,Vi) < Cji ₁ _{{ h}_i) e _Ic d{xj, Xk) < _{bj k} _. _{{ h k )} _€ _I'_b X e c m

where Iq and Ig are defined to indicate that they are not necessarily equivalent

to Ic and Ib although defined similarly.

Analysis in [7] relies basically on the results obtained in [8] for the distance constraints. Authors propose two algorithms to solve C — P M M C . The first one is a polynomial algorithm which performs a binary search over the opti mum objective value z and requires data to be rational numbers. The second algorithm is a strongly polynomial one which employs the general parametric approach suggested by Megiddo [14].

Binary search algorithm is based on two stages. In the first stage an interval of prespecified length that contains the optimum objective function value is found by performing a bisection search over a finite set of 2: values and in the second stage the exact optimal value of ^ is found. S L P is used to check for the feasibility of distance constraints at each iteration. Final step is to apply a shortest path algorithm to find the exact value of 2.

Parametric approach depends on the results of Megiddo [14] for converting a (strongly) polynomial algorithm for a given combinatorial problem into a strongly polynomial algorithm to solve the parametric version of this combi natorial problem.

Let F{z) = mh\{L(Eh, Ei) — d{vh,Vi) \ \ < h < i < n} where L{Eh,Ei) is the shortest direct path in LN{z) and a direct path is defined to be a path whose intermediate nodes are all A^-nodes and terminal nodes are two distinct £■-nodes. It was shown by Tansel et al. [15] that an equivalent version of separation conditions can be stated in terms of shortest direct paths. For some

(37)

value of F{z) is attained for some direct path on LN{z)^ so with each value of z an optimizing direct path can be associated. The real line can be decomposed into finite set of intervals on which all z have the same optimizing direct path in each interval, i.e. F{z) is linear in each interval. At least one and at most two of these intervals contain z*.

For a specified value of z an algorithm which uses a shortest path algorithm as a subroutine, is used to compute the value of F(z). This algorithm is the primary algorithm for solving the parametric version of the problem with z being the parameter.

The algorithm is initiated by some uncertainty interval Iq which contains z*. The shortest path algorithm is applied parametrically with arc lengths that are some linear functions of z. Since this algorithm applies additions, subtractions, and comparisons only, it generates linear functions. For the comparison of two linear functions, the intersection point z', called the critical value, is found. The sign of F(z') is computed so that whether z' < z* or not is determined. In either case the interval of uncertainty can be reduced. So the algorithm can proceed to next step, without a need to specify a value for z in the current interval. This step is called comparison resolution step. This step is continued until termination where an interval containing z* is left with the following properties:

There is the same optimizing pair for all values of z in the interval, i.e. F(z) is linear over this interval, so z* can easily be computed. The complexity of the parametric approach is 0 (mn^(m + n.)^).

2.4 Biobjective Multifacility Minimax and Vec

tor Minimization

Tansel,Francis and Lowe [16] consider biobjective multifacility minimax prob lem on tree networks, which involves as objectives the maximum of the weighted

(38)

distances between specified pairs of new and existing facilities and maximum of the weighted distances between specified pairs of new facilities. The Biobjective Multifacility Minimax Problem B M M can be stated as follows:

vector minimize where f { X ) M X ) M X ) { f { X ) : x e T ^ } { MX) , M X ) )

max {wjid{xj,Vi) : (j,i) € /c } max {vjkd{xj,xk) : (j,k) € h }

[16] characterizes efficient points of B M M by making use of separation conditions and provides an 0 (m^(m + 7i)^) procedure to construct the efficient frontier which is the set of two tuples (^1,2:2) constituting the objective values of efficient points.

First the problem is transformed into an equivalent form in terms of distance constraints, i.e. Z = (2:1,22) is to be vector minimized subject to

d{xj,Vi) < zi/wji , {j,i) e Ic

d{xj,xk) < z-ilvjk , { j , k ) e l B

The graph LN{Z) is constructed associated with the above D C . Then it is shown that the following are equivalent.

(a) A location of vector X is efficient.

(b) At least one of the arcs (A(y·, Nk)·, {j, k) € Ib is in a tight path in LN{Z) where Z = f { X ) ·

Further general results are provided which unify the necessary and sufficient conditions for efficiency of a broad class of location problems which involve t (t > 1) minimax type objectives.

(39)

CHAPTER 2. EXISTING THEORY FOR TREE NETWORKS ₂₆

vector minimize { / ( ^ ) · ^ ^ T ’”'} where f { X ) = ( f i { X ) , f t { X ) )

fr{X) = max [max u.) : {j, i) G T 0 Ic},

max {v^ji^d{xj,xk) : {j,k) G F 0 Is)], 0 < ?· < i

F is assumed to be a nonempty subset of Ic U Ib, and weights tut. and are

positive for each 1 < r < t. f r( X ) is defined as the r-th objective.

For the ¿-objective multifacility minimax problem a linkage network L Nbc

is constructed. The node set of LNbc is {N\^...,Nm} U {Ei^...,En) and the

arc set is as follows: For each r, 1 < r < t if (j, i) € F f\ Ic then there is an arc ar{Nj, Ei) of length Zrivf- and if (j, k) e F 0 Ib then there is an arc

ar{Nj,Nk) of length Zr/vji^. Thus there exist several arcs between a pair of nodes of L Nb c· It is proven in [16] that X is efEcient if arid only if for every r € {1, with > 0, at least one arc associated with the r-th objective is in a tight path in L Nb c·, where Z = f { X ) .

2.5 Other Approaches

Erkut, Francis, Lowe, and Tamir [6] consider the multifacility location problem on tree networks subject to distance constraints. All constraints and the ob jective function are arbitrary nondecreasing functions of any finite collection of tree distances between pairs of new and existing facilities and between distinct pairs of new facilities. It is shown in [6] that such problems are equivalent to mathematical programming problems which, when each function is expressed using only maximization and summation operations on nonnegatively weighted arguments, are linear programming problems of polynomial dimensions. This result may constitute another partial answer to the question why tree networks are more tractable than cyclic network problems since they have equivalent mathematical programming formulations, while cyclic network versions of the same problems do not.

(40)

We also consider two papers by Chhajed and Lowe [2, 3] which are the only papers related to more general graphs than trees. The main concern in [2] is the minisum problem with mutual communication, but their approach is applicable to node restricted version of the minimax problem with mutual communication. The minisum problem is reformulated in the form of a graph theoretic Node Selection Problem defined on a special graph which is solved in polynomial time when the graph that denotes the interaction between pairs of new facilities has the special structure of series-parallel graphs.

' In [3], authors consider a generic multifacility location problem, which sub sumes as special cases several jV*'P-Hard location problems. The generic prob lem is solved in polynomial time for the k-tree structured interaction between new facilities. This paper identifies the broadest efficiently solvable classes of several difficult problems which includes the node restricted version of the minimax problem with mutual communication.

The problem we consider in this thesis is a feasibility problem whereas works in [2, 3] consider the related optimization form. The basic deviation of our approach from that of [2] and [3] is twofold: First, we consider the continuous version of the problem while [2, 3] restrict the locations of new facilities to finitely many candidate points. Second, we require that the interaction between new facilities has a tree structure whereas in [2] and [3] the problem is solved for series-parallel and ¿--tree structured interactions. Hence our approach is a generalization of [2] and [3] in one respect while it is a restriction in the other.

2.6 D C

is

M V - C o m p l e t e

on General Networks

Up to now, we have provided the basic theory for tree networks, and cited only two works on networks more general than trees that covered the node restricted version of the related minimax problem as subcases. In this section we provide the basic result by Kolen [1 2] regarding the distance constraints on general networks.

(41)

The problem of finding a clique of size c of a given graph is known to be A/^'P-Complete (see [9]).The problem CL IQ U E which we state next, is reduced to the distance constraints problem of deciding whether there exists a feasible solution to the given set of distance constraints. So the distance constraints problem is also A/^P-Complete.

C L IQ U E

In sta n c e : A graph G = (V,E) with V = and an integer c.

Q u estio n : Does there exist a subset C C V of cardinality c such that [vj, G E i f { v ^ , V k ] C V ?

Let DC — d denote the problem of deciding whether there exists a feasible solution to the given set of distance constraints. DC — d is stated next.

DC-d

In sta n c e : /1 graph G' — (V',E') with V = th €. Ai, lengths

e(e) e 2+, e e E \ Cji e Q+, \ < j < rn and \ < i < n, bjk G Q+,

I < j < k < m.

Q u estio n : Is there a set X = {.cj, . . . , on G' such that

d{xj,Vi) < Cji , 1 < j < m , 1 < z < n, d{xj,Xk) < bjk , 1 < i < ^’ < m?

Now we state the basic result regarding the distance constraints on general networks.

T h e o re m 2.2 DC - d is AfV-Complete.

Proof: DC — d belongs to the class AfV since by using standard shortest path techniques we can test whether a given solution satisfies the bounds in polynomial time.

We shall reduce the problem C L I Q U E to DC — d. Let an instance of C L I Q U E be given by G = (V, E) with V = {u i,...,u,i} and an integer c. The

(42)

corresponding instance of DC — d is given hy V = V \J W C U C {p} U {<7} U {r}, where VF = { u ; i , a n d f/ = E' = {[p» v . ] n , · ] , [u,·, w,·],

[wi,Ui] : i = U e E, i < j } , m = 3c, ((e) = 1 for all

e € £', Cji = lor I < j < m, 1 < * < n, bjk — 1 for \ < j < k < n. (See example in Figure 2.4 with c = 3.)

We claim that G = {V,E) contains a clique of size c if and only if there exists points xi,...,Xm on G' = {V',E') such that the weighted distances are less than or equal to the given upper bounds, i.e.

7) ^ I5 ^(^j+2c j ^ 1 ) J l,...,c (2.9) d{^xj^Xj-\-c) ^ 1) ^j+2c) ^ 1) J

d{ xi^xj^2c) < 1 , 1 < * < i < c. (2.11)

Let x\^...^xzc be the points on G' = {V',E') satisfying (2.9), (2.10) and (2.11). Since d{p,q) = d{q,r) = 1, from (2.9) and (2.10) we have Xj e K, say Xj E Vj, Xj+c = and Xj+2c = Uj, j = l,...,c . It follows from (2.11) that

[vi,Uj] E E', i.e., [vi,Vj] E E, i < j. Hence {vj : j = l,...,c} is a clique in the graph G = (l/,^ ).

Let {vj : j = 1, ...,c) be a clique of size c in G. Define Xj = vj, xj+c = wj, Xj^2c = Uji j = l,...,c . Then xi,...,X3c satisfy (2.9), (2.10) and (2.1 1). □

V/ w ,

(G)

(G')

(43)

Chapter 3 DISTANCE CONSTRAINTS

AND EXPAND/INTERSECT

METHOD IN GENERAL

METRIC SPACES

In this chapter we deviate from the network context and introduce a new approach to solve distance constraints in general metric spaces. To pose the problem in its general form, let L be a metric space with distance d that satisfies the usual axioms of nonnegativity, symmetry and triangle inequality of a metric. Some well known instances of (L,d) are obtained by taking L to be the A’-dimensional Euclidean space and d to be ^p-norm. Our particular interest in the next chapter will be in the case where L is an embedded network and d{x, y) is the length of a shortest path between x and y in L. The main results we give in this chapter are true for arbitrary metric spaces.

We have previously defined distance constraints on networks. The definition of DC on general metrics is similar. We take ui,...,u„ be n fixed points in L, rather than vertices in (7, with u, being the location of existing facility i. New facilities are to be placed at points .rj, ...Xm any where in the location space to

(44)

satisfy distance bounds on specified pairs of facilities. So we have: ^ Cji X \ ,..■ , Xyyi G L (;V0 e Ic

(i,

k )

e

Ib {DCA) {DC.2)

Again Cji, bjk are nonnegative finite constants and Ic and Ib specify the pairs of facilities for which there is a bound on their separation.

In Chapter 2, we have defined an auxiliary network called the Linkage Network L N which conveniently represented the data of the problem. Since, construction of L N does not rely on the specific location space, an equivalent auxiliary network L N is also valid for DC defined in general metric spaces. Now, we denote the portion of L N spanning only A j’s and the arcs between them by L Nb- Figure 3.1 shows an example of a linkage network and related L Nb.

(LN^)

Figure 3.1: Example of L N and Related L Nb

In the next section we give a new approach to solve DC in general metric spaces for the case when L Nb kas a tree structure. The basic idea of the

method depends on successively performing two set operations EXPANSION and INTERSECTION defined on subsets of the location space.

(45)

CHAPTER 3 DISTANCE CONSTRAINTS AND ... 32

3.1 E X P A N D /IN T E R S E C T Method for Gen

eral Metrics

Given a nonempty subset S oi L and a nonnegative constant r, the expansion of S by r is the set of all points in L for which there exists j/ in 5 with d(x, y) < r. We denote the expansion of S by r by N{S,r). N{S,r) includes all points of L that are reachable from at least one point in S within r distance units. For example, if L is the plane, d is the Euclidean distance, and S is the ball centered at X with radius a, then N{S^ ?·) is the ball centered at x with radius o: + r. (Figure 3.2)

Figure 3.2: Expansion of S by r (in the Plane with Euclidean Distance)

The definition of expansion implies x G N{S,r) if and only if x £ N{y,r) for some point y G S if and only if x E ijyes ^ { y A ’)· Hence, we have N{S ,r) — U y e s ^ i V A ’)· With this observation we may think of N{S,r) as the neighborhood of S within r distance units (this explains the choice of our notation A^(·,/·)).

Note that the definition of expansion does not require any assumptions on S other than it being nonempty. S may be finite, infinite, connected, disconnected, open or closed. If S is compact, then any expansion of S is also compact provided that r is finite and L is closed.

First, let us consider DC(l). Since we are looking for a point x in L such that d{x,Vi) < c,·, i ^ I = the feasible set for DC{1) is S = Dig/A^(y,, c,). Each neighborhood yV(u,-,c,) is nonempty since we assume Ci

Polynomially solvable cases of multifacility distance constraints on cyclic networks

CYCLIC NETWORKS

By

Naile Giilcan Ye§ilk6kgen

July, 1993

ABSTRACT

POLYNOMIALLY SOLVABLE CASES OF MULTIFACILITY

DISTANCE CONSTRAINTS ON CYCLIC NETWORKS

Naile Giilcan Ye§ilk6kgen

M.S. in Industrial Engineering

Supervisor: Assoc. Prof. Barbaros Q. Tansel

July, 1993

GENEL SERIMLERDE ÇOKTESISLI UZAKLIK KISITLARI

PROBLEMİNİN POLİNOM ZAMANDA ÇÖZÜLEBİLİR

DURUMLARI

Naile Gülcan Yeşilkökçen

Endüstri Mühendisliği Bölümü Yüksek Lisans

Tez Yöneticisi: Doç. Dr. Barbaros Ç. Tansel

Temmuz, 1993

Contents

INTRODUCTION

1.1

Introduction and Overview

1.2

Networks, Embedding, and Distance

1.3

Distance Constraints and m-Center Prob­

lem with Mutual Communication

EXISTING THEORY FOR

TREE NETWORKS

2.1

Convexity on Tree Networks

2.1.1

C o n v ex ity o f D ista n ce

2.1.2

Im p lica tio n s o f C o n v ex ity o f D ista n c e

2.2

Distance Constraints on Tree Networks

2.2.1

S in gle F acility C ase

2.2.2

M u ltifa cility C ase

2.3

Minimax Problem with Mutual Commu­

nication

2.3.1

D ista n c e C on strain ed

on Tree N etw ork s

2.4

Biobjective Multifacility Minimax and Vec­

tor Minimization

2.5

Other Approaches

2.6

D C

is

M V - C o m p l e t e

on General Networks

Chapter 3

DISTANCE CONSTRAINTS

AND EXPAND/INTERSECT

METHOD IN GENERAL

METRIC SPACES

(i,

e

3.1

E X P A N D /IN T E R S E C T Method for Gen­

eral Metrics

Distance Constraints and m-Center Prob

Minimax Problem with Mutual Commu

Biobjective Multifacility Minimax and Vec

E X P A N D /IN T E R S E C T Method for Gen