Skaler denklemlerde kararlılık analizi

Adıyaman Üniversitesi

Fen Bilimleri Dergisi 4 (2) (2014) 109-149

Skaler Denklemlerde Kararlılık Analizi

Özlem Ak Gümüş

Adıyaman Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, Adıyaman akgumus@adiyaman.edu.tr

Özet

Bu çalışmada, skaler denklemlerin kararlılığını belirlemek için kullanılan kararlılık metotları verilmiştir. Bu metotlar açıklanmış, bu metotlar ile ilgili olarak teoremlere yer verilmiştir. Sonuca kolay bir şekilde ulaşmak için kararlılık tabloları oluşturulmuştur. İlgili örnekler verilmiştir. Son olarak, çalışma boyunca üzerinde durulan kararlılık testleri karşılaştırılmış ve birbirlerine göre avantajı incelenmiştir.

Anahtar Kelimeler: Kararlılık, Fark denklemleri, Skaler denklemler, Kararlılık testleri.

Stability Analysis in Scalar Equations Abstract

In this paper, it is given stability methods used for indicating stability of scaler equations. These methods are explained, the theorems as regard with these methods are given. For reaching to the result easily, stability tables are constituted. Related examples are given. Finaly, stability methods which are given along this study are compared; and advantages relative to each other of these methods are investigated.

Keywords: Stability, Difference equations, Scalar equations, Stability test.

1. Giriş

Fark denklemlerinin kararlılığı üzerine şimdiye kadar çeşitli çalışmalar yapılmış ve bunun sayesinde de önemli bilgilere ulaşılmıştır. Acaba genel fark denklemlerinin özel bir hali olan ve “skaler denklemler” olarak da bilinen reel değerli homojen fark denklemlerinin kararlılığını belirleyen metotlar nelerdir? İşte bu sorunun cevabı çalışma konumuzu

110

oluşturmuştur. Ayrıca bu metotların birbirine göre avantajı incelenmiştir. Bu metotlar, verilen skaler denklemi çözmeden skaler denklemin karakteristik polinomu yardımıyla, kararlılık testi için pratik bir hesaplama gerektirir [1-6,8]. Öncelikle çalışmamızla ilgili bazı tanımları hatırlayalım.

Tanım 1.1 a_k1,a_k2,,a₀R olmak üzere k. mertebeden bir skaler denklem

0 2 1 2 0 1          k) a _x(n k ) a _ x(n k ) a x(n) n ( x k k  (1.1) formunda tanımlanır [7].

Tanım 1.2 (1.1) ile verilen skaler denklemin karakteristik polinomu

0 1 1 1 a a a ) ( D k k k A           

olmak üzere; D_A()0 denkleminin köklerine “öz değer” denir [7].

Tanım 1.3 (1.1) ile verilen denklemin asimtotik kararlı olması için gerek ve yeter şart

n ,.., , i ; i 1 12  [7].

2. Skaler Denklemler için Kararlılık Testleri

Skaler denklemin karakteristik polinomu yardımıyla, kök yer teknikleri ve açık kök belirlenmesi etkili bir biçimde uygulanabilir. Burada, tablosal teknikler ile basit ve sistematik bir şema ortaya çıkarılmıştır., Hesaplama ve uygulama basitliklerinden dolayı, tablo teknikleri büyük oranda dikkat çekmiştir. Bu teknikler skaler denklemin karakteristik polinomunu kullanılarak ikinci dizi belirleyicilerinin hesaplamalarını gerektirir. O zaman kararlılık şartları tablodaki elemanlardan kolayca elde edilebilir [1-6,8]. Şimdi bu testleri inceleyelim.

2.1. Marden-Jury Testi

[3] de verilen bu kararlılık testinde bir skaler fark denkleminin karakteristik polinomu D(z)d₀d₁zd_nzn (2.1.1) şeklinde tanımlansın. Bu test



D_i(z)



_in_o 



D₀(z)D₁(z)D_n(z)



şeklinde bir polinom dizisi oluşturarak D z nin kararlılığını inceler. Bu polinom dizisi;

 

) z ( D d ) z ( D d ) z ( Di1  i,0 i  i,ni *i (2.1.2)

111

bağıntısı kullanılarak oluşturulur. D z_i( ); (n i ). mertebeden polinomu i n i n , i , i , i i(z) d d z d z D  0 1  _  olmak üzere ve D (z) *

i , D z nin karşılıklı polinomu olup

 

i n i i n i i n i i i n i z z D z d d z d z

D*_{( )}  ₍ 1₎ _,  _,1 _ _,0  şeklinde tanımlanır. Aynı zamanda n n n * z d z d d ) z ( D ) z (

D0    1  0 şeklindedir. Denklem (2.1.2) kullanılarak dizilerin

elemanları ile olan ilişkisi göz önüne alınırsa; i0,1,2,,n olmak üzere; ) z ( D_{i 1} d (d d z d z d zni) i n , i , i , i , i , i        2  2 1 0 0 ( ,0 ) 1 1 , 1 , , , i n i i n i i n i i n i i n i d d z d z d z d _{ }  _        ) z ( Di 1 di dini (di,0di,1 di,nidi,n i1)z 2 , 2 0 ,        1 1 1 , , 1 , 0 , ) (        ni ni i i n i i n i i d d d z d 

yazılabilir. Temel şart aşağıdaki teoremde olduğu gibi verilebilir.

Teorem 2.1.1 (2.1.1) ile verilen D z polinomunun tüm sıfırlarının birim çember içine

 

düşmesi için  _i d_i,0 0, i1, 2, ,n [3]. 2.2 Hu’nun Kararlılık Testi

Bu test yardımıyla oluşturulan tabloda Marden-Jury Testinde kullanılan polinomlar dizisiyle basit ilişkili



S_i(z)



_in_0 simetrik polinomlardan oluşan yeni bir dizi tanımlanmıştır [3]. Yeni polinom düzenlemesi ile oluşturulan bu tablo uygulaması, iki boyutlu ve çok boyutlu sistemlerin kararlılığını test edecek sade ve sistemli bir tekniğin bulunmasına yol açmıştır.





n i i(z)

S _0 simetrik poliomların yeni bir dizisi,



S(z)





S (z)S (z) Sn(z)



n i

i 0  0 1  (2.2.1)

verilsin. Si(z),(ni). mertebeden polinomu;

i n i n , i , i , i i(z) S S z S z S  ₀ ₁  _  ile , , , 0,1, , (( 1) / 2) i j i n i j

S S _{ } j Int n şeklinde tanımlanır. Burada Int(.), tam değer

fonksiyonudur. İlk iki





n i i(z) S _0 polinomu; ) z ( D ) z ( D ) z ( S0  0  0* (2.2.2) ve ) z ( D ) z ( D ) z ( S1  1  1* (2.2.3)

112

olarak verilir ki, burada D z D z D z₀( ), ₀*( ), ₁( ) ve D1*(z) denklem (2.1.2) ile verilen





n i i(z)

D _0

Marden Jury dizisi polinomlarıdır.





n i i(z)

D _0 deki polinomlar yardımıyla S_i1( ),z i0

simetrik polinomları ) z ( S z ) z ( S ) z ( ) z ( S_i1  1 1 _{i i}  1_{i i1} (2.2.4) bağıntısı ile hesaplanır. Buradaki katsayılar aşağıdaki şekilde verilir:

0 1 0 1, i i, i i S q d  i n , i , i , i i i S d d q 2  ₀  ₀ _ 1 0    _{i, i} i S q  Teorem 2.2.1 Dk1(z)dk,0Dk(z)dk,nkDk*(z) ve D (z) z (d D (z) dk,n kDk(z)) * k , k * k     0  1 1

olmak üzere, Denklem (2.2.1)’de verilen





n i i(z)

D _0 Marden Jury dizisinin polinomları arasındaki bağıntı * ( ) ( ) ( ) i i i S z D z D z (2.2.5) şeklindedir [3].

Bundan sonra



S_i(z)



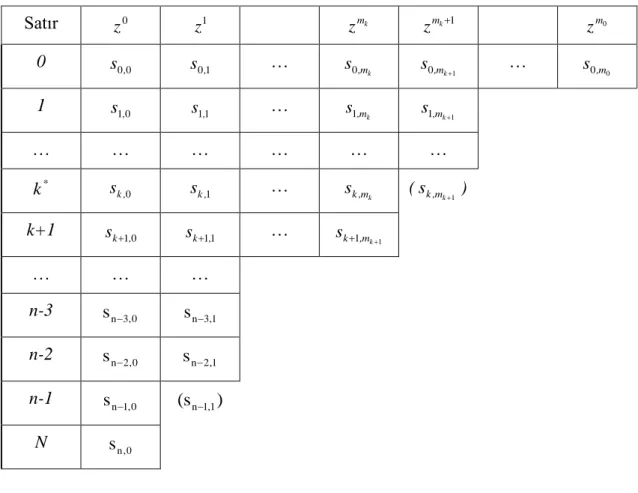
n_i0 simetrik polinomların dizisini oluşturup yeni bir tablo vereceğiz. Yeni tablonun elemanlarıyla ilgili uygun kararlılık koşulları da verilecektir.

Tablo 2.1. Hu’nun Kararlılık Tablosu

Satır 0 z z 1 _zmk _zmk1 _zm0 0 s_0,0 s _0,1 … k m , s₀ 1 0,mk s … 0 0 m, s 1 s _1,0 s _1,1 … k m , s₁ 1 1,mk s … … … … * k sk,0 s k,1 … sk,m_k (sk,m_k₁) k+1 s_k1,0 s_k1,1 … 1 1  ,mk k s … … … n-3 _{sn3,0 sn3,1} n-2 s_n2,0 s_n2,1 n-1 _{sn1,0 (sn1,1)} N _sn,0

113

İlk satırın elemanları satır “0”, denklem (2.2.2) de verilen S₀(z) polinomunun katsayıları olup S_0,j d_0,jd_{0,n j} , j0,1, ,m₀ şeklindedir. İkinci satırın elemanları, satır “1” denklem (2.2.3) de verilen S₁(z) nin katsayılarıdır ve aşağıdaki formla hesaplanır.

)) ( ) ( ( )) ( ) ( ( )) ( ) ( ( ) ( ) ( ) ( * 0 0 1 , 0 * 0 1 0 0 , 0 0 , 0 * 0 0 , 0 1 * 0 , 0 0 0 , 0 1 z D z D z d z D z z D d z D d z D d z z D d z D d z S n n n            ) z (

D₀ nin katsayılarını kullanarak S_1,j d_0,0(d_0,j d_0,nj1)d_0,n(d_0,j1d_0,nj), j0,1,m₁ yazılabilir. Sonraki satırdaki elemanlar aynı şekilde Teorem 2.2.1 de verilen bağıntı yardımıyla hesaplanabilir. Buna göre genel bağıntı ve katsayılar

, 1( 1, 1, 1) 1 2, 1 i j i i j i j i i j S _ S_ S_{ } _S_{ } , i2,3, , ,n j0,1, m_i,             tek i n , ) i n ( çift i n , ) i n ( mi 1 2 1 2 1 veya mi Int[ (ni)] 2 1

şeklindedir. Tablo 2.1, mi Int[ (ni)]

2 1

ile birlikte Si(z), i0,1,,n polinomunun

katsayılarını yarıya düşürerek oluşturulan simetrik polinomların basit bir şeklidir. Yinede n-i tek sayılı satırlar için

S

i,m_i1 elemanları bir sonraki satırın elemanı olan Si1,m_i1 hesaplanmasında gereklidir. Bu nedenle biz onları sol elemanların kopyası olduğunu belirtmek için tabloda parantez içerisine yerleştirdik. Matematiksel olarak

i m , i S 1 , i , i, 1, 2, 1 i m i m

S _ S n i tek i  n şeklinde ifade edilebilir.

Tablo 2.1 in yapısı sürekli zaman sistemleri için kullanılan Routh Tablosuna çok benzer; şayet n tek ise m m (n 1)

2 1

0

1    dir. Yani tablonun ilk iki satırı aynı sayı

elemanlarına sahiptirler. Böylece elemanların satırı her sırada bir azalacaktır. Şayet n çift ise

n m

2 1

0  dir. Elemanların sayılarının azalması satır 1 den başlayacaktır. Son iki satır olan n-1

ve n hep bir elemana sahip olacaktır. Buradan (n-i) tek sayılı satırlardaki ( )

1

,mi i

S

kopyalanmış elemanları içermediği anlaşılır. Aşağıdaki teorem yeni tabloya uyumlu olarak denk kararlılık koşulları vermektedir.

114

Teorem 2.2.2 d_n 0 ile birlikte D z nin bütün sıfırlarının birim çember içine düşmesi için

 

 D(1)0,(1)nD(1)0 ve S_i,0 0,i1,2,n1 veya 0 2 , , 2 , 1 , 0 ₂ 0 ,    n  i i n veq

S  veya S_i,0  ,q_i 0 i1,3,,n2, ntek veya

,0 0 , 0, 2, , 2 ; 0 0 0; 2, 4, , 2,

i i

S  i n q  ve q  i n n çift

denk olan şartlardan biri yerine getirilmelidir. 2.3 Jury Testi I (n) 0 ( ) n k k k F z a z 





,  üzerinde n. dereceden polinom dizisi olsun.



, varyasyonu reel

sayılar dizisindeki farklı işaretlerin sayısını göstersin. F z nin karşılıklı polinomu

 

F(z)

olmak üzere, eğer F(z)F(z) ise F z nin simetrik olduğu söylenebilir.

 

F z( ) _n(z)

olduğunda F(z) znF(1/z) dir. Burada F(z), F z nin eşleniğidir. Biz;

 

F z , reel

 

katsayılı polinomu üzerinde çalıştığımızda katsayılar değişmez.     n k k k n(z) a z F ) z ( F 0 , F 1( ) ve F(1)0 (2.2.6) olsun. Reel durumda, genelliği kaybetmeden a_n 0 olduğunu varsayalım. F z nin

 

kararlığının belirleme formunun incelenmesinde azalan mertebeli polinomların bir dizisi bulunur. JT ve daha sonra MJT de kullanılan polinom dizisi



F_i(z)



_in_0 şeklinde tanımlansın.

Burada    i k k ) i ( k i(z) a z F 0

formunda elde edilen polinom dizisi,



F_i(z)



_in_0 ve ) n ( ) n ( ) n ( ) n ( ) n ( n ) n ( ) n ( n n ) n ( n a a a a a a ) ( F     _1 1  _2 2  ₂ 2 ₁  ₀ karakteristik polinomunun katsayıları yardımıyla aşağıdaki tabloyu oluşturabiliriz [7].

Tablo 2. 2. Jury’nin Kararlılık Tablosu

Satır 0 1 2 . . . k . . . n2 n1 n 1 2 ) ( 0 n a a₁(n) a₂(n) . . . a_k(n) . . . a_n(n_)₂ a_n(n_)₁ a_n(n) ) (n n a a_n(n_)₁ a_n(n_)₂ . . . a_n(n_)_k . . . a(₂n) a₁(n) a₀(n) 3 4 ) 1 ( 0  n a a₁(n1) a₂(n1) . . . a_k(n1) . . . a_n(n_₂1) a_n(n_11) ) 1 ( 1   n n a a_n(n_₂1) a_n(_n₃1) . . . a_n(n__k1_)₁ . . . a₁(n1) a₀(n1)

115 5 6 ) 2 ( 0  n a a₁(n2) a₂(n2) . . . a_k(n2) . . . a_n(_n₂2) ) 2 ( 2   n n a a_n(n_32) a_n(n_₄2) . . . a_n(n__k2)₂ . . . a₀(n2)     2n-5 2n-4 ) 3 ( 0 a a₁(3) a₂(3) a₃(3) ) 3 ( 3 a a₂(3) a₁(3) a₀(3) 2n-3 a₀(2) a₁(2) a₂(2)

Teorem 2.3.1 F z nin asimtotik kararlı olması için;

 

i) F(1)>0 ve (-1)nF(1)0

ii) a₀(n1)  a_n(n_₁1) 0, a₀(n2)  a(_nn_₂2) 0,, a₀(2)  a₂(2) 0

şartları sağlanmalıdır. Burada (n 1)

k a  ve (n 2) k a  katsayıları; ) n ( ) n ( k n ) n ( n ) n ( k ) n ( k a a a a a 0 1   _ , _{(n ) (n )} k n ) n ( n ) n ( k ) n ( k a a a a a 1 0 1 1 1 1 1 2         _ ,  k=0,1,…,n-1 k=0,1,…,n-2 ile hesaplanır [7].

2.4. Jury Testi II (Raible Tablosu)

Jury bu test ile verilen bir skaler denklemin karakteristik polinomu yardımıyla birim çember içine ve dışına düşen köklerin hesaplanabileceğini, böylece başka bir irdelemeye gerek kalmadan asimtotik kararlılığın tesbit edilebileceği üzerinde durmuştur [6].

) z ( F ) z (

Fn  , (2.2.6) denklemi ile verilen reel katsayılı polinomu yardımıyla elde edilen azalan dereceli polinomun katsayıları

: Fn 1 ) n ( ) n ( n ) n ( ) n ( n ) n ( n a a a a a 0 0 1 1     , (n) (n) n ) n ( ) n ( n ) n ( n a a a a a 1 0 1 1 2      ,.., (n) n(n) n ) n ( ) n ( ) n ( a a a a a 1 0 1 0    : 2  n F _{(n )} (n ) n ) n ( ) n ( n ) n ( n a a a a a _{1 0} 1 1 1 0 1 1 2 2           , (n ) (n ) n ) n ( ) n ( n ) n ( n a a a a a 1 1 1 1 1 0 1 2 2 3           ,... (n ) (nn ) n ) n ( ) n ( ) n ( a a a a a 1 2 1 1 1 0 1 1 1 0        _{ } 

116 ) 2 ( 1 ) 2 ( 2 ) 2 ( 0 ) 2 ( 1 ) 1 ( 0 ) 2 ( 0 ) 2 ( 2 ) 2 ( 0 ) 2 ( 2 ) 1 ( 1 ) 2 ( 0 ) 2 ( 2 ) 2 ( 0 ) 2 ( 2 ) 1 ( 1 1: , , a a a a a a a a a a a a a a a F       , : F0 ) ( ) ( ) ( ) ( ) ( a a a a a 0 00 1 0 0 0 1 0 0  

ile verilir. Raible tablosunun her bir satırı bir polinomu simgeler. F z polinomunun birim

 

çember içindeki ve dışındaki kök sayılarını sırasıyla i F ve

 

(F) şeklinde gösterelim. O halde aşağıdaki teoremi verebiliriz.

Teorem 2.4.1. Raible tablosunun ilk kolonunda sıfır olmadığı düzenli durum için; (1) Eğer (n)0 n a ise , İ(F) = +{ , ,…, , (0)} 0 ) 1 ( 1 ) 2 ( 2 ) 1 ( 1 a a a a n n n n     ( 1) ( 2) (1) (0) 1 2 1 0 ( )F {ann ,ann , ,a ,a }        (2) Eğer a(nn) 0ise ,

 

( 1) 1 { _nn , İ F   a _ (n ) n a 22   , … , a1(1), (0) 0 } a (F){ a(_nn₁1), a(_nn₂2), … , a₁(1), a₀(0)}

ile kök sayıları hesaplanır [6].

Teorem 2.4.2 F z nin asimtotik kararlı olması için

 

i F

 

n olmasıdır [6]. 2.5 Reel MJT (Modifiye Edilmiş Jury Testi)

JT’nin modifiye edilmiş versiyonu ilk kez Schur-Cohn minörleri, daha sonra iç determinantları elde etmek amacıyla kullanılmıştır [1]. 2 2x boyutunda matrisin determinant hesabı ise kararlılığın belirlenmesinde kolaylık sağlar. Reel-MJT aşağıdaki polinom dizisini kullanarak oluşturulabilir.                            ] ) ( [ 1 )] ( ) ( [ )] ( ) ( [ ) ( 1 ) 1 ( 1 1 ) 1 ( 0 ) 2 ( 0 1 ) 1 ( 1 1 ) 1 ( 0 ) ( ) ( 0 i i i i i i n n n n n n n n n n i F a z F a a z F a z F a z F a z F a z F 0 4 3 2 1 , , n , n i , n i , n i ,         (2.2.7)

Elde edilen her polinom, bir önceki polinomun katsayılarına bağlı olarak aşağıdaki şekilde elde edilir. F z_n( ) ve F_n( )z karşılıklı polinomu

) ( 0 ) ( 1 2 ) ( 2 2 ) ( 2 1 ) ( 1 ) ( ) ( nn n n n n n n n n n n n z a z a z a z a z a z a F   _   _    

117 ) n ( n ) n ( n ) n ( n n ) n ( n ) n ( n ) n ( n (z) a z a z a z a z a z a F        _  _1  2 2 2 2 1 1 0  olmak üzere (n ) (n ) (n ) n n ) n ( n n ) n ( n n (z) a z a z a z a z a F 0 1 1 1 2 1 2 1 2 1 1 1 1                polinomunu elde edelim. ( ) ( ) ( ) ( ) 1 ( ) ( ) 2 1( ) 0 0 1 0 2 n n n n n n n n n n n n n F_ z  a a z a a _z  a a_ z    ( ) ( ) 2 ( ) ( ) ( ) 2 0 2 0 1 ( 0 ) n n n n n a a z a a z a ( ) ( ) ( ) ( ) ( 1) ( ) ( ) ( 2) ( ) ( ) 2 ( ) ( ) ( ) 2 0 1 2 2 1 ( ) n n n n n n n n n n n n n n n n n n n n n n a a z a a z  a a z  a _ a z a a z_ a               _  (z) [a a a a ]z [a a a a ]  F_{n1 1}(n) _n(n) ₀(n) (_nn₁) n1 ₂(n) _n(n) ₀(n) _n(n₂)



0 2



0 2 1 0 1 2 2 0 2.a a a ]z [a a a a ]z [a ] [a ] a [ (_nn) _n(n) (n) (n)  (_nn) _n(n) (n) (n)  _n(n)  ( ) olup katsayılar, ) ( 1 ) ( 0 ) ( ) ( 1 ) 1 ( 1 n n n n n n n n a a a a a _   _ ) n ( n ) n ( ) n ( n ) n ( ) n ( n a a a a a 2 0 2 1 2        ) n ( ) n ( ) n ( n ) n ( n ) n ( a a a a a 1 _{2 0 2} 2     ) n ( ) n ( ) n ( n ) n ( n ) n ( a a a a a 1 0 1 1 1     2 0 2 1 0 [a ] [a ] a n(n) (n) ) n (   

şeklinde bulunur. Benzer işlemlerle

) n ( ) n ( ) n ( n ) n ( n n (z) a z a z a z a F_2  _₂2 2 ₂ 2 2 ₁ 2  ₀ 2 polinomunun katsayıları ) n ( ) n ( n ) n ( n ) n ( ) n ( n a a a a a 1 1 1 1 1 2 1 0 2 2             ) n ( n ) n ( n ) n ( ) n ( ) n ( a a a a a 1 3 1 1 1 2 1 0 2 2        _{ } ) n ( n ) n ( n ) n ( ) n ( ) n ( a a a a a 21 1 1 1 1 1 0 2 1        _{ } 2 1 1 2 1 0 1 0 (a ) (a ) a(n )  (n )  _n(_n )

elde edilir. Aşağıdaki çizelge üzerinde, katsayılar arasındaki ilişkiyi daha açık bir şekilde görebiliriz.

118

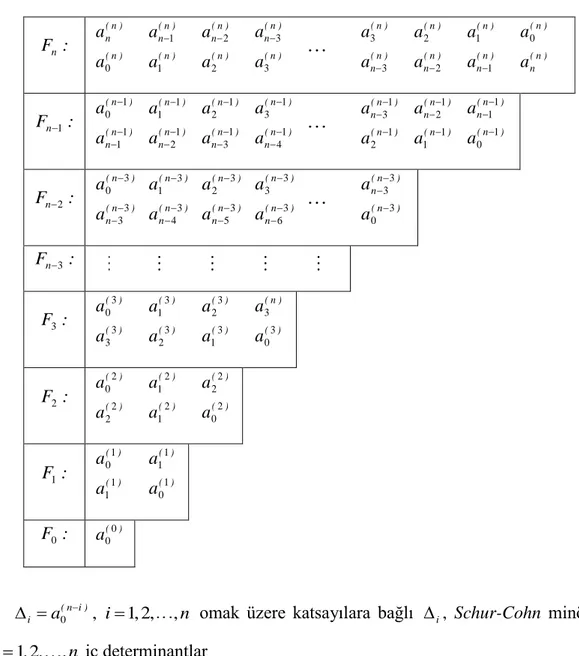
Tablo 2.3. Modifiye Edilmiş Jury Tablosu

) i n ( i a  

 0 , i1, 2, ,n omak üzere katsayılara bağlı i, Schur-Cohn minörleri ve

 _i, i1,2,,n iç determinantlar                              2 ) 1 ( 1 ) 1 ( 0 ) 1 ( 1 ) 1 ( 0 ) ( 0 ) ( i i n i n i n n n n n n n i a a a a a a n i i i , , 4 , 3 2 1     (2.2.8)

ile verilir. F z nin kararlı olması için gerek ve yeter şart aşağıdaki gibi belirtilebilir.

 

Teorem 2.5.1. (2.2.6) da verilen F(z)_n[z] polinomu için F(1)0, (1)nF(1)0 olmak üzere; : F_n ) n ( ) n ( n a a 0 ) n ( ) n ( n a a 1 1  ) n ( ) n ( n a a 2 2  ) n ( ) n ( n a a 3 3   ) n ( n ) n ( a a 3 3  (nn) ) n ( a a 2 2  (nn) ) n ( a a 1 1  n(n) ) n ( a a₀ : F_{n 1} ) n ( n ) n ( a a 1 1 1 0    ) n ( n ) n ( a a 1 2 1 1    ) n ( n ) n ( a a 1 3 1 2    ) n ( n ) n ( a a 1 4 1 3     ) n ( ) n ( n a a 1 2 1 3    ) n ( ) n ( n a a 1 1 1 2    ) n ( ) n ( n a a 1 0 1 1    : Fn 2 _{(n )} n ) n ( a a 3 3 3 0    ) n ( n ) n ( a a 3 4 3 1    ) n ( n ) n ( a a 3 5 3 2    ) n ( n ) n ( a a 3 6 3 3     ) n ( ) n ( n a a 3 0 3 3    : Fn 3      : F3 _{( )} ) ( a a 3 3 3 0 ) ( ) ( a a 3 2 3 1 ) ( ) ( a a 3 1 3 2 ) ( ) n ( a a 3 0 3 : F₂ ) ( ) ( a a 2 2 2 0 ) ( ) ( a a 2 1 2 1 ) ( ) ( a a 2 0 2 2 : F₁ ) ( ) ( a a 1 1 1 0 ) ( ) ( a a 1 0 1 1 : F0 ) ( a00

119 a) i 0, i1, 2, ,n 1 b) n çift, 1 0, 3 0,..., 1 0     n    , c) n tek, 2 0, 4 0,..., 1 0     n    ,

yukarıdaki denk olan şartlardan biri yerine getirilmelidir [1]. 2.6 Reel-BT (Bistritz Testi)

[2] de verilen bu kararlılık metodunda BT’de kullanılan polinom dizisi



T_i(z)



n_i0 ile gösterilsin.    i k k ) i ( k i(z) t z T 0

ile tanımlanan dizinin şematik olarak gösterilmesinde ilk satır n. mertebeden polinom, ikinci satır (n-1). dereceden polinomdur ve azalan mertebeyle devam eder.

Bistritz F z kararlılığını aşağıdaki şekilde verilen

 



T_i(z)



n_i0 simetrik polinom dizisi kullanarak araştırdı. Reel-BT için

                   z ) z ( T ) z ( T ) z ( z ) z ( F ) z ( F ) z ( F ) z ( F ) z ( T i i i n n n n i 2 1 2 1 1  2 3 0 1 , , n , n i n i n i        (2.2.9)

formuna sahibiz. Ayrıca;

) i ( ) i ( i i i t t ) ( T ) ( T 1 0 2 0 1 2 2 0 0         , in2,n3,,0 (2.2.10)

geçerlidir. Ti(z) simetrik olduğu için

) i ( k i ) i ( k t

t  _ , k 0,1,,iyazılabilir. O halde aşağıdaki

teoremi verelim.

Teorem 2.6.1 Denklem (2.2.6) da verilen F(z)_n[z] polinomu Teorem 2.5.1. deki şartlar yerine getirildiğinde kararlıdır. Ayrıca, T_i(0)t₀(i) 0, i n 1, n2, , 0 ve



1 ₁ 1 ₀ 1



0

varT ( ),T _( ), ,T ( )

v_{n n n}  şeklindedir.

(2.2.9) numaralı denklemden F z kök dağılımının belirlenmesi için bir çizelge

 

120 ( 2) ( 2) ( ) 0 1 ( 1) ( 1) ( 1) ( 1) 0 0 1 1 , 0,1,..., i i i k k i i i i k k t t t k i t t t t            _{ }    

olup



T_i(z)



_in_0 dizisi için aşağıda tanımlanan çizelge formu düzenlenir. Ayrıca



T_i(z)



n_i0

polinomları simetrik olduğundan dolayı sadece girişlerin yarısı değerlendirilir [2]. Tablo 2.4. Reel Bistritz Tablosu

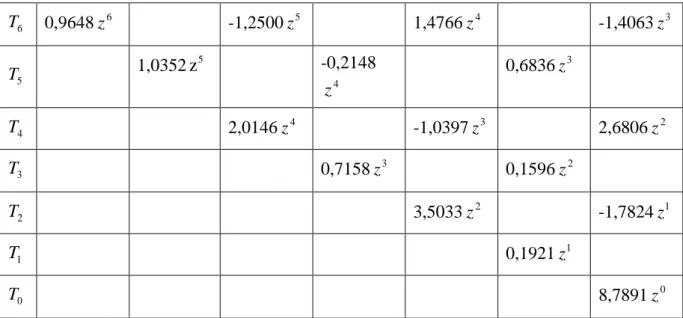
: T_n (n) t0 ) n ( t1 ) n ( t2 … : T_{n 1} (n ) t0 1  (n ) t₁ 1 t(₂n1) … : T_{n 2} (n ) t0 2  (n ) t1 2  _… : T2 ) ( t02 ) ( t₁2 : T₁ t0(1) : T₀ ( ) t00

Şimdi verilen bu iki test arasındaki ilişkiyi inceleyelim. 2.6.a Reel - MJT ile Reel - BT Arasındaki İlişki

Biz reel – MJT de faydalandığımız



F_i(z)



n_i0 ve reel-BT de faydalandığımız





n i i(z)

T _0 dizileri arasındaki ilişkiyi araştıracağız. Sonuç bizim amacımız açısından önemlidir. Reel-BT den elde edilen Schur-Cohn minörleri ve iç determinantları elde edelim.

Denklem (2.2.9) dan n satır ve i=n için

1 1 2 1 2 1     n n n T (z )T F ve 1 ₁ 2 1 2 1   _{  } n n n T (z )T F (2.2.11) denklemine ulaşırız. Böylece;

( ) ( ) ( 1) ( ) ( ) ( 1) 0 0 0 0 ( ) ( ) ( ) ( ) ( ) ( 1) 0 0 0 0 1 1 1 1 , 2 2 2 2 , n n n n n n n n n n n n n n n n a t t a t t a a t a a t            (2.2.12)

elde ederiz. Denklem (2.2.11) i kullanarak ve (2.2.9) numaralı denklemden alınan T in n

121 2  n T z T ) z )( z ( Tn n n    1 1 )) z ( T ) z ( T ) z ( T (_{n n1} 2_{n n1} _{n n1} 1  n T z T T zT ) z ( T_{n n n n n n} n     2 1 1 1 z T ) z ( T ) z ( T_{n n n n} n   ₁ 1 ₁ 2 _    _  2 2  n T z T ) z ( T T ) z ( T_{n n n n n} n   ₁ 1 ₁ 2 1 2 1 2 1 2 _     _  2 2 1  n zT T (z ) t t T T t t n ) n ( ) n ( n n ) n ( ) n ( 1 2 1 2 1 1 1 0 0 1 1 0 0     _{   }           _{ }   _     (n ) n ) n ( ) n ( n n ) n ( ) n ( t ) z ( T t t T T t t 1 0 1 0 1 0 1 1 0 0 1 2 1 2 1 ) n ( ) n ( n ) n ( a a t₀ 1   ₀ ) n ( ) n ( n ) n ( a a t0   0           _{   }   _{  (n )} n ) n ( ) n ( n ) n ( ) n ( n n n ) n ( ) n ( t ) z ( T ) a a ( ) a a ( T T t t 1 0 1 0 0 1 1 0 0 1 2 1 2 1           _{    }  _{ } _{(n )} n ) n ( n ) n ( n ) n ( n n ) n ( n n ) n ( ) n ( t ) z ( T a T a T ) z ( a T a T t t 1 0 1 0 0 1 1 1 0 0 1 2 1 2 1 1 2 1 2 1 ) n ( n n ) n ( n n ) n ( n n ) n ( t )) z ( T T ( a ) T ) z ( T ( a T t 1 0 1 0 1 1 0 1 2 1 2 1 1 2 1 2 1                  _{ }   ) n ( n ) n ( n ) n ( n n ) n ( t )) z ( F a ) z ( F a ( T t 1 0 0 1 0       n_{(n )} n ) n ( t F T t 1 0 1 1 0       _(nn ₎ n n n t F T zT ₁ 0 1 1 2 2 1      2 1 1 0 1 2 1   )  n n  n n ( n zT T t F _

122 2 1 1 0 0 1 0 1 2 1       (n ) n  n ) n ( ) n ( n T zT t t t F 2 1 0 1 0 1 2 1       n ) n ( n ) n ( n t T t zT F z ) z ( T ) z )( z ( T T n n n n      1 1 2  ) z z z ( 12  1 2  n zT 2znTn1(z)zTn1(z)Tn1(z)Tn(z) 2 2 1  n zT z _nT_n (z) z _nT_n (z) T_n (z) T_n(z) 2 1 2 1 2 1 1 1 1          2 2 1  n zT T (z) T (z) T (z) t t z ) z ( T t t z (n ) n n n ) n ( n ) n ( ) n ( 2 1 2 1 2 1 1 1 1 0 0 1 1 0 0     _{    } ) n ( n ) n ( n ) n ( n ) n ( ) n ( t ) z ( T t ) z ( T ) z ( t ) z ( T t t z 1 0 1 0 1 0 1 1 0 0 2 1 1 2 1          ) n ( n n ) n ( n n ) n ( n ) n ( ) n ( t )) z ( F ) z ( F ( t )) z ( F ) z ( F ( t ) z ( T t t z ₁ 0 1 0 0 1 1 0 0 2 1 2 1            ) n ( n ) n ( n ) n ( n ) n ( n ) n ( n ) n ( ) n ( t )) z ( F t ) z ( F t ( ) z ( F t ) z ( F t ) z ( T t zt 1 0 1 0 0 1 0 0 1 1 0 0 2 1 2 1 2 1 2 1             ) n ( ) n ( ) n ( n ) n ( ) n ( n n ) n ( ) n ( t t t ) z ( F t t ) z ( F ) z ( T t zt 1 0 1 0 0 1 0 0 1 1 0 0 2 1 2 1 2 1 2 1           _      _   ) n ( ) n ( n ) n ( n n n ) n ( ) n ( n t a ) z ( F a ) z ( F ) z ( T t zt zT ₁ 0 0 1 1 0 0 2 2 1         2 2 1  n T _{(n )} ) n ( n ) n ( n n n ) n ( ) n ( zt a ) z ( F a ) z ( F ) z ( T t t 1 0 0 1 1 0 0        ) n ( ) n ( n ) n ( n n n ) n ( ) n ( zt a ) z ( F a ) z ( F ) z ( T t t 1 0 0 1 1 0 0        _(nn ₎ n ) n ( ) n ( t F ) z ( T t t 1 0 1 1 1 0 0        ( ) ( ) 1 ( ) 0 ( ) n n n n n n F_ a F z a F z ( ) ( ) 0 1 ( ) ( ) n n n n n n a F z a F z F z      

123 olduğundan, 2 1 1 0 0 1 0 1 2 1       _{ } n n ) n ( ) n ( ) n ( n T ) z ( T t t t ) z ( F 2 1 0 1 0 1 2        n ) n ( n ) n ( n T t T t F

olarak bulunur. Böylece,

2 1 0 1 0 1 2 1       n ) n ( n ) n ( n t T t zT F 2 1 0 1 0 1 2 1        n ) n ( n ) n ( n t T t T F ve katsayılar ( 1) ( ) ( 1) ( 1) ( 2) ( 1) ( ) ( 1) 1 0 0 0 0 0 0 0 ( 1) ( 1) ( ) ( 1) ( 1) ( 2) ( 1) ( 1) ( 1) ( 2) 0 1 0 0 0 0 0 1 0 0 1 . , . 2 1 1 2 , 2 2 n n n n n n n n n n n n n n n n n n n n n a t t t t a t t a a t t t t a a t t                           (2.2.13)

şeklinde elde edilir. Denklem (2.2.11) i kullanarak (2.2.9) dan alınan T_n1 in değiştirilmesiyle;

2 2 ( 1) ( ) ( 2) ( ) ( 1) ( 2) 2 0 0 0 2 0 0 0 3 ( 1) ( ) ( 2) ( ) ( 1) ( 2) 2 0 0 0 2 0 0 0 3 1 1 1 (2 ) . 2 2 2 1 1 1 (2 ) 2 2 2 n n n n n n n n n n n n n n n n n n F t t t T t t t zT F t t t T t t t T                      (2.2.14) ulaşırız. Böylece; ) 3 ( 0 ) 2 ( 0 ) 1 ( 0 ) ( 0 ) 2 ( 2 ) 2 ( 0 ) 3 ( 0 ) 2 ( 0 ) 1 ( 0 ) ( 0 ) 2 ( 0 ) ( 0 ) 2 ( 0 ) 1 ( 0 ) 2 ( 2 ) 2 ( 0 ) 2 ( 0 ) ( 0 ) 2 ( 0 ) 1 ( 0 ) 2 ( 0 ) 3 ( 0 ) 2 ( 0 ) 1 ( 0 ) ( 0 ) 2 ( 0 ) ( 0 ) 2 ( 0 ) 1 ( 0 ) 2 ( 2 2 1 2 1 ) 2 1 2 ( ) 2 1 2 ( 2 1 . . . 2 1 ) 2 1 2 ( 2 1 2 2 2                                       n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n t t t t a a t t t t t t t t a a t t t t a t t t t t t t t a (2.2.15)

124

Teorem 2.6.2 i=n-2, n-3,…,1 için reel-MJT ve reel-BT satırları arasındaki ilişki

1 1        i ) i ( i ) i ( i i ) i ( i ) i ( i T y T x F zT y T x F (2.2.16)

denklemleriyle verilir. Burada

( ) ( ) ( ) ( ) 0 ( ) 0 ( ) ( 1) 0 0 , i i i i i i i i a a a x y t t      ve x(i),y(i)R şeklindedir Sonuç 2.6.1 in2,n3,,2 için _{(i )} ) i ( i ) i ( ) i ( ) i ( ) i ( ) i ( i ) i ( a a a t t a a a 1 0 0 0 2 0 0 1 1 1 0      _   geçerlidir.

Teorem 2.6.3 Reel-MJT ve Reel-BT’nin her satırının katsayıları,

                  _     0 0 1 3 2 2 1 1 1 0 0 1 0 0 2 0 1 0 1 0 0 i ,..., n , n i t. t n i t t t. t a a a (i) (i ) ) n ( ) n ( ) n ( ) n ( ) i ( ) i ( i ) i (

ile birbirine bağlanır ve

               1 2 1 2 1 1 0 0 1 0 1 0 0 ,..., n , n i t. t n i t a a a ) i ( ) i ( ) n ( ) i ( ) i ( i ) i ( bağıntısı geçerlidir.

2.6.b Schur-Cohn Minörleri ve İç Determinantlar

Daha önceki bölümde elde edilen sonuçlarla birlikte, şimdi Schur-Cohn minörlerini ve iç determinantları reel-BT den elde edebiliriz. Önce Schur-Cohn minörleri hakkında bilgi verelim. Aşağıdaki sonuç i; Schur-Cohn minörlerini reel-BT den nasıl elde edilebileceğini göstermektedir. Teorem 2.6.4 _i (t(n i )t(n i)[ _i t(n i )t(n ) _i ] i 1,2,...,n 2 1 2 2 1 2 1 0 1 0 1 0 1 0         _     _bağıntsı

125 Teorem 2.6.5           _       ,.. , i . t ,.. , i t i ) i n ( i ) i n ( i 4 2 2 1 3 1 1 0 1 0

ile hesaplanır. Burada    _{i i} _i,i1, 2,...,n ve ₀ 1 dir.

2.7 Hu’nun Modifiye Edilmiş Tablosu Yardımıyla Kararlılık Testi

Hu’nun tablosunu oluştururken MJT tablosuna ihtiyaç vardır. Bu yüzden MJT yi tekrar gözden geçirelim. n. mertebeden verilen bir skaler denklemin karakteristik polinomu;

n nz d z d d ) z (

D  0 1  şeklinde tanımlansın. Burada, dj, j1,2,,n reel ve n sistemin mertebesidir. MJT deki polinomlar ve katsayıları için daha önce kullandığımız F ve f harfleri yerine D ve d harflerini kullanacağız. MJT Tablo 2.5 de verildiği gibidir [3].

Tablo 2.5. MJT Satır D_i(z) 0 z z 1 z 2  zn2 zn1 z n 0 D₀(z) d_0,0 d_0,1 d_0,2  d0,n2 d0,n1 d0,n 1 D₁(z) d1,0 d 1,1 d1,2  d1,n2 d1,n1 2 D₂(z) d2,0 d2,1 d2,2  d2,n2       n-1 D_{n 1} (z) d_n1,0 d_n1,1 N D_n(z) d_n,0

MJT formunun bir polinom dizisi,



D(z)



_in_0 



D₀(z)D₁(z)D_n(z)



olmak üzere;

)) ( ) ( ( 1 ) ( ,0 , * 1 1 d D z d D z P z D i i in i i i i      ile n n n * z d z d d ) z ( D ) z ( D0    1  0 ve       1 0 1 1 , i i d P , -1 0 , diğer durumlarda i 

126

alalım. Şimdi modifiye edilmiş bir Hu Tablosu (MHT) elde edeceğiz, öyle ki





n i i(z)

H _0 ile gösterilen simetrik polinom dizisi MJT’de kullanılan





n

i i(z)

D _0 dizisiyle, basit bir ilişki içindedir. Yani; H_i(z)D_i(z)D_i*(z), i0,1,,n olmak üzere

)) z ( D d ) z ( D d ( P ) z ( D i,n i i i, i* i * i 0 1 1 1    _   denklemini takiple; * * 1( 1( ) 1( )) ( ,0 , ) ( ) ( ,0 , ) ( ) i i i i i n i i i i n i i zP_ D_ z D_ z  zd d _ D z  d zd _ D z

yazılabilir. Sağ taraftaki işlemlere devam edilirse; zd D z_{i,0 i}( )d_{i n i, }D z_i( )d D z_{i,0 i}*( )zd_{i n i, }D z_i*( ) ) z ( D d ) z ( D d ) z ( D zd ) z ( D zd i, i i, i * i , i * i , i0  0  0  0  )) z ( D ) z ( D ( d )) z ( D ) z ( D ( zd i, i i* * i i , i     0 0 (d_i,ni d_i,0)D_i(z)z(d_i,nid_i,0)D_i*(z) ) z ( D ) d d ( z ) z ( D ) d d ( )) z ( D ) z ( D ( d ) z (1 _{i,0 i}  _i*  _{i,n i} _{i,0 i}  _i,ni  _{i,0 i}*    A(D(z) D (z)) BD(z) CD*(z) i i * i i     (2.2.16) elde edilir. Burada A(1z)d_i,0, B(di,nidi,0), Cz(di,ni di,0 ) alınmıştır.

) z ( CD ) z ( BDi  i*         _{    }  )) z ( D d ) z ( D d ( P B _{i , i i ,n i i}* i 1 1 1 1 0 1 2 1          _{    }   )) z ( D d ) z ( D d ( P z C * i , i i i n , i i 1 0 1 1 1 1 2 1 ) z ( CD ) z ( BD_i  _i*



(Bd z Cd )D (z) ( Bd z Cd )



P_i i , i , i i ,n i i1,0 1 1 1 1 0 1 1 0 1 2 1               

ve C zBbağıntıları elde edilir. Denklem (2.2.16) ve son eşitlikten; )) z ( D ) z ( D ( zP_{i1 i1}  _i*_1 A(D_i(z)D_i*(z))B(D_i(z)zD_i*(z)) + (d d )(D (z) D (z)) P B * i i i n , i , i i 1 1 1 1 0 1 2          (2.2.17)

eşitliğine ulaşırız. D_i(z) ve D_i*(z) nın katsayıları kullanılarak;

i n , i , i d zd B A  ₀ _

127 i n i i zd d zB A  _,0 _, veya i , i ( z) d ) z ( A 1 ₀ 1  0 0 i, , i i n , i d ) h d ( B _  

yazabiliriz ve Czh_i,0 olarak buluruz. (2.2.17) numaralı denklemdeki A, B ve C değerleri yerine konulursa ve Hi(z)Di(z)Di*(z) kullanılırsa;



( z ) H (z) z H (z)



P ) z ( H i i i i i i 1 1 1 1 1 1 1           (2.2.18) bulunur. Burada; 0 1 0 1, i i, i i h q d  1 0 0 2    _  _{i i, i, i,n} i h d d q  1 0 2 1 1 0 1 2 1            i, i i i n , i , i i i h q P ) d d ( P B  (2.2.19)

şeklindedir. Hu’nun Tablosu (HT) ile karşılaştırıldığında, Modifiye Edilmiş Hu Tablosunun (MHT) oluşturulma prosedüründe iki tane modifikasyon vardır.

(i) Denklem (2.2.18) de verilen her polinom dizisi P_i1 e bölünür.

(ii) Denklem (2.2.19) deki _i faktörü P ye bölünür. _i2

Aşağıdaki teorem denklem (2.2.18) ile MJT de kullanılan denklem arasındaki ilişkiyi tanımlar.

Teorem 2.7.1. MJT de kullanılan denklem (2.2.18) deki



H_i(z)



n_i0 dizisi ve denklem





n i i(z)

D _0 dizisi arasındaki ilişki bize;

) z ( D ) z ( D ) z ( Hi  i  i* i0,1,,n (2.2.20) verir. Teorem 2.7.1 in ispatı yukarıda elde edilen bulgular sayesinde çok açıktır.





n i i(z)

H _0 dizisini oluştururken yukarıdaki prosedür kolaylıkla tablo tekniği kullanılarak uygulanabilir. MHT ve HT aynı forma sahiptir ve bu Tablo 2.6 da verilmiştir.

128

Tablo 2.6. Hu’nun Modifiye Edilmiş Tablosu

Satır 0 z z 1  _zmk _zmk1  _zm0 0 h0,0 h 0,1  h0,m_k h0,mk₁  h0 m, 0 1 h 1,0 h 1,1  h1,mk h1,mk1          * k hk,0 hk,1  hk,mk (hk,mk1) k+1 hk1,0 hk1,1  hk1,mk1     n-3 hn3,0 hn3,1  n-2 hn2,0 hn2,1 n-1 hn1,0 (hn1,1) N hn,0

Tablo 2.6 nın ilk sırasındaki elemanlar H₀(z)D₀(z)D₀*(z) katsayılarıdır. Katsayılara göre bu terimler h0,j djdn j , j0,1,...,m0 şekilde yazılabilir. İkinci sıra,

birinci satır elemanları H1(z)D1(z)D1*(z) katsayılarıdır. O halde,

H₁(z)D₁(z)D₁*(z)

(d_0,0D₀(z)d_0,nD*₀(z))z1(d_0,0D₀*(z)d_0,nD₀(z))

d_0,0(D₀(z)z1D*₀(z))d_0,n(z1D₀(z)D₀*(z))

olarak elde edilir. Burada katsayılar h_1,j d_0,0(d_0,jd_{0,n j 1})d_0n(d_0,j1d_{0,n j} ),

1

0,1,...,

j m şeklindedir. Daha sonraki sırada bulunan elemanlar

1 , , 1 1, 1 1 1 , ( ( ) ) i i i j i j i i j i h j h h h P       

   ,i1, 2,..., ,n j0,1,...,m_i bağıntısına bağlı olarak (2.2.18) numaralı denklem kullanılarak hesaplanabilir. n-i’nin tek olduğu satırlar için

1

, i , i,

i m i m

h _ h n i tek , i=1,2,…,n-1 ve _i,q_i ve _i faktörleri (2.2.19) denklemlerinde verilmiştir ve i. satırdaki m sayısı i