Mustafa Emin GÜRLEK
Dumlupınar Üniversitesi
Lisansüstü Eğitim Öğretim ve Sınav Yönetmeliği Uyarınca Fen Bilimleri Enstitüsü İnşaat Mühendisliği Anabilim Dalında
YÜKSEK LİSANS TEZİ Olarak Hazırlanmıştır.
Danışman: Dr. Öğr. Üyesi Mustafa Halûk SARAÇOĞLU
Mustafa Emin GÜRLEK’ in YÜKSEK LİSANS tezi olarak hazırladığı Tabakalı Kompozit Kirişlerin Sonlu Farklar Metodu İle Analizi başlıklı bu çalışma, jürimizce Dumlupınar Üniversitesi Lisansüstü Eğitim Öğretim ve Sınav Yönetmeliğinin ilgili maddeleri uyarınca değerlendirilerek kabul edilmiştir.
11/05/2018 Prof. Dr. Önder UYSAL
Enstitü Müdürü, Fen Bilimleri Enstitüsü ……….
Dr. Öğr. Üye. Nuran BAĞIRGAN
Bölüm Başkanı, İnşaat Mühendisliği Bölümü ………. Dr. Öğr. Üye. Mustafa Halûk SARAÇOĞLU
Danışman, İnşaat Mühendisliği Bölümü ...…………...
Sınav Komitesi Üyeleri
Dr. Öğr. Üye. Mustafa Halûk SARAÇOĞLU
İnşaat Mühendisliği Bölümü, Dumlupınar Üniversitesi ……….
Dr. Öğr. Üye. Burak KAYMAK
İnşaat Mühendisliği Bölümü, Dumlupınar Üniversitesi ……….
Dr. Öğr. Üye. Uğur ALBAYRAK
Bu tezin hazırlanmasında Akademik kurallara riayet ettiğimizi, özgün bir çalışma olduğunu ve yapılan tez çalışmasının bilimsel etik ilke ve kurallara uygun olduğunu, çalışma kapsamında teze ait olmayan veriler için kaynak gösterildiğini ve kaynaklar dizininde belirtildiğini, Yüksek Öğretim Kurulu tarafından kullanılmak üzere önerilen ve Dumlupınar Üniversitesi tarafından kullanılan İntihal Programı ile tarandığını ve benzerlik oranının % 8 çıktığını beyan ederiz. Aykırı bir durum ortaya çıktığı takdirde tüm hukuki sonuçlara razı olduğumuzu taahhüt ederiz.
TABAKALI KOMPOZİT KİRİŞLERİN SONLU FARKLAR METODU İLE ANALİZİ Mustafa Emin GÜRLEK
İnşaat Mühendisliği, Yüksek Lisans Tezi, 2018 Tez Danışmanı: Dr. Öğr. Üyesi Mustafa Halûk SARAÇOĞLU
ÖZET
Bu çalışmada; tabakalı kompozit kirişlerin gerilme ve şekil değiştirme analizleri sonlu farklar yöntemi kullanılarak yapılmıştır. Analizlerde farklı mesnet koşulları ve farklı yüklemeler etkisi altındaki kirişler, Euler-Bernoulli ve Timoshenko kiriş teorilerine göre incelenmiştir. İncelenen bu kirişler farklı tabaka sayıları ve farklı oryantasyon açılarına sahiptirler. Tabakalı kompozit kirişler, düzlem gerilme problemi olarak ele alınmıştır. Gerilme ve şekil değiştirme analizleri yapılırken ilgili bünye bağıntıları ve denge denklemleri için bazı kabuller yapılmıştır. Üç boyutlu doğrusal olmayan şekil değiştirme ifadeleri, iki boyutlu ve doğrusal şekil değiştirme ifadelerine indirgenmiştir. Bu diferansiyel denklemlerin çözümü için merkezi sonlu fark ifadeleri kullanılmıştır. Her sonlu fark düğüm noktası için merkezi sonlu fark ifadesi yazılmıştır. Daha sonra bu ifadeler sınır şartlarına göre tekrar düzenlenmiştir. Elde edilen bünye bağıntıları ve denge denklemlerinin çözümü için açık kaynak kodlu olan DEV-C++ V 5.8.3 editörü kullanılarak bir bilgisayar programı geliştirilmiştir. Geliştirilen bu program kullanılarak sayısal uygulamalar yapılmıştır. Literatürde bulunan örnek problemler çözülerek geliştirilen bilgisayar programının doğruluğu test edilmiştir.
Sonuç olarak tabaka dizilişleri ve sınır şartları farklı tabakalı kompozit kirişlerin yük altındaki gerilme ve şekil değiştirme davranışları ortaya konulmuştur. Elde edilen sonuçlar tablo ve grafiklerle sunulmuştur.
Anahtar Kelimeler: Gerilme, Oryantasyon Açısı, Sonlu Farklar Metodu, Şekil Değiştirme, Tabakalı Kompozit Kiriş,
ANALYSIS OF LAMINATED COMPOSITE BEAMS BY FINITE DIFFERENCE METHOD
Mustafa Emin GÜRLEK Civil Engineering, M.S. Thesis, 2018
Thesis Advisor: Assist. Prof. Dr. Mustafa Halûk SARAÇOĞLU
SUMMARY
In this study; stress and displacement analysis of laminated composite beams were performed using finite difference method. In the analyzes, different support conditions and beams under different loading conditions were investigated according to Euler-Bernoulli and Timoshenko beam theories. These examined beams have different lamination scheme and different orientation angles. Laminated composite beams are considered as plane stress problem. When stress and strain analyzes were carried out, some assumptions were made for related constitutive and equilibrium equations. The three-dimensional non-linear strain expressions were reduced to two-dimensional and linear strain expressions. The central finite difference relations were used to solve these differential equations. For each finite difference node a centered finite difference statement was written. These expressions were then rearranged according to the boundary conditions. A computer program has been developed using the open-source DEV-C++ V 5.8.3 editor for solving the obtained constitutive and equilibrium equations. Numerical applications were performed using this developed program. The sample problems in the literature have been solved and the accuracy of the developed computer program has been tested.
As a result, stress and displacement behavior of laminated composite beams under loads which has different boundary conditions , lamination scheme and orientation angle were presented. The results were presented in tables and graphs.
Keywords: Finite Difference Method, Laminated composite beams, Orientation Angle, Strain, Stress,
TEŞEKKÜR
Yüksek lisans eğitimim süresince tüm bilgi ve tecrübelerini esirgemeden paylaşan ve başarıya ulaşmam için her daim desteklerini üzerimde hissettiren değerli hocam Dr. Öğr. Üyesi Mustafa Halûk SARAÇOĞLU’ na sevgi ve saygı ile teşekkür ederim.
Ayrıca çalışmalarım boyunca maddi ve manevi desteklerini esirgemeyen sevgili eşim ve aileme teşekkür ederim.
İÇİNDEKİLER Sayfa ÖZET ……… v SUMMARY ………... vi ŞEKİLLER DİZİNİ ……….. x ÇİZELGELER DİZİNİ ………. xiii SİMGELER VE KISALTMALAR DİZİNİ ……….. xv 1. GİRİŞ ……….... 1 1.1. Literatür Araştırması ………... 3
2. TABAKALI KOMPOZİT KİRİŞLERİN ANALİZİ ……… 7
2.1. Yer Değiştirme ve Şekil Değiştirmeler ………. 11
2.2. Tabaka Bünye Bağıntıları ……….. 15
2.3. Euler-Bernoulli Kiriş Teorisi ……… 17
2.3.1. Euler-Bernoulli kiriş teorisi için denge denklemleri ……… 18
2.3.2. Euler-Bernoulli kiriş teorisi için eğilme ………... 21
2.3.3. Euler-Bernoulli kiriş teorisi için gerilme ……….. 22
2.4. Timoshenko Kiriş Teorisi ………... 23
2.4.1. Timoshenko kiriş teorisi için denge denklemleri ………... 23
2.4.2. Timoshenko kiriş teorisi için eğilme ……… 26
2.4.3. Timoshenko kiriş teorisi için gerilme ……….. 26
3. SONLU FARKLAR YÖNTEMİ İLE KİRİŞ ANALİZİ ……… 27
3.1. Sonlu Farklar Yönteminin Kiriş Denklemine Uygulanması ………... 29
3.1.1. Sabit veya hareketli mesnet ………... 31
3.1.2. Ankastre mesnet ………... 32
İÇİNDEKİLER(devam)
Sayfa
4. GELİŞTİRİLEN BİLGİSAYAR PROGRAMI ……… 37
4.1. Verilerin Kullanıcıdan Alınması ……… 37
4.2. Analizlerin Yapılması ……… 38
4.3. Elde Edilen Sonuçların Dosyaya Yazdırılması ………... 40
4.4. Geliştirilen Programın Bir Örnek Üzerinde Anlatılması ………... 40
4.5. Akış Diyagramı ………... 45
5. ÖRNEKLER ………. 47
5.1. Rijitliklerle İlgili Örnekler ………... 47
5.2. Euler-Bernoulli Kiriş Teorisi İle İlgili Örnekler ………. 50
5.3. Timoshenko Kiriş Teorisi İle İlgili Örnekler ………... 64
6. SONUÇ VE ÖNERİLER ……….. 71
7. KAYNAKLAR DİZİNİ ……… 75 8. ÖZGEÇMİŞ
ŞEKİLLER DİZİNİ
Şekil Sayfa
1.1. Kompozit malzemelerin sınıflandırılması. ……….. 1
1.2. Yayılı yükle yüklenmiş basit kiriş. ……….. 2
1.3. Yayılı yükle yüklenmiş ve bağlanmamış iki tabakalı basit kiriş. ……… 2
1.4. Yayılı yükle yüklenmiş ve bağlanmış iki tabakalı basit kiriş. ………... 3
2.1. Liflerle güçlendirilmiş tek yönlü tabaka. ………... 7
2.2. Oryantasyon açısı. ………... 7
2.3. Farklı lif oryantasyonlarına sahip tabakalardan oluşan kiriş kesiti. ………. 8
2.4. Düşey yükle yüklenmiş kiriş için teorilere göre yer değiştirmeler. ……… 9
2.5. Tabakalı kompozit kiriş için kullanılan koordinat sistemi ve ………... 11
tabaka numaraları. 2.6. Yapılan kabullere göre kiriş parçasının şekil değiştirmemiş ve şekil ………... 12
değiştirmiş geometrisi. 2.7. Tabakalar arası gerilme ve şekil değiştirme değişimleri. ………... 14
2.8. Bir kiriş elemanındaki kuvvet ve moment bileşenleri. ……… 18
2.9. Tabakalı kirişin geometrisi ve atalet momenti. ………... 21
3.1. Tabakalı kompozit kirişin sonlu fark ağı . ………... 28
3.2. Sonlu fark ağı oluşturulmuş kiriş. ………... 30
3.3. Sabit veya hareketli mesnet düğüm noktası. ………... 31
3.4. Ankastre mesnet düğüm noktası. ……… 32
3.5 Serbest uç düğüm noktası. ………... 33
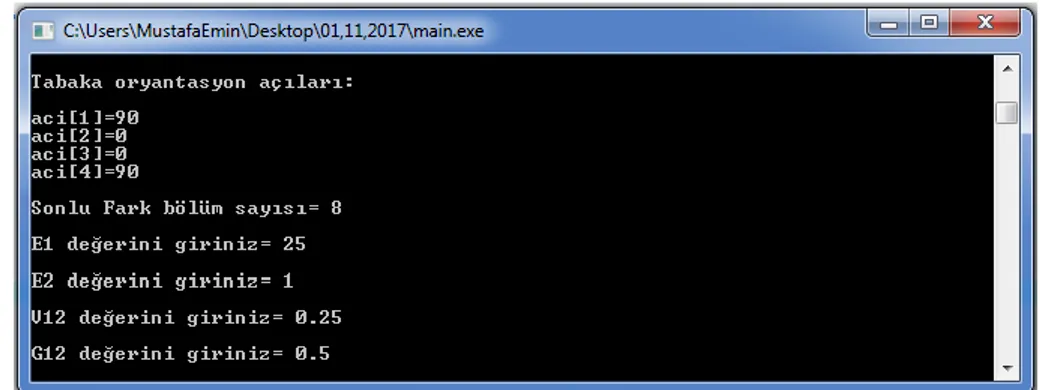
4.1. Geliştirilen programın giriş ekranı. ………... 37
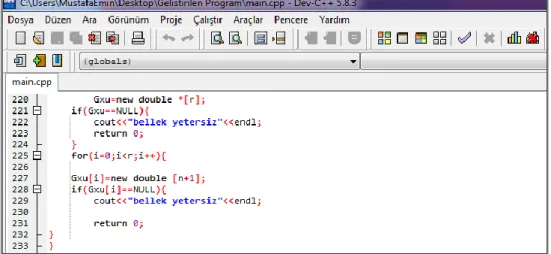
4.2. Programda gerilmeler için yer ayırma işleminden oluşan bir bölüm. ………... 38
4.3. İki ucu basit mesnetli tabakalı kompozit kiriş. ……….... 40
4.4. Örneğe ait kirişin boyutları, tabaka sayısı ve koordinatları. ………... 41
ŞEKİLLER DİZİNİ (devam)
Şekil Sayfa
4.6. Örneğe ait kirişe etki eden yük ve sınır şartı seçimi. ………... 42
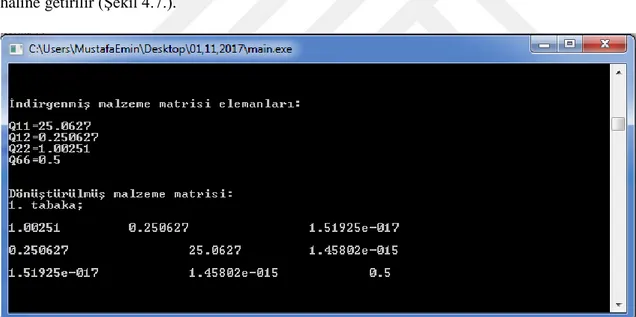
4.7. Kirişe ait indirgenmiş ve dönüştürülmüş indirgenmiş malzeme ………. 42
matris elemanları. 4.8. Kirişe ait eğilme katılık matrisi ve dönüştürülmüş eğilme katılık ……….. 43
matris elemanları. 4.9. A katsayı matrisi ve sonlu fark düğüm noktalarındaki çökme değerleri. ……….... 43
4.10. B katsayı matrisi ve sonlu fark düğüm noktalarındaki moment değerleri. ………. 44
4.11. Kirişin sonlu fark düğüm noktalarındaki gerilme değerleri. ……….. 44
4.12. Geliştirilen bilgisayar programına ait akış diyagramı. ……….... 45
5.1. Karbon/epoksi malzemesinden oluşan simetrik çapraz tabaka ( 00/900 )s. …... 48
5.2. Bor/epoksi malzemesinden oluşan simetrik tabakalı ……….. 49
kompozit kiriş ( 300 /00/900/-450 )s. 5.3. Simetrik tek tabakalı kompozit kiriş ( 00 )s. ……… 50
5.4. Simetrik tek tabakalı ( 00 )s kirişin orta nokta çökme değerleri. ……….. 51
5.5. Simetrik tabakalı kompozit kiriş ( 00/450/-450/900 )s. ……….. 52
5.6. İki ucu basit mesnetli simetrik tabakalı kompozit ………... 52
kirişin ( 00 /450/-450/900 )s eğilme momenti değerleri. 5.7. İki ucu basit mesnetli simetrik tabakalı kompozit kirişin ……… 53
x=50 düğüm noktasındaki gerilme değerleri. 5.8. İki ucu basit mesnetli simetrik tabakalı kompozit kirişin ………... 54
x=10 düğüm noktasındaki gerilme değerleri. 5.9. İki ucu basit mesnetli simetrik tabakalı kompozit kirişin ……….... 55
x=80 düğüm noktasındaki gerilme değerleri. 5.10. İki ucu ankastre mesnetli kompozit tabakalı kiriş. ………... 56
5.11. Bir ucu ankastre diğer ucu serbest kompozit tabakalı kiriş. ………... 57
5.12. Beş tabakadan oluşturulmuş simetrik kompozit tabakalı kiriş. ……….... 58
5.13. Simetrik tek tabakalı ( 00 )s ve çapraz tabakalı ( 00 /900 )s kompozit ………... 60 kirişlerin E1/E2 oranına bağlı olarak orta noktasındaki boyutsuzlaştırılmış
ŞEKİLLER DİZİNİ (devam)
Şekil Sayfa
5.14. Simetrik tek tabakalı ( 00 )s kompozit kirişin oryantasyon açısına bağlı ……... 61 olarak orta nokta boyutsuz çökme değerlerinin eğrisel değişimi.
5.15. Üzerinde tekil yük bulunan iki ucu basit mesnetli kompozit tabakalı kiriş. ……. 62 5.16. Üzerinde tekil yük bulunan simetrik tabakalı kompozit ………. 63
kiriş ( 00
/450/-450/900 )s.
5.17. Üzerinde tekil yük bulunan simetrik tabakalı ( 00/450/-450/900 )s ………... 63 kompozit kirişin gerilme grafiği.
5.18. İki ucu basit mesnetli kompozit tabakalı kiriş. ……….... 64 5.19. İki ucu ankastre mesnetli kompozit tabakalı kirişin a/h oranına göre ………. 66
boyutsuz çökme değerleri.
5.20. Üç eşit tabakadan oluşmuş iki ucu basit mesnetli kompozit tabakalı kiriş. ………. 66 5.21. Üzerinde tekil yük bulunan iki ucu ankastre mesnetli kompozit ……….. 68
tabakalı kiriş.
ÇİZELGELER DİZİNİ
Çizelge Sayfa
5.1. Karbon/epoksiye ait malzeme özellikleri. ………... 47 5.2. Karbon/epoksi malzemesine ait malzeme matris elemanları ( 00/900 )s. …………. 48 5.3. Bor/epoksiye ait malzeme özellikleri. ………. 49 5.4. Bor/epoksi malzemesine ait eğilme katılık matrisi D ve uzama ………... 50 ij
katılık matrisi A ( 30ij 0/00/900/-450 )s.
5.5. Simetrik tek tabakalı kompozit kirişe ( 00 )s ait malzeme ve kesit özellikleri. …… 51 5.6. Simetrik tabakalı kompozit kirişe ( 00/450/-450/900 )s ait ………. 51
malzeme ve kesit özellikleri.
5.7. İki ucu ankastre mesnetli kirişe ait malzeme ve kesit özellikleri. ……… 56 5.8. İki ucu ankastre mesnetli, farklı tabaka sayısı ve oryantasyon açılarına …………. 56
sahip kompozit tabakalı kirişin orta nokta boyutsuz çökme değerleri.
5.9. Bir ucu ankastre diğer ucu serbest kompozit tabakalı kirişin, farklı tabaka …... 58 sayısı ve oryantasyon açılarına göre uç nokta boyutsuz çökme değerleri.
5.10. Beş tabakadan oluşturulmuş simetrik konsol kirişe ait malzeme ………. 58 ve kesit özellikleri.
5.11. Simetrik ve farklı oryantasyon açılarına sahip kompozit tabakalı …………... 59 konsol kirişin uç nokta çökme değerleri.
5.12. Simetrik tek tabakalı ( 00 )s ve çapraz tabakalı ( 00 /900 )s kompozit ………... 59 kirişlerin E1/E2 oranına bağlı olarak orta noktasındaki boyutsuzlaştırılmış
çökme değerleri.
5.13. Simetrik tek tabakalı ( 00 ) kompozit kirişin oryantasyon açısına ……… 60 bağlı olarak orta noktasındaki boyutsuzlaştırılmış çökme değerleri.
5.14. Üzerinde tekil yük bulunan iki ucu basit mesnetli kompozit tabakalı kirişe ……… 61 ait malzeme ve kesit özellikleri.
5.15. Üzerinde tekil yük bulunan iki ucu basit mesnetli kompozit tabakalı kirişlerin ... 62 orta nokta boyutsuz çökme değerleri.
5.16. Simetrik tabakalı kompozit kirişe ( 00/450/-450/900 )s ait malzeme ve …………... 63 kesit özellikleri.
ÇİZELGELER DİZİNİ(devam)
Çizelge Sayfa
5.18. İki ucu basit mesnetli, farklı tabaka sayısı ve oryantasyon açılarına sahip ……... 65 kompozit tabakalı kirişin Timoshenko kiriş teorisine göre orta nokta
boyutsuz çökme değerleri.
5.19. İki ucu ankastre mesnetli, farklı tabaka sayısı ve oryantasyon açılarına …………. 65 sahip kompozit tabakalı kirişin Timoshenko kiriş teorisine göre orta nokta
boyutsuz çökme değerleri.
5.20. Üç eşit tabakadan oluşan tabakalı kompozit kirişe ait malzeme ve ………. 66 kesit özellikleri.
5.21. İki ucu basit mesnetli, farklı elastisite oranları ve a/h oranlarına sahip ……... 67 kompozit tabakalı kirişin Timoshenko kiriş teorisine göre orta nokta
boyutsuz çökme değerleri.
5.22. Üzerinde tekil yük bulunan iki ucu basit mesnetli kompozit tabakalı ……… 67 kirişlerin a/h oranlarına göre orta nokta boyutsuz çökme değerleri.
5.23. Üzerinde tekil yük bulunan iki ucu ankastre mesnetli kompozit tabakalı ………... 68 kirişlerin a/h oranlarına göre orta nokta boyutsuz çökme değerleri.
SİMGELER VE KISALTMALAR DİZİNİ
Simgeler Açıklama
a Kirişin x yönündeki boyutu b Kirişin y yönündeki boyutu h Kiriş kalınlığı
k Tabaka numarası
K Kayma düzeltme katsayısı N Toplam tabaka sayısı
q Kirişe z ekseninde etkiyen düzgün yayılı yük F Kirişe z ekseninde etkiyen tekil yük
( x1,x2,x3 ) Malzeme eksen takımı ( x,y,z ) Global eksen takımı
Oryantasyon açısı
0, ,0 0
u v w Kirişin yük etkisinde orta düzlem yer değiştirmeleri ,
x y
Eksenel dönme
Ei Elastisite modülü yy
I Kirişin h kalınlığındaki atalet momenti b
xz
G Eşdeğer kayma modülü b
xx
E Eşdeğer elastisite modülü Gij Kayma modülü
ij Şekil değiştirme ij Gerilme ij v Poisson oranı x
SİMGELER VE KISALTMALAR DİZİNİ(devam)
Simgeler Açıklama Mij Eğilme momenti Q(x,y) Kesme kuvveti
( )k ij
Q Her tabaka için indirgenmiş malzeme matris elemanları ( )k
ij
Q Her tabaka için dönüştürülmüş indirgenmiş malzeme matris elemanları
ij
D Eğilme katılık matrisi elemanları *
ij
D Dönüştürülmüş eğilme katılık matrisi elemanları
ij
A Uzama katılık matris elemanları *
ij
A Dönüştürülmüş uzama katılık matris elemanları
x Doğrusal denklem takımında bilinmeyenler için oluşturulan vektör
b Doğrusal denklem takımında bilinenler için oluşturulan karşı taraf vektörü
A ,
B Doğrusal denklem takımı katsayı matrisi Zi Düğüm noktası , d Türev simgesi1. GİRİŞ
Kompozit malzeme, iki veya daha fazla malzemenin makro seviyede birbiri içerisinde çözünmeyecek şekilde birleştirilmesiyle oluşturulan yeni malzemelerdir. Kompozit malzemeler bor, cam ve grafit gibi yüksek dayanımlı ince liflerin epoksi, reçine gibi bağlayıcı bir matris malzeme içine yerleştirilmesi ile değişik üretim yöntemleri kullanılarak elde edilirler.
Kompozitin bileşenleri kimyasal olarak birbirlerini etkilemezler. Eğer malzemeler birbiri içerisinde çözünürse ve atom seviyesinde bir karışım söz konusu olursa, bu tür malzemeler kompozit değil alaşım olur.
Kompozitler, genel olarak matris ismi verilen bir ana malzeme ve takviye elemanı ismi verilen daha mukavim bir malzemeden oluşturulur. Bu iki malzeme grubundan, takviye malzemesi kompozit malzemenin mukavemet ve yük taşıma özelliğini, matris malzeme ise plastik deformasyona geçişte oluşabilecek çatlak ilerlemelerini önleyici rol oynamakta ve kompozit malzemenin kopmasını geciktirmektedir.
Kompozit malzeme üretiminde genel olarak mekanik dayanım, yorulma dayanımı, aşınma dayanımı, rijitlik, hafiflik, elektrik iletkenlik, ısıl iletkenlik, akustik, kırılma tokluğu, ekonomik olmaları, estetiklik gibi özelliklerin geliştirilmesi amaçlanmaktadır (Jones, 1999:2).
Günümüzde kompozit malzemeler inşaat ve yapı sektörü, uzay teknolojisi, denizcilik sektörü, robot teknolojisi, otomotiv, savunma sanayi, spor malzemeleri gibi neredeyse artık her alanda kullanılmaktadır.
Kompozit malzemelerin sınıflandırılması oldukça zordur. Malzemedeki takviye elemanlarının şekil ve yerleştirilmesine göre yaygın olarak kullanılan sınıflandırılması aşağıdaki (Şekil 1.1.)’ de verilmektedir (http://kisi.deu.edu.tr/mehmet.zor/).
Şekil 1.1. Kompozit malzemelerin sınıflandırılması. A) Elyaflı Kompozitler B) Parçacıklı Kompozitler
Bu çalışmada da en eski ve en yaygın kullanım alanına sahip olan tabakalı kompozitler kullanılmıştır.
Liflerle güçlendirilmiş kompozit malzemeler tabaka denilen ince katmanlardan oluşurlar. Kullanılan malzemede en büyük eğilme rijitliğine ulaşmak için iki veya daha fazla tabaka bir araya getirilerek tabakalı yapılar oluşturulur.
(Şekil.1.2.)’ de görülen genişliği b yüksekliği h uzunluğu a olan ve üzerinde q yayılı yükü ile yüklenmiş elastisite modülü E olan bir basit kirişin orta noktasındaki çökme değeri
4 0
5 q a
w =
384 E I
ile hesaplanabilir. Burada I kiriş kesitinin ağırlık merkezinden geçen yatay eksene göre atalet momentidir.a b h q 4 4 0 3 3 5 q a 5 q a = = 12 b h E b h E 12 384 384 w 3 b h I= 12
Şekil 1.2. Yayılı yükle yüklenmiş basit kiriş.
Genişliği b yüksekliği h uzunluğu a elastisite modülü E olan iki adet kirişe q yayılı yükü yüklenirse bu durumda basit kirişin orta noktasındaki çökme değeri 2 kat azalacaktır (Şekil 1.3).
a b h h q 3 b h I= 6 4 3 0 3 3 5 q a 5 q a = = 6 b h 384 384 E b h E 6 w
Bu iki kiriş çivi, vida, yapıştırıcı gibi malzemelerle birbirlerine kusursuzca bağlandıklarında kiriş kesitinin yüksekliği 2h olacak ve orta nokta çökme değeri 8 kat azalacaktır (Şekil 1.4.). a b h h 4 4 0 3 3 5 q a 5 q a = = 1.5 384 2b h 384 E b h E 3 w q 3 3 b (2h) 2bh I= 3 12
Şekil 1.4. Yayılı yükle yüklenmiş ve bağlanmış iki tabakalı basit kiriş.
Bu örneklerden de anlaşılacağı gibi tabakalar bir araya getirilerek kusursuzca bağlandıklarında eğilme rijitliğinde büyük bir artış olacaktır.
1.1. Literatür Araştırması
Kompozit malzemelerin son yıllarda yapı ve inşaat alanlarında kullanımının hızlı bir şekilde arttığı gözlemlenmektedir. Kompozit malzemelerden oluşan yapı elemanlarından bir tanesi de tabakalı kompozit kirişlerdir. Tabakalı kompozit kirişlerin yapısal davranışları ve karakteristik özellikleri ele alındığında statik ve dinamik yükler altında gösterecekleri davranışların çok iyi bilinmesi gerekir. Çünkü göstermiş oldukları bu davranışların yapı için avantaj veya dezavantajları tercih sebebi olacaktır. Bu sebeple tabakalı kompozit kirişlerin analizi ile ilgili günümüze kadar bir takım teoriler ve sayısal çözüm yöntemleri geliştirilmiştir.
Bu çalışmalarda genel olarak şekil değiştirme, eğilme, burkulma ve titreşim analizleri ele alınmıştır. Yapılan analizlerde genel olarak iki teori üzerinde durulmuştur. Bunlardan ilki Euler-Bernoulli Kiriş teorisi diğeri ise Timoshenko Kiriş teorisidir. Timoshenko Kiriş teorisinin Euler-Bernoulli Kiriş teorisinden farkı, analizlerde kesme kuvvetinin de etkilerini dikkate almasıdır. Ayrıca bu iki teoriden başka daha karışık olan Yüksek Mertebe Kiriş teorileri de analizlerde kullanılmıştır. Yapılan literatür çalışmalarında tabaklı kompozit kirişlerle ilgili en temel kaynaklar arasında (Wang vd., 2000; Reddy, 2004; Carrera vd., 2011) bulunmaktadır.
(Dökmeci, 1973) Elastik tabakalı kompozit kirişlerin gerilme ve şekil değiştirme analizleri için termo-elastodinamiğin üç boyutlu teorisini kullanmıştır. İncelediği kirişlerde her bir tabaka farklı kalınlıkta ve farklı anizotrop malzemeden oluşmuştur.
(Khdeir ve Reddy, 1997) İnce ve kalın çapraz tabakalı kompozit kirişlerin eğilme analizini yapmışlardır. Euler-Bernoulli, Timoshenko ve yüksek mertebeden kiriş teorileriyle farklı sınır şartları ve farklı yüklemeler altındaki simetrik ve anti simetrik çapraz tabakalı kirişler için çözümler yapmışlardır. Buna ek olarak tabaka sayısı, kayma deformasyonu ve elastisite modülleri arasındaki oranın, kirişin şekil değişikliğine olan etkisini incelemişlerdir.
(Loja ve Barbosa, 2001) Anizotrop çok katmanlı kalın ve ince kirişlerin statik ve dinamik davranışlarını incelemişlerdir. Bu çalışmada yer değiştirmenin doğrusal olmadığı kabul edilerek, sonlu elemanlar modelini geliştirmek için yüksek mertebeden kayma deformasyon teorisini kullanmışlardır. Geliştirdikleri bu model ile kalın izotrop ve anizotrop kirişlerin yer değiştirme, gerilme ve doğal frekans değerlerinin çözümü ile gerçek değerler arasındaki sonuçların iyi bir uyum sağladığını görmüşlerdir.
(Aydoğdu, 2005) Simetrik çapraz tabakalı kompozit kirişlerin titreşim analizini Ritz metodunu kullanarak yapmıştır. Kirişlerin farklı sınır koşullarını ve altı farklı serbestlik derecesi kombinasyonlarını dikkate almıştır. Ayrıca çalışmada parabolik, hiperbolik, birinci mertebe ve üstel şekilde tanımlanan yüksek mertebe kiriş teorilerini kullanmıştır.
(Tahani, 2007) Tabakalı kompozit kirişlerin analizini, tabaka bazlı yer değiştirme teorilerini kullanarak yapmıştır. Bunun için iki farklı teori geliştirmiştir. İlk olarak mevcutta bulunan tabakalı plak teorisine, tabakalı kiriş teorisini uyarlamıştır. İkinci olarakta plak ve kabuk teorilerinin geliştirilmesinde kullanılan teorileri uygulamıştır. Çapraz ve açılı tabakalı örnekleri sonlu elemanlar paket programıyla çözerek teorinin kesinliğini değerlendirmiştir.
(Jun vd., 2008) Genel tabakalı kompozit kirişler için dinamik sonlu elemanlar metodu geliştirmişlerdir. Geliştirdikleri bu metotla Poisson etkisi, malzeme yapısı, narinlik oranı, kayma deformasyonu ve sınır koşullarının doğal frekanslar üzerindeki etkilerini incelemişlerdir.
(Boay ve Wee, 2008) Tabakalı kompozit kirişlerin eğilme, burkulma ve serbest titreşim analizleri için kapalı form çözümleri geliştirmişlerdir. Burada elde ettikleri kapalı formu, kirişin etkin eğilme modülünü belirlemek için kullanmışlardır. Belirledikleri etkin eğilme modülünü çeşitli sınır şartlarına sahip tabakalı kompozit kirişin eğilme, burkulma ve serbest titreşim analizlerinde uygulamışlardır.
(Catapano vd., 2011) Tabakalı kompozit kirişlerin lineer statik analizini, iki ucu basit mesnetli çapraz tabakalı kirişler üzerinde, kiriş eksenine dik yükler etki ettirerek farklı uzunluk/kalınlık oranlarına sahip kirişler için incelemişlerdir. Ayrıca yönetici denklemleri virtüel yer değiştirme prensibi ile elde etmişlerdir.
(Chen vd., 2011) Üzerinde sinüsoidal yük bulunan iki ucu basit mesnetli çapraz tabakalı kompozit kirişin, gerilme ve şekil değiştirmelerini geliştirdikleri düzenlenmiş gerilme çifti teorisi ile analiz etmişlerdir. Elde ettikleri sonuçları Euler-Bernoulli ve Timoshenko gerilme çifti teorileriyle karşılaştırmışlar ve yakın sonuçlar elde etmişlerdir.
(Aguiar vd., 2012) Eşdeğer tek katmanlı teorileri (Euler-Bernoulli, Timoshenko ve Yüksek dereceden kayma deformasyon kiriş teorileri) göz önünde bulundurarak, farklı en kesitlere sahip tabakalı kompozit kirişlerin statik analizi için karışık ve yer değiştirmeye dayanan sonlu eleman modelini geliştirmişlerdir. Bu çalışmada Hellinger-Reissner ilkesini, Euler-Bernoulli ve Timoshenko kiriş teorileri için, karışık formülasyonlar ile tutarlı olan yönetici denklemleri oluşturmakta kullanmışlardır.
(Vo ve Thai, 2012) Çeşitli rafine edilmiş kayma deformasyon teorilerini kullanarak tabakalı kompozit kirişlerin statik davranışlarını incelemişlerdir. Geliştirilen teoremin yönetici denklemleri, sınır koşulları ve gerilme bileşenleri gibi bazı açılardan Euler-Bernoulli kiriş teorisine benzerlik gösterdiğini vurgulamışlardır. Analizlerinde üzerinde düzgün yayılı ve tekil yük bulunan simetrik ve anti simetrik çapraz tabakalı kompozit kirişler için sayısal sonuçlar elde etmişlerdir. Buna ek olarak lif açılarının ve dizilimlerinin; kayma deformasyon parametresi, uzama-eğilme-kayma-burulma üzerindeki etkilerini de araştırmışlardır.
(Manoach vd., 2013) Yapmış oldukları çalışmada tabakalar arası ayrışmaya uğrayan tabakalı kompozit kirişlerin, dinamik davranışının deneysel ve sayısal analizlerini gerçekleştirmişlerdir.
(Abadi ve Daneshmehr, 2014) Tabakalı kompozit kirişlerin burkulma analizi için düzenlenmiş gerilme çifti teorisine dayanarak geliştirdikleri teoremi kullanmışlardır. Minimum potansiyel enerji prensibi uygulayarak Euler-Bernoulli ve Timoshenko kiriş teorileri için yönetici denklemleri, başlangıç ve sınır şartlarını oluşturmuşlardır. Geçiş denklemlerinde Forier serilerini kullanarak çözüm yapmışlardır. Malzeme uzunluk ölçü parametresinin, kiriş kalınlığının ve kiriş uzunluğunun tabakalı kompozit kiriş davranışına etkisini incelemişlerdir. Burada burkulma analizi için [ 0/90/0 ] ve [ 90/0/90 ] oryantasyon açılarına sahip tabakalardan oluşturulmuş kirişler kullanılmıştır.
(Afshin ve Taheri-Behrooz, 2015) Winkler tipi elastik zemin üzerinde bulunan, düşey yükle yüklenmiş tabakalı kompozit kirişin, davranışını ve tabakalar arası gerilme dağılımını Reddy’nin teoremini kullanarak elde etmişler. Ayrıca yük tipi, elastik temel rijitliği ve boyut
oranlarını içeren çeşitli parametrelerin tabakalar arasındaki gerilme dağılımına etkisini incelemişlerdir.
(Özütok ve Madenci, 2017) Karışık tip sonlu elemanlar yöntemiyle yüksek mertebeden kayma deformasyon teorisine dayalı tabakalı kompozit kirişlerin statik analizini yapmışlardır. Kullanılan teori, tabakalı kompozit kirişin kalınlığı boyunca kayma gerilmesinin doğrusal olmayan dağılımını içermektedir. Buna ek olarak karışık sonlu elemanlar denklemlerini, Gâteaux diferansiyel yöntemini kullanarak elde etmişlerdir. Sonuç olarak deplasman, dönme, eğilme, kesme kuvveti ve yüksek mertebe eğilme momentlerini, Euler-Bernoulli ve Timoshenko kiriş teorileriyle elde etmiş oldukları sonuçlar ile karşılaştırmışlardır.
(Nguyen vd., 2017) Tabakalı kompozit kirişlerin statik, burkulma ve titreşim analizleri için trigonometrik seriler ile analitik çözümler yapmışlardır. Lagrange denklemlerini kullanarak yönetici denklemleri oluşturmuşlardır. Ayrıca oryantasyon açıları ve malzeme anizotropisinin uzunluğun derinliğe oranı üzerindeki etkilerini; deplasmanlar, gerilmeler, doğal frekanslar, kritik burkulma yükleri ve ilgili mod şekilleri elde ederek incelemişlerdir.
(Sayyad ve Ghugal, 2017) Kompozit tabakalı yapılarda eğilme, burkulma ve serbest titreşim davranışları ile ilgili ve bunların analizleri için gerekli teoriler hakkında geniş bir literatür taraması yaparak çalışmalarında 515 adet referans göstermişlerdir.
Tabakalı kompozit kirişler izotrop ve ortotrop kirişlere göre daha iyi mekanik özelliklere sahiptir. Bu nedenle pek çok araştırmacı konu ile ilgili çalışmalar yapmışlardır. Yaptıkları bu çalışmalarda farklı problemleri ve çözüm yöntemlerini incelemişlerdir. Bu çalışmada tabakalı kompozit kirişlerin statik analizi sonlu farklar metodu kullanılarak yapılmıştır.
2. TABAKALI KOMPOZİT KİRİŞLERİN ANALİZİ
Liflerle güçlendirilmiş tabaka, matris malzemesi ve liflerden oluşur. Bu tabakalarda en büyük dayanım lif yönlerindeyken, life dik doğrultuda daha düşük değerlere sahiptir. Liflerle güçlendirilmiş tek yönlü tabaka ortotrop malzeme gibi davranır.
x
2x
1x
3Şekil 2.1. Liflerle güçlendirilmiş tek yönlü tabaka.
(Şekil 2.1.)’deki gibi X1 malzeme koordinat ekseni lif yönüne paralel, X2 tabaka düzleminde ve lif yönüne dik, X3 ise tabaka düzlemine dik olarak alınabilir. Tabakanın ortotrop malzeme özellikleri teorik yaklaşımla veya laboratuvarlarda yapılan deneylerden elde edilebilir. Lif ekseni ile global ekseni (x,y,z) arasındaki açı oryantasyon açısıdır (Şekil 2.2.). Bu oryantasyon açısı 0 0
90
90 arasında değişmektedir (Reddy, 2004: 86-90; Saraçoğlu ve Özçelikörs, 2011).
x
1x
z=x
3y
x
2
Şekil 2.2. Oryantasyon açısı.
Tabakalı kompozit kirişler farklı oryantasyon açısına sahip tabakaların bir araya getirilmesiyle oluşurlar (Şekil 2.3.).
900
0 0
y
z
x
Şekil 2.3. Farklı lif oryantasyonlarına sahip tabakalardan oluşan kiriş kesiti.
Tabakalı kompozit kirişlerin analizi için bugüne kadar pek çok yöntem geliştirilmiştir. Bu yöntemlerden en çok kullanılanları Euler-Bernoulli kiriş teorisi de denilen klasik tabakalı kompozit kiriş teorisi ve kesme kuvvetinin etkilerini de dikkate alan Timoshenko kiriş teorisidir. Ayrıca bu konu ile ilgili yüksek mertebe tabakalı kompozit kiriş teorileri de geliştirilmiştir (Şekil 2.4.).
z
Z,w
X
,u
( , )
u w
0 0( ,
u w
)
( , )
u w
0 x w 0 x w 0 0( ,
u w
)
0 x w x
( , )
u w
0 0( ,
u w
)
0 x w 0 x w x
x
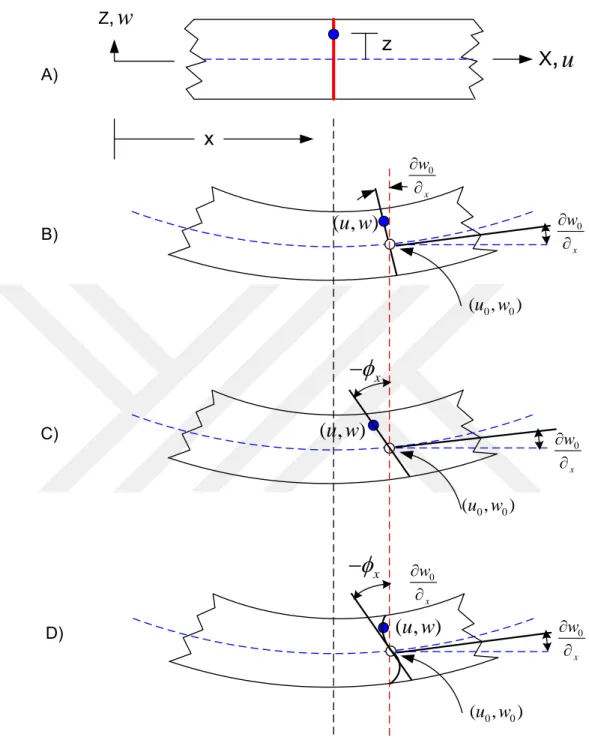
A) B) C) D)Şekil 2.4. Düşey yükle yüklenmiş kiriş için teorilere göre yer değiştirmeler (Reddy, 2004: 672). A) Şekil değiştirmemiş kiriş.
B) Euler-Bernoulli kiriş teorisi. C) Timoshenko kiriş teorisi.
D) 3. Mertebe kayma deformasyon kiriş teorisi.
Düşey yükle yüklenmiş kirişte yer değiştirme tarif edilirken x ekseninde u , y ekseni v , z ekseninde w kullanılır. u ,0 v ve 0 w ise orta düzlemin yer değiştirmeleridir. Euler-Bernoulli 0
0 0 ( , , ) ( , ) x u x y z u x y z w 0 0 ( , , ) ( , ) y v x y z v x y z w ( 2.1 ) 0 ( , , ) ( , ) w x y z w x y Timoshenko kiriş teorisine göre yer değiştirmeler şu şekildedir.
0 ( , , ) ( , ) x( , ) u x y z u x y z x y 0 ( , , ) ( , ) y( , ) v x y z v x y z
x y ( 2.2 ) Burada x ve -ysırasıyla y ve x eksenlerine göre dönmeyi tanımlar.0 x z x u w
0 y z y v w ( 2.3 )İkinci mertebe kiriş teorisine göre yer değiştirmeler şu şekildedir. 2 0 ( , , ) ( , ) x( , ) x( , ) u x y z u x y z x y z x y 2 0 ( , , ) ( , ) y( , ) y( , ) v x y z v x y z x y z x y 0 ( , , ) ( , ) w x y z w x y ( 2.4 )
Reddy’ nin üçüncü mertebe teorisine göre yer değiştirmeler şu şekildedir.
3 0 2 0 4 ( , , ) ( , ) ( , ) ( )( ) 3 x x x u x y z u x y z x y z w h 3 0 2 0 4 ( , , ) ( , ) ( , ) ( )( ) 3 y y y v x y z v x y z x y z w h 0 ( , , ) ( , ) w x y z w x y ( 2.5 )
Yük altında şekil değiştiren tabakalık kompozit kirişin yer değiştirme alanı tarifi her bir teori için farklıdır (Reddy, 2004: 110-112).
2.1. Yer Değiştirme ve Şekil Değiştirmeler
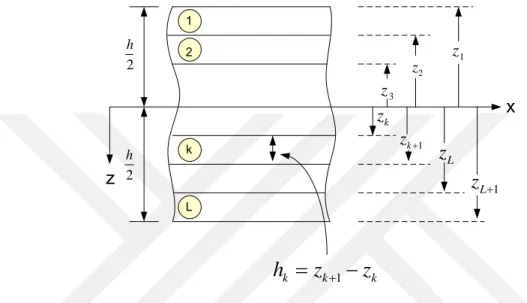
Toplam kalınlığı h olan ve N adet tabakadan oluşmuş bir kirişin tabaka numaraları (Şekil 2.5.)‘ teki gibi sıralanmıştır. Genel olarak k numaralı tabakanın kalınlığı hk zk1zk
olarak tanımlanır. z0 ‘da ki xy düzlemi kirişin orta düzlemidir.
1 2 k L 2 h 2 h 1 z 2 z 3 z k z 1 k z L
z
1 Lz
1 k k kh
z
z
z
x
Şekil 2.5. Tabakalı kompozit kiriş için kullanılan koordinat sistemi ve tabaka numaraları (Reddy, 2004: 113).
Kiriş teorilerinde yer değiştirme ve şekil değiştirme hesapları için aşağıdaki kabul ve kısıtlamalar yapılır.
1) Tabakalar birbirine mükemmel bir şekilde yapıştırılmışlardır. Bundan dolayı şekil değiştirme esnasında tabakalar beraber hareket ederler.
2) Her tabakanın malzemesi lineer elastik ve üç düzlemde malzeme simetrisine sahiptir(mesela ortotrop).
3) Her bir tabaka sabit kalınlığa sahiptir.
4) Şekil değiştirmeler ve deplasmanlar küçüktür.
5) Tabakanın alt ve üst yüzeylerindeki enine kayma gerilmeleri sıfırdır.
Bu kabullere göre kiriş üzerindeki (x,y,z) koordinatlarına sahip bir nokta şekil değiştirdikten sonra (x+ u ,y+ v ,z+ w ) koordinatına hareket eder (Reddy, 2004: 114).
Euler-Bernoulli kiriş teorisine göre x eksenindeki u yer değiştirmesi, y eksenindeki v yer değiştirmesi ve z eksenindeki w yer değiştirmesi aşağıdaki eşitliklerle ifade edilir.
0 0 ( , , ) ( , ) x u x y z u x y z w 0 0 ( , , ) ( , ) y v x y z v x y z w 0 ( , , ) ( , ) w x y z w x y ( 2.6 )
(Şekil 2.6.)’ da Euler-Bernoulli kiriş teorisine göre kiriş üzerindeki bir noktanın yer değiştirmesi görülmektedir. x z 0
w
0u
0w
x
0w
x
x z 0w
0u
0w
x
0w
x
z xŞekil 2.6. Yapılan kabullere göre kiriş parçasının şekil değiştirmemiş ve şekil değiştirmiş geometrisi.
Üç boyutlu doğrusal olmayan şekil değiştirmeler genel olarak aşağıdaki eşitliklerde verilmiştir. 2 2 2 1 2 xx u u v w E x x x x 2 2 2 1 2 yy v u v w E y y y y 2 2 2 1 2 zz w u v w E z z z z
1 2 xy u v u u v v w w E y x x y x y x y ( 2.7 ) 1 2 xz u w u u v v w w E z x x z x z x z 1 2 yz v w u u v v w w E z y y z y z y z
Bu eşitlikler içindeki bazı diferansiyel ifadeler küçük olduğu için ihmal edilebilirler. 2 u x , 2 u y , 2 u z , 2 v x , 2 v y 2 v z , u u x y , v v x y , u u x z , v v x z u u y z , v v y z , 2 w z , w w x z , w w y z
Buna göre şekil değiştirme ve yer değiştirme arasındaki eşitliğin ihmaller sonrasında lineer hale gelmiş şekli aşağıdaki eşitliklerdeki gibidir.
2 1 2 xx u w x x 2 1 2 yy v w y y zz w z ( 2.8 ) 1 2 xy u v w w y x x y 1 2 xz u w z x 1 2 yz v w z y
Daha sonra ( 2.6 ), ( 2.8 )’in yerine yazılırsa yeni eşitlikler elde edilir.
2 2 0 0 0 2 1 2 xx u w w z x x x 2 0 0 0 0 0 1 2 xy u v w w w z y x x y x y 2 2 0 0 0 2 1 2 yy v w w z y y y ( 2.9 )
0 0 1 0 2 xz w w x x 0 0 1 0 2 yz w w y y 0 zz
Kabullere göre xz,
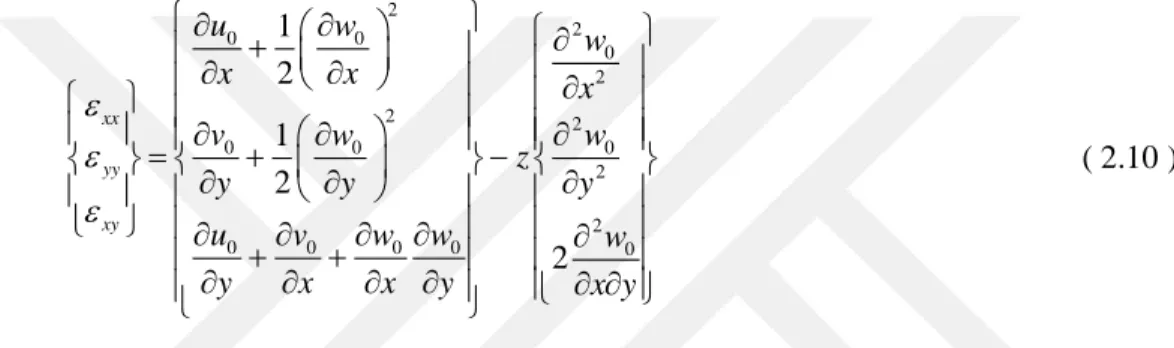
yz ve zz sıfır olduğu için geriye kalan üç tane şekil değiştirme eşitliği dikkate alınır.2 2 0 0 0 2 2 2 0 0 0 2 2 0 0 0 0 0 1 2 1 2 2 xx yy xy u w w x x x v w w z y y y u v w w w y x x y x y ( 2.10 )
Liflerle güçlendirilmiş kompozit tabakalı kirişte her tabakanın ortotrop olduğu ve Hooke Kanununa uyduğu kabul edilir. Şekil değiştirmeler tabakalı kiriş kalınlığı boyunca sürekli olmasına rağmen, gerilmeler ise her bir tabakada farklılık gösterebilir (Şekil 2.7.). Gerilmeler her bir tabaka için malzeme katsayılarına bağlı olarak değişir (Reddy, 2004: 115-117). z z x xx B) A) z xx C)
Şekil 2.7. Tabakalar arası gerilme ve şekil değiştirme değişimleri. A) Tabakalı kiriş kesiti.
B) Düzlem şekil değiştirme değişimi. C) Gerilme değişimi.
2.2. Tabaka Bünye Bağıntıları
Tabaka bünye bağıntıları, tabakada oluşan gerilmeler ile şekil değiştirmeler arasındaki ilişkiyi verir. Tabakalı kirişler birden fazla ortotrop tabakadan oluşurlar. Yapılan kabullere göre kalınlığa dik düzlemde kayma gerilmeleri xz 0 ve
yz0’ dır. zz0 olduğu için zz 0 kabul edilir. Bununla birlikte kiriş kalınlığı kiriş uzunluğuna göre ince olduğu için, kiriş düzlem gerilme problemi olarak çözülebilir.Düzlem gerilme problemiyle ilgili lineer bünye bağıntıları k’ncı ortotrop tabaka için şu şekildedir.
k k k ij Q 11 11 12 11 22 12 22 22 66 12 12 0 0 0 0 2 k k Q Q Q Q Q ( 2.11 )Bu eşitliklerde 11 lif eksenine paralel yöndeki eksenel gerilmedir. 22 lif eksenine dik ve tabaka düzlemindeki eksenel gerilmeyi, 12 ise tabaka düzlemine dik olan kayma gerilmesini ifade eder. Burada değerleri ise k’ncı tabaka için ilgili eksenlerdeki şekil değiştirmelerdir. Gerilme ve şekil değiştirme arasındaki ilişkiyi k
ij
Q indirgenmiş malzeme matrisi kurar. Qij k , k tabakasının Poisson Oranları, Elastisite Modülleri ve Kayma Modülü kullanılarak aşağıdaki eşitlikten elde edilebilirler.
1 11 12 21 1 E Q
, 12 12 2 21 1 12 21 12 21 1 1 E E Q
, 2 22 12 21 1 E Q
, Q66G12 ( 2.12 )Burada; E1 lif yönündeki, E2 ise life dik yöndeki Elastisite Modülleridir. G ise 12 x -x1 2 düzlemindeki kayma modülüdür. 12ve 21ise ilgili yönlerdeki Poisson oranlarıdır.
Kompozit tabakalı kirişlerde lif eksenleri kiriş eksenine göre farklı yönlenmiş ortotrop tabakalardan oluştuğu için hepsi aynı (x,y,z) koordinat eksenine dönüştürülmelidir. Bu dönüşüm işlemi aşağıdaki eşitlikler kullanılarak yapılır.
2 2 11 2 2 22 2 2 12
cos sin sin 2
sin cos sin 2
cos sin cos sin cos sin
k k xx yy xy ( 2.13 )
Malzeme eksen takımına göre ifade edilen gerilme ifadeleri yerine bünye bağıntılarındaki ( 2.11 ) konulursa aşağıdaki bağıntıya ulaşılır.
2 2 11 11 12 2 2 12 22 22 2 2 66 12
cos sin sin 2 0
sin cos sin 2 0
cos sin cos sin cos sin 0 0 2
k k xx yy xy Q Q Q Q Q ( 2.14 )
Şekil değiştirmelerin dönüştürülmesinde ise aşağıdaki eşitlik kullanılır.
2 2 11 2 2 22 2 2 12
cos sin cos sin
sin cos cos sin
sin 2 sin 2 cos sin
2 2 xx yy xy ( 2.15 )
( 2.15 ) ile tanımlanan eşitlik ( 2.14 ) ’ te yerine yazıldığında tabakalı kirişin problem ekseni olan (x,y,z) eksenlerine göre k’ncı ortotrop tabaka için bünye bağıntıları elde edilir.
2 2 2 2 11 12 2 2 2 2 12 22 2 2 2 2 66
cos sin sin 2 0 cos sin cos sin sin cos sin 2 0 sin cos cos sin cos sin cos sin cos sin 0 0 sin 2 sin 2 cos sin 2
k k xx xx yy yy xy xy Q Q Q Q Q ( 2.16 ) Yukarıdaki eşitlikte bulunan matris çarpım işlemleri sonucunda aşağıdaki eşitlik elde edilir. 11 12 16 12 22 26 16 26 66 k k xx xx yy yy xy xy Q Q Q Q Q Q Q Q Q ( 2.17 )
Elde edilen bünye bağıntılarındaki dönüştürülmüş indirgenmiş malzeme matrisi elemanlarının açık ifadeleri aşağıdaki gibidir (Saraçoğlu ve Özçelikörs, 2011).
4 2 2 4
11 11cos 2 12 2 66 sin cos 22sin Q Q
Q Q
Q
2 2
4 4
12 11 22 4 66 sin cos 12 sin cosQ Q Q Q Q
4 2 2 4
22 11sin 2 12 2 66 sin cos 22cos Q Q
Q Q
Q
3
316 11 12 2 66 sin cos 12 22 2 66 sin cos
Q Q Q Q
Q Q Q
( 2.18 )
3
326 11 12 2 66 sin cos 12 22 2 66 sin cos
Q Q Q Q
Q Q Q
2 2
4 4
66 11 22 2 12 2 66 sin cos 66 sin cos
Q Q Q Q Q Q
Yukarıda verilen eşitliklerde kullanılan θ, oryantasyon açısını ve
Q Q Q11, 12, 22,Q66
katsayıları ise ( 2.12 )’ de verilen indirgenmiş malzeme matrisi elemanlarıdır (Reddy, 2004: 117-119).
2.3. Euler-Bernoulli Kiriş Teorisi
Bernoulli kirişi adını önemli buluşlara imza atan Jacob Bernolli’den sonra almıştır. Daniel Bernoulli ve Leonard Euler de bu kullanışlı teoriyi ortaya koyan ilk bilim insanlarıdır. 19. yüzyıla gelene kadar bu teori büyük ölçekte kabul görmemiştir. Fakat “Eiffel Tower” ve “Ferris Wheel” yapılarında kullanılan teori başarılı olunca hızla önemi artmış ve mühendisliğin yapıtaşlarından biri haline gelmiştir.
Euler-Bernoulli kiriş teorisinde varsayılan kabuller aşağıdaki şekildedir (Reddy, 2004: 112-113).
1) Deformasyon öncesinde çubuk eksenine dik olan en kesitler (yani enine normaller) deformasyon sonrasında yine çubuk eksenine dik kalırlar.
2) Enine normaller uzayıp kısalmazlar.
3) Enine normaller şekil değiştirmeden sonra orta düzleme dik kalacak şekilde dönerler. İlk iki kabulden dolayı enine yer değiştirmeler kalınlık koordinatından bağımsızdırlar ve enine normaller şekil değiştirmezler.
0 zz
( 2.19 )
Üçüncü kabule göre enine kayma şekil değiştirmeleri sıfırdır.
0
xz
0 yz
( 2.20 )2.3.1. Euler-Bernoulli kiriş teorisi için denge denklemleri
Kompozit tabakalı kirişlerin Euler-Bernoulli kiriş teorisine göre eğilmesinin hesabında gerilme-şekil değiştirme ilişkilerinden faydalanılır. Eğer düzlem kuvvetler sıfırsa, düzlem yer değiştirmeler de (u ,0 v ) sıfırdır. Buna göre kirişin herhangi bir yerindeki eğilme momentleri; 0
0
yy xy
M M ( 2.21 )
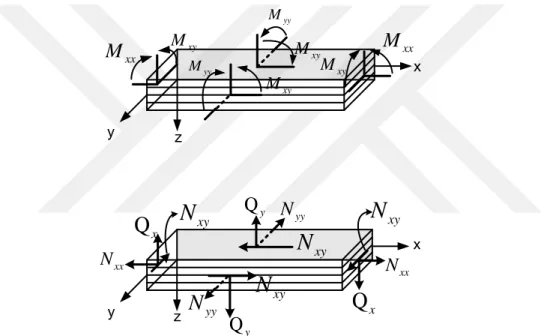
olarak kabul edilir. Bir kiriş elemanındaki kuvvet ve moment bileşenlerinin pozitif yönleri (Şekil 2.8.) ‘ de verilmiştir.
xx
M
Mxy yy M xy MM
xx xy M y x xy M yy M z y z x xxN
xxN
Q
y yyN
xyN
xyN
N
xy xyN
yyN
Q
yQ
xQ
xŞekil 2.8. Bir kiriş elemanındaki kuvvet ve moment bileşenleri.
Euler-Bernoulli kiriş teorisine göre kesit içerisinde oluşacak iç momentlerin eğrilik cinsinden ifadesi aşağıdaki eşitlikteki gibidir.
2 0 2 11 12 16 2 0 12 22 26 2 16 26 66 2 0 2 xx yy xy w x M D D D w M D D D y D D D M w x y ( 2.22 )
Bu eşitlikte kullanılan “w0” kiriş orta düzleminin çökme fonksiyonunu, D11,D12,D22,D16,D26,D66 ise eğilme katılık matrisi elamanlarını göstermektedir. Eğilme katılık matrisi elemanları aşağıdaki eşitlikten bulunmaktadır.
3 3 1 1 1 ( ) 3 N k ij ij k k k D Q z z
( 2.23 )(Eşitlik 2.22)’ nin tersi alınarak eğriliklerin momentler cinsinden ifadesi elde edilebilir. 2 0 2 * * * 11 12 16 2 * * * 0 12 22 26 2 * * * 16 26 66 2 0 2 xx yy xy w x M D D D w D D D M y D D D M w x y ( 2.24 ) Burada * ij
D , D ’nin dönüştürülmüş eğilme katılık matris elamanlarını belirtir. (Eşitlik ij
2.21) ifadesini varsayarak yukarıdaki ifademizin son hali aşağıdaki gibi olur. ( 2.21 ) ile tanımlanan eşitlik ( 2.24 )’ te yerine yazıldığında ifadenin son hali aşağıdaki gibi olur.
2 * 0 11 2 xx w D M x , 2 * 0 12 2 xx w D M y , 2 * 0 16 2 xx w D M x y ( 2.25 ) Dönüştürülmüş eğilme katılık matris elemanları aşağıdaki eşitliklerden hesaplanır.
1 22 66 26 26 D D D D D 2 16 26 12 66 D D D D D 3 12 26 22 16 D D D D D * 11 1 12 2 16 3 D D D D D D D ( 2.26 ) * * 11 ( 22 66 26 26) / D D D D D D * * 12 ( 16 26 12 66) / D D D D D D * * 16 ( 12 26 22 16) / D D D D D D
(Eşitlik 2.25) ve (Eşitlik 2.26) ifadesi Poisson etkisi D ve anizotrop kayma çifti 12* * 16
D ,
Bu etkiler sadece uzun kirişler için yani uzunluk-genişlik oranı çok büyük olduğunda ihmal edilebilir. Çökmenin (w0), y koordinatından bağımsız olması tabaka dizilişine bağlıdır.
Açılı tabakalardan oluşan kirişlerde uzunluk-genişlik oranı, burulma eğriliğini ihmal edebilmek için oldukça büyük olmalıdır. Bu çalışmada dikkate alınan tabakalı kirişlerin, Poisson oranının ve kayma çiftinin eğilme üzerindeki etkilerinin ihmal edilebilmesi için yeterince uzun olduğu kabul edilir (a/h > 10).
Bundan dolayı kiriş orta düzleminin çökmesi (w0), sadece kiriş ekseni koordinatına (x) bağlı olur.
0 0( )
w w x ( 2.27 )
( 2.25 )’ teki D ve 12* * 16
D ihmal edildiğinde aşağıdaki eşitlik elde edilir.
2 * 0 11 2 xx w D M x ( 2.28 )
(Eşitlik 2.28)’ i Euler-Bernoulli kiriş teorisinde kullanabilmek için aşağıdaki tarifler yapılır. M x( )bMxx
,
Q(x)=bQx,
3 * * 11 11 12 b xx yy b E h D I D ,
3 12 yy bh I ( 2.29 )Buradaki eşitliklerde M; b genişliğindeki eğilme momentini, Q; b genişliğindeki kesme kuvvetini,
E
xxb eşdeğer Elastisite modülünü, h tabakalı kirişin toplam kalınlığını ve Iyytabakalı kirişin y eksenine göre atalet momentini ifade etmektedir.Bu tarifler ( 2.28 )’ de yerine yazıldığında aşağıdaki eşitlikler elde edilir. 2 0 2 b xx yy w M x E I ve ya 2 0 2 ( ) xxb yy w M x E I x ( 2.30 )
Eğilme momentinin birinci türevini aldığımızda kesme kuvvetini verecektir.
Q xx x M x ve ya Q(x) M x ( 2.31 )
b
x
h
y
y
z
312
yybh
I
a
z
Şekil 2.9. Tabakalı kirişin geometrisi ve atalet momenti.
Tabakalı kirişler için Euler-Bernoulli kiriş teorisine göre hareket denklemi aşağıdaki eşitliklerden elde edilir.
2 2 0 xx M q x ( 2.32 )
Bu eşitlikte Mxx, (Şekil 2.8.)’ de gösterilen eğilme momentidir. q ise kiriş düzlemine dik etki eden x’ e bağlı yayılı yük fonksiyonudur.
Tabakalı kirişler için hareket denklemlerinin çözümü için bazı sınır şartlarının kabul edilmesi gerekir. Bu sınır şartları yukarıda tarif edilen, geometrik sınır şartı ve kuvvet sınır şartlarıdır. Geometrik sınır şartı için çökme ve dönme, kuvvet sınır şartı için ise kesme kuvveti ve eğilme momenti dikkate alınır.
Geometrik sınır şartı; çökme: w , dönme: 0 w0
x
Kuvvet sınır şartı; kesme kuvveti: Q(x) M x( )
x
, eğilme momenti:M x ( )
Bu şekilde Euler-Bernoulli kiriş teorisi için denge denklemleri elde edilmiş olur (Reddy, 2004: 167-169).
2.3.2. Euler-Bernoulli kiriş teorisi için eğilme
Statik eğilme altındaki kompozit tabakalı kiriş için, Euler-Bernoulli kiriş teorisine göre eğrilik ve eğilme momenti arasındaki ilişkiyi gösteren diferansiyel denklem aşağıdaki gibidir.
2 0 2 ( ) b xx yy d w M x dx E I ( 2.33.a )
4 0 4 ˆ b xx yy d w E I q dx ( 2.33.b )
Bu ifadelerde ˆq kiriş genişliği ile düşey yayılı yükün çarpımıdır ( ˆq q b).
(Eşitlik 2.33.a) eğilme momentinin hesabında, (Eşitlik 2.33.b) ise hiperstatik kirişlerin çözümünde daha uygundur.
Bu eşitliklerin çözümü için tabakalı kompozit kirişlerin mesnetlenme durumlarına göre farklı sınır şartları oluşur. Örnek olarak bazı sınır şartları aşağıda gösterilmiştir.
Sabit ve hareketli mesnet: w0 0, M x( )0
Serbest uç: Q(x) M x( ) 0 x , M x( )0 Ankastre mesnet: w0 0, dw0 0 dx
2.3.3. Euler-Bernoulli kiriş teorisi için gerilme
Düşey yükle yüklenmiş kompozit tabakalı kirişte oluşan gerilmeler her tabakada farklılık gösterebilir. İlgili tabakadaki oluşacak olan gerilmeler aşağıdaki eşitliklerden elde edilir. 2 0 2 11 12 16 2 0 12 22 26 2 16 26 66 2 0 2 k k xx yy xy w x Q Q Q w z Q Q Q y Q Q Q w x y ( 2.34.a ) * * * 11 12 16 11 12 16 * * * 12 22 26 12 22 26 * * * 16 26 66 16 26 66 0 0 k M Q Q Q D D D z Q Q Q D D D b Q Q Q D D D ( 2.34.b ) ( ) ( ) * ( ) * ( ) * 11 11 12 12 16 16 ( ) ( , ) ( ) k k k k xx M x z x z Q D Q D Q D b ( 2.34.c ) ( ) ( ) * ( ) * ( ) * 12 11 22 12 26 16 ( ) ( , ) ( ) k k k k yy M x z x z Q D Q D Q D b ( 2.34.d )
( ) ( ) * ( ) * ( ) * 16 11 26 12 66 16 ( ) ( , ) ( ) k k k k xy M x z x z Q D Q D Q D b ( 2.34.e )
Bu eşitliklerde k indisi tabaka numarasını belirtmektedir. Genellikle tabakalı kompozit kirişlerde en büyük gerilme, kirişin en üst yüzeyi veya en alt yüzeyinde oluşmaz. Kiriş kalınlığı boyunca en büyük gerilmenin bulunduğu yer tabaka dizilişine bağlıdır (Reddy, 2004: 169-170).
2.4. Timoshenko Kiriş Teorisi
Timoshenko kiriş teorisi Euler-Bernoulli kiriş teorisinin geliştirilmiş halidir. Timoshenko kiriş teorisine göre yapılan hesaplamalarda kayma ve dönme etkisi de göz önüne alındığından elde edilen sonuçlar Euler-Bernoulli kiriş teorisine göre her zaman daha büyük çıkmaktadır. Timoshenko kiriş teorisi gerçeğe daha yakın sonuçlar veren bir teoridir. Özellikle yüksek kesitli kirişlerde daha uygun sonuçlar verdiğinden bu teori, kalın kiriş teorisi olarak ta bilinir.
Timoshenko kiriş teorisine göre kiriş üzerinde seçilen bir noktanın yer değiştirmesi (Şekil 2.4.)’ teki gibidir.
Timoshenko kiriş teorisi kabullerine göre, Euler-Bernoulli kiriş teorisinde olduğu gibi, kiriş kesiti yine düzleminde rijittir ve deformasyondan önce çubuk eksenine dik olan kiriş kesiti deformasyondan sonra yine çubuk eksenine dik olarak kalır. Fakat kiriş kesiti, şekil değiştirmeden sonra orta düzleme dik kalacak şekilde dönmez. Buna göre xx,xz,
yz değiştirmeleri sıfırdan farklıdır ve hesaplanması gerekir.2.4.1. Timoshenko kiriş teorisi için denge denklemleri
Tabakalı kompozit kirişlerin Timoshenko kiriş teorisine göre yer değiştirmeleri ve dönme ifadeleri (Eşitlik 2.2) ve (Eşitlik 2.3) ‘ teki gibidir.
Timoshenko Kiriş Teorisine göre kesitte oluşacak momentlerin ve kesme kuvvetlerinin eğrilikler cinsinden ifadesi aşağıdaki eşitliklerdeki gibidir.
11 12 16 12 22 26 16 26 66 X xx y yy xy y x x M D D D M D D D y D D D M y x ( 2.35.a )